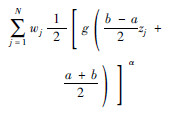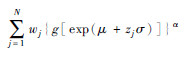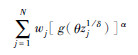2. 中国运载火箭技术研究院, 北京 100076
2. China Academy of Launch Vehicle Technology, Beijing 100076, China
在工程结构的优化设计及可靠性分析中, 普遍存在着参数的不确定性, 因此需要对参数的不确定性进行定量化描述, 利用不确定性分析方法进行参数统计分析、结构优化设计、可靠性分析等[1]。不确定性分析方法包括概率统计方法、非概率凸集方法以及模糊方法。对于一些实际工程问题, 结构输入参数可能需要同时采用以上3种方法进行定量化描述, 不确定性的多源性问题以及概率与非概率条件下的相容性问题也得到了深入研究[2-3]。
以概率统计为基础的不确定性传递分析得到了最为广泛的研究, 其中结构可靠性分析技术取得了丰硕的研究成果, 经过几十年的发展形成具有代表性的3类技术:近似解析法[4-5]、数值模拟法[6-7]和代理模型法[8-9]。近似解析法以计算功能函数的矩为基础, 以FORM和SORM方法为代表, 将原功能函数在设计点处线性或二次展开, 该类方法的精度不仅受限于设计点的确定精度, 而且不适用于功能函数高度非线性的复杂问题。数值模拟法则避开了对功能函数的近似, 对于结构响应函数的形式没有要求, 以Monte Carlo法、重要抽样法等为代表, 然而对于一般问题, 数值模拟法需要大量抽样并估计功能函数的值才能得到合理的结果, 尤其对于小失效概率的工程问题, 其计算代价无法承受。随着可靠性分析技术的发展与工程应用的需求, 建立代理模型来表示原结构输入-输出关系模型, 进而利用代理模型进行可靠性分析的思路得到了发展, 常用的代理模型有Kriging、支持向量机等, 然而可靠性分析的精度依赖于代理模型的精度, 训练样本的选择与控制技术也正在不断研究发展中。
在以上几类成熟方法发展的基础上, 直接估计结构系统输出响应的概率密度函数, 进而将其在失效域积分进行可靠性分析的思路受到了研究者们的青睐。其中, 极大熵准则得到了广泛的研究[10-15]。通过在一实数点处的Taylor级数展开式可看出一个正的变量的任一阶分数矩包括了其大量的整数矩的信息[12], 利用分数矩能够引入更多的被估计变量信息, 基于分数矩的极大熵准则进一步提高了概率密度函数估计的精度与效率[12-15], 因此得到了很大的发展。
极大熵准则利用熵与不确定性的联系直接估计变量的概率密度分布, 然而其计算精度与效率很大程度上取决于熵最大优化模型中的约束条件—变量分数矩的求解精度与效率, 因为寻求最大熵值过程中, 只有在求解输出响应函数的分数矩信息时才会涉及结构响应函数的估计, 尤其是针对有限元辅助设计的隐式输入-输出模型, 高效的分数矩求解方法可以很大程度地降低模型的调用次数, 从而大幅提升计算效率。目前针对分数矩求解的专项研究比较少, 因此, 本文研究了3种高效的分数矩求解方法, 可从根本上解决计算效率的问题。同时, 通过与极大熵准则融合, 提供了一种先进的可靠性分析方法。此外, 基于本文的矩求解方法可为基于矩的可靠性分析以及稳健优化等应用提供很好的技术支撑[16-17]。
1 分数矩概念分数矩的引入进一步促进了极大熵准则的发展与推广, 基于分数矩的极大熵准则表达式如式(1)所示, 通过式(1)中熵的最大优化估计结构输出响应Y的概率密度函数fY(y)。
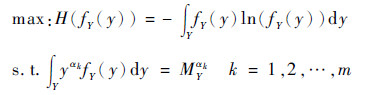
|
(1) |
式中:H(fY(y))为fY(y)的信息熵; MYαk为Y的αk阶分数矩, 用于熵最大优化过程中提供被估计变量的有限信息作为约束, 而且一般仅需提供被估计量的低阶分数矩信息[12-13]。
分数矩的计算需要变量为正的随机量, 即假设结构系统的输出响应函数Y=g(X)为正的随机量, X=(X1, X2, …, Xn)T(n为输入的维数)为模型随机输入变量的向量, Y的α阶分数矩可以表示为
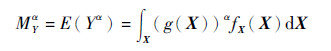
|
(2) |
式中:α为一个任意实数。
分数矩的优势可通过如下推导看出。将Yα进行Taylor级数展开, 进而E(Yα)可表示为
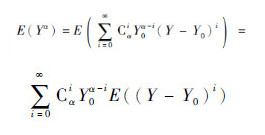
|
(3) |
式中:Cαi=α!/[i!(α-i)!]; Y0为任一实数。
将(Y-Y0)i进行二项展开, 进而式(3)可以表示为
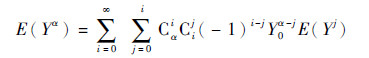
|
(4) |
由式(4)可以看出, 一个正的随机变量的分数矩包含了大量的整数矩信息[12], 因此, 采用分数矩作为约束, 可以为极大熵准则提供更多的被估计变量信息, 提高函数估计精度。由此可见, 分数矩的计算是极大熵准则的核心与关键。
2 分数矩求解方法 2.1 降维积分方法高维模型替代(High Dimensional Model Representation, HDMR)方法近年得到了大量的研究[18], 其能够合理且有效地近似一个复杂且为隐式关系的实际模型。采用基于HDMR的降维积分(Dimension Reduction Integration, DRI)方法可求解结构输出响应的分数矩。Cut-HDMR[19]是常用的方法之一, 文献[12]对Cut-HDMR进行了改进。对输出响应函数Y=g(X)进行自然对数转化:
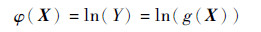
|
(5) |
将φ(X)按Cut-HDMR[19]形式展开, 表达为
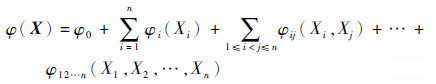
|
(6) |
式中:
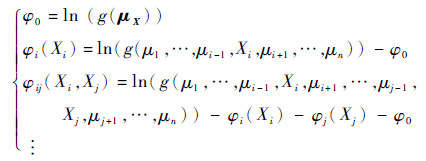
|
(7) |
式中:μX=[μ1, μ2, …, μn]T为结构输入向量X的均值向量。
按照Cut-HDMR方法只保留式(6)中展开项的常数项与一阶项, 进而得到简化与近似的结构输出响应函数:
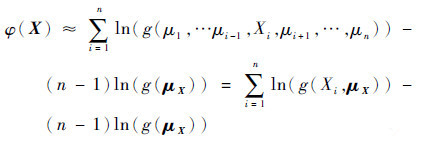
|
(8) |
对式(8)进行逆变换, 得到原始的输出响应函数为
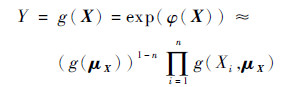
|
(9) |
由式(9)可以看出, 输出响应函数近似地表达为n个一元函数的乘积形式, 从而为分数矩的计算作好了铺垫。DRI方法给出一个正的输出响应变量的α阶分数矩, 可以按式(10)推导[12-13]:
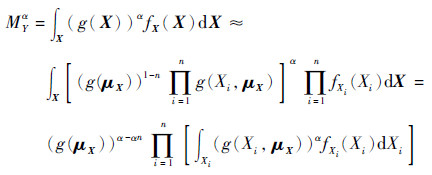
|
(10) |
可以看出, 式(10)建立了一个多元函数分数矩与一元函数分数矩的关系, 也即DRI方法将一个多元函数分数矩的求解近似转化为多个一元函数分数矩求解后再乘积的形式, 式(10)也可以用来求解输出响应的整数矩, 只需令α为整数即可。可以通过高斯积分准则来求解一元函数的积分, 表 1给出了常用的几种分布类型的一元函数高斯积分表达式[19]。本文在具体的积分计算时采用五点高斯积分准则, 表 2给出了积分数据[20], 其中wj为积分权重, zj为积分点。
| 积分准则 | 积分权重与点 | j=1 | j=2 | j=3 | j=4 | j=5 |
| 高斯-埃尔米特 | wj | 1.13×10-2 | 0.222 1 | 0.533 3 | 0.222 1 | 1.13×10-2 |
| zj | -2.857 0 | -1.355 6 | 0 | 1.355 6 | 2.857 0 | |
| 高斯-勒让德 | wj | 0.236 9 | 0.478 6 | 0.568 9 | 0.478 6 | 0.236 9 |
| zj | -0.906 2 | -0.538 5 | 0 | 0.538 5 | 0.906 2 | |
| 高斯-拉盖尔 | wj | 0.521 8 | 0.398 7 | 7.59×10-2 | 3.61×10-3 | 2.34×10-5 |
| zj | 0.263 6 | 1.413 4 | 3.596 4 | 7.085 8 | 12.641 |
2.2 稀疏网格积分方法
以Smolyak准则为基础的稀疏网格积分(Sparse Grid Integration, SGI)方法[21]是将多元函数的求积公式用合适的一元函数求积公式的张量积组合来表达。
假定w1si和U1si表示第i个变量的一维空间中的权重和积分点, 其可以由一元函数的高斯积分、Clenshaw-Curtis、梯形准则等方法得到[22]。假定精度水平为k(k≥0), 则n元函数对应的n维空间中所有积分点组成的集合Unk可以通过Smolyak准则[21]选取。
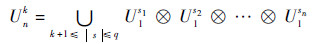
|
(11) |
式中:⊗表示张量积计算; q=k+n; |s|=s1+ s2+…+sn。
集合Unk中相应于第l个积分点ξl=[ξls1s1,ξls2s2, …, ξlsnsn]T∈Unk的权重wl可以依据Smolyak准则确定。

|
(12) |
因此, 式(2)中给出的多元函数积分可以通过式(13)所示的SGI方法求得, 其计算结果能够达到2k+1阶多项式精度[23]。
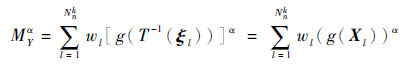
|
(13) |
式中:wl和ξl∈Unk分别为依据稀疏网格选点技术得到的n维变量空间中的积分权重和积分点; Nnk为选取的积分点的个数; 基本变量X从原始空间向积分点ξ空间的变换函数为T(·), T-1(·)为其反函数; ξl与Xl分别为2个空间的对应点。例如对于正态分布, 选取高斯-埃尔米特多项式的零点作为一维积分点时, 有Xl=T-1(ξl)= μX + ξlCσX, CσX为对角线元素为各变量标准差的n×n维矩阵。采用式(13)进行积分求解时, 不需要计算g(T-1(ξl))的具体表达式, 只需将积分点处的ξl值变换到Xl空间, 进而估计相应的结构输出响应函数值。类似地, 式(13)也可以计算输出响应的整数矩。
2.3 无迹变换方法无迹变换(Unscented Transformation, UT)方法是由Julier和Uhlmann[24]引入来通过非线性转换估计分布的均值和协方差信息, 被广泛应用于卡尔曼滤波技术中[25]。其基本思想是根据输入变量的均值和协方差等一些分布特征确定一组Sigma点和对应的权重, 进而利用确定的Sigma点近似估计被估计函数的矩信息。UT方法与Monte Carlo法最重要的差别在于前者用到的点是根据特定的法则产生的, 而后者用到的点是随机产生的。UT方法产生p个Sigma点以及它们对应的权重, 权重信息并不代表概率信息, 它们可正可负, 唯一需要满足的条件就是权重之和必须为1。
常用的UT方法称为标准UT方法, 标准UT方法选取一些Sigma点来捕捉输入变量前二阶矩的信息, 而Sigma点的个数p与输入变量的维数n呈线性关系。目前, 学者们发展了很多方法来定义Sigma点及其权重系数, Sigma点及权重都是与非线性的功能函数无关的。Sigma点必须能够反应均值、方差以及球面对称性。
本文介绍一种二阶UT中选取2n+1个Sigma点的标准抽样技术[24]。对称的选取2n+1个Sigma点, 这组Sigma点能够匹配n维随机向量的均值和协方差以及所有的高阶奇次矩阵。
所选取的Sigma点s及相应的权重W如下:
当i=0时,
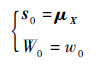
|
(14) |
当i=1, 2, …, n时,
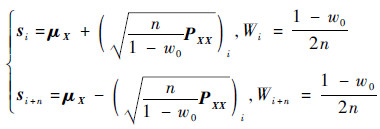
|
(15) |
式中:PXX为输入协方差矩阵; ()i指选取第i列或行; 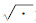
因此, 对于式(2)中的多维变量积分MYα可以由式(16)求得
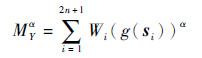
|
(16) |
在结构可靠性工程领域, 通常用结构功能函数的估计次数来表征本文方法的计算效率, 因为对于以有限元形式表征的结构输入-输出模型, 单次的模型调用会花费数秒甚至数分钟的时间, 减少模型的调用次数, 也即函数估计次数, 可从根本上提高计算效率。本节对3种分数矩求解方法的函数估计次数进行分析。
对于DRI方法, 通过式(10)可看出, 将一个多元函数的α阶分数矩近似转化为n个一元函数α阶分数矩乘积的形式, 而一元函数估计的次数是非常小的。根据高斯积分的特点, 对于均匀分布、正态分布等对称分布, 由表 2可看出其高斯积分点包含zi=0点, 经表 1所示的数值积分表达式转化后即需计算g(μX), 而式(10)中已计算g(μX), 该结果可重复利用, 因此对于该类对称分布的变量, 其对应的一元函数估计次数为Ni-1。DRI方法的函数估计次数记为NDRI, 即[12]

|
(17) |
式中:k为输入变量概率分布具有对称性的输入变量个数; Ni为高斯积分点的个数。
SGI方法调用函数次数是与所选择的精度水平k以及输入变量维数n有关。根据被积分函数的复杂程度确定k的取值, 一般情况下取2或3即可满足要求, 相应的函数估计次数NSGI为
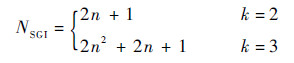
|
(18) |
UT方法选取2n+1个Sigma点并计算相应的函数值, 因此UT方法的函数估计次数NUT为

|
(19) |
例如, 对于一个包含6个正态随机输入变量的问题, 由于各特征点对应的函数值只需计算一次, 所得响应值在求解各阶次分数矩时可重复使用, 因此, 对于DRI方法, 选择五点高斯积分时计算量为25;采用SGI方法时, 当k取2时调用模型13次, 当k取3时调用模型85次; 若选择UT方法, 则计算量为13。综上可看出, 本文3种方法的函数估计次数均较少, 很大程度提高了分数矩的计算效率。
3.2 适用性分析基于分数矩的极大熵准则能够准确高效地估计结构输出响应的概率密度函数, 进而直接积分即可进行结构可靠性分析。在使用时, 需要被估计函数为正的随机量。在结构可靠性工程领域, 可采用2种思路进行结构可靠性分析:①估计结构输出响应的概率密度分布, 进而以结构输出门限值为积分下限进行积分即可得到结构的失效概率; ②直接估计结构功能函数的概率密度分布, 进而直接以0为积分上限对其积分即可得到失效概率。在机械结构分析中, 位移、应力等输出响应一般可处理为正的随机量, 进而可直接计算结构输出响应的分数矩并估计概率密度分布。也可按第2种方式, 先构建结构的功能函数, 此处可以将功能函数构建为商的形式, 即G=ΔL/ΔC, ΔC为结构输出响应, ΔL为设定的门限值, 从而避免了传统功能函数形式G=ΔL-ΔC引入的负值, 进而可直接对其运用极大熵准则, 失效概率求解的积分区域可缩减至0到1。然而, 若对于一个任意函数, 其存在负值为一种普遍情况, 这时基于分数矩的极大熵密度估计技术就存在一定的使用限制, 这种情况下往往可以将函数加上一个较大的正常数, 进而可运用该方法得到其在坐标轴上平移后的概率密度分布, 进而再进行平移转换。
对于本文3种分数矩求解方法, 其在求解分数矩问题时的适用性分析如下所述。
DRI方法通过对输出响应函数的变换, 用多个一元函数分数矩乘积求解一个多元函数的分数矩, 解决了多维积分的“维数灾难”问题。然而, 通过式(10)的转换过程可以看出, 输入向量X的联合概率密度函数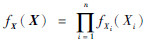
SGI方法被广泛地应用于随机不确定性的传递中, 同时在微分方程的求解以及数值积分、差值等方面发挥了很大作用, 是一种能够有效用于多维复杂问题的离散化方法[22]。SGI方法对多元积分问题具有很好的适用性, 针对不同的输入分布类型, 可以采用任何类型的一维积分点进行适应匹配, 实现过程灵活简单。此外, SGI方法的使用对与输入变量是否具有相关性无要求, 可根据问题的复杂程度及实际需求选择核实的精度水平, 因此, SGI方法对于大部分的分数矩求解问题普遍适用。
UT方法效率远高于Monte Carlo等一般数值模拟方法, 尤其针对非线性程度不高的问题, 可以高效地且仅采用2n+1次函数调用即能求得函数的低阶矩。然而, 其精度有限, 如果所研究问题的非线性程度较高, 则UT方法的精度水平会下降[24]。实际上, 若用UT方法进行分数矩计算, 尤其是式(1)中所述的极大熵准则分数矩约束计算时, UT方法的精度已能满足使用要求, 因为仅仅只需要几个低阶次的分数矩就可以提供输出响应函数的大量整数阶矩信息。然而, 若需要计算复杂函数的更高阶矩信息时, 则可采用高阶UT方法[25]。此外, 同SGI方法, UT方法也适用于结构输入变量相关时的矩信息计算。
4 算例分析本节将DRI、SGI、UT 3种分数矩求解方法应用于数值及工程算例中结构输出响应的分数矩计算, 同时, 采用Monte Carlo法在抽取104样本情况下验证上述方法的正确性以及高效性。Ncall代表各方法的函数估计次数。
4.1 数值算例文献[26]提出了一个著名的概率风险评估模型, 该模型已被广泛应用于结构输入变量的重要性分析等指标验证中[20]。在本算例中, 将本文方法应用于该模型以对其分数矩进行求解, 该模型表达为

|
(20) |
式中:X1和X2为每年发生事件的个数, 是开始事件; X3~X7为元件的失效率, 是基本事件。上述所有变量分布均为对数正态分布, 均值与误差因子如表 3所示[26]。利用本文所给3种方法求得分数矩的结果见表 4。
| α | DRI | SGI(k=2) | UT | SGI(k=3) | Monte Carlo |
| -0.3 | 13.228 | 13.228 | 13.825 | 13.243 | 13.208 |
| -0.05 | 1.535 | 1.535 | 1.543 | 1.535 | 1.535 |
| 0.62 | 5.217×10-3 | 5.171×10-3 | 5.146×10-3 | 5.204×10-3 | 5.209×10-3 |
| 1.3 | 1.856×10-5 | 1.743×10-5 | 1.859×10-5 | 1.838×10-5 | 1.849×10-5 |
| 1 | 2.197×10-4 | 2.131×10-4 | 2.190×10-4 | 2.186×10-4 | 2.190×10-4 |
| 2 | 6.407×10-8 | 5.202×10-8 | 6.265×10-8 | 6.142×10-8 | 6.445×10-8 |
| 3 | 2.449×10-11 | 1.313×10-11 | 1.386×10-11 | 2.008×10-11 | 2.640×10-11 |
| Ncall | 36 | 15 | 15 | 113 | 104 |
从表 4可以看出, 利用DRI、SGI、UT方法进行分数矩计算所得的结果均与Monte Carlo法在104抽样情况下的计算结果吻合得很好, 反映了3种分数矩求解方法在计算输出响应函数分数矩时具有较高的精度。同时, 利用3种方法求得了输出响应函数的低阶整数矩信息, 可看出即使矩信息数值非常小, 所得计算结果也能很好得接近Monte Carlo数值仿真结果。此外, 对于SGI方法, 为了对比分析不同精度水平时的计算结果, 分别在精度水平取k=2和k=3时的分数矩结果, 可以看出对于本算例, 当取精度水平k=2时, 已经可以得到较高精度的计算结果。
此外, 表 4中的函数估计次数Ncall清晰地对比反映出了DRI、SGI、UT 3种方法的计算效率。相比于Monte Carlo法, 均只需要少量次数的函数估计便可得到高精度的计算结果, 很大程度减少了计算代价。因此, 以上方法可为极大熵准则在很小计算量的情况下提供较为精确的分数矩约束信息, 能够有效地促进基于极大熵准则的可靠性分析方法在工程中的应用。
4.2 工程算例为了更好地验证本文3种方法的工程适用性, 本节算例将其应用于一个平面十杆桁架结构中[20], 结构概图如图 1所示。水平和竖直杆的长度和弹性模量均为L和E, 杆的横截面积为Ai(i=1, 2, …, 10)。作用在节点处的载荷Pi(i=1, 2, 3)如图 1所示。设L、Ai(i=1, 2, …, 10)、E和Pi(i=1, 2, 3)为15个服从正态分布的随机变量, 分布参数如表 5所示。本节算例为隐式输入-输出模型, 可通过ANSYS进行有限元分析得出各输入状态下的输出响应值。
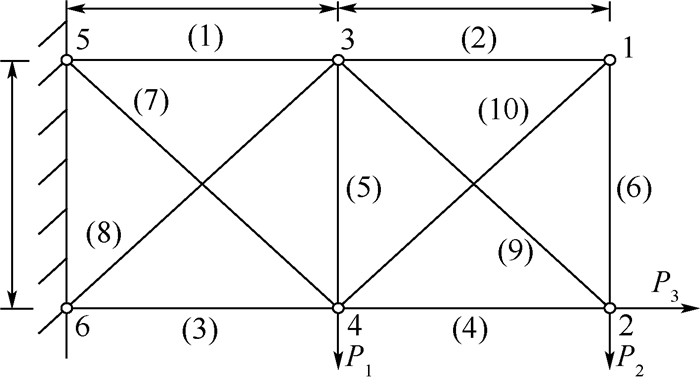
|
| 图 1 平面十杆桁架结构示意图 Fig. 1 Schematic diagram of a plane ten-bar truss structure |
| 输入变量 | 均值 | 变异系数 |
| Ai/m2 | 0.001 | 0.15 |
| E/GPa | 100 | 0.05 |
| L/m | 1 | 0.05 |
| P1/kN | 80 | 0.05 |
| P2/kN | 10 | 0.05 |
| P3/kN | 10 | 0.05 |
运用本文3种方法可直接计算十杆桁架结构在载荷作用下响应的分数矩信息, 考虑到可靠性分析模型中, 可利用极大熵准则直接估计结构功能函数的概率密度函数, 因此以2节点纵向位移阀值为0.003 5 m作为约束条件构建结构系统失效模型。由于考虑到分数矩只适用于正的变量, 故设该模型的功能函数为G=0.003 5/Δy, Δy为节点2纵向的位移。利用本文3种方法求得分数矩的结果见表 6。
| 方法 | 分数矩 | Ncall | ||||
| d=-1.5 | d=-0.47 | d=0.08 | d=1.8 | d=2.5 | ||
| DRI | 0.787 4 | 0.925 0 | 1.013 7 | 1.382 8 | 1.585 6 | 61 |
| SGI(k=2) | 0.786 1 | 0.924 8 | 1.013 7 | 1.383 0 | 1.585 6 | 31 |
| UT | 0.792 9 | 0.926 3 | 1.013 5 | 1.382 1 | 1.586 9 | 31 |
| Monte Carlo | 0.786 3 | 0.924 6 | 1.013 7 | 1.384 0 | 1.587 2 | 104 |
对于以有限元形式表征的隐式十杆复杂模型, 3种方法对结构功能函数的分数矩求解效果同4.1节的数值算例, 结果数值十分接近Monte Carlo法计算结果, 再次验证了3种方法的计算精度。因此对于一般工程问题, 在利用密度估计思路进行可靠性分析时, 对于很大程度决定计算精度的分数矩约束信息的计算可选择性地采用本文3种分数矩求解方法, 能够确保提供的约束信息较好地吻合被拟合函数的真实信息。
各方法在隐式模型上的应用更能体现出方法本身的计算效率, 少量的有限元仿真分析次数即表征了较低的计算代价, 从表 6可看出3种方法只需数十次的有限元仿真即可得到高精度的计算结果, 很大程度缩短了计算时间, 也反映出其只需要很小的计算代价即可提供高精度的矩信息, 为后续极大熵准则等方法的应用奠定了很好的基础。
5 结论随着结构可靠性分析方法的发展, 直接估计结构输出概率密度分布, 进而积分进行概率不确定性条件下可靠性分析的求解思路在工程应用方面具有较大的潜力。针对被广泛研究的极大熵准则, 待估计函数的分数矩的求解精度与效率很大程度上决定了整个密度估计的精度与效率。
1) 本文研究了降维积分(DRI)方法、稀疏网格积分(SGI)方法及无迹变换(UT)方法3种分数矩求解方法, 介绍了分数矩求解原理及过程, 给出了各方法的计算效率, 并分析了各方法的适用性。
2) 通过数值与具有隐式输入-输出关系的工程算例验证了3种分数矩求解方法在计算变量分数矩时具有较大的优势, 验证了本文方法均只需要少量的函数估计次数即可获得较高精度的计算结果。
3) 选择性地应用3种分数矩求解方法进行结构系统分数矩的计算, 可有效推动极大熵等密度估计技术在工程结构可靠性分析中的推广应用, 进而促进结构可靠性分析技术的工程适用性。
| [1] |
王晓军, 杨海峰, 邱志平, 等. 基于测量数据的不确定性结构分析的模糊理论[J].
北京航空航天大学学报, 2010, 36 (8): 887–891.
WANG X J, YANG H F, QIU Z P, et al. Fuzzy theory for uncertain structural analysis based on measurement data[J]. Journal of Beijing University of Aeronautics and Astronautics, 2010, 36 (8): 887–891. (in Chinese) |
| [2] | WANG X J, WANG L, ELISHAKOFF I, et al. Probability and convexity concepts are not antagonistic[J]. Acta Mechanica, 2011, 219 (1-2): 45–64. DOI:10.1007/s00707-010-0440-4 |
| [3] | QIU Z P, WANG L. The need for introduction of non-probabilistic interval conceptions into structural analysis and design[J]. Science China-Physics, Mechanics & Astronomy, 2016, 59 (11): 114632. |
| [4] | ZHAO Y G, ONO T. A general procedure for first/second-order reliability method (FORM/SORM)[J]. Structural Safety, 1999, 21 (2): 95–112. DOI:10.1016/S0167-4730(99)00008-9 |
| [5] | KIUREGHIAN A D. The geometry of random vibrations and solutions by FORM and SORM[J]. Probabilistic Engineering Mechanics, 2000, 15 (1): 81–90. |
| [6] |
吕震宙, 宋述芳, 李洪双, 等.
结构机构可靠性及可靠性灵敏度分析[M]. 北京: 科学出版社, 2009.
LU Z Z, SONG S F, LI H S, et al. Reliability and reliability sensitivity analysis of structural and mechanism[M]. Beijing: Science Press, 2009. (in Chinese) |
| [7] | MELCHERS R E. Importance sampling in structural system[J]. Structural Safety, 1989, 6 (1): 3–10. DOI:10.1016/0167-4730(89)90003-9 |
| [8] | ZHANG L G, LU Z Z, WANG P. Efficient structural reliability analysis method based on advanced Kriging model[J]. Applied Mathematical Modelling, 2015, 39 (2): 781–793. DOI:10.1016/j.apm.2014.07.008 |
| [9] | ROCCO C, MORENO J. Fast Monte Carlo reliability evaluation using support vector machine[J]. Reliability Engineering and System Safety, 2002, 76 (3): 237–243. DOI:10.1016/S0951-8320(02)00015-7 |
| [10] | JAYNES E. Information theory and statistical mechanics[J]. Physical Review, 1957, 108 (2): 171–190. DOI:10.1103/PhysRev.108.171 |
| [11] | INVERARDI P, TAGLIANI A. Maximum entropy density estimation from fractional moments[J]. Communications in Statistics-Theory and Methods, 2003, 32 (2): 327–345. DOI:10.1081/STA-120018189 |
| [12] | ZHANG X F, PANDEY M D. Structural reliability analysis based on the concepts of entropy, fractional moment and dimensional reduction method[J]. Structural Safety, 2013, 43 : 28–40. DOI:10.1016/j.strusafe.2013.03.001 |
| [13] | ZHANG L G, LU Z Z, CHENG L, et al. A new method for eva-luating Borgonovo moment-independent importance measure with its application in an aircraft structure[J]. Reliability Engineering and System Safety, 2014, 132 : 163–175. DOI:10.1016/j.ress.2014.07.011 |
| [14] |
张磊刚, 吕震宙, 陈军. 基于失效概率的矩独立重要性测度的高效算法[J].
航空学报, 2014, 35 (8): 2199–2206.
ZHANG L G, LU Z Z, CHEN J. An efficient method for failure probability-based moment-independent importance measure[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35 (8): 2199–2206. (in Chinese) |
| [15] | LI B Y, ZHANG L G, ZHU X J, et al. Reliability analysis based on a novel density estimation method for structures with correlations[J]. Chinese Journal of Aeronautics, 2017, 30 (3): 1021–1030. DOI:10.1016/j.cja.2017.04.005 |
| [16] |
郭健彬, 曾声奎, 陈云霞. 稳健协同优化方法的改进和应用[J].
火力与指挥控制, 2010, 35 (4): 32–35.
GUO J B, ZENG S K, CHEN Y X. Improvement and application of multidisciplinary robust design optimization method[J]. Fire Control and Command Control, 2010, 35 (4): 32–35. (in Chinese) |
| [17] | GUO J B, ZHAO Z T, ZHAO J Y, et al. Integral robust design method based on maximum tolerance region[J]. Journal of Donghua University, 2014, 31 (6): 737–740. |
| [18] | LI G, ROSENTHAL C, RABITZ H. High dimensional model representations[J]. Journal of Physical Chemistry, 2001, 105 (33): 7756–7777. |
| [19] |
张旭方, PANDEYM D, 张义民. 结构随机响应计算的一种数值方法[J].
中国科学:技术科学, 2012, 42 (1): 103–114.
ZHANG X F, PANDEY M D, ZHANG Y M. A numerical method for calculating the random response of structures[J]. Scientia Sinica Technologica, 2012, 42 (1): 103–114. (in Chinese) |
| [20] |
张磊刚. 不确定性结构的局部和矩独立灵敏度方法研究[D]. 西安: 西北工业大学, 2015.
ZHANG L G. Study of local and moment-independent sensitivity analysis method for structures with uncertainty[D]. Xi'an: Northwestern Polytechnical University, 2015(in Chinese). |
| [21] | SMOLYAK S A. Quadrature and interpolation formulas for tensor products of certain classes of functions[J]. Soviet Mathematics Doklady, 1963, 4 : 240–243. |
| [22] | GERSTNER T, GRIEBEL M. Numerical integration using sparse grids[J]. Number Algorithms, 1998, 18 (3-4): 209–232. |
| [23] | ZHANG L G, LU Z Z, CHENG L, et al. Moment-independent regional sensitivity analysis of the complicated models with great efficiency[J]. International Journal for Numerical Methods in Engineering, 2015, 103 (13): 996–1014. DOI:10.1002/nme.v103.13 |
| [24] | JULIER S J, UHLMANN J K. Unscented filtering and nonlinear estimation[J]. Proceedings of the IEEE, 2004, 92 (3): 401–422. DOI:10.1109/JPROC.2003.823141 |
| [25] |
张勇刚, 费玉龙, 武哲民, 等. 一种高阶无迹卡尔曼滤波方法[J].
自动化学报, 2014, 40 (5): 838–848.
ZHANG Y G, FEI Y L, WU Z M, et al. A high order unscented Kalman filtering method[J]. Acta Automatica Sinica, 2014, 40 (5): 838–848. (in Chinese) |
| [26] | IMAN R L. A matrix-based approach to uncertainty and sensitivity analysis for fault tree[J]. Risk Analysis, 1987, 7 (1): 21–33. DOI:10.1111/risk.1987.7.issue-1 |