复杂工程系统通常包含许多不同功能的子系统,并且系统的任务成功要求系统成功完成多个连续非重叠的子阶段[1]。在每个阶段中,同一组件的工作方式、环境条件、系统的配置以及失效判据等会随着阶段的改变而改变。通常把在这种具有多个任务的系统称为多阶段任务系统(Phased-Mission System,PMS)。PMS的可靠性评估目前已经得到广泛的研究,大致可概括为解析法和仿真法2种形式。其中解析法又可以细分为3种:①组合法[2],通常使用二元决策图(Binary Decision Diagram,BDD)解决不可修复的PMS;②状态空间法[3-4],主要基于Markov模型,解决组件的可维修性,但是其规模会随系统组件数量的增长呈指数增长趋势;③模块化方法[5-8],结合了组合法和状态空间法的优点。
PMS可靠性评估中常常假设各个单元的失效是相互独立的,这种假设能够为具体求解带来很大方便,但是不能完全真实地反映实际情况。PMS中相似单元在同一阶段以及同一单元在多个阶段具有一定的相关性,若简单地在系统各单元失效相互独立的假设下进行系统可靠性分析与计算,常常会导致过大误差。PMS中往往存在由于某种共同的原因,简称共因(Common Cause,CC),造成多个组件失效,从而导致系统失效,即共因失效(Common Cause Failure,CCF)。
根据共因导致多个组件的失效概率相同与否,共因失效可分为对称性共因失效(各组件失效的概率相同)和非对称性共因失效(各组件的失效概率既可能因组件而异,也可能随时间变化)。在非对称性共因失效研究方面,学者们普遍认为共因对受其影响的单元的作用存在不同概率。文献[9]首次提出了随机共因失效(Probabilistic CCF, PCCF)的概念及其逻辑门。文献[10]在此基础上分析了静态与动态容错系统的可靠性。文献[11]提出了改进的显性和隐性方法,分析在内部与外部多个共因影响下系统的可靠性。文献[12]又进一步分析了PCCF影响下的多阶段任务系统可靠性。
现有共因失效研究主要限于单阶段任务系统,然而PMS的共因失效(特别是随机共因失效)更复杂,尤其是在系统和组件具有动态行为的情况下,现有面向PMS的随机共因失效算法不适用于系统的动态性。例如,系统中出现的诸如顺序相关、功能相关等动态逻辑,BDD方法无法解决此类问题;此外,现有的研究通常假设不同的共因之间统计独立,这与实际系统也存在一定差距。针对这些问题,本文提出一种新的模块化方法,首先,利用BDD方法对系统静态模块进行求解,利用Markov模型对系统动态模块进行求解;其次,计算扩展共因之间的概率,使其适用于互斥、相互独立和统计相关等不同统计关系,从而使分析结果更符合实际情况。
1 基本假设条件本文在考虑随机共因失效情况下研究PMS可靠性评估问题,遵循以下基本假设条件:
1) 组件是不可修复的。
2) 系统存在随机共因失效,且不同共因之间存在相关性。
3) 系统不同组件之间的失效概率都是相互独立的。
4) 组件失效服从指数分布。
5) Cij表示第i个阶段出现的第j个共因,其出现在阶段i开始时刻且在i阶段结束时结束,即该共因对组件影响时间为阶段持续时间。
2 共因事件模型由于共因的存在,PMS中的多个组件可能会在一个或多个阶段内同时发生失效,但在PMS工作运行过程中共因并不是必然发生,因此根据共因是否发生可以将系统的样本空间划分为不同事件。假设系统中有m个阶段,存在L个共因,根据这L个共因发生与否可以将系统的样本空间划分为2L个不相交的事件:若阶段1中有L1个共因,阶段2中有L2个共因,以此类推阶段i有Li个共因,则有i=1,2,…,m;j=1,2,…,Ln(n=1, 2, …, m)。每个事件称为一个随机共因事件,使用En表示,则有E1表示L个共因都不发生,E2表示L个共因中仅有阶段1中的第一个共因(即C11)发生,以此类推E2L表示L个共因都发生。En逻辑表达式为
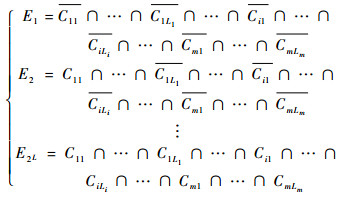
|
(1) |
式中:L1+L2+…+Lm=L。
P(En)为En的发生概率,有
利用共因的发生概率就可以由式(1)计算各个En的发生概率。目前,研究通常假设不同共因之间是相互独立的,从而可以很方便地计算每个En的概率。但现实中多个共因之间的关系要复杂得多,利用贝叶斯理论可以对En的概率计算模型进行扩展[8],使其包含互斥、相互独立和统计相关等关系,支持可靠性分析评估。限于篇幅,本文以2个共因为例,给出各种情况下每个En的概率计算公式,多个共因时的计算公式可以此类推。
假设存在2个共因C11和C12,其发生概率分别为P1和P2。则共因发生相关性的表达式如下所示:
1) 当共因之间为互斥关系时,有
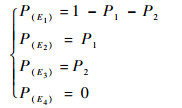
|
(2) |
2) 当共因之间相互独立时,有
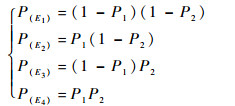
|
(3) |
3) 当共因之间统计相关时,若
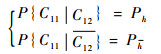
|
则
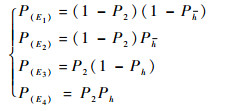
|
(4) |
本文采用模块化建模方法,综合利用BDD和Markov模型对PMS进行建模,使用隐式替代法考虑随机共因失效的影响,从而实现对PMS的可靠性进行评估[13]。
3.1 基础方法理论1) BDD模型
基于香农定理,BDD方法可以表示为if-then-else的形式[14-15]。BDD主要使用布尔函数表达,故障树在转换为BDD时,由于不同底事件的排序会得到不一样的BDD,相应的计算量也有所不同。本文采用结构式中的从上至下、从左到右的排序方法[16-17]。
2) Markov模型
使用Markov模型对动态模块进行求解的分析步骤如下:
步骤1 定义动态模块M的状态空间。
步骤2 描绘状态转移图。根据系统特征以及步骤1总结的状态空间来绘制状态转移图。
步骤3 定义模块M在时刻t的状态为Si(Si∈W),其概率用Pi(t)表示。
步骤4 建立状态转移方程。使用步骤3的定义以及步骤2的状态转移图建立状态转移方程。
步骤5 求解状态转移方程,得出阶段i结束时刻Ti模块M的各个状态Si的状态概率。
步骤6 计算系统总的失效概率。根据系统功能需求,将每个失效模式的概率相加即为系统失效概率。
3.2 引入共因失效的基本思路如前所述,系统中若不考虑共因失效,常常会使系统可靠性过于理想化,因此在PMS的可靠性评估中应考虑共因失效的影响,且应尽可能考虑共因之间的各种统计关系(如第2节所述)。共因失效影响的引入分为以下步骤:
步骤1 建立所有随机共因的事件空间En, 其中包含所有随机共因发生和不发生的组合。
步骤2 在不考虑随机共因的影响下,构建系统的可靠性模型,分析模型得出所需要的状态空间。
步骤3 由步骤2的状态空间,计算每个状态空间下每个静态模块所涉及组件在每个随机共因事件影响下的条件故障概率。
步骤4 评估系统在每个随机共因事件影响下的条件故障概率。
步骤5 用一个全概率公式将随机共因失效的影响加入整个系统的故障概率中。
3.3 PMS可靠性评估步骤在引入共因失效的基本思路指导下,考虑随机共因失效的PMS可靠性评估主要分为以下5步:
步骤1 按第2节给出的模型及算法构建PMS工作运行过程事件空间,并计算各中随机共因事件的概率。
步骤2 在不考虑随机共因失效的情况下,构建系统的可靠性模型。其主要步骤如下:
1) 首先,将每个阶段用故障树表示,再根据多阶段任务系统的特点得到系统级的故障树;其次,根据Rauzy方法[18]将系统级故障树进行整合得到系统级相互独立的模块,再将每个独立模块作为底事件组成系统级故障树;最后,将系统故障树模型转化并化简为系统级最简BDD模型。
2) 根据其逻辑结构特点将上述的独立模块进行静态模块和动态模块归类。使用与、或、表决等静态逻辑门的为静态模块;包含至少一个功能相关、冷备份等动态逻辑门的为动态模块。
步骤3 计算步骤2所得到的系统级失效BBD模型中每个静态模块组件的条件失效概率。此时应考虑随机共因失效对组件的影响,即计算条件失效概率。若随机共因事件En发生时组件x受k个共因影响,则静态模块中组件x在随机共因事件En发生时的随机失效概率为
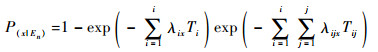
|
(5) |
式中:λix为组件x在阶段i的内部失效率;λijx为组件x受共因Cij影响的失效率;Tij为组件x受共因Cij影响的持续时间;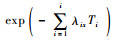
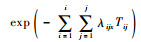
步骤4 评估系统在随机共因失效影响下的条件失效概率P(PMSfails|En)。对于步骤2得到的失效模型,使用BDD方法对静态模块进行求解,使用Markov模型对动态模块进行求解;进而再计算整个系统的失效概率。其中静态模块中的组件失效概率已由步骤3得到,根据实际的逻辑关系可以很容易求得静态模块的条件失效概率;使用Mdy表示动态模块,则动态模块在随机共因失效影响下的条件失效概率为

|
(6) |
式中:PM为动态模块的内部失效概率,通过将组件的内部失效率作为动态模块对应Markov链的转移率计算而得;同理Pci为动态模块受随机共因失效影响下的失效概率,通过将组件由共因导致的失效率作为动态模块对应Markov链的转移率计算而得。
步骤5 评估整个系统的可靠性概率。
根据全概率公式得出系统由于某个随机共因事件影响的失效概率为
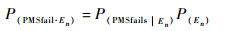
|
则系统受所有随机共因事件影响下的失效概率为
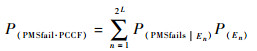
|
因此系统受随机失效影响下的可靠性概率为
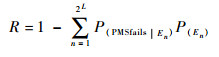
|
(7) |
卫星是一个典型的PMS,本文以文献[16]给出的地球同步轨道卫星为例,分析其在首次变轨中受PCCF影响所得到的任务系统可靠性概率。卫星首次变轨经历太阳捕获、地球捕获、地球指向、远地点点火准备和远地点点火等5个阶段,其所涉及的组件及分系统介绍详见表 1。
| 分系统 | 单机 | 符号 | 简介 |
| 姿轨控 | 姿态控制计算机 | A | 含Aa和Ab共2台,冷备份 |
| 陀螺 | B | 含Ba、Bb和Bc共3台,3取2 | |
| 数字太阳敏感器 | C | 含Ca、Cb、Cc和Cd共4台,其中仅Ca和Cb热备份 | |
| 红外地球敏感器 | D | 含Da和Db共2台,热备份 | |
| 星敏感器 | E | 含Ea、Eb和Ec共3台,3取2 | |
| 推进 | 490 N发动机 | F | 1台F |
| 10 N推力器 | G | 含Ga和Gb共2套,热备份 |
系统所涉及的具体参数描述如下:
1) 系统中存在3个共因:C41、C51和C52。对应失效概率分别为PC41=0.7,PC51=0.6,PC52=0.4。C41分别与C51、C52统计独立;C51与C52统计相关。其中:
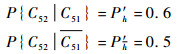
|
2) 组件的失效率描述。组件的内部失效率分别为:λA=2.44, λB=1.22, λC=6.10, λD= 2.44, λF=1.72, λG=1.22(单位均为10-8 min-1);组件由于共因所导致的失效率分别为:λ41(A)=2, λ41(C)=3, λ41(E)=6, λ41(G)=7, λ51(B)=1, λ51(D)=2, λ51(F)=3, λ52(A)=5, λ52(C)=6, λ52(E)=2, λ52(G)=4(单位均为10-4 min-1)。
3) 阶段持续时间。每个阶段的持续时间分别为:T1=45, T2=698, T3=35, T4=120, T5=57(单位均为min)。
4.2 可靠性建模与评估构建卫星首次变轨过程中的随机共因事件空间如式(8)所示:

|
(8) |
计算各共因失效事件的失效概率:
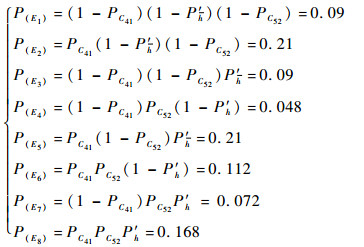
|
首先,采用故障树对所涉及的5个任务阶段建模(详见文献[16])。根据模块化思想,将整个系统总结为8个独立的子模块,分别为
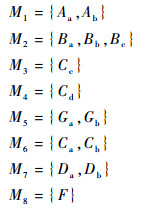
|
其中:M1为动态模块,其他为静态模块。各阶段的BDD模型详见文献[16],并将其简化为系统级的BDD模型如图 1所示,图中Mji表示在第i阶段的Mj。
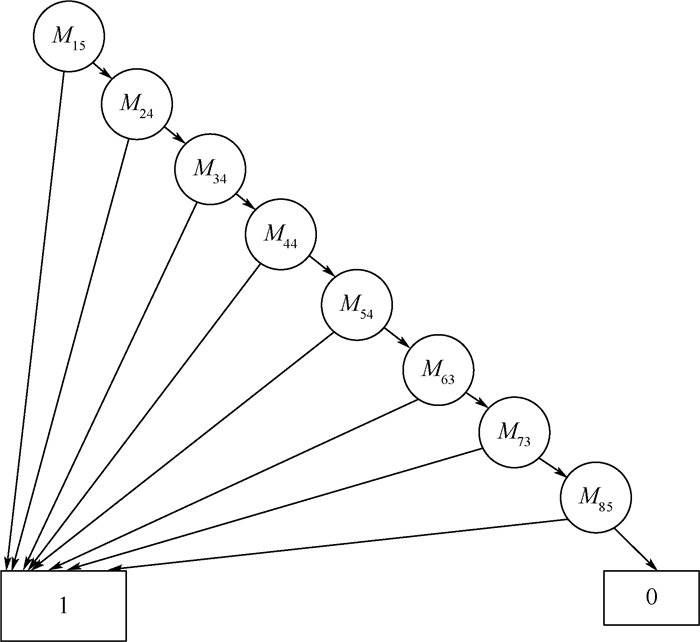
|
| 图 1 系统BDD模型 Fig. 1 BDD model of system |
由式(6)计算组件条件的失效概率如表 2所示。由系统BDD模型可知系统失效所涉及的模块为M24、M34、M44、M54、M63、M73和M85。
| 模块 | 组件 | E1/10-5 | E2 | E3 | E4/10-5 | E5 | E6 | E7 | E8 |
| M24 | Ba4 | 1.086 | 1.086×10-5 | 1.086×10-5 | 1.086 | 1.086×10-5 | 1.086×10-5 | 1.086×10-5 | 1.086×10-5 |
| Bb4 | 1.068 | 1.068×10-5 | 1.068×10-5 | 1.068 | 1.068×10-5 | 1.068×10-5 | 1.068×10-5 | 1.068×10-5 | |
| Bc4 | 1.068 | 1.068×10-5 | 1.068×10-5 | 1.068 | 1.068×10-5 | 1.068×10-5 | 1.068×10-5 | 1.068×10-5 | |
| M63 | Ca3 | 4.746 | 4.746×10-5 | 4.746×10-5 | 4.746 | 4.746×10-5 | 4.746×10-5 | 4.746×10-5 | 4.746×10-5 |
| Cb3 | 4.746 | 4.746×10-5 | 4.746×10-5 | 4.746 | 4.746×10-5 | 4.746×10-5 | 4.746×10-5 | 4.746×10-5 | |
| M34 | Cc4 | 5.478 | 0.035 4 | 5.478×10-5 | 5.478 | 0.035 4 | 0.035 4 | 5.478×10-5 | 0.035 4 |
| M44 | Cd4 | 5.478 | 0.035 4 | 5.478×10-5 | 5.478 | 0.035 4 | 0.035 4 | 5.478×10-5 | 0.035 4 |
| M54 | Ga4 | 1.068 | 0.080 6 | 1.068×10-5 | 1.068 | 0.080 6 | 0.080 6 | 1.068×10-5 | 0.080 6 |
| Gb4 | 1.068 | 0.080 6 | 1.068×10-5 | 1.068 | 0.080 6 | 0.080 6 | 1.068×10-5 | 0.080 6 | |
| M73 | Da3 | 1.891 | 1.891×10-5 | 1.891×10-5 | 1.891 | 1.891×10-5 | 1.891×10-5 | 1.891×10-5 | 1.891×10-5 |
| Db3 | 1.891 | 1.891×10-5 | 1.891×10-5 | 1.891 | 1.891×10-5 | 1.891×10-5 | 1.891×10-5 | 1.891×10-5 | |
| M85 | F5 | 1.643 | 1.643×10-5 | 0.0170 | 1.643 | 0.017 0 | 1.643×10-5 | 0.017 0 | 0.017 0 |
评估系统在随机共因失效影响下的条件失效概率。其中M2~M8采用BDD求解所得失效表达式如式(9)所示;M1的Markov模型如图 2所示,求解Markov模型所得微分方程为式(10),其中PSi代表状态Si的失效概率;系统失效表达式为式(11)。由式(7)、式(9)和式(10)可求得每个模块在共因失效时间影响下的失效概率,如表 3所示。
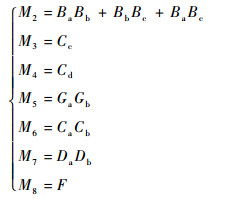
|
(9) |
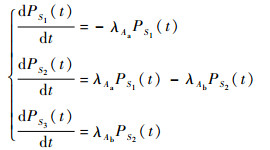
|
(10) |
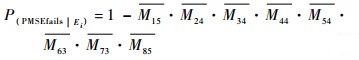
|
(11) |

|
| 图 2 M1对应的的Markov模型 Fig. 2 Markov model of M1 |
| 模块 | E1 | E2 | E3 | E4 | E5 | E6 | E7 | E8 |
| M15 | 1.000×10-8 | 0.009 87 | 1.000×10-8 | 0.009 64 | 0.009 87 | 0.004 22 | 0.009 64 | 0.004 22 |
| M24 | 3.422×10-10 | 3.422×10-10 | 3.422×10-10 | 3.422×10-10 | 3.422×10-10 | 3.422×10-10 | 3.422×10-10 | 3.422×10-10 |
| M63 | 2.252×10-9 | 2.252×10-9 | 2.252×10-9 | 2.252×10-9 | 2.252×10-9 | 2.252×10-9 | 2.252×10-9 | 2.252×10-9 |
| M34 | 5.478×10-5 | 0.0354 | 5.478×10-5 | 5.478×10-5 | 0.035 4 | 0.035 4 | 5.478×10-5 | 0.035 4 |
| M44 | 5.478×10-5 | 0.035 4 | 5.478×10-5 | 5.478×10-5 | 0.035 4 | 0.035 4 | 5.478×10-5 | 0.035 4 |
| M54 | 1.141×10-10 | 0.006 5 | 1.141×10-10 | 1.141×10-10 | 0.006 5 | 0.006 5 | 1.141×10-10 | 0.006 5 |
| M73 | 3.576×10-10 | 3.576×10-10 | 3.576×10-10 | 3.576×10-10 | 3.576×10-10 | 3.576×10-10 | 3.576×10-10 | 3.576×10-10 |
| M85 | 1.643×10-5 | 1.643×10-5 | 0.017 0 | 1.64 3×10-5 | 0.017 0 | 1.643×10-5 | 0.017 0 | 0.017 0 |
由式(11),参考表 3的数据可得系统在随机共因失效事件影响下的条件失效概率(保留10位有效数字):

|
由式(11)计算系统可靠性概率为
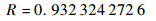
|
在不考虑共因影响的情况下,卫星首次变轨的任务成功概率为0.999 881 49[16],但由于卫星在执行任务过程中存在共因事件,尽管随机共因失效的概率并不高,但是仍然使得系统的任务成功概率降低了约6.8%,且随着工作时间的累积,其影响效果还会逐渐增大。因此,对于卫星等PMS来说,随机共因事件是一个不容忽视的可靠性影响因素。
5 结论1) 利用贝叶斯理论扩展了PMS中随机共因失效的概率模型,使其具有更大的适用范围。
2) 提出了将随机共因失效引入PMS可靠性评估的基本思路,并给出了详细的可靠性评估步骤。
3) 给出了分别利用BDD和Markov模型以及全概率公式进行求解的概率模型。
4) 通过案例分析,一方面验证了方法的可行性和有效性,另一方面确认了如果不考虑共因失效的影响,可靠性评估结论将过于乐观。
在后续研究中,笔者将在考虑系统组件存在维修活动以及级联失效关系情况下,研究如何对PMS可靠性进行评估,并进一步优化本文提出的建模分析方法,使其更加有效、便捷。
| [1] | XING L, AMARI S V. Reliability of phased-mission systems[M]. Berlin: Springer, 2008: 349-368. |
| [2] | XING L, LEVITIN G. BDD-based reliability evaluation of phased-mission systems with internal/external common-cause failures[J]. Reliability Engineering and System Safety, 2013, 112 : 145–153. DOI:10.1016/j.ress.2012.12.003 |
| [3] | WU X Y, YAN H, LI L. Numerical method for reliability analysis of phased mission system using Markov chains[J]. Communication Statistics-Theory and Method, 2012, 41 (21): 3960–3973. DOI:10.1080/03610926.2012.697969 |
| [4] | WU X Y, WU X Y. Extended object-oriented Petri net model for mission reliability simulation of repairable PMS with common cause failures[J]. Reliability Engineering and System Safety, 2015, 136 : 109–119. DOI:10.1016/j.ress.2014.11.012 |
| [5] | SHRESTHA A, XING L, DAI Y. Reliability analysis of multi-state phased-mission systems with unordered and ordered states[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part A:Systems and Humans, 2011, 41 (4): 625–636. DOI:10.1109/TSMCA.2010.2089513 |
| [6] | LU J M, WU X Y. Reliability evaluation of generalized phased-mission systems with repairable components[J]. Reliability Engineering and System Safety, 2014, 121 : 136–145. DOI:10.1016/j.ress.2013.08.005 |
| [7] | MO Y, XING L, AMARI S. A multiple-valued decision diagram based method for efficient reliability analysis of non-repairable phased-mission systems[J]. IEEE Transactions on Reliability, 2014, 63 (1): 320–330. DOI:10.1109/TR.2014.2299497 |
| [8] | WANG D, TRIVEDI K S. Reliability analysis of phased-mission system with independent component repairs[J]. IEEE Transactions on Reliability, 2007, 56 (3): 540–551. DOI:10.1109/TR.2007.903268 |
| [9] | XING L, WANG W. Probabilistic common-cause failures analysis[C]//Proceeding of the 2008 Annual Reliability and Maintainability Symposium. Piscataway, NJ: IEEE Press, 2009: 354-358. |
| [10] | XING L, BODDU P, SUN Y, et al. Reliability analysis of static and dynamic fault-tolerant systems subject to probabilistic common-cause failures[J]. Journal of Risk and Reliability, 2010, 224 (1): 43–53. |
| [11] | WANG C, XING L, LEVITIN G. Explicit and implicit methods for probabilistic common-cause failure analysis[J]. Reliability Engineering and System Safety, 2014, 131 (3): 175–184. |
| [12] | WANG C, XING L, LEVITIN G. Probabilistic common cause failures in phased-mission systems[J]. Reliability Engineering and System Safety, 2015, 144 : 53–60. DOI:10.1016/j.ress.2015.07.004 |
| [13] | OU Y, DUGAN J B. Modular solution of dynamic multi-phase systems[J]. IEEE Transaction on Reliability, 2004, 53 (4): 499–508. DOI:10.1109/TR.2004.837305 |
| [14] | XING L, AMARI S V. Binary decision diagrams and extensions for system reliability analysis[M]. Boston: John Wiley & Sons, 2015. |
| [15] | LI S, SI S, DUI H, et al. A novel decision diagrams extension method[J]. Reliability Engineering and System Safety, 2014, 126 : 107–115. DOI:10.1016/j.ress.2014.01.017 |
| [16] |
张华, 宗益燕, 韦锡峰, 等. 地球同步轨道卫星多阶段任务可靠性建模[J].
航天器环境工程, 2016, 33 (4): 439–445.
ZHANG H, ZONG Y Y, WEI X F, et al. Phased-mission system reliability modeling of geostationary satellite based on mission profile[J]. Spacecraft Environment Engineering, 2016, 33 (4): 439–445. (in Chinese) |
| [17] |
朱海鹏. 基于BDD的多阶段任务系统可靠性建模分析[D]. 成都: 电子科技大学, 2010: 37-38.
ZHU H P. Reliability modeling and analysis method for PMS based on BDD[D]. Chengdu: University of Electronic Science and Technology of China, 2010: 37-38(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10614-2010234447.htm |
| [18] | RAUZY A. New algorithms for fault tree analysis[J]. Reliability Engineering and System Safety, 1993, 40 (3): 203–211. DOI:10.1016/0951-8320(93)90060-C |



