2. 北京遥感设备研究所, 北京 100854
2. Beijing Remote Sensing Equipment Institute, Beijing 100854, China
无源定位技术在信号处理领域应用广泛,不仅在雷达[1]、声呐[2]和导航等传统领域持续发挥作用,而且在无线通信、传感器网络[3-4]等新兴商业领域中得到了应用。分布式定位站通过接收未知辐射源信号,可提取与目标位置有关的观测量信息,如到达角度(Angle of Arrival, AOA)、到达时差(Time Difference of Arrival, TDOA)[5]、到达频差(Frequency Difference of Arrival, FDOA)[6]和信号到达强度(Received Signal Strength, RSS)[7]等信息,利用一种或多种观测量信息[8],通过求解观测量信息与目标位置参数的几何定位方程,可以获得目标的位置估计。
该几何定位方程对目标位置参数非线性,而且非凸,所以不易求解,很多文献都对该问题进行了深入研究。迭代定位算法[9-10]作为传统的无源定位算法,通过泰勒级数展开,在较小的观测量噪声下可以达到克拉美罗界(Cramer-Rao Lower Bound, CRLB),但需要较准确的初始值估计,计算量大而且存在定位发散问题。球面内插(Spherical Interpolation, SI)算法[11]和球面相交(Spherical Intersection, SX)算法[12]是2种闭式算法,不需迭代运算而且计算量小,但定位性能达不到最优。Chan和Ho提出了经典的两步加权最小二乘(Two-Step Weighted Least Squares, TS-WLS)算法[13],该算法可以得到目标位置的闭式解析解,不需初始值和迭代运算,在较小的观测量噪声下能达到CRLB。Einemo和So[14]通过改进TS-WLS算法,将其应用在分布式MIMO[14-16]雷达中,借助外辐射源得到了非辐射目标的位置估计。然而这些研究都是建立在定位站位置准确已知的基础上,实际中难以实现。文献[17]考虑了定位站位置误差的存在,发现定位站位置误差会对目标定位性能有较大的影响,通过将定位站位置统计分布信息引入到加权矩阵中,提出一种存在定位站位置误差下的时差定位算法,改善了目标定位精度。在定位站与目标具有相对运动时,又提出了一种存在定位站位置和速度误差下的时频差联合定位算法[18],提高了目标的位置和速度估计精度。即使这样,存在定位站位置误差下的定位与不存在定位站位置误差下的定位相比,定位性能也相差甚大。标校源的使用有效缓解了这一问题,文献[19]使用位置已知的标校源,通过测量来自该标校源的时差观测量,结合预测时差值,可估计定位站的位置偏差,从而改善定位站位置,极大地提高了目标的定位精度。
上述文献只考虑了对单目标的定位研究,对多目标定位却研究很少。文献[20]在定位站位置不确定情况下,提出了一种渐进有效的定位不相交多目标时差定位算法,其中不相交性可以来自时间、频率或两者都有,从而消除模糊便于估计每个目标的观测量信息,该算法可以对多目标进行有效定位,但需要目标位置假设,而且需要对定位站和目标进行联合估计,增大了运算量。在此基础上,文献[21]提出了一种新的定位不相交多目标的时差定位算法,该算法不需要初始值估计,避免了定位站和目标的联合估计,降低了计算量,而且在较低的测量噪声和定位站位置误差下,对远、近场目标的定位性能均能达到CRLB。如前所述,定位站位置误差对单目标的定位性能有较大影响,对多目标定位而言,也具有相同的结论。
本文研究不相交多目标的时差定位问题,通过使用位置已知的标校源改善定位站位置,减小定位站位置不确定性对多目标定位性能的影响,提高对多目标的定位精度。首先对标校源辅助的多目标时差定位进行CRLB性能分析,并与未使用标校源辅助的多目标时差定位CRLB对比,发现标校源的使用理论上可以大幅提高多目标的定位精度。因此,本文提出了一种使用标校源的多目标时差定位闭式算法,该算法基于加权最小二乘估计,分为2个阶段:第1阶段使用来自标校源的时差观测量,改善定位站位置,并估计对应的位置误差统计特性;第2阶段使用更新的定位站位置,利用TS-WLS算法实现对多目标的高精度定位。该算法不需要目标位置假设和迭代运算,没有局部收敛和定位发散问题,只对目标位置进行估计,避免了定位站和目标的联合估计,算法计算复杂度较小。而且相比于单目标定位算法,本文算法可考虑并利用来自不同目标的定位观测量误差相关性信息,从而完善定位算法加权矩阵,不仅可同时估计多个目标的位置信息,而且提高了目标定位精度。算法定位性能分析和仿真结果表明,在较小的时差观测误差和定位站位置误差下,对多目标的定位性能可以达到CRLB。
1 定位场景本文使用多定位站对三维空间的不相交多目标进行时差定位,定位场景如图 1所示。设有K个目标(图中“△”表示),位置分别为uko=[xko, yko, zko]T, k=1, 2, …, K,则需估计的多目标位置参数可表示为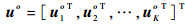

|
| 图 1 多目标定位场景 Fig. 1 Multi-source localization scenario |
定位站接收来自目标和标校源的信号,通过与参考定位站(设为s1定位站)的接收信号进行相关,可估计相应的TDOA,乘以信号传播速度,得到信号到达距离差(Range Difference of Arrival, RDOA)。来自第k个目标的RDOA观测量可表示为

|
(1) |
式中:i=2, 3, …, M;k=1, 2, …, K;ri1, k为RDOA观测值;Δri1, k为RDOA观测误差;ri1, ko为RDOA真实值,可表示为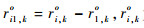
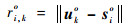
|
(2) |
式中:‖ ‖为2-范数。
来自第k个目标的所有RDOA观测量可表示为rk=[r21, k, r31, k, …, rM1, k]T=rko+Δrk,rko为RDOA真值向量,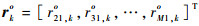
假设来自已知标校源的RDOA校正观测量可估计,并有
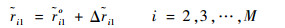
|
(3) |
式中: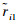


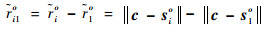
|
(4) |
式中: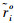
来自标校源的所有校正RDOA观测量可表示为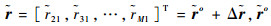
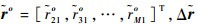
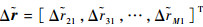
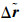
由于定位站存在位置误差,所以真实位置sio未知,含误差的定位站位置si已知,可表示为
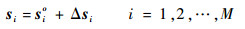
|
(5) |
式中:Δsi为第i个定位站的位置误差向量。
M个含有位置误差的定位站位置可用3M×1维向量s表示
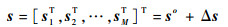
|
(6) |
式中:so为真实定位站位置,可表示为so=[s1oT, s2oT, …, sMoT]T;Δs为定位站位置误差向量,Δs=[Δs1T, Δs2T, …, ΔsMT]T,设Δs为零均值高斯随机矢量,且协方差矩阵为Qβ。
假设误差项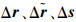
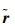
CRLB可衡量确定性参数估计的有效性,由参数估计的无偏性推导而来,是无偏估计所能达到的最小方差,可由Fisher信息矩阵J获得。在第1节描述的定位场景下,令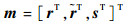
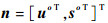
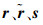
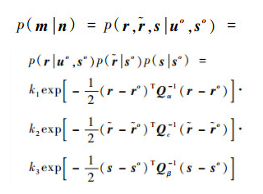
|
(7) |
式中:
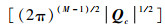
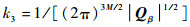
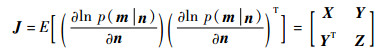
|
(8) |
式中:

|
(9) |
其中:∂ro/∂uo为K(M-1)×3K维矩阵,∂ro/∂uo= 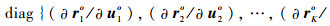
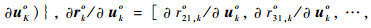
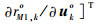
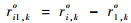
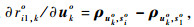
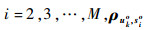
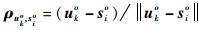
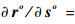
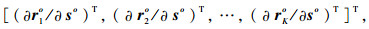
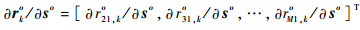
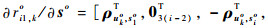
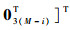
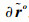
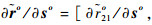
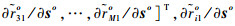
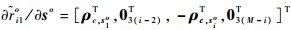
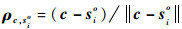
令C(n)=J-1,则矩阵C(n)的左3K×3K块矩阵即为不相交多目标位置的无偏估计CRLB,可用C(u)表示。对式(8)应用分割矩阵求逆公式[20]可得

|
(10) |
式中:X-1为不存在定位站位置误差时的CRLB;由文献[19]的附录Ⅱ推导可知,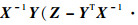
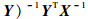
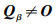
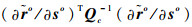

|
(11) |
式中:C(u)1为未使用标校源时的CRLB;C(u)2为使用标校源时的CRLB;Γ表示引入标校源后的定位性能改善程度,经分析知Γ为半正定矩阵,意味着标校源的引入会提升(若不提升,至少不会降低)对多目标的无源定位性能。可通过举例直观说明这一结论。
以2个目标为例,设目标1位置为[2 000, 2 500, 3 000]m,目标2位置为=[600, 650, 550]m,标校源位置已知,设为[1 500, 1 550, 1 500]m,定位站实际位置如表 1所示。来自两目标和已知标校源的RDOA观测量平均误差功率均设为σr2=10-3 m2,Qα、Qc、Qβ 3种协方差矩阵的构造方式可具体见第4节。
| m | |||
| 定位站 | 位置坐标 | ||
| x | y | z | |
| s1 | 300 | 100 | 150 |
| s2 | 400 | 150 | 100 |
| s3 | 300 | 500 | 200 |
| s4 | 350 | 200 | 100 |
| s5 | -100 | -100 | -100 |
| s6 | 200 | -300 | -200 |
对两目标的位置估计CRLB随定位站位置误差的变化如图 2所示,f(C(u)1)和f(C(u)2)分别为C(u)1和C(u)2的主对角线元素之和的平方根,用来表征CRLB的大小,σs为定位站位置误差标准差。虚线表示目标1的CRLB曲线,实线表示目标2的CRLB曲线,其中带有“○”的曲线表示未使用标校源,带有“□”的曲线表示使用标校源。从图中可以明显看出,不管对目标1还是目标2,标校源的使用可以大幅提高定位性能:对目标1,当定位站位置噪声功率σs2>-20 dB时,定位性能至少可以改善8dB;对目标2,当定位站位置噪声功率σs2>-20 dB时,定位性能至少可以改善4 dB。

|
| 图 2 多目标定位CRLB比较 Fig. 2 CRLB comparison of multi-source localization |
本节为本文闭式定位算法的理论推导和定位性能分析。首先利用来自标校源的校正RDOA观测量估计定位站位置误差,进而改善定位站位置;然后基于校正的定位站位置,引入冗余变量,将RDOA定位方程伪线性化,使用TS-WLS定位算法获得多目标的位置估计。最后通过定位性能分析评估该算法的有效性。
3.1 定位算法本文定位算法分为2个阶段:第1阶段借助标校源校正定位站位置,通过一步闭式运算估计定位站位置误差,不需迭代运算,占整个算法计算量的比重较小;第2阶段使用校正的定位站位置对多目标进行TS-WLS定位,使用更多的时差观测量信息,且需要进行两步WLS算法,占整个算法计算量的比重较大。
1) 第1阶段:校正定位站位置
由于标校源位置已知,结合定位站位置可以预测RDOA,与校正RDOA观测值的差异可以提供定位站位置误差和时差观测误差的信息,利用该信息可以校正定位站位置。由第1节可知,校正RDOA观测量可表示为
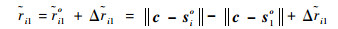
|
(12) |
式中:i=2, 3, …, M。sio、s1o未知,si、s1已知,可对其进行泰勒展开处理,忽略二阶及高阶项得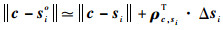
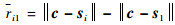
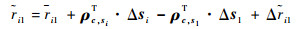
|
(13) |
对所有的校正RDOA与预测RDOA可用以下矩阵形式表示:
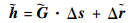
|
(14) |
式中:Δs为待估计的定位站位置误差项;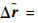
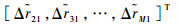

|
(15) |
其中: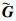
由于Δs统计分布具有先验知识,Δs为零均值高斯随机矢量,且协方差矩阵为Qβ。对非确定性参数或随机参数估计,可使用贝叶斯高斯-马尔可夫理论[19],Δs的最小线性均方误差估计为
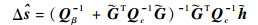
|
(16) |
因此定位站位置可改善为

|
(17) |
式中: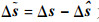
由式(16)可推导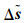
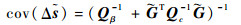
|
(18) |
定位站位置校正前后的协方差矩阵差值可表示为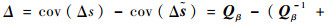
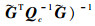
2) 第2阶段:TS-WLS定位
定位站位置经校正后,可使用TS-WLS算法进行多目标定位。TS-WLS算法分为2步:第1步引入冗余变量将RDOA定位方程伪线性化,使用WLS算法估计目标位置和冗余变量;第2步利用目标位置与冗余变量的约束关系,结合第1步估计结果构建线性方程,再次使用WLS算法,估计最终多目标位置。
第1步:由第1节可知,对第k个目标满足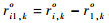
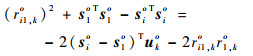
|
(19) |
式中:无误差项ri1, ko、sio可由相应的误差项代替,即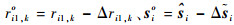
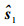

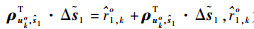
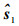
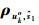

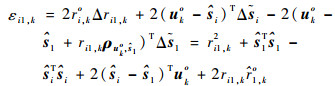
|
(20) |
式中:距离参量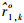

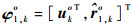
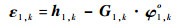
|
(21) |
式中: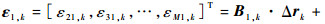
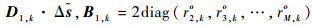
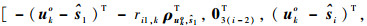
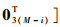
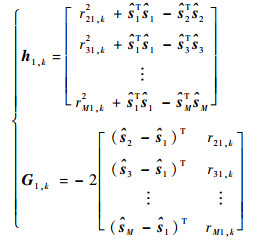
|
(22) |
由于K个目标的RDOA观测量基于相同的定位站位置误差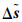

|
(23) |
式中: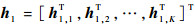
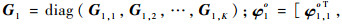
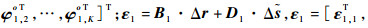

使用WLS算法求解式(23),其WLS解为
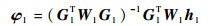
|
(24) |
式中:W1为加权矩阵,若取W1=cov(ε1)-1,则WLS估计与近似ML估计等效。由于Δr与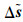

|
(25) |
当RDOA观测误差和校正后的定位站位置误差足够小,采用扰动法[13]可得φ1的协方差矩阵
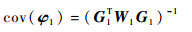
|
(26) |
第2步:由于φ1中含有冗余变量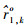
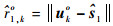
在第1步WLS解中,φ1, k(1:3)为第k个目标的位置估计,φ1, k(4)为第k个目标到校正后参考定位站的距离估计。令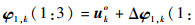
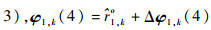
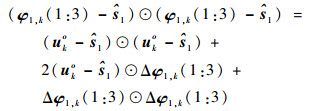
|
(27) |

|
(28) |
式中:⊙表示Schur积,即元素与元素相乘,且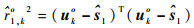
令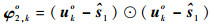
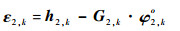
|
(29) |
式中: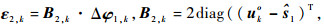
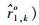
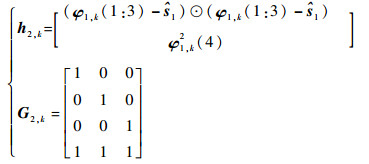
|
(30) |
扩展到K个目标,可用以下矩阵方程表示:
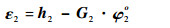
|
(31) |
式中: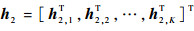

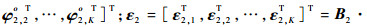
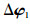
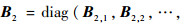
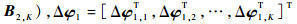
再次使用WLS算法,式(31)的WLS解为
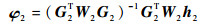
|
(32) |
式中:W2为加权矩阵,取W2=cov(ε2)-1,根据式(26),并结合ε2的表达式可得
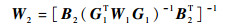
|
(33) |
将式(31)代入式(32)并结合式(33),可得φ2的协方差矩阵
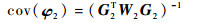
|
(34) |
根据φ2o的定义,第k个目标的最终位置估计可表示为
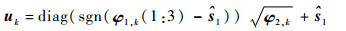
|
(35) |
式中:sgn为符号函数,可消除平方根运算产生的符号模糊,使最终解与第1步WLS解的符号保持一致。
注意到,在求解加权矩阵W1和W2时,需要目标和定位站的真实位置,均不可获得。为便于算法实现,可令W1=Qα-1,代入式(24)获得目标位置的初始估计值,结合定位站位置校正值,由式(25)更新W1,从而改善目标位置估计。使用第1步WLS解可得到加权矩阵W2。
综上所述,使用标校源对多目标的时差定位算法实现步骤如下:
步骤1 根据校正RDOA观测量,通过式(16)估计定位站位置误差,通过式(17)校正定位站位置。
步骤2 令W1为RDOA观测量协方差矩阵的逆,代入式(24)获得目标位置的初始估计值。
步骤3 根据初始目标位置,通过式(25)更新W1,代入式(24)获得第1步WLS的改善目标位置。
步骤4 根据第1步WLS解,通过式(33)构建W2,代入式(32)获得第2步WLS解。
步骤5 由式(35)得到多目标的最终位置估计。
3.2 性能分析本节对多目标定位算法的定位精度进行分析,并与CRLB比较,评估算法的有效性。
由式(35)可得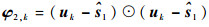
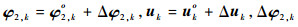
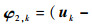
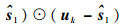
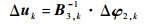
|
(36) |
式中: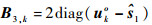
扩展到K个目标,则定位误差Δu与第2步WLS解的估计误差Δφ2的关系可表示为
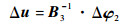
|
(37) |
式中: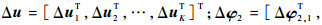
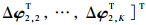
忽略B3中的定位站位置误差,由式(37)可得多目标最终位置估计的协方差矩阵
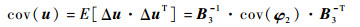
|
(38) |
式中:cov(φ2)由式(34)获得。将式(34)、式(33)和式(25)分别代入式(38)中,经化简可得

|
(39) |
式中: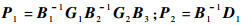
根据矩阵求逆引理,式(39)可整理得
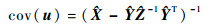
|
(40) |
式中: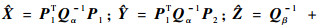
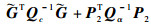
将式(40)与式(10)比较可知,cov(u)与C(u)具有相同的结构,而且表达式内的对应矩阵也具有相同的结构,文献[19, 21]均对两者的关系进行了分析。设定3个条件:①定位站位置误差相比于标校源与定位站距离足够小,即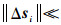
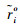
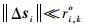
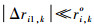
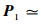
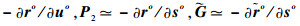
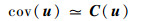
|
(41) |
综上,在定位站位置误差和RDOA观测误差均足够小,或标校源与目标距离定位站均足够远时,本文定位算法可以实现有效估计,定位性能理论上可以达到CRLB。
4 仿真分析本节将通过计算机仿真验证本文闭式算法的定位性能。采用6定位站,定位站真实位置坐标如表 1所示,带误差的定位站位置通过在定位站真实位置的基础上叠加零均值高斯白噪声获得,定位站位置误差协方差矩阵结构设为Qβ=σs2Rs,Rs=diag(10, 10, 10, 2, 2, 2, 10, 10, 10, 40, 40, 40, 20, 20, 20, 3, 3, 3),σs为定位站位置误差标准差,即各定位站具有不同的位置误差,但每个定位站各位置坐标误差相同。来自目标和标校源的RDOA观测量通过在对应真值的基础上叠加一定强度的零均值高斯白噪声产生,设协方差矩阵结构分别为Qα=σr2Rt,Qc=σr2Rc,其中σr为RDOA观测量误差标准差,σr2=10-3 m2,Rt=blkdiag(R1, R2, …, RK),R1=R2=…=RK=Rc=R,R为(M-1)×(M-1)维矩阵,其对角元素为1,其余元素为0.5。假设不同目标产生的RDOA观测量互相独立。定位性能用均方误差(Mean Square Error, MSE)表征,即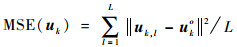
进行以下3项仿真:仿真1为基于标校源辅助的单目标定位性能仿真;仿真2为基于标校源辅助的多目标定位性能仿真;仿真3探究标校源位置对多目标定位性能的影响。
1) 仿真1
单目标定位几何构型如图 3所示,目标位置设为uo=[2 000, 2 500, 3 000]T m,标较源位置设为c=[1 500, 1 550, 1 500]T m。

|
| 图 3 仿真1目标定位几何构型 Fig. 3 Geometry for source localization in Simulation 1 |
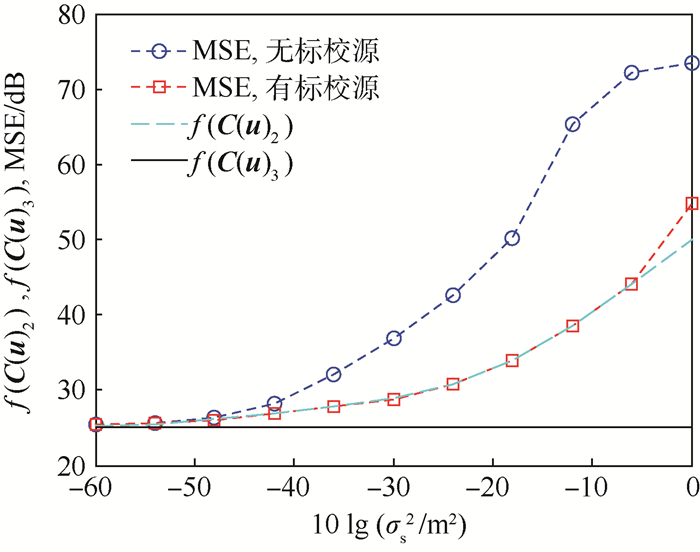
在标校源辅助下,使用本文算法对单目标的定位性能仿真如图 4所示。“□”为单目标定位性能(MSE)随定位站位置误差的变化曲线,虚线表示使用标校源校正定位的CRLB,实线表示没有定位站位置误差下的CRLB(f(C(u)3))。为便于比较,同时进行了不存在标校源时的单目标定位性能(MSE)仿真,用“○”表示。
|
| 图 4 单目标定位性能比较 Fig. 4 Comparison of single source localization performance |
从图 4中可以看出,当定位站位置误差小于-6 dB时,本文算法的定位精度可以达到CRLB,即可以对单目标进行有效定位;当定位站位置误差大于-6 dB时,发生门限效应,定位精度迅速偏离CRLB;当定位站位置误差大于-50 dB时,采用标校源辅助的单目标定位性能要优于未采用标校源辅助的单目标定位性能,且随着定位站位置误差的增大,性能改善程度更加明显;使用标校源校正定位,定位性能仍达不到没有定位站位置误差下的定位精度。
2) 仿真2
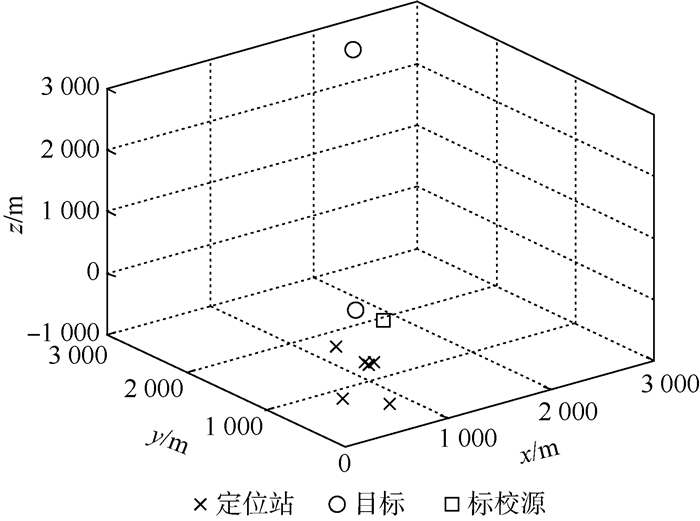
多目标定位几何构型如图 5所示,符号含义同仿真1。为简化处理,本仿真仅对2个不相交目标进行定位,目标数量可多于2个。设目标1为远场目标,位置为u1o=[2 000, 2 500, 3 000]T m,目标2为近场目标,位置为u2o=[600, 650, 550]T m,标校源位置为c=[750, 500, 400]T m,定位站位置不变。
|
| 图 5 仿真2目标定位几何构型 Fig. 5 Geometry for source localization in Simulation 2 |
在标校源辅助下,使用本文算法对2个目标的定位性能仿真如图 6所示。曲线含义同仿真1,在此不再赘述,其中定位性能较差的一组曲线为目标1的定位性能曲线,定位性能较好的一组曲线为目标2的定位性能曲线。

|
| 图 6 多目标定位性能比较 Fig. 6 Comparison of multi-source localization performance |
从图 6中可以看出,不管是对近场目标还是远场目标,采用本文算法均可以完成有效定位。当定位站位置误差小于-12 dB时,对目标1的定位精度可以达到CRLB;当定位站位置误差大于-12 dB时,发生门限效应;当定位站位置误差大于-24 dB时,本方算法的定位性能要明显优于未采用标校源辅助的定位性能,但达不到没有定位站位置误差下的定位精度。当定位站位置误差小于-12 dB时,对目标2的定位精度可以达到CRLB;当定位站位置误差大于-6 dB时,发生门限效应;当定位站位置误差大于-24 dB时,本方算法的定位性能要明显优于未采用标校源辅助的定位性能。
3) 仿真3
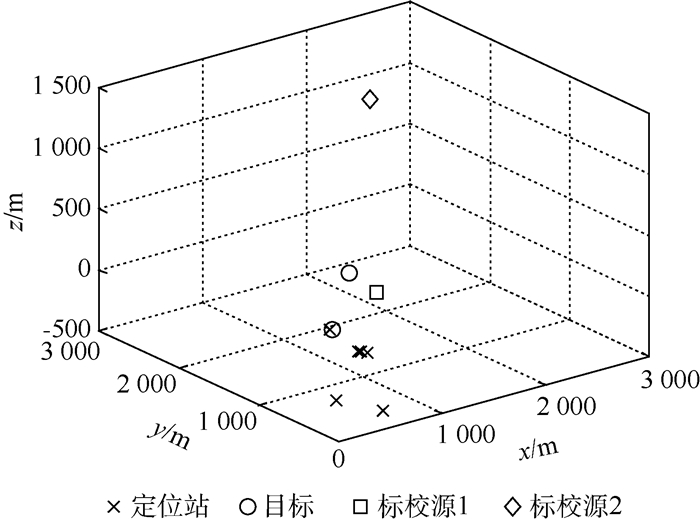
多目标定位几何构型如图 7所示。对2个不相交目标进行仿真,设目标1位置为u1o=[314, 483, 209]T m,目标2位置为u2o=[600, 650, 550]T m,标校源1位置为c1=[750, 500, 400]T m,标校源2位置为c2=[1 500, 1 550, 1 500]T m,定位站位置不变,同仿真1。
|
| 图 7 仿真3目标定位几何构型 Fig. 7 Geometry for source localization in Simulation 3 |
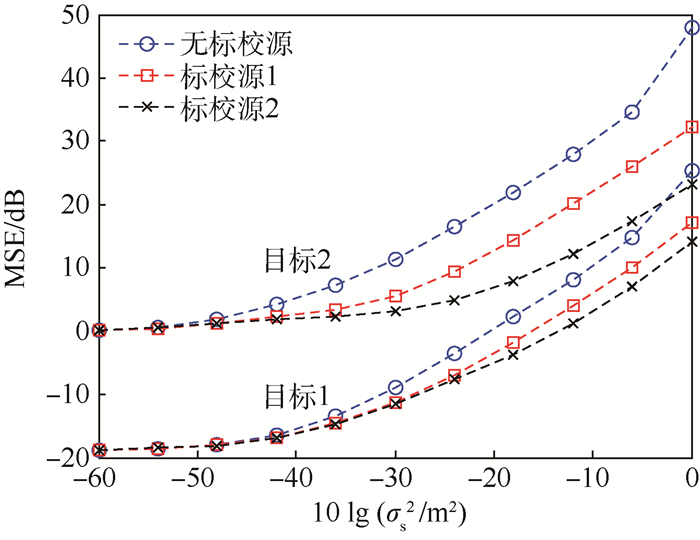
改变标校源位置,采用本文算法对两目标的定位性能仿真如图 8所示。“□”表示使用标校源1进行校正定位时目标位置估计性能随定位站位置误差的变化曲线,“×”表示使用标校源2校正定位时的定位性能曲线,“○”表示无标校源辅助下的定位性能曲线。其中定位性能较好的一组曲线为目标1的定位性能曲线,定位性能较差的一组曲线为目标2的定位性能曲线。
|
| 图 8 改变标校源位置时多目标定位性能比较 Fig. 8 Comparison of multi-source localization performance via changing calibration position |
从图 8中可以看出,无论标校源处于位置1还是位置2,不管对目标1还是目标2,本文算法的定位性能均优于未使用标校源时的定位性能。但标校源位置不同,对目标的定位性能改善程度也不同:对目标1,在定位站位置误差大于-18 dB时,采用标校源1定位精度至少改善4 dB,采用标校源2定位精度至少改善5.8 dB;对目标2,在定位站位置误差大于-24 dB时,采用标校源1定位精度至少改善7 dB,采用标校源2定位精度至少改善11.6 dB。
文献[19]表明,若使用差分校正(Differential Calibration, DC)技术,标校源离未知目标越近,定位性能改善程度越大。但仿真3结果表明,采用本文算法进行定位,离未知目标(目标1或目标2)更远的标校源反而提供了更好的定位性能。这是因为DC技术与本文算法对定位站位置的校正机理不同,至于如何设置标校源位置,使本文算法对定位精度的改善做出更大贡献仍有待研究。
5 结论本文提出了一种基于标校源辅助的不相交多目标时差定位算法。
1) 首先利用标校源校正定位站位置,然后基于校正的定位站位置,通过TS-WLS算法对多目标进行时差定位。
2) 该算法不需要初始值估计,不用对定位站和目标位置进行联合估计,通过闭式代数运算同时估计多目标位置,降低了计算量。
3) 标校源的引入虽增加了部分计算复杂度,但经CRLB分析表明,使用标校源理论上可以提高对多目标的定位精度。
4) 对该算法进行了定位性能分析和仿真验证,仿真结果表明:①对多目标,不管是近场目标还是远场目标,使用标校源校正技术均可以提高目标定位精度;②在定位站位置误差和时差观测误差较小时,算法定位性能可以达到CRLB;③标校源的位置不同,对多目标的定位精度改善程度不同。
| [1] | YANG H, CHUN J. An improved algebraic solution for moving target localization in non-coherent MIMO radar systems[J]. IEEE Transactions on Signal Processing, 2016, 64 (1): 258–270. DOI:10.1109/TSP.2015.2477803 |
| [2] | LI Y R, HO K C. Efficient closed-form estimators for multi-static sonar localization[J]. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51 (1): 600–614. DOI:10.1109/TAES.2014.140482 |
| [3] | SHI J, FAN L, ZHANG X L, et al. Multi-target positioning for passive sensor network via bistatic range space projection[J]. Science China Information Science Letter, 2016, 59 : 019302:1–-019302:3. |
| [4] | LIU C, FANG D Y, JIANG H B, et al. RSS distribution-based passive localization and its application in sensor networks[J]. IEEE Transactions on Wireless Communications, 2016, 15 (4): 2883–2895. DOI:10.1109/TWC.2015.2512861 |
| [5] | WANG Y, HO K C. TDOA positioning irrespective of source range[J]. IEEE Transactions on Signal Processing, 2017, 65 (6): 1447–1460. DOI:10.1109/TSP.2016.2630030 |
| [6] | NGUYEN N H, DOGANCAY K. Single-platform passive emitter localization with bearing and Doppler-shift measurements using pseudolinear estimation techniques[J]. Signal Processing, 2016, 125 : 336–348. DOI:10.1016/j.sigpro.2016.01.023 |
| [7] | YIN F, ZHAO Y X, FREDRIK G, et al. Received-signal-strength threshold optimization using Gaussian processes[J]. IEEE Transactions on Signal Processing, 2017, 65 (8): 2164–2177. DOI:10.1109/TSP.2017.2655480 |
| [8] | NGUYEN N H, DOGANCAY K. Multistatic pseudolinear target motion analysis using hybrid measurements[J]. Signal Processing, 2017, 130 : 22–36. DOI:10.1016/j.sigpro.2016.06.004 |
| [9] | FOY W H. Position-location solution by Taylor-series estimation[J]. IEEE Transactions on Aerospace and Electronic Systems, 1976, 12 (2): 187–194. |
| [10] | TORRIERI D J. Statistical theory of passive location systems[J]. IEEE Transactions on Aerospace and Electronic Systems, 1984, 20 (2): 183–198. |
| [11] | SMITH J O, ABEL J S. Closed-form least-squares source location estimation from range-difference measurements[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1987, 35 (12): 1661–1669. DOI:10.1109/TASSP.1987.1165089 |
| [12] | SCHAU H C, ROBINSON A Z. Passive source localization employing intersecting spherical surfaces from time-of-arrival differences[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1987, 35 (8): 1223–1225. |
| [13] | CHAN Y T, HO K C. A simple and efficient estimator for hyperbolic location[J]. IEEE Transactions on Signal Processing, 1994, 42 (8): 1905–1915. DOI:10.1109/78.301830 |
| [14] | EINEMO M, SO H C. Weighted least squares algorithm for target localization in distributed MIMO radar[J]. Signal Processing, 2015, 115 : 144–150. DOI:10.1016/j.sigpro.2015.04.004 |
| [15] | YANG H, CHUN J, CHASE D. Hyperbolic localization in MIMO radar system[J]. IEEE Antennas Wireless Propagation Letter, 2015, 14 : 618–621. DOI:10.1109/LAWP.2014.2374603 |
| [16] | REZA M V, MICHAEL R B. On the CRLB of TDOA-FDOA estimation from MIMO signals[C]//IEEE/ION Postion, Location & Navigation Symposium-plans. Piscataway, NJ: IEEE Press, 2016: 772-778. |
| [17] | HO K C, KOVAVISARUCH L, PARIKH H. Source localization using TDOA with erroneous receiver positions[C]//Proceedings of the International Symposium on Circuits and Systems. Piscataway, NJ: IEEE Press, 2004: 453-456. |
| [18] | HO K C, LU X N, KOVAVISARUCH L, et al. Source localization using TDOA and FDOA measurements in the presence of receiver location errors:Analysis and solution[J]. IEEE Transactions on Signal Processing, 2007, 55 (2): 684–696. DOI:10.1109/TSP.2006.885744 |
| [19] | HO K C, YANG L. On the use of a calibration emitter for source localization in the presence of sensor position uncertainty[J]. IEEE Transactions on Signal Processing, 2008, 56 (12): 5758–5772. DOI:10.1109/TSP.2008.929870 |
| [20] | YANG L, HO K C. An approximately efficient TDOA localization algorithm in closed-form for locating multiple disjoint sources with erroneous sensor positions[J]. IEEE Transactions on Signal Processing, 2009, 57 (1): 4598–4615. |
| [21] | SUN M, HO K C. An asymptotically efficient estimator for TDOA and FDOA positioning of multiple disjoint sources in the presence of sensor location uncertainties[J]. IEEE Transactions on Signal Processing, 2011, 59 (7): 3434–3440. DOI:10.1109/TSP.2011.2131135 |



