2. 上海航天设备制造总厂, 上海 200245
2. Shanghai Aerospace Equipment Manufacturing Factory, Shanghai 200245, China
工作流技术逐渐成为大型企业管理业务流程的主要工具,其中工作流建模是工作流管理的基础,也是决定业务流程管理是否科学的先决条件,因此需要利用过程挖掘思想进行工作流建模,确保业务流程模型的有效性和准确性。过程挖掘是从事件日志中发现过程、控制、数据、组织和社会结构等信息的重要工具,该工具有助于分析和改进已经实施的业务过程,是实现工作流建模的重要工具[1]。同时过程挖掘也是实现工作流过程建模的基础,是工作流管理的最基本工作,也是工作流分析的前提条件[2]。
过程挖掘的基本思想由Cook和Wolf[3]提出,目标是从软件过程的事件日志中自动发现过程模型。Agrawal等[4]最早将过程挖掘算法应用到工作流管理中,假设活动之间相互独立,利用活动之间的先后关系构造活动之间的依赖性。Pinter和Golani[5]对Agrawal等[4]的算法进行了拓展,将活动的开始时间和完成时间分开,从而检测任务之间的并行关系。Herbst和Karagiannis[6]进一步考虑了事件日志中存在的重名活动对活动依赖关系识别的影响,在前人的基础上加入了重名活动识别的预处理过程,提出了MerfeSeq、SplitSeq和SplitPar 3个算法。Schimm[7]提出了一种以获取完备且最小过程模型为目标的算法,该模型需要产生日志中记录的全部活动,但是该模型在出现隐藏活动或者非自由选择结构时会出错。Greco等[8]以挖掘过程模型的层次树为目标,这些模型从不同的抽象层次描述事件日志。目前,对过程挖掘算法研究贡献最大的是van der Aalst教授及其团队。2004年,van der Aalst等[9]首先提出了基于工作流网络(Workflow net,WF-net)行为推理的α算法,可以在事件日志完备的情况下,发现合理的SWF-net(Structural Workflow net)。为了解决工作流中存在的各种特殊结构的问题,α算法发展成为一系列的算法——α系列算法。α+算法[10]在α算法的基础上,考虑了短循环结构的挖掘,可以成功发现事件日志中的循环结构,得到一个合理的SWF-net。tsinghua-α算法[11]考虑了事件日志中的活动不为原子活动,即每个活动都由一个START和一个COMPLETION活动组成,用活动之间的重叠关系修正了α算法中的规则,使得整个算法更加严谨,但是该算法对事件日志的要求较高,实用性并不高。α++算法[12]是在α+算法基础上的拓展,考虑了事件日志中的非自由选择结构,该算法提出了3类活动间接依赖关系的发掘方法,可以发现日志中存在的所有非自由选择结构,不足的是该算法会挖掘太多冗余关系,出现较严重的过拟合情况。α#算法[13]是在α+算法上的另一拓展,从挖掘隐藏活动入手,用隐藏活动和不可见任务作为非自由选择结构的构成要素。α*算法[14]是在经典α算法上的拓展,提出了可以发现事件日志中重名活动的规则,该算法作为α算法的预处理步骤,可以识别日志中命名不同但内容重复的活动,使得α算法的准确率明显提高。α系列算法在工作流模型基本结构和特殊结构的识别上有较高的准确率,但是其无法消除噪声的干扰,在对含有噪声的事件日志进行挖掘时,准确率会明显下降。
为了消除事件日志中的噪声影响,van der Aalst等[15]提出了Petri网模型同活动因果矩阵的关系,将形式化的Petri网转化成数学化的矩阵模型,进而引入遗传算法对工作流模型进行迭代和进化,从而可以消除日志中的噪声干扰,同时得到较为完善的结论。李莉等[16]沿用活动因果矩阵的思想,将变异粒子群算法与过程挖掘融合起来,增强算法跳出局部最优的能力,提高了算法的运行速度。宋炜和刘强[17]同样在因果矩阵的启发下,采用模拟退火算法实现过程挖掘,实现了对工作流中基本结构和特殊结构的挖掘。黄黎等[18]在李莉等[16]的基础上定义基于时序行为的老化因子,并引入高斯变异的多种群协作的自适应策略,对粒子群算法进行改进,提高了算法的稳定性和收敛速度。以上都是基于进化算法的过程挖掘算法,这些算法在准确率上有很好的表现,但是当初始因果矩阵比较复杂,即工作流长度较大时,迭代算子太大导致算法运行时间很长,算法效率较低。
本文提出了一种基于统计α算法的过程挖掘算法,旨在同时满足高准确性和高效率2个目标,将α系列算法和进化算法的优势结合起来。本文主要贡献点如下:①提出了一种重名活动识别和处理方法,解决了α系列算法目前没有解决的重名活动处理,将重名活动识别和处理作为α算法的预处理活动,消除重名活动对于依赖关系识别的影响,显著提高了算法的准确率。②提出了一种统计α算法,通过概率计算有效消除了事件日志中的噪声影响,明显提高了算法的准确率,并保证了算法的运行效率。③考虑了工作流中常常出现的非自由选择结构,提出一个新的识别非自由选择结构的算法,在尽量少的添加间接依赖关系的前提下,保证了非自由选择结构的识别率和准确性。
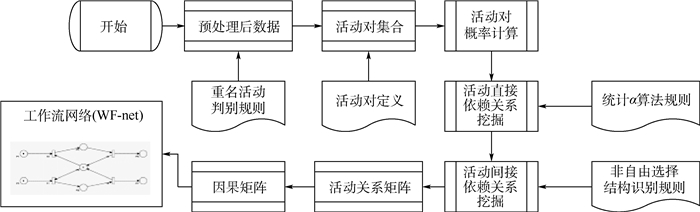
1 统计α算法体系本文提出的基于统计α算法的过程挖掘算法方案如图 1所示,主要包含2个模块:预处理模块和过程挖掘模块。其中,预处理模块主要包括完备事件日志的提取、循环结构识别与处理、重名活动识别与处理3个步骤。首先根据完备事件日志的定义从数据库中挑选符合条件的事件日志作为过程挖掘的基础;然后采用文献[19]中对于循环结构的识别规则,挖掘出长度不同的循环结构,并将循环结构体用一个活动集合来代替,从而消除循环结构对于重名活动的影响;最后利用本文提出的重名活动识别算法,将事件日志中的重名活动进行分类识别和处理,以消除重名活动对于活动依赖关系判断的影响。在过程挖掘模块中,首先给出活动依赖关系定义,并说明直接依赖与间接依赖之间的差异性;然后在此基础上给出统计α算法的详细算法思路;最后在统计α算法得到的直接依赖关系的基础上,进一步对非自由选择结构中产生的间接依赖进行挖掘,从而完善活动间的依赖关系得到活动关系矩阵。在得到最终的活动关系矩阵之后,根据因果矩阵的构造规则,可以将活动关系矩阵转化成因果矩阵进而得到对应的WF-net[15]。

|
| 图 1 基于统计α算法的过程挖掘方案 Fig. 1 Scheme of process mining based on statistical α-algorithm |
事件日志是工作流执行过程中产生的重要信息,在事件日志中往往会记录工作流中每个活动的名称、开始时间和执行人等信息。考虑到事件日志中往往会缺失活动的结束时间,每个活动的持续时间并不是一个可以直接从事件日志中得到的信息,很难在WF-net中引入持续时间的限定,赋时WF-net无法从目前的事件日志中得到。因此,本文提出的过程挖掘算法重点在于活动之间依赖关系的挖掘,通过构造活动关系矩阵,间接得到因果矩阵,进而生成WF-net。
本文挖掘的活动依赖关系分为直接依赖和间接依赖2个方面。若有活动集合T,存在事件日志W⊆T,有a, b∈T,若a和b有依赖关系:
1) 若存在a·∩·b≠∅∨·a∩b·≠∅,则称a和b存在直接依赖。直接依赖关系主要有表 1中4种关系。
| 直接依赖关系分类 | 符号 | 定义 |
| 顺序关系 | a > Wb | a, b∈σ={…, a, b, …} |
| 因果关系 | a→Wb | a > Wb∧b≯Wa |
| 选择关系 | a#Wb | a≯Wb∧b≯Wa |
| 并行关系 | a‖Wb | a > Wb∧b > Wa |
2) 若不存在a·∩·b≠∅∨·a∩b·≠∅,则称a和b存在间接依赖。间接依赖关系主要指间接因果关系,用记号a↦Wb表示。
由直接依赖关系定义可以看到,过程挖掘算法的挖掘结果同事件日志的完备性有着重要关系,不完备的事件日志往往得到错误的结果。因此,在使用过程挖掘算法之前需要给出完备事件日志的定义。
定义1(完备事件日志) 令T为活动集合,有事件日志W⊆T,W为完备事件日志当且仅当:①对于任意日志W′⊆T,满足>W′⊆>W∧→W′⊆→W∧#W′⊆#W∧‖W′⊆‖W;②对于任意t∈T,满足∃σ⊆W:t∈σ。
完备事件日志是判断活动间依赖关系的前提条件,日志的完备性要求每种可能出现的流程轨迹至少出现一次。本文中所有算法都是基于完备事件日志基础之上的,在当今大数据的环境中,由于数据量足够大,可以认为拿到的事件日志都是完备的。
1.2 重名活动识别算法重名活动是过程挖掘中一种常见的特殊结构,表 2给出了某临床路径工作流的事件日志部分内容,活动t25和t45记录着同样的活动“医患交流”,记t25和t45为重名活动。为了区分同一条流程轨迹中的重名活动,用记号δi(A, ni)表示在流程轨迹δi中第ni个活动A。然而通过对于事件日志内容的具体分析可以发现,t25所表示的“医患交流”指的是手术前医患对于手术的沟通,t45显然代表了术后医生对于患者的询问。虽然t25和t45具有相同的文字描述,但是两者的实际意义并不相同。如果将两者当作重名活动来判断会导致活动依赖关系判别出现错误,因此需要将重名活动判别作为过程挖掘的预处理步骤。
| 活动序号 | 活动名称 |
| | |
| 25 | 医患交流 |
| 26 | 手术室准备 |
| 27 | 药物准备 |
| 28 | 手术工具准备 |
| 29 | 最后确认 |
| | 手术阶段 |
| 41 | 术后整理 |
| 42 | 送病人回病房 |
| 43 | 送水送药 |
| 44 | 病人休息 |
| 45 | 医患交流 |
| 46 | 病情讨论 |
| | |
循环结构同样是工作流中常见的特殊结构,多出现在发生资源等待或者返工的情况下。当循环结构出现时,必然会出现大量重名活动接连出现,为了简化重名活动判别过程,本文使用文献[19]中给出的对于循环结构的识别作为预处理,以消除循环结构对于重名活动判别的影响。
本文对于重名活动的判别基于重名活动之上,考虑那些命名相同的活动是否具体含义也相同。将重名活动根据其具体活动内容是否相同分为2种:活动内容相同的称为重复性重名活动,简称重复活动(Duplicate Activities,DA);活动内容不同的称为非重复性重名活动(Homonyms Activities,HA)。为了探索重名活动在何时为重复活动,本文以活动组(activities group)为单位,给出基于活动组的重复活动的定义。
定义2(活动组) 对于任意流程轨迹δi∈W,如果δi中活动A∈δi,A的2个前驱活动Tp、Tpp和2个后继活动Ts、Tss,则将{Tpp,Tp,A,Ts,Tss}这样一个有序集合记作一个活动组,记作GA。如果δi中存在重名活动δi(A, n), δi(A, m)∈δi,且两者对应的活动组分别为GA和GA′,若GA和GA′中包含的除了A之外的元素相同,但元素排列顺序不同,则称为2个活动组相等,记作GA=GA′。
定义3(重复活动) 对于任意流程轨迹δi∈W,如果δi中存在重名活动δi(A, n), δi(A, m)∈δi,且两者对应的活动组分别为GA和GA′,若GA和GA′中除了活动A之外的其他活动对应相等,则活动δi(A, n)和活动δi(A, m)可以定义为重复活动。
对于事件日志W中的某条流程轨迹δi∈W,如果在δi中存在重名活动δi(A, n), δi(A, m)∈δi,Tp和Ts分别为活动δi(A, n)的前驱任务和后继任务,Tpp为Tp的前驱活动,Tss为Ts的后继活动;Tp′和Ts′分别为活动δi(A, m)的前驱任务和后继任务,Tpp′为Tp′的前驱活动,Tss′为Ts′的后继活动。活动δi(A, n)和活动δi(A, m)对应的活动组分别为GA和GA′,U为重复活动集合。结合上述定义2和定义3,给出重复活动判别规则如下:
1) 若GA=GA′,Tp=Tp′且Ts=Ts′,则〈δi(A, n), δi(A, m)〉∈U。
2) 若GA=GA′,Tp=Tp′,Ts≠Ts′,Ts=Tss′,且Tss=Ts′,则〈δi(A, n), δi(A, m)〉∈U。
3) 若GA=GA′,Tp≠Tp′,Ts=Ts′,Tp=Tpp′,且Tpp=Tp′,则〈δi(A, n), δi(A, m)〉∈U。
4) 若GA=GA′,Tp≠Tp′,Ts≠Ts′,Tp=Tpp′,Tpp=Tp′,Ts=Tss′,且Tss=Ts′,则〈δi(A, n), δi(A, m)〉∈U。
5) 若GA≠GA′,Tp=Tp′,Ts≠Ts′且Ts #WTs′,则〈δi(A, n), δi(A, m)〉∈U。
6) 若GA≠GA′,Tp≠Tp′,Ts=Ts′且Tp #WTp′,则〈δi(A, n), δi(A, m)〉∈U。
7) 若GA≠GA′,Tp≠Tp′,Tp #WTp′,Ts≠Ts′且Ts #WTs′,则〈δi(A, n), δi(A, m)〉∈U。
8) 若GA≠GA′,Tp≠Tp′,Tp #WTp′,Ts≠Ts′,Ts=Tss′,且Tss=Ts′,则〈δi(A, n), δi(A, m)〉∈U。
9) 若GA≠GA′,Ts≠Ts′,Ts #WTs′,Tp≠Tp′,Tp=Tpp′,且Tpp=Tp′,则〈δi(A, n), δi(A, m)〉∈U。
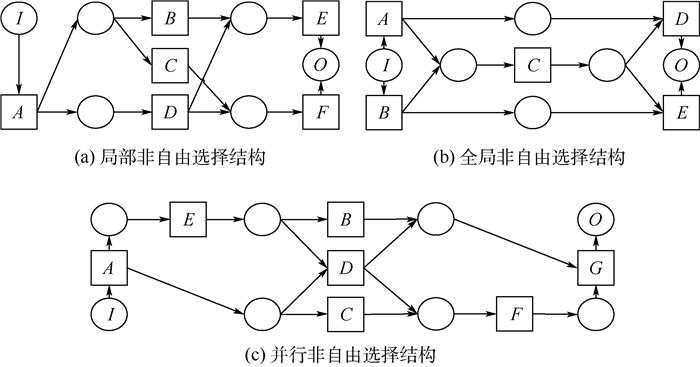
1.3 非自由选择结构识别与分析非自由选择结构是工作流中又一种常见的特殊结构,通常情况下非自由选择结构由间接因果依赖关系导致。不考虑循环结构的影响,非自由选择结构可分为如图 2所示的三大类:局部非自由选择、全局非自由选择和并行非自由选择。在图 2(a)中,对于活动E和F的选择取决于其之前对活动B和C的选择,2个选择包含在同一个并行活动中,选择的结果总能最终到达库所O,不影响后续工作流,因此称为局部非自由选择。在图 2(b)中,对于活动D和E的选择取决于对于活动A和B的选择,这2个选择结构并不在同一个结构之下,更可能中间隔着若干个活动,因此称为全局非自由选择。在图 2(c)中,若不考虑间接依赖,很容易忽略活动D和G之间的依赖关系,而此时用于并行关系的存在,如果在活动B和D之间选择了D,则会发生工作流网在F处发生死锁,此情况不同于图 2(a),称为并行非自由选择。
|
| 图 2 非自由选择结构分类 Fig. 2 Classification of non-free-choice constructs |
通过以上分析可以发现:非自由选择结构的产生总是由另一个选择结构导致的,前一个选择结构对于活动的选择往往决定了后面某个选择结构的结果。因此为了探索非自由选择结构,需要考察各个选择结构之间的关联,探索两者之间可能存在的依赖关系,为此本文首先给出几个活动关系定义。
定义4(活动关系补充) 令N=(P, T, F)为一个不包含循环结构的工作流网络,F为流关系,W为工作流事件日志,T为活动集合,其中a, b∈T:
1) a◁Wb,当且仅当a#Wb, 且∃c∈T, c→Wa, c→Wb。
2) a▷Wb,当且仅当a#Wb, 且∃c∈T, a→Wc, b→Wc。
3) a≫Wb,当且仅当a≯Wb,对于流程轨迹σ={t1, t2, …, tn},有i, j∈{1, 2, …, n}满足i < j, ti=a, tj=b,对于任意k∈{i+1, …, j-1},满足tk≠a∧tk≠b∧¬(tk◁Wa or tk▷Wa)。
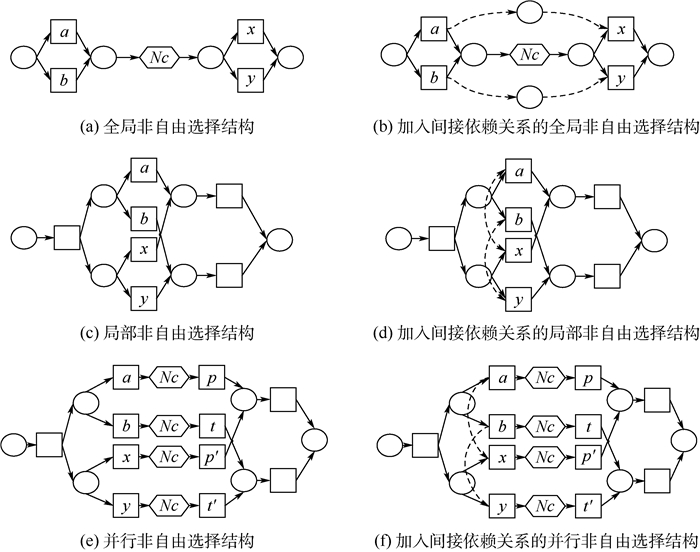
基于定义4,在不包含循环结构的情况下,给出间接依赖(↦W)判断规则:令W为完备事件日志,N=(P, T, F)=α(W)是为利用统计α算法对事件日志W进行挖掘得到的WF-net,在N中有2次选择关系a#Wb, x#Wy,且选择关系a#Wb不发生在x#Wy之后:
规则1 若a≫Wx∧b≫Wy,¬(a≫Wy∨b≫Wx), 则a↦Wx∧b↦Wy。
规则2 若¬(a≫Wx)∧(a≫Wy)∧¬(b≫Wx)∧¬(b≫Wy), a▷Wx∧b▷Wy, ¬(a▷Wy)∧¬(b▷Wx), 则a↦Wx∧b↦Wy。
规则3 若¬(a≫Wx)∧¬(a≫Wy)∧¬(b≫Wx)∧¬(b≫Wy), ∃p, t, p′, t′:a≫Wp, b≫Wt且x≫Wp′, y≫Wt′,有p▷Wp′∧t▷Wt′∧¬(p▷Wt′)∧¬(t▷Wp′), 则a↦Wx∧b↦Wy。
在上述3条规则中,规则1针对全局非自由选择结构,如图 3(a)所示,选择结构a#Wb, x#Wy在时间上存在着一定的前后顺序,即存在a≫Wx∧b≫Wy,但是在事件日志却不存在a≫Wy∨b≫Wx,说明对于x, y的选择由选择结构a#Wb决定,因此需要加入间接依赖关系a↦Wx∧b↦Wy(见图 3(b))。规则2、规则3针对局部和并行非自由选择结构,如图 3(c)、(e)所示,2个选择结构a#Wb, x#Wy在时间上不存在前后顺序,4个活动的发生次序不确定,此时考察选择关系之后的活动。若存在a▷Wx∧b▷Wy,且¬(a▷Wy)∧¬(b▷Wx),此时2个选择结构均为非自由选择,活动a和x必须并行发生,或者活动b和y并行发生,因此活动a和x、b和y相互之间存在间接依赖关系(见图 3(d))。若不存在a▷Wx∨b▷Wy,考察2个并行关系的后续活动,若有活动p, t, p′, t′:a≫Wp, b≫Wt, x≫Wp′, y≫Wt′,满足规则2中的条件:p▷Wp′∧t▷Wt′∧¬(p▷Wt′)∧¬(t▷Wp′),则同样有a↦Wx∧b↦Wy。
|
| 图 3 间接依赖判断规则 Fig. 3 Rules to judge indirect relations |
由于经典α系列算法要求事件日志中不包含噪声,同时要求事件日志完备。而在如今数据量日益增大的条件下,完备事件日志不再是一个难以达到的条件,而事件日志中的噪声却逐渐成为一个无法控制的干扰因素。为了解决噪声的干扰,有学者提出将α算法和遗传算法等进化算法结合起来,将因果矩阵作为迭代算法的基本算子,尽管该方法在消除噪声方面有较好的效果,但是却由于变异、交叉次数过多导致算法运行时间较长,算法效率较低。本文提出的统计α算法借用了概率计算的思想来消除噪声干扰提高算法准确率,同时算法的运行时间也可以维持在较低的水平。本文提出的基于统计α算法的过程挖掘具体方案如图 4所示。
|
| 图 4 基于统计α算法的过程挖掘步骤 Fig. 4 Steps of process mining based on statistical α-algorithm |
本文提出的统计α算法以活动对为单位,通过每2个活动之间的活动关系进一步分析整个工作流程中所有活动间的相关关系。首先给出活动对的定义。
定义5(活动对) 对于任意一个事件日志W,假设有流程轨迹δi={…, Ti, Ti+1, …}⊆W(i=1, 2, …),流程轨迹中的元素按照执行时间的先后顺序排列,则活动对(Activities Couple,AC)可定义如下:
活动对{
FA,第1个活动名称(Ti);
SA,第2个活动名称(Ti+1);
f,发生概率;
R,活动关系=顺序关系(默认)
}
活动对是一个具有多个属性的结构体。
定义6(同前活动对) 对于任意活动对AC(A, B),若存在一个活动对和它有相同的第1个活动A,第2个活动却不相同,则称之为AC(A, B)的同前活动对,记作#AC(A, B)。
定义7(转置活动对) 对于任意活动对AC(A, B),若存在1个活动对的第1个活动等于它的第2个活动,第2个活动等于它的第1个活动,则称之为AC(A, B)的转置活动对,记作-AC(A, B)。
活动对中的发生概率f根据该活动对在事件日志中的出现次数计算得到。对于活动对AC(Ti, Ti+1)的概率:
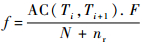
|
式中:f=AC(Ti, Ti+1).F表示该活动对的出现次数,需要遍历所有事件日志获得;N为流程轨迹数;nr=nr(Ti)+nr(Ti+1)为活动Ti和活动Ti+1重名活动的数目总和。
在计算活动对概率之后,可以在此基础上进一步判别活动对的活动关系R,具体算法步骤如图 5所示。
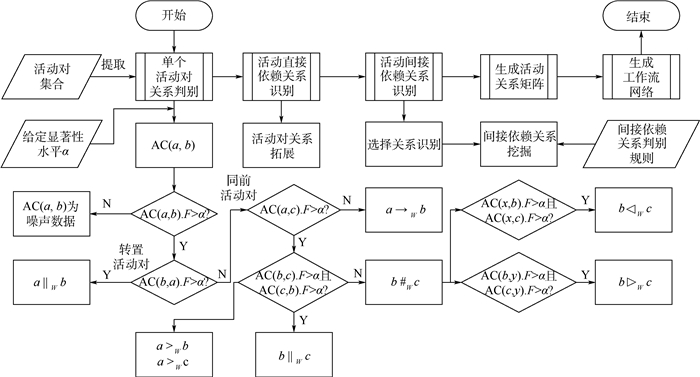
|
| 图 5 统计α算法算法步骤 Fig. 5 Steps of statistical α-algorithm |
步骤1 单个活动对关系判别。本文对于活动关系的判别建立在每个活动对的关系之上,而对于单个活动对的关系判别则是基于经典α算法中的判别规则加以改进。具体算法如下。
输入:活动对集合Array(AC);显著性水平α。
输出:更新活动关系后的活动对集合。
Foreach(AC(a, b) in Array(AC))
If(AC(a, b).F < α){
AC(a, b)为噪声数据;
Array(AC).Remove(AC(a, b))}
Else{
-AC(a, b)=AC(b, a)//转置活动对
If(AC(b, a).F>α){
a‖Wb}
Else{
#AC(a, b)=AC(a, c)//同前活动对
If(AC(a, c).F < α){
a→Wb}
Else{
a>Wb; a>Wc
If(AC(b, c).F>α & & AC(c, b).F>α){
b‖Wc}
Else{
b#Wc
If(AC(x, b).F>α & & AC(x, c).F>α){
b◁Wc}
If(AC(b, y).F>α & & AC(c, y).F>α){
b▷Wc}
}}}
}
步骤2 活动直接依赖关系识别。在得到了单个活动对关系之后,需要将活动对间的关系进行整合以得到多个活动间的关系,这里给出几个活动关系整合规则:
1) 因果关系的传递性:若有a→Wb∧b→Wc,则a→Wc。
2) 并行关系的不确定性:当a‖Wb∧b‖Wc时,若有a‖Wc,则a‖Wb‖Wc;若a#Wc,则活动(a‖Wb)#W(b‖Wc),2个选择关系共用同一个的活动b(或者重复活动b)。
3) 选择关系的不确定性:当a#Wb∧b#Wc时,若有a#Wc,则a#Wb#Wc;若a‖Wc,则活动(a#Wb)‖W(b#Wc),2个选择关系共用同一个活动b(或者重复活动b),这种情况经常出现非自由选择结构,需要进一步判别。
步骤3 活动间接依赖关系识别。在完成活动直接关系的识别后,按照上文的叙述,需要重新对选择关系活动进行考察,挖掘选择关系之间可能存在的间接依赖关系,以完善活动关系。
步骤4 生成工作流网络。将直接活动关系和间接活动关系进行整合,得到活动关系矩阵。将活动关系矩阵转化为因果矩阵,并据此生成工作流网络。
2 实验与结果验证本文采用仿真数据和真实案例分别对提出的算法进行有效性验证。由于本文提出的算法基于大量数据的基础之上,因此为了实验数据满足数量上的要求,本文以仿真数据进行实验为主,真实数据则是为了进一步对算法进行验证。仿真数据的产生原理在文献[20]的基础上加以改进,主要分为如下4个步骤:
步骤1 确定流程轨迹长度。流程轨迹长度是最影响算法运行效率的指标,而为了尽量多得出现包含各种不同的活动关系,需要轨迹达到一定的长度。为了均衡两者之间的矛盾,本文将仿真数据分为3类,分别用于对重名活动、非自由选择结构和统计α算法进行验证。
步骤2 确定事件日志规模。事件日志规模主要指流程轨迹的数目,该数目需要保证足够多的数量以确保事件日志的完备性。本文考虑5种事件日志规模:200、400、600、800和1 000条流程轨迹。
步骤3 确定噪声规模。噪声类型主要分为5种:①删除流程轨迹的某个活动;②调换流程轨迹中某2个活动;③随机替换流程轨迹中的某个活动;④随机在流程轨迹添加一个随机活动;⑤人为地生成重名活动,并随机替换已有的活动。噪声规模按照文献[20]中的表述,噪声最少有一个,最多不可超过轨迹长度的1/3,本文将噪声规模主要分为5%、10%和20% 3种规模,以检测不同情况下统计α算法对于噪声的抗干扰性。
步骤4 确定活动执行的优先度。为了得到非自由选择结构,本文将对选择结构中的活动人为设置执行优先度,优先度越高,选择结构中该活动的发生几率越高。执行优先度等级设置为如下4种:
1) Level1:无优先级,所有活动有同样的执行优先度,设为0.5。
2) Level2:低优先级,活动执行优先度在0.4~0.6之间。
3) Level3:中优先级,活动执行优先度在0.25~0.75之间。
4) Level4:高优先级,活动执行优先度在0.01~0.09之间。
2.1 仿真实验与算法性能分析本节为了多方面验证本文提出算法的有效性,将实验分为3个部分:重名活动识别算法验证实验、统计α算法验证实验和非自由选择结构识别算法验证实验。3个实验有各自的侧重点,因此对于实验数据的安排同样有所区别。
2.1.1 重名活动识别算法的验证实验由于重名活动识别是在统计α算法之前,因此在重名活动识别中暂时不考虑活动执行的优先度等级,同时为了保证重名活动不被其他噪声所干扰,噪声类型也只选择类型⑤,噪声规模按照5%、10%和20% 3种来进行实验,实验数据安排如表 3所示。该实验的评价指标有3个:识别率(是否能准确捕捉每一个重名活动)、准确率(重名活动中重复活动识别准确率)和运行效率(算法运行时间)。该实验的对比算法为Herbst和Karagiannis[6]提出的重名活动识别算法。
| 数据编号 | 流程轨迹长度 | 事件日志规模 | 噪声类型 | 噪声规模/% | 优先度等级 |
| C1 | 22 | 200 | ⑤ | 5 | Level1 |
| C2 | 22 | 200 | ⑤ | 10 | Level1 |
| C3 | 22 | 200 | ⑤ | 20 | Level1 |
| C4 | 42 | 200 | ⑤ | 5 | Level1 |
| C5 | 42 | 200 | ⑤ | 10 | Level1 |
| C6 | 42 | 200 | ⑤ | 20 | Level1 |
得到的实验结果如表 4所示。2个算法在识别率和准确率上一致,可能由于重名活动数量并不多的关系,两者在这2个方面没有任何差异。在运行时间上,本文提出的算法要优于文献[6]算法,因为本文在重名活动识别时,以活动组作为最小单位,减少了算法迭代和比较的内容,算法时间上有明显减少。
| 数据编号 | 重名活动数量 | 本文算法 | 文献[6]算法 | |||||
| 识别率/% | 准确率/% | 运行时间/ms | 识别率/% | 准确率/% | 运行时间/ms | |||
| C1 | 2对 | 100 | 100 | 10.12 | 100 | 100 | 15.12 | |
| C2 | 3对 | 100 | 100 | 10.14 | 100 | 100 | 15.36 | |
| C3 | 5对 | 100 | 100 | 10.80 | 100 | 100 | 15.66 | |
| C4 | 3对 | 100 | 100 | 21.33 | 100 | 100 | 30.54 | |
| C5 | 5对 | 100 | 100 | 21.35 | 100 | 100 | 30.87 | |
| C6 | 9对 | 100 | 100 | 21.55 | 100 | 100 | 31.03 | |
2.1.2 统计α算法的验证实验
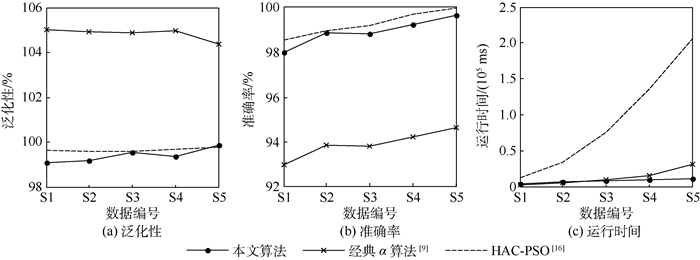
由于非自由选择结构识别是在统计α算法之后进行,因此本节暂时不考虑非自由选择结构的影响,优先度等级统一设置为Level1。由于统计α算法在重名活动识别的基础之上,因此这里噪声类型设置为①~④。主要考虑的实验因素为事件日志规模和噪声规模,即一因素三水平和另一因素五水平的实验,具体实验数据安排如表 5所示。该实验的衡量指标有3个:泛化性g(本文用数据量的2/3作为算法训练样本,用剩下的1/3数据进行拟合,泛化性g=Nd/Nm+noise,Nd为拟合数据中活动数目,Nm为算法得到模型中的活动数目,noise表示噪声规模。g的值越接近1越好,g的值大于1表示算法得到的模型中噪声过多,g的值太小表明算法中遗漏的活动太多)、准确率a(活动关系准确率)和运行时间t。该部分的对比算法为经典α算法[9]、基于变异粒子群算法的过程挖掘算法(HAC-PSO)[16]。
| 数据编号 | 流程轨迹长度 | 事件日志规模 | 噪声类型 | 噪声规模/% | 优先度等级 |
| S1~S5 | 42 | 200~1 000 | ①~④ | 5 | Level1 |
| S6~S10 | 42 | 200~1 000 | ①~④ | 10 | Level1 |
| S11~S15 | 42 | 200~1 000 | ①~④ | 20 | Level1 |
实验结果如表 6所示。为了分别比较事件日志规模和噪声规模对最终结果的影响,本文采用控制变量的方法分别考察这2个因素对3个评价指标的影响。图 6为3种算法在噪声规模同样为5%的情况下,泛化性、准确率和运行时间3个指标的对比情况。可以看到,在噪声规模相同的情况下,统计α算法和HAC-PSO的泛化性和准确率表现差不多,两者都是比较接近100%。而经典α算法在泛化性上出现了明显的超出100%的现象,说明受到了噪声的较大影响,同样经典α算法的准确率也是低于另外2个算法5%左右,正好是噪声规模的大小。而运行时间上,经典α算法和统计α算法都维持在一个较低的水平,但是HAC-PSO的运行时间却远远高于这2种算法。在噪声规模为10%和15%时有着类似的结果。
| 数据编号 | 本文算法(α=0.05) | 经典α算法[9] | HAC-PSO[16] | ||||||||
| 泛化性/% | 准确率/% | 运行时间/ms | 泛化性/% | 准确率/% | 运行时间/ms | 泛化性/% | 准确率/% | 运行时间/ms | |||
| S1 | 99.10 | 97.98 | 3 350 | 105.00 | 92.98 | 2 289 | 99.65 | 98.56 | 12 651 | ||
| S2 | 99.16 | 98.88 | 5 830 | 104.90 | 93.86 | 4 820 | 99.58 | 98.96 | 33 624 | ||
| S3 | 99.52 | 98.82 | 7316 | 104.88 | 93.82 | 9 213 | 99.58 | 99.19 | 75 623 | ||
| S4 | 99.36 | 99.25 | 9 833 | 104.95 | 94.22 | 15 632 | 99.69 | 99.69 | 136 362 | ||
| S5 | 99.88 | 99.65 | 11 369 | 104.36 | 94.65 | 30 205 | 99.78 | 99.96 | 206 534 | ||
| S6 | 101.02 | 97.23 | 4 069 | 111.02 | 86.88 | 2 441 | 99.16 | 98.03 | 12 543 | ||
| S7 | 100.56 | 97.79 | 6 151 | 110.56 | 87.25 | 4 922 | 99.23 | 98.15 | 34 123 | ||
| S8 | 100.23 | 98.56 | 8 536 | 110.23 | 88.36 | 9 365 | 99.26 | 98.45 | 76 245 | ||
| S9 | 100.20 | 98.33 | 10 623 | 110.20 | 89.12 | 15 664 | 99.32 | 98.32 | 132 013 | ||
| S10 | 99.93 | 99.21 | 12 988 | 109.93 | 89.35 | 30 157 | 99.49 | 98.98 | 214 756 | ||
| S11 | 100.98 | 97.56 | 4 419 | 114.98 | 82.36 | 2 674 | 98.52 | 97.23 | 13 025 | ||
| S12 | 100.56 | 97.88 | 6 496 | 114.56 | 83.65 | 5 155 | 98.62 | 97.53 | 34 216 | ||
| S13 | 100.23 | 98.65 | 9 441 | 114.43 | 82.98 | 9 998 | 99.15 | 98.68 | 77 487 | ||
| S14 | 100.59 | 98.98 | 14 635 | 115.09 | 84.98 | 17 897 | 99.48 | 99.32 | 140 259 | ||
| S15 | 100.20 | 99.52 | 19 062 | 114.35 | 83.66 | 32 390 | 99.60 | 99.56 | 219 874 | ||
|
| 图 6 相同噪声规模下的算法结果对比 Fig. 6 Comparison of algorithm results under the same noise scale |
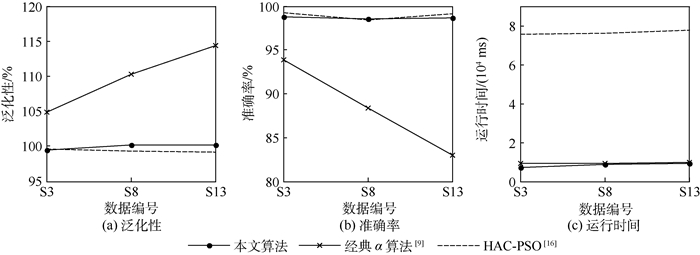
图 7给出了事件日志规模为600,噪声规模不同情况下,泛化性、准确率和运行时间3个指标的对比情况。可以看到,在噪声规模增加的情况下,统计α算法和HAC-PSO可以在泛化性和准确率上保持较好的水平,而经典α算法随着噪声规模的增加,泛化性快速增加,并且超过100%,准确率直线下降,可见经典α算法受噪声的影响十分大。而随着噪声规模增加,统计α算法运行时间也有小幅增加,而经典α算法则基本保持不变,HAC-PSO的运行时间远超过前2种算法。
|
| 图 7 相同事件日志规模下的算法结果对比 Fig. 7 Comparison of algorithm results under the same event log scale |
总结来说,统计α算法在泛化性和准确率上要明显优于经典α算法,与HAC-PSO基本持平。但是在算法运行时间上却明显优于HAC-PSO,基本与经典α算法持平,兼具了两者的优点,实现了算法的高准确率和高效率。
2.1.3 非自由选择结构识别算法的验证实验非自由选择结构在统计α算法的基础是在噪声消除的基础之上进行的,因此这里不再考虑噪声对算法的影响。为了使非自由选择结构发生几率足够大,活动执行优先度等级直接设置为Level4,具体实验数据安排如表 7所示。该算法的衡量指标有3个:识别率(是否能识别每一个非自由选择结构,本文利用识别数目来表达识别率)、准确率(识别出来的非自由选择结构是否准确)、间接依赖数目(间接依赖数目过少会导致非自由选择结构的遗漏,过多会导致模型过于冗余,工作流运行效率低。当准确率和识别率达到较高水平时,间接依赖数目越少越好)和运行时间(不包括统计α算法的时间)。该算法的对比算法为α++算法。
| 数据编号 | 流程轨迹长度 | 事件日志规模 | 优先度等级 |
| F1 | 50 | 600 | Level4 |
| F2 | 60 | 600 | Level4 |
| F3 | 70 | 600 | Level4 |
| F4 | 80 | 600 | Level4 |
| F5 | 90 | 600 | Level4 |
实验结果如表 8所示。可以看到,本文提出的算法在识别率上偶尔会低于α++算法,但准确率能达到较好的水平。从2种算法挖掘出的间接依赖数目来看,α++算法[12]挖掘出更多的间接依赖,但是2个算法的准确率表现却没有差异,可见α++算法中产生了许多冗余依赖关系。在运行时间方面,本文算法相较于α++算法略有优势。综合来看,虽然本文算法在识别率上表现不如α++算法,但是该算法能在尽量少的间接依赖数目下得到同样准确率的结果,因此本文算法同样具有足够的竞争力。
| 数据编号 | 非自由选择结构数量 | 本文算法 | α++算法[12] | |||||||
| 识别数目 | 准确率/% | 间接依赖数目 | 运行时间/ms | 识别数目 | 准确率/% | 间接依赖数目 | 运行时间/ms | |||
| F1 | 5 | 5 | 100 | 14 | 1 025 | 5 | 100 | 20 | 1 562 | |
| F2 | 6 | 6 | 100 | 18 | 1 365 | 6 | 100 | 32 | 1 845 | |
| F3 | 7 | 7 | 100 | 20 | 1 852 | 7 | 100 | 36 | 2 214 | |
| F4 | 8 | 7 | 100 | 22 | 1 955 | 8 | 100 | 42 | 2 456 | |
| F5 | 9 | 9 | 100 | 28 | 2 123 | 9 | 100 | 50 | 2 814 | |
2.2 真实数据实验与分析
本文真实数据来自于内蒙古某三甲医院临床路径系统中产生的事件日志,这里选用急性阑尾炎的事件日志作为实验数据,表 9给出该病种事件日志分析后的基本信息。真实数据实验主要选取如下衡量指标:重名活动识别率cr、重名活动准确率ca、模型泛化性mg、模型准确率ma、非自由选择结构识别率fr、非自由选择结构准确率fa和运行时间t。实验对比算法为α++算法[12]、基于遗传算法的过程挖掘(GA)[15]、文献[6]算法和HAC-PSO[16]。
| 病种名称 | 流程轨迹长度 | 事件日志规模 | 重名活动数量 | 噪声类型 | 噪声规模/% | 非自由选择结构数量 |
| 急性阑尾炎 | 53 | 200 | 10对 | ①~④ | 6 | 2 |
实验结果如表 10所示。可以看到,本文提出的算法有着如下优势:①可以处理更多的特殊结构,如重名活动、非自由选择结构等;②在识别率和准确率上与现有算法相比并没有什么差距;③在保证准确率的情况下同样保证了运行效率,运行时间远优于GA和HAC-PSO。
3 结论
本文提出了一种基于统计α算法的过程挖掘算法,从工作流事件日志中挖掘有用的信息,实现了工作流模型的建立。
1) 在经典α系列算法的基础上增加了重名活动识别与处理,并将该过程作为α算法的预处理活动,以消除重名活动对活动依赖关系识别的干扰。
2) 运用统计学的思想结合经典α算法的规则,形成统计α算法,消除了事件日志中噪声的干扰问题,同时保证了算法较高的运行效率。
3) 提出了一种新的非自由选择结构识别算法,在保证了较高的识别率和准确率的情况下,尽量少得添加间接依赖关系,消除了冗余的活动依赖关系。
通过仿真实验和真实数据实验,验证了本文算法的有效性和优越性。后续工作主要是非自由选择结构识别率的进一步提高以及隐藏活动的挖掘,进一步完善该算法。
| [1] |
闻立杰. 基于工作流网的过程挖掘算法研究[D]. 北京: 清华大学, 2007.
WEN L J. Studies on algorithms for process mining based on WF-net[D]. Beijing: Tsinghua University, 2007(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10003-2008088148.htm |
| [2] |
曾庆田. 过程挖掘的研究现状与问题综述[J].
系统仿真学报, 2007, 19 (s1): 275–280.
ZENG Q T. A survey of research issues and approaches on process mining[J]. Journal of System Simulation, 2007, 19 (s1): 275–280. (in Chinese) |
| [3] | COOK J E, WOLF A L. Automating process discovery through event-data analysis[C]//Proceedings of the 17th International Conference on Software Engineering. New York: ACM, 1995: 73-82. |
| [4] | AGRAWAL R, GUNOPULOS D, LEYMANN F. Mining process models from workflow logs[C]//International Conference on Extending Database Technology. Berlin: Springer, 1998: 467-483. |
| [5] | PINTER S S, GOLANI M. Discovering workflow models from activities' lifespans[J]. Computers in Industry, 2004, 53 (3): 283–296. DOI:10.1016/j.compind.2003.10.004 |
| [6] | HERBST J, KARAGIANNIS D. Workflow mining with InWoLvE[J]. Computers in Industry, 2004, 53 (3): 245–264. DOI:10.1016/j.compind.2003.10.002 |
| [7] | SCHIMM G. Mining exact models of concurrent workflows[J]. Computers in Industry, 2004, 53 (3): 265–281. DOI:10.1016/j.compind.2003.10.003 |
| [8] | GRECO G, GUZZO A, PONTIERI L, et al. Discovering expre-ssive process models by clustering log traces[J]. IEEE Transactions on Knowledge and Data Engineering, 2006, 18 (8): 1010–1027. DOI:10.1109/TKDE.2006.123 |
| [9] | VAN DER AALST W M P, WEIJTERS T, MARUSTER L. Workflow mining:Discovering process models from event logs[J]. IEEE Transactions on Knowledge and Data Engineering, 2004, 16 (9): 1128–1142. DOI:10.1109/TKDE.2004.47 |
| [10] | DEMEDEIROS A K A, DONGEN B F, VAN DER AALST W M P, et al. Process mining for ubiquitous mobile systems: An overview and a concrete algorithm[C]//International Workshop on Ubiquitous Mobile Information and Collaboration Systems. Berlin: Springer, 2004: 151-165. |
| [11] | WEN L, WANG J, VAN DER AALST W M P, et al. A novel approach for process mining based on event types[J]. Journal of Intelligent Information Systems, 2009, 32 (2): 163–190. DOI:10.1007/s10844-007-0052-1 |
| [12] | WEN L, VAN DER AALST W M P, WANG J, et al. Mining process models with non-free-choice constructs[J]. Data Mi-ning and Knowledge Discovery, 2007, 15 (2): 145–180. DOI:10.1007/s10618-007-0065-y |
| [13] | WEN L, WANG J, SUN J. Mining invisible tasks from event logs[M]//LI Q, FENG L, PEI J, et al. Advances in data and web management. Berlin: Springer, 2007: 358-365. |
| [14] | LI J, LIU D, YANG B. Process mining: Extending α-algorithm to mine duplicate tasks in process logs[M]//SUI Q, YANG D, WANG T. Advances in web and network technologies, and information management. Berlin: Springer, 2007: 396-407. |
| [15] | DEMEDEIROS A K A, WEIJTERS A J M M, VAN DER AALST W M P. Using genetic algorithms to mine process models: Representation, operators and results[R]. Eindhoven: Eindhoven University of Technology, 2005. |
| [16] |
李莉, 李洪奇, 谢绍龙. 基于变异粒子群算法的过程挖掘[J].
计算机集成制造系统, 2012, 18 (3): 634–638.
LI L, LI H Q, XIE S L. Process mining based on mutation-particle swarm optimization[J]. Computer Integrated Manufacturing System, 2012, 18 (3): 634–638. (in Chinese) |
| [17] |
宋炜, 刘强. 基于模拟退火算法的过程挖掘研究[J].
电子学报, 2009, 37 (s1): 135–139.
SONG W, LIU Q. Business process mining based on simulated annealing[J]. Acta Electronica Sinica, 2009, 37 (s1): 135–139. (in Chinese) |
| [18] |
黄黎, 谭文安, 许小媛. 一种基于时序行为的流过程协同重构算法[J].
计算机工程与科学, 2017, 39 (5): 897–903.
HUANG L, TAN W A, XU X Y. Cooperative streaming process reengineering based on sequential behaviors[J]. Computer Engineering & Science, 2017, 39 (5): 897–903. (in Chinese) |
| [19] | DEMEDEIROS A K A, DONGEN B F, VAN DER AALST W M P, et al. Process mining: Extending the α-algorithm to mine short loops[R]. Eindhoven: Eindhoven University of Technology, 2004. |
| [20] | VAN DER AALST W M P, DONGEN B F, HERBST J, et al. Workflow mining:A survey of issues and approaches[J]. Data & Knowledge Engineering, 2003, 47 (2): 237–267. |



