可视化技术是诸多数据密集型领域的一种重要研究手段。近年来,等值面算法在三维数据场可视化方面得到了广泛地应用和发展。Lorensen和Cline[1]于1987年提出的MC(Marching Cubes)算法作为等值面提取最为流行的经典算法,其原理简单易于实现,自从被提出以来,得到了业界广泛地使用,包括生物化学[2]、生物医学[3-4]、数字雕刻[5]、环境科学[6]、自然现象呈现[7]以及可视化算法分析[8]等。但经典的MC算法也有一些不足之处,如存在拓扑结构的二义性[9]、对高分辨率数据集计算效率低[10-11]及产生的结果集规模庞大[12]等问题。
近年来,针对MC算法的改进层出不穷。本文着眼于MC算法产生结果集规模庞大这一问题,介绍了现阶段主要的改进方法,并且介绍了一种基于简化构型的SMC(Simplified Marching Cubes)算法。根据简化构型的特点,针对SMC算法的两方面问题提出了一种改进的OSMC(Octree based Simplified Marching Cubes)算法,依次介绍了算法的八叉树构建、八叉树收缩和三角片提取3步。在实验与讨论的部分通过对MC算法、SMC算法、OSMC算法三者实验数据的对比,从表面形态、三角片削减率和分辨率增长3个方面说明OSMC算法的优势并探讨了其原因。
1 相关研究成果近年来,越来越多的高分辨率数据集被投入使用。MC算法产生庞大的三角片数量给后期的渲染造成了很大压力,同时也加重了存储负担。不少研究人员针对这一问题,提出了诸多解决方案。总体上看,这一问题的解决方案大致分为两类。
第一类是对生成的网格数据采取网格削减算法。如Schroeder等[13]于1992年提出的渐进网格算法与Garland和Heckbert[14]于1997年提出的二次误差边折叠算法。这类算法的输入是多边形网格数据,是在规模较大的网格数据已经被生成之后再采用一定方式来删除顶点面片等几何元素,是一种事后补救方法。这类方法通常处理费时,并且建立辅助结构会占据大量存储空间,并不是针对本文提出问题的理想解决方案,因此不作过多探讨。
第二类是采取避免生成较多三角片的表面重建方法。相比于事后削减的方法,这一类方法利用了图像数据的特点,效率更高。Montani等[15]提出了一种离散化的DiscMC算法,这种算法通过将插值点选择在体元边的中点,提高了相邻体元间的三角形共面的概率。然后再将共面的三角形合并成平面多边形,以此来减少三角片。其在2000年又进一步改进了此方法,提高了DiscMC算法对等值面的逼近程度[16]。Shu等[17]于1995年提出一种自适应的MC算法,这种算法在执行过程中不断地重复对体数据划分子体,直到在子体内寻找到相对于等值面的误差在一定范围内逼近表面。这样就能够实现使用较少的三角片来表示等值面。Shekhar等[18]于1996年针对Shu等[17]的方法削减程度不足的问题又提出了一种使用了八叉树结构削减三角片的算法,其中使用了表面追踪技术,避免了处理空体元。在体元合并中评估误差,保证误差在给定阈值之内,最后修补缝隙、生成三角片。八叉树是在表面重建算法中重要的一种数据结构,能够用于代表隐函数[19-20]和自适应提取等值面[21-22]。
上述几种方法均是利用了等值面局部形态特点来进行三角片削减,Cui和Liu[23]于2008年与Vignoles等[24]于2011年各自提出了一种不同于上述几种方法简化思路的算法。2种算法实现细节有所不同,但其核心思想一致,都使用了一种简化后的体元构型,为方便起见将文献[13-14]提出的方法统一称作SMC算法。使用简化后的构型,减少了部分体元中提取三角片的数量,从而削减了三角片数,同时提高了计算效率,并且不会存在二义性问题。SMC算法在对低分辨率数据使用时产生的表面与MC算法差别显著,逼近程度低于MC算法,故未能有广泛应用。但随着近年来高分辨率数据得到越来越多的应用,简化构型的优势便体现出来。在高分辨率数据上,SMC算法和MC算法产生的表面的形态差别变得几乎可以忽略不计,故其为MC算法的合理替代方案,并且广泛应用于实践之中。但由于简化构型仅是在体元内部的简化,无法考虑等值面局部形态特征,因而SMC算法存在较大的改进空间。主要体现在如下2个方面:
1) 对于部分数据集,SMC算法削减率较低。原因在于并非所有的简化构型都比MC算法构型具有更少的三角片数,若数据场内有相当比例活动体元正属于这类构型,则SMC算法无法削减这些体元的三角片数。
2) 无法很好地应对分辨率的提高。原因在于体数据分辨率提高后体元数量会大大增加,仅是体元内部的简化无法应对体元总数的增加带来的影响。
本文提出的OSMC算法,既利用了简化构型的优点,同时也考虑了等值面局部形态特征。OSMC算法与SMC算法产生的表面形状完全相同,但三角片数量更少。并且对于具有较多平坦区域的数据集,OSMC算法能有效地弥补SMC算法削减程度不足的问题,同时还能够较好地应对数据集分辨率的增长。
2 OSMC算法 2.1 简化构型SMC算法中的简化构型是基于MC算法构型做出的简化模型。
假设等值面sc={(x, y, z):F(x, y, z)=c},其中sc为等值面集合,(x, y, z)为点的坐标,F为映射函数,c为等值面的值。若等值面穿过了2个相邻体素所构成的边,体素位置坐标分别为Vl(xl, yl, zl)和Vh(xh, yh, zh),相应体素值分别为Il < c和Ih≥c, 在MC算法中插值点的位置应采用式(1)计算:
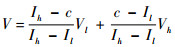
|
(1) |
若将插值点的位置总取为Vh,即
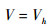
|
(2) |
则会使一部分三角形的顶点位置重合,如此操作,便会导致生成的三角形产生退化。对MC算法的所有基本构型采取式(2)的操作即形成简化构型,即SMC算法构型。图 1和图 2中对比显示了15种MC算法构型与其对应的SMC算法构型。可以看出在简化构型中一部分三角形在顶点移动后退化消失,导致多种构型产生的三角形减少甚至消失,也直接导致最终产生的等值面的三角形的数量会相应减少。

|
| 图 1 MC算法构型 Fig. 1 MC algorithm configuration |

|
| 图 2 SMC算法构型 Fig. 2 SMC algorithm configuration |
将基于简化构型提取出三角片所构成的表面成为SMC表面。SMC表面相比于MC表面有如下3个特点:①SMC表面的所有三角片的顶点都是体素点;②组成SMC表面的三角片只有3种可能形状和有限种法线方向;③与MC表面相比,SMC表面位置略向高于等值面的方向偏移,形成一定的系统误差,此误差随着数据集分辨率的提高而减少。
OSMC算法是基于八叉树的特性来实现局部共面三角片的合并。OSMC算法一共分为3步:八叉树构建、八叉树收缩以及三角片提取,流程如图 3所示。2.2~2.4节分别对这3个步骤进行详细说明。
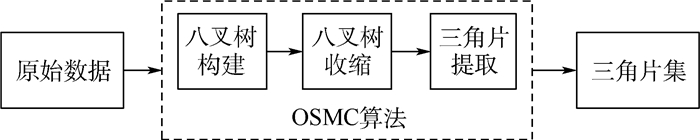
|
| 图 3 OSMC算法流程 Fig. 3 Flowchart of OSMC algorithm |
无论是MC算法还是SMC算法,插值和提取三角片等计算都是针对活动体元。活动体元的8个顶点体素根据其体素值大小共有256种有限的情况,每一种情况即是一个体元状态(cube configuration)。若令体元C的8个端点体素值依次为I0,I1,…,I7,则体元状态的计算方法如下:

|
(3) |
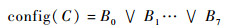
|
(4) |
式中:Bi为体元状态; isovalue为等值面的值; Ii为体素值; ∨符号代表位运算或。
config(C)不为0或255的体元即为活动体元。标准MC算法是通过全维度扫描所有体元,逐个求取体元状态config(C)来寻找活动体元,而往往活动体元只占全部体元总数的很小一部分,这导致算法近80%的计算时间花费在访问非活动体元上。为了提高时间效率,不少算法采用其他方式去寻找活动体元,例如文献[21]采用八叉树组织图像数据,文献[18]的表面追踪。但这些方法都有一定的局限性,往往只适用于某些有特殊性的场合。例如文献[21]的方法主要针对一次预处理、多次重建的应用场合;而文献[18]的方法必须人工选择种子体元作为输入参数。一般场合下,数据场体素值分布情况应当是完全未知的,任何一个体元都必须至少被遍历到一次才能获取其体元状态。所以为了不失一般性,OSMC算法采用遍历所有体元的方式寻找活动体元。实际上,任何方法只要能利用实际应用场合的特点找到活动体元,都可以替代全部遍历的方式。采用何种方式取决于对算法时间效率和通用性的权衡。
2.2.2 为活动体元创建节点对每一个活动体元,需要为其创建对应的节点。OSMC算法采用指针式八叉树,其任意节点N均包含父节点p和8个子节点c0,c1,…,c7的指针以及一个数据域data,为了让每个节点总能指代自然数表示的立方体范围,八叉树对空间按2的幂划分。因此OSMC算法的八叉树T所指代的空间尺寸应为大于体数据最长维的最小的2的幂。设数据场为:DF={(x, y, z), x∈[0, w], y∈[0, h], z∈[0, d]},则T的深度计算式为
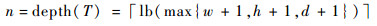
|
(5) |
则T实际所能表示的最大空间包围盒R(T)在3个坐标轴上范围均为[0, 2n-1]。对T中任意非叶节点,其子节点对应着将父节点空间范围各个维度等分之后的子立方体空间范围。依据这样的划分方式,利用节点之间的父子关系即可以求出N所指代的空间包围盒R(N)。对于叶子节点,R(N)的3个维度的上下界均相等,即有
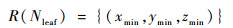
|
(6) |
因而叶节点Nleaf可以与一个三维坐标对应。树的初始状态只包含一个根节点。每当找到一个活动体元C(x, y, z),为其建立叶节点需要确定其在各层的层内索引ki, 0≤i≤n-1。层内索引反映了从根节点建立叶节点的路径,利用八叉树空间划分与体元坐标二进制位的对应关系,能够求得层内索引。层内索引的求法如下:
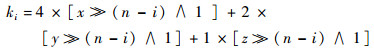
|
(7) |
式中:符号“∧”代表位运算与;符号“»”代表位运算逻辑右移。
本步骤执行到对所有活动体元都有对应的节点为止。经过此步形成的八叉树有如下2个特点:①八叉树的所有叶节点与活动体元坐标一一对应。②所有的叶子节点均处在同一深度。
2.3 八叉树收缩八叉树收缩是一个自底向上迭代的过程。从八叉树depth(T)-1层节点开始,尝试将子节点的信息归并到父节点,相应节点内的体元合并成为更大的“超体元”(super cell),若成功则删除子节点。这一步骤的关键是判断节点能够收缩的条件。为此首先提出“共面构型”的概念,共面构型是指满足如下任意条件之一的体元构型:
1) 该体元为空体元。
2) 该体元构型内含有三角片且三角片均在同一平面。
3) 该体元构型内不含三角片,但其互补构型内含有三角片且三角片均在同一平面。
图 1和图 2中符合条件2)的构型均为第8、9号构型;符合条件3)的为第1、2号构型;其余10种构型为非共面构型。
OSMC算法收缩节点的基本原理是:对八叉树上的一个节点N,若其子节点c0,c1,…,c7中分别提取的三角片构成集合Tc,Tc中所有三角片均共面且有相同的法向量,则此三角片集合组成的形状等价于对N提取三角片集合TN所组成的形状,且一定有Card(TN)≤Card(Tc)成立。这样使用更少的三角片组成相同平面区域就能实现三角片数量的削减。显然只有属于共面构型的c0, c1, …, c7才能满足此条件,共面构型为有限种可枚举的情况,因此上述原理不难被证明。这样节点收缩的问题便转化为子节点中提取的三角片是否共面的问题。
在空间解析几何中,平面方程一般形式为Ax+By+C′z=D,三元组(A, B, C′)是决定法线方向的参数。而D值反映了其空间位置。2个三角片若共面,则其一定具有相同的法线方向和D值。通过2.1节对构型的分析可以得知,共面构型内三角片所在的平面方程形式只可能是如表 1的13种可能。
| 构型 | 三角片类型 | 平面方程类型 |
 |
正三角形 | x+y+z=c |
| x+y-z=c | ||
| x-y-z=c | ||
| x-y+z=c | ||
 |
一般直角三角形 | x+y=c |
| x-y=c | ||
| y+z=c | ||
| y-z=c | ||
| x+z=c | ||
| x-z=c | ||
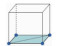 |
等腰直角三角形 | x=c |
| y=c | ||
| z=c |
对于位置在数据场原点的共面构型的体元C0(0, 0, 0),三角片的方程A0x+B0y+C0z=D0是由体元状态config(C0)唯一决定的。因为方程形式只有有限种,所以可以建立两者的函数映射关系:方程:config(C)→(Ac, Bc, Cc, Dc)和法向量:config(C)→(Ac, Bc, Cc)。一般地,对于共面构型体元C(xc, yc, zc),其三角片所在平面方程相对C0存在一个平移关系,方程解析式为
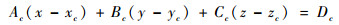
|
(8) |
令D=Acxc+Bcyc+Cczc+Dc,则四元组(Ac, Bc, Cc, Dc)就能够反映体元C中三角片相对于整个数据场F的平面方程。又由于具有映射关系:方程:config(C)→(Ac, Bc, Cc),所以二元组〈config(C), D〉即能充分反映体元的三角片位置信息。八叉树的所有叶节点,由于和活动体元一一对应,所以其形式为
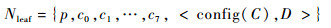
|
(9) |
综上所述,八叉树T上任意一个节点N能收缩,其子节点c0, c1, …, c7必须满足如下条件:
1) 若N为叶节点,非空ci为共面构型。
2) 若N不为叶节点,非空ci为收缩成功的节点。
3) 对于任意非空的ci, cj, i≠j,有
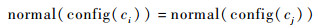
|
(10) |
4) 对于任意非空的ci, cj, i≠j,有Di=Dj。
收缩操作首先对倒数第2层节点执行,每成功执行一次收缩操作,当前节点记录下的从子节点继承来的D值,并利用config(c0), config(c1), …, config(c7)计算config(N),同时删掉子节点。当某个节点收缩操作失败后,其父节点也不再进行收缩,直到所有的节点都不能再收缩后结束。可以采用FIFO的容器实现这样自底向上的迭代操作。
2.4 三角片提取八叉树T收缩完成后,叶节点不再都处于同一深度,一部分节点对应单体元,即处在depth(T)层的节点。而在depth(T)层之上的叶节点对应的是“超体元”。超体元即是收缩了下层节点后形成的广义体元。对单体元和超体元,提取三角片的方法有所不同。OSMC算法本步骤采用程序遍历八叉树叶节点,依次判断节点属于单个体元还是超体元。对其分别用不同的方法求取三角片集合TN,直到所有叶节点都被访问为止。
2.4.1 对单体元的三角片提取节点N对应单个体元即说明N的父节点收缩失败。由2.1节对SMC算法的分析可知其生成三角片的顶点都位于体素点上。对N的三角片提取可直接使用SMC算法的查找表,根据体元状态索引即可获取三角片体元顶点的组成方式,而三角片顶点的位置可由节点空间范围R(N)确定,这样就得到三角形集合TN,即

|
(11) |
超体元节点N中虽然三角片的顶点依然是体素点,但不一定是超体元的8个顶点。如图 4所示。
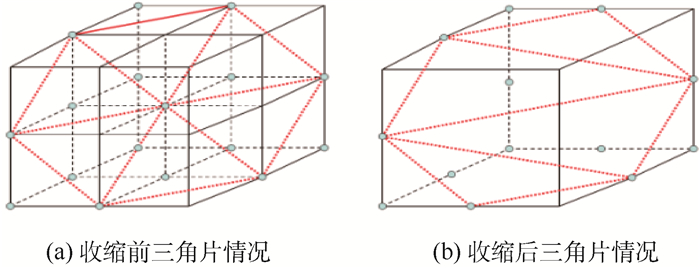
|
| 图 4 超体元提取三角片 Fig. 4 Triangle extraction for super cell |
从该超体元对应的八叉树节点数据域中可以获得三角片空间位置信息〈config(N), DN〉,则三角片所在的平面方程参数〈AN, BN, CN, DN〉便可以求取。因为三角片的顶点实在超体元边上,需要使用标准MC算法的查找表来确定被穿过的体元边集合EN和三角片的集合TN的信息,即
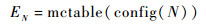
|
(12) |

|
(13) |
之后再采用空间解析几何的方法,通过EN中每一条体元边ei的直线方程与平面方程ANx+BNy+CNz=DN联立求解三角片顶点位置,公式如下:
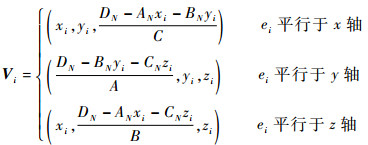
|
(14) |
本节将通过实验证明OSMC算法的优越性。本文算法采用C++实现,实验硬件平台为Intel(R) Xeon(R) X5650 6核CPU,内存32 GB,操作系统为64位Windows 7。所有实验均在相同的软硬件环境下进行。
3.1 公开数据集实验OSMC算法被应用于公开数据集上进行测试。图 5为MC算法、SMC算法和OSMC算法分别对尺寸为256像素×256像素×128像素的Engine数据集重建表面后形成的模型预览图。可以看出,表面的整体形态上三者区别并不明显,而将图像的局部进行放大后,如图 6所示,可以看出MC表面与SMC表面细节上略有差别,而OSMC表面与SMC表面是完全一致的。也就是OSMC表面对等值面的逼近误差与SMC算法是相同的。该误差产生的原因是因为使用了SMC算法简化构型,在分辨率不算高的Engine数据上能够在细节上体现出与MC表面的区别。

|
| 图 5 3种算法对Engine数据产生的表面全视图 Fig. 5 Isosurface full view of three algorithms on Engine data set |

|
| 图 6 细节表面图 Fig. 6 Detailed surface |
图 7为MC算法、SMC算法和OSMC算法在Engine数据集局部位置三角片集合的构成情况。从对比图中可以看出:SMC算法在形状不规则的区域的三角片密度低于MC算法,但在平坦区域的三角片密度和MC算法一样;OSMC算法在平坦区域合并了大部分共面三角片,使角片密度降低,而在形状不规则区域三角片密度和SMC算法相同。综合起来看,OSMC算法相比于MC算法,既在形状不规则区域具有较低三角片密度,也在平坦区域有更少三角片密度,不过细节部分略有损失。而与SMC算法比较而言,细节部分保存完好,更显优势。
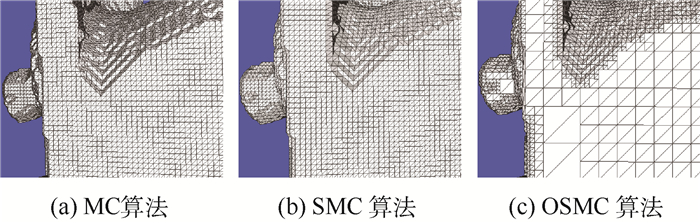
|
| 图 7 表面三角片构成情况 Fig. 7 Composition of surface triangle |
表 2列举了9组数据集分别在MC算法、SMC算法、OSMC算法下重建表面生成的三角片总数,以及OSMC算法对MC、SMC算法的削减率对比。可以看出,对于不同的数据集,算法的削减程度有所差别。SMC算法在对总体形态不规则程度较高的数据集上相比MC算法有较好的削减率,例如Skull、Lobster数据集。OSMC算法的削减程度则相对较低,但也依然超过了SMC算法。在具有较大比例规则表面的数据集上,OSMC算法表现非常出色,在SMC算法的基础上依然有显著的削减,例如Engine、Fan、Table和Teapot数据集,并且可以很好地保留SMC算法的所有细节。
| 数据集 | 三角片数 | 削减率/% | ||||
| MC算法 | SMC算法 | OSMC算法 | OSMC较SMC算法 | OSMC较MC算法 | ||
| Engine | 622764 | 432370 | 259479 | -40.0 | -58.3 | |
| Fan | 508928 | 370256 | 179179 | -51.6 | -64.8 | |
| Table | 475548 | 439692 | 90073 | -79.5 | -81.1 | |
| Teapot | 745152 | 508798 | 304008 | -40.2 | -59.2 | |
| Bonsai | 644340 | 435994 | 372986 | -14.5 | -42.1 | |
| Skull | 1842404 | 1114208 | 1033229 | -7.3 | -43.9 | |
| Backpack | 3985836 | 2876044 | 2066527 | -28.1 | -48.2 | |
| Phantom | 7457316 | 5296868 | 3557633 | -32.8 | -52.3 | |
| Lobster | 1245556 | 721914 | 632738 | -12.4 | -49.2 | |
3.2 人类肺部结节CT数据实验
将OSMC算法应用于真实的人类肺部结节CT数据,数据的最大分辨率为55像素×55像素×120像素。
如图 8所示,人类肺部结节形状不规则,细节部分很多。细节部分对于诊断病情却至关重要,而OSMC算法在这方面表现得很好,对细节刻画很仔细,能够生成和SMC算法完全一样的网格。

|
| 图 8 3种算法人体肺部结节数据产生的网格和表面全视图 Fig. 8 Mesh and isosurface full view of three algorithms on human pulmonary nodule data set |
表 3列出了针对不同病人的完全不同的肺部结节CT数据,以及MC、SMC和OSMC算法生成的三角片的个数。可以看出,对于不同的肺部结节数据,尽管OSMC与SMC算法生成的网格形状是完全一样的,但是OSMC算法生成的三角片更少,最多能少20%左右。
| 数据集 | 三角片数 | 削减率/% | ||||
| MC算法 | SMC算法 | OSMC算法 | OSMC较SMC算法 | OSMC较MC算法 | ||
| 肺部结节1 | 11652 | 7524 | 6498 | -13.64 | -44.23 | |
| 肺部结节2 | 1992 | 1366 | 1160 | -15.08 | -41.77 | |
| 肺部结节3 | 3704 | 2564 | 2012 | -21.53 | -45.68 | |
| 肺部结节4 | 17360 | 10744 | 9198 | -14.39 | -47.02 | |
| 肺部结节5 | 16212 | 10098 | 8623 | -14.61 | -46.81 | |
| 肺部结节6 | 25052 | 16258 | 13583 | -16.45 | -45.78 | |
| 肺部结节7 | 44344 | 25638 | 24213 | -5.56 | -45.40 | |
| 肺部结节8 | 19972 | 11714 | 11350 | -3.11 | -43.17 | |
| 总计 | -10.80 | -45.37 | ||||
图 9展示了图 8中肺部结节上不平滑的一个小触角处生成的网格形状。可以看出,OSMC和SMC算法生成的形状完全一样,但是在SMC算法生成的形状一致的几个相邻三角片处,OSMC算法能够合并简化网格,使生成的三角片数量减少。
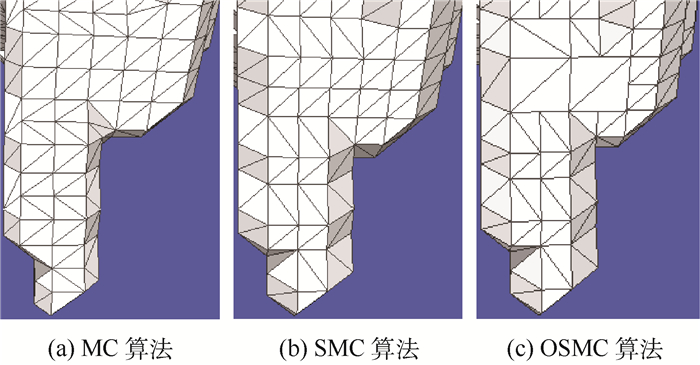
|
| 图 9 3种算法人体肺部结节CT数据结果表面细节三角片构成情况 Fig. 9 Triangles mesh part view of three algorithms on CT human pulmonary nodule data set |
综上,OSMC算法在面对等值面较粗糙细节较多的数据时,能够完整地保留等值面的所有细节部分,不会改变生成的等值面的形状,并且在相对平滑的部分完成合并简化,有效地减少了生成的三角片的数量。
3.3 地质数据实验笔者还在真实的地质断面分离数据上测试了OSMC算法,其中最大数据的分辨率为1 000像素×1 000像素×500像素。图 10展示了MC、SMC和OSMC算法对同一个地质断面数据生成的等值面,由于分辨率很高,可以看出,OSMC算法生成的结果与MC算法很相近,与SMC算法完全一样。

|
| 图 10 3种算法对地质体数据产生的表面全视图 Fig. 10 Isosurface full view of three algorithms on geological data set |
表 4列出了在7个不同的地质断面分离数据上使用这3个算法生成的等值面的三角片个数以及相对于标准MC、SMC算法,OSMC算法生成三角片的数量的减少比率。显然,OSMC算法在此类数据上表现非常好,相对于MC和SMC算法,OSMC算法生成的三角片数量都远少于前者,减少比率最高可以达到80%,平均都在50%以上。
| 数据集 | 三角片数 | 削减率/% | ||||
| MC算法 | SMC算法 | OSMC算法 | OSMC较SMC算法 | OSMC较MC算法 | ||
| 地质体1 | 4216160 | 3068372 | 1569472 | -48.85 | -62.77 | |
| 地质体2 | 3570748 | 3044366 | 1123834 | -63.09 | -68.53 | |
| 地质体3 | 3998268 | 3018910 | 1068565 | -64.60 | -73.27 | |
| 地质体4 | 7187412 | 5691550 | 1902811 | -66.57 | -73.53 | |
| 地质体5 | 2374620 | 1788710 | 764733 | -57.28 | -67.80 | |
| 地质体6 | 3348048 | 2714290 | 639024 | -76.46 | -80.91 | |
| 地质体7 | 33408 | 26202 | 14492 | -44.70 | -56.62 | |
| 总计 | -63.40 | -71.35 | ||||
图 11展示了OSMC算法之所以表现的如此优异的原因。因为地质断面数据在其外部边缘处非常平滑,并且数据量巨大,传统的MC和SMC算法对每一个小的区域都要生成一个三角片。但其实这些三角片都是共面并且完全一样的,而OSMC算法可以将这些很多共面的小的三角片合并成一个大的三角片。这样既没有改变等值面的形状,并且大大减少了处于边缘的平滑的部分三角片数量。MC算法需要生成几万乃至几十万个三角片,但是OSMC算法只需要几百或者几千个就可以了。
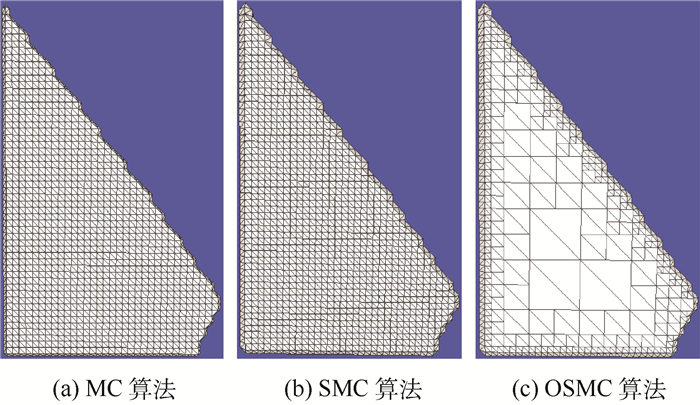
|
| 图 11 地质体数据集上平滑部分的三角片构成情况 Fig. 11 Triangle mesh of flat area of geological data set |
图 12展示了在地质断面部分MC、SMC和OSMC算法生成的等值面的结果。可以看出,OSMC算法生成的等值面与SMC算法完全一样,没有丢失任何原本的断面信息,并且在局部共面的地方进行了合并简化,使生成的三角片相应减少。

|
| 图 12 地质体数据集上非平滑部分的三角片构成情况 Fig. 12 Triangle mesh of uneven area of geological data set |
综上可以看出,本文OSMC算法在这种局部相对平滑的数据表现非常好。一方面,其生成的等值面的三角片数量较MC和SMC算法有很大比例的减少; 另一方面,在需要精细刻画的局部,OSMC算法没有因为合并而改变原本等值面的形状,也就没有丢失任何信息。
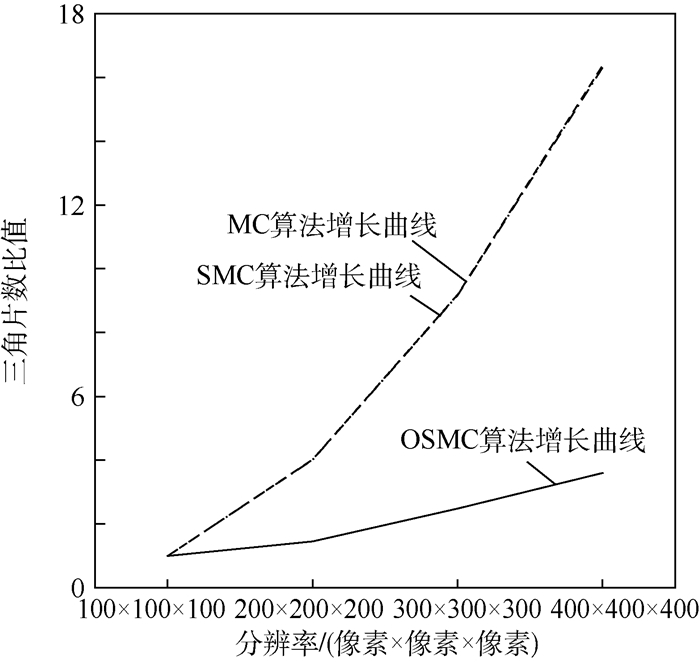
3.4 分辨率增长下的实验表 5和表 6分别列举了Table数据集和四面体数据集中MC算法、SMC算法和OSMC算法在数据集分辨率增加为原来的1、2、3、4倍时,三角片数量的增长情况。可以看出,当数据集分辨率变为原来的n倍后,MC算法和SMC算法的三角片数量变为接近原来的n2倍。而OSMC算法则以低于n2的速度增长。图 13和图 14中通过曲线来反映增长趋势,由于MC算法和SMC算法增长倍率相差很小,故曲线几乎合并为一条,而OSMC算法的倍率曲线则明显较低。其原因在于OSMC算法在八叉树收缩的步骤中合并了局部平坦区域中的体元,在分辨率提升的情况下,虽然这些区域的体元密度增加,但仍然会合并成相同的超体元。
| 分辨率/(像素×像素×像素) | MC算法 | SMC算法 | OSMC算法 | |||||
| 三角片数 | 与1倍分辨率比值 | 三角片数 | 与1倍分辨率比值 | 三角片数 | 与1倍分辨率比值 | |||
| 197×70×101 | 111652 | 1.00 | 103056 | 1.00 | 7028 | 1.00 | ||
| 394×140×203 | 475548 | 4.26 | 439692 | 4.27 | 10196 | 3.49 | ||
| 591×210×304 | 1045120 | 9.36 | 955408 | 9.27 | 17464 | 5.84 | ||
| 788×280×406 | 1920724 | 17.20 | 1786762 | 17.34 | 25334 | 10.33 | ||
| 分辨率/(像素×像素×像素) | MC算法 | SMC算法 | OSMC算法 | |||||
| 三角片数 | 与1倍分辨率比值 | 三角片数 | 与1倍分辨率比值 | 三角片数 | 与1倍分辨率比值 | |||
| 100×100×100 | 55868 | 1.00 | 37438 | 1.00 | 7028 | 1.00 | ||
| 200×200×200 | 224648 | 4.02 | 150152 | 4.01 | 10196 | 1.45 | ||
| 300×300×300 | 513332 | 9.19 | 343384 | 9.17 | 17464 | 2.48 | ||
| 400×400×400 | 914936 | 16.38 | 610738 | 16.31 | 25334 | 3.60 | ||

|
| 图 13 Table数据增长曲线 Fig. 13 Table data growth curves |
|
| 图 14 四面体数据增长曲线 Fig. 14 Tetrahedral data growth curves |
从图 13和图 14中还可以看出,对于具有更大比例平坦表面的数据集,如四面体数据集,其增长曲线相比Table数据集更低。根据OSMC算法的特点不难推断,若数据集不规则表面比例增大,则OSMC算法增长曲线会向MC和SMC算法的增长曲线靠近。这也说明OSMC算法削减程度与数据集表面的形态特征有关。
4 结论本文在简化构型等值面的基础上提出了普适通用的OSMC算法,使用八叉树结构合并了等值面局部的部分共面三角片。
1) OSMC算法相对于SMC算法能进一步减少三角片的数量,同时保证生成表面的形态与其完全一致。
2) OSMC算法的削减效果在具有较多平坦区域的数据集上表现显著,能有效弥补SMC算法对这类数据集削减程度不足的问题。
3) OSMC算法对实验数据的平均削减率为55.1%,高于SMC算法的29.7%,在面对高分辨率的地质数据时其最高削减率达到了80%,平均也超过了50%,效果尤为明显。
4) 在数据集分辨率逐渐增大的情况下, OSMC算法的结果集规模会以低于MC算法和SMC算法的速率增长。
OSMC算法也存在如下2方面的问题:一是合并体元的条件设置局限在共面构型上,限制了削减率的进一步提升。二是八叉树的划分方式可能会把共面三角片分在非兄弟节点上,这样的情况在收缩时无法合并。所以下一步的研究方向是改善算法的合并条件以及八叉树的收缩过程,进一步增加算法的削减率。
附录A:生成SMC简化构型查找表为快速处理体元,需要为SMC简化构型构造有256个入口的查找表,SMC查找表的构建基于MC算法的查找表。首先需要对体元的各个顶点的边按图A1的方式编号。

|
| 图 A1 体元顶点与边 Fig. A1 Number of vertices and edges of cell |
MC算法查找表共有256行,每一行是由形式为{〈e0, e1, e2〉, 〈e3, e4, e5〉, …}的三元组构成,对于任意一种体元状态,可从中获取三角形顶点所在边的索引和三角形的组合方式〈ei, ej, ek〉。而对于SMC算法,由于三角片的顶点不在位于体元边上,而是体元顶点上,那么单个三角片就不再使用3条边索引表示,而是使用3个顶点索引表示。即:〈Vi, Vj, Vk〉,从标准MC算法查找表构建SMC算法查找表的步骤如下:
算法 SMC构型查找表生成算法
输入:MC构型查找表T输出。
输出:SMC构型查找表ST。
Begin
For cube state i from 0 to 255
Get triangles from T[i]
For each triangle
Get the three edge indices
Get two vertex indices for each edge
Caculate three intersected points
for the three edge
If(the three vertices are not equal)
then
Find the cube vertex where the three intersected points locate
Record the cube vertex index to ST[i]
End
附录B:生成三角片平面方程查找表在八叉树收缩时需要根据三角片方程和法向量来合并体元,这些方程和法线的参数在算法执行时动态计算会造成较大的开销,所以也需要像MC算法一样构造查找表来提升效率。构造Equation表基于简化构型,需要利用附录A构造的SMC查找表。
Equation表同样有256个入口,每个入口对应三角片方程参数(A, B, C, D)。具体构造方法是遍历256种体元构型,判断其中三角片是否为共面构型,若为共面构型,判断其方程类型为表 1中的哪一种,根据不同方程类型和体元顶点坐标反求方程参数。伪代码如下:
算法 三角片方程查找表生成算法
输入:SMC构型查找表T输出。
输出:三角片方程查找表Eq。
Begin
For cube state i from 0 to 255
if(i is coplanar configration)
Get vertices V on the plane using T[i]
Get the triangle t using T[i]
If(t is equilateral triangle)
Solve (A, B, C, D) using V
If(t is isosceles right-angle triangle)
Find the plane which t is pararell with
Solve (A, B, C, D) using V
If(t is non-isosceles right-angle triangle)
Find the axis t is pararell with
Solve (A, B, C, D) using V
Set (A, B, C, D) to Eq[i]
else
Set Eq[i] to invalid value
End
| [1] | LORENSEN W E, CLINE H E. Marching cubes: A high resolution 3D surface construction algorithm[C]//ACM Siggraph Computer Graphics. New York: ACM, 1987, 21(4): 163-169. |
| [2] | HEIMBACH I, RHIEM F, BEULE F, et al. pyMolDyn:Identification, structure, and properties of cavities/vacancies in condensed matter and molecules[J]. Journal of Computational Chemistry, 2017, 38 (6): 389–394. DOI:10.1002/jcc.24697 |
| [3] | YIM P J, VASBINDER G B C, HO V B, et al. Isosurfaces as deformable models for magnetic resonance angiography[J]. IEEE Transactions on Medical Imaging, 2003, 22 (7): 875–881. DOI:10.1109/TMI.2003.815056 |
| [4] | BRONSON J R, SASTRY S P, LEVINE J A, et al. Adaptive and unstructured mesh cleaving[J]. Procedia Engineering, 2014, 82 : 266–278. DOI:10.1016/j.proeng.2014.10.389 |
| [5] | FERLEY E, CANI M P, GASCUEL J D. Practical volumetric sculpting[J]. The Visual Computer, 2000, 16 (8): 469–480. DOI:10.1007/PL00007216 |
| [6] | STEIN R, SHIH A M, BAKER M P, et al. Scientific visualization of water quality in the Chesapeake bay[C]//IEEE Visualization Conference. Piscataway, NJ: IEEE Press, 2000: 509-512. |
| [7] | TREMBILSKI A. Two methods for cloud visualisation from weather simulation data[J]. The Visual Computer, 2001, 17 (3): 179–184. DOI:10.1007/PL00013405 |
| [8] | KIM K, WITTENBRINK C M, PANG A. Data level comparison of surface classification and gradient filters[C]//Volume Graphics 2001. Berlin: Springer, 2001: 19-34. |
| [9] | NIELSON G M, HAMANN B. The asymptotic decider: Resolving the ambiguity in marching cubes[C]//Proceedings of the 2nd Conference on Visualization'91. Piscataway, NJ: IEEE Press, 1991: 83-91. |
| [10] | RECK F, DACHSBACHER C, GROSSO R, et al. Realtime iso-surface extraction with graphics hardware[C]//Eurographics. Geneva: Eurographics, 2004: 1-4. |
| [11] | JOHANSSON G, CARR H. Accelerating marching cubes with graphics hardware[C]//Proceedings of the 2006 Conference of the Center for Advanced Studies on Collaborative Research. Armonk: IBM Corporation, 2006, 6: 39. |
| [12] | NEWMAN T S, YI H. A survey of the marching cubes algorithm[J]. Computers & Graphics, 2006, 30 (5): 854–879. |
| [13] | SCHROEDER W J, ZARGE J A, LORENSEN W E. Decimation of triangle meshes[C]//ACM Siggraph Computer Graphics. New York: ACM, 1992, 26(2): 65-70. |
| [14] | GARLAND M, HECKBERT P S. Surface simplification using quadric error metrics[C]//Proceedings of the 24th Annual Conference on Computer Graphics and Interactive Techniques. New York: ACM Press/Addison-Wesley Publishing Co., 1997: 209-216. |
| [15] | MONTANI C, SCATENI R, SCOPIGNO R. Discretized marching cubes[C]//Proceedings of the Conference on Visualization'94. Piscataway, NJ: IEEE Press, 1994: 281-287. |
| [16] | MONTANI C, SCATENI R, SCOPIGNO R. Decreasing isosurface complexity via discrete fitting[J]. Computer Aided Geometric Design, 2000, 17 (3): 207–232. |
| [17] | SHU R, ZHOU C, KANKANHALLI M S. Adaptive marching cubes[J]. The Visual Computer, 1995, 11 (4): 202–217. DOI:10.1007/BF01901516 |
| [18] | SHEKHAR R, FAYYAD E, YAGEL R, et al. Octree-based decimation of marching cubes surfaces[C]//7th Annual IEEE Conference on Visualization. Piscataway, NJ: IEEE Press, 1996: 335-342. |
| [19] | OHTAKE Y, BELYAEV A, ALEXA M, et al. Multi-level partition of unity implicits[C]//ACM Siggraph 2005 Courses. New York: ACM, 2005: 173. |
| [20] | KAZHDAN M, HOPPE H. Screened poisson surface reconstruction[J]. ACM Transactions on Graphics (TOG), 2013, 32 (3): 29. |
| [21] | WILHELMS J, VAN GELDER A. Octrees for faster isosurface generation[J]. ACM Transactions on Graphics (TOG), 1992, 11 (3): 201–227. DOI:10.1145/130881.130882 |
| [22] | WESTERMANN R, KOBBELT L, ERTL T. Real-time exploration of regular volume data by adaptive reconstruction of isosurfaces[J]. The Visual Computer, 1999, 15 (2): 100–111. |
| [23] | CUI S H, LIU J. Simplified patterns for extracting the isosurfaces of solid objects[J]. Image and Vision Computing, 2008, 26 (2): 174–186. DOI:10.1016/j.imavis.2007.02.003 |
| [24] | VIGNOLES G L, DONIAS M, MULAT C, et al. Simplified marching cubes:An efficient discretization scheme for simulations of deposition/ablation in complex media[J]. Computational Materials Science, 2011, 50 (3): 893–902. DOI:10.1016/j.commatsci.2010.10.027 |



