在以往仿真技术中,仿真系统与真实系统的关系在结构上是分离的、在运行上是离线的、在地位/角色上是辅助的。随着应用需求的变化,仿真系统和真实系统开始出现融合的趋势,如嵌入式仿真[1]、在线仿真[2]等概念。而且,近年来在复杂系统和自然现象等研究领域[3]出现了虚实共生和平行执行[4]的概念,强调仿真系统/人工系统与真实系统之间在结构上相互依存、时间上并行执行(不一定同步)。在装备作战运用和维修保障领域中,实时决策[5]、在线规划、健康管理、精确维修等需求日益迫切,建立与装备共生、平行的仿真系统是解决此类问题的一种新途径,在此背景下,装备平行仿真技术应运而生。
以装备维修保障领域为例,武器装备结构的复杂性和运行工况条件的时变性使得装备故障率和维修保障难度增加,装备一旦发生故障,不仅影响武器装备作战效能的发挥,而且停机时间长、停机费用高,这就要求对装备进行精确维修。传统维修方式如修复性维修和定时维修存在"过维修"和"欠维修"的问题,已不能满足精确维修需要。随着状态监测技术的发展,基于状态的维修(Condition Based Maintenance,CBM)能有效减少停机时间、降低维修费用、提高装备可用度,已成为实现装备精确维修的重要手段。CBM是指通过内部传感器或外部监测设备获得装备状态信息,据此对装备健康状态进行评价,为维修决策提供依据。其中,剩余寿命(Remaining Useful Life,RUL)预测是CBM的关键环节[6]。RUL是指装备从当前时刻至发生故障时刻的时间长度,准确的RUL预测是维修规划的前提和依据,且根据实时监测数据自适应修正RUL预测结果成为重要研究方向[7]。当前的RUL预测方法中模型不具备与装备的双向交互能力,不支持模型参数自适应调整和模型输出自适应校正,模型参数是已知的或者根据历史数据以离线估计的方式得到,成为阻碍实现RUL自适应预测的重要因素。
装备平行仿真技术为解决RUL自适应预测问题提供了有效技术途径,针对装备RUL自适应预测需求,利用平行仿真技术可实现预测模型演化,不断逼近装备真实退化状态,实现RUL的在线、实时、自适应预测,称此技术为面向装备RUL预测的平行仿真技术。
1 装备平行仿真理论装备平行仿真是系统建模与仿真领域的新兴技术,已经成为研究前沿和热点。装备平行仿真是一种新的仿真应用模式,旨在将仿真系统和武器装备通过双向交互同时运行在一起,仿真系统以在线的方式实时获取装备信息,用于在线修正仿真模型,仿真结果可以动态地反馈给装备并影响武器装备的运行,从而提升武器装备的自身性能,以及运用和保障效能[8]。以这种模式运行的仿真系统称之为平行仿真系统,平行仿真系统是对装备的仿真,包括武器装备全部或部分环节、特性的仿真模型。
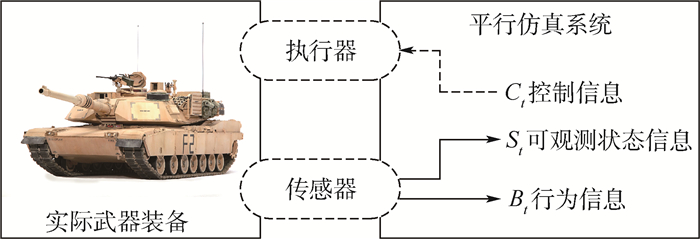
在装备平行仿真中,实际武器装备和平行仿真系统通过传感器、执行器进行双向交互。传感器给平行仿真系统提供实际武器装备信息,执行器使得平行仿真系统对实际武器装备执行控制等操作。一些实际武器装备或其子系统并不可控,此时执行器不一定存在。装备平行仿真示意图如图 1所示。由传感器提供的实际武器装备信息可以划分为2类,即在时刻t的实际武器可观测装备状态信息St和行为信息Bt。
|
| 图 1 装备平行仿真示意图 Fig. 1 Schematic of equipment parallel simulation |
St反映了实际武器装备在给定时刻多个内部状态变量的取值,可以将实际武器装备状态划分为已知状态Sa和未知状态Sua。由于武器装备的复杂性,很难获得装备的完全状态信息St=Sa∪Sua。例如,获取装备的完全状态信息可能会消耗大量时间或者经过密集计算,当平行仿真系统利用这些信息时可能已经出现信息过时的情况。除此之外,一些状态变量能够利用传感器进行观测,而一些状态变量却不可观测。Bt反映了状态信息中不能反映的可计量的实际武器装备信息。在面向装备RUL预测的平行仿真中,主要涉及状态信息St。
实际武器装备能够受控于平行仿真系统发送的控制信息Ct,根据控制信息的执行方式,可以划分为自动控制信息CtA和手动控制信息CtM。由于控制信息的获取需要经过平行仿真系统一定时间的计算或推理,因此Ct是离散控制信息。控制信息Ct只在一定受限时间内有效,经过一定时间后可能是无效信息,此时有效的控制信息可能就变为Ct+1。在面向装备RUL预测的平行仿真中,平行仿真系统的反馈为RUL及其概率密度函数(Probability Density Function,PDF),但RUL及其PDF都属于隐含控制量,没有直接体现在Ct中,RUL、PDF反馈给装备维护人员后,由装备维护人员根据反馈结果和维修经验进行维修决策,进而利用执行器对实际武器装备或其子系统进行修复、更换等视情维修操作。
虽然平行仿真中的"平行"在英文中翻译为"parallel",但与并行仿真中"parallel"有本质不同,装备平行仿真中的"平行"与平行系统理论中的"平行"具有相同的内涵,是指实际系统和仿真系统的平行互动关系。装备平行仿真的理论缘起与平行系统理论[9-10]、动态数据驱动应用系统(Dynamic Data Driven Application System,DDDAS)[11-13]、共生仿真[14]、在线仿真等理论范式密切相关,文献[8]已作详细综述,但是也存在明显差异。平行系统理论强调基于Agent的建模,DDDAS、共生仿真、在线仿真中实际系统和仿真系统不存在平行关系,共生仿真强调利用假设分析(What-If Analysis,WIA)方法进行多脚本仿真,在线仿真是与离线仿真相对的概念,实际系统和仿真系统之间的连接是其基本特征。在以上相关技术中,仿真模型侧重于一次性构建,属于相对固定和特定的模型,具体表现在模型参数固定、不具备数据同化能力,即仿真模型不具备演化能力[15]。平行仿真的建模技术属于演化建模或适应性建模,与以往仿真技术相比,模型演化是平行仿真技术在建模方式上的核心内涵和主要技术特征。平行仿真系统通过模型演化使得仿真模型输出不断逼近装备真实状态,提高仿真系统预测的准确性。此外,平行仿真技术还具有虚实共生、数据驱动、高效运行的特点[8]。
目前,国内仿真领域的专家学者正在逐步开展装备平行仿真技术研究,主要面向装备指挥决策支持领域[16]、维修保障领域[17]及航天控制仿真领域,针对指挥决策支持的平行仿真研究相对较多,如毛少杰[18-19]、邱晓刚[5]、窦林涛[20]等,目前处于框架建立和关键技术讨论阶段,在航天控制仿真领域中,王会霞[21]讨论了平行仿真技术的特点,给出了其在导弹控制系统仿真验证中的应用框架,本文的研究针对的是装备维修保障领域中平行仿真技术研究,且主要关注演化建模技术。
2 面向RUL预测的平行仿真框架面向装备RUL预测的平行仿真是指构建与实际武器装备平行运行的仿真系统即平行仿真系统,实际武器装备和平行仿真系统通过特定接口互联在一起,并利用状态监测技术以在线形式实时感知装备退化状态以驱动仿真模型状态和参数更新,实现仿真模型演化,得到更为准确的RUL预测结果,并将预测结果反馈给装备维护人员,为维修决策提供实时数据支持,提升实际武器装备的保障效能。
2.1 建模分析模型是仿真的基础,建立恰当的模型是面向装备RUL预测平行仿真的前提。模型的恰当主要表现在3个方面:一是所建立模型应该符合建模意图,即利于RUL预测;二是所建立的模型应该易于进行状态估计;三是所建立模型应该能反映装备潜在的特性和规律。传统的寿命预测、可靠性评估等理论注重的是对装备失效数据的研究,相关的理论方法已经十分完善,这些分析方法都是建立在大量失效数据的基础之上的。然而随着制造工艺的提高,产品寿命延长、可靠性提高,很难得到装备的失效数据,即便采用加速寿命试验方法也存在试验周期长、试验成本高等突出问题。装备完成特定功能是由其性能参数所表征的,受环境应力、负荷的影响,装备性能参数随时间退化是不可避免的,性能退化是导致装备故障的主要原因,故装备故障机理可通过性能退化过程进行解释分析。相较于失效数据,与装备健康状态相关的随机退化信号是可以通过状态监测技术获得的,如振动监测和油液分析,充分挖掘和利用这些退化数据,能够有效分析装备的可靠性和RUL。因此,基于性能退化建模是首选建模方向。
为便于描述装备动态变化的退化状态并对装备退化状态进行估计,宜建立装备退化状态空间模型(State Space Model,SSM),包括状态方程和观测方程。然而,受退化数据有限的制约,直接建立装备退化SSM十分困难。考虑到运行环境、内部结构对装备性能退化的影响具有随机性和不确定性,利用随机过程模型进行装备退化建模分析是比较合理的选择。基于随机过程模型的装备性能退化建模通过利用随机过程拟合装备某一性能退化量的变化轨迹来描述设备退化的趋势,以此来预测设备达到失效阈值的时间。Wiener过程不仅能描述具有增加或减小趋势的非单调退化过程,而且具有良好的数学性质,即容易得到RUL的PDF解析解,有利于实时预测,因此本文选用Wiener过程。故将SSM和Wiener过程结合在一起构建装备退化SSM既有利于装备退化状态估计,也有利于刻画装备退化规律。本文所提的演化建模框架是以基于Wiener SSM(WSSM)的性能退化建模为基础的。
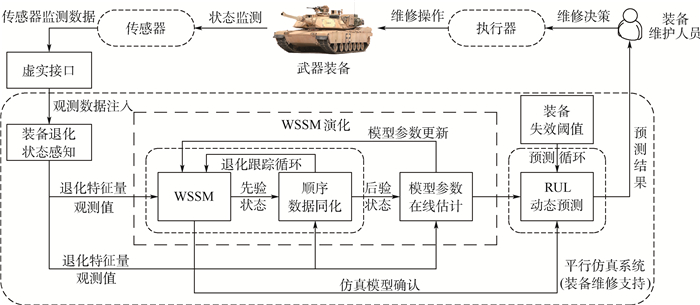
2.2 演化建模框架面向装备RUL预测的平行仿真示意图如图 2所示。其具体过程为:利用传感器等监测设备对武器装备退化状态进行实时监测并得到监测数据,经虚实接口传输到平行仿真系统中,平行仿真系统首先对装备退化状态进行在线感知,主要涉及数据降噪、缺失数据处理等数据预处理技术,得到反映装备退化状态的特征量,并与WSSM输出不断进行数据同化,实现装备退化状态的跟踪循环,结合参数在线估计算法对WSSM中未知参数进行实时估计,实现模型参数演化,不断逼近装备真实退化状态,进而得到演化后的WSSM,并利用装备失效阈值实时预测装备RUL及其PDF,平行仿真系统将预测结果反馈给装备维护人员,以此作为视情维修决策的重要依据,利用执行器对武器装备进行备件更换等维修操作,从而提高装备保障效能。
|
| 图 2 面向装备RUL预测的平行仿真示意图 Fig. 2 Schematic of equipment RUL prediction oriented parallel simulation |
数据同化(Data Assimilation,DA)和参数在线估计是实现WSSM演化的关键。由于装备退化数据的动态注入,平行仿真系统必须具备数据同化能力,以提高仿真系统的适应能力和预测能力。数据同化将最新观测数据引入WSSM中,减少WSSM噪声的影响,通过不断校正WSSM输出结果使得WSSM预测轨迹更加接近真实情况,常用的数据同化算法有卡尔曼滤波(Kalman Filter,KF)[22]、粒子滤波(Particle Filter,PF)等。参数在线估计算法用于演化WSSM未知参数,期望最大化(Expectation Maximum,EM)算法是目前常用的用于估计SSM未知参数的算法。由于此演化建模框架以WSSM为基础,使其还考虑了历史监测数据和监测噪声对RUL的影响,使得RUL预测结果更为准确合理。
2.3 基于WSSM的装备性能退化建模 2.3.1 Wiener过程与MLE-IG法Wiener过程可记为
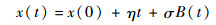
|
(1) |
式中:x(0)为初始退化状态,一般设为0;η、σ为未知参数,η为漂移系数,σ为扩散系数;B(t)为标准Brownian运动,且服从均值为0、方差为t的正态分布,即B(t)~N(0, t)。设装备失效阈值为w,则装备剩余寿命T定义为退化过程首次通过失效阈值的时间:

|
(2) |
Wiener过程具有以下性质:
1) Wiener过程属于无后效性的齐次Markov过程。
2) 在不同时间段内,x(t)的增量Δxi相互独立。
3) 独立增量Δxi服从均值为ηΔti、方差为σ2Δti的正态分布,即Δxi~N(ηΔti, σ2Δti)。
Wiener过程的数学期望E(x(t))=ηt是时间t的线性函数,漂移系数是反映退化过程的重要参数,Wiener过程的方差var(x(t))=σ2t表征了退化过程在时刻t的不确定性,因此对参数η、σ2的实时估计是实现准确RUL预测的前提。由于E(x(t))=ηt是线性形式,故Wiener过程适宜于描述线性退化系统。以往对Wiener过程中参数η、σ2的估计利用极大似然估计(Maximum Likelihood Estimation,MLE)方法,由于Δxi~N(ηΔti, σ2Δti),则Δxi的PDF为

|
(3) |
则其似然函数为
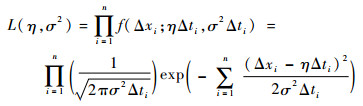
|
(4) |
对似然函数取对数,得其对数似然函数
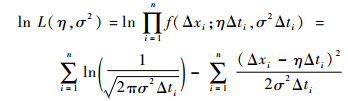
|
(5) |
对数似然函数分别对η、σ2求偏导数,并令偏导数为0,即
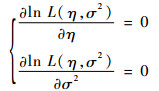
|
(6) |
可求得参数η、σ2的极大似然估计值:
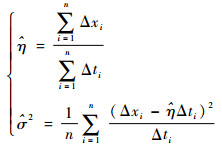
|
(7) |
得到参数估计值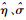
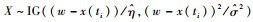
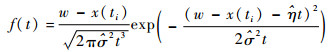
|
(8) |
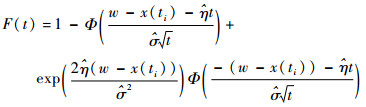
|
(9) |
称此传统方法为MLE-IG法。注意到,MLE-IG法无法实现模型状态、参数的演化,且未考虑监测噪声和历史数据的影响,得到的RUL预测结果必然存在较大误差。
2.3.2 Wiener状态空间模型为考虑历史数据的影响和漂移系数的不确定性,将漂移系数η扩展成退化漂移状态ηk,即
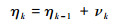
|
(10) |
式中:νk~N(0, ε2),标准差ε表征了ηk的不确定性。
装备退化状态监测中受传感器测量精度以及装备运行工况的影响,精确的退化状态数据无法直接测量得到,考虑测量噪声的影响,观测方程可写为

|
(11) |
式中:πk~N(0, ϕ2),ϕ2为测量噪声的方差。得到模型
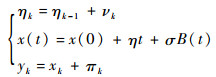
|
(12) |
进一步,通过对x(t)进行Euler离散化,可以得到WSSM为
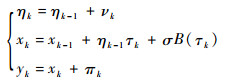
|
(13) |
式中:τk=tk-tk-1为传感器采样间隔,并假设初始退化状态x0、初始退化漂移状态η0、漂移状态噪声ν1, ν2, …, νk,以及Brownian运动B(τ1), B(τ2), …, B(τk)和传感器监测噪声π1, π2, …, πk相互独立。方程包含2个状态,即退化状态x和漂移状态η。由式(13)所知,二者存在相关性,故难以同时进行估计。为解决此问题,可将x、η合成为一个扩展状态z,即zk=(ηk, xk)T,WSSM可进一步记为

|
(14) |
式中: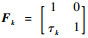


|
(15) |
作为动态数据驱动的仿真理论,平行仿真能提高RUL预测精度的关键在于不断地将实际装备退化状态观测数据与WSSM输出结果进行数据同化,即校正装备退化SSM输出。数据同化算法是联系观测数据和WSSM的桥梁,是实现退化状态预测的基础。本文利用KF算法实现数据同化,KF能在状态线性变化和误差高斯分布情况下得到状态最优估计,其实质是对装备退化状态进行跟踪。利用KF实现WSSM输出校正主要包括预测和更新2个步骤。
步骤1 预测
利用时刻k-1扩展状态zk-1的后验估计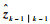
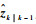
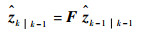
|
(16) |

|
(17) |
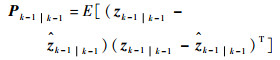
|
(18) |
步骤2 更新
利用k时刻扩展状态zk的先验估计
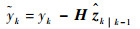
|
(19) |

|
(20) |
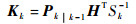
|
(21) |
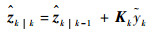
|
(22) |
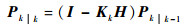
|
(23) |
式中: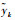
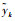
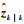
WSSM中未知参数θ为μ0、Σ0、Q、ϕ,μ0和Σ0分别为初始隐藏状态z0的数学期望和协方差矩阵,即z0~N(μ0, Σ0)。θ为装备退化特性和规律的重要特征,但是在应用中这些参数是未知且可变的,需要根据装备退化数据对θ进行在线估计。实际上,θ的初始值可通过同一型号装备的历史数据估计得到,然而同一型号装备也存在差异,加之装备运行环境等因素的影响,利用同一型号历史数据估计未知参数存在很大误差,因此根据装备退化状态数据对参数θ进行在线估计能有效提高平行仿真系统预测的准确性。MLE是常用的估计算法,然而由于WSSM中存在隐藏状态,MLE并不适用。EM算法是一种能有效估计含隐藏状态模型参数的迭代算法,平行仿真系统利用EM算法可对WSSM中未知参数θ进行实时、在线估计。定义隐藏状态和测量数据分别为Zk=(z1, z2, …, zk)、Yk=(y1, y2, …, yk)。
在采样时刻k、EM算法第l步时,参数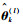
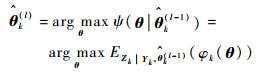
|
(24) |
式中:φk(θ)为Zk、Yk的联合对数似然函数;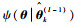
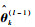
1) E步
根据Bayesian定理和Markov性质,φk(θ)可展开为
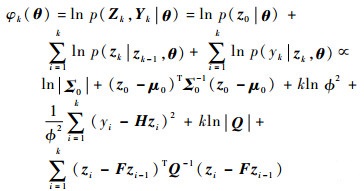
|
(25) |
将式(25)代入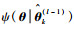

|
(26) |
进一步推导,有
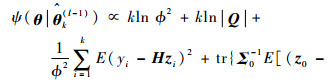
|
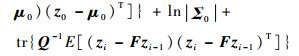
|
(27) |
式中:tr为矩阵迹运算。为计算式(27),需首先计算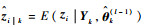

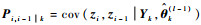
平滑增益为
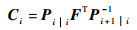
|
(28) |
平滑状态向量为
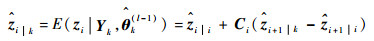
|
(29) |
平滑状态向量的协方差矩阵为
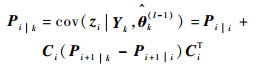
|
(30) |
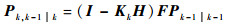
|
(31) |
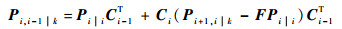
|
(32) |
根据式(28)~式(32),式(27)中的3项数学期望可记为

|
(33) |
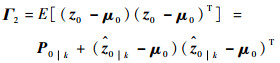
|
(34) |
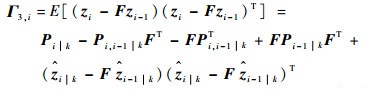
|
(35) |
根据式(33)~式(35),可得联合对数似然函数的数学期望

|
(36) |
2) M步
EM算法第l步时未知参数θ的估计可利用对式(36)取偏导数并令偏导数为0求得,即
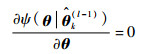
|
(37) |
求解可得参数θ的在线估计值,即
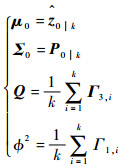
|
(38) |
至此,得到第l步的未知参数估计值即完成一次迭代
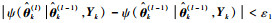

根据式(2)可知,RUL定义为从当前时刻至退化状态首次到达失效阈值w的时间间隔。由于xk和ηk都是随机变量,所以RUL的PDF不再服从IG分布,为实时预测RUL的PDF,下面进行k时刻RUL计算的推导。根据Wiener过程性质知,WSSM中以xk、ηk为条件的RUL的PDF服从IG分布,即

|
(39) |
式中:Tk为第k个监测时刻的剩余寿命,其PDF可以写为
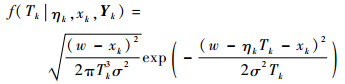
|
(40) |
由于zk=(ηk, xk)T是双变量,易知其服从二维正态分布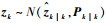
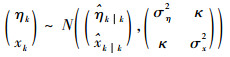
|
其PDF可展开为
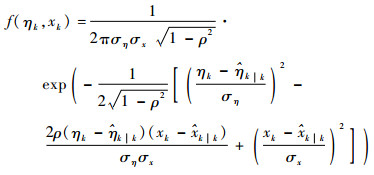
|
(41) |
式中:ρ=κ/σησx为xk和ηk的相关系数,κ=cov(ηk, xk)为xk和ηk的协方差。根据Bayesian定理和全概率公式,求解积分可得k时刻RUL的PDF解析表达式为

|
(42) |
根据式(42),平行仿真系统能够实时计算RUL的PDF,为视情维修决策提供数据支撑。
5 应用实例为验证面向装备RUL预测的平行仿真框架的可行性和有效性,尤其是对平行仿真系统中模型演化方法即数据同化算法和参数在线估计算法及RUL预测的验证,基于开源数据对本文方法进行验证。
5.1 开源退化数据与特征提取作为数据驱动的模型演化范式,装备性能退化数据是面向装备RUL预测平行仿真的研究基础。本文拟采用美国NASA官方网站提供的NSF I/UCR中心的IMS(Intelligent Maintenance Systems)轴承全寿命试验数据[23]进行方法验证。此权威数据已被维修保障领域研究人员广泛用于相关理论和方法的验证。试验数据采样频率20 kHz,数据长度20 480,采集时间范围2004-02-12T10:32:39—2004-02-19T06:22:39,每10 min采集1次,8 d内共收集到984组数据,时间分布为连续的164 h。在全寿命周期试验后期,轴承1出现了外沟槽故障。
为兼顾退化特征量对退化过程的敏感性和平稳性,选择振动信号的均方根值(Root Mean Square,RMS)作为退化特征量,其计算公式为
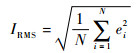
|
(43) |
式中:N为采样点数;ei为第i个采样点的振动加速度。轴承1的振动信号均方根值如图 3所示。轴承1的RMS在第532个监测时刻发生明显变化,在第980个监测时刻均方根值最大,随后装备发生外沟槽故障,因此将第532个监测时刻作为退化状态估计的起点,失效阈值为第980个监测时刻对应的均方根值0.725 mm/s2,即w=0.725。

|
| 图 3 全寿命试验中轴承1的均方根值 Fig. 3 RMS of the 1st bearing in life test |
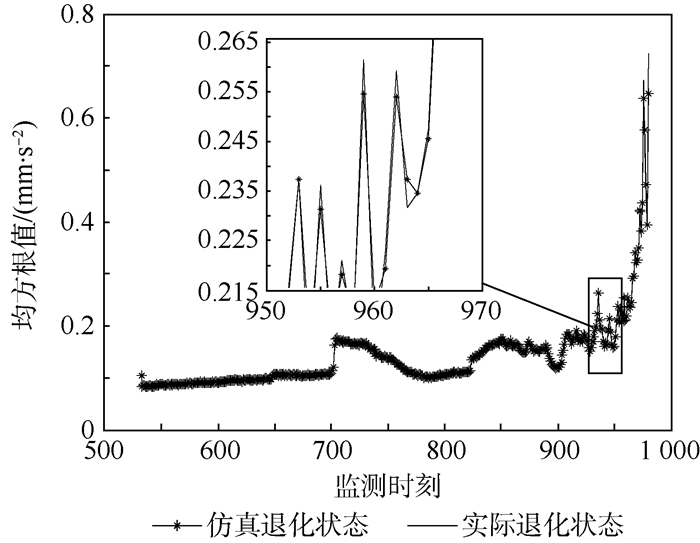
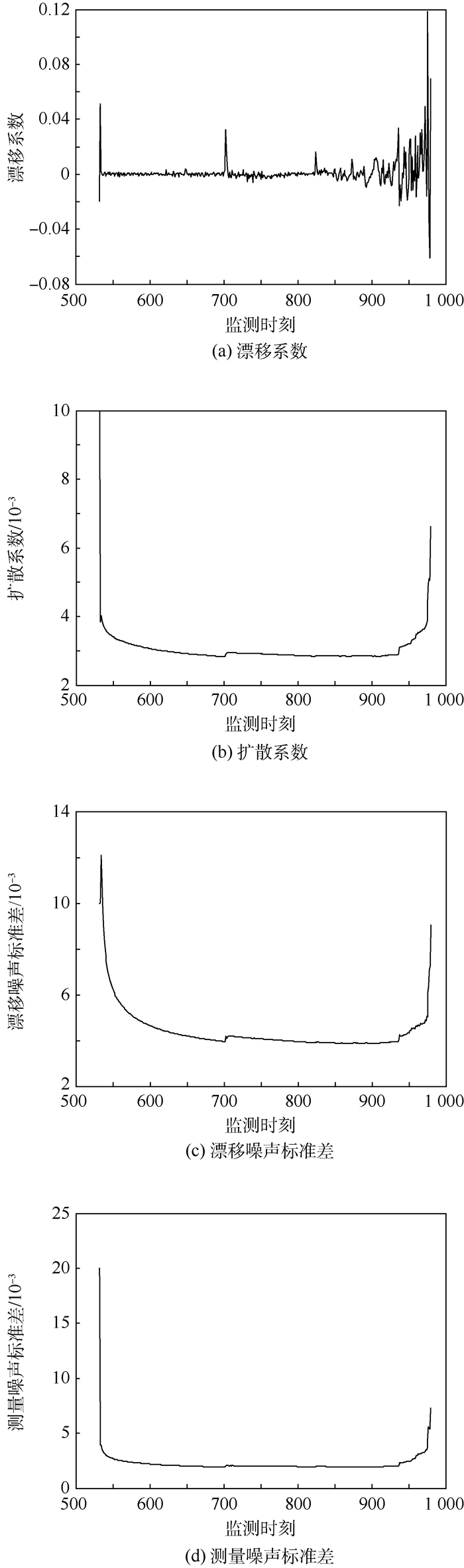
WSSM参数初始设置为x0=0、η0=0.01、ε=0.01、σ=0.01、τ=1、ϕ=0.02。图 4为仿真退化状态与实际观测退化状态的对比图,基于数据同化和参数在线估计的WSSM演化方法能有效仿真轴承的退化过程。图 4、图 5均以第532个监测时刻为起点。
|
| 图 4 退化状态对比 Fig. 4 Comparison of degradation state |
|
| 图 5 WSSM未知参数在线演化 Fig. 5 Online evolution of unknown parameters for WSSM |
为量化退化状态对比结果,利用均方根误差(Root Mean Square Error,RMSE)来进行度量,RMSE计算公式为

|
(44) |
式中:m为监测时刻数目。经计算,仿真退化状态与实际观测退化状态的均方根误差仅为1.891%,充分说明平行仿真方法能有效建模和仿真轴承的性能退化过程。相应地,随着轴承性能退化数据的动态注入,平行仿真系统利用数据同化算法和EM算法对参数向量θ进行在线演化,在第532~980个监测时刻的在线演化结果如图 5所示。
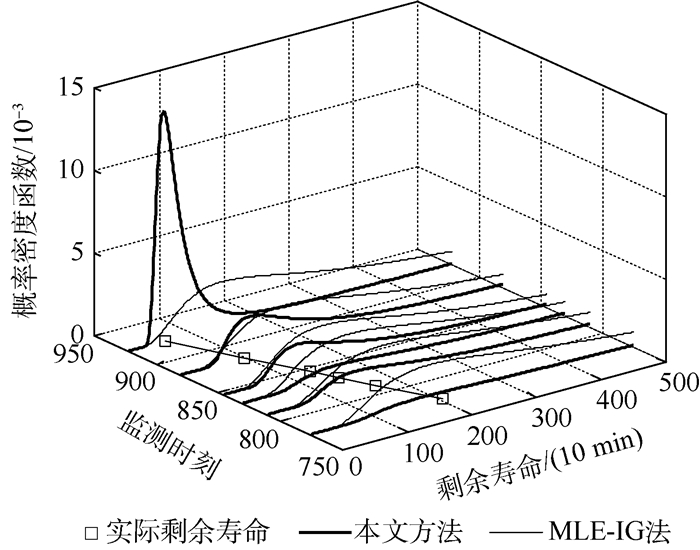
图 5结果表明,模型参数随着观测退化数据的积累能很快收敛,在第700个监测时刻附近和第930个监测时刻后,由于轴承退化状态的变化较为剧烈,使得参数发生明显变化,这也正体现了平行仿真中模型演化的重要性。在每一个监测时刻,一旦模型中的参数实现在线演化,对应地RUL的PDF就能通过式(42)计算得到。图 6给出了6个不同监测时刻上预测的RUL的PDF曲线。

|
| 图 6 不同监测时刻上预测的RUL的PDF Fig. 6 PDF of RUL predicted at different monitoring time points |
图 6中,在每一个监测时刻,实际的剩余寿命均落在剩余寿命概率密度曲线的范围内,实际剩余寿命位于PDF峰值对应的剩余寿命附近,而且随着轴承性能退化数据的动态注入和累积,剩余寿命的PDF越来越尖锐,右偏态特性越小,说明模型参数越来越准确,剩余寿命预测的不确定性不断降低,实现了轴承剩余寿命的在线、实时、自适应预测,能为装备维护人员维修决策提供重要依据。本文所用的Wiener过程描述的是一维退化量情形,针对多维退化量下RUL预测问题,本文方法仍然有较强适用性。若多特征量相互独立,可分别使用本文方法进行RUL预测,根据RUL预测的最小值安排维修决策;若多特征量相关,可先利用主成分分析(Principal Component Analysis,PCA)法得到若干反映原多特征量的独立主成分及其对应权值,进行加权求和后,得到一个无量纲的综合特征量,对此综合特征量利用本文方法仍然可以得到满意的RUL预测结果。
5.3 不同方法的比较利用本次试验得到的轴承退化数据,采用MLE法离线估计漂移系数和扩散系数,得到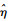
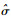
|
| 图 7 MLE-IG法与本文方法的对比 Fig. 7 Comparison between MLE-IG method and proposed method |
MLE-IG法中得到第k个监测时刻的剩余寿命期望值
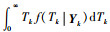
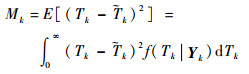
|
(45) |
|
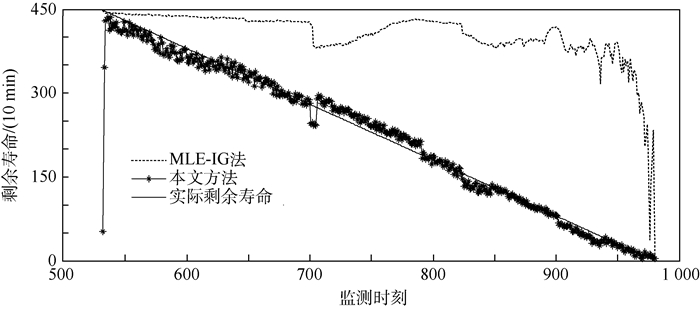
| 图 8 预测的剩余寿命期望值与实际剩余寿命对比 Fig. 8 Comparison between expectation of predictive RUL and bearing actual RUL |
式中: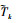
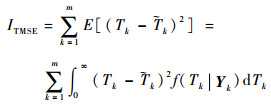
|
(46) |
总均方差越小表明RUL预测结果越准确,MLE-IG法和本文方法的总均方差分别为13.345 5、0.352 2,说明利用平行仿真方法预测RUL的精度远高于传统方法,充分证明了本文方法的有效性。
6 结论1) 本文率先将装备平行仿真技术引入装备维修保障领域,以虚实互动的思想解决装备剩余寿命自适应预测问题,提出了面向装备(RUL)预测的平行仿真框架,并以某轴承开源退化数据为数据驱动源进行了实例验证。
2) 实例仿真结果表明,平行仿真方法能有效建模并以高逼真度仿真装备的退化过程,仿真退化状态与实际观测退化状态的均方根误差仅为1.891%。
3) 平行仿真方法不仅考虑了利用实时动态注入的退化数据演化WSSM,包括基于KF算法的数据同化和基于EM算法的参数在线估计,同时考虑了历史监测数据和监测噪声对RUL的影响,使得RUL预测结果更为准确合理。
4) 较于传统的MLE-IG法,基于平行仿真方法预测装备RUL具有PDF右偏特性小、PDF峰值接近实际RUL的特点,能有效提高装备RUL预测精度,总均方差为0.352 2,远远小于MLE-IG法的13.345 5,实现了装备RUL的自适应预测,同时利用平行仿真方法预测装备RUL还具有在线、实时的特点。
本文方法还存在一定局限性。①WSSM适宜仿真装备性能线性退化的情况,在退化过程非线性很强情况下,预测精度会明显降低,这就需要研究面向非线性退化装备RUL预测的平行仿真技术;②受装备复杂度和环境因素等影响,装备性能退化过程具有较强的不确定性,呈现出多阶段性的特点,这就要求利用实时退化数据自适应选择适宜仿真模型,即需要研究模型自适应更替技术。
致谢
感谢北京仿真中心航天系统仿真重点实验室蔡继红研究员和北京航空航天大学自动化科学与电气工程学院宋晓教授对本文的贡献。
| [1] |
李伟, 李宗毅, 翟中敏. 嵌入式仿真技术及其在军事上的应用[J].
系统仿真学报, 2009, 21 (21): 6968–6971.
LI W, LI Z Y, ZHAI Z M. Embedded simulation and its application in military[J]. Journal of System Simulation, 2009, 21 (21): 6968–6971. (in Chinese) |
| [2] | DAVIS W J. On-line simulation: Need and evolving research requirements[M]//BANKS J. Handbook of simulation: Principles, methodology, advances, applications and practices. Hoboken: Wiley, 1998: 465-516. |
| [3] | AYDT H, TURNER S J, CAI W T, et al. Research issues in symbiotic simulation[C]//Proceedings of the 2010 Winter Simulation Conference. Piscataway, NJ: IEEE Press, 2010: 1213-1222. |
| [4] | CHEN B. KD-ACP:A software framework for social computing in emergency management[J]. Mathematical Problems in Engineering, 2014, 21 (3): 35–38. |
| [5] |
邱晓刚, 胡艮胜. 面向辅助决策的平行系统思考[J].
指挥与控制学报, 2016, 2 (3): 230–233.
QIU X G, HU G S. The consideration of parallel system for decision support[J]. Journal of Command and Control, 2016, 2 (3): 230–233. (in Chinese) |
| [6] | GEBRAEEL N, ELWANY A, PAN J. Residual life predictions in the absence of prior degradation knowledge[J]. IEEE Transactions on Reliability, 2009, 58 (1): 106–117. DOI:10.1109/TR.2008.2011659 |
| [7] | SI X S, WANG W B, HU C H, et al. Remaining useful life estimation-A review on the statistical data driven approaches[J]. European Journal of Operational Research, 2011, 213 (1): 1–14. DOI:10.1016/j.ejor.2010.11.018 |
| [8] |
葛承垄, 朱元昌, 邸彦强, 等. 装备平行仿真技术的基础理论问题[J].
系统工程与电子技术, 2017, 39 (5): 1169–1177.
GE C L, ZHU Y C, DI Y Q, et al. Basic theoretical issues of equipment parallel simulation technology[J]. System Engineering and Electronics, 2017, 39 (5): 1169–1177. DOI:10.3969/j.issn.1001-506X.2017.05.33 (in Chinese) |
| [9] |
王飞跃. 平行系统方法与复杂系统的管理和控制[J].
控制与决策, 2004, 19 (5): 485–489.
WANG F Y. Parallel system methods for management and control of complex systems[J]. Control & Decision, 2004, 19 (5): 485–489. (in Chinese) |
| [10] | WANG F Y. Parallel control and management for intelligent transportation systems:Concepts, architectures, and applications[J]. IEEE Transactions on Intelligent Transportation Systems, 2010, 11 (3): 630–638. DOI:10.1109/TITS.2010.2060218 |
| [11] | DAREMA F. Dynamic data driven application systems[EB/OL]. [2016-07-01]. http://www.cise.nsf.gov/dddas. |
| [12] | HUANG Y, VERBRAECK A. A dynamic data-driven approach for rail transport system simulation[C]//Proceedings of the 2009 Winter Simulation Conference. Piscataway, NJ: IEEE Press, 2009: 2553-2562. |
| [13] | GU F. Dynamic data driven application system for wildfire spread simulation[D]. Atlanta: Georgia State University, 2010. |
| [14] | FUJIMOTO R, LUNCEFORD D, PAGE E, et al. Grand challenges for modeling and simulation: 350[R]. Schloss Dagstuhl: Parallel/Distributed Simulation Working Group, 2002. |
| [15] |
葛承垄, 朱元昌, 邸彦强, 等. 装备平行仿真理论框架研究[J].
指挥与控制学报, 2017, 3 (1): 48–56.
GE C L, ZHU Y C, DI Y Q, et al. Theoretical framework for equipment parallel simulation[J]. Journal of Command and Control, 2017, 3 (1): 48–56. (in Chinese) |
| [16] |
陈淼, 孙强, 王东科. 平行系统在反导指挥控制中的应用[J].
指挥控制与仿真, 2017, 39 (1): 70–72.
CHEN M, SUN Q, WANG D K. Application of parallel system method in command and control for anti-missile system[J]. Command Control & Simulation, 2017, 39 (1): 70–72. (in Chinese) |
| [17] |
葛承垄, 朱元昌, 邸彦强, 等. 装备精确维修平行仿真系统及关键技术研究[J].
现代防御技术, 2016, 44 (6): 162–168.
GE C L, ZHU Y C, DI Y Q, et al. Research on parallel simulation system and essential technology for equipment precision maintenance[J]. Modern Defence Technology, 2016, 44 (6): 162–168. (in Chinese) |
| [18] |
毛少杰, 周芳, 楚威, 等. 面向指挥决策支持的平行仿真系统研究[J].
指挥与控制学报, 2016, 2 (4): 315–321.
MAO S J, ZHOU F, CHU W, et al. Parallel simulation systems for command and decision support[J]. Journal of Command and Control, 2016, 2 (4): 315–321. (in Chinese) |
| [19] |
孙黎阳, 楚威, 毛少杰, 等. 面向C4ISR系统决策支持的平行仿真框架[J].
指挥信息系统与技术, 2015, 6 (3): 56–61.
SUN L Y, CHU W, MAO S J, et al. Parallel simulation framework for C4ISR system command decision support[J]. Command Information System and Technology, 2015, 6 (3): 56–61. (in Chinese) |
| [20] |
窦林涛, 初阳, 周玉芳, 等. 平行仿真技术在指控系统中的应用构想[J].
指挥控制与仿真, 2017, 39 (1): 62–69.
DOU L T, CHU Y, ZHOU Y F, et al. Conception of the application of parallel simulation technology in command and control system[J]. Command Control & Simulation, 2017, 39 (1): 62–69. (in Chinese) |
| [21] |
王会霞. 平行仿真技术研究[J].
航天控制, 2016, 34 (6): 64–67.
WANG H X. Research on parallel simulation technology[J]. Aerospace Control, 2016, 34 (6): 64–67. (in Chinese) |
| [22] | KALMAN R E. A new approach to linear filtering and prediction problems[J]. Transactions of the ASME-Journal of Basic Engineering, 1960, 82 (1): 35–45. DOI:10.1115/1.3662552 |
| [23] | MORTADA M. Diagnosis of rotor bearings using logical analysis of data[J]. Journal of Quality in Maintenance Engineering, 2011, 17 (4): 371–397. DOI:10.1108/13552511111180186 |



