旋转弹在飞行过程中绕自身纵轴连续滚转,在无控条件下可有效降低气动不对称、结构不对称和推力偏心等扰动因素所带来的弹道散布,提高落点精度,在制导控制条件下可省掉滚转控制回路,简化控制系统组成,因而旋转体制为众多弹箭类武器系统所采用。但是,弹体的旋转也使旋转弹在空气动力学特性、飞行力学特性、控制理论与方法等方面明显有别于非旋转弹,并带来一些特殊问题,如马格努斯效应、陀螺效应等,使得旋转弹在俯仰和偏航方向的运动存在交叉耦合作用[1]。在旋转弹控制系统设计中,需要考虑各种耦合因素,不仅包括以马格努斯效应为表现形式的气动交联、以陀螺效应为表现形式的惯性交联,而且包括舵机系统延迟引起的控制交联。在复杂的飞行环境下弹体自身会受到各种不确定性因素的干扰,这都给旋转弹控制系统设计带来了较大挑战[2-3]。
相关学者在旋转弹控制系统设计领域开展了较为深入研究,并取得了一定的研究成果。文献[4-5]分析了双通道控制旋转弹的各种耦合特性,并采用前馈补偿解耦方法实现了旋转弹基于过载驾驶仪的静态解耦控制。文献[6]采取对角占优解耦控制方法设计了弹体动力学环节以及执行机构动力学环节的解耦控制器。上述中基于前馈补偿解耦和对角占优解耦方法需要对模型有较为精确的认识,而且所设计的补偿器并不能确保系统在全频域段具有较好的解耦效果,从而学者将现代控制系统设计方法应用于旋转弹控制系统设计。文献[7]采用动态逆方法进行姿态控制器设计,该方法可有效处理动力学中的非线性因素。文献[8-10]采用鲁棒H∞控制方法进行旋转弹控制器设计,具有良好的鲁棒性和自适应能力。由于滚动时域优化(RHO)方法,又被称为模型预测控制,对模型精度要求不高,且具有较好的解耦控制能力[11],其被学者应用于导弹控制领域[12-13],并取得了较好的控制效果。本文在文献[11]的基础上,提出一种基于指令滤波器的RHO控制方法,并将其应用于旋转弹解耦控制,在不同的弹体旋转速度下取得了较好的解耦控制效果,确保了飞行指令的稳定跟踪。
1 旋转弹动力学模型由于旋转弹在飞行过程中以一定角速度绕其纵轴连续滚转,为了便于分析,引入准弹体坐标系,建立旋转弹动力学模型。准弹体坐标系中旋转弹的质心运动动力学方程组和导弹绕质心转动的动力学方程组分别为[14]
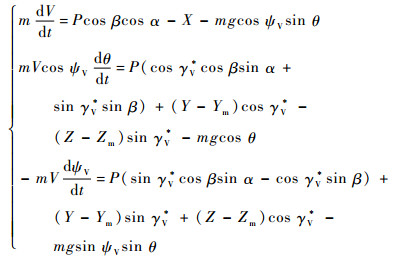
|
(1) |

|
(2) |
式中:m为旋转弹质量;g为重力加速度;V为飞行速度;为旋转速度;D为弹体直径;P为推力;X为阻力;Y为升力;Z为侧向力;Ym为沿着升力方向的马格努斯力;Zm为沿着侧向力方向的马格努斯力;α为迎角;β为侧滑角;γV*为速度准倾斜角;θ为弹道倾角;ψV为弹道偏角;ωx、ωy、ωz为旋转弹转动角速度;Jx、Jy、Jz为旋转弹转动惯量;Mxσx为滚转力矩对尾翼安装角的偏导数;Mxωx为滚转力矩对弹体绕纵轴旋转角速度的偏导数;Myβ为偏航力矩对侧滑角β的一阶偏导数;Myσy为偏航力矩对偏航舵偏角σy的一阶偏导数;Myωy为偏航力矩对弹体转动角速度ωy的一阶偏导数;My"为偏航力矩对弹体无因次旋转角速度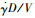

为了简化控制系统设计,需要对弹体动力学方程组(1)和(2)进行简化,不失一般性,作如下假设:
1) 假设在一小段飞行过程中,弹体的速度不变,弹体的转速不变。
2) 假设在控制系统设计的相关研究中,忽略重力作用。
3) 假设迎角α、侧滑角β、偏航角ψ、弹道偏角ψV、偏航角微分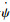
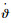
4) 假设控制舵产生的升力和弹体受到的总升力相比是小量。
当重点考虑弹体短周期运动时,可假定速度的方向不变,而只考虑弹轴的摆动运动,即假定弹道倾角θ和弹道偏角ψV在弹体运动短周期内基本保持不变,可近似为零,并根据小角度假设条件,有如下近似关系式成立[1]:
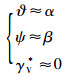
|
(3) |

|
(4) |
将式(3)和式(4)代入式(1)和式(2)整理化简后可得如下所示旋转弹动力学模型:
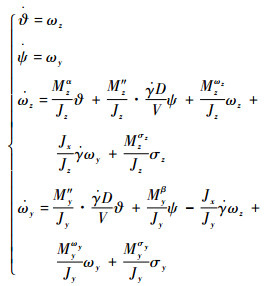
|
(5) |
对于轴对称弹体,有Jy=Jz,Mzα=Myβ,Mz"=My",Mzωz=Myωy,Mzσz=Myσy。
令法向加速度ay、侧向加速度az为系统输出,根据法向加速度和侧向加速度的定义有
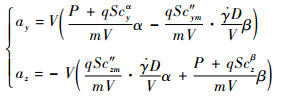
|
(6) |
式中:q为动压;S为机翼参考面积;cyα为升力系数对迎角α的导数;cym"为升力系数对弹体无因次旋转角速度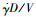
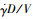
根据式(3),ay和az可由式(7)近似得到
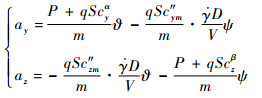
|
(7) |
考虑建模误差和外界干扰,将式(5)和式(7)写成如下状态空间形式:
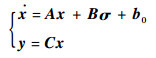
|
(8) |
式中: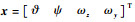
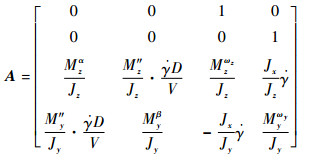
|
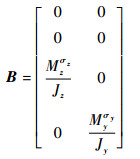
|
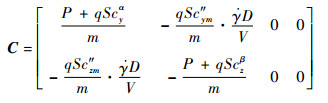
|
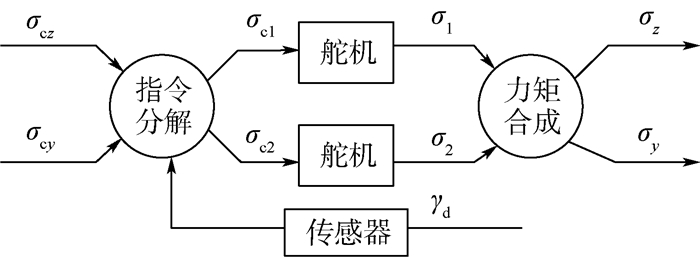
舵机系统的指令执行框图如图 1所示。
|
| 图 1 舵机系统的指令执行框图 Fig. 1 Command execution block diagram of servo system |
弹体的控制指令σcy、σcz形成于非旋转的准弹体坐标系下,根据传感器测量得到此时弹体相对于准弹体坐标系的滚转角γd,将σcz、σcy进行分解,得到弹体坐标系下的控制指令σc1、σc2,σc1、σc2经舵机驱动舵面偏转,从而得到弹体坐标系下舵面偏转角σ1、σ2和控制力矩,最后再将σ1、σ2和控制力矩合成到准弹体坐标系下的舵机响应σz、σy和控制力矩。
舵机响应传递函数为
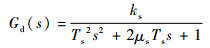
|
(9) |
式中:ks为舵机系统增益;Ts为舵机系统时间常数;μs为舵机系统阻尼。
根据图 1所示的指令执行框图和舵机响应传递函数,可得舵机系统的传递函数矩阵为[1]
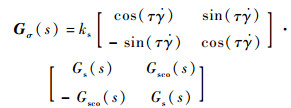
|
(10) |
式中:τ为从滚转角γ的测量到控制指令的生成并分解输入到实际舵机系统所需的时间;Gs(s)和Gsco(s)分别为前向通道传递函数和耦合通道传递函数,其表达式分别为
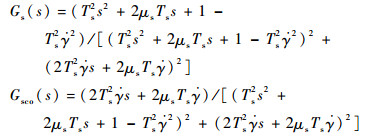
|
可以看出,旋转弹旋转导致控制通道出现耦合,随着转速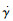
当忽略转速变化且仅考虑舵机系统在常值指令输入下的稳态输出时,则准弹体系中舵机系统的动力学模型可简化为
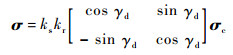
|
(11) |
式中:σc=[σcz σcy]T为准弹体坐标系中控制指令;kr表征了舵机系统由于弹体滚转出现的幅值衰减特性;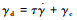
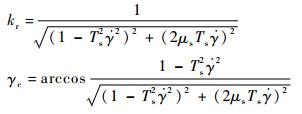
|
将式(11)代入式(8)可得考虑舵机系统动态特性的旋转弹动力学模型
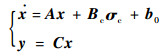
|
(12) |
式中:Bc表达式为
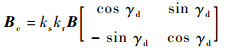
|
采用以下指令滤波器[15]得到加速度指令信号:
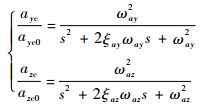
|
(13) |
式中:ayc和azc分别为法向加速度指令和侧向加速度指令;ayc0和azc0分别为法向加速度指令滤波器和侧向加速度指令滤波器的输入信号;ξay和ξaz分别为法向加速度指令滤波器和侧向加速度指令滤波器的阻尼;ωay和ωaz分别为法向加速度指令滤波器和侧向加速度指令滤波器的自然频率。
将指令滤波器式(13)写成状态空间的形式

|
(14) |
式中:指令滤波器状态向量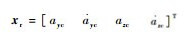
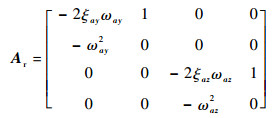
|
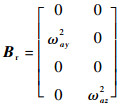
|

|
RHO优化控制的性能指标如下所示[16]:

|
(15) |
式中:tf和t0分别为区间的上界和下界;Qp和QI分别为跟踪误差和跟踪误差积分的加权阵;Rr为控制量的加权阵;yI为积分误差,可由下式得到

|
(16) |
综合旋转弹线性状态方程、指令滤波器状态方程和积分误差方程得到增广状态方程为
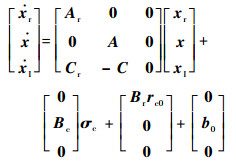
|
(17) |
将式(17)写成对应的如下形式:

|
(18) |
式中:AR、BR、bR、b表达式分别为
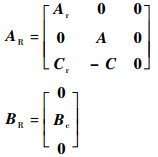
|

|
基于增广状态方程式(18)将性能指标式(15)重新写成
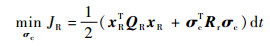
|
(19) |
式中:
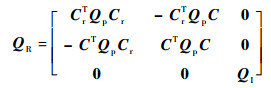
|
对控制量进行设计,先构造如下Hamilton函数[17]:
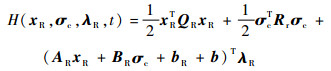
|
(20) |
式中:λR为时变拉格朗日乘子向量。
σc使得Hamilton函数值最小的必要条件为∂H/∂σc=0,有
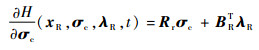
|
(21) |
由于
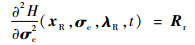
|
(22) |
式中:Rr为正定矩阵;H为σc的二次型,则满足式(21)的σc可使H值最小。求式(21)的解为
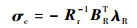
|
(23) |
将时变拉格朗日乘子向量λR设计成状态xR的线性组合,有
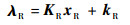
|
(24) |
式中:KR和kR为参数变量。
对于时变拉格朗日乘子向量λR有如下等式成立[18]:
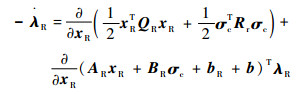
|
(25) |
整理式(25)可得
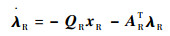
|
(26) |
将式(24)两边对时间t求导得
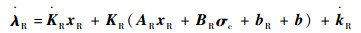
|
(27) |
将式(23)代入式(27)得
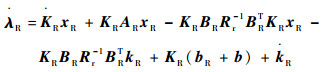
|
(28) |
根据式(26)和式(28)得
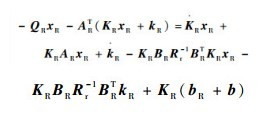
|
(28) |
整理式(29)得
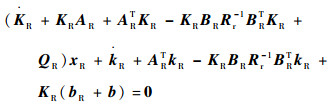
|
(30) |
由式(30)对于任意的状态向量xR都成立,则可以得到如下2个黎卡提微分方程:
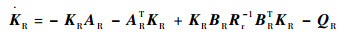
|
(31) |
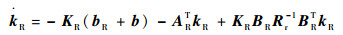
|
(32) |
通过求解式(31)和式(32)所示的黎卡提微分方程得到参数变量KR和kR。由于式(32)中模型不确定项b未知,且RHO方法对模型精度要求不高,可用以下黎卡提微分方程近似计算kR[11]:
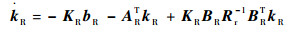
|
(33) |
由于KR和kR在有限时域区间[t0 tf]边界tf可以稳定在任意一个常值上,认为KR和kR在时域边界tf为0。在有限时域内对式(31)和式(33)进行反向积分,得到KR(t0)和kR(t0)[11]。通过式(34)计算得到控制器增益

|
(34) |
式中:FR=[Fr Fx FI]为控制器增益,Fr、Fx和FI分别为对应指令滤波器状态、旋转弹状态和积分误差状态的控制器增益; fR为针对建模误差的补偿控制器增益。
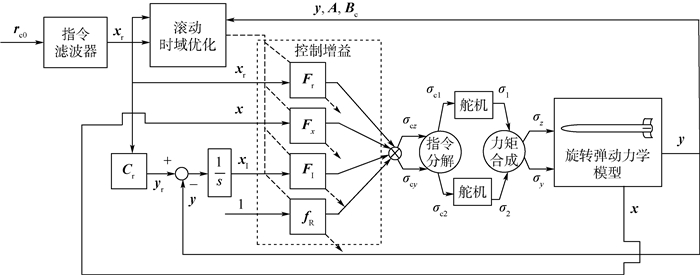
基于RHO控制器结构如图 2所示。通过式(35)计算得到控制量

|
(35) |
|
| 图 2 基于RHO的控制系统结构 Fig. 2 Structure of control system based on RHO |
为了验证控制系统的鲁棒性,在原有气动参数基础上加上15%作为建模误差,并在旋转弹准弹体坐标俯仰通道施加30 sin(2πt) N·m的干扰信号。指令滤波器参数为
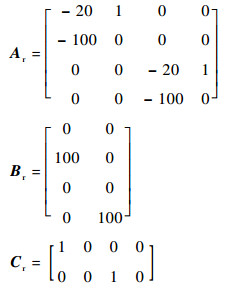
|
RHO控制器设计参数为
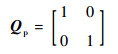
|
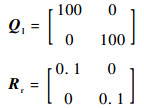
|
旋转弹质量m=465 kg,机翼参考面积S=0.070 9 m2,弹体直径D=0.3 m,舵机系统增益ks=10;舵机系统时间常数Ts=0.016;舵机系统阻尼μs=0.5;飞行速度V=1 200 m/s。
法向加速度指令为幅值100 m/s2的阶跃信号,侧向加速度指令为0,仿真结果如图 3所示,分别给出了转速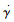
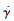

|
| 图 3 基于RHO控制器的仿真结果 Fig. 3 Simulation results based on RHO controller |
1) 旋转弹旋转导致控制通道出现耦合,随着转速的提高,舵机系统前向通道传递函数的增益将减小,舵机系统耦合通道传递函数的增益将增大,控制通道耦合加剧。
2) 在进行基于指令滤波器的RHO控制器设计中,将控制量设计为增广状态向量的线性组合。控制量中包含增广状态向量的部分充分利用反馈信息以达到保障基本稳定飞行的目的;截距控制量用来抑制建模误差和外界干扰的影响。
3) 本文设计的RHO控制器在滚动的时域区间内实时对控制参数进行更新,有效抑制了建模误差和外界干扰的影响,使得系统输出能够较好地跟踪指令信号,实现解耦控制。
| [1] |
杨树兴, 赵良玉, 闫晓勇.
旋转弹动态稳定性理论[M]. 北京: 国防工业出版社, 2014: 1-20.
YANG S X, ZHAO L Y, YAN X Y. Dynamic stability theory of spinning projectile[M]. Beijing: National Defence Industry Press, 2014: 1-20. (in Chinese) |
| [2] |
周伟. 旋转弹动态稳定性与鲁棒变增益控制[D]. 北京: 北京理工大学, 2016: 1-30.
ZHOU W. Dynamic stability and robust variable gain control of spinning projectile[D]. Beijing: Beijing Institute of Technology, 2016: 1-30(in Chinese). |
| [3] | ZHOU W, YANG S X, DONG J L. Coning motion instability of spinning missiles induced by hinge moment[J]. Aerospace Science and Technology, 2013, 30 (1): 239–245. DOI:10.1016/j.ast.2013.08.008 |
| [4] |
陈罗婧, 刘莉, 于剑桥. 双通道控制旋转导弹自动驾驶仪解耦控制研究[J].
北京理工大学学报, 2008, 28 (1): 11–14.
CHEN L J, LIU L, YU J Q. Decoupling control of a double-channel control rolling missile autopilot[J]. Transaction of Beijing Institute of Technology, 2008, 28 (1): 11–14. (in Chinese) |
| [5] |
陈罗婧, 刘莉, 于剑桥. 双通道控制旋转导弹自动驾驶仪回路数学变换及其耦合性分析[J].
北京理工大学学报, 2007, 27 (10): 847–850.
CHEN L J, LIU L, YU J Q. Transform and coupling analysis of double-channel control rolling missile autopilot loop[J]. Transaction of Beijing Institute of Technology, 2007, 27 (10): 847–850. DOI:10.3969/j.issn.1001-0645.2007.10.001 (in Chinese) |
| [6] |
袁天保, 刘新建, 秦子增. 自旋弹弹导弹动力学与控制[J].
宇航学报, 2006, 27 (2): 217–220.
YUAN T B, LIU X J, QIN Z Z. Dynamic and control of spinning ballistic missile[J]. Journal of Astronautics, 2006, 27 (2): 217–220. (in Chinese) |
| [7] |
闫晓勇, 李克勇, 杨树兴. 基于动态逆理论的自旋弹控制方法[J].
弹箭与制导学报, 2009, 29 (5): 83–86.
YAN X Y, LI K Y, YANG S X. The control method of spinning missile based on dynamic inversion[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2009, 29 (5): 83–86. (in Chinese) |
| [8] | THEODOULIS S, WERNERT P. Flight control for a class of 155 mm spin-stabilized projectiles with course correction fuse[C]//AIAA Guidance, Navigation, and Control Conference. Reston: AIAA, 2011: 241-245. |
| [9] | THEODOULIS S, GASSMANN V, WERNERT P. Guidance and control design for a class of spin-stabilized fin-controlled projectiles[J]. Journal of Guidance, Control, and Dynamics, 2013, 36 (2): 517–531. DOI:10.2514/1.56520 |
| [10] | THEODOULIS S, SEVE F, WERNERT P. Robust gain-scheduled autopilot design for spin-stabilized projectiles with a course-correction fuze[J]. Aerospace Science and Technology, 2015, 42 : 477–489. DOI:10.1016/j.ast.2014.12.027 |
| [11] | WARD D G, BARRON R L. A self-designing receding horizon optimal flight controller[C]//Proceedings of the American Control Conference. Washington, D. C. : Barron Associates, 1995: 3490-3494. |
| [12] | FAWZY M, ABOELELA M A S, RHMAN O A E, et al. Design of missile control system using model predictive control[J]. The Online Journal on Computer Science and Information Technology, 2011, 1 (3): 64–70. |
| [13] | BACHTIAR V. Multi-objective design of model predictive control and its application in missile autopilot and guidance[D]. Melbourne: University of Melbourne, 2016. |
| [14] |
钱杏芳, 林瑞雄, 赵亚男.
导弹飞行力学[M]. 北京: 北京理工大学出版社, 2006: 60-70.
QIAN X F, LIN R X, ZHAO Y N. Missile flight aerodynamics[M]. Beijing: Beijing Institute of Technology Press, 2006: 60-70. (in Chinese) |
| [15] | SONNEVELDT L, CHU Q P, MULDER J A. Nonlinear flight control design using constrained adaptive backstepping[J]. Journal of Guidance, Control, and Dynamics, 2007, 30 (2): 322–335. DOI:10.2514/1.25834 |
| [16] |
陈伟, 冯高鹏, 邓坤. 基于滚动时域优化的变后掠角飞机修正控制律设计[J].
南京航空航天大学学报, 2017, 49 (1): 96–104.
CHEN W, FENG G P, DENG K. Design of retrofit control law based on receding horizon optimal technique for variable sweep wing aircraft[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2017, 49 (1): 96–104. (in Chinese) |
| [17] | KIRK D E. Optimal control theory an introduction[M]. New York: Dover Puchblications, 2004: 90-93. |
| [18] | TODOROV E. Optimal control theory[M]. Massachusetts: MIT Press, 2006: 1-15. |



