“低慢小”目标的探测是一个世界性难题,困难主要源于以下3个方面[1-2]:①飞行高度“低”,一般在1000m以下,地面雷达观测时会有大量杂波进入接收机,尤其在建筑密集的城市环境中,探测难度更大。②飞行速度“慢”,一般小于200km/h,其回波信号处于杂波主瓣区,容易与鸟群等低速杂波混淆。为防止过多虚警,雷达往往设置速度阈值,导致低速的低空小目标被滤除。③雷达散射截面积(RCS)“小”,目标信噪比低,雷达反射信号忽隐忽现,目标不易被发现与识别。随着无人机技术的日渐成熟,其作为一种典型的“低慢小”目标,严重威胁航班安全运行[3-4]。
雷达系统通常包括检测和跟踪2个部分。其中,检测部分将目标从噪声和杂波环境中提取出来,获得目标的速度、位置等状态信息;跟踪部分对目标下一刻的状态进行预测,进而形成稳定航迹。在常规雷达系统中,检测与跟踪部分通常分别考虑和设计[5-6]。实际上,二者是相互影响的。检测是跟踪的前提,良好的检测是保证跟踪性能的基础;同时,跟踪能进一步完善检测结果,利用跟踪获得的目标动态特征能够提高检测能力[7-8]。因此,本文提出一种基于Rao-Blackwellized蒙特卡罗数据关联的检测跟踪联合优化算法,对雷达目标检测与跟踪进行交互处理,将跟踪结果反馈给检测部分,提高雷达系统对低空小目标的检测能力,同时保证下一步的精确跟踪。
1 检测跟踪联合优化技术雷达系统在完成目标检测之后,通常将波门内超过一定阈值的量测数据通过跟踪算法进行关联[9]。如将跟踪结果反馈至检测中心,进而根据该反馈信息调整波门内的检测阈值,改善检测结果,此类算法即可称为检测跟踪联合优化算法。王云奇[10]结合目标、环境等先验知识的辅助,量化分析检测性能与跟踪性能的关系,实现检测和跟踪的耦合。刘红亮、严俊坤等[11-12]提出一种航迹恒虚警的目标检测跟踪一体化算法,根据帧虚警概率调整预测波门内的检测门限,完成目标检测与跟踪的联合优化过程。闫学昭[13]采用DSP等硬件编程方法,搭建了雷达目标检测与跟踪交互处理模块,将跟踪结果反馈至检测系统,在提高检测准确率的前提下实现了精确跟踪。
综上所述,这些算法的共同点在于基于一定规则降低波门内的检测阈值,以牺牲波门内局部虚警率为代价提升局部目标的检测率[11]。可见,波门的设置至关重要,如果波门面积(体积)过小,则可能将检测目标排除在外;如果波门面积(体积)过大,则可能引入过多虚警,导致计算机过载。针对此缺点,本文提出一种基于Rao-Blackwellized蒙特卡罗数据关联的检测跟踪联合优化算法。该算法采用序贯蒙特卡罗(Sequential Monte Carlo, SMC)(又称为粒子滤波)方法实现多目标跟踪,由于粒子能够用于表示多种不同的数据关联假设,基于SMC方法的多目标跟踪算法可视为多假设跟踪(Multiple Hypothesis Tracking, MHT)的推广[14]。此外,Rao-Blackwellizion方法的应用能提高算法的准确率和效率,采用卡尔曼滤波或扩展卡尔曼滤波等方法估计目标状态,将SMC方法仅用于数据关联估计,使得联合后验分布由混合高斯表示,比纯粹的SMC方法具有更小的方差。同时,本文算法能够根据粒子的分布范围确定波门大小,在考虑粒子权重的前提下,利用检测单元与所有粒子的相对位置对检测门限进行修正。
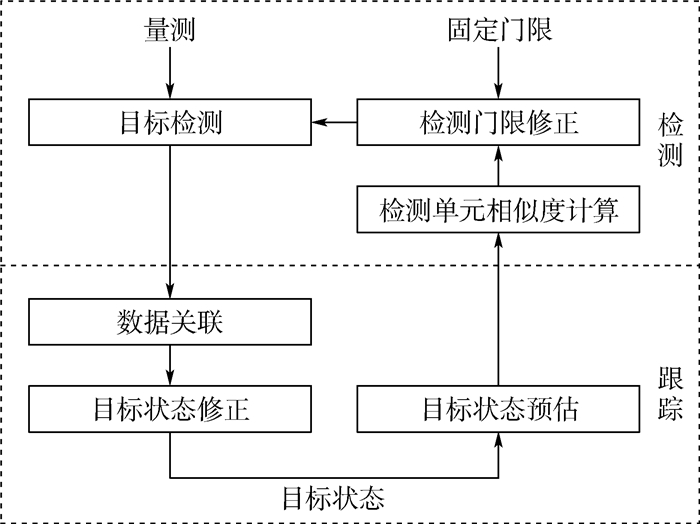
2 基于SMC的检测跟踪联合优化算法本文提出一种基于Rao-Blackwellized蒙特卡罗数据关联的检测跟踪联合优化算法,包括检测和跟踪2个部分,将粒子滤波跟踪获取的目标状态信息反馈至检测部分,以修正相关检测单元的检测门限,实现检测与跟踪的联合优化,算法流程如图 1所示,详细步骤如下:
|
| 图 1 目标检测跟踪联合优化算法流程图 Fig. 1 Flowchart of joint optimization algorithm for target detection and tracking |
步骤1 粒子滤波目标状态预估。
以一组N个粒子表示目标的当前状态{wk-1(i), ck-1(i), mk-1(i), Pk-1(i):i=1, 2, …, N},基于每个粒子i=1, 2, …, N在k-1时刻的预估值mk-1(i)和协方差Pk-1(i)对k时刻的目标状态进行卡尔曼预估:
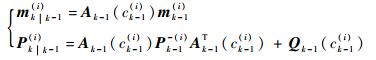
|
(1) |
式中:ck-1(i)为数据关联指数;Ak-1和Qk-1分别为k-1时刻的转换矩阵和过程噪声矩阵;mk|k-1(i)和Pk|k-1(i)分别为粒子i在k时刻的预估状态和协方差。
计算每个粒子新的非归一化权重为
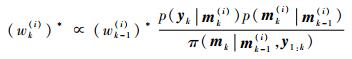
|
(2) |
式中:wk-1(i)为粒子权重;yk为k时刻的量测; y1:k为1~k时刻的所有量测;π(mk|mk-1(i), y1:k)为前一时刻的重要性分布;p(mk(i)|mk-1(i))为目标的动态模型,描述了目标的随机动态;p(yk|mk(i))为测量模型,描述了基于目标当前状态的测量值分布。
进行权重归一化处理:
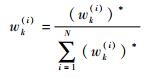
|
(3) |
步骤2 检测单元相似度计算。
基于高斯概率分布函数计算检测单元uk与每个粒子预估位置的空间相似度:
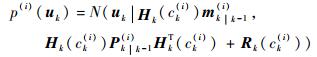
|
(4) |
式中:Hk和Rk分别为k时刻的量测模型矩阵和量测噪声矩阵;N(·)表示检测单元与粒子预估位置的相似度。
结合每个粒子的权重,得到每个检测单元与所有粒子群预估位置的空间相似度为
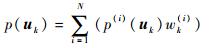
|
(5) |
步骤3 检测门限修正。
利用步骤2计算所得的每个检测单元与所有粒子群预估位置的空间相似度,对每个检测单元的固定检测门限θ进行修正[15-16],修正后的检测门限表示为

|
(6) |
式中:γ为门限修正强度参数。
该模型的合理性在于:对于与粒子预估位置相距较远的检测单元,其为目标量测的概率较小,则p(uk)值趋近于0,e-γp(uk)值趋近于1,以至于不对阈值进行修正;对于与粒子预估位置相距较近的检测单元,其为目标量测的概率增大,则p(uk)值增大,且0 < e-γp(uk) < 1。参数γ能够调节该指数函数模型的非线性属性,较大的γ值能够强化模型对检测门限的影响; 相反,较小的γ值会弱化以上影响。在目标检测过程中,对于小弱目标,一般会设置较低的检测门限,通过跟踪算法剔除杂波和虚警,并通过本文算法进一步降低预估区域的检测门限;对于回波较强的目标,可适当提高检测门限,以减少虚警数量,提高跟踪效率。
步骤4 目标检测。
根据步骤3计算所得的检测门限,由式(7)判断检测单元中是否存在目标:
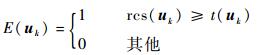
|
(7) |
式中:rcs(uk)为检测单元uk处的量测回波强度值,若该值大于或等于检测门限,则数据确认为目标(E(uk)=1),由yk表示,反之则无目标(E(uk)=0)。
步骤5 数据关联。
假设马尔可夫模型为m次,则数据关联指数ck取决于先前的m个关联结果ck-m:k-1,假设虚警在量测空间V中均匀分布,卡尔曼滤波的量测相似度计算如下:
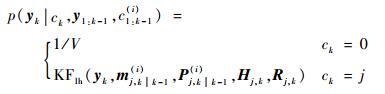
|
(8) |
式中:j=1, 2,…, T,T为目标数目;KFlh(·)代表卡尔曼滤波器测量相似度估计;Hj, k和Rj, k分别为目标j的量测模型矩阵和量测噪声矩阵。
对于j=1, 2,…, T,有
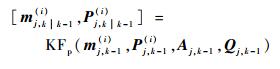
|
(9) |
式中:KFp(·)代表卡尔曼滤波的预估部分;mj, k-1(i)和Pj, k-1(i)分别为粒子i目标j的预估值和协方差;Aj, k-1和Qj, k-1分别为动态模型转换矩阵和目标j的过程噪声矩阵。
数据关联结果由最优重要性分布决定,其概率分布结果计算如下:
1) 计算非归一化噪声关联概率:

|
(10) |
式中:
2) 为每个目标j=1, 2,…, T计算非归一化目标关联概率:
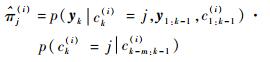
|
(11) |
式中: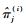
3) 归一化重要性分布:
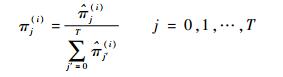
|
(12) |
4) 概率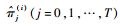
步骤6 粒子滤波目标状态修正。
基于数据关联结果ck(i)对每个粒子进行卡尔曼滤波更新:
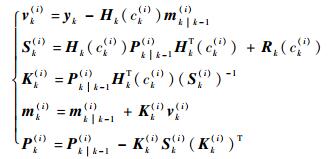
|
(13) |
式中:mk(i)和Pk(i)分别为粒子i在k时刻更新后的估计值和协方差;vk(i)、Sk(i)和Kk(i)为过程变量。
重新计算粒子权重并估计有效粒子数:
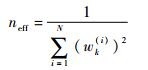
|
(14) |
如有效粒子数过低(如neff < N/4),则进行重采样。
3 实验结果分析本节分别针对仿真数据和雷达实测数据,评价本文算法的有效性,评价指标包括目标数Nd、虚警数Nfa、检测率Pd、虚警率Pfa、工作特征(Receiver Operator Characteristic, ROC)曲线、均方根误差(Root-Mean-Square Error, RMSE)等。
3.1 仿真数据根据雷达目标散射原理,RCS随目标与雷达的相对角度变化,具有起伏特性。雷达回波起伏与RCS值相关,雷达与目标间角度的变化导致雷达回波强度变化,最终决定雷达图像中像素灰度值的大小。同时,低空雷达具有较宽的垂直波束,接收的回波中容易混入地杂波而导致虚警。本节的仿真数据以瑞利分布模拟地杂波,以4类χ2分布模拟低空目标的RCS概率密度分布[17]。
模拟低空目标的4类χ2分布概率密度函数为

|
(15) |
式中:
模拟地杂波的瑞利分布概率密度函数为
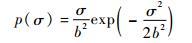
|
(16) |
式中:b为瑞利系数。
以离散维纳过程速度模型建立杂波环境中的单目标运动模型,其中目标的状态可以写为
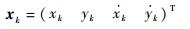
|
(17) |
式中:(xk, yk)为二维直角坐标系中的目标位置;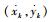
离散动态可以表示为线性、时不变构造方程:
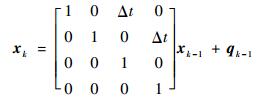
|
(18) |
式中:qk-1为离散高斯过程白噪声,矩特征为

|
(19) |
其中:时间步长设定为Δt=0.1;过程噪声的功率谱密度设定为q=0.1。
为构造杂波测量环境,如果测量值为噪声,则数据关联指数ck设定为0,如果为真实目标则设定为1。杂波测量值均匀地分布在空间[-5, 5]×[-4, 4]中。真实目标的测量模型与附加的高斯噪声成线性关系。因此,可以将联合测量相似度表示为
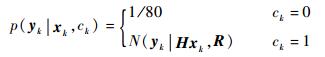
|
(20) |
量测噪声矩阵为

|
(21) |
数据关联的先验值完全独立,写为

|
(22) |
说明量测为杂波的概率是pc,量测为目标的概率是1-pc。pc代表了杂波在量测中所占的比例,该值越大,跟踪的难度也越大。
如图 2所示,经过240步仿真,目标从(-4, -0.2)出发,在0~1.0 s以速度(1, 0)匀速运动,在1.1~3.0 s完成右转弯,在3.1~3.5 s以速度(0, -1)匀速运动,在3.6~5.5 s完成左转弯,在5.6~8.0 s以速度(1, 0)匀速运动,在8.1~10.5 s完成左转弯,在10.6~14.0 s以速度(0, 1)匀速运动,在14.1~16.5 s完成左转弯,在16.6~19.0 s以速度(-1, 0)匀速运动,在19.1~21.0 s完成左转弯,在21.1~21.5 s以速度(0, -1)匀速运动,在21.6~23.5 s完成右转弯,在23.6~24.0 s以速度(-1, 0)匀速运动,直至结束。杂波概率为0.3。针对4类目标RCS模型,按照图 2中的雷达目标运动轨迹,经过1000次蒙特卡罗仿真并取平均值,图 3给出不同杂波概率条件下(pc=0.1, 0.3, 0.5)的ROC曲线和RMSE曲线,对比了采用本文算法对检测门限进行修正前后的跟踪结果,粒子数为10。

|
| 图 2 雷达目标仿真运动轨迹 Fig. 2 Simulation of radar target motion trajectory |
由图 3中4类模型的ROC曲线可见,本文算法均明显改善了4类目标模型的检测效果,其中,模型1的检测效果稍差,模型2~模型4的检测效果逐渐改善,这是由目标的散射特性决定的。具体而言,模型1的典型目标为前向观察的小型喷气飞机,模型2的典型目标为螺旋桨推进飞机、直升机等,模型3的典型目标为喷气飞机、大型民用客机,模型4的典型目标为侧向观测的导弹与高速飞行体等。显然,模型1的检测难度最大,模型2~模型4的检测难度逐渐降低。由于目标检测阈值在修正前后均采用了数据关联算法剔除杂波,pc值对ROC曲线的影响不大。由图 3中4类模型的RMSE曲线可见,pc值对RMSE曲线的作用明显,当pc值提高时,RMSE明显提高,跟踪效果变差。同时发现,当杂波比例较低时(pc=0.1, 0.3),量测中的虚警较少,跟踪精度(RMSE)较高,此时,本文算法利用跟踪结果对检测门限进行反馈修正,能够进一步提高跟踪精度。但是,当杂波比例较高时(pc=0.5),杂波和虚警在量测中的比例达到50%,此时由于目标量测较少,导致跟踪精度(RMSE)降低。由实验结果可见,如果阈值设置过低(θ < 1.5),检测门限经过修正后的跟踪结果反而可能进一步恶化,这可能是由于过低的阈值引入部分虚警导致的。因此,当虚警比例较高时,建议适当提高阈值(θ>1.5),采用检测门限反馈修正算法能够在一定程度上改善跟踪结果,确保算法收敛。

|
| 图 3 雷达目标仿真运动跟踪效果 Fig. 3 Simulation results of radar target motion tracking |
针对4类目标RCS模型,表 1~表 4给出了粒子数N为10、50和100的情况下,本文算法给定不同分割阈值时的RMSE值,杂波比例均设定为pc=0.1。通过对以上4组数据的分析,粒子数对检测结果影响不大,粒子数较多时的检测结果有时甚至稍逊于粒子数较少的时候。其原因在于本文算法采用Rao-Blackwellization方法将单目标跟踪与数据关联分开处理,将SMC(粒子滤波)方法用于数据关联,采用较少的粒子数,实现杂波与虚警量测中的多目标跟踪,可视为MHT的推广。Rao-Blackwellized粒子滤波的理论基础是某些滤波方程可以闭合的形式计算,其他采用蒙特卡罗采样,而不是对所有方程都采用采样方法。Rao-Blackwell的思想实现了较小的估计方差,其可视为用无穷集合去替代有限集合,往往能得到更为准确的结果。
| θ | RMSE | ||
| N=10 | N=50 | N=100 | |
| 0.5 | 0.1287 | 0.1289 | 0.1294 |
| 1.0 | 0.1314 | 0.1313 | 0.1318 |
| 1.5 | 0.1342 | 0.1336 | 0.1347 |
| 2.0 | 0.1375 | 0.1380 | 0.1375 |
| 2.5 | 0.1406 | 0.1409 | 0.1408 |
| 3.0 | 0.1437 | 0.1441 | 0.1446 |
| θ | RMSE | ||
| N=10 | N=50 | N=100 | |
| 0.5 | 0.1266 | 0.1265 | 0.1265 |
| 1.0 | 0.1273 | 0.1270 | 0.1267 |
| 1.5 | 0.1282 | 0.1279 | 0.1280 |
| 2.0 | 0.1291 | 0.1296 | 0.1291 |
| 2.5 | 0.1311 | 0.1305 | 0.1307 |
| 3.0 | 0.1325 | 0.1328 | 0.1329 |
| θ | RMSE | ||
| N=10 | N=50 | N=100 | |
| 0.5 | 0.1266 | 0.1264 | 0.1264 |
| 1.0 | 0.1264 | 0.1265 | 0.1264 |
| 1.5 | 0.1268 | 0.1259 | 0.1267 |
| 2.0 | 0.1270 | 0.1272 | 0.1271 |
| 2.5 | 0.1284 | 0.1283 | 0.1282 |
| 3.0 | 0.1291 | 0.1296 | 0.1285 |
| θ | RMSE | ||
| N=10 | N=50 | N=100 | |
| 0.5 | 0.1266 | 0.1269 | 0.1265 |
| 1.0 | 0.1262 | 0.1258 | 0.1263 |
| 1.5 | 0.1266 | 0.1265 | 0.1262 |
| 2.0 | 0.1263 | 0.1265 | 0.1260 |
| 2.5 | 0.1272 | 0.1266 | 0.1272 |
| 3.0 | 0.1275 | 0.1275 | 0.1275 |
3.2 实测数据
基于一组S波段非相参雷达数据和一组S波段相参雷达数据,在前期研究成果的基础上,采用本文算法进行处理,并与现有经典算法进行对比分析,2组数据的采样周期均为2.5s。第1组测试数据为S波段非相参雷达采集的图像序列,图中目标为一架波音737客机,分辨率1024×1024,量程22km,共120帧。图 4给出了某帧图像的检测跟踪结果。其中,图 4(a)在原始图像中标定了目标位置,分别采用固定阈值(Fixed Threshold, FT)、单元平均恒虚警(Cell Average-ConstantFalseAlarmRate, CA-CFAR)和本文算法进行目标检测;图 4(b)为目标跟踪结果。实验结果表明,目标检测阈值设置为θ=70时,FT算法在引入228个虚警的前提下能够检测到目标,CA-CFAR算法不仅能检测到目标,且将虚警数降为25个,基于前期研究成果[18],结合本文算法,粒子数为10,能够检测到小弱目标,且将虚警数减少到2个。图 4(b)为检测阈值设定为θ=120时,本文算法的目标跟踪结果,此时120帧图像的目标检测累积之和为Nd=119,Nfa=3,所有信息叠加在雷达背景图像上,3个虚警位置疑为未形成轨迹的低空未知目标。

|
| 图 4 S波段非相参雷达目标检测与跟踪结果 Fig. 4 Target detection and tracking results of S-band incoherent radar |
为比较各类算法的鲁棒性,表 5给出了设置不同分割阈值的情况下,各类算法处理120帧雷达图像获取的目标数和虚警数总和,包括FT、CA-CFAR、最小选择恒虚警(Small of-Constant False Alarm Rate, SO-CFAR)和本文算法。形态学处理(Morphological Processing, MP)是一种经典的图像处理算法,对于剔除雷达图像中由单个像素组成的杂波信息,效果良好[19]。此处,将MP算法作为所有算法的后处理,将“腐蚀”和“膨胀”处理相结合,既能剔除虚警,又能将属于同一目标的多个量测区域重新联通,避免将目标信息误认为虚警。由表 5可见,当检测到的目标数为114时,FT的虚警数为3539,CA-CFAR的虚警数为2469,而SO-CFAR的虚警数为3541。本文算法在设定不同阈值时,几乎能检测到所有目标,虚警数最小值仅为1。总体而言,本文算法最优,CA-CFAR算法优于FT算法,SO-CFAR算法甚至略逊于FT算法,其原因在于SO-CFAR算法通常将局部检测阈值设置过低,容易导致较高虚警率。
| θ | FT+MP | CA-CFAR+MP | SO-CFAR+MP | 本文算法+MP | |||||||
| Nd | Nfa | Nd | Nfa | Nd | Nfa | Nd | Nfa | ||||
| 30 | 119 | 16030 | 114 | 3320 | 119 | 16053 | 120 | 3504 | |||
| 40 | 119 | 9357 | 114 | 2469 | 119 | 9368 | 120 | 1032 | |||
| 50 | 116 | 5674 | 113 | 1886 | 116 | 5679 | 120 | 329 | |||
| 60 | 114 | 3539 | 111 | 1492 | 114 | 3541 | 120 | 105 | |||
| 70 | 112 | 2077 | 109 | 1124 | 112 | 2077 | 120 | 36 | |||
| 80 | 112 | 1197 | 110 | 774 | 112 | 1197 | 119 | 16 | |||
| 90 | 109 | 645 | 107 | 473 | 109 | 645 | 119 | 10 | |||
| 100 | 108 | 331 | 107 | 284 | 108 | 331 | 119 | 6 | |||
| 110 | 106 | 147 | 105 | 136 | 106 | 147 | 119 | 3 | |||
| 120 | 104 | 44 | 104 | 41 | 104 | 44 | 119 | 1 | |||
第2组测试数据在某雷达测试外场,由S波段相参雷达采集的轻小型无人机目标数据,该无人机目标沿正北偏西方向逐渐远离雷达飞行,量程6km。门限θ为目标RCS值,典型无人机目标的RCS值很小,属于小弱目标。
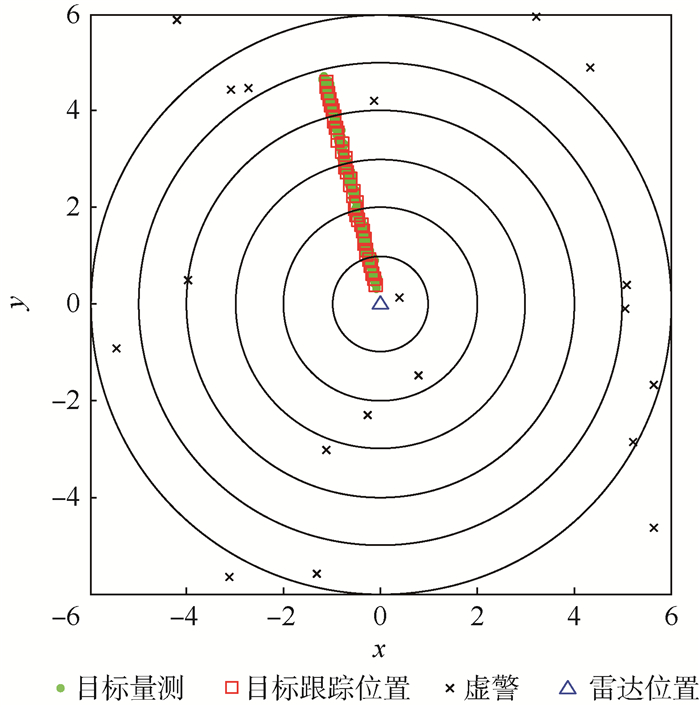
图 5中,采样周期为360个。表 6对比了设定不同θ值时的检测结果。本文算法将粒子数设定为10,能够在检测到339个无人机目标的情况下将虚警数降低到17。相参雷达已经剔除了静止的背景地物回波,且对虚警具有一定的抑制作用,本文算法的作用主要在于跟踪目标的同时提高对小弱目标的检测能力。
|
| 图 5 S波段相参雷达无人机目标检测与跟踪结果 Fig. 5 UAV target detection and tracking results of S-band coherent radar |
| θ | FT算法 | 本文算法 | |||
| Nd | Nfa | Nd | Nfa | ||
| 0.01 | 327 | 21 | 339 | 21 | |
| 0.02 | 273 | 21 | 339 | 21 | |
| 0.03 | 201 | 17 | 339 | 17 | |
4 结论
本文结合SMC方法计算的粒子范围确定波门大小,在考虑粒子权重的前提下,利用检测单元与所有粒子的相对位置对检测门限进行修正,提高对小弱目标的检测能力。通过将本文算法与其他经典算法进行对比,得出以下结论:
1) 由仿真结果可见,本文算法对于各种类型雷达目标的检测结果均有明显改善,在杂波比例较低时,对跟踪精度也有一定提高。
2) 本文算法分别对每个目标进行卡尔曼滤波预估、更新和测量相似度估计,比纯粹的粒子滤波方法效率更高,以较少的粒子数就能实现对目标的精确跟踪。
3) 将本文算法与前期研究成果相结合,并应用于S波段非相参雷达采集的图像序列,检测结果表明,本文算法能够改善局部区域内的目标检测结果,优于其他经典算法。
4) 将本文算法应用于S波段相参雷达数据,能够提高对低空无人机目标的检测跟踪能力。
| [1] |
韩崇昭, 朱洪艳, 段战胜, 等.
多源信息融合[M]. 北京: 清华大学出版社, 2006: 320-365.
HAN C Z, ZHU H Y, DUAN Z S, et al. Multi-source information fusion[M]. Beijing: Tsinghua University Press, 2006: 320-365. (in Chinese) |
| [2] | ASLAN M S, SARANL A. Threshold optimization for tracking a nonmaneuvering target[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 37 (2): 2844–2859. |
| [3] |
吕信明. 军用无人机的发展及对策[J].
国防科技, 2013, 34 (1): 5–7.
LV X M. Military UAV development and countermeasures[J]. National Defense Science & Technology, 2013, 34 (1): 5–7. (in Chinese) |
| [4] |
何煦. 对低空小型无人机的对抗方法研究[J].
中国新通信, 2016, 18 (15): 147–149.
HE X. Research on countermeasures against low-altitude small UAV[J]. China New Telecommunications, 2016, 18 (15): 147–149. DOI:10.3969/j.issn.1673-4866.2016.15.123 (in Chinese) |
| [5] | RICHARDS M A. Fundamentals of radar signal processing[M]. New York: McGraw-Hill, 2005: 1-15. |
| [6] | SKOLNIK M I. Introduction to radar systems[M]. New York: McGraw-Hill, 2002: 5-10. |
| [7] | BAR-SHALOM Y, LI X R, KIRUBARAJAN T. Estimation with application to tracking and navigation: Theory algorithms and software[M]. New York: John Wiley & Sons, Inc., 2001: 35-42. |
| [8] | LI X R, JILKOV V P. Survey of maneuvering target tracking, Part Ⅴ:Multiple-model methods[J]. IEEE Transactions on Aerospace and Electronic Systems, 2005, 41 (4): 1255–1321. DOI:10.1109/TAES.2005.1561886 |
| [9] | BLACKMAN S S. Multiple hypothesis tracking for multiple target tracking[J]. IEEE Aerospace and Electronic Systems Magazine, 2004, 19 (1-2): 5–18. |
| [10] |
王云奇. 知识辅助检测跟踪一体化算法研究[D]. 成都: 电子科技大学, 2014: 4-12.
WANG Y Q. Research of detection-tracking-integration algorithm with knowledge-aided[D]. Chengdu: University of Electronic Science and Technology of China, 2014: 4-12(in Chinese). |
| [11] |
刘红亮, 周生华, 刘宏伟, 等. 一种航迹恒虚警的目标检测跟踪一体化算法[J].
电子与信息学报, 2016, 38 (5): 1072–1078.
LIU H L, ZHOU S H, LIU H W, et al. An integrated target detection and tracking algorithm with constant track false alarm rate[J]. Journal of Electronics & Information Technology, 2016, 38 (5): 1072–1078. (in Chinese) |
| [12] |
严俊坤, 刘红亮, 戴奉周, 等. 一种具有恒虚警性质的检测跟踪联合处理算法[J].
电子与信息学报, 2014, 36 (11): 2666–2671.
YAN J K, LIU H L, DAI F Z, et al. Joint detection and tracking processing algorithm with constant false alarm rate property[J]. Journal of Electronics & Information Technology, 2014, 36 (11): 2666–2671. (in Chinese) |
| [13] |
闫学昭. 雷达目标检测与跟踪交互处理[D]. 大连: 大连海事大学, 2011: 35-40.
YAN X Z. Radar target detection and tracking interactive processing[D]. Dalian: Dalian Maritime University, 2011: 35-40(in Chinese). |
| [14] | KOKKALA J, SÄRKKÄ S. Combining particle MCMC with Rao-Blackwellized Monte Carlo data association for parameter estimation in multiple target tracking[J]. Digital Signal Processing, 2015, 47 : 84–95. DOI:10.1016/j.dsp.2015.04.004 |
| [15] | MCHUGH J M, KONRAD J, SALIGRAMA V, et al. Foreground-adaptive background subtraction[J]. IEEE Signal Processing Letters, 2009, 16 (5): 390–393. DOI:10.1109/LSP.2009.2016447 |
| [16] | STAUFFER C, GRIMSON E. Learning patterns of activity using real-time tracking[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22 (8): 747–757. DOI:10.1109/34.868677 |
| [17] |
黄培康, 殷红成, 许小剑.
雷达目标特性[M]. 北京: 电子工业出版社, 2005: 114.
HUANG P K, YIN H C, XU X J. Radar target characteristics[M]. Beijing: Publishing House of Electronics Industry, 2005: 114. (in Chinese) |
| [18] |
陈唯实, 李敬. 基于空域特性的低空空域雷达目标检测[J].
航空学报, 2015, 36 (9): 3060–3068.
CHEN W S, LI J. Radar target detection in low-altitude airspace with spatial features[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36 (9): 3060–3068. (in Chinese) |
| [19] | GONZALEZ R C, WOODS R E, EDDINS S L. Digital image processing using MATLAB[M]. Englewood Cliffs: Prentice Hall, 2009: 261-268. |



