飞行汽车的种类很多,固定翼飞行汽车因其较好的飞行性能和航程等优势,近年来逐渐成为国内外研究的重点[1-4]。对于采用固定翼的飞行汽车,其起飞过程时间很短, 但作为地面行驶和飞行阶段之间的过渡过程,是飞行汽车应用中的关键阶段。
由于飞行汽车在地面行驶状态和飞行状态的驱动方式不同,因而飞行汽车动力系统的匹配和对应的驱动策略就很重要,然而近年来国内外鲜有针对性的成果。
本文针对某型飞行汽车,通过动力学分析和仿真建模,针对起飞阶段进行了动力匹配计算,分析了双模式驱动的优势,并在其基础上进行了传动系统优化分析。
1 双模式驱动与最佳切换时刻的定义 1.1 双模式驱动对于固定翼飞行汽车[1-4],起飞阶段的驱动力可以类似于飞机,由螺旋桨提供。然而螺旋桨的效率与进距比关系密切,在车速较低时螺旋桨提供的驱动力有限[1-2, 5]。与之相对的,轮胎在这一阶段能够持续提供稳定的驱动力;这部分如果能够得到妥善利用,对于提高起飞阶段的加速性能大有裨益。如果能够充分利用轮胎在低速时提供的大驱动力,整个起飞阶段的加速性能都将得到提高。
当车速逐渐提升,进距比也随之增大,螺旋桨逐渐工作到高效率区;另一方面,升力的增长影响附着条件,轮胎能提供的驱动力越来越小;高速下螺旋桨由提供驱动力成为了必然选择。
综合考虑整个起飞阶段,当速度较低时由轮胎提供驱动力,使得整车能够更快的加速;当轮胎驱动力不足时改由螺旋桨驱动,直至达到起飞速度,即双模式驱动,较之单纯的螺旋桨驱动,更能充分利用发动机功率,起飞的加速时间和滑跑距离也都将得到优化。因而对于双模式驱动的研究具有重要意义。
1.2 最佳切换时刻采用双模式驱动的控制策略可以充分利用发动机功率,2种驱动模式切换时刻的选择成为关键。为了更好地分析这个问题,需要定义“最佳切换时刻”的概念,即对于采用双模式驱动起飞策略的飞行汽车,以在起飞加速过程中能够保持正常的行驶状态为前提,起飞过程中必然存在一个或几个时间点,在该时间点将发动机动力输出由轮胎转换至螺旋桨,可以使起飞过程加速时间、滑跑距离最短。将这一个或几个时间点定义为最佳切换时刻。本文的理论计算和优化过程都将以最佳切换时刻作为对象,后续将不再赘述。
2 动力学分析 2.1 双模式驱动行驶状态的分类按照双模式驱动的思想,飞行汽车在运行过程中大致可以分为3种状态:
1) 地面运行。机翼不展开,此时的受力情况与普通的汽车类似,发动机的扭矩通过轮胎转变为驱动车辆前进的驱动力。
2) 起飞阶段。轮胎驱动,机翼展开,与地面运行状态的主要区别在于升力,主要出现在起飞滑跑的前半段。
3) 螺旋桨驱动。机翼展开,受力情况与普通飞机类似,应用在起飞阶段及飞行阶段。
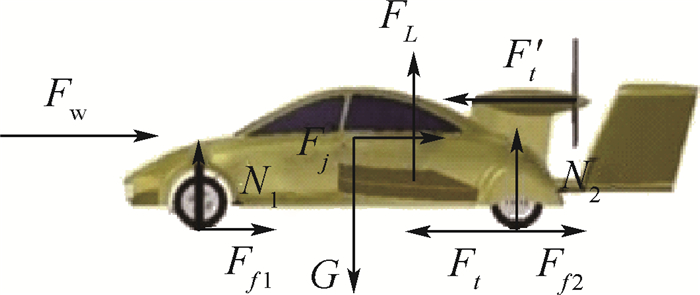
图 1给出了飞行汽车运行过程中可能受到的所有力[6-7]。图中水平方向上:Ft和Ft′,分别为轮胎和螺旋桨提供的驱动力;飞行汽车为后驱,故轮胎驱动力作用于后轮;Ff1和Ff2分别为前后轮胎受到的滚动阻力;Fw为整车受到的迎风阻力。Fj为整车受到的加速阻力。竖直方向上:G为整车受到的重力;N1、N2分别表示前轮、后轮受到的地面支持力;FL为机翼提供的升力。
本文在分析时,为简便忽略了一些实际问题的因素,对受力模型进行了如下简化:
1) 认为前后轮载荷平均分配,忽略由于质心不平分轴距带来的一系列影响,该影响包括但不限于:后轮载荷所决定的附着力的限制、前后轮滚动阻力的大小、起飞过程中整车姿态变化导致的升阻力特性变化等。
2) 不针对力矩做分析,将车速达到起飞车速(升力、重力相平衡)作为分析的终点。
3) 不考虑爬坡阻力Fi的影响,认为在起飞过程中沿着水平路面行驶。
2.2 飞行汽车动力学建模本文参考一般车辆的受力分析特征[6-7],建立的飞行汽车动力学模型为
水平方向:
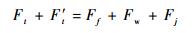
|
(1a) |
竖直方向:
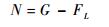
|
(1b) |
将水平方向的各项计算过程展开,得
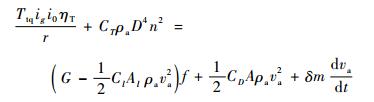
|
(2) |
式中:Ttq为发动机输出的转矩;ig为各挡位传动比;i0为主减速器传动比;ηT为传动系统机械效率;r为车轮半径;CT、Cl和CD分别为螺旋桨拉力系数、机翼升力系数和迎风阻力系数;D为螺旋桨直径;n为螺旋桨转速;Al为机翼投影面积;f为滚动阻力系数, 根据路面状况的不同会有很大区别;A为换算的迎风面积;ρa为地面状况的空气密度,考虑到飞行汽车飞行高度不超过2000m,在计算过程中认为空气密度在整个运行范围内变化不大;δ为旋转质量换算系数,由经验公式求得[7];m为整车质量;va为整车前进速度,在不考虑风速的情况下,整车相对于空气的速度等于整车的前进速度。
需要说明的是,3种形式模式下的受力情况并不相同,实际计算中应用的受力模型如下:
1) 地面运行。
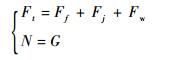
|
(3) |
FL在这一阶段忽略。
2) 起飞阶段。纯轮胎驱动。
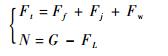
|
(4) |
3) 螺旋桨驱动。
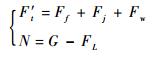
|
(5) |
根据2.2节所建立的动力学模型,对该飞行汽车进行动力匹配计算[8-13]。飞行汽车的基本参数如表 1所示。
| 参数 | 数值 |
| 载荷W/N | 6500 |
| 起飞速度/(km·h-1) | 110 |
| 升阻比K | 10 |
| 迎风面积A/m2 | 2 |
| 车轮半径r/m | 0.52 |
| 螺旋桨传动比i | 2.43 |
| 螺旋桨直径D/m | 1.8 |
| 机翼投影面积Al/m2 | 9 |
3.1 发动机选型计算
对于飞行汽车来说,发动机的选型由平飞时所需的功率作为重要参考。
飞行器巡航所需的推力为
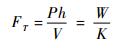
|
(6) |
式中:h为稳定飞行的高度;V为飞行速度。
提供这些推力所需的功率为

|
(7) |
将飞行汽车的参数代入式(7),得P=50.56kW。
本文选用的发动机外特性如图 2所示。

|
| 图 2 发动机外特性曲线 Fig. 2 External characteristic curves of engine |
主减速器传动比根据最高挡(直接挡)下的最高车速进行计算,根据动力学模型:Ft=Ff+Fw+Fj,最高车速运行状态,加速阻力Fj为0,则
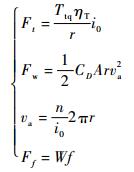
|
(8) |
利用发动机相关数据:最大转矩为127N·m,最大转矩转速为5500r/min,即可求得主减速器传动比i0。
3.2.2 一挡传动比一挡传动比根据最大爬坡度的要求,根据动力学模型:Ft=Ff+Fw+Fj+Fi,爬坡过程认为保持很低车速匀速前进,Fw、Ff均认为是0,则
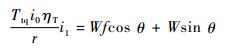
|
(9) |
式中:θ为爬坡坡度。
根据主减速器传动比及爬坡度要求,即可求得一挡传动比i1。
3.2.3 中间挡传动比对于中间挡,当一挡和最高挡确定后,通常按照等比级数分配。同时,为避免各挡之间换挡困难,相邻两挡之间的传动比一般不超过1.7~1.8。
根据以上原则,用于匹配选定发动机的传动系统传动比为:i0=3.2;i1=2.4;i2=1.8;i3=1.34;i4=1。
4 双模式驱动行驶状态仿真在节气门全开状态下,汽车原地起步连续换挡加速时间为

|
(10) |
式中:第1项为车辆原地起步阶段,即车速从0增加到最低稳定车速时所需的时间,第2项为从最低稳定车速连续换挡加速到最高车速所需要的时间,主要取决于换挡规律,第3项为换挡过程中所需要的时间;g为重力加速度,计算时取为9.8m/s2; Δtm为司机换挡所需的反应时间,根据经验取0.2~0.5s,本文在计算过程中取为0.5s。
以上述加速时间计算公式为基础,根据理论受力模型和参数选取,利用Simulink建立了模拟行驶状态的仿真模型[14-16]。
仿真模型有四大部分,分别对应计算轮胎驱动力、螺旋桨驱动力、迎风阻力和滚动阻力,根据受力计算前进的加速度,进而通过积分求得整车的加速时间和滑跑距离。加速时间按照式(10)计算,仿真中计算连续换挡加速时间和换挡过程的延迟时间。需要说明的是,由于原地加速时间受离合器接合规律的影响,很难在仿真模型中体现,因此在仿真模型中,忽略了这部分加速时间。对于最低稳定车速的选取,参考同等整备质量的车辆。
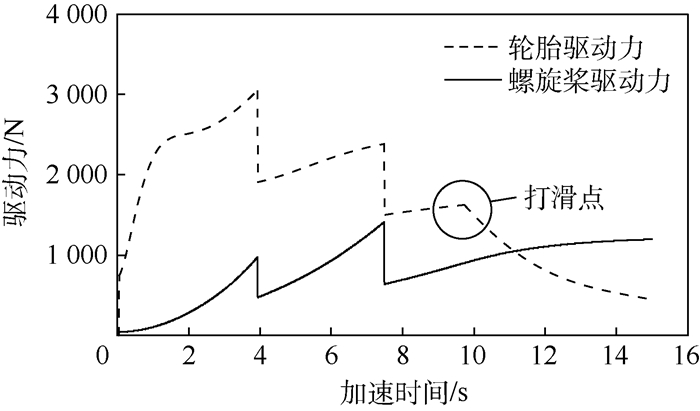
5 双模式驱动控制及最佳切换时刻分析 5.1 最佳切换时刻的选取2.1节进行受力分析时提到,起飞阶段驱动与地面运行最大的区别在于升力的影响,升力随车速的提高而增大,受此影响轮胎与地面的附着力减小,轮胎能提供的驱动力也逐渐变小。当车速增大到某一值时,达到轮胎的打滑界限,如图 3所示。
|
| 图 3 起飞阶段轮胎驱动力与对应发动机转速下螺旋桨驱动力 Fig. 3 Wheel driving force and propeller driving force under the same engine speed during takeoff stage |
起飞滑跑开始阶段,螺旋桨的效率低,此时轮胎驱动力远高于对应发动机转速下螺旋桨提供的推力。随着发动机转速和车速的提升,螺旋桨提供的推力逐渐增大,而轮胎驱动力由于传动比以及升力的影响,呈现阶梯状减小的趋势。轮胎与螺旋桨所能提供的驱动力,在二挡末相等。
综合以上2个因素,初步确定在发动机由二挡切换到三挡时,脱开轮胎驱动,转为纯螺旋桨驱动。
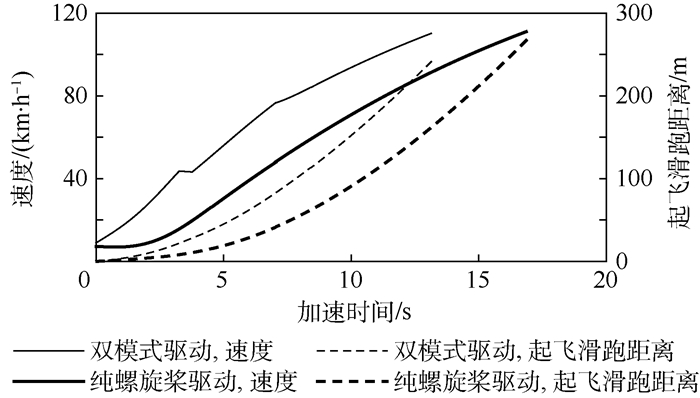
5.2 双模式驱动与纯螺旋桨驱动对比在同样的工况下(初速度、目标速度、载荷等),分别计算采取双模式驱动策略以及纯螺旋桨驱动2种起飞方式的加速时间和起飞滑跑距离,最终结果如图 4所示。
|
| 图 4 起飞过程加速曲线 Fig. 4 Accelerating curves during takeoff stage |
加速时间及起飞滑跑距离计算结果如表 2所示。
| 驱动方式 | 加速时间/s | 起飞滑跑距离/m |
| 纯螺旋桨驱动 | 16.87 | 276 |
| 双模式驱动 | 13.15 | 240 |
| 优化率/% | 22.05 | 13.04 |
从表 2中可以看出,采用双模式的驱动策略,可以有效提升起飞阶段的动力性能。
5.3 双模式驱动下各参数对起飞性能的影响 5.3.1 传动比对于飞行汽车来说,不同的传动比会导致2个因素发生改变。以一挡传动比为例,较大的传动比使得:①一挡期间轮胎的驱动力更大;②一挡换二挡时的车速更低,使得飞行汽车在一挡加速持续时间更短。对于缩短起飞滑跑距离来说,前者有利,后者不利,因此从定性分析的角度很难判断传动比的变化对结果产生的影响。
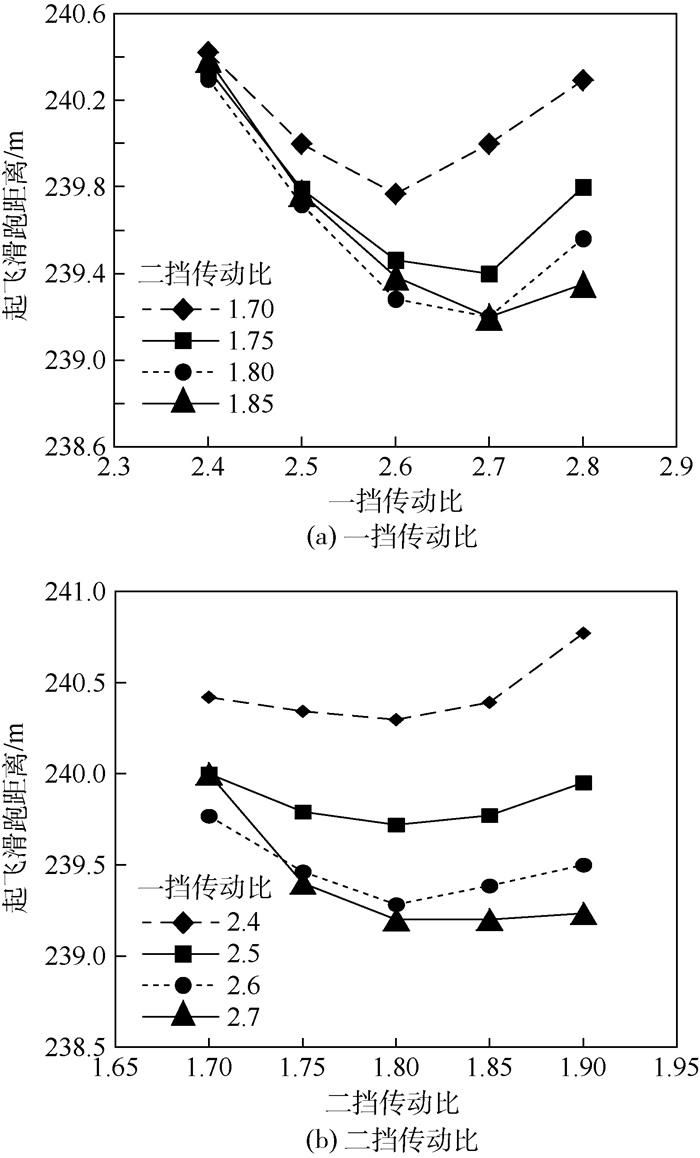
通过仿真计算,一挡、二挡传动比变化对起飞性能的影响结果如图 5所示。
|
| 图 5 传动比对起飞滑跑距离的影响 Fig. 5 Influence of transmission ratio on takeoff running distance |
从图 5(a)可以看出,当二挡传动比不变时,随着一挡传动比的增大,起飞滑跑距离呈现先递减后递增的变化趋势,即对于不同的二挡传动比,都有一个最佳的一挡传动比使得起飞滑跑距离最短。而且可以看出,随着二挡传动比的增大,该最佳一挡传动比值也逐渐增大。本文讨论的飞行汽车,当二挡传动比从1.70增大到1.85时,最佳的一挡传动比从2.6增大到2.7。
从图 5(b)可以看出,当一挡传动比不变时,随着二挡传动比的增大,起飞滑跑距离呈现先递减后递增的变化趋势,即对于不同的一挡传动比,也存在一个最佳的二挡传动比使得起飞滑跑距离最短。这与一挡传动比对起飞滑跑距离的影响规律一致。
通过优化分析看出,一挡选择2.7、二挡选择1.80是飞行汽车传动比的更优选择。然而,由于总体来说起飞滑跑时间比较短,传动比的优化对于缩短起飞滑跑距离产生的作用很有限(仅有0.5%),所以在进行传动比的选择时,应以概念设计为核心,动力性要求可以适当弱化。
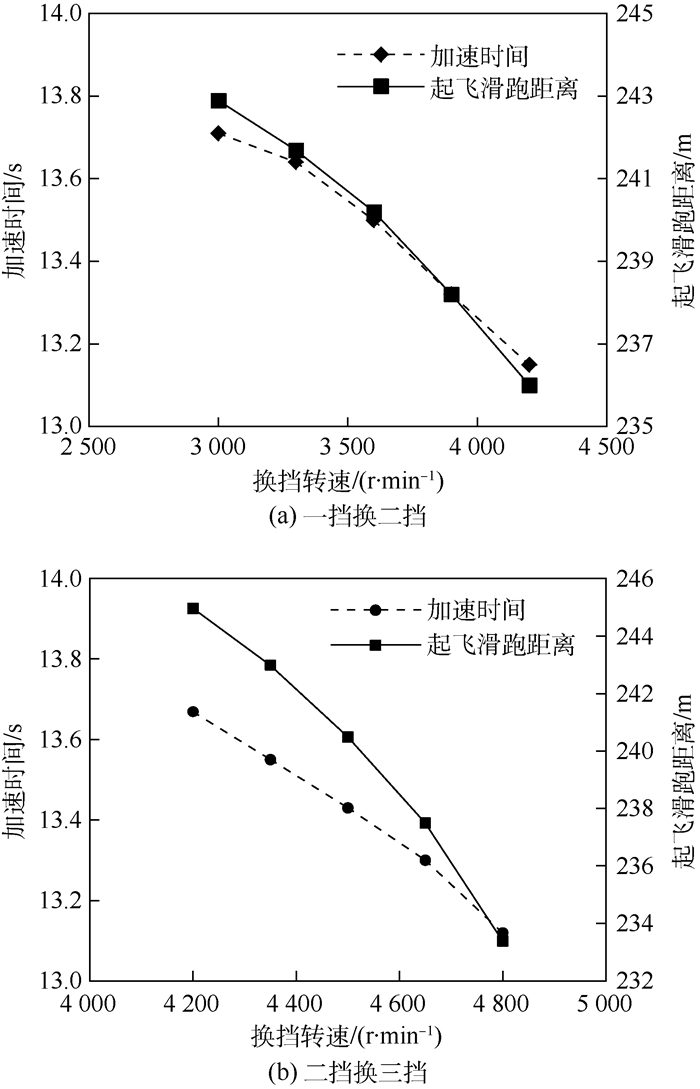
5.3.2 换挡转速换挡转速的影响受发动机特性影响较大,对于本文选用的发动机,其峰值转矩出现在4800r/min前后,更高的换挡转速可以充分利用发动机的高转矩区;同时,轮胎提供的驱动力大于纯螺旋桨驱动力,换挡转速越高,则轮胎驱动的持续时间越长,相应的飞行汽车起飞滑跑距离越短。其影响具体如图 6所示。
|
| 图 6 换挡转速对加速时间和起飞滑跑距离的影响 Fig. 6 Influence of shifting speed on acceleration time and takeoff running distance |
如图 6所示,增大换挡转速能缩短约5%的加速时间和起飞滑跑距离,所以,在起飞阶段尽可能延迟换挡有益于提升动力性能。同时也应该注意到,转速越高意味着车速也会越快,有可能造成轮胎打滑,所以换挡转速不能无限制的提高。
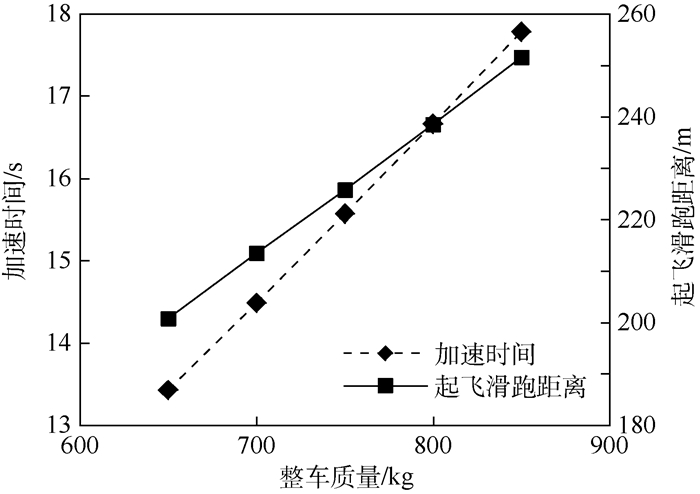
5.3.3 整车设计参数整车质量对加速时间和起飞滑跑距离的影响如图 7所示。整车质量越重,所需加速时间越长,起飞滑跑距离越长。
|
| 图 7 整车质量对加速时间和起飞滑跑距离的影响 Fig. 7 Influence of vehicle quality on acceleration time and takeoff running distance |
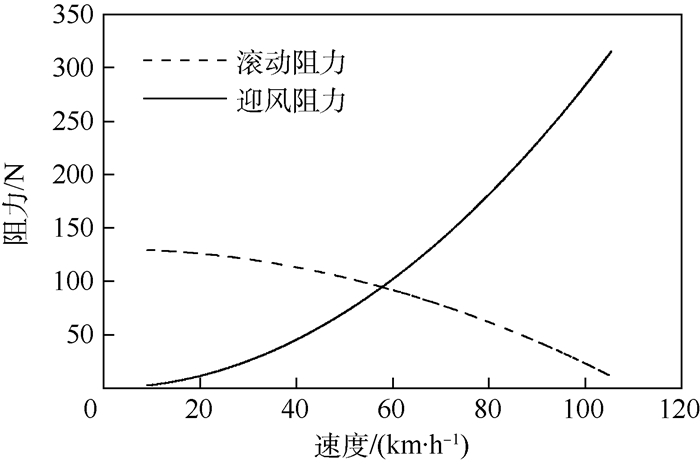
整车所受的阻力包括滚动阻力和迎风阻力,其所占比重变化规律如图 8所示。
|
| 图 8 滚动阻力和迎风阻力与车速的关系 Fig. 8 Relationship between wheel and windward resistance and vehicle speed |
随着车速的增大,迎风阻力逐渐成为主要因素,对于飞行汽车来说,从设计上减小迎风阻力也是提升动力性能的重要途径。
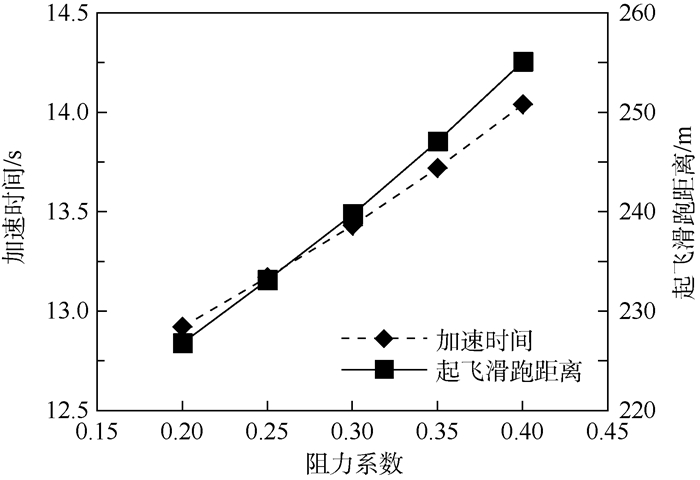
整车质量为800kg时阻力系数变动对起飞性能的影响如图 9所示。阻力系数越大,起飞的加速时间越长,滑跑距离越大。
|
| 图 9 阻力系数对加速时间和起飞滑跑距离的影响 Fig. 9 Influence of drag coefficient on acceleration time and takeoff running distance |
路上行驶与空中飞行,不单单是2种运行状态,两者所处的环境条件、发动机工况、正常运行状态所需要的适应性系数等参数也有很大区别[17]。一般来说,乘用车的发动机经常工作在中低转速,而飞行器的发动机通常工作在高转速。本文选用的发动机转矩峰值出现在4800r/min,高于一般的乘用车发动机。
选取适应性系数不同的发动机外特性曲线进行对比,分析发动机适应性系数对加速性能产生的影响。
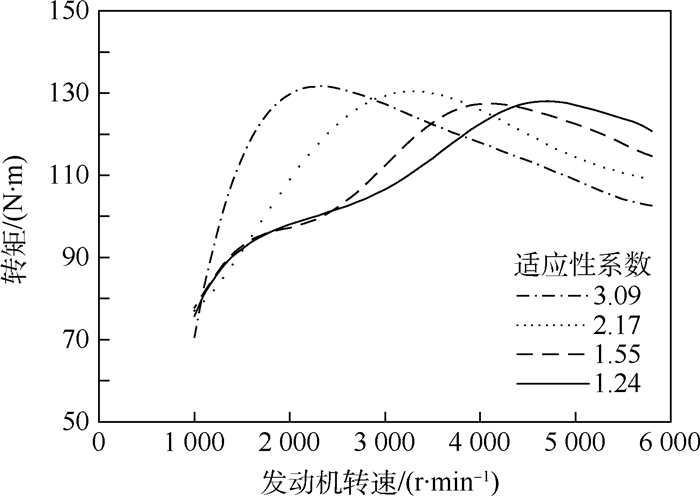
用于计算的外特性曲线如图 10所示。
|
| 图 10 不同发动机转矩特性曲线 Fig. 10 Different engine torque characteristic curves |
分别以图 10中4条特性曲线作为发动机外特性,按照双模式驱动的控制策略作为起飞策略进行计算,图 11、图 12分别为加速过程中加速时间和起飞滑跑距离的对比。
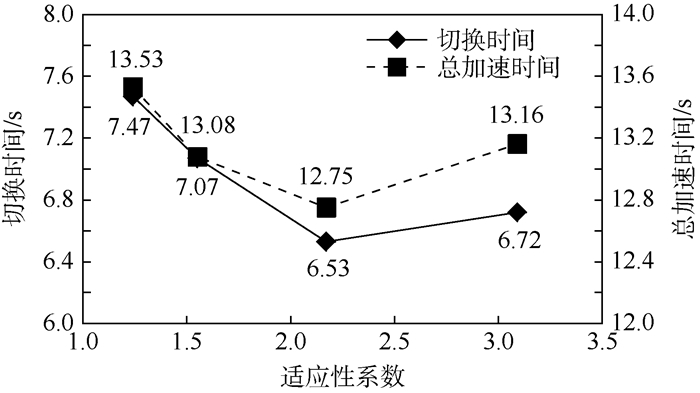
|
| 图 11 发动机适应性系数对切换时间和总加速时间的影响 Fig. 11 Influence of engine adaptability coefficient on switching time and take-off acceleration time |

|
| 图 12 发动机适应性系数对切换时刻行驶距离和总起飞滑跑距离的影响 Fig. 12 Influence of engine adaptability coefficient on running distance at switching time and running distance of take-off stage |
由图 11、图 12可以看到,当适应性系数增大时,起飞性能得到提升;适应性系数在2.2附近时,起飞滑跑距离最短,加速到起飞速度所需的时间也最少;在最高转矩和功率相差不大的情况下,匹配程度不同的发动机在切换前的加速时间和起飞滑跑距离甚至相差10%以上。分析原因,因为在起飞阶段,特别是轮胎驱动阶段发动机的常用工作转速在2000~4000r/min,过高或过低的峰值转速,都会因为扭矩特性的峰值区不能得到很好的利用而造成动力性能的恶化。当发动机的高转矩区向低速区域移动时,发动机的转矩能够更好地被利用,故而加速性能得到了提升。综上,对于发动机外特性的考虑,需要综合2种情况:①如果侧重起飞机动性,则应该在满足飞行工况的前提条件下,尽可能地使发动机的高转矩区向低转速方向靠拢,提高适应性系数;②如果侧重飞行安全性,则应该使发动机的高转矩区域向飞行额定转速靠近,适应性系数适当减小,采取其他方式来提升起飞性能。
6 结论1) 本文采用双模式的驱动策略,相比纯螺旋桨驱动,能有效提升起飞阶段的动力性能,缩短起飞滑跑阶段的时间和距离。
2) 最佳切换时刻出现在轮胎驱动力和螺旋桨驱动力相等的位置;考虑到换挡产生的驱动力变化,以换挡点作为切换点有利于改善行驶稳定性。
3) 在进行传动系统参数的选取时,应以起飞阶段轮胎驱动工况作为对象进行匹配和优化设计,尤其要注意的是,因为升力的影响,在进行挡位和换挡策略的设计时,要以避免车轮打滑作为边界条件。
4) 对于飞行汽车,空气动力性能的影响较一般汽车而言更加明显,迎风阻力在起飞阶段成为主要阻力源。
5) 与飞行汽车相匹配的发动机,适应性系数应根据起飞阶段发动机常用工况进行选取;与车用发动机不同,较大的适应性系数,不仅对提高起飞动力性无益,还会使飞行阶段工作恶化。
| [1] |
李根, 马铁林, 林海英, 等. 飞行汽车研究进展及技术难点[C]//探索创新交流: 中国航空学会青年科技论坛文集: 第7集. 北京: 航空工业出版社, 2016: 133-139.
LI G, MA T L, LIN H Y, et al. Research development and technical difficulties of flying car[C]//Exploration, Innovation, Exchange: Essays on the Youth Science and Technology Forum of China Aviation Society: Seventh. Beijing: Aeronautical Industry Press, 2016: 133-139(in Chinese). |
| [2] | RAJASHEKARA K, WANG Q, MATSUSE K. Flying cars:Cha-llenges and propulsion strategies[J]. IEEE Electrification Magazine, 2016, 4 (1): 46–57. DOI:10.1109/MELE.2015.2509901 |
| [3] |
朱保利, 程磊, 吴恢鹏. 飞行汽车概念设计与气动特性分析[J].
机械工程师, 2014 (5): 87–89.
ZHU B L, CHENG L, WU H P. Conceptualdesign and aerodynamic characteristics analysis of flying car based on CFD[J]. Mechanical Engineer, 2014 (5): 87–89. (in Chinese) |
| [4] |
王拖连, 杨世文, 薛姣, 等. 陆空两用飞行汽车发展现状与展望[J].
公路与汽运, 2011 (4): 12–16.
WANG T L, YANG S W, XUE J, et al. The development status and prospect of airphibian flying car[J]. Highway and Automotive Applications, 2011 (4): 12–16. (in Chinese) |
| [5] |
刘沛清.
空气螺旋桨理论及其应用[M]. 北京: 北京航空航天大学出版社, 2006.
LIU P Q. Air propeller theory and its application[M]. Beijing: Beihang University Press, 2006. (in Chinese) |
| [6] |
邹晓敏, 刘刚. 车辆道路行驶阻力的模拟及测量[J].
质量与认证, 2012 (12): 58–61.
ZOU X M, LIU G. Simulation and measurement of driving resistance of vehicle road[J]. China Quality Certification, 2012 (12): 58–61. (in Chinese) |
| [7] |
李晓甫, 赵克刚, 黄向东, 等. 汽车行驶阻力模型参数的确定[J].
汽车工程, 2011, 33 (8): 645–648.
LI X F, ZHAO K G, HUANG X D, et al. Determination of parameters in vehicle driving resistance model[J]. Automotive Engineering, 2011, 33 (8): 645–648. (in Chinese) |
| [8] |
张杰, 吴森堂. 一种变体飞行器的动力学建模与动态特性分析[J].
北京航空航天大学学报, 2015, 4 (1): 58–64.
ZHANG J, WU S T. Dynamic modeling for a morphing aircraft and dynamic characteristics analysis[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 4 (1): 58–64. (in Chinese) |
| [9] |
林学东.
汽车动力匹配技术[M]. 北京: 中国水利水电出版社, 2010.
LIN X D. Vehicle power matching technology[M]. Beijing: China Water and Power Press, 2010. (in Chinese) |
| [10] |
杨连生.
内燃机性能及其与传动装置的优化匹配[M]. 北京: 学术期刊出版社, 1988.
YANG L S. Performance of internal combustion engine and its optimal matching with transmission[M]. Beijing: Academic Periodical Press, 1988. (in Chinese) |
| [11] |
曲建清, 宋辉. 无人机总体与起飞性能匹配性设计优化[J].
飞行力学, 2013, 31 (3): 225–229.
QU J Q, SONG H. Design optimization of UAV configuration and takeoff performance[J]. Flight Dynamics, 2013, 31 (3): 225–229. (in Chinese) |
| [12] | ZHOU M, ZHAO L, ZHANG Y, et al. Pure electric vehicle power-train parameters matching based on vehicle performance[J]. International Journal of Control & Automation, 2015, 8 (9): 53–62. |
| [13] | ZHANG L, HAO G, YANG X, et al. The electric vehicle power design and the matching characteristics analysis of the transmi-ssion system[J]. Telkomnika Indonesian Journal of Electrical Engineering, 2013, 11 (11): 6352–6357. |
| [14] |
吴大卫, 李寒冰, 李书, 等. 基于仿真模型的短距起飞性能优化[J].
北京航空航天大学学报, 2014, 40 (6): 756–761.
WU D W, LI H B, LI S, et al. Short takeoff performance optimization based on simulation model[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40 (6): 756–761. (in Chinese) |
| [15] |
张威, 张景海, 隗海林, 等. 汽车动力学仿真模型的发展[J].
汽车技术, 2003 (2): 1–4.
ZHANG W, ZHANG J H, HUAI H L, et al. Development of vehicle dynamic simulation model[J]. Automobile Technology, 2003 (2): 1–4. (in Chinese) |
| [16] |
冯超. 基于Matlab/Simulink的电动汽车仿真模型设计与应用[D]. 北京: 中国科学院大学, 2013.
FENG C. The simulation model design and application of the electric vehicle based on Matlab/Simulink[D]. Beijing: University of Chinese Academy of Sciences, 2013(in Chinese). |
| [17] |
张雪文, 徐明亮, 杨欣. 汽油发动机的动力特性分析[J].
机械制造与自动化, 2012, 41 (1): 47–49.
ZHANG X W, XU M L, YANG X. Dynamic characteristics of gasoline engines[J]. Machine Building Automation, 2012, 41 (1): 47–49. (in Chinese) |