2. 北京航空航天大学机械工程及自动化学院, 北京 100083
2. School of Mechanical Engineering & Automation, Beijing University of Aeronautics and Astronautics, Beijing 100083, China
在平面带移动副多杆机构的研究中,机构的分支(或回路[1])指的是在不拆开给定参数机构的情况下,其连续运动所能达到的位置[2-4]。由于带移动副机构的复杂性,机构的分支往往是几个离散的运动空间。在同一个分支内,机构从一个位形转换到另一个位形不需要破坏其物理的连接。若机构的分支中存在阻挠机构运动的死点,此点为分支点,分支点将分支分为多个子分支。在子分支内,机构可以连续、平滑的运动且不存在任何奇异点。国内外很多学者提出了一系列理论对其进行分析,Ting、Wang[2-4]等根据机构的环路特点,将Stephenson六连杆机构分成2个环路,并引入关节旋转空间的概念,根据输入角和输出角之间的相互关系得到影响机构运动的奇异点。韩建友等[5-7]提出了解域综合方法,根据解曲线的映射特点构建平面多连杆机构的平面解域,继而得到机构的分支和分支缺陷。宋黎等[8-9]通过构建邻接矩阵的方法生成优先生成树,得到含复铰有移动副平面机构的分支,将机构的运动链分析及运动分析很好的结合。Plecnik和McCarthy[10]提出了自动创建平面单自由度多杆机构的运动生成算法,通过共同边缘建立循环方程对机构的分支进行分析,并对Stephenson Ⅲ型机构精确点位置进行了研究。Parrish等[11]将建立的单自由度环方程算法与连杆邻接图结合,运用到多杆多环单自由度机构中,得到9种六杆机构及71种八杆机构的环路自动生成算法。祖义祯和邓华[12]将弧长法运用到平面连杆机构的运动路径求解中,并提出了精确定位运动路径奇异点的计算方法,该方法能有效判断不同分段等情况下机构的提升形态特点。李佳等[13]提出了杆组特征值的概念,构建了带移动副机构的杆组拓扑图,导出了全移动副机构杆组的构件数和移动副之间的匹配关系。李占贤等[14]借助球面解析几何理论,采用解析法得到二自由度带移动副球面机构位置正逆解,并进一步得到机构速度和加速度的正逆解,丰富了球面机构的构型。Sultan和Kalim[15]先根据机构的环路式及微分法对齿轮五杆曲柄滑块机构进行轨迹分析,再引入Levenberg-Marquardt算法对机构的轨迹进行误差分析,减小误差,得到机构更加精确的轨迹。Soh和Ying[16]设计了一种平面六连杆和八连杆滑块机构运动生成方法,得到15种不同类型单自由度平面六连杆和八连杆机构,并将其运用到了多功能轮椅的改造设计中。Saleh[17]提出了一种带移动副和旋转副的闭环连杆机构轨迹生成方法,其中包括几何反演、分支以及奇异性等一系列运动特征。
在一定程度上,带移动副机构扩大了机构的运动范围,在工业的应用上有很重要的意义。目前,对平面多环连杆机构的死点和分支研究的较透彻的方法主要有雅可比矩阵分析法[6]和等效四杆法[18]等。雅可比矩阵分析法主要针对给定机构的几个运动位置,通过判断位置之间的关系来判断机构的运动缺陷,该方法简便且易于编程实现,对于特定位置的缺陷判断有重要的意义。而等效四杆法通过机构4个不同的瞬心构建等效四杆机构,从而推导复杂机构的死点,该方法主要用于种判断复杂机构的死点,不能判断机构分支和运动缺陷。本文在前人研究的基础上,提出了一种适用于计算机编程的方法,对带移动副平面六连杆机构的运动特性进行识别。该方法首先基于关节旋转空间的概念[1-3],将带移动副平面六连杆机构分成2部分,包括对带移动副四环链输入输出关系识别及带移动副五环链关节旋转空间识别;其次根据2个链路的共同作用得到2种带移动副的平面六连杆机构的分支以及机构各个关节在死点、分支点及各个极限位置处的具体位型。本文方法能得到带移动副平面六连杆机构运动中所有连杆的运动顺序以及运动范围,并且通过分支之间的关系能直观地判定机构的运动缺陷。
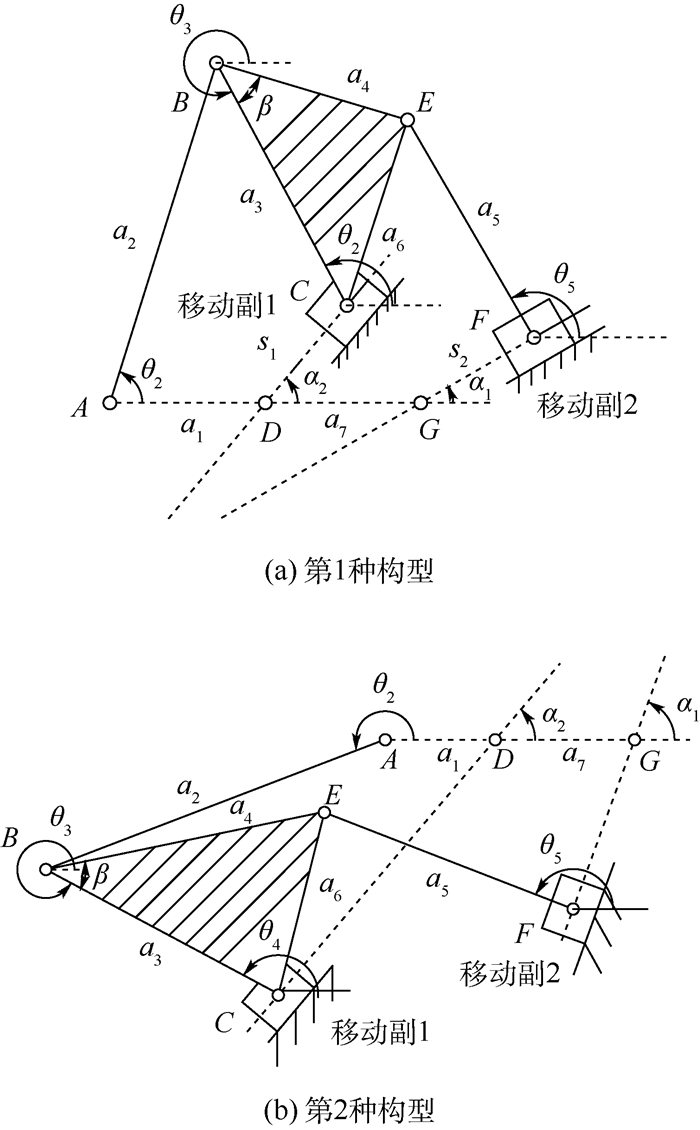
1 带移动副四环链死点识别任何带移动副平面多连杆机构都包含一个或多个带移动副四环链,如图 1、图 2所示,2种带移动副平面六连杆机构都包含带移动副四环链ABCD。分析带移动副四环链是分析带移动副平面六连杆机构的基础。

|
| 图 1 带2个移动副平面六连杆机构 Fig. 1 Planar six-bar linkage with two sliding pairs |
|
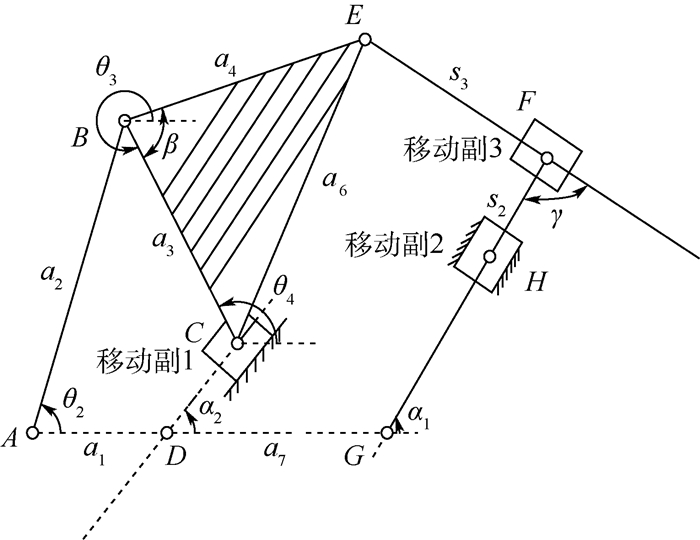
| 图 2 带3个移动副平面六连杆机构 Fig. 2 Planar six-bar linkage with three sliding pairs |
根据欧拉环方程,四环链ABCD的环式可表示为[3]

|
(1) |
式中:a1、a2、a3为连杆长度;s1为移动副1在导路上移动的距离;θ2、θ3为对应连杆的运动角度;α2为移动副1导路倾斜角度。
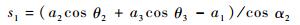
|
(2) |
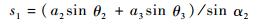
|
(3) |
消除s1,式(1)可表示为
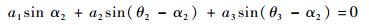
|
(4) |
当θ2、θ3为输入、输出参数时,式(4)表示θ2、θ3输入-输出关系模型,利用半角公式x3=tan(θ3/2),令sinθ3=2x3/(1+x32),cosθ3=(1-x32)/(1+x32),代入式(4)中,简化可得一个一元二次式,即
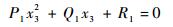
|
(5) |
式中:
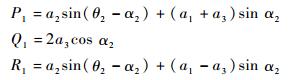
|
当P1≠0时,若要带移动副四环链型存在,即x3存在解,则式(5)必须满足:
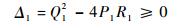
|
(6) |
整理得

|
(7) |
式中:
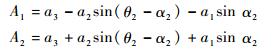
|
当Δ1=0时,即A1=0或A2=0时,表示四环链处在死点位置,其中或不能同时为0。不论带移动副四环链连杆参数的差异,四环链处于死点位置时,忽略外五环链ABEFG的影响,其构型都如图 3所示,2种构型的区别在于AB杆及滑块位置的区别。

|
| 图 3 AB杆处于极限位置的2种构型 Fig. 3 Two configurations of AB bar in limit positions |
1) A1=0且A2≠0,即a3=a2sin(θ2-α2)+a1sin α2,可根据等式得到死点处AB杆的具体位置,BC杆垂直于滑块1的导路s1,其中,0 < θ2 < α2+π,θ4=±π/2+α2,滑块在D点处导路的上方。
2) A2=0且A1≠0,即a3=-a2sin(θ2-α2)-a1sin α2,可根据等式得到死点处AB杆的具体位置,BC杆也垂直于滑块1的导路s1,其中,α2+π≤θ2 < 2π,θ4=±π/2+α2,滑块在D点处导路的下方。
根据式(5)及式(6),可根据输入角得输出角:
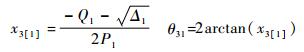
|
(8a) |
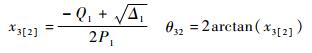
|
(8b) |
对于带移动副的平面五连杆机构ABEFG,不论其是带1个移动副的平面五连杆机构,还是带2个移动副的平面五连杆机构,其自由度都为2,根据一个驱动关节,可得带移动副平面五连杆机构在此驱动关节下的关节旋转空间,即输入变量与输出变量之间的运动范围。
2.1 带1个移动副五环链机构带1个移动副平面五连杆机构的环式可根据欧拉公式表示为
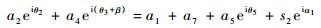
|
(9) |
式中:a4、a5、a7为连杆长度;s2为移动副2在导路上移动的距离;θ3+β、θ5为对应连杆的运动角度;α1为移动副2轴线与水平方向的夹角。
根据其实部和虚部,式(9)可表示为
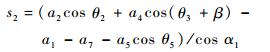
|
(10a) |
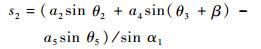
|
(10b) |
消除s2,式(9)可表示为
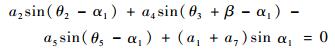
|
(11) |
利用半角公式x5=tan(θ5/2),令sin θ5=2x5/(1+x52),cos θ5=(1-x52)/(1+x52),代入式(11)中,则式(11)同样可表示为一元二次式:
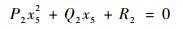
|
(12) |
式中:
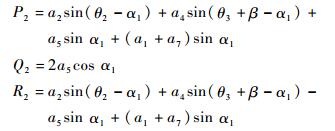
|
当P2≠0,式(12)有解必须满足:
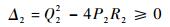
|
(13) |
整理得
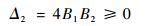
|
(14) |
式中:

|
(15a) |

|
(15b) |
式(14)产生θ2与θ3之间的关节旋转空间,其中,B1=0及B2=0表示关节旋转空间的边界,对于带移动副的平面五连杆机构ABEFG,当其处于死点位置,其有如图 4所示的2种构型。
|
| 图 4 EF杆处于极限位置的2种构型 Fig. 4 Two configurations of EF bar in limit positions |
1) B1=0且B2≠0, 即a5=(a1+a7)sin α1+a2sin(θ2-α1)+a4sin(θ3+β-α1),可根据等式得到在死点处EF杆的具体位置,其中,θ5=±π/2+α1,此时,EF杆垂直于移动副2的运动导路GF且移动副2在G点处导路的上方。
2) B2=0且B1≠0,即a5=-(a1+a7)sin α1-a2sin(θ2-α1)-a4sin(θ3+β-α1),同样可根据等式得到死点处EF杆的具体位置,同样,θ5=±π/2+α1,但EF垂直于滑块2的运动导路GF且移动副2在G点处导路的下方。
通过式(13),可得θ5:
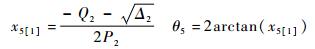
|
(16a) |
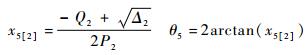
|
(16b) |
每个解对应一种机构构型,其中arctan(x5)在(-π/2, π/2)变化,与之一一相对应的θ5在(-π, π)变化。
2.2 带2个移动副五环链机构一个带3个移动副平面六连杆机构包含一个带1个移动副的四环链以及一个带2个移动副的五环链,五环通过拉伸旋转转变成四环。因此,带3个移动副平面六连杆机构的分支识别取决于四环ABCDA和五环ABEFGA的相互作用,其五环欧拉环式可表示为

|
(17) |
式中:s3为移动副3在导路上移动的距离;α1+γ为移动副3导路倾斜角度。
根据其实部和虚部,式(17)表示为

|
(18a) |
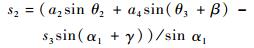
|
(18b) |
消除s2,式(17)可表示为
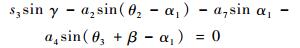
|
(19) |
令s3为未知数,式(19)的判别式为
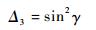
|
(20) |
在式(20)中,sin2γ≥0恒成立;当sin γ≠0时,对于每对θ2和θ3,s3有唯一确定值;但当sin γ=0,s3有无穷大解,在这种情况下的机构是无用的,因此,要满足机构存在,必须sin γ≠0。
3 分支识别方法 3.1 带2个移动副平面六连杆机构分支识别方法对于2种带移动副平面六连杆机构,其分支识别采用不同方法,判别方法可用如图 5所示的流程图表示。

|
| 图 5 带2个移动副平面六连杆机构分支识别流程 Fig. 5 Flowchart of branch identification of planar six-bar linkage with two sliding pairs |
对于带2个移动副平面六连杆机构,根据式(14)可得六连杆机构的可动范围,即其关节旋转空间。
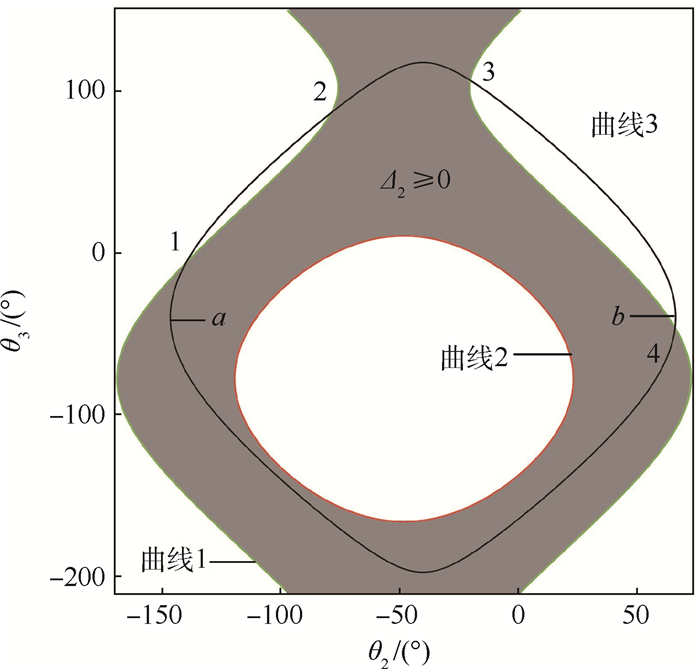
联立式(4)及式(15a),可得带2个移动副平面六连杆机构中EF杆处于第1种构型的关节角。同样,联立式(4)及式(15b),可得带2个移动副平面六连杆机构中EF杆处于第2种构型的关节角。根据第1、2节,可得在带移动副平面六连杆机构中四环链的死点位置。如图 6所示,利用Maple软件对一定参数下带2个移动副平面六连杆机构进行仿真分析,得到θ2-θ3分支曲线。其中,曲线1表示EF杆处于第1种构型的关节旋转曲线边界,曲线2表示EF杆处于第2种构型的关节旋转曲线边界,曲线1与曲线2构成的阴影部分为带2个移动副平面六连杆机构的θ2-θ3关节旋转空间,曲线3为带移动副四环ABCD的θ2-θ3输入输出曲线,与关节旋转空间边界交于1、2、3、4等4个点,这4个点表示整个机构在运动构成中产生的分支点,根据机构的分支点,将整个机构的运动分成2个分支2-3、1-4。对曲线3进一步分析,根据第1节,此参数中带移动副四环本身有2个死点a、b。对此进一步分析:
|
| 图 6 带2个移动副平面六连杆机构分支曲线 Fig. 6 Curve of branches of planar six-bar linkage with two sliding pairs |
1) 死点a在关节旋转空间的阴影范围内,整个机构运动过程中,此死点是存在的,将1-4分支分成2个子分支1-a以及a-4。
2) 死点b不在关节旋转空间的阴影范围内,机构在运动过程中,并不能达到1-2曲线,因此b在此参数的带移动副平面六连杆机构中不存在。
3.2 带3个移动副平面六连杆机构分支识别方法由于带3个移动副平面六连杆机构不需要判定关节旋转空间,即当γ≠0时,EF杆没有限制,因此只需要得到其带移动副四环链的输入输出曲线,从而得到四环链死点。
3.3 带移动副平面六连杆机构雅可比矩阵分析法联立式(10a)、式(10b)、式(18a)、式(18b)分别对θ3、θ5、α1、α2求导,整理得雅可比矩阵行列式[6]为
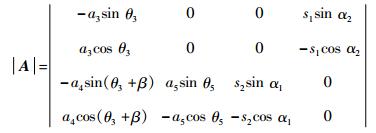
|
(21) |
将式(21)展开并求其行列式的值为

|
(22) |
式中:Δ4=sin(θ5-α1)sin(θ3-α2), α1、α2由2个移动副运动导路角度决定。
当Δ4=0时,带移动副平面六连杆机构处于奇异点位置,根据机构所处具体位置以及Δ4值的特点,可分析各个位置之间是否存在运动缺陷。
4 实例 4.1 带2个移动副平面六连杆机构分支及死点判断实例图 1为带2个移动副平面六连杆机构,某实例尺寸参数如表 1所示。
| 参数 | 数值 |
| a1 | 2.4 |
| a2 | 5.5 |
| a3 | 4.8 |
| a4 | 4.2 |
| a5 | 2.5 |
| a7 | 2.4 |
| β/(°) | 45 |
| α1/(°) | 30 |
| α2/(°) | 50 |
根据表 1中带2个移动副平面六连杆机构的参数及上述对带2个移动副平面六连杆机构分支识别方法,利用Maple软件得到θ2-θ3的分支曲线,如图 7所示。

|
| 图 7 带2个移动副平面六连杆机构实例的分支曲线 Fig. 7 Curve of branches of planar six-bar linkage with two sliding pairs |
计算出当EF杆处于极限位置时机构的分支点,如表 2所示。
| 分支点 | θ2/(°) | θ3/(°) | θ4/(°) | θ5/(°) |
| 1 | -161.4 | -28.6 | 16.4 | 120 |
| 2 | -141.6 | -92.2 | -47.2 | -60 |
| 3 | -105.5 | 55.3 | 100.3 | 120 |
| 4 | -15.6 | 91.3 | 136.3 | 120 |
| 5 | 7.9 | -152.7 | -107.7 | -60 |
| 6 | 72.6 | -74.6 | -29.6 | 120 |
根据图 7和表 2,以及机构的分支点,整个机构分成如下3个分支:1-2、3-4、5-6。
根据第1节计算可得,当带移动副平面六连杆机构处于死点位置时,机构在2种构型处,θ2分别为-162.7°、82.6°,如图 7所示,θ2在82.6°处时并不满足关节旋转空间的范围。因此在带2个移动副平面六连杆机构的运动范围内,θ2=82.6°并不属于此参数机构中的带移动副平面六连杆机构死点。根据上述理论,可得带移动副平面六连杆机构的死点如表 3所示。
死点的存在将机构的分支1-2分成2个子分支,分别是1-a、a-2。
4.2 带3个移动副平面六连杆机构分支及死点判断实例图 2为带3个移动副平面六连杆机构,某实例尺寸参数如表 4所示。
| 参数 | 数值 |
| a1 | 3 |
| a2 | 6 |
| a3 | 5.2 |
| a4 | 5 |
| a7 | 4 |
| β/(°) | 50 |
| γ/(°) | 30 |
| α1,α2/(°) | 30 |
根据第1、2节可得,带3个移动副平面六连杆机构的关节旋转空间主要由γ影响,当γ≠0时,不需要考虑其关节旋转空间,根据第1节,可得在此参数下机构的死点,如表 5所示。
| 死点 | θ2/(°) | θ3/(°) | θ4/(°) |
| a | -78.9 | -40.0 | 10.0 |
| b | -158.9 | -40.0 | 10.0 |
影响带3个移动副平面六连杆机构运动的因素主要是四环链ABCD,通过Δ1=0,可得到四环链死点a、b,代入式(8)及式(4),进而得到死点处机构各连杆的具体位置。
4.3 基于雅可比矩阵分析法的带移动副平面六连杆机构分支判断实例对于雅可比矩阵分析法,给定2个运动位置参数θ2=-50°及θ2=10°。令A点为原点,将AD设为x轴,AD逆时针旋转90°后设为y轴,建立坐标系。根据表 1,带2个移动副平面六连杆机构参数给定时,在2个位置处的位置坐标参数如表 6所示。
| 参数 | 位置1 | 位置2 |
| θ2/(°) | -50 | 10 |
| B | (3.54, -4.21) | (5.42, 0.96) |
| E | (2.94, -0.06) | (1.75, -1.10) |
| F | (1.32, 1.85) | (-0.12, -2.97) |
| Δ4 | 0.25 | -0.34 |
图 8为带2个移动副平面六连杆机构在可行运动范围内的Δ4与θ2关系曲线。其中,Δ41表示θ2=-50°的Δ4的值,Δ42表示θ2=10°的Δ4的值。根据雅可比矩阵分析法,θ2 2个位置处Δ4值的符号不同,说明存在运动缺陷。而根据本文方法,在表 1所示的机构参数下,由表 2所示的分支点及图 7所示的分支曲线,当θ2=-50°时,机构在分支3-4中,θ2=10°时,机构在分支5-6中,而2个分支之间存在运动缺陷4-5,因此2个位置之间存在运动缺陷。

|
| 图 8 带2个移动副平面六连杆机构Δ4随θ2变化曲线 Fig. 8 Change of Δ4 with θ2 for planar six-bar linkage with two sliding pairs |
通过计算可知,2种方法都能应用到带移动副平面六连杆机构的运动缺陷判定中,但切入点不同,雅可比矩阵分析法针对机构的运动位置,对各个位置之间的运动缺陷进行判断,而关节旋转空间分析法是将机构整个运动的运动分支曲线和分支点求出来,从而判断机构的运动是否存在运动缺陷。实例表明,关节旋转空间分析法在具体点之间的运动缺陷判断没有雅可比矩阵分析法直观方便,但通过分支识别图也能快速识别出来。其次,关节旋转空间分析法能得到机构极限位置的所有分支点、死点以及所有关节在极限位置的角度,对于判断机构在极限位置的构型有重要的作用。另外,关节旋转空间分析法通过分支识别图能将机构的运动范围、运动顺序、运动缺陷清晰地表达出来。
5 结论1) 根据欧拉公式,消去移动副移动距离对环路的影响,得到机构在极限位置的具体构型。
2) 结合三角换元法和判别式法,得到机构极限位置各个关节的具体角度,为带移动副平面六连杆机构的设计与制造提供了一定的理论基础。
3) 2个链路的结合(四环链和五环链)可准确得到抑制机构运动移动副六连杆链的分支点、死点,并得到机构的运动分支及所有分支的具体运动范围。通过实例验证及与雅可比矩阵分析法比较,得到本文方法能判断一定参数下的带移动副平面六杆机构的运动缺陷和运动顺序,以及2种方法各自的侧重点和优缺点,有助于探讨多环平面机构的一般研究方法。
| [1] | CHASE T R, MIRTH J A. Circuits and branches of single degree-of-freedom planar linkages[J]. Journal of Mechanical Design, 1993, 115 (2): 223–230. DOI:10.1115/1.2919181 |
| [2] | TING K L, WANG J, XUE C, et al. Full rotatability and singularity of six-bar and geared five-bar linkages[J]. Journal of Mechanisms and Robotics, 2010, 2 (1): 298–300. |
| [3] | TING K L, DOU X. Classification and branch identification of Stephenson six-bar chains[J]. Mechanism & Machine Theory, 1996, 31 (31): 283–295. |
| [4] | WANG J, TING K L, XUE C. Discriminant method for the mo-bility identification of single degree-of-freedom double-loop linkages[J]. Mechanism & Machine Theory, 2010, 4 (5): 740–755. |
| [5] |
杨通, 韩建友, 崔光珍, 等. 给定两连杆运动面的Watt-Ⅰ六连杆机构空间解域综合方法[J].
农业机械学报, 2014, 45 (10): 307–312.
YANG T, HAN J Y, CUI G Z, et al. Synthesis of Watt-Ⅰ six-bar linkage based on spatial solution region for given two coupler plans[J]. Transactions of the Chinese Society of Agricultural, 2014, 45 (10): 307–312. DOI:10.6041/j.issn.1000-1298.2014.10.048 (in Chinese) |
| [6] |
韩建友, 崔光珍, 杨通, 等. 六连杆机构四位置运动生成的解域综合理论与方法[J].
北京航空航天大学学报, 2014, 40 (9): 1170–1175.
HAN J Y, CUI G Z, YANG T, et al. The solution region synthesis theory and method of six-bar linkages with 4-position[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40 (9): 1170–1175. (in Chinese) |
| [7] |
崔光珍, 韩建友, 杨通. 给定4R开链的八杆机构解域综合理论与方法[J].
农业机械学报, 2015, 46 (4): 331–337.
CUI G Z, HAN J Y, YANG T. Solution region synthesis method of eight-bar linkages for 4R open chain[J]. Transactions of the Chinese Society of Agricultural Machinery, 2015, 46 (4): 331–337. DOI:10.6041/j.issn.1000-1298.2015.04.049 (in Chinese) |
| [8] |
宋黎, 陈磊. 含复铰有移动副平面运动链的结构类型综合方法[J].
机械科学与技术, 2009, 28 (3): 295–300.
SONG L, CHEN L. A method for structural type synthesis of planar kinematic chains with multiple joints and sliding joints[J]. Mechanical Science and Technology for Aerospace, 2009, 28 (3): 295–300. (in Chinese) |
| [9] |
宋黎, 廖爱红, 聂松辉. 含复铰有移动副平面机构运动分析数学模型的自动建立方法[J].
机械科技与技术, 2012, 31 (2): 47–52.
SONG L, LIAO A H, NIE S H. A method for automatically establishing model for kinematic analysis of planar mechanism with multiple joints and prismatic pair[J]. Mechanical Science and Technology for Aerospace, 2012, 31 (2): 47–52. (in Chinese) |
| [10] | PLECNIK M M, MCCARTHY J M. Kinematic synthesis of Stephenson Ⅲ six-bar function generators[J]. Mechanism & Machine Theory, 2016, 97 (9): 112–126. |
| [11] | PARRISH B E, MCCARTHY J M, EPPSTEIN D. Automated generation of linkage loop equations for planar one degree-of-freedom linkages, demonstrated up to 8-bar[J]. Journal of Mechanisms and Robotics, 2015, 7 (1): 14–22. |
| [12] |
祖义祯, 邓华. 基于弧长法的平面连杆机构运动分析[J].
浙江大学学报(工学版), 2011, 45 (12): 2159–2168.
ZU Y Z, DENG H. Kinematic analysis of planar pin-bar linkages by arc-length method[J]. Journal of Zhejiang University(Engineering Science), 2011, 45 (12): 2159–2168. DOI:10.3785/j.issn.1008-973X.2011.12.014 (in Chinese) |
| [13] |
李佳, 孔建益, 廖汉元, 等. 全移动副机构的型综合[J].
中国机械工程, 2012, 23 (18): 2165–2168.
LI J, KONG J Y, LIAO H Y, et al. Type synthesis of mechanism with all prismatic pairs[J]. China Mechanical Engineering, 2012, 23 (18): 2165–2168. DOI:10.3969/j.issn.1004-132X.2012.18.005 (in Chinese) |
| [14] |
李占贤, 杨志杰, 于江. 移动副驱动的2-DOF球面并联机构运动学分析[J].
机械设计与制造, 2011 (11): 216–218.
LI Z X, YANG Z J, YU J. Kinematic analysis of a 2-DOF spherical parallel mechanism driven by sliding pair[J]. Machinery Design & Manufacture, 2011 (11): 216–218. DOI:10.3969/j.issn.1001-3997.2011.11.084 (in Chinese) |
| [15] | SULTAN A, KALIM A. On the kinematics and synthesis of a geared five-bar slider-crank mechanism[J]. Proceedings of the Institution of Mechanical Engineers Part C-Journal of Mechanical Engineering Science, 2011, 225 (5): 1253–1261. DOI:10.1177/2041298310392650 |
| [16] | SOH G S, YING F. Motion generation of planar six-and eight-bar slider mechanisms as constrained robotic systems[J]. Journal of Mechanisms and Robotics, 2015, 7 (3): 975–978. |
| [17] | SALEH M A. Singularity traces of single degree-of-freedom planar linkages that include prismatic and revolute joints[J]. Journal of Mechanisms and Robotics, 2015, 8 (5): 15–18. |
| [18] | WANG J, TING K L, ZHAO D X. Equivalent linkages and dead center positions of planar single-degree-of-freedom complex linkages[J]. Journal of Mechanisms and Robotics, 2015, 7 (4): 1–6. |



