2. 中央军委联合参谋部 第55研究所, 北京 100094
2. The 55 th Institute, Joint Staff Department of the Central Military Commission, Beijing 100094, China
人工神经网络(Artificial Neural Network,ANN)凭借其强大的分类和自学习能力,已在故障诊断领域展现了良好的性能和应用价值[1-3]。但是传统ANN存在训练时间长、收敛速度慢、易陷入局部最优等局限性,这也影响了对故障诊断实时性和准确性的要求。
回声状态网络(Echo State Network, ESN)是一种基于储备池计算模型的新型递归神经网络[4],其储备池生成独立于训练过程,内部神经元随机稀疏连接,只需对储备池输出权值采用线性回归方法进行训练。ESN不仅训练算法简捷易实现,还能获得全局最优的输出权值,在非线性预测领域引起了学术界的广泛关注,并已得到成功应用[5-8],但在模式识别领域方面的应用研究还处于起步阶段[9-10]。
虽然ESN发展潜力巨大,但仍面临一些理论和实际问题有待解决。由于储备池生成的随机性,导致网络模型往往与具体问题不相关,而储备池的适应性问题对网络性能至关重要,目前有关储备池优化的研究主要集中在改变神经元类型[5]、改进网络拓扑结构[11]和优化网络参数[12]等方面。同时,ESN的训练算法还不成熟,为控制模型规模,相关学者通过子集选择方法[13]剔除了无关网络节点,但是这种基于梯度的方法效率并不高[14],且容易得到次优结果;正则化方法是一种有效的特征选择方法,它能够在计算输出权值的同时控制模型的复杂程度,相关学者进行了多种正则化稀疏模型的研究[15-18],取得了良好的效果,在兼顾性能的同时还进一步提高了模型的可解释性。
基于以上分析,本文提出了一种基于L1/2范数正则化的改进ESN,并将其应用于故障诊断问题中。通过神经可塑性机制对储备池进行优化,利用BCM规则(Bienenstock-Cooper-Munro rule)进行储备池连接权矩阵预训练,以期提升储备池的动态适应性能。在输出权值矩阵训练计算过程中,将L1/2正则子引入目标函数惩罚项,并进行改进使其在零点附近光滑,以克服迭代数值振荡问题,通过半阈值迭代法完成模型的求解过程。本文提出的模型在末制导雷达和机载电台的故障诊断中取得了良好的应用效果,具有较高的准确率。
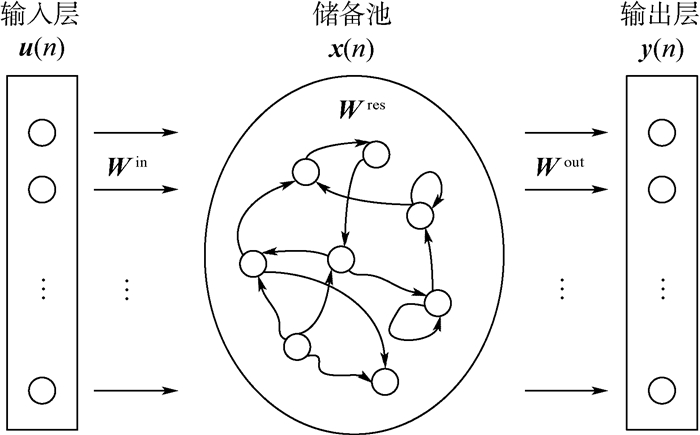
1 基于ESN的分类基本原理传统ESN模型结构如图 1所示。图中:u(n)∈RL、x(n)∈RN和y(n)∈RM分别为n时刻的输入信号、状态向量和输出向量。ESN的状态方程[19]为
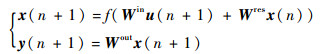
|
(1) |
|
| 图 1 ESN模型结构 Fig. 1 Architecture of ESN model |
式中:Win∈RN×L、Wres∈RN×N和Wout∈RM×N分别为输入权值矩阵、储备池连接权矩阵和输出权矩阵,Win和Wres在训练前随机生成并保持不变,Wout是唯一需要通过训练计算得到的权值矩阵;f(·)为储备池内部神经元的激励函数,通常为S型函数。
在分类问题中,给定K对训练样本集{u(n), y(n)}n=1K,u(n)为样本数据,输出变量y(n)为其对应的类别标识,当输入样本数据属于j类别时,则相应第j个输出单元为+1,其余单元为0。由于网络的回声状态属性,为避免在网络稳定之前任意初始状态对变量的影响,通常会舍弃初始的暂态过程。假设舍弃的网络状态长度为K0,储备池状态矩阵X和输出矩阵Y可以表示为
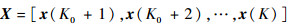
|
(2) |

|
(3) |
式中:实际训练长度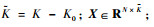

因此,网络的训练过程即为求解以下线性回归问题:

|
(4) |
回归方程可以通过伪逆法求解得到,则目标函数L(·)和输出权值估计矩阵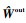
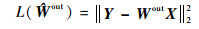
|
(5) |
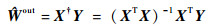
|
(6) |
式中:‖·‖2为L2范数;X†为矩阵X的伪逆。
伪逆法虽然计算简单便捷,且输出权值为无偏估计,但是存在过拟合问题,即训练误差很小,而测试误差却很大,这是由于计算过程中会产生较大方差,严重影响了模型的泛化能力。
2 储备池连接权矩阵优化在传统ESN模型中,储备池内部的连接关系及连接权矩阵Wres均为随机产生,并在训练过程中保持不变,然而储备池的内部结构对ESN分类及预测性能具有重要影响。由于突触可塑性机制能够根据输入信号刺激的活动改变储备池内部突触的强度,在可塑性准则的作用下,输入信号中所蕴含的结构信息可以在储备池训练过程中得到学习,实现连接权值的修正。本节利用BCM规则对储备池内部连接权值进行改进。
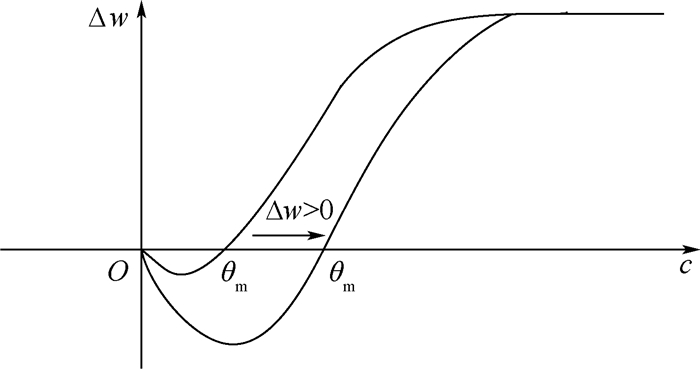
BCM规则[20]遵循Hebbian学习原理,其通过一个相当于稳定器功能的滑动阈值来控制突触的变化,阈值的改变能够控制神经元活动的增强或减弱,这一自我调节的可塑特性能够改善储备池的学习稳定性。BCM规则不仅对前后突触的时间移动平均值起作用,还能够调节突触后的活动,当积极权值变化水平较高时,减少相应的改变量。在BCM规则下,阈值大小与突触变化速率呈反比关系,当突触变化速率增加时,阈值处于较小值,反之阈值也相应增加,这也就意味着修正阈值决定了突触效能改变的方向,原理如图 2所示。
BCM规则有多种变式,本文采用如下一种形式:
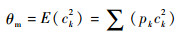
|
(7) |

|
(8) |
|
| 图 2 突触权值修正规则 Fig. 2 Synaptic weight modification rule |
式中:xj为突触前神经元输入;ck为突触后神经元输出,其等于所有输入神经元的加权和,即ck= 
由式(8)和图 2可以看出,BCM规则可以使神经元根据特定输入形成一种选择能力[21],当Δw=0时权值收敛,此时对应神经元输出c=0或c=θm的情况。此外,可塑性也是BCM规则的一个重要特点,本文改进的式(7)中,1/θm为学习速率,与标准BCM规则中学习速率为恒定常数不同,当输入分布变化使相应环境改变时,神经元连接权重就不再稳定而发展成为另一种选择特性。
经典ESN的连接权值产生是一种与具体“问题”无关的通用随机方式,本节通过引入BCM规则对储备池连接权值进行自组织优化,使得权值与训练样本输入数据相适应,并可根据输入样本的改变而做出相应调整,增强了ESN系统的适应性和样本训练过程中的数据拟合能力,进而实现提高测试样本分类准确度的目的。
3 基于L1/2范数正则化的回声状态网络 3.1 光滑L1/2范数正则化模型为克服普通线性最小二乘法出现的病态不适定问题,平衡模型的拟合能力与泛化能力,考虑在ESN的目标函数中增加正则化项,这种正则化方法已成为解决稀疏问题的有效工具,其一般具有如下形式:
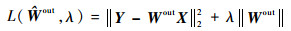
|
(9) |
式中:等号右边第1项为误差项,第2项为正则化惩罚项;λ为控制后项大小的惩罚系数。
正则化模型是一种系数收缩方法,利用惩罚项平衡模型的偏差与方差,控制输出权值幅值,改善模型求解的稳定性。
由于在改善机器学习过拟合问题上的优异表现,基于L2范数正则化的岭回归模型[15]已在ESN连接权重学习算法中得到广泛应用,作为一种光滑的凸优化模型,岭回归算法可以输出解析形式的权值解:

|
(10) |
由式(10)可以看出,由于XTX的对角元素添加了正常数项,避免了在线性回归问题中出现不可逆的状态矩阵,但是L2范数正则化模型无法得到稀疏化的解,不能通过特征选择来控制模型规模。
为了使式(9)得到稀疏化的解,基于L1范数正则化模型[22]的研究开始逐渐流行。模型惩罚项选择兼具L2范数优点的L1范数,可以利用其特征选择能力产生稀疏解,并控制网络规模[23]。但是L1范数正则化模型的目标函数在零点附近非光滑且不可微,常规求导优化方法不能直接应用,增加了模型求解的复杂程度;而且模型得到的往往不是最稀疏的解,甚至在某些变量选择情况下可能会产生不一致性问题[24]。
L1/2正则子[25]为解决特征提取及变量选择问题提供了一个新的思路,实验[26]已经证明L1/2范数正则化模型较流行的L1范数模型有更稀疏的解,且鲁棒性更优。本文利用L1/2正则子的优良性质,将其与ESN结合,在目标函数中增加L1/2正则项:
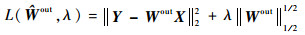
|
(11) |
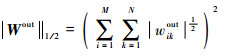
|
(12) |
但是L1/2正则子在零点处并非光滑,这会造成数值学习训练出现振荡现象。为克服上述问题,提高正则化效率,本文通过一个零点附近的光滑函数g(x)逼近|x|函数,改进L1/2正则项,改进后的误差目标函数及光滑函数为

|
(13) |

|
(14) |
式中:输出权矩阵函数g(Wout)∈RM×N;a为一个较小的正常数。
3.2 L1/2-ESN模型对于L1/2范数正则化模型的求解,虽然通过重赋权迭代算法[26]可以将其转化为L1/2范数模型进行求解,但是计算速度及复杂度依然不够理想。对应于软硬阈值迭代算法,半阈值迭代法[27]是解决L1/2正则化问题的一种快速而有效的手段,因此本文结合半阈值迭代法针对光滑L1/2-ESN模型的输出权值进行求解推导。
令R0M×N={Z=(z1, z2, …, zM)T, zi≠0},若W∈R0M×N为式(11)所示正则化模型的解,根据W的最优化一阶条件,可得
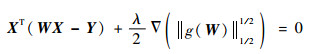
|
(15) |
式中:∇(‖·‖1/21/2)为正则项的梯度。
在式(15)两边同乘任意正参数μ,变为

|
(16) |
如果∇(‖·‖1/21/2)存在,则表明算子Rλ, 1/2(·)=(I+∇(‖·‖1/21/2))-1对任意正实数的正则化参数λ均有定义,且有

|
(17) |
定义Bμ(W)=W+μXT(Y-WX),则正则化模型的解可以固定表示为W=Rλμ,1/2(Bμ(W)),进一步给出算子Rλ,1/2的定义函数。
令
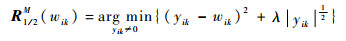
|
(18) |
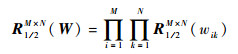
|
(19) |

|
(20) |

|
(21) |
定理[27]已经证明,从D1/2M映射到R1/2M的算子存在非线性对角化的形式,特记为
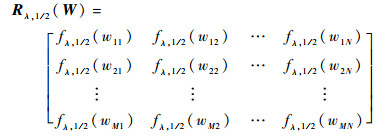
|
(22) |
式中:
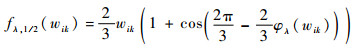
|
(23) |

|
(24) |
此时,若最小化目标函数的解为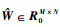
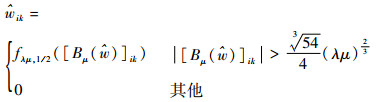
|
(25) |
综上所述,光滑L1/2-ESN模型的输出权值可以通过式(26)进行迭代更新:
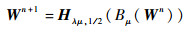
|
(26) |
式中:Hλμ, 1/2为半阈值迭代算子。若∀Z∈RM×N,则算子定义为
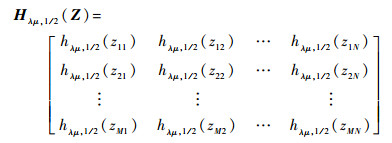
|
(27) |
式中:
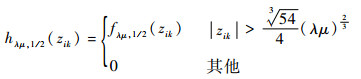
|
(28) |
针对ESN储备池随机生成的稀疏网络结构,考虑引入BCM规则对随机权重进行调整以改善储备池的动态性能,提高其对样本数据的适应性。同时在网络训练学习阶段,考虑在目标函数中添加光滑L1/2范数正则项,如式(11)所示,构建L1/2-PESN(L1/2-Plasticity Echo State Network)模型。与传统ESN模型相比,L1/2-PESN模型在保证泛化能力的基础上,能够产生更稀疏的解,以更优秀的鲁棒性求解表现实现对模型规模的有效控制。结合半阈值迭代法,可以对模型进行快速有效的求解,本文提出的L1/2-PESN模型结构如图 3所示,其训练算法具体实现步骤如下:

|
| 图 3 L1/2-PESN模型结构 Fig. 3 Architecture of L1/2-PESN model |
步骤1 设定相关网络参数。包括储备池规模、谱半径和稀疏程度;随机初始化储备池输入权值Win和内部连接权值Wres。
步骤2 连接权值Wres预训练。利用BCM规则进行Wres的无监督学习训练,调整Wres以优化储备池对样本的适应性。
步骤3 网络状态采样。根据网络方程更新状态变量,舍弃暂态过程的预热数据,形成状态矩阵X。
步骤4 计算输出权值Wout。利用半阈值迭代法对目标函数的光滑L1/2范数正则化模型进行求解,得到Wout。
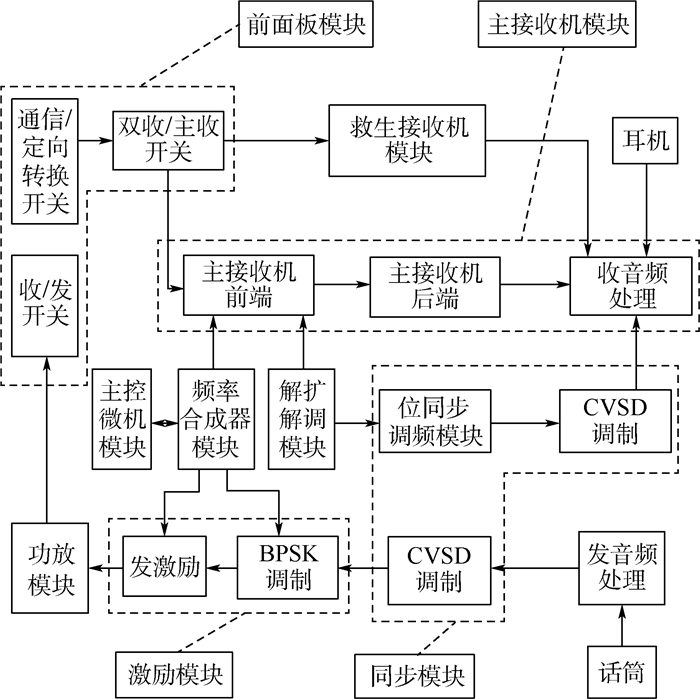
4 机载电台故障诊断实例分析某型超短波机载通信电台具有抗干扰通信功能,用于现代电子战条件下的地空和空空指挥通信,可与空军现役地空超短波抗干扰通信系统实现兼容。该电台采用模块化设计结构,其组成如图 4所示,整机由前面板模块、主接收机模块、救生接收机模块、主控微机模块、同步模块、频率合成器模块、激励模块、解扩解调模块和功放模块共9个SRU(Shop Replaceable Unit)组成。
|
| 图 4 机载通信电台组成 Fig. 4 Composition of airborne communication station |
以“电台不受控制”这一故障现象为例,对电台进行故障模块定位,涉及的测试参数包括+5 V电压(c1)、1553B总线电压(c2)、UUT收信端电压(c3)、UUT发信端电压(c4)、UUT收信端功耗(c5)、UUT发信端功耗(c6)。可能存在故障的模块为前面板模块(d1)和主控微机模块(d2)。以某部队175组实测故障数据为样本,表 1给出了经过精确离散化处理后的部分诊断数据,“1”表示正常,“0”和“2”分别表示低于下限和高于上限的情况。
| 序号 | 测试参数 | 故障模块 | |||||
| c1 | c2 | c3 | c4 | c5 | c6 | ||
| 1 | 2 | 0 | 1 | 1 | 1 | 1 | d1 |
| 2 | 1 | 2 | 1 | 2 | 1 | 2 | d2 |
| | | | | | | | |
| 174 | 1 | 1 | 1 | 1 | 1 | 2 | d2 |
| 175 | 1 | 2 | 1 | 0 | 1 | 1 | d1 |
随机选取故障数据的80%作为训练样本,剩余20%为测试样本。设置ESN储备池规模N=50,谱半径λmax=0.75,稀疏程度D=20%,输入单元L=8,输出单元M=3,针对L1/2-PESN模型,在训练开始前先利用BCM规则对Wres进行50次迭代的预训练。为比较分析各方法效果,本文引入在故障诊断领域广泛应用的BP神经网络(Back Propagation Neural Network, BPNN)、传统ESN、BCM-ESN、L1/2-ESN与本文提出的L1/2-PESN模型进行对比,其中BPNN采用单隐层的3层网络结构,隐层节点数量采用交叉验证获得,隐层激活函数为S型函数。表 2给出了各方法的性能对比结果,训练测试时间及诊断结果为分别进行100次实验后得到的平均值。
| 方法 | 储备池生成时间/s | 训练时间/s | 诊断正确率/% |
| BPNN | 43.76 | 79.6 | |
| 传统ESN | 0.49 | 14.13 | 88.4 |
| BCM-ESN | 6.04 | 14.37 | 90.5 |
| L1/2-ESN | 0.36 | 16.78 | 91.2 |
| L1/2-PESN | 6.58 | 16.64 | 93.1 |
从表 2中BPNN与传统ESN对比的实验结果可以看出,由于BPNN在训练过程中收敛速度较慢,而传统ESN的训练过程得以简化,避免了传统神经网络易陷入局部最小等问题,使得传统ESN的诊断正确率较BPNN相比提高了8.8%,训练时间的消耗也显著降低,这也证明了传统ESN具有比BPNN更加优异的性能表现。
进一步观察分析可知,仅利用BCM规则对ESN的Wres进行优化后,储备池的生成时间明显高于传统ESN模型,这是由于要对Wres进行预训练迭代学习造成的。但是故障诊断的正确率有了一定提高,这也证明了BCM准则对储备池适应性的优化是合理有效的。进一步比较L1/2-ESN与传统ESN可知,二者的训练时间相当,L1/2-ESN仅比ESN消耗稍高一些,但是由于引入了L1/2范数惩罚项,有效避免了过拟合,借助于模型的特征选择能力,诊断正确率上较传统ESN有了更优越的表现。
综合对比各诊断模型的性能表现,本文提出的L1/2-PESN模型具有最好的效果,诊断正确率最高,这也证明了本文方法在提升储备池动态性能和提升ESN泛化能力上的优越性。同传统ESN相比,虽然储备池生成需要一定的时间消耗,但是这一阶段是在训练开始前独立进行的,因此这部分额外的时间消耗对实际应用影响不大。实验结果表明,L1/2-PESN模型在机载电台模块级故障诊断问题中具有不错的应用前景。
5 结论1) 本文提出的L1/2-PESN模型在储备池生成过程中通过引入BCM规则对储备池连接权值进行自组织优化,使得权值与训练样本输入数据相适应,并可根据输入样本的改变而做出相应调整,改善了储备池的动态适应性能和样本训练过程中的数据拟合能力。
2) 借助于L1/2正则子优秀的稀疏性表现,对储备池进行了有效的输出特征选择,在控制网络规模的同时提升了模型的泛化能力。基于机载电台的故障诊断实验结果表明,本文方法较BPNN和传统ESN模型,具有良好的稳定性及更高的诊断准确率。
| [1] | CHINE W, MELLIT A, LUGHI V, et al. A novel fault diagnosis technique for photovoltaic systems based on artificial neural networks[J]. Renewable Energy, 2016, 90 : 501–512. DOI:10.1016/j.renene.2016.01.036 |
| [2] | UNAL M, ONAT M, DEMETGUL M, et al. Fault diagnosis of rolling bearings using a genetic algorithm optimized neural network[J]. Measurement, 2014, 58 : 187–196. DOI:10.1016/j.measurement.2014.08.041 |
| [3] | SHATNAWI Y, AL-KHASSAWENEH M. Fault diagnosis in internal combustion engines using extension neural network[J]. IEEE Transactions on Industrial Electronics, 2014, 61 (3): 1434–1443. DOI:10.1109/TIE.2013.2261033 |
| [4] | JAEGER H. The "echo state" approach to analysing and training recurrent neural networks-with an erratum note[R]. Bonn: German National Research Center for Information Technology GMD Technical Report, 2001. |
| [5] | LUN S X, YAO X S, QI H Y, et al. A novel model of leaky integrator echo state network for time-series prediction[J]. Neurocomputing, 2015, 159 : 58–66. |
| [6] | VARSHNEY S, VERMA T. Half hourly electricity load prediction using echo state network[J]. International Journal of Science and Research, 2014, 3 (6): 885–888. |
| [7] | MORANDO S, JEMEI S, HISSEL D, et al. ANOVA method applied to proton exchange membrane fuel cell ageing forecasting using an echo state network[J]. Mathematics and Computers in Simulation, 2017, 131 : 283–294. DOI:10.1016/j.matcom.2015.06.009 |
| [8] |
许美玲, 韩敏. 多元混沌时间序列的因子回声状态网络预测模型[J].
自动化学报, 2015, 41 (5): 1042–1046.
XU M L, HAN M. The model of factor echo state network prediction for multivariate chaotic time series[J]. Acta Automatica Sinica, 2015, 41 (5): 1042–1046. (in Chinese) |
| [9] |
郭嘉, 雷苗, 彭喜元. 基于相应簇回声状态网络静态分类方法[J].
电子学报, 2011, 39 (3A): 14–18.
GUO J, LEI M, PENG X Y. Static classification method based on corresponding cluster echo state network[J]. Acta Sinica, 2011, 39 (3A): 14–18. (in Chinese) |
| [10] | SCARDAPANE S, UNCINI A. Semi-supervised echo state networks for audio classification[J]. Cognitive Computation, 2017, 9 (1): 125–135. DOI:10.1007/s12559-016-9439-z |
| [11] | SONG Q S, FENG Z R. Effects of connectivity structure of complex echo state network on its prediction performance for nonlinear time series[J]. Neurocomputing, 2010, 73 (10-12): 2177–2185. DOI:10.1016/j.neucom.2010.01.015 |
| [12] | MARTIN C E, REGGIA J A. Fusing swarm intelligence and self-assembly for optimizing echo state networks[J]. Computational Intelligence and Neuroscience, 2015, 2015 (5-6): 642429. |
| [13] | DUTOIT X, SCHRAUWEN B, VAN CAMPENHOUT J, et al. Pruning and regularization in reservoir computing[J]. Neurocomputing, 2009, 72 (7): 1534–1546. |
| [14] | KUMP P, BAI E W, CHAN K, et al. Variable selection via RIVAL(removing irrelevant variables amidst Lasso iterations) and its application to nuclear material detection[J]. Automatica, 2012, 48 (9): 2107–2115. DOI:10.1016/j.automatica.2012.06.051 |
| [15] | SHI Z, HAN M. Support vector echo-state machine for chaotic time-series prediction[J]. IEEE Transactions on Neural Networks, 2007, 18 (2): 359–372. DOI:10.1109/TNN.2006.885113 |
| [16] |
刘建伟, 李双成, 罗雄麟. p范数正则化支持向量机分类算法[J].
自动化学报, 2012, 38 (1): 76–87.
LIU J W, LI S C, LUO X L. Classification algorithm of support vector machine via p-norm regularization[J]. Acta Automatica Sinica, 2012, 38 (1): 76–87. (in Chinese) |
| [17] |
韩敏, 李德才. 基于替代函数及贝叶斯框架的1范数ELM算法[J].
自动化学报, 2011, 37 (11): 1344–1350.
HAN M, LI D C. An norm 1 regularization term ELM algorithm based on surrogate function and Bayesian framework[J]. Acta Automatica Sinica, 2011, 37 (11): 1344–1350. (in Chinese) |
| [18] | ZOU H, HASTIE T. Regularization and variable selection via the elastic net[J]. Journal of the Royal Statistical Society, 2005, 67 (2): 301–320. |
| [19] | LUKOŠEVIČIUS M, JAEGER H. Reservoir computing approaches to recurrent neural network training[J]. Computer Science Review, 2009, 3 (3): 127–149. DOI:10.1016/j.cosrev.2009.03.005 |
| [20] | CASTELLANI G C, INTRATOR N, SHOUVAL H, et al. Solutions of the BCM learning rule in a network of lateral interacting nonlinear neurons[J]. Network:Computation in Neural Systems, 1999, 10 (2): 111–121. DOI:10.1088/0954-898X_10_2_001 |
| [21] | LEFORT M, BONIFACE Y, GIRAU B. Self-organization of neural maps using a modulated BCM rule within a multimodal architecture[C]//Brain Inspired Cognitive Systems 2010. Berlin: Springer, 2010: 26-38. |
| [22] | TIBSHIRANI R. Regression shrinkage and selection via the lasso[J]. Journal of the Royal Statistical Society, 1996, 58 (1): 267–288. |
| [23] |
彭义刚, 索津莉, 戴琼海, 等. 从压缩传感到低秩矩阵恢复:理论与应用[J].
自动化学报, 2013, 39 (7): 981–994.
PENG Y G, SUO J L, DAI Q H, et al. From compressed sensing to low-rank matrix recovery:Theory and applications[J]. Acta Automatica Sinica, 2013, 39 (7): 981–994. (in Chinese) |
| [24] | ZOU H. The adaptive lasso and its oracle properties[J]. Journal of the American Statistical Association, 2006, 101 (476): 1418–1429. DOI:10.1198/016214506000000735 |
| [25] | XU Z, ZHANG H, WANG Y, et al. L 1/2 regularization[J]. Science China Information Sciences, 2010, 53 (6): 1159–1169. DOI:10.1007/s11432-010-0090-0 |
| [26] | DAUBECHIES I, DEVORE R, FORNASIER M, et al. Iteratively reweighted least squares minimization for sparse recovery[J]. Communications on Pure and Applied Mathematics, 2010, 63 (1): 1–38. |
| [27] | XU Z, CHANG X, XU F, et al. L1/2 regularization:A thresholding representation theory and a fast solver[J]. IEEE Transactions on Neural Networks and Learning Systems, 2012, 23 (7): 1013–1027. DOI:10.1109/TNNLS.2012.2197412 |
| [28] | ZENG J, LIN S, WANG Y, et al. L1/2 regularization:Convergence of iterative half thresholding algorithm[J]. IEEE Transactions on Signal Processing, 2014, 62 (9): 2317–2329. DOI:10.1109/TSP.2014.2309076 |



