柔性微动机构是一种依靠结构的弹性变形来传递确定的力和运动的机构[1-2]。因为应用柔性结构代替了传统的运动副,所以避免了传统运动副存在的间隙、摩擦和装配等缺点,具有高精度、高寿命和可微型化等优点。柔性微动机构在众多领域都有重要应用,例如精密仪器、微加工、微装配、纳米技术、生物工程和航空航天等领域[3-5],其性能直接影响到这些领域的发展。
刚度是评价柔性微动机构的重要性能指标之一,不仅影响到机构的定位精度以及动态性能,还是其他性能指标求解的基础。目前刚度有多种求解方法[6-7],应用较普遍的有伪刚体模型法、有限元方法、刚度矩阵法和柔度矩阵法。其中伪刚体模型法[8-9]是将柔性结构简化为刚体机构,并结合能量原理来求解刚度,该方法思路简单,但精度不高。有限元方法[10-11]是一种精确较高的数值解法,应用软件能够求解任意复杂结构的刚度,但不能得到相应的解析解。刚度矩阵法[12]和柔度矩阵法[13-14]是2种比较相近的方法,应用已知单元的刚度或柔度来组装求解整体的刚度或柔度,精度较高,并具有较规范的求解过程。上述方法一般应用于求解柔性结构中单个输入外力与单个输出位移之间的关系,即柔度或刚度,但在实际情况中,有时需要求解柔性结构在多个外部载荷作用下,其输出位移与这些输入外力之间的关系。
对于多输入柔性微动机构的输出位移,本文将柔度矩阵法与刚体上力或位移的规律相结合,并通过叠加和协调原理来求解。应用该方法求解结构对称型微动夹持器输出位移与驱动力和夹持力间的关系式,并将求解结果与有限元分析结果进行比对,结果表明该方法具有足够的精度,能够用于多外力微动机构的结构分析与优化。应用MATLAB软件对该结构进行基于所求关系式的参数分析,并得到机构参数设计时所需的理论依据。
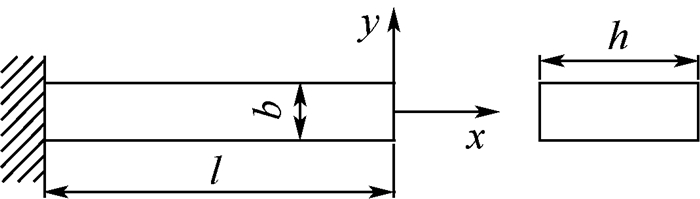
1 多外力下输出位移求解原理 1.1 柔性单元末端力与末端位移的关系矩形杆单元i的几何参数及相应坐标系如图 1所示,设末端在x-y平面内外力Fi作用下的位移为Ui,可得

|
(1) |
|
| 图 1 矩形杆单元 Fig. 1 Square bar element |
式中:Ci为矩形杆单元的柔度矩阵。
若将其视为悬臂梁,则根据材料力学基本原理可求得Ci为
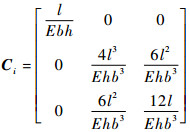
|
(2) |
式中:E为材料的弹性模量;b、h和l为矩形杆的几何参数。
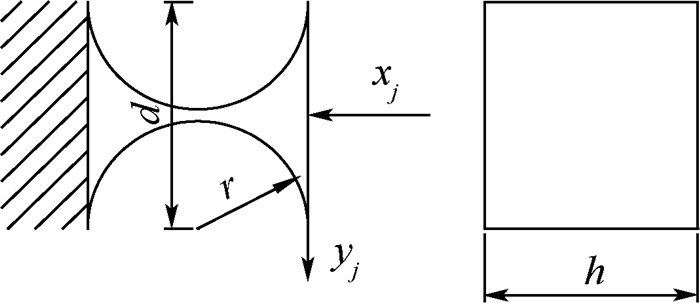
柔性铰链单元j几何参数及相应坐标系如图 2所示,设末端在xj-yj平面内外力Fj作用下的位移为Uj,同样可得形如式(1)的公式,对应的矩阵Cj可从文献[15]中获得。
|
| 图 2 柔性铰链单元 Fig. 2 Compliant hinge element |
在三维坐标系中,施加于刚体上点k处的外力可表示为向量Fk=[Fx,Fy,Fz,Mx,My,Mz]T,Fx,Fy和Fz为沿坐标轴方向的力,Mx,My和Mz为绕坐标轴的力矩。为得到刚体的力平衡方程,需要将作用在不同点处的外力平移到同一点处,设作用在刚体上A点处的外力向量为FA,将其平移到B点时表示为FB,由A点到B点的力平移转换矩阵表示为VAB,若已知A点坐标为(xA,yA,zA),B点坐标为(xB,yB,zB),则由力平移定理可得
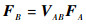
|
(3) |
式中:
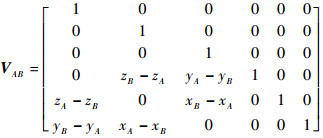
|
在三维坐标系中,可用向量Un=[dx,dy,dz,θx,θy,θz]T来描述刚体的位移,其中dx、dy和dz为刚体上点n沿坐标轴的线位移,θx、θy和θz为刚体绕点n处坐标系各轴的角位移。刚体运动在不同点处的表示不同,设某刚体上的A点和B点,且A点到B点的位移转换矩阵为PAB,该刚体位移在A点处的表示为UA,在B点的表示为UB,则根据刚体平面运动规律可得
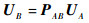
|
(4) |
式中:
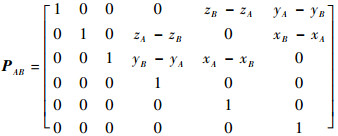
|
对于外力向量或位移向量,在不同的坐标系中会有不同的表现形式,需要应用坐标变换矩阵进行转化,对于外力和位移,坐标变换矩阵是相同的。设向量在三维坐标系Oi中表示为FOi,当坐标系O2绕坐标系O1的m轴转动θ角度时,相应的坐标变换矩阵为Rm(θ),则有
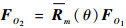
|
(5) |
式中:
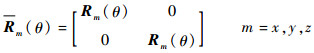
|
其中:
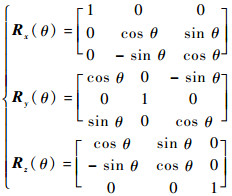
|
从位移角度分析,通过对整体结构的划分,可根据结构的串并联关系得到整体位移与各部分位移之间的关系,即叠加关系或协调关系,若拆分部分不是末端柔度已知的单元,则继续拆分。如此循环,直到拆分部分全为末端柔度已知的单元。从力角度分析,在上述拆分的过程中同样会得到整体外力与其拆分部分外力之间的关系,即力平衡关系。综合上述关系,便可通过已知单元末端柔度建立整体结构上力与位移的关系。
当整体结构由各单元串联组成时,整体位移等于各单元对整体位移贡献量之和,即叠加关系。每个单元对整体位移的贡献量为假设该单元单独变形,其他单元为刚体时,对应产生的整体位移。例如,某平面型支链由3个杆单元串联而成,即整体位移与各单元位移为叠加关系,如图 3所示,各单元在其单元坐标系Om中的单元柔度分别为C1、C2和C3,文献[16]给出了在整体坐标系3中该支链末端刚度C的求解公式为
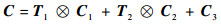
|
(6) |

|
| 图 3 三连杆串联支链 Fig. 3 Serial chain of three bars |
式中:运算符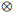
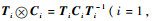
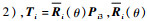
当整体可以看作各单元并联组成时,整体位移与各单元位移为协调关系,可假设相交部分为刚性单元来求解协调关系式,并联立相交单元上的力平衡关系式来求解整体上的力与位移的关系式。
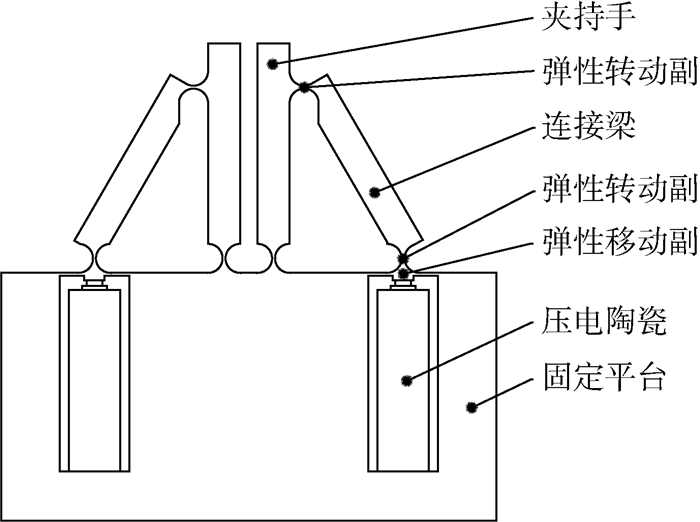
2 微动夹持器的输出位移求解 2.1 微动夹持器结构模型本文提出了一种微动夹持器如图 4所示,该结构由两侧对称放置的压电陶瓷提供动力,并通过弹性移动副和连接梁传递到左右2个夹持手,实现夹持动作。
|
| 图 4 微动夹持器结构模型 Fig. 4 Structural model of micro-motion gripper |
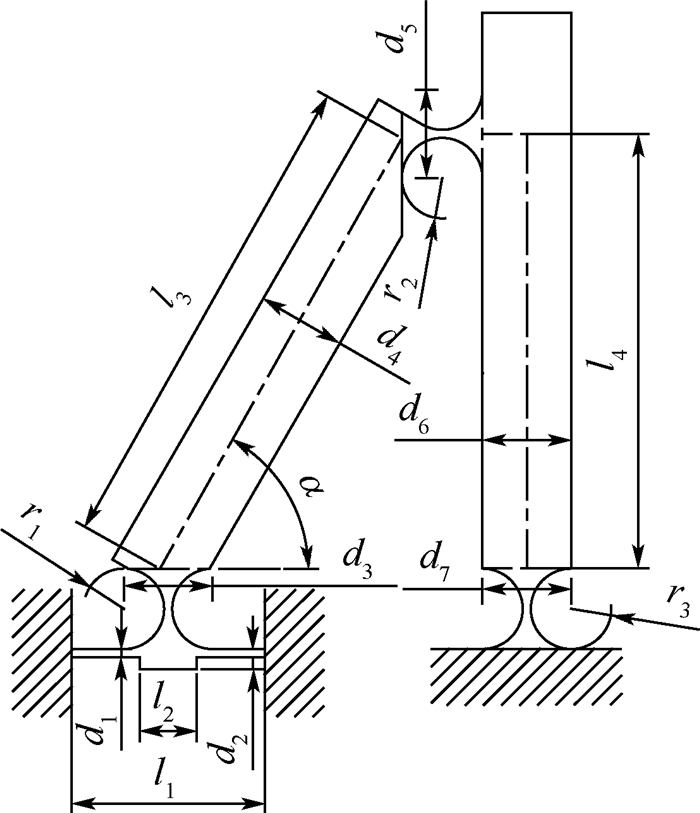
微动夹持器的参数模型如图 5所示,在实际应用中,该夹持器不仅需要完成夹持动作,还需要提供特定的夹持力,以便完成特定的夹持任务。
|
| 图 5 微动夹持器参数模型 Fig. 5 Parameterized model of micro-motion gripper |
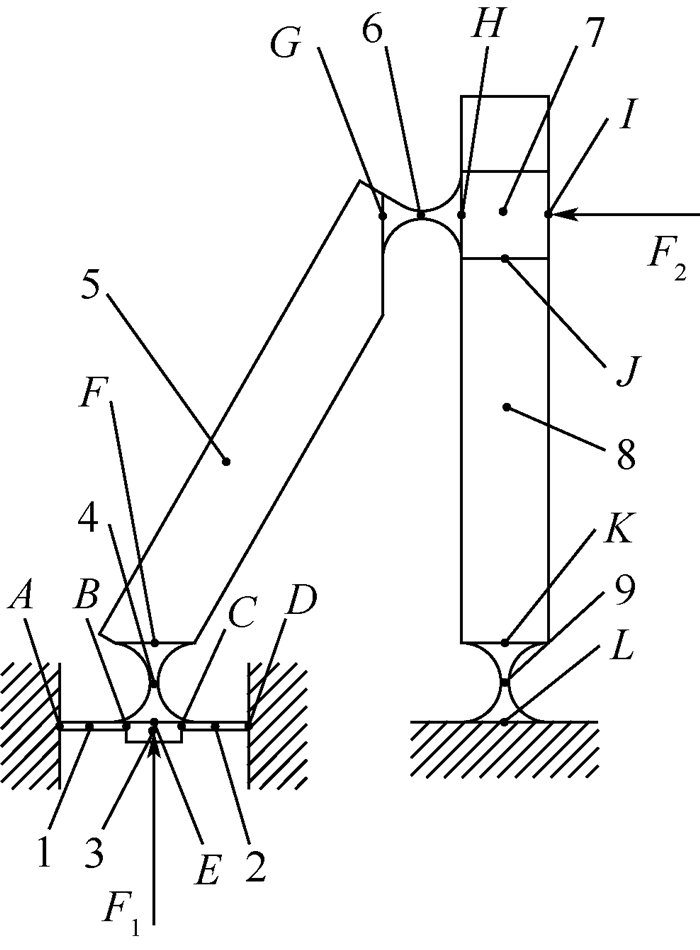
首先对整体结构进行单元划分,各单元分别编号为1~9,单元之间的连接点及输入输出点分别用字母A~L来表示。为简化计算,现将单元3和7视为刚体。定义外力F1为单元3的外力,外力F2为单元7的外力,微动夹持器力学模型如图 6所示。为了得到完成夹持动作并提供特定夹持力时所需要的驱动力,需要建立外力F1、F2和I点位移UI的关系式。
|
| 图 6 微动夹持器力学模型 Fig. 6 Mechanical model of micro-motion gripper |
由分析可得,UI是刚性单元7在I点的位移,单元7的位移是单元6和8末端位移在该处的协调,单元8末端位移又是单元8和9的位移叠加,单元6末端位移是单元3、4、5和6的位移叠加,刚体单元3的位移又是单元1和2末端位移在该处的协调,而实际求解则需倒序进行。
规定在坐标系Ok中,单元i对单元j的作用力在v点处的向量表示为kFvij,单元i在点j处的位移向量表示为kUji,由点i到点j的力平移转换矩阵为Vijk,由点i到点j的位移转换矩阵为Pijk。Rij为坐标系Oi到坐标系Oj的坐标变换矩阵,Ci表示单元i在其单元坐标系中的柔度矩阵。
2.3.1 单元3的位移求解建立如图 7所示坐标系,并将单元3视为刚体。根据矩形杆的柔度计算式(1)可得单元1和2的位移
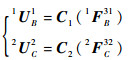
|
(7) |
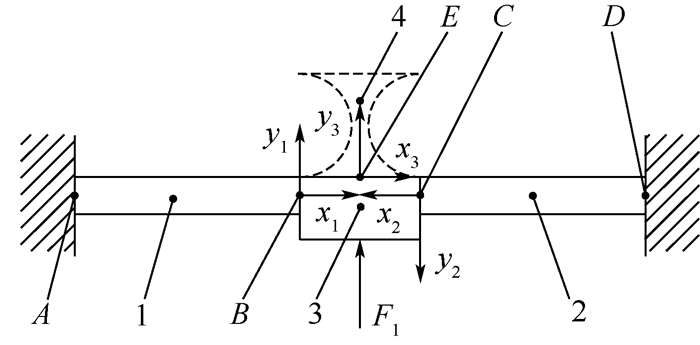
|
| 图 7 单元3结构 Fig. 7 Structure of Element 3 |
由刚体单元3上位移或力的关系式可得
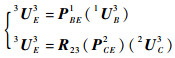
|
(8) |
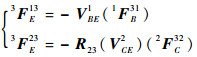
|
(9) |
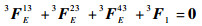
|
(10) |
式中:3F1为外力F1在坐标系O3中的向量表示。
将式(7)~式(9)代入式(10)整理可得
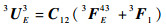
|
(11) |
式中:
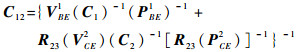
|
建立如图 8所示坐标系,首先求解当单元3刚性化时, 由柔性单元4、5和6引起的单元6的末端柔度,根据单元4、5和6间的串联关系可得
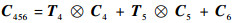
|
(12) |
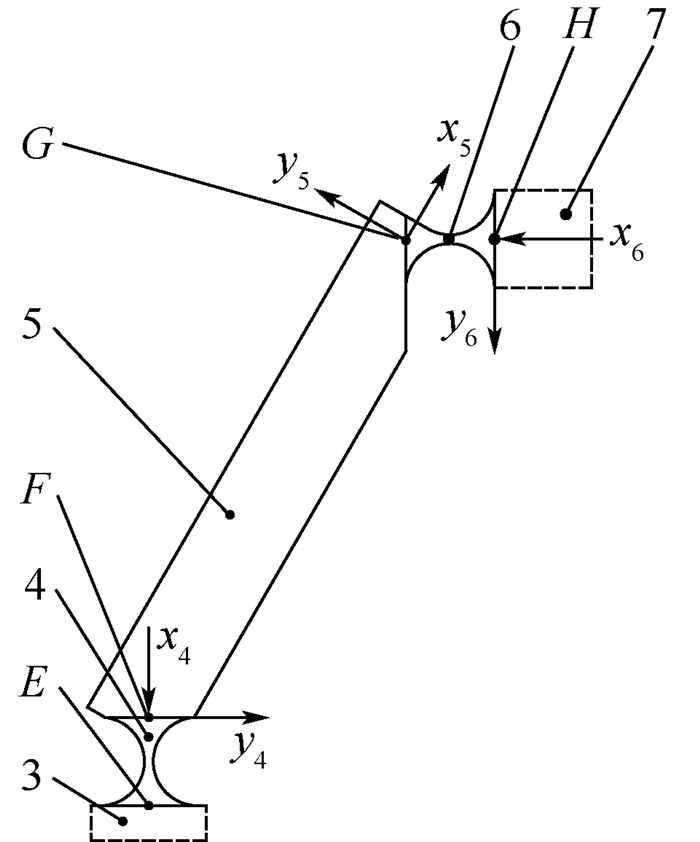
|
| 图 8 单元6结构 Fig. 8 Structure of Element 6 |
式中:T4=R46PFH4;T5=R56PGH5。
单元6末端的实际位移由2部分叠加而成,即单元4、5和6对其贡献量和单元3对其贡献量,则有
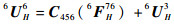
|
(13) |
视单元4、5和6为刚体时可得
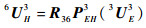
|
(14) |
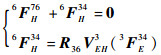
|
(15) |
将式(14)和式(15)代入式(13)整理可得
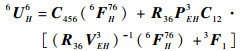
|
(16) |
首先求解单元8和9串联支链末端柔度,建立如图 9所示坐标系,根据单元8和9的串联关系可得
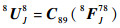
|
(17) |
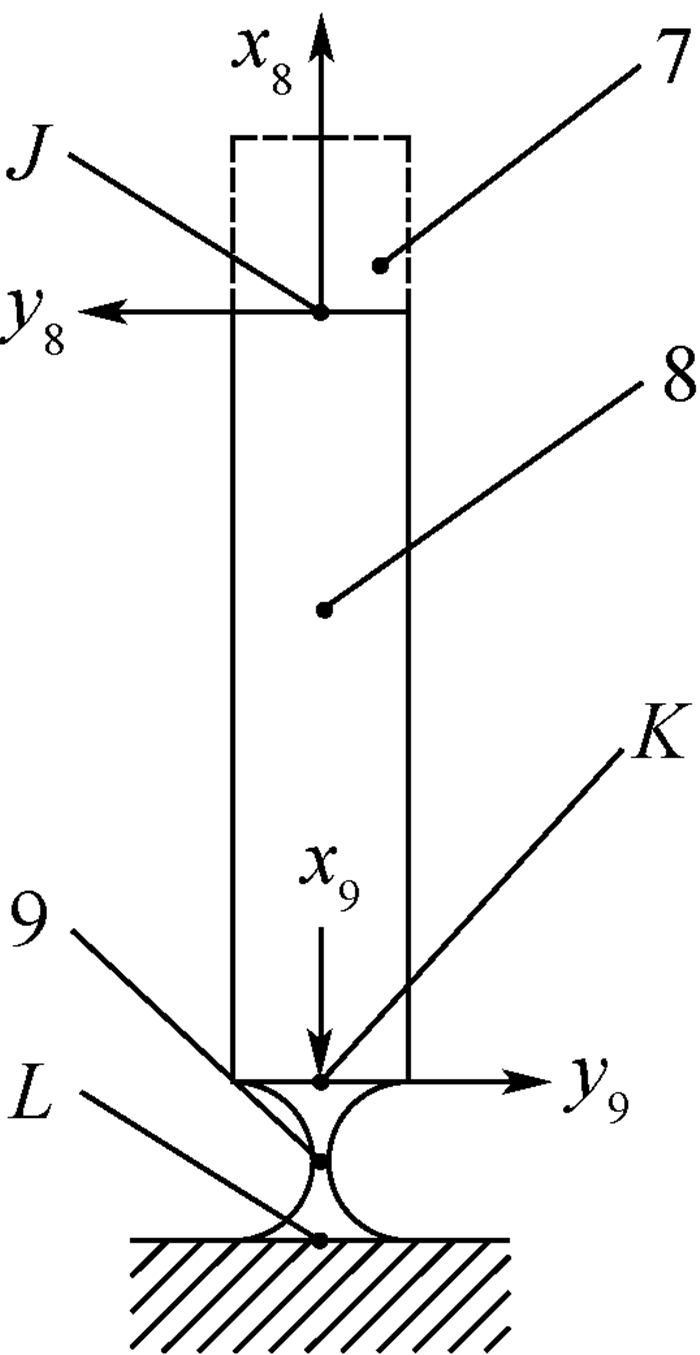
|
| 图 9 单元8和单元9的串联支链结构 Fig. 9 Structure of series chain of Element 8 and 9 |
式中: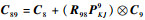
建立如图 10所示坐标系,为简化计算,视单元7为刚体,根据单元7的外力平衡可得
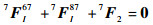
|
(18) |

|
| 图 10 单元7结构 Fig. 10 Structure of Element 7 |
式中:7F2为外力F2在坐标系O7中的向量表示。
根据单元7上力和位移的关系可得
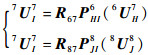
|
(19) |
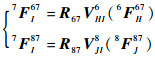
|
(20) |
联立式(11)、式(16)~式(20),整理可得单元7上I点位移7UI7与输入力3F1和7F2间的关系为

|
(21) |
式中:
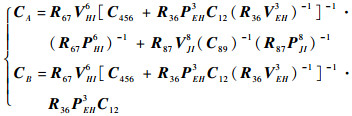
|
为了验证理论分析的准确性,现将理论值与有限元分析结果进行比对。设定几何参数为:l1=24 mm,l2=7 mm,d1=1 mm,d2=1.5 mm,l3=62 mm,l4=54 mm,d4=d6=11 mm,r1=r2=r3=5 mm,α=π/3 rad,d3=d5=d7=11 mm,厚度b= 15 mm。利用软件ANSYS 15.0对该模型进行有限元分析,首先将三维模型导入到软件中,选取实体单元Solid186,设定材料为60Si2Mn,即设定材料弹性模量E为206 GPa,泊松比μ为0.27,剪切模量G为79 GPa,进行网格划分如图 11所示。约束固定平台,在C处施加驱动力F1,在L处施加夹持力F2, 提取L处的位移。

|
| 图 11 微动夹持器有限元网格划分模型 Fig. 11 Finite element meshing model of micro-motion gripper |
F2选取0~20 N内的5组值,F1选取10~50 N内的5组值,两者相互组合得到25组输入数对,对其进行理论计算与有限元分析,对比结果如表 1所示。
| 外力 | 位移uIy | 位移uIx | |||||||
| F2/N | F1/N | 理论值/μm | 有限元分析值/μm | 相对误差/% | 理论值/μm | 有限元分析值/μm | 相对误差/% | ||
| 0 | 10 | -1.31 | -1.42 | 7.7 | -0.122 | -0.132 | 7.6 | ||
| 20 | -2.62 | -2.84 | 7.7 | -0.245 | -0.265 | 7.5 | |||
| 30 | -3.93 | -4.27 | 7.9 | -0.367 | -0.397 | 7.6 | |||
| 40 | -5.24 | -5.69 | 7.9 | -0.490 | -0.530 | 7.5 | |||
| 50 | -6.56 | -7.12 | 7.8 | -0.612 | -0.663 | 7.7 | |||
| 5 | 10 | 0.020 9 | 0.047 8 | 56 | 0.003 75 | 0.007 45 | 49 | ||
| 20 | -1.29 | -1.37 | 5.8 | -0.119 | -0.125 | 4.8 | |||
| 30 | -2.60 | -2.80 | 7.1 | -0.241 | -0.258 | 6.5 | |||
| 40 | -3.91 | -4.22 | 7.3 | -0.364 | -0.390 | 6.6 | |||
| 50 | -5.22 | -5.65 | 7.6 | -0.486 | -0.523 | 7.1 | |||
| 10 | 10 | 1.34 | 1.46 | 8.2 | 0.132 | 0.142 | 7.0 | ||
| 20 | 0.041 7 | 0.095 6 | 56 | 0.007 51 | 0.014 9 | 49 | |||
| 30 | -1.27 | -1.33 | 4.5 | -0.115 | -0.118 | 2.5 | |||
| 40 | -2.58 | -2.75 | 6.2 | -0.237 | -0.250 | 5.2 | |||
| 50 | -3.89 | -4.17 | 6.7 | -0.360 | -0.382 | 5.7 | |||
| 15 | 10 | 2.68 | 2.92 | 8.2 | 0.256 | 0.281 | 8.8 | ||
| 20 | 1.37 | 1.50 | 8.6 | 0.134 | 0.146 | 8.2 | |||
| 30 | 0.062 6 | 0.143 | 56 | -0.011 3 | -0.022 3 | 49 | |||
| 40 | -1.25 | -1.28 | 2.3 | -0.111 | -0.110 | 1.0 | |||
| 50 | -2.56 | -2.70 | 5.2 | -0.234 | -0.242 | 3.3 | |||
| 20 | 10 | 4.02 | 4.38 | 8.2 | 0.382 | 0.418 | 8.6 | ||
| 20 | 2.71 | 2.97 | 8.7 | 0.260 | 0.284 | 8.4 | |||
| 30 | 1.40 | 1.53 | 8.4 | 0.141 | 0.154 | 8.4 | |||
| 40 | 0.083 5 | 0.191 | 56 | 0.015 | 0.029 8 | 49 | |||
| 50 | -1.23 | -1.24 | 0.8 | -0.107 | -0.103 | 3.9 | |||
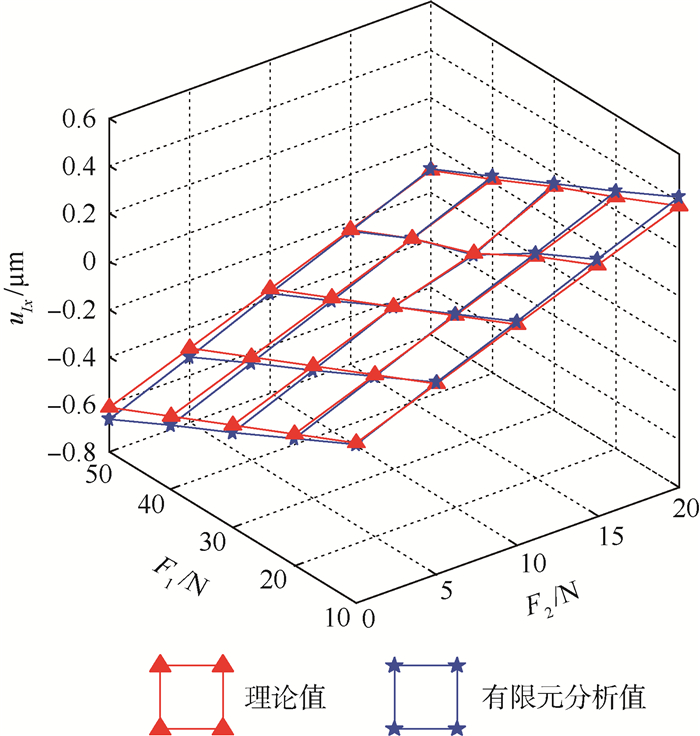
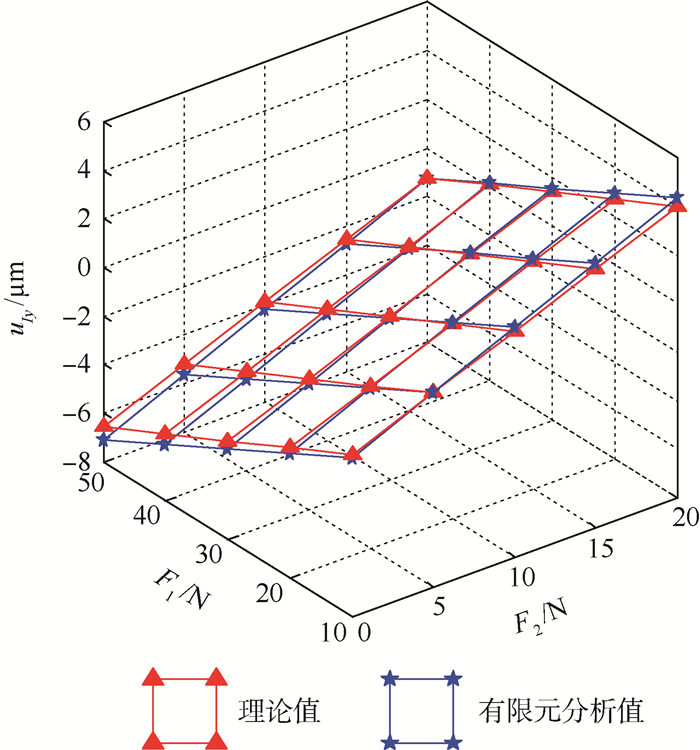
表 1中uIx和uIy分别表示单元7上的I点在坐标系O7中沿x轴和y轴的位移量,数据分析表明理论值与有限元分析值的相对误差多数在9%以内,而每5组中存在1组相对误差较大,这些误差较大的数据均发生在所求位移很小的时候,即F1和F2对输出位移的作用效应相当之时两者产生的位移几乎完全抵消。当F1作用效应相对F2较大时,对比值误差相对较小,如图 12和图 13所示。
|
| 图 12 uIx的理论值与有限元分析值 Fig. 12 Theoretical analysis and finit element analysis results of uIx |
|
| 图 13 uIy的理论值与有限元分析值 Fig. 13 Theoretical analysis and finit element analysis results of uIy |
理论与有限元分析所求得的uIx和uIy位移云图均为平面,当一个输入力为定值时,另一输入力与输出位移之间均为近似线性关系。对于uIx和uIy而言,相应的理论值与有限元分析结果基本一致,考虑到有两者之间的差别,其原因可能有以下几个方面:①在理论计算中,由于对单元3和7进行了刚化处理,忽略了其本身的实际变形。②应用的柔性单元关系式要求端面均布受力,忽略了实际中单元端面受力不均匀的现象,这种界面的微观受力情况有待进一步研究。③位移计算中应用了叠加原理,忽略了叠加对象相互间的影响。
4 基于解析式的参数分析在第2节中,获得了单元7上I点位移7UI7与输入力3F1和7F2间的解析表达式(21),为通过参数优化设计提高柔性夹持器性能提供了依据。式(21)涉及到2个外力,可以通过建立两者之间的线性关系,得到只与结构参数有关的因变量,即外力与输出位移之间的柔度。
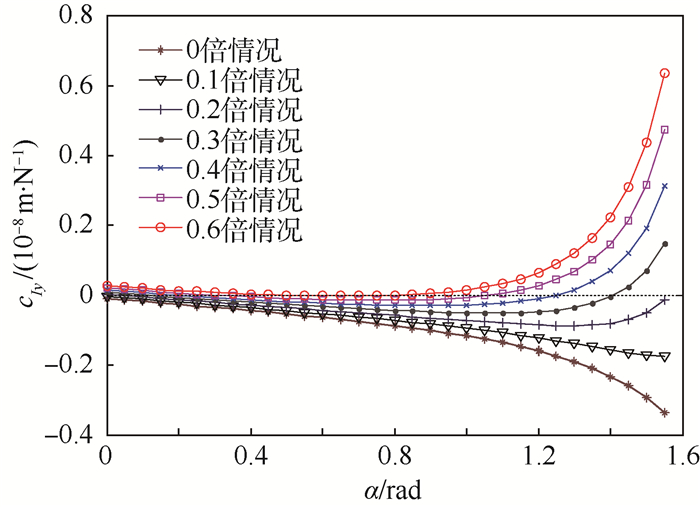
现将夹持力F2设定为驱动力F1的0、0.1、0.2、0.3、0.4、0.5和0.6倍大小的7种情况,且每种情况下都存在输出位移uIx与外力F1之间的柔度系数cIx和输出位移uIy与外力F1之间的柔度系数cIy。结构参数α代表着连接梁的倾斜程度,对微动夹持器的驱动力与输出位移之间的关系具有重要影响。以α为参数自变量,则可得α与的cIx之间的关系如图 14所示,α与cIy之间的关系如图 15所示。

|
| 图 14 参数α与柔度系数cIx的关系曲线 Fig. 14 Relation curves of parameter α and compliance coefficient cIx |
|
| 图 15 参数α与柔度系数cIy的关系曲线 Fig. 15 Relation curves of parameter α and compliance coefficient cIy |
从图 14和图 15中可以看出,在0、0.1和0.2倍的情况下柔度系数cIx和cIy在α的整个取值范围上均为负值,在0.3和0.4倍情况下柔度系数cIx和cIy在α小于1.3 rad的取值上为负值,在0.6及以上倍数的情况下柔度系数cIx和cIy在α的绝大部分取值上均为正值,由于柔度取正值时不能完成正常的夹持动作,因此在仅改变α值的情况下,该夹持手最多可以提供0.5倍驱动力大小的夹持力。
单元7上I点沿y向位移为夹持器的主运动方向,因此从图 15中可以看出,若要获得较大的夹持范围,即柔度较大,在0和0.1倍情况下,在满足其他条件的情况下应使α尽可能取大值;在0.2倍的情况,应使α取值在1.3 rad左右;对于0.4和0.5倍的情况,应使α取值在0.8 rad左右。
5 结论1) 本文结合柔度矩阵法和刚体受力与移动规律得到了求解多外力作用下柔性机构输出位移解析解的方法,从而满足了实际情况中多外力作用情况的工程需要。该方法具有普遍适用性,能为一般柔性机构的性能分析和进一步的参数优化提供方法支持。
2) 运用该方法求解了两外力下的微动夹持器的输出位移,并与有限元方法的计算结果进行了对比。结果表明该方法具有可靠的精度及规范的求解过程。给出了机构参数α与柔度的解析表达式,根据关系曲线对结构参数α的选择做了定性分析,表明了该方法在参数优化方面的实际应用价值。
| [1] | SARAJILIC E, YAMAHATA C, CORDERO M, et al. Three-phase electrostatic rotary stepper micromotor with a flexural pivot bearing[J]. Journal of Microelectromechanical System, 2012, 19 (2): 338–394. |
| [2] |
于靖军, 郝光波, 陈贵敏, 等. 柔性机构及其应用[J].
机械工程学报, 2015, 51 (13): 53–68.
YU J J, HAO G B, CHEN G M, et al. State-of-art of compliant mechanisms and their applications[J]. Journal of Mechanical Engineering, 2015, 51 (13): 53–68. (in Chinese) |
| [3] |
李静, 庞岩, 冯咬齐, 等. 柔性航天器姿控执行机构微振动集中隔离与分散隔离对比研究[J].
航天器环境工程, 2016, 33 (1): 58–64.
LI J, PANG Y, FENG Y Q, et al. Comparison of concentrated and distributed isolations of micro vibrations in flexible spacecraft attitude actuators[J]. Spacecraft Environment Engineering, 2016, 33 (1): 58–64. (in Chinese) |
| [4] | LI Y, XU Q. A totally decoupled piezo-driven XYZ flexure parallel micropositioning stage for micro/nanomanipulation[J]. IEEE Transactions on Automation Science and Engineering, 2011, 8 (2): 265–279. DOI:10.1109/TASE.2010.2077675 |
| [5] | FUCHIWAKI O, AOYAMA H. Design and control of versatile micro robot for microscopic manipulation[M]. Livermore: American Society for Precision Engineering, 2001: 22-29. |
| [6] |
郑洋洋, 宫金良, 张彦斐. 基于传递矩阵法的柔性杠杆放大机构刚度分析[J].
北京航空航天大学学报, 2017, 43 (4): 849–856.
ZHENG Y Y, GONG J L, ZHANG Y F. Rigidity analysis of a flexible lever magnifying mechanism based on transfer matrix method[J]. Journal of Beijing University of Aeronautics and Astronautics, 2017, 43 (4): 849–856. (in Chinese) |
| [7] | NI Y, DENG Z, WU X, et al. Modeling and analysis of an over-constrained flexure-based compliant mechanism[J]. Measurement, 2014, 50 (1): 270–278. |
| [8] |
于靖军, 毕树生, 宗光华, 等. 基于伪刚体模型法的全性机构位置分析[J].
机械工程学报, 2002, 38 (2): 75–78.
YU J J, BI S S, ZONG G H, et al. Kinematics analysis of fully compliant mechanisms using the pseudo-rigid-body model[J]. Journal of Mechanical Engineering, 2002, 38 (2): 75–78. (in Chinese) |
| [9] | HER I, CHANG J. A linear scheme for the displacement analysis of micropositioning stages with flexure hinges[J]. Journal of Mechanical Design, 1994, 116 (3): 770–776. DOI:10.1115/1.2919449 |
| [10] |
李育文, 张华, 杨建新, 等. 6-UPS并联机床静刚度的有限元分析和实验研究[J].
中国机械工程, 2004, 15 (2): 112–115.
LI Y W, ZHANG H, YANG J X, et al. Finite element analysis and experimental study for the stiffness of a 6-UPS parallel kinematic machine[J]. China Mechanical Engineering, 2004, 15 (2): 112–115. (in Chinese) |
| [11] |
栾玉亮, 荣伟彬, 孙立宁. 基于有限元方法的3-PPSR大长径比柔性并联机器人刚度模型分析[J].
机器人, 2014, 36 (6): 730–736.
LUAN Y L, RONG W B, SUN L N. Analysis on stiffness model of 3-PPSR flexible parallel robot with high aspect based on finite element method[J]. Robot, 2014, 36 (6): 730–736. (in Chinese) |
| [12] |
于靖军, 毕树生, 宗光华. 空间全柔性机构位置分析的刚度矩阵法[J].
北京航空航天大学学报, 2002, 28 (3): 323–326.
YU J J, BI S S, ZONG G H. Stiffness matrix method for displacement analysis of full spatial compliant mechanisms[J]. Journal of Beijing University of Aeronautics and Astronautics, 2002, 28 (3): 323–326. (in Chinese) |
| [13] |
张德福, 赵磊. 基于柔度矩阵法的整体式XY光学微调整机构研究[J].
仪器仪表学报, 2014, 35 (2): 269–275.
ZHANG D F, ZHAO L. Research of monolithic XY micro-adjustment mechanism based on compliance matrix[J]. Chinese Journal of Scientific Instrument, 2014, 35 (2): 269–275. (in Chinese) |
| [14] |
于靖军, 毕树生, 宗光华, 等. 3自由度柔性微机器人的静刚度分析[J].
机械工程学报, 2002, 38 (4): 7–10.
YU J J, BI S S, ZONG G H, et al. Analysis for the static stiffness of a 3DOF parallel compliant micromanipulator[J]. Chinese Journal of Mechanical Engineering, 2002, 38 (4): 7–10. (in Chinese) |
| [15] |
吴鹰飞, 周兆英. 柔性铰链的设计计算[J].
工程力学, 2002, 19 (6): 136–140.
WU Y F, ZHOU Z Y. Design of flexure hinges[J]. Engineering Mechanics, 2002, 19 (6): 136–140. (in Chinese) |
| [16] | KOSEKI Y, TANIKAWA T, KOYACHI N, et al. Kinematic analysis of a translational 3-d of micro-parallel mechanism using the matrix method[J]. Advanced Robotics, 2002, 16 (3): 251–264. DOI:10.1163/156855302760121927 |



