近年来,翼身融合(Blended-Wing-Body, BWB)布局飞行器由于具有提高气动效率、降低油耗、排放和噪声等方面的潜力[1-3]而逐渐成为研究热点,是一种有希望取代常规布局的未来民机布局形式。为了能进一步发挥其优势,研究者提出在BWB布局上应用一种被称为分布式动力(distributed propulsion)的新的发动机布局形式[4-6]。该布局相比传统的集中吊挂式布局,具有更低的冲压阻力、浸润面积、结构重量和噪声等多项潜在优势。BWB与分布式动力系统耦合布局的特点是在BWB机身上表面后部沿翼展方向布置若干个进气口靠近或半埋入机身的发动机或风扇,这会使机身上表面的边界层被发动机摄入,即产生了边界层吸入(Boundary Layer Ingestion, BLI)效应。该效应会使得分布式动力BWB飞机的气动特性显著不同于集中吊挂式布局[7-10]。已有一些研究者针对这一问题展开了相关研究。
Rodriguez[11]研究了带3台发动机的BWB飞机动力系统的布置形式,比较了吊挂式和埋入式进气口对气动特性的影响,并进行了初步的多学科优化设计,研究表明采用埋入式进气口布局的飞机具有较高的推进效率和气动效率。Lundbladh和Grönstedt[12]研究了不同进气形式的分布式动力BWB飞机在巡航条件下的效率问题,发现埋入式进气口对降低飞机的起飞重量和油耗、提升巡航效率是有利的。Liou等[13]对分布式动力BWB飞机整流罩的气动设计问题进行了初步研究,发现在重新设计整流罩形状后,整流罩表面的激波减弱,全机升力系数提高。闫万方等[14]研究了部分设计参数对分布式动力BWB飞机全机气动特性的影响,发现在这些参数中,流量系数(Mass Flow Rate, MFR)和进气口弦向位置对飞机气动特性影响显著。
相比吊挂式发动机布局,分布式动力BWB飞机具有更长、面积更大的整流罩,且更靠近机身,会影响到飞机上表面流场,因此研究其对飞机机体气动特性的影响是有意义的。本文采用数值模拟与敏感度分析相结合的方法对分布式动力BWB飞机的整流罩设计参数进行研究,获得其对飞机气动特性影响的敏感度并分类,从中选择典型参数分析单变量对气动特性影响的原因,并分析多参数对气动特性的耦合影响。
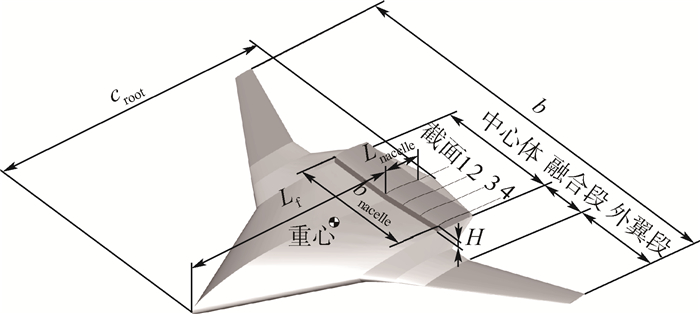
1 模型和方法 1.1 模型定义本文所研究的分布式动力BWB飞机的气动布局如图 1所示[14]。该布局由中心体、融合段和外翼段组成,在中心体后部沿展向布置有分布式动力系统。动力系统前后部分别为进、排气边界,上表面为整流罩。飞机的主要几何参数标注于图 1,其展长b=68.2 m,机身对称面弦长(即机身长度)croot=44.6 m,重心到机头的距离Lcg=27.3 m。动力系统的位置和外形尺寸取值如下(均以与机身对称面弦长croot的比值表示):进气边界弦向位置(定义为动力系统进气边界到机头的距离)Lf=0.8croot,整流罩长度Lnacelle =0.13croot,进气边界高度H=0.02croot,整流罩展向长度bnacelle=0.48croot。
|
| 图 1 分布式动力BWB飞机的气动布局 Fig. 1 Aerodynamics configuration of distributed propulsion BWB aircraft |
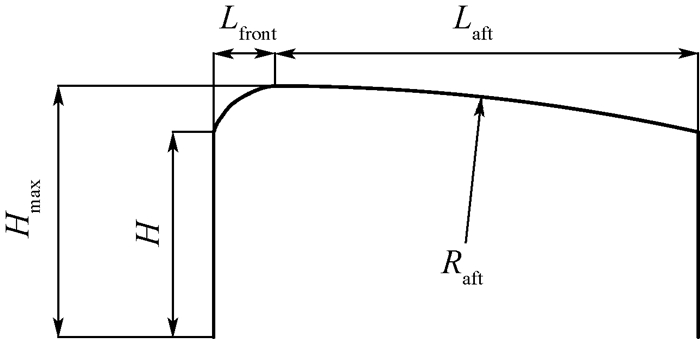
对于整流罩的参数化描述,本文参照文献[15]给出整流罩外形的定义方式。从对称面沿展向等距离布置4个控制截面作为设计变量,每个截面的几何参数定义如图 2所示。
|
| 图 2 整流罩截面几何参数定义 Fig. 2 Geometric parameter definition of nacelle section |
从图 2可见,整流罩截面外形由前后2段组成。前段外形的设计参照传统的发动机整流罩,为NACA-1系翼型[16],其长度为Lfront,高度为Hmax -H(Hmax为整流罩的最大高度)。后段为圆弧,半径为Raft,表达式为
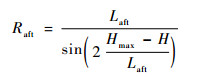
|
(1) |
在本研究中,给定动力系统的H和整流罩长度Lnacelle(Lnacelle=Lfront+Laft)不变,并选定Lnacelle作为无量纲参考长度。于是可以定义2个新的几何参数:整流罩厚度t和整流罩厚度位置x。
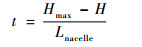
|
(2) |
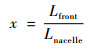
|
(3) |
由上述定义可知,由每个截面的t和x的组合可唯一确定该截面形状。整流罩曲面形状由这4个截面放样给出,可知由ti和xi(i=1, 2, 3, 4)总共8个参数即可唯一确定整流罩形状。为了便于研究,需要选取一个基准构型。参照文献[15]中对二维情形下整流罩参数进行研究,设定基准构型的ti=0.047,xi=0.29(i=1, 2, 3, 4)。此外,为确定动力系统的边界条件,还需用到流量系数MFR和排气方向τ。MFR的定义为
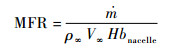
|
(4) |
式中:ṁ为流入进气口的空气的质量流率;ρ∞为远前方来流的密度;V∞为远前方来流的速度。基准条件下MFR=0.68。排气方向τ的定义为排气气流方向与排气边界法向的夹角,当排气方向斜向上时为正值,基准条件下τ=0°。
1.2 数值方法及验证本文的数值计算以三维定常RANS方程作为控制方程,使用有限体积法对其进行空间离散,并使用具有二阶精度的耦合方法求解,湍流模型为一方程S-A模型。动力系统进气口的边界条件类型为压力出口,动力系统喷口的边界条件类型为质量流量入口。计算所使用的网格模型为C-H型网格,其结构如图 3所示。

|
| 图 3 计算网格结构 Fig. 3 Structure of computation mesh |
本文研究中出现的气动力和力矩系数包括升力系数CL、阻力系数CD和俯仰力矩系数CM,其定义分别为:CL=L/(0.5ρ∞V∞2Sref),CD=D/(0.5ρ∞V∞2Sref),CM=M/(0.5ρ∞V∞2Srefc)。式中:L、D和M分别为飞机的升力、阻力和俯仰力矩(包含整流罩表面);力矩M的取矩点为重心;c为飞机的平均气动弦长;Sref为飞机的参考面积。
以下对本文所用的计算网格进行验证。为确定合适的网格规模,对网格规模递增的3套网格分别进行计算,对比结果见表 1,基准计算条件为飞行高度Hflight=11 000 m,马赫数Ma=0.85,迎角α=2.8°。可见,网格1的计算结果与网格3相差较大,而网格2的计算结果与网格3较为接近,且计算开销小于网格3。
| 算例名称 | 网格规模 | CL | CD |
| 网格1 | 907 563 | 0.411 2 | 0.021 63 |
| 网格2 | 1 378 251 | 0.413 7 | 0.020 71 |
| 网格3 | 2 055 448 | 0.416 0 | 0.020 56 |
另外,需要选取合适的壁面网格高度,因为壁面网格高度足够小才能准确地描述边界层内流动,但过小的壁面网格高度会降低网格质量。对3套规模相同、壁面网格高度递减的网格计算结果进行了对比,对比结果如表 2所示。可见,网格4的计算结果与网格2相差较大,而网格2与网格5的计算结果较为接近。从表 1和表 2的验证结果可以看出,网格2的数值模拟结果在精度与效率之间取得了平衡,因此本文选取网格2作为数值模拟的基准网格。
| 算例名称 | 壁面网格高度/m | CL | CD |
| 网格2 | 5×10-4 | 0.413 7 | 0.020 71 |
| 网格4 | 1×10-3 | 0.414 8 | 0.020 52 |
| 网格5 | 3×10-4 | 0.413 9 | 0.020 76 |
2 结果和讨论 2.1 参数敏感度分析
本文采用Morris法分析整流罩外形设计参数对飞机气动系数的敏感度。Morris法是一种全局敏感度分析法,具体流程为:①将n个参数的定义域映射到[0, 1]区间并离散化为p个水平,构成n维p水平的采样空间;②选定重复采样次数r;③进行r次随机抽样,每次抽样都可以获得1组n个参数的基本效应(elementary effect)值;④对每个参数,计算r个基本效应的平均值d和标准差S,这2个量分别表示该参数对目标函数的敏感度和该参数与其他参数的耦合作用程度[17]。
根据Morris法的步骤,首先选择1.1节给出的决定整流罩形状的8个参数作为研究对象,并给出这8个参数在各自的基准值Pi附近的变化区间。由于各参数的量纲和量级可能各异,因此,需要对参数的变化区间作归一化[15]。本文将归一化后的参数变化区间称为参考变化区间,第i个参数的参考变化区间[l*, u*]i定义为
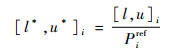
|
(5) |
式中:Piref为第i个参数对应的参考特征量;u、l分别为该参数实际变化区间的上、下界。本文以整流罩长度Lnacelle作为整流罩各截面厚度和厚度位置对应的参考特征量。考虑几何约束和参数的一般变化范围,将参数的参考变化区间上下界设为6%和-4%,由此可知参数的实际变化区间,如表 3所示。
| 参数 | Pi | [Pi -l, Pi +u] |
| ti(i=1, 2, 3, 4) | 0.047 | [0.007, 0.107] |
| xi(i=1, 2, 3, 4) | 0.29 | [0.25, 0.35] |
此外还应为Morris法选定合适的抽样次数,若抽样次数太小,则无法获得有意义的统计平均值;反之则会导致过大的计算开销。综合考虑这2个因素,并参考二维翼型Morris敏感度分析的经验[15],将本研究的抽样次数取为r=50。
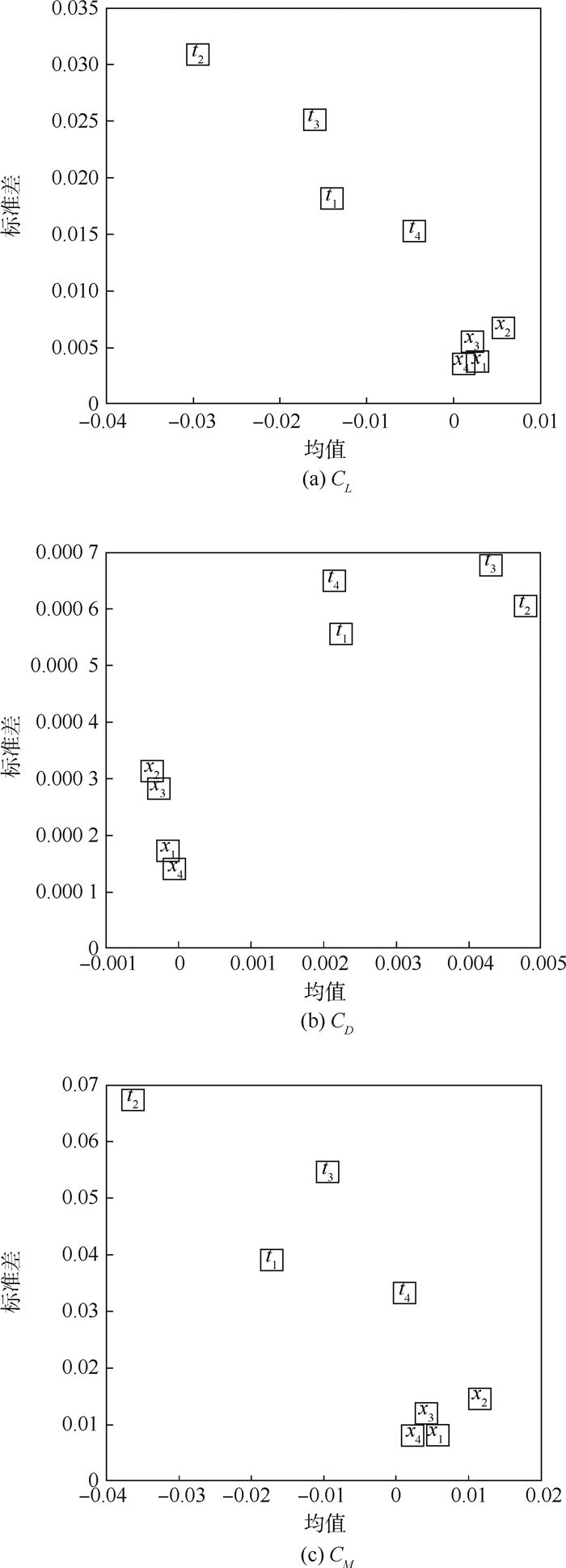
使用Morris法计算了上述8个参数在巡航状态下(条件见1.2节)对气动系数的敏感度和耦合作用,计算结果如图 4所示。
|
| 图 4 Morris法计算的各参数对气动系数影响的均值与标准差 Fig. 4 Mean values and standard deviations of effects of parameters on aerodynamic coefficients with Morris method |
从图中可知,总体而言,各截面厚度ti对气动系数影响较大,厚度位置xi影响较小,这与二维结果是一致的。从均值绝对值的对比可以看出,对CL敏感度较大的参数排序为t2、t3、t1、x2;对CD敏感度较大的参数排序为t2、t3、t1、t4;对CM敏感度较大的参数排序为t2、t1、x2、t3。从标准差的对比可以看出,对气动系数影响较大的参数与其他参数的相互作用也较明显,反之亦然,这与二维研究的结果也是一致的。另外,从图 4中均值的符号可以看出,CL敏感度较大的参数对CL的基本效应均值为负数。
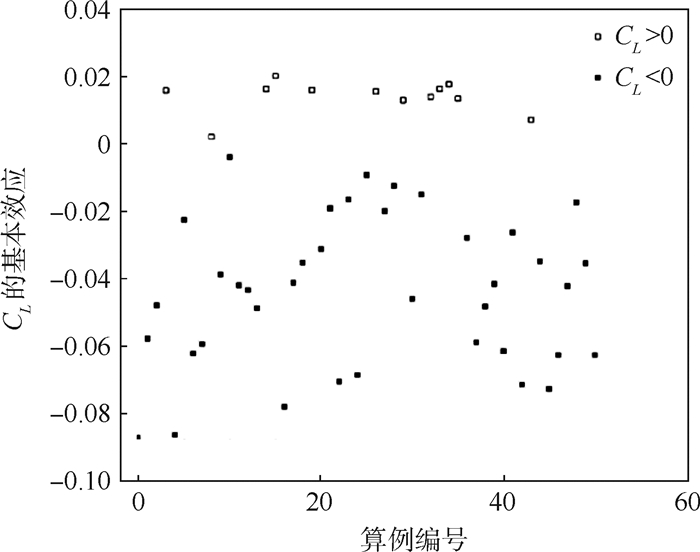
图 5为参数t2对CL的基本效应分布图,可以看出在样本中的大多数点处,基本效应是绝对值较大的负值,即在大多数点处,厚度的增加造成升力减少。这是因为这些点所对应的构型下,整流罩厚度的变化跨越了线性和非线性区间的分界点,厚度的增加会使得整流罩发生局部失速,或者使得失速区域扩大,从而造成升力的下降。这与采用了相同整流罩构型的二维翼型Morris法分析结果中,CL敏感度较大的参数对CL的基本效应均值为正数[15]不同。因此在本设计中,为了获得较好的气动特性,应当对三维整流罩的厚度加以限制使其保持在线性区间。
|
| 图 5 t2对CL的基本效应分 Fig. 5 Distribution of CL elementaryeffect with respect to t2 |
t2是整流罩参数中对所有气动系数敏感度最大的一个。基准构型下,气动系数随t2的变化规律见表 4。可见,随t2的增大,CL、CD和CM都单调增大。
| t2 | CL | CD | CM |
| 0.007 | 0.411 3 | 0.019 72 | 0.037 6 |
| 0.047 | 0.413 7 | 0.020 71 | 0.044 9 |
| 0.087 | 0.416 4 | 0.022 02 | 0.052 7 |
因整流罩的剖面形状类似圆头尖尾的低速翼型,在分析整流罩几何参数对气动特性的影响时,可以把整流罩视为BWB飞机机身后部上表面固定放置的一段展弦比不大(约3.7)的机翼表面。从对带BLI效应的二维翼型的研究中[15]可知,在设定的参数变化区间内,随整流罩厚度的增大,整流罩发生了失速,CL先增大后减小,压差阻力系数一直增大,CM变化趋势和CL一致。而从表 4中气动系数随t2的变化规律可以看出,在设定的相同变化区间内整流罩未发生失速,这与二维研究结果是不同的。
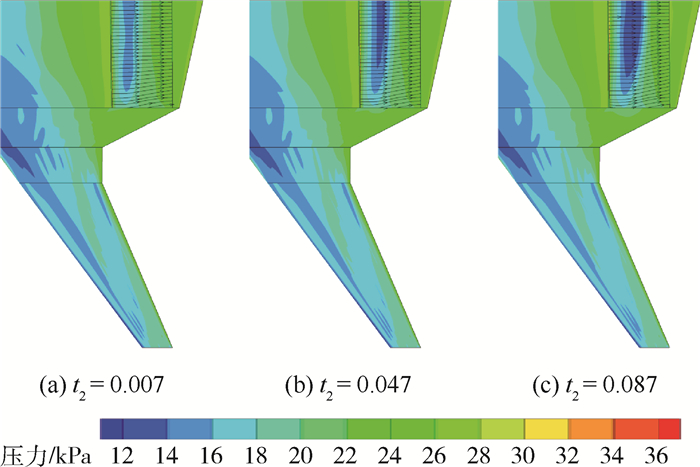
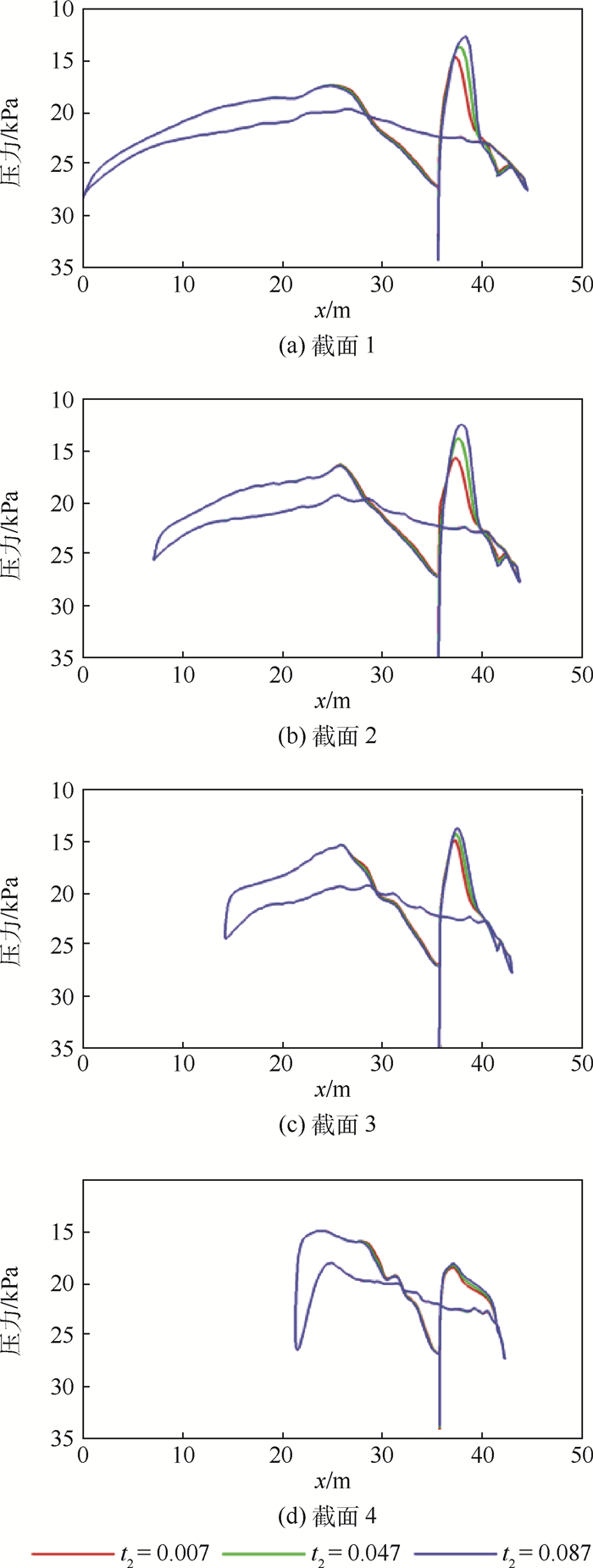
图 6为t2变化时的压力云图和流线图,图 7为t2变化对各截面压力分布的影响。从图中可以看出,t2变化主要影响整流罩表面的压力分布,基本不影响进气边界前的机体压力分布。在t2所在的截面2,t2增大使得当地的压力峰值增大,背风面的压力也随之增大。t2增大也使得其他截面的压力峰值增加了,且增加的幅值随与截面2的距离增加而降低。这是由于t2的变化不仅改变了当地截面的形状,还影响了展向流动,从而影响到整个截面的压力分布。另外,从整流罩表面流线还可以看出,靠近对称面的整流罩表面流线较为平顺,与平直翼的流线相似;靠近整流罩端面的流线向后缘收缩,体现出三维效应;t2增大还使得流线略向内收缩,表明此时三维效应略微增强。
|
| 图 6 t2变化时的压力云图和流线图 Fig. 6 Pressure contours and stream lineswith variation of t2 |
|
| 图 7 t2变化时的各截面压力分布 Fig. 7 Pressure distribution on cross sections with variation of t2 |
x4是4个截面的最大厚度位置变量中对气动系数敏感度最小的一个。气动系数随x4的变化规律见表 5,可见随x4增大,3个气动系数的变化量很小。与2.2.1节的结果对比可知,整流罩厚度位置的影响比厚度要弱,这也与Morris敏感度分析法的结果一致。
| x4 | CL | CD | CM |
| 0.25 | 0.413 5 | 0.020 70 | 0.044 7 |
| 0.29 | 0.413 7 | 0.020 71 | 0.044 9 |
| 0.33 | 0.413 7 | 0.020 68 | 0.044 8 |
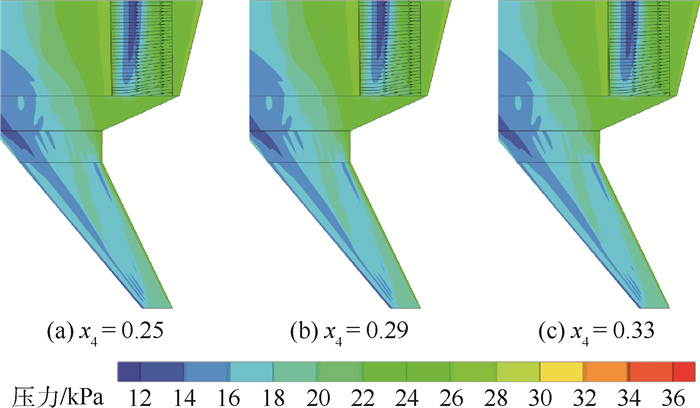
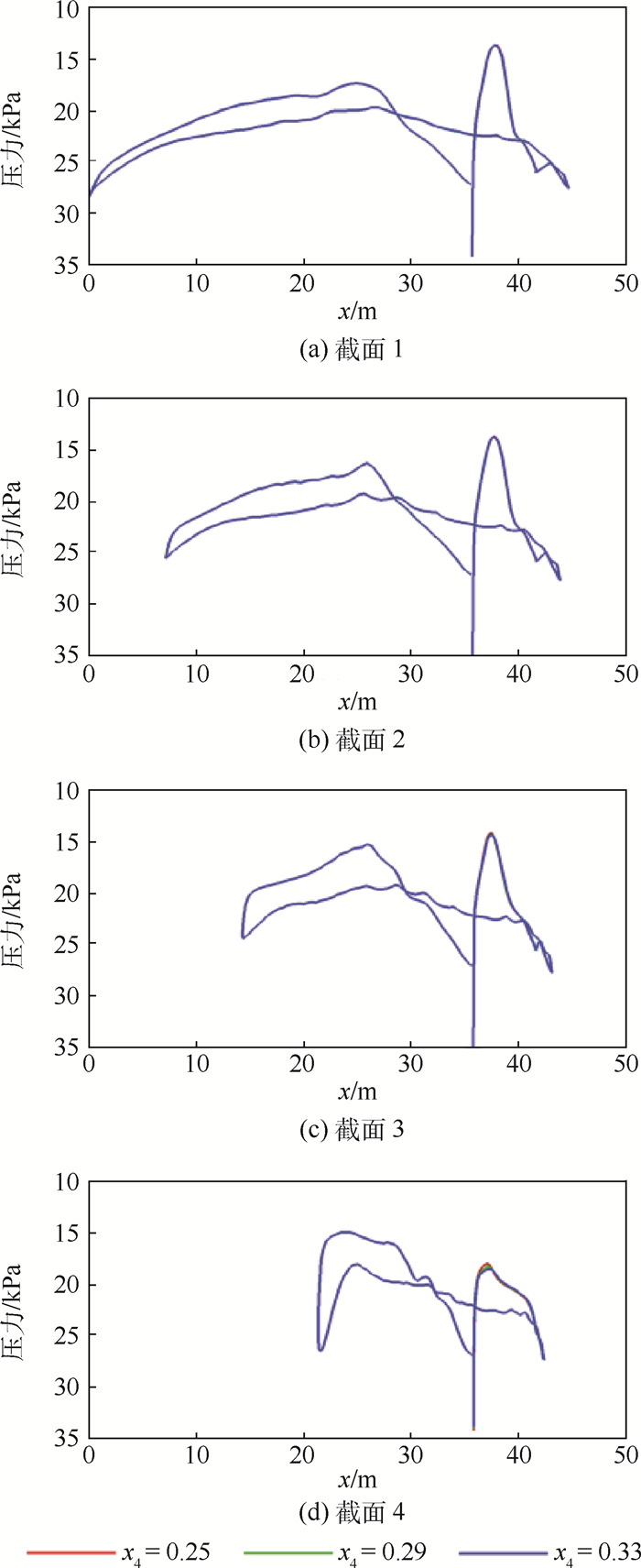
图 8为x4变化时的压力云图和流线图,图 9为x4变化对各截面压力分布的影响。从图中可以看出,x4的后移使得当地截面的压力峰值略微降低,这与二维结果是一致的。从其影响范围看,除对当地截面整流罩压力峰值有一定影响外,对机体表面和其他截面压力分布的影响很小。
|
| 图 8 x4变化时的压力云图和流线图 Fig. 8 Pressure contours and stream lines with variation of x4 |
|
| 图 9 x4变化时的各截面压力分布 Fig. 9 Pressure distribution on cross sections with variation of x4 |
分布式动力推进BWB布局其他基本设计参数在基准值附近变化时[14],整流罩对气动特性的影响规律可能不同。由于推进系统的布局参数众多,为了找到其中的关键参数,首先对基本设计参数进行了初步的敏感度区间分析,结果见表 6。
| 参数 | CL | CD |
| 流量系数 | 1.8 | 0.525 |
| 排气方向 | 1.34 | 0.32 |
| 进气边界弦向位置 | 0.392 | 0.28 |
| 进气边界高度 | 0.068 6 | 0.04 |
| 弦向整流罩长度 | 0.025 7 | 0.038 6 |
| 展向流量分布 | 0.019 5 | 0.024 |
| 展向进气位置分布 | 0.006 8 | 0.027 |
从表 6中可以看出,流量系数、排气方向和进气边界弦向位置这3个参数区间敏感度较大。以下分析这些参数在基准值附近变化时,整流罩关键参数t2对气动特性的影响规律。
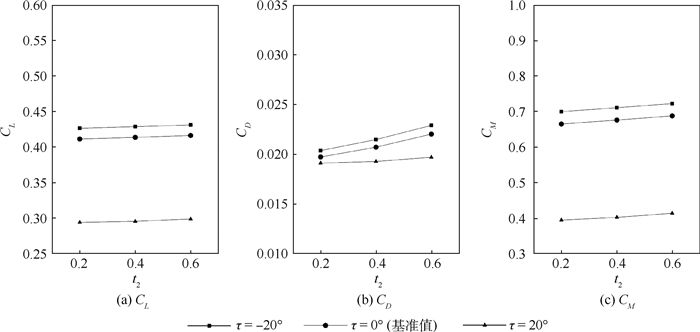
2.3.1 排气方向推进系统的排气对飞机尾部附近的流场有引射作用,因此排气方向τ会影响飞机的气动特性。图 10为不同τ下,CL、CD和CM随t2的变化。
|
| 图 10 不同τ下气动系数随t2的变化 Fig. 10 Variation of aerodynamic coefficients with t2 at different τ |
从图 10中可以看出,在τ取不同值时,CL、CD和CM随t2单调增加的趋势是不变的。且CL-t2和CM-t2曲线的斜率也基本不变,也就是说τ的变化不改变气动系数随t2的变化规律。当τ=20°时,CD随t2增加的斜率明显下降,此时CD几乎不随t2变化而变化。另外,当τ=20°时,CL和CM随t2变化的曲线都大幅向下移动,表明斜向上方的排气会使得气动特性大幅恶化。
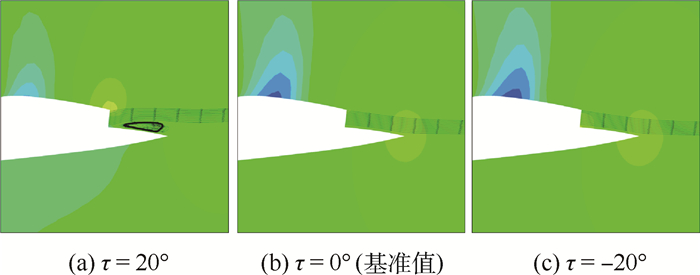
图 11为不同τ对应的局部压力分布和流线图。从图 11 (a) 中可见,由于布局的原因,τ=20°时排气方向与排气口后的机体表面产生了一个较大的夹角,在夹角处产生了分离,造成了气动特性的恶化。从图 11(c)中可见,τ=-20°时由于排气口后机体表面约束了气流的偏转,排气方向与τ=0°时相差不大,因此气动特性与τ=0°时相差不大。另一方面由于气流上沿仍产生了角度不大的偏转,因此,整流罩表面的流动也受其影响,低压区略有扩大,从而CL、CD均有所增大。
|
| 图 11 不同τ下的压力云图和流线图 Fig. 11 Pressure contours and stream lines at different τ |
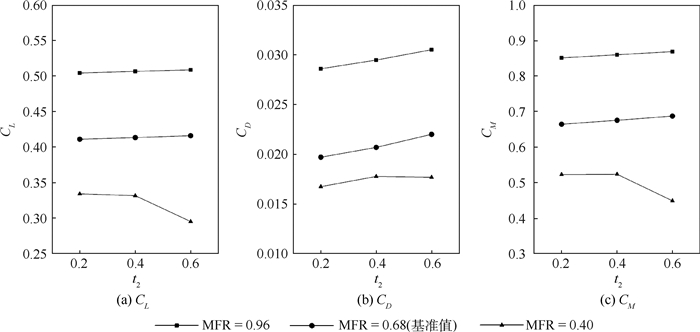
流量系数是BLI耦合布局中的重要参数,其变化会显著影响耦合布局的气动特性。图 12为不同MFR下气动系数随t2的变化。
|
| 图 12 不同MFR下气动系数随t2的变化 Fig. 12 Variation of aerodynamic coefficients with t2 at different MFR |
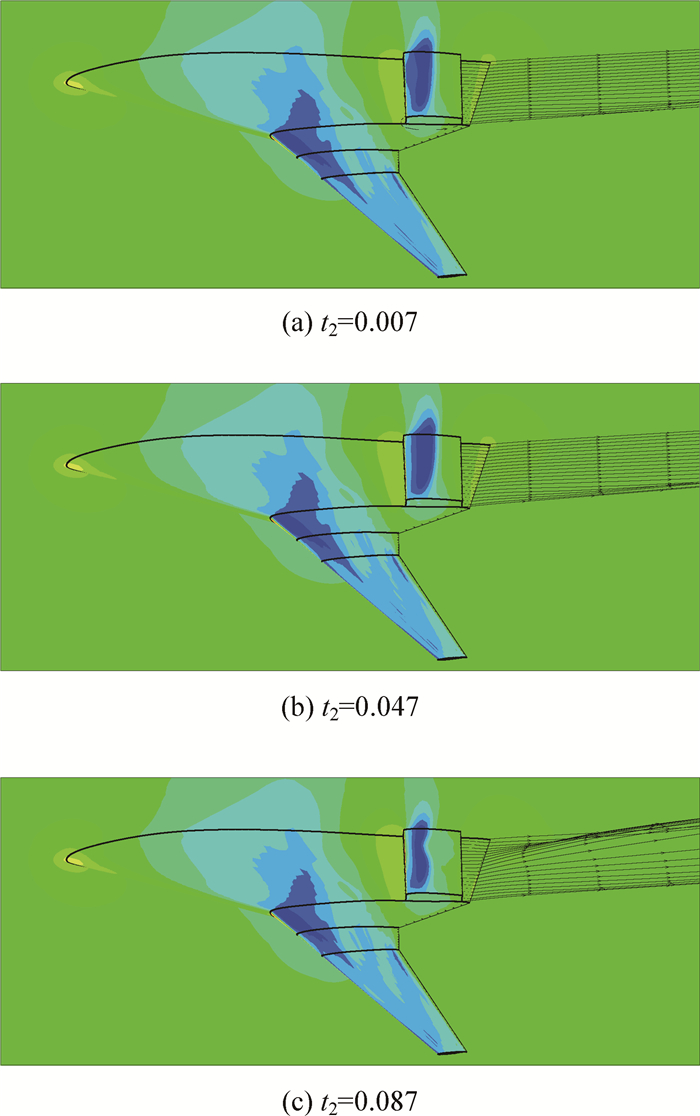
从图 12中可以看出,与基准状况相比,在MFR增大时,CL、CD和CM随t2单调增加的趋势不变且斜率基本一致。而MFR减小至0.40时,CL、和CM随t2先基本不变后减小,CD随t2先增加后减小。图 13为MFR=0.40时,不同t2对应的压力分布和流线图。从图 13中可见,当t2减小时,整流罩表面低压区的前缘局部后移,低压区略有变小。t2增加时,低压区的后缘局部前移,低压力区明显变小。观察图 13(c)的流线可知,在t2截面对应的位置,机身后部的流线明显向上偏折,这是因为t2增加使得当地气流发生了后缘分离,机身后部的气流减速,从而喷流的流线向上偏折。可见整流罩局部厚度增加的构型在MFR过小时,会导致当地的气流发生后缘分离,进而造成升力降低、阻力增加以及喷口流线偏折。
|
| 图 13 MFR=0.40时飞机表面和对称面压力云图及喷口流线图 Fig. 13 Pressure contours of aircraft surface and symmetric plane and stream lines of nozzle at MFR=0.40 |
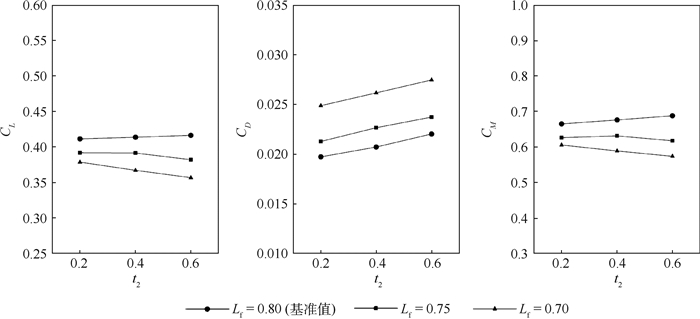
进气边界弦向位置Lf是BLI耦合布局中进排气系统的重要位置参数。图 14为不同Lf下气动系数随t2的变化。由于几何约束,进排气系统无法再向后移动,因此研究Lf向前移动不同距离时t2的影响规律。
|
| 图 14 不同Lf下气动系数随t2的变化 Fig. 14 Variation of aerodynamic coefficients with t2 at different Lf |
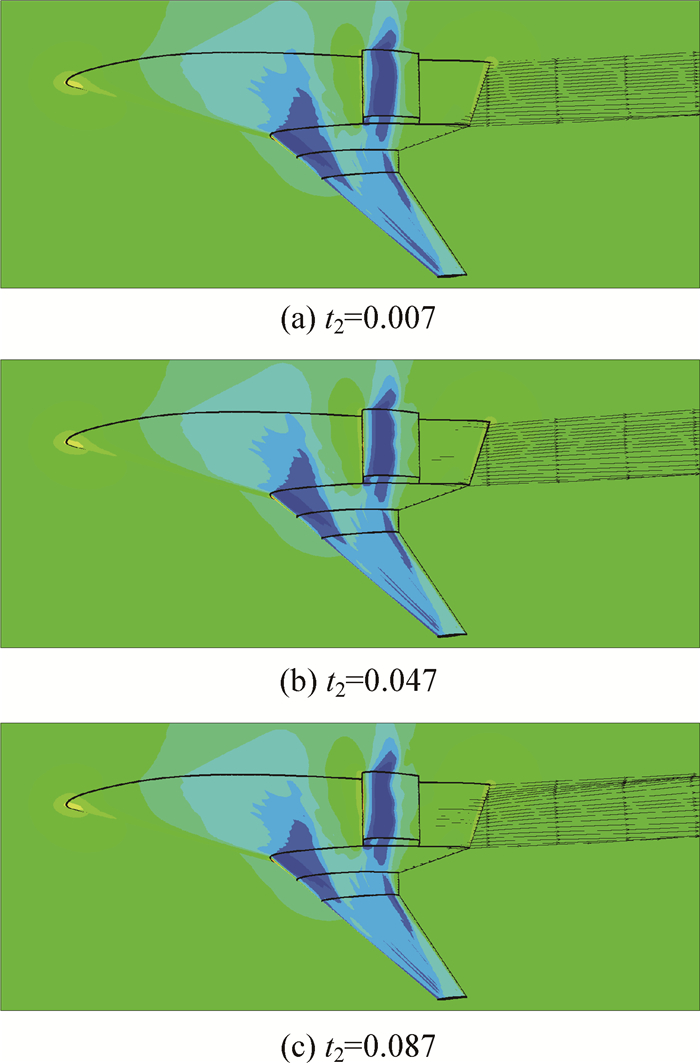
从图 14中可以看出,Lf减小至0.75时,CL和CM随t2先增加后减小;Lf减小至0.70时,CL和CM随t2的增加而减小;所有Lf下CD均随t2单调增加,且Lf越靠前CD越大。这说明随着进排气系统的前移,整流罩的失速特性和气动特性也变差了。图 15为Lf=0.70时,不同t2对应的压力分布和流线图。可见在t2=0.007时,整流罩表面后部即已经存在分离区,t2的增大使得分离区也随之增大,从而愈加恶化了气动特性,t2=0.087时截面2后部的喷口气流也出现了偏折现象。这是由于进气边界的前移使得整流罩前缘过早地遭遇上翼面未经充分加速的气流,整个整流罩表面的气流能量不足,从而更容易失速。
|
| 图 15 Lf=0.70时飞机表面和对称面压力分布及喷口流线图 Fig. 15 Pressure contours of aircraft surface and symmetric plane and stream lines of nozzle at Lf=0.70 |
Morris敏感度分析结果表明,在整流罩设计参数中,t2和t3对气动系数的耦合作用较强,下面分析原因。定义这2个参数同时产生增量(增量可以是正值或负值)时,气动系数的增量为dcoup,这2个参数单独产生增量时气动系数的增量之和为dline。易知dline即为dcoup的线性主部。再定义两者的相对差别为(dline-dcoup)/dcoup,可知相对差别越大,代表这2个变量的耦合作用越强。考虑到参数参考变化区间的长度,将参数增量设为±4%。基于以上分析,将这2个参数产生增量时相对差别的变化规律列于表 7。
| 气动系数 | 算例 | dcoup | dline | 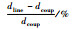 |
| CL | 1 | -0.012 4 | -0.009 8 | -21.1 |
| 2 | -0.028 7 | -0.002 1 | -92.8 | |
| CD | 1 | -0.002 6 | 0.003 2 | 24.4 |
| 2 | -0.003 8 | -0.004 7 | 21.3 | |
| CM | 1 | 0.045 2 | -0.041 8 | -7.5 |
| 2 | -0.040 5 | -0.019 1 | -147.1 | |
| 注:算例1、2分别代表t2和t3同时减少和同时增加。 | ||||
从表 7中可见,t2和t3同增时,两者对气动系数的耦合作用比两者同减时更强。这是因为整流罩厚度增加后发生了失速,其表面难以维持附着流动,气动系数的非线性增强。这与二维情形下t与Lf的耦合变化影响趋势是相同的[15]。
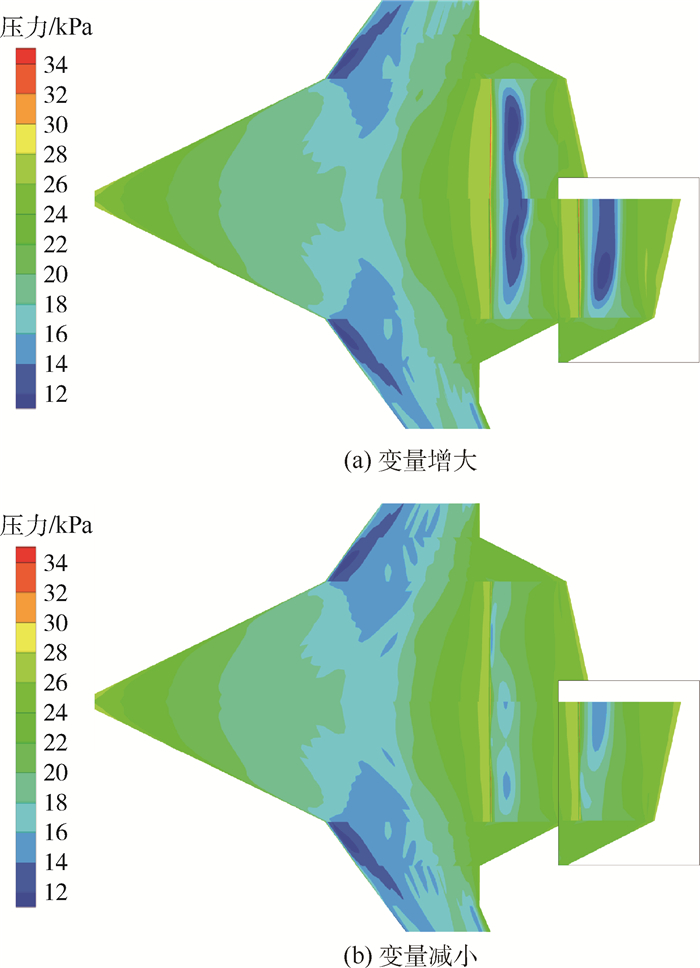
图 16为t2和t3耦合变化时的压力分布图,每图的上半部分为t2和t3同时变化;下半部分为t2单独变化,小图为t3单独变化。从图中可以看出,t2和t3同增时的影响更强,低压区显著减小。t2和t3同减时类似,整流罩表面的低压区几乎消失,其效果比t2和t3单独变化时更强。
|
| 图 16 t2和t3耦合变化时的压力分布 Fig. 16 Pressure distribution with coupled variation of t2 and t3 |
本文使用Morris敏感度分析法,结合数值模拟,研究了BLI效应下分布式动力BWB布局飞机的整流罩设计参数对气动特性的影响,获得以下结论:
1) 对整流罩4个截面的厚度和最大厚度位置共8个参数进行了气动特性敏感度分析,结果表明:特征截面2和3的最大厚度对气动特性影响相对较大,其他参数影响相对较小。总体而言,厚度参数比最大厚度位置参数的敏感度更大且与其他参数耦合作用更强,这与二维的分析结果一致。
2) 特征截面2最大厚度对气动特性影响较大的主要原因为:截面厚度变化使得当地截面翼型的厚度和弯度增加,从而改变本地截面的压力分布,增大升力和压差阻力系数;截面厚度的变化还改变了展向流动,使得其他截面的压力分布产生变化,并影响整流罩沿翼展的流线分布。
3) 当流量系数和进气口弦向位置减小时,截面最大厚度增大对气动特性影响更为显著,这是因为在这两种情况下,整流罩表面来流速度较低,截面最大厚度增大会使得整流罩发生失速,影响整流罩表面压力分布和喷口后气流方向,从而影响升力和阻力。
4) 特征截面2和3的最大厚度同时变化时对气动特性的耦合作用较强,这是因为两者同时增大使整流罩表面的失速区域进一步扩大,增加了气动特性的非线性。
| [1] | LIEBECK R H. Design of the blended wing body subsonic transport[J]. Journal of Aircraft, 2004, 41 (1): 10–25. DOI:10.2514/1.9084 |
| [2] | QIN N, VAVALLE A, MOIGNE L A, et al. Aerodynamic considerations of blended wing body aircraft[J]. Progress in Aerospace Sciences, 2004, 40 (6): 321–343. DOI:10.1016/j.paerosci.2004.08.001 |
| [3] | LABAN M, ARENDSEN P, ROUWHORST W, et al. A computational design engine for multi-disciplinary optimisation with application to a blended wing body configuration[C]//9th AIAA/ASSMO Multidisciplinary Analysis and Optimization Conference. Reston: AIAA, 2002. |
| [4] | KIM H, LIOU M F, LIOU M S. Mail-slot nacelle shape design for N3-X hybrid wing body configuration[C]//51st AIAA/SAE/ASEE Joint Propulsion Conference. Reston: AIAA, 2015: 3805. |
| [5] | KO A. The multidisciplinary design optimization of a distributed propulsion blended-wing-body aircraft[D]. Blacksburg: Virgina Polytechnic Institute and State University, 2003. https://vtechworks.lib.vt.edu/handle/10919/27257 |
| [6] | GOHARDANI A S, DOULGERIS G, SINGH R. Challenges of future aircraft propulsion:A review of distributed propulsion technology and its potential application for the all electric commercial aircraft[J]. Progress in Aerospace Sciences, 2011, 47 (5): 369–391. DOI:10.1016/j.paerosci.2010.09.001 |
| [7] | KIM H D, BROWN G V, FELDER J L. Distributed turboelectric propulsion for hybrid wing body aircraft[C]//9th International Powered Lift Conference. London: Royal Aeronautical Society, 2008. |
| [8] | HILEMAN J I, SPAKOVSZKY Z S, DRELA M, et al. Airframe design for silent fuel-efficient aircraft[J]. Journal of Aircraft, 2010, 47 (3): 956–969. DOI:10.2514/1.46545 |
| [9] | KO A, LEIFSSON L T, SCHETZ J A, et al. MDO of a blended-wing-body transport aircraft with distributed propulsion: AIAA-2003-6732[R]. Reston: AIAA, 2003. |
| [10] | KO A, SCHETZ J A, MASON W H. Assessment of the potential advantages of distributed-propulsion for aircraft[C]//XVIth International Symposium on Air Breathing Engines (ISABE). Reston: AIAA, 2003: 71-79. |
| [11] | RODRIGUEZ D L. Multidisciplinary optimization method for designing boundary-layer-ingesting inlets[J]. Journal of Aircraft, 2009, 46 (3): 883–894. DOI:10.2514/1.38755 |
| [12] | LUNDBLADH A, GRÖNSTEDT T. Distributed propulsion and turbofan scale effects[C]//ISABE 2005, 17th Symposium on Airbreathing Engine. Reston: AIAA, 2005. |
| [13] | LIOU M S, KIM H J, LIOU M F. Aerodynamic design of the hybrid wing body with nacelle: N3-X propulsion-airframe configuration[C]//34th AIAA Applied Aerodynamics Conference. Reston: AIAA, 2016: 3875. |
| [14] |
闫万方, 吴江浩, 张艳来. 分布式推进关键参数对BWB飞机气动特性影响[J].
北京航空航天大学学报, 2015, 41 (6): 1055–1065.
YAN W F, WU J H, ZHANG Y L. Effects of distributed propulsion crucial variables on aerodynamic performance of blended wing body aircraft[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41 (6): 1055–1065. (in Chinese) |
| [15] |
项洋, 吴江浩, 张艳来. BLI效应下整流罩设计对翼型气动特性的影响[J].
北京航空航天大学学报, 2016, 42 (5): 945–952.
XIANG Y, WU J H, ZHANG Y L. Effects of cowling design on aerodynamic performance of airfoil with BLI[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016, 42 (5): 945–952. (in Chinese) |
| [16] | NICHOLS M R, KEITH A L. Investigation of a systematic group of NACA 1-series cowlings with and without spinners: NACA-Report-950[R]. Washington, D. C. : U. S. Government Printing Office, 1950. |
| [17] | MORRIS M D. Factorial sampling plans for preliminary computational experiments[J]. Technometrics, 1991, 33 (2): 161–174. DOI:10.1080/00401706.1991.10484804 |



