空间任意两坐标系的旋转变换常用描述方法是方向余弦矩阵、欧拉角和四元数,且它们之间都存在相互对应的转化关系[1-3]。若空间任意两坐标系间没有明确的旋转关系,则用方向余弦矩阵描述更加方便,但需求解9个参数;欧拉角表示坐标旋转变换的方式为依次绕着坐标系的3个坐标轴按固定次序旋转3次,共有12种转位次序[4-5];若仅绕着空间某任意一条轴一次转位实现坐标变换,则用四元数法描述更为方便[6-7]。由于四元数表示方法简单,且不存在奇异性,故广泛应用于飞行器控制、捷联惯导系统、刚体旋转运动等领域,且在姿态控制、更新及姿态解算算法等领域已有大量深入的研究[8-11]。
欧拉角虽然形象直观,易理解,但该方法是按照固定坐标轴旋转次序进行坐标旋转的,很容易造成万向节锁(gimbal lock)现象[12-13]。理论上,欧拉旋转可以靠3次固定坐标轴顺序旋转实现物体的任意转动,但实际上如果在旋转中不幸让某些坐标轴重合,便会丢失一个方向上的旋转能力,在这种状态下无论怎么旋转都不可能得到某些想要的旋转效果,除非打破原先设定的旋转顺序或者同时旋转3个坐标轴。由于万向节锁的存在,欧拉旋转无法实现球面平滑差值。
尽管四元数可以避免万向节锁现象,只需一个4维的参数就可以执行绕任意过原点的向量旋转,方便快捷,而且可以提供平滑插值;但其理解较困难,不直观,因为其多了一个维度,相较于欧拉旋转更复杂。在需要保存大量角位移时(比如存储动画数据),比欧拉角多出的33%的数据量也是相当可观的。目前四元数有许多在不同应用领域的优化研究, 但其优化的实质并非是减少四元数的维数[14-15]。
为了避免欧拉角的局限性,同时尽可能地减少坐标系旋转所需表示的参数个数,本文详细研究了两位置坐标旋转变换的通用表示法,首次提出了一种三元角两位置坐标旋转变换方法,它对坐标旋转变换提供了一种新思路,且对复合运动的描述较四元数和欧拉角而言更为便捷。
1 三元角相关概念及参数定义三元角坐标旋转变换方法核心内容是:空间任意2个相同原点的直角坐标系,通过2次旋转便可实现其重合,且3个角参数便可唯一确定其坐标旋转变换矩阵。
空间任意坐标系两位置变换过程如图 1所示。为方便描述,本文在所有图示和推导过程中,1系代表初始坐标系(初系),2系代表进行一次转位后的过渡坐标系,3系代表末坐标系(末系)。为了更加直观表示由3系到2系的转位过程,这里将该过程从图 1总过程图中单独提取出来,如图 2所示。

|
| 图 1 三元角坐标变换方式示意图 Fig. 1 Schematic diagram of ternary angle coordinate transformation |
|
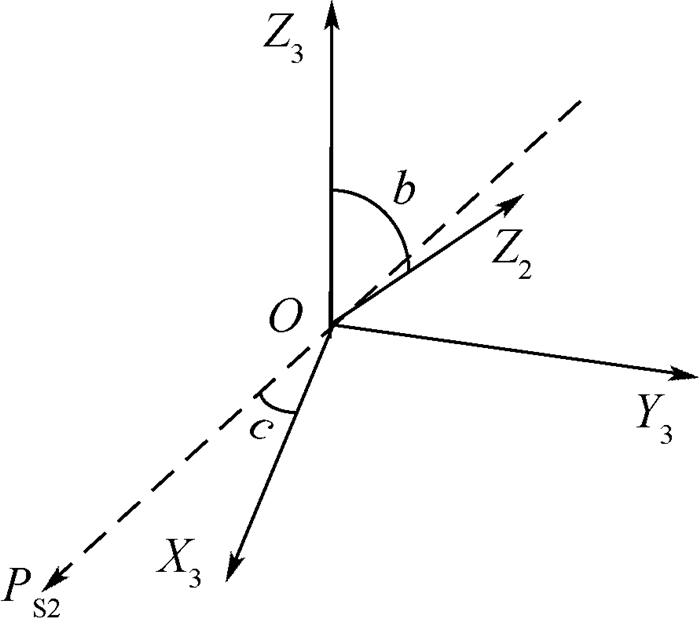
| 图 2 末系到初系先偏转过程简图 Fig. 2 Process diagram of deflection first from last coordinate system to initial coordinate system |
三元角法的3个参数分别为:偏矢角c、偏转角b和旋转角a。相关参数及概念定义如下:
1) 偏矢轴PS 在t0时刻对1系进行惯性凝固,将此时的Z轴定义为惯性转轴Zi, 将此时的XOY平面定义为惯性平面Si,在Si平面内某条轴与Zi轴垂直且相交于原点,该轴除了可以进行自身旋转,同时与Zi轴进行半固连,伴随Zi轴一同旋转,定义该轴为偏矢轴PS。
2) 偏矢角c 偏矢轴PS绕Zi轴(规定逆时针为正方向)旋转到Xi轴时所转过的角度定义为偏矢角c(0°, 360°)。
3) 偏转角b 1系Z轴在坐标旋转过程中绕着偏矢轴PS(规定逆时针为正方向)旋转到3系Z轴时所转过的角为偏转角b(0°, 360°)。
4) 旋转角a 1系在旋转至3系的过程中,绕惯性转轴(规定逆时针为正方向)旋转过的角度定义为旋转角a(0°, 360°)。
三元角方法的特点:按本节定义,空间任意两坐标系1系和3系,从1系到3系的变换可以经过两次旋转实现,一次是绕惯性转轴Zi轴旋转,另一次是绕偏矢轴PS旋转,且这2次旋转相互独立,互不影响,不分先后顺序。这2次旋转有2种次序组合方式,2种次序的变换最终得到的参数内容是相同的。与欧拉角变换方法相比,不会因为绕坐标轴旋转次序的不同而出现不同参数内容的情况;同时,在旋转变换过程中,Zi轴或PS轴可以是1系上的某坐标轴,也可以不是其自身坐标轴,从而使三元角方法相对于欧拉角的旋转方式相对自由;另外,由于惯性转轴Zi和偏矢轴PS始终垂直,不存在重合的情况,从而避免了出现万向节锁现象。
2 三元角变换矩阵无论是先绕惯性转轴Zi轴旋转,后绕偏矢轴PS旋转(简称先旋后偏方式),还是先绕偏矢轴PS旋转,后绕惯性转轴Zi轴旋转(简称先偏后旋方式),最后得到的旋转角a、偏转角b、偏矢角c这3个参数内容以及旋转矩阵都是相同的。为了说明这2种转位次序具有相同的参数内容,在三元角变换矩阵的求取过程中对先偏后旋和先旋后偏2种方式都进行了变换矩阵的求取。为了更加直观地说明任何两坐标系按本文提出的方式进行2次转位便可实现重合,这里采用由末系到初系的方式进行变换矩阵的推导。
2.1 由末系到初系按先偏后旋方式推导 2.1.1 先偏转如图 1和图 2所示, Z3轴绕着偏矢轴PS2顺时针旋转角b到达Z2轴,使3系与2系重合,偏矢轴PS2与X3轴的夹角为偏矢角c, 则由3系旋转到2系的四元数表示为

|
(1) |
将q1用旋转矩阵表示为

|
式中:
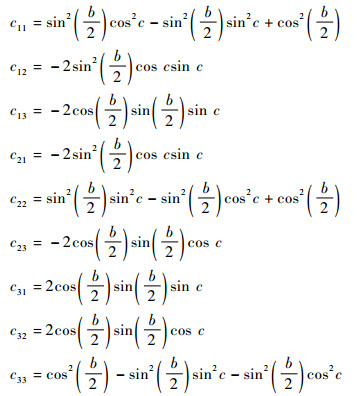
|
如图 1所示,偏转过后再由2系绕Z2(Z1)轴顺时针旋转角a到1系,由2系到1系的旋转矩阵表示形式为
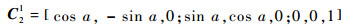
|
(2) |
得到由末系到初系的旋转矩阵最终表示形式为:Cmc=C31=C21C32,即

|
(3) |
式中:
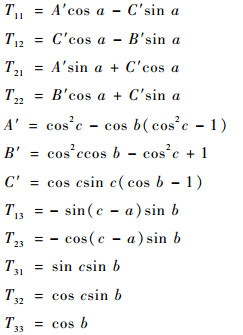
|
因为本文方法中的3个角度参数是固定的,并没有限制两位置的旋转次序(即先偏后旋和先旋后偏),若式(3)表示的三元角公式正确,则只要按照三元角两位置旋转方法要求找到3个参数,从末系到初系按照先偏后旋和先旋后偏的方式得出的三元角矩阵应该是相同的。2.2.1节和2.2.2节将进行验证。
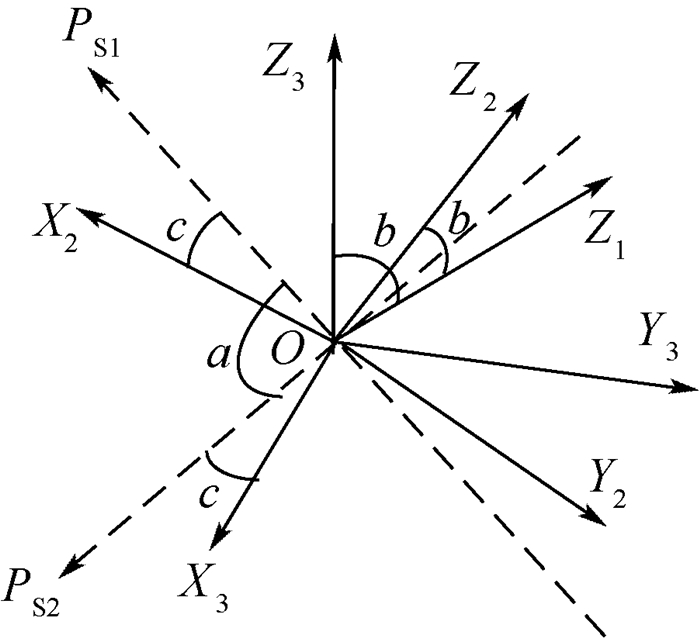
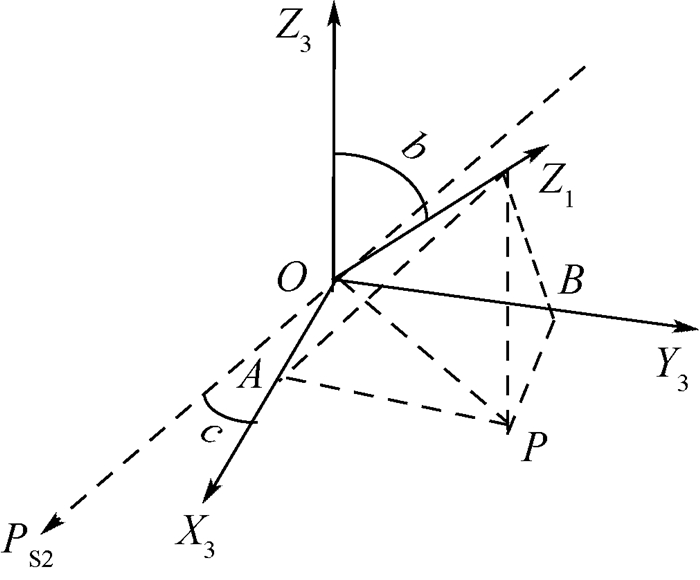
2.2.1 先旋转如图 3所示,若3系(末系)绕着初始坐标系的Z1轴顺时针旋转角a到2系,将该过程用四元数表示,需要分析求取旋转轴Z1相对参考系3的位置矢量。为了分析方便,作图如图 4所示。
|
| 图 3 末系到初系先旋后偏过程图 Fig. 3 Process diagram of rotation first deflection second from last coordinate system to initial coordinate system |
|
| 图 4 末系到初系先旋转过程图 Fig. 4 Process diagram of rotation first from last coordinate system to initial coordinate system |
过点Z1向X3OY3平面做一条垂线,交该平面于点P, 过点P分别向OX3轴和OY3轴做垂线,分别交于点A和点B,连接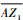
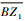
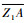
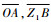
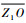
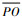

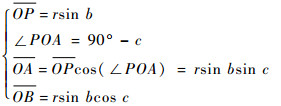
|
则有
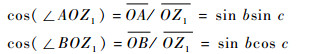
|
则用四元数表示该旋转过程为

|
(4) |
式中:l0=cos 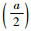
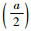
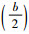
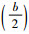
将q2用旋转矩阵表示为

|
式中:
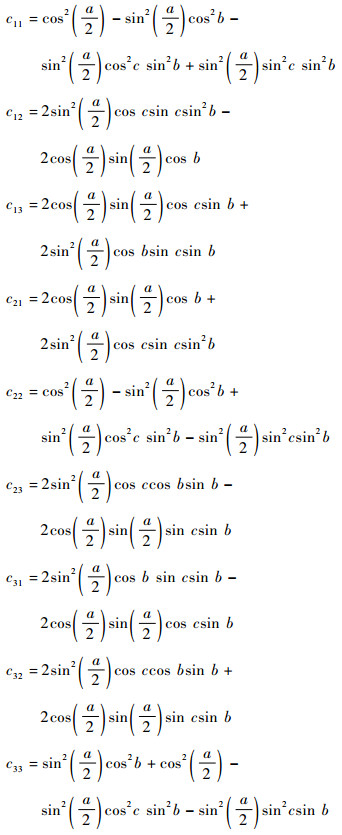
|
如图 5所示,由2系的Z2轴绕着偏矢轴PS1轴顺时针旋转角b使Z2轴与Z1轴重合,即2系与1系重合。用四元数表示为

|
(5) |
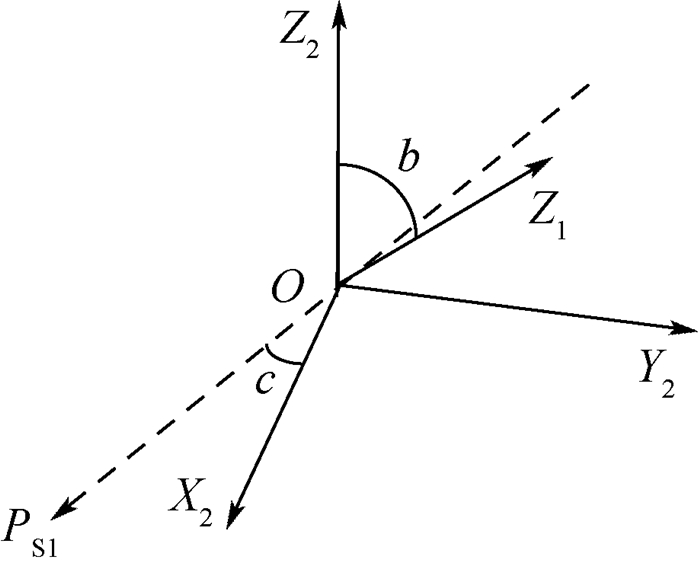
|
| 图 5 末系到初系后偏转过程图 Fig. 5 Process diagram of post deflection from last coordinate system to initial coordinate system |
将q3用旋转矩阵表示为

|
式中:
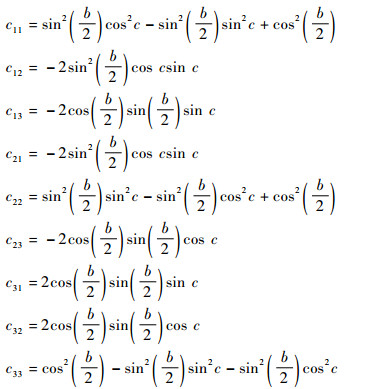
|
经过计算,有Cm′c′=C31=C21C32=Cmc,验证了末系到初系三元角矩阵Cmc的正确性。推导出三元角的旋转矩阵表示形式后,便可建立其与欧拉角和四元数的关系。
3 三元角与欧拉角、四元数之间的转换关系 3.1 三元角与欧拉角的转换关系在实际运用中,欧拉角常用来表示运载体的姿态,其姿态角常采用312的转序进行描述,(通常,在3转位中,按绕Z轴顺时针转为正,)其绕Z轴、X轴和Y轴所转过的角度分别称为航向角ψ(0°,360°)、俯仰角θ(-90°,90°)和横滚角γ(-180°,180°)。将末系(3系)到初系(1系)的坐标旋转变换用上述欧拉角表示,对照式(3),则欧拉角与三元角关系为
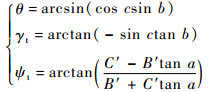
|
(6) |
式中:ψt、γt分别为航向角和横滚角的真值,如表 1和表 2所示。
| T22 | T21 | ψ |
| →0 | + | 90° |
| →0 | - | -90° |
| + | + | ψt |
| + | - | ψt |
| - | + | ψt+180° |
| - | - | ψt-180° |
3.2 三元角与四元数的转换关系
用q=(q0, q1, q2, q3)表示由末系(3系)到初系(1系)旋转四元数,对照式(3),则三元角与四元数关系为
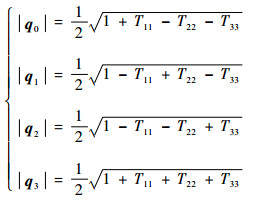
|
(7) |
各个元素的符号按式(8)确定:
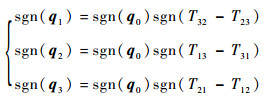
|
(8) |
在惯性导航领域,目前比较先进的误差抑制方式是旋转调制技术,有单轴旋转调制和双轴旋转调制,单轴旋转调制中有连续旋转调制和偏置旋转调制等,双轴旋转调制有16次序转位等,但其都是绕着自身坐标系的坐标轴进行偏置或旋转[16-18]。
理论上,如果惯性测量单元(IMU)的Z轴在旋转调制时进行晃动,则会增加其误差的可观测性。为了更全面的分析旋转调制技术,这里定义一种复合旋转调制方式,按本文提出的相关定义,坐标系绕着t0时刻经惯性凝固后的Z轴进行逆时针旋转,旋转周期为10 s,同时,规定偏矢角c为25°,坐标系绕着本文中定义的偏矢轴按周期T=2 s的正弦方式进行小角度偏转,偏转角度最大幅值为20°。该条件下的坐标变换描述用三元角表示为
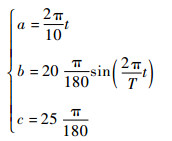
|
(9) |
如式(6)和式(7)所示,若用四元数和欧拉角表示时则会极其复杂,可见,用三元角描述该运动时更加方便简洁,相较于其他2种方法更适合对复合运动的描述。
用三元角法进行该种复合运动轨迹的MATLAB仿真,如图 6所示。经过简单的分析和判断,仿真的运动轨迹与设计的相符。

|
| 图 6 坐标系的三维变换效果图 Fig. 6 Three-dimensional effect graphs of coordinate transformation |
为简单起见,假设用该种复合旋转方式对IMU的常值误差进行调制,IMU 3个轴向上陀螺的常值漂移为0.01(″)/s, 则分别用单轴旋转调制和该种复合旋转调制进行仿真分析, 其中单轴旋转调制的周期为10 s,2种方式的调制效果如图 7和图 8所示, 3个陀螺常漂在导航系X、Y、Z轴上的总投影分别为εx、εy、εz。

|
| 图 7 常值漂移单轴旋转调制效果分析 Fig. 7 Analysis on effect of single-axis rotation modulation with constant drift |
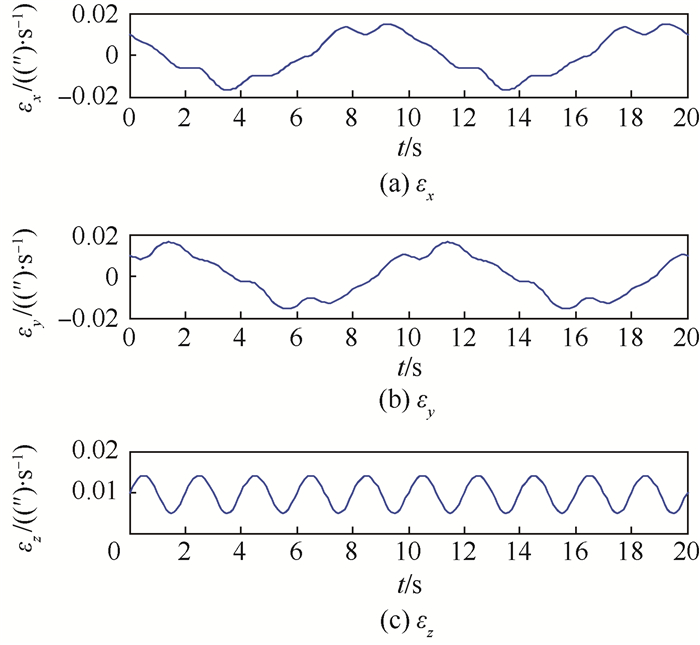
|
| 图 8 常值漂移复合旋转调制效果分析 Fig. 8 Analysis on effect of compound rotation modulation with constant drift |
从图 7和图 8中可以看出,单轴和复合旋转调制都能将XOY平面内的误差调制掉,但单轴旋转调制对Z轴上的常值漂移却没有调制效果;由于复合调制中将Z轴进行小角度偏转,增加了Z方向上常值误差的可观测性,从而将常值误差由0.01(″)/s调制为0.009 7(″)/s,即每小时比单轴旋转调制减少了1.08″的漂移量。可见,通过简单设计的复合调制对Z轴上的常值漂移有一定的调制效果。
通过研究三元角方法,为旋转调制提供了新的思路——复合旋转调制。三元角法可以更加方便地设计复合运动的形式,为下一步进行IMU常值误差、标度因数误差和安装误差调制情况的分析提供了有力的数学手段。上述举例只是反映了三元角在复合旋转调制中的应用,除此之外,该方法还可广泛应用于三维动画设计、姿态仿真等其他领域。
5 结论1) 三元角坐标旋转变换方法,是一种仅需2次转位便可实现空间任意两坐标系旋转变换的通用方法,具有普适性,且与四元数和欧拉角在思维角度与描述方法上具有较大区别,其对坐标旋转变换提供了一种全新的思路。
2) 对较复杂的复合运动过程,用四元数或欧拉角描述时,除直接理解上的困难外,在运动的数学表达上也会极为复杂。三元角本身就是从偏转和旋转的角度出发进行表示的,故对复合运动的描述会更加方便、更易理解,且根据方法需要,定义了偏矢轴、偏矢角、偏转角和旋转角等全新概念,体现了一种区别于四元数和欧拉角的新的坐标变换思路和视角。
3) 三元角在转位次数及参数上,相对于四元数和欧拉角,具有较明显优势:三元角转位次数(2次)比欧拉角(3次)少,且避免了欧拉角因要按固定3次转位而造成的万象节锁现象;维数上,三元角(三维)比四元数(四维)少,且和欧拉角(三维)比也没有额外增加。此外,三元角和欧拉角参数表示的都是角度,故相较于四元数,受参数浮点数舍入误差累计的影响较小。
4) 三元角坐标旋转变换方法对IMU旋转调制技术的研究提供了新的思路和数学手段。可在此基础上,借助三元角进一步研究IMU的复合旋转调制技术。
| [1] | DIEBEL J. Representing attitude:Euler angles, unit quaternions, and rotation vectors[J]. Matrix, 2006, 58 (15-16): 1–35. |
| [2] |
余杨, 张洪钺. 圆锥运动及其影响的3种描述方法[J].
北京航空航天大学学报, 2008, 34 (8): 956–960.
YU Y, ZHANG H Y. Three description of coning motion and its influence[J]. Journal of Beijing University of Aeronautics and Astronautics, 2008, 34 (8): 956–960. (in Chinese) |
| [3] |
尹剑, 陈红, 杨萌, 等. 捷联姿态计算中方向余弦与四元数法分析比较[J].
四川兵工学报, 2015, 36 (9): 106–110.
YIN J, CHEN H, YANG M, et al. Analysis and comparison of direction cosine matrix and quaternion methods for strapdown inertial navigation attitude algorithm[J]. Journal of Sichuan Ordnance, 2015, 36 (9): 106–110. (in Chinese) |
| [4] | HUANG Z, LI Y W, GAO F. The expression of the orientation of a spatial moving unit by Euler angle[J]. Journal of Yanshan University, 2002, 26 (3): 189–192. |
| [5] |
李跃军, 阎超. 飞行器姿态角解算的全角度双欧法[J].
北京航空航天大学学报, 2007, 33 (5): 505–508.
LI Y J, YAN C. Improvement of dual-Euler method for full scale Eulerian angles solution of aircraft[J]. Journal of Beijing University of Aeronautics and Astronautics, 2007, 33 (5): 505–508. (in Chinese) |
| [6] |
刘俊峰. 三维转动的四元数表述[J].
大学物理, 2004, 23 (4): 39–43.
LIU J F. Three dimensional rotation represented by quaternion[J]. College Physics, 2004, 23 (4): 39–43. (in Chinese) |
| [7] |
邢燕. 四元数及其在图形图像处理中的应用研究[D]. 合肥: 合肥工业大学, 2009: 1-8.
XING Y.Research on quaternion and its applications in graphics and image processing[D].Hefei:Hefei University of Technology, 2009:1-8(in Chinese). http://cdmd.cnki.com.cn/article/cdmd-10359-2010036953.htm |
| [8] |
封文春, 林贵平. 四元数在弹射座椅性能仿真中的应用[J].
北京航空航天大学学报, 2006, 32 (8): 881–884.
FENG W C, LIN G P. Application of quaternion in ejection seat performance simulation[J]. Journal of Beijing University of Aeronautics and Astronautics, 2006, 32 (8): 881–884. (in Chinese) |
| [9] | ZHANG R H, JIA H G, CHEN T, et al. Attitude solution for strapdown inertial navigation system based on quaternion algorithm[J]. Optics and Precision Engineering, 2008, 16 (10): 1963–1970. |
| [10] |
袁赣南, 张涛. 四元数UKF超紧密组合导航滤波方法[J].
北京航空航天大学学报, 2010, 36 (7): 762–766.
YUAN G N, ZHANG T. Quaternion unscented Kalman filtering for ultra-tight integration[J]. Journal of Beijing University of Aeronautics and Astronautics, 2010, 36 (7): 762–766. (in Chinese) |
| [11] | XIA X, JING W, LI C, et al. Time-shared scheme design for attitude control system during space separation[J]. Aerospace Science and Technology, 2011, 15 (2): 108–116. DOI:10.1016/j.ast.2010.06.005 |
| [12] | VASS G. Avoiding gimbal lock[J]. Computer Graphics World, 2009, 32 (6): 10–11. |
| [13] |
赵庆涛, 邢建平, 王康, 等. 基于体感识别的人形机器人姿态控制策略研究[J].
互联网天地, 2016, 13 (5): 14–24.
ZHAO Q T, XING J P, WANG K, et al. Research on humanoid robot posture control strategy based on somatosensory recognition[J]. China Internet, 2016, 13 (5): 14–24. (in Chinese) |
| [14] |
刘建洲. 四元数体上的矩阵及其优化理论[J].
数学学报, 1992, 35 (6): 831–838.
LIU J Z. Matrix and its optimization theory on quaternion[J]. Acta Mathematica Sinica, 1992, 35 (6): 831–838. (in Chinese) |
| [15] | SCHMIDT J, NIEMANN H.Using quaternions for parametrizing 3-d rotations in unconstrained nonlinear optimization[C]//Proceedings of the Vision Modeling and Visualization Conference, VMV.[S.l.]:Aka Gmbh, 2001:399-406. |
| [16] |
徐烨烽, 吕妍红, 仇海涛. 基于MEMS器件的旋转调制式航姿参考系统设计[J].
北京航空航天大学学报, 2010, 36 (11): 1343–1347.
XU Y F, LV Y H, QIU H T. Design of rotation modulation on AHRS based on MEMS sensor[J]. Journal of Beijing University of Aeronautics and Astronautics, 2010, 36 (11): 1343–1347. (in Chinese) |
| [17] |
赵晓伟, 李江, 党宁, 等. 基于单轴连续旋转调制的方位对准技术[J].
导弹与航天运载技术, 2016 (1): 26–30.
ZHAO X W, LI J, DANG N, et al. Research on azimuth alignment technology based on the single axis continuous rotation modulation[J]. Missiles and Space Vehicles, 2016 (1): 26–30. (in Chinese) |
| [18] |
蔡山波. 双轴旋转捷联惯导系统旋转控制算法研究[D]. 北京: 北京理工大学, 2016.
CAI S B.Control algorithm of dual-axis rotation SINS framework[D].Beijing:Beijing Institute of Technology, 2016(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10007-1016717719.htm |



