2. 北京航空航天大学 中法工程师学院, 北京 100083
2. Ecole Centrale de Pékin, Beijing University of Aeronautics and Astronautics, Beijing 100083, China
湍流大涡模拟已经在工程中得到了越来越广泛的应用。大涡模拟将流动分为可解尺度流动和亚格子尺度流动,对可解尺度流动直接求解,对于亚格子尺度流动,则通过建立亚格子模型的方法将其对可解尺度流动的影响模化。要建立比较准确的亚格子模型需要对湍流中的小尺度流动现象有深刻的认识,而湍流中很多小尺度流动结构都可以用速度梯度张量(以下简称梯度张量)描述。在流体微团运动过程中,其所携带的梯度张量也会不断发生变化,这一过程称为梯度张量的拉格朗日动力学演化(以下简称演化),对这一演化过程的研究可以帮助人们理解很多小尺度流动结构的物理本质。
随着最近30年来计算和试验技术的发展,湍流中梯度张量方面的研究得到了极大的关注[1-12]。人们首先发现了湍流中有关梯度张量的一些统计规律[4],比如Kerr等[5-6]发现应变率张量的特征值分布偏离高斯分布;Sreenivasan和Antonia[7]发现纵向速度梯度扭率为负。而为了解释这些统计规律背后的物理原因,很多学者都提出了各种梯度张量的演化模型[4, 8-11]。这些演化模型一般都需要确定一个时间尺度作为演化的无量纲时间,Yu和Meneveau[13]指出均匀各向同性湍流中可用当地Kolmogorov时间作为演化的时间尺度。但目前剪切湍流和各向异性湍流中梯度张量演化的研究比较少,在这些复杂湍流中梯度张量演化的时间尺度是否依然是当地Kolmogorov时间也需验证。本文通过对槽道湍流中应变率张量的拉格朗日自相关函数的统计验证当地Kolmogorov时间作为梯度张量演化时间尺度的普适性。
1 理论基础Kolmogorov时间是湍流中最小涡的时间尺度,定义[14]为
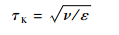
|
(1) |
式中:ν为流体的运动黏性系数;ε为单位质量流体的耗散率:
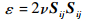
|
(2) |
式中:Sij为脉动应变率。
Kolmogorov时间的概念来自于Kolmogorov的K41理论。湍流中,从大尺度输入的能量(如槽道湍流中的平均剪切)维持湍流的流动,而大尺度上雷诺数一般在103量级以上,意味着大尺度的运动中黏性作用远小于惯性,因此大尺度的涡很不稳定,容易破碎成更小的涡。在这个过程中湍流的能量从大尺度传递到小尺度,而随着涡的长度尺度变小,相应的特征雷诺数也会变小,当小涡的雷诺数达到1甚至1以下时,黏性会占据主导作用,小涡的能量会被黏性耗散掉,不会产生更小的涡。这些湍流中最小涡的尺度被称为Kolmogorov微尺度[14],分别为Kolmogorov长度ηK=(ν3/ε)1/4,Kolmogorov速度vK=(νε)1/4和Kolmogorov时间τK。由这些Kolmogorov微尺度组成的雷诺数正好为1,这说明小于Kolmogorov微尺度的流动结构中,黏性耗散效应非常明显,此时小涡不会破碎成更小的涡,而是直接通过黏性耗散转化为热能。湍流中最小涡的尺度就是Kolmogorov微尺度。
因为梯度张量的演化包含了许多小尺度流动的信息,使用Kolmogorov时间作为其时间尺度应当是合适的。不过Yu和Meneveau[13]在研究中通过统计应变率张量等物理量的拉格朗日时间自相关函数指出:因为湍流的间歇性,梯度张量演化的时间尺度应该为当地Kolmogorov时间τK, r= 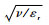
这里所说的拉格朗日时间自相关是和欧拉方法下的时间自相关对应的。一般所说的时间自相关是指欧拉方法下的自相关,可以定义时间自相关函数(一些文献中亦称为时间自相关系数)为[15]

|
(3) |
式中:u(x, t)和u(x, t+τ)分别为流场中坐标为x的一固定点在t时刻和t+τ时刻的随机变量的值。
对于统计定常的湍流,时间自相关函数只与时间间隔τ有关而与起始时刻t无关。
拉格朗日时间自相关与欧拉方法下的时间自相关不同点在于,拉格朗日时间自相关中u(x, t)和u(x, t+τ)不是同一固定点处不同时刻的随机变量的值,而是同一流体微团不同时刻的随机变量的值。
从上述标量物理量的时间自相关函数出发,可以定义二阶张量的拉格朗日时间自相关函数,如应变率张量的拉格朗日时间自相关函数[13]可定义为
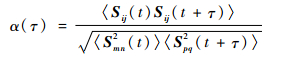
|
(4) |
式中:S(t)和S(t+τ)分别为随流粒子在t时刻和t+τ时刻所处位置处的应变率张量。为简化,下文均用自相关函数代指拉格朗日时间自相关函数。
Yu和Meneveau[13]确定梯度张量演化的时间尺度的做法是:在一个均匀各向同性湍流场中选择一些正方体子区域,统计这些子区域中的随流粒子应变率张量、梯度张量和旋转率张量等物理量随时间的变化,使用随流粒子周边区域的当地Kolmogorov时间对变化过程进行无量纲化,再使用式(4)计算自相关函数。
由K41理论可知,湍流的一些统计性质的预测依赖于平均耗散率,而湍流具有强间歇性,流场中耗散率的分布是不均匀的,整个流场的平均耗散率并不能影响某个区域当地的湍流发展。因此Kolmogorov提出了强化Kolmogorov相似假设(RKSH)对K41理论进行了补充[16]。RKSH理论使用当地耗散率代替全场平均耗散率。Yu和Meneveau[13]认为在研究梯度张量的演化时,也要考虑湍流间歇性的影响。当地耗散率大的区域,流体微团运动状态改变更快,因而自相关函数下降更快,当地耗散率小的区域,流体微团运动状态改变慢,因而自相关函数下降也慢,因此在统计自相关函数时,将耗散率的间歇性影响考虑进来,采用当地Kolmogorov时间作为时间尺度对自相关函数无量纲化,则不同区域的自相关函数曲线下降段应当是重合的。Yu和Meneveau[13]在均匀各向同性的盒子湍流中确实观察到了这一现象,这表明在均匀各向同性湍流中,梯度张量演化的时间尺度主要由当地耗散率决定。
上述结论是在均匀各向同性湍流中得到的,而实际流动往往是各向异性的。目前在各向异性湍流中关于梯度张量演化时间尺度的研究还比较少,因此本文在各向异性的槽道湍流中进行了相关的统计研究。
为减少计算量,本文只统计应变率张量的自相关函数。在梯度张量演化过程中,随着流体微团运动状态的改变,梯度张量的自相关函数会随时间下降,其下降速度反映了演化速度的快慢。作为梯度张量的2个分量,应变率张量和旋转率张量的自相关函数在演化过程中也会随时间下降,并且它们的下降速度受到梯度张量演化的影响,因此可以一定程度反映演化速度的快慢。在这3个自相关函数中,应变率张量的自相关函数会比其他两者更快下降到0附近[13],因此本文用应变率张量自相关函数作为衡量梯度张量演化速度的参考,以减少需要统计的时间长度。本文希望通过统计槽道湍流中不同y+区间应变率张量自相关函数的变化规律,验证存在平均剪切和壁面效应时梯度张量演化的时间尺度是否依然与当地耗散率有关。这项工作一方面可以帮助了解各向异性湍流和各向同性湍流的区别,另一方面也可以帮助梯度张量演化模型更好地应用于实际流动。
2 数值模拟方法 2.1 流场计算本文在槽道流场计算中,使用程序求解滤波后涡量形式的无量纲Navier-Stokes方程。将滤波运算运用于涡量形式的无量纲Navier-Stokes方程,得到槽道流场的控制方程:
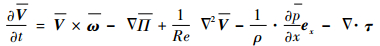
|
(5) |
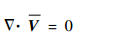
|
(6) |
式中:所有变量均为无量纲物理量;V为可解尺度速度;ω为可解尺度涡量;Π为脉动总压;ρ为流体密度;∂p/∂x为流向平均压力梯度;ex为流向单位向量;τ为亚格子应力,本文使用动力模式亚格子模型[17]计算τ;Re为特征雷诺数,本文计算时取Re=7 000,雷诺数中的特征长度为半槽宽H,特征速度为截面平均流速Um。流动为不可压。
本文使用谱方法进行数值离散,在流向和展向使用Fourier级数展开,在法向使用Chebyshev-配置法,关于计算程序和数值方法的更详细内容可以参考文献[18-20]。计算使用的网格数在流向,展向和法向3个方向上均为128,流向计算域长度为4πH, 展向计算域长度为2πH,流向和展向均为周期性边界条件。
2.2 粒子计算进行自相关函数的计算时,本文需要用到同一流体微团在不同时间步的物理量信息,为此需要在流场中追踪流体微团的运动。本文在流场中加入600个随流体流动的粒子模拟流体微团的运动,计算2 400个时间步,记录每一个粒子在每个时间步的位置、速度和速度梯度,通过四阶Runge-Kutta时间推进获得下一时间步粒子所在位置,即
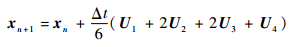
|
(7) |
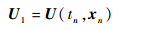
|
(8) |
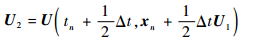
|
(9) |
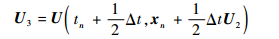
|
(10) |
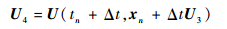
|
(11) |
式中:xn为tn时间步粒子坐标,由tn时间步粒子坐标和流场信息,可以插值得到tn时间步粒子的速度U1,之后由式(9)计算中间时间步粒子速度U2,依次类推获得中间速度U3、U4,再由式(7)计算得到tn+1时间步粒子坐标xn+1。
通过四阶Runge-Kutta时间推进本文可以获得600个粒子在每个时间步的位置,由每个时间步流场信息可以获得600个粒子在每个时间步的速度梯度,进而得到应变率张量Sij在不同时间步的值。
3 统计方法及结果分析 3.1 统计方法Yu和Meneveau[13]在统计中选取的子区域是正方体子区域,而本文选取的子区域是沿法向分割出来的子区间,这些子区间相当于不同y+处x-z平面上的薄层。本文希望研究的是槽道中流场的各向异性对梯度张量演化的时间尺度的影响,而流场在x-z平面上是均匀的,因此本文采用此种方法选取子区域,对比的是不同y+区间之间自相关函数的变化。
对自相关曲线无量纲化时,本文使用了2种无量纲的方法。
第1种方法使用每个粒子的当地Kolmogorov时间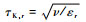
在统计每一个粒子的εr时,本文并没有使用球积分的方法。原因在于:①槽道流场中在靠近壁面处有很强的平均剪切,随y+减小耗散率会迅速增大,使用球积分的方法会使获得的εr有明显误差;②如果在靠近壁面处使用球积分,做积分的球会碰到壁面。基于这些原因,本文使用x-z平面上的圆的面积分代替Yu和Meneveau[13]在各向同性湍流统计中使用的球积分来计算粒子所在位置的当地耗散率εr。εr的计算公式为
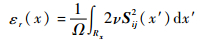
|
(12) |
式中:Rx表示以粒子所在位置x为中心r为半径x-z平面上的圆;Ω为这个圆的面积。
在统计中,分别取r为4、8、16个流向网格长度这3种积分半径,获得了3种结果。一个流向网格长度在对数区约为12个Kolmogorov长度,在黏性底层约为27个Kolmogorov长度。
第2种方法是对每个y+区间采用该区间自己的平均Kolmogorov时间τK, y进行无量纲化, 即
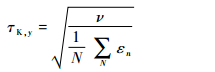
|
(13) |
式中:N为落在要统计的y+区间内的样本数;εn为第n个样本的耗散率。
因为本文使用的流场是统计定常的湍流流场,进行统计时起始时刻t0的选取并不会对结果造成影响,所以同一个粒子在不同时间步可以看成不同的统计样本。表 1为统计使用的子区间(按到壁面的无量纲距离y+计算)。
| 序号 | y+范围 | 粒子样本数 |
| 1 | 0~4 | 100 680 |
| 2 | 8~12 | 19 116 |
| 3 | 16~20 | 16 501 |
| 4 | 24~28 | 13 596 |
| 5 | 32~36 | 13 365 |
| 6 | 40~44 | 12 072 |
| 7 | 48~52 | 11 663 |
| 8 | 52~66 | 29 073 |
| 9 | 80~94 | 22 411 |
| 10 | 108~122 | 20 331 |
| 11 | 136~150 | 19 610 |
| 12 | 164~178 | 16 608 |
| 13 | 288~312 | 18 123 |
| 14 | 376~400 | 40 832 |
槽道湍流中物理量梯度在靠近壁面处远大于流场中央,所以在划分区间时区间宽度在靠近壁面处较窄,在远离壁面时本文将区间宽度放宽以增加样本数量。
需要注意的是,使用式(4)进行统计时,其中的应变率张量使用的速度偏导是去除流向平均速度梯度〈∂u/∂y〉的。原因在于,槽道湍流中,靠近壁面区域的流向速度沿法向有比较大的梯度,如果不去除平均剪切对应变率张量的影响,那么计算出来的自相关函数在时间间隔τ→∞时将不会下降到0,因为平均剪切一直存在,这使得统计结果总具有相关性,而这是由平均流在壁面附近的强剪切导致的,体现的是平均剪切在大尺度流动中的影响,不是流体微团自身运动过程中不同时刻应变率张量相关性的体现。本文所研究的应变率张量的自相关函数反映的是小尺度流动中的特征,所以在计算自相关函数时要去除平均剪切对计算结果的影响。
3.2 统计结果按照3.1节中的方法,本文使用式(4)进行统计,以当地耗散率εr的积分半径r为4个流向网格长度为例。结果如图 1、图 2所示(图中横纵坐标变量均无单位),纵坐标为应变率张量自相关函数,横坐标为无量纲时间。
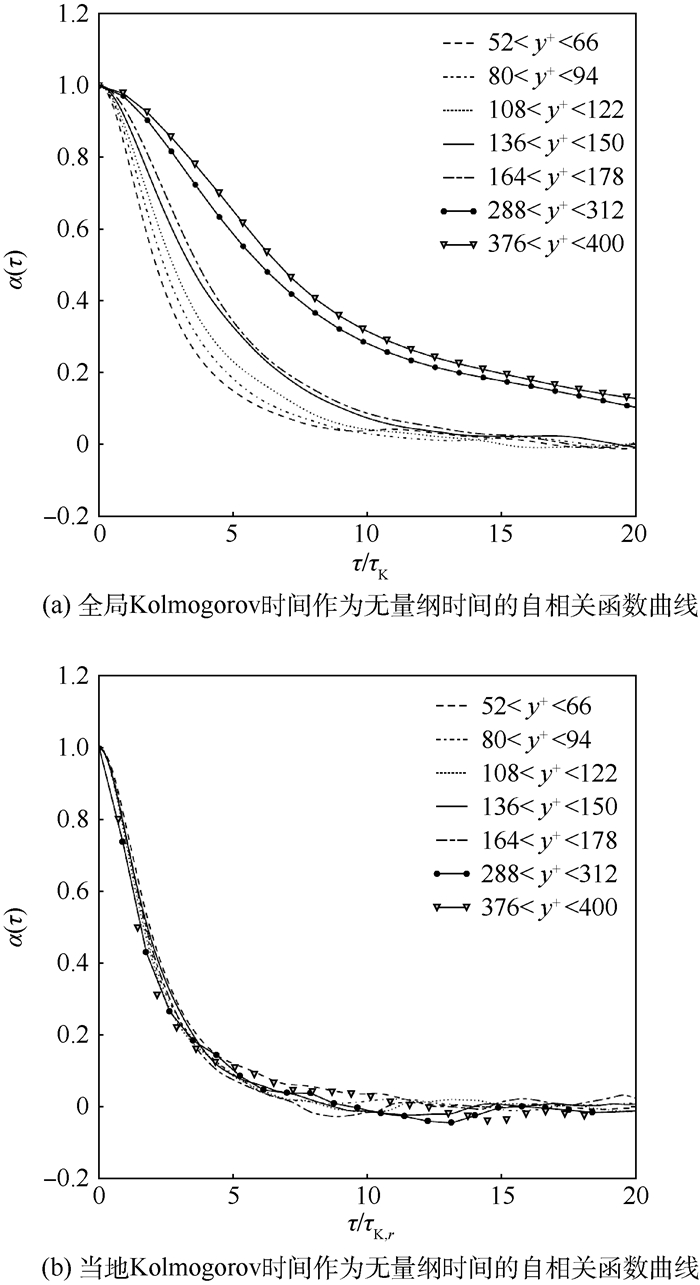
|
| 图 1 52<y+<400时应变率张量自相关函数下降曲线 Fig. 1 Decline curves of auto-correlation function of strain-rate tensor in 52 < y+ < 400 region |

|
| 图 2 0<y+<52时应变率张量自相关函数下降曲线 Fig. 2 Decline curves of auto-correlation function of strain-rate tensor in 0 < y+ < 52 region |
图 1(a)显示在对数区中,若以整个流场的平均Kolmogorov时间(以下简称全局Kolmogorov时间)作为时间尺度,不同y+区间自相关函数下降速度不同。在图 1(b)中以当地Kolmogorov时间作为时间尺度对自相关函数无量纲后,不同y+区间自相关函数下降曲线重合到一起。
本文发现,在黏性底层和过渡层(0<y+<52)中,以当地Kolmogorov时间作为时间尺度对自相关函数无量纲后,不同y+区间自相关函数下降曲线是分散的,越接近壁面,下降速度越慢,如图 2(b)所示,在这些区域当地耗散率并不再决定梯度张量演化的时间尺度。图 2(a)显示使用全局Kolmogorov时间对自相关函数无量纲化结果反而更好。
除了以4个流向网格(r=4网格长度)作为积分半径计算εr以外,本文还统计了以8、16个流向网格(r=8网格长度、r=16网格长度)作为积分半径的εr计算的τK, r进行无量纲化的结果,以及每个y+区间使用该区间自己的τK, y进行无量纲化的结果,如图 3所示。
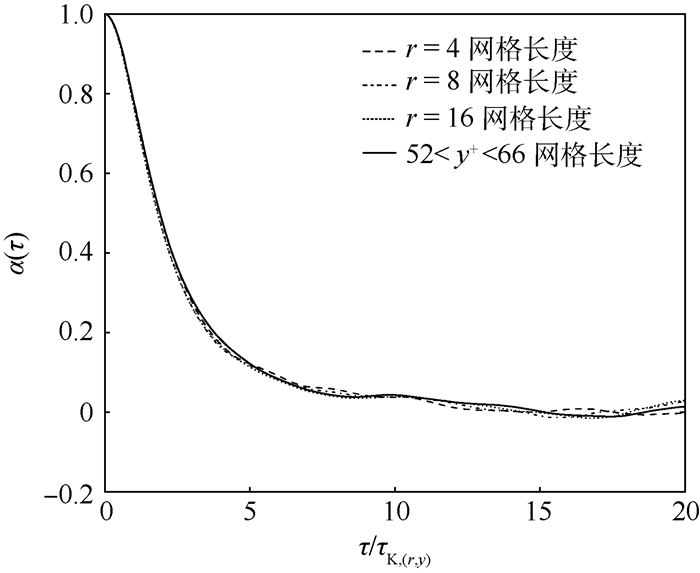
|
| 图 3 52<y+<66区间不同无量纲方式对比 Fig. 3 Comparison among different dimensionless patterns in 52 < y+ < 66 region |
图 3显示,在52<y+<66区间上,取r为4、8、16个流向网格长度的εr来计算τK, r进行无量纲化得到的自相关函数的下降曲线是完全重合的,使用τK, r和使用该y+区间的τK, y进行无量纲得到的结果区别也极小。在其他y+区间上,本文也得到了类似的结果。
3.3 结果分析对于如式(4)的自相关函数α(τ),其取值范围为[-1, 1],τ=0时Sij(t)=Sij(t+τ),α(τ)为其最大值1。τ>0时Sij的任何变化都会在短时间内使α(τ)减小,表示t+τ时刻Sij不再与t时刻的Sij相同,Sij变化速度越快,α(τ)减小速度也越快。在短时间内,不论应变率张量受到何种因素影响,只要在这一因素影响下Sij发生了改变,就会导致自相关函数下降。
而从长期来看,经过20个当地Kolmogorov时间后,不同y+区间的自相关函数都下降到了0附近。这意味着在20τK, r的时间里,应变率的历史效应基本已被消除。图 1(b)显示在对数区中该过程更快,只需要(5~10)τK, r的时间。
关于梯度张量的演化过程,可以通过对Navier-Stokes方程求偏导来对这一过程进行数学上的描述[13]:
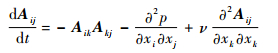
|
(14) |
式中:A为梯度张量(Aij=∂ui/∂xj);p为除以流体密度的压力。
梯度张量可以分解为应变率张量和旋转率张量,因此式(14)不仅反映了哪些因素会导致流体微团的梯度张量发生变化,也可以间接说明哪些因素会导致应变率张量发生变化,进而导致自相关函数的下降。
式(14)右端第1项表示的是梯度张量对自身所施加的影响,称为自相互作用项; 右端第2项表示压力变化对梯度张量的影响,表明流体微团周围压力梯度的不均匀会导致梯度张量的变化; 右端第3项表示黏性剪切的影响。
在湍流中,黏性剪切、压力梯度的不均匀和梯度张量自身的自相互作用都会对流体微团的运动状态造成影响,使得不同时刻流体微团的梯度张量不再相同,表现为自相关函数随时间下降。
均匀各向同性湍流中,Yu和Meneveau[13]使用τK, r对各子区域的自相关函数进行无量纲化后,发现不同子区域自相关函数下降曲线重合。这说明均匀各向同性湍流中,在式(14)右端3项共同作用下,不同区域梯度张量经历的演化过程是相同的,只是因为湍流的间歇性,经历这一过程的快慢不同,当地耗散率大的区域演化速度快,当地耗散率小的区域演化速度慢。
在槽道湍流中,越靠近壁面,平均剪切越强,导致湍流更加活跃,当地耗散率也因此增大。这种当地耗散率增大的趋势并不是湍流的间歇性导致的,而是近壁区的强平均剪切导致的。
对数区中不同y+区间使用τK, r进行无量纲化后自相关函数下降曲线重合,这说明在对数区中,虽然流场中存在各向异性,靠近壁面处当地耗散率会因为平均剪切而有所增大,但这一因素的影响并不明显,决定演化过程快慢的依然是当地耗散率。本文认为在这些区域,梯度张量经历的演化过程应当与均匀各向同性湍流中的演化过程相同。
而在黏性底层和过渡层中,不同y+区间使用τK, r进行无量纲化后自相关函数下降曲线是分散的。这一结果说明在这些区域梯度张量演化过程的快慢不仅仅由当地耗散率决定,平均剪切增强导致当地耗散率增大时,梯度张量演化速度并没有同等程度的加快。
关于靠近壁面处应变率张量的自相关函数下降曲线分散的原因,一个可能的解释是在靠近壁面处出现了强脉冲结构影响了速度分布的间歇性[19]。为了进一步明确物理机制,未来还需要更深入的研究。图 2(a)可能在一定程度上体现了这种间歇性之间的相似性。
4 结论本文通过对槽道湍流中不同y+区间应变率张量的自相关函数的统计,有如下发现:
1) 对数区中,梯度张量演化的时间尺度依然为当地Kolmogorov时间,这一点与均匀各向同性湍流相同。
2) 黏性底层和过渡层中,随到壁面无量纲距离y+的减小,以当地Kolmogorov时间衡量,梯度张量演化速度变慢。本文认为在这些区域中,梯度张量的演化偏离了均匀各向同性的湍流中的演化模式,这使得当地耗散率不再决定梯度张量演化的时间尺度。
3) 槽道湍流中除了湍流的间歇性会使当地耗散率增大外,平均剪切也会使当地耗散率增大,而平均剪切并不会加快梯度张量的演化速度。未来在槽道湍流中,可能应考虑引入平均剪切来修正当地Kolmogorov时间τK, r作为演化的时间尺度。
| [1] | CHEVILLARD L, MENEVEAU C. Lagrangian dynamics and statistical geometric structure of turbulence[J]. Physical Review Letters, 2006, 97 (17): 174501. DOI:10.1103/PhysRevLett.97.174501 |
| [2] | OOI A, SORIA J, CHONG M S, et al. A study of the evolution and characteristics of the invariants of the velocity-gradient tensor in isotropic turbulence[J]. Journal of Fluid Mechanics, 1999, 381 (1): 141–174. |
| [3] | ATKINSON C, CHUMAKOV S, BRRMEJO-MORENO I, et al. Lagrangian evolution of the invariant of the velocity gradient tensor in a turbulent boundary layer[J]. Physics of Fluids, 2012, 24 (10): 677–686. |
| [4] | MENEVEAU C. Lagrangian dynamics and models of the velocity gradient tensor in turbulent flows[J]. Annual Review of Fluid Mechanics, 2011, 43 (1): 219–245. DOI:10.1146/annurev-fluid-122109-160708 |
| [5] | KERR R M. Histograms of helicity and strain in numerical turbulence[J]. Physical Review Letters, 1987, 59 (7): 783–786. DOI:10.1103/PhysRevLett.59.783 |
| [6] | ASHURST W T, KERSTEIN A R, KERR R M, et al. Alignment of vorticity and scalar gradient with the strain rate in simulated Navier-Stokes turbulence[J]. Physics of Fluids, 1987, 30 (8): 2343–2353. DOI:10.1063/1.866513 |
| [7] | SREENIVASAN K R, ANTONIA R A. The phenomenology of small-scale turbulence[J]. Annual Review of Fluid Mechanics, 1997, 29 (1): 435–472. DOI:10.1146/annurev.fluid.29.1.435 |
| [8] | GIRIMAJI S S, POPE S B. A diffusion model for velocity gradients in turbulence[J]. Physics of Fluids A:Fluid Dynamics, 1990, 2 (2): 242–256. DOI:10.1063/1.857773 |
| [9] | MARTIN J, DOPAZO C, VALION L. Dynamics of velocity gradient invariants in turbulence:Restricted Euler and linear diffusion models[J]. Physics of Fluids, 1998, 10 (8): 2012–2025. DOI:10.1063/1.869717 |
| [10] | JEONG E, GIRIMAJI S S. Velocity-gradient dynamics in turbulence:Effect of viscosity and forcing[J]. Theoretical and Computational Fluid Dynamics, 2003, 16 (6): 421–432. DOI:10.1007/s00162-002-0084-7 |
| [11] | FANG L, BOS W J T, JIN G D. Short-time evolution of Lagrangian velocity gradient correlations in isotropic turbulence[J]. Physics of Fluids, 2015, 27 (12): 457–472. |
| [12] | FANG L, ZHANG Y J, FANG J, et al. Relation of the fourth-order statistical invariants of velocity gradient tensor in isotropic turbulence[J]. Physical Review E, 2016, 94 (2): 023114. DOI:10.1103/PhysRevE.94.023114 |
| [13] | YU H, MENEVEAU C. Lagrangian refined Kolmogorov similarity hypothesis for gradient time-evolution in turbulence flows[J]. Physical Review Letters, 2010, 104 (8): 084502. DOI:10.1103/PhysRevLett.104.084502 |
| [14] |
TENNEKES H, LUMLEY J. 湍流初级教程[M]. 施红辉, 林培锋, 金浩哲, 译. 北京: 科学出版社, 2015: 14-15.
TENNEKES H, LUMLEY J.A first course in turbulence[M].SHI H H, LIN P F, JIN H Z, translated.Beijing:Science Press, 2015:14-15(in Chinese). |
| [15] |
张兆顺, 崔桂香, 许春晓.
湍流理论与模拟[M]. 北京: 清华大学出版社, 2005: 11.
ZHANG Z S, CUI G X, XU C X. Theory and modeling of turbulence[M]. Beijing: Tsinghua University Press, 2005: 11. (in Chinese) |
| [16] | STOLOVITZKY G, KAILASNATH P, SREENIVASAN K R. Kolmogorov's refined similarity hypothesis[J]. Physical Review Letters, 1992, 69 (8): 1178–1181. DOI:10.1103/PhysRevLett.69.1178 |
| [17] |
张兆顺, 崔桂香, 许春晓.
湍流大涡模拟的理论与应用[M]. 北京: 清华大学出版社, 2008: 101-104.
ZHANG Z S, CUI G X, XU C X. Theory and application of large eddy simulation of turbulence[M]. Beijing: Tsinghua University Press, 2008: 101-104. (in Chinese) |
| [18] |
周海兵. 标量湍流的数值研究[D]. 北京: 清华大学, 2003: 39-45.
ZHOU H B.Numerical research of scalar turbulence[D].Beijing:Tsinghua University, 2003:39-45(in Chinese). http://d.wanfangdata.com.cn/Thesis_Y815711.aspx |
| [19] | XU C X, ZHANG Z S, TOONDER J M J, et al. Origin of high kurtosis levels in the viscous sublayer.Direct numerical simulation and experiment[J]. Physics of Fluids, 1996, 8 (7): 1938–1944. DOI:10.1063/1.868973 |
| [20] | FANG L, SHAO L, BERTOGLIO J P, et al. The rapid-slow decomposition of the subgrid flux in inhomogeneous scalar turbulence[J]. Journal of Turbulence, 2011, 12 (8): 1–23. |



