2. 中国外星海上测控部, 江阴 214431
2. China Satellite Maritime Tracking and Controlling Department, Jiangyin 214431, China
风险不确定性作为风险评估结果的一种测度表征,为风险决策者提供额外的风险附加信息,以供决策者做出合理风险决策。在工程实际中,系统定量化风险评估不确定性的刻画、传播以及不确定性对风险决策的影响作为热点问题备受关注[1-2],特别是在航天、航空、核电等领域,精确的基础可靠性数据无法获取时,风险不确定性对风险决策的影响尤为重要。
风险不确定性分为2类[3]:一类是由系统内部行为的偶然性产生的随机不确定性(也称为客观不确定性);另一类是由风险评估者对系统信息、知识的缺乏而产生的认知不确定性(也称为主观不确定性)。随着对风险不确定性的认知进一步加深,单一概率分布无法刻画不确定性的所有属性[4],特别是在数据不精确、知识不完备的情形下,无法处理认知不确定性。针对认知不确定性的刻画,Moens和Hanss[5]采用区间分析方法框架刻画认知不确定性;Rohmer和Baudrit[6]采用可能性分布刻画地震风险模型、数据不确定性,构建了基于模糊区间分析方法的地震风险不确定性模型;Agarwal等[7]提出基于证据理论的不确定性量化方法,用于多属性优化设计;Shah等[8]采用证据理论对认知不确定性建模与传播。
当风险模型中同时存在随机不确定性与认知不确定性时,Guyonnet等[4]提出一种混合不确定性分析框架;Rao等[9]采用动态故障树与蒙特卡罗模拟相结合的方法对核反应堆电能供给系统进行风险不确定性刻画与传播;Baraldi和Zio[10]采用事件树与蒙特卡罗模拟相结合对核电厂风险混合不确定性进行对比研究,分别给出概率、可能性以及概率-可能性框架下的不确定性传播特性。上述方法只考虑风险模型输入变量为不确定性的混合不确定性,并没考虑风险模型输入变量分布参数的不确定性,对此,Baudrit等[11]又提出双层蒙特卡罗混合不确定性分析框架。
Baudrit等[11]在构建双层蒙特卡罗混合不确定性传播框架时,认知不确定性分布参数完全正依赖,或者完全独立,无法处理变量分布参数之间存在非完全依赖时的混合不确定性传播。对此,本文提出一种考虑认知不确定性分布参数相互依赖的混合不确定性传播方法,针对双层蒙特卡罗不确定性抽样独立性或完全正依赖的不足,构建了认知不确定性分布参数统一的依赖性模型,实现分布参数的完全依赖、部分依赖以及独立传播。针对双层蒙特卡罗参数独立时计算代价大的难题,将可能性分布等概率转化为证据信度空间,并引入随机集理论计算方法实现认知不确定性分布参数的独立传播。以氢氧发动机贮箱共底漏气率为算例,验证了本文方法的有效性和可行性。
1 认知不确定性刻画与传播方法 1.1 D-S证据理论D-S证据理论最先由Dempster[12]提出并经Shafer[13]完善。相比于概率理论,D-S证据理论同时具备处理不确定性和冲突信息的能力,特别是在信息不完备时专家信息合成方面,具有明显的优势[14]。在有限元素的离散空间里,D-S证据理论可视为概率理论的一般化描述。由于概率理论必须满足可加性原则,概率测度只能分配给相互独立的事件,而D-S证据理论可将信度测度分配到一个或多个事件的组合。特别地,如信度测度只分配给独立事件时,则D-S证据理论退化为主观贝叶斯概率框架。此时,信度函数刻画概率的上下界。另外,在D-S证据理论中,各信息源用来合成证据时,无需先验信息。
在D-S证据理论中,辨识框架Θ为所有可能发生的元素命题集,Θ中所有可能非空独立子集或命题称为幂集,记为
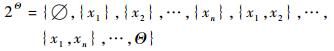
|
(1) |
子集或命题X的信任程度通过基本信度(概率)分配函数m来实现,且满足以下性质:
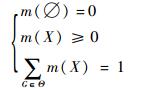
|
(2) |
定义1 给定辨识框架Θ,基本概率分配(Basic Probability Assignment,BPA)定义为:m:2Θ→[0, 1]。
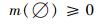
|
(3) |
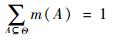
|
(4) |
定义2 给定辨识框架Θ,信度函数Bel定义为
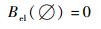
|
(5) |
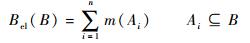
|
(6) |
式中:Bel(B)为所有B的子集信度和。
定义3 给定辨识框架Θ,似然函数Pl定义为
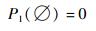
|
(7) |
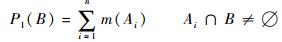
|
(8) |
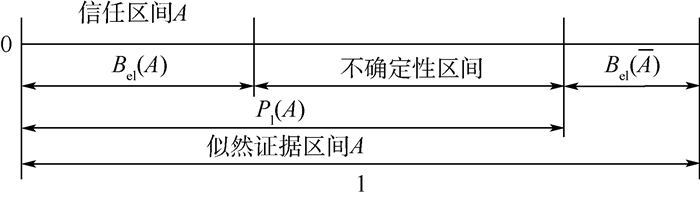
通常,信度函数和似然函数可被理解为区间概率,信度函数Bel可被解释为概率区间下界,似然函数Pl被解释为概率区间的上界。事实上,事件A的信度函数和似然函数区间Pl(A)-Bel(A)是其认知不确定性测度,也可被解释为事件A真值的不精确性[15],如图 1所示。
|
| 图 1 D-S证据理论信度区间关系 Fig. 1 Relationship between belief intervals of D-S evidence theory |
在概率理论框架下,事件A的概率与其补集之和为1,然而,由图 1可知,D-S证据理论框架下,事件A的信度与其信度补集之和小于1。另外,信度函数与似然函数有如下关系:
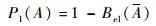
|
(9) |

|
(10) |
若不确定性信息m1和m2相对独立,通常采用加法原则生成一个新的BPA[16],D-S证据合成规则为[17]

|
(11) |
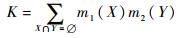
|
(12) |
式中:K为m1与m2的冲突系数。K=0时,m1与m2无冲突;K=1时,m1与m2完全冲突。
1.2 可能性理论可能性理论具备处理信息不精确、知识不完备情形下的不确定性能力,不同于概率理论(使用单一概率测度),可能性理论采用一对集合函数(可能性测度和必然性测度)来刻画不确定性[18]。模糊集作为可能性理论不确定性刻画的常用方法,在此给出模糊集理论简要叙述,详细内容见文献[19]。
模糊集Ã中元素集为(a1, a2, …, an),元素ai(i=1, 2, …, n)的隶属函数μi表征ai属于集合Ã的隶属程度,其值介于区间[0, 1][20]。Dubois[20]定义了隶属度的描述:μÃ(u)=1时表示u完全属于集合Ã,μÃ(u)>μÃ(v)表示u的可能性大于v,若存在元素ai,使得μÃ(ai)=1,则模糊集Ã是常规模糊集。
可能性理论框架下,可能性测度∏和必要性测度N分别定义如下[21]。
集合U中的元素y构成的子集A有可能性测度:
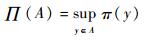
|
(13) |
对应的,必要性测度N(A)定义为
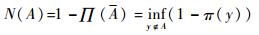
|
(14) |
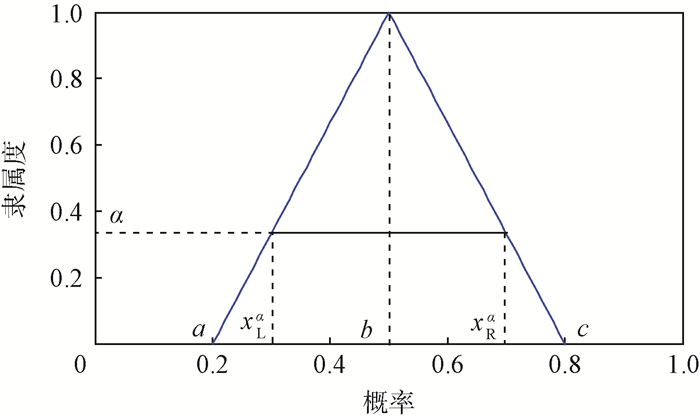
α-截集通常用来处理模糊数计算,α-截集为一区间数Aα={x∈U, μÃ(x)≥α},表明在区间内各元素的隶属度大于等于α,如图 2所示,三角模糊分布α-截集下界xLα和上界xRα可通过式(15)求得:
|
| 图 2 三角模糊分布对应的α-截集区间 Fig. 2 α-cut interval corresponding to triangular fuzzy distribution |
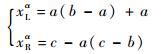
|
(15) |
模糊数α-截集运算法则如下:

|
(16) |
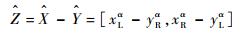
|
(17) |
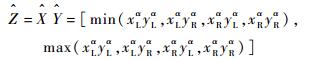
|
(18) |
采用α-截集计算可能性分布时,设定认知不确定性分布参数相互完全依赖[1],但在工程实际中,认知不确定性分布参数存在部分依赖、独立或者完全依赖情形[22]。对此,本文对认知不确定性分布参数的依赖性进行进一步分析,提出认知不确定性分布参数依赖性系数的概念,具体分析如下。
传统基于可能性分布下不确定性传播分析框架,获取一个随机α值后,可能性变量Yi, i=1, 2, …, n的α-截集Aiα的信度水平均为α,此时假设各输入变量之间完全正相关(依赖)。当可能性变量之间非完全依赖或者独立时,变量α-截集Aiα具有不同的信度水平α,以及可能性变量的信度区间Aiα与另一变量信度区间Ajα相关,本文通过2个可能性变量α-截集区间Aiα的模与信度水平α的变化率关系来定义其线性依赖性关系,k∈[-1, 1]定义为两模糊数依赖性系数。可能性分布参数Y1和Y2依赖性模型如下:

|
(19) |
由于Aiα是α的函数,A1α与A2α的依赖性进一步可通过不同的α-截集来刻画。
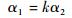
|
(20) |
式中:设定k=±1时,表示Y1与Y2完全正(负)依赖;0<k<1时,表示Y1与Y2部分正依赖;-1<k<0时,表示Y1与Y2部分负依赖;当k=0时,表示Y1与Y2相互独立。在此特别指出,依赖性系数k可根据工程实际不确定性分布参数相互关系取其他数值范围,以及可能存在非线性依赖关系,本文不作进一步研究。
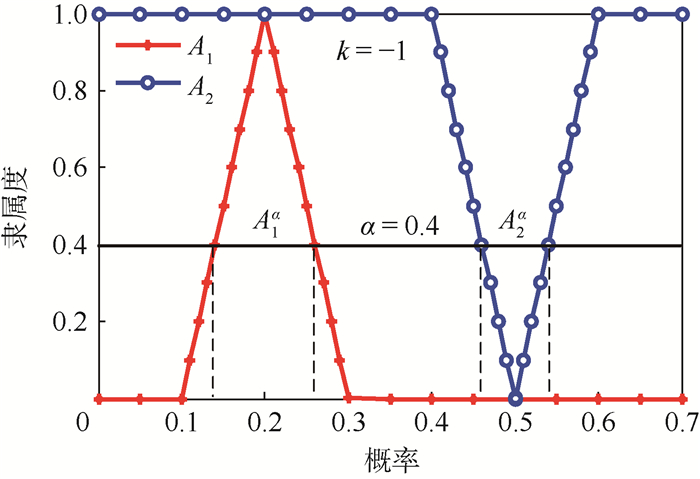
在此,给出认知不确定性分布参数依赖情形下参数认知不确定性的变化过程。以完全负依赖k=-1时为例说明,当两模糊数完全负依赖时,随着α增大,参数Y1的α-截集A1α区间减小,认知不确定性变小;参数Y2的α-截集A2α区间增大,认知不确定性变大。具体变化过程如图 3所示。
|
| 图 3 认知不确定性分布参数完全负依赖模型 Fig. 3 Total negative dependency model of epistemic uncertainty distribution parameter |
在混合不确定性传播过程处理中,各种不确定性依赖关系通过式(20)设置相对应的α-截集来实现,2.2节给出了认知不确定性分布参数非独立情形下的混合不确定性传播框架,2.3节给出了认知不确定性分布参数独立情形下的混合不确定性传播框架。
2.2 分布参数非独立时混合不确定性传播在2.1节不确定性依赖性模型的基础上,本节给出不确定性分布参数非独立情形下混合不确定性传播的分析框架。
风险模型R=f(Y1, Y2, …, Yn),输入变量Yi(i=1, 2, …, n),其中,前k个输入变量[Y1, Y2, …, Yk]为概率分布pY1(y1|θ1), pY2(y2|θ2), …, pYk(yk|θk),分布参数向量为θj=[θj, 1, θj, 2, …, θj, m], j=1, 2, …, k,服从可能性分布,其由可能性分布向量表示为πθj(θj)=[πθj, 1(θj, 1), πθj, 2(θj, 2), …, πθj, mj(θj, mj)]。输入向量[Yk+1, Yk+2, …, Yl, …, Yn]为可能性分布,表示为[πYk+1(yk+1), πYk+2(yk+2), …, πYl(yl), …, πYn(yn)]。
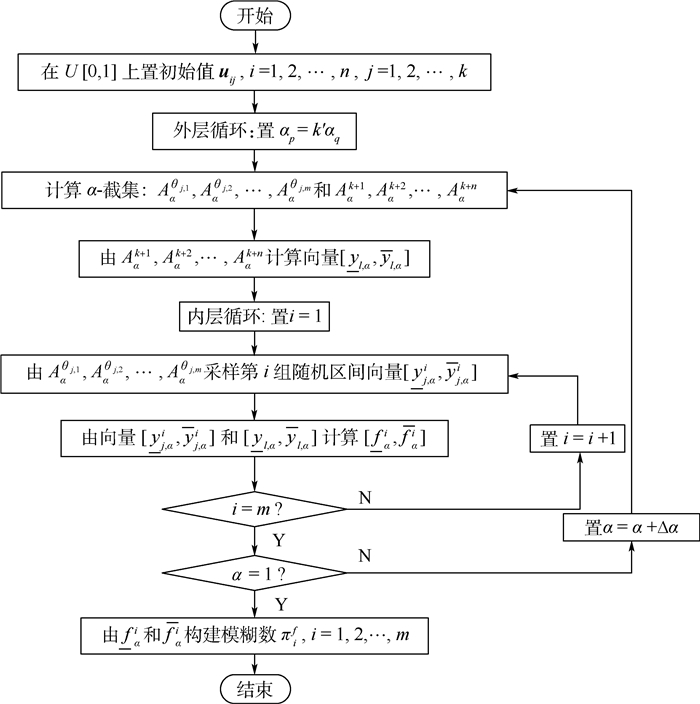
在双层不确定性传播框架下,基于蒙特卡罗-模糊扩展原则的混合不确定性传播通过蒙特卡罗数值模拟与模糊扩展原理实现,蒙特卡罗实现概率分布采样,模糊集用以处理认知不确定性。在此需要指出的是,按照文献[11]的传播框架,认知不确定性分布参数每次循环生成一个α-截集,即所有认知不确定性分布参数具有同一α信度水平。考虑变量参数依赖情形下,每次生成随机矩阵uij(i=1, 2,…, n, j=1, 2, …, k,n-k为认知不确定性分布参数个数)以给出不同的信度水平,并定义参数依赖性关系:αp=k′αq(k′为依赖性系数), Yp与Yq相互依赖。具体方法流程如图 4所示。
|
| 图 4 参数非独立时的混合不确定性传播流程 Fig. 4 Hybrid uncertainty propagation flowchart under independent distribution parameters |
具体步骤如下:
步骤1 生成随机采样矩阵uij,uij∈U[0, 1],i=1, 2, …, n, j=1, 2, …, k,U服从均匀分布。
步骤2 αp=k′αq, p≠q,开始外层循环。
步骤3 计算概率分布参数向量[θj, 1, θj, 2, …, θj, m], j=1, 2, …, k与可能性分布向量[Yk+1, Yk+2, …, Yl, …, Yn]α-截集Aαθj, 1, Aαθj, 2, …, Aαθj, m和Aαk+1, Aαk+2, …, Aαk+n,并由Aαk+1, Aαk+2, …, Aαk+n计算[yl, α, yl, α], l=k+1, k+2, …, n。
步骤4 i=1,开始内层循环。
步骤5 由步骤1和步骤3计算概率分布向量[Y1, Y2,…, Yk]的随机区间[yj, αi, yj, αi]。
步骤6 由步骤3和步骤5计算[fαi, fαi],fαi与fαi为第i次随机采样α-截集的上下界:
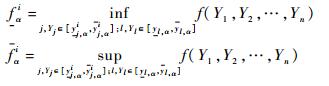
|
步骤7 如果i≠m,i=i+1并返回步骤5;否则继续步骤8。
步骤8 如果α≠1,α=1并返回步骤3;否则构建m个可能性分布函数πif, i=1, 2, …, m并结束。
执行完上述流程后,生成m个可能性分布πif, i=1, 2, …, m,并作为风险模型输出Z=f(Y1, Y2, …, Yn),m为随机变量的采样次数。
集合A包含于风险模型Z的输出域UZ,则集合A的可能性测度与必要性测度为

|
(21) |
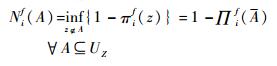
|
(22) |
另外,可由m个可能性测度与必要性测度计算出信度函数Bel(A)与似然函数Pl(A)[11]:
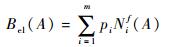
|
(23) |
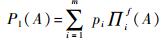
|
(24) |
式中:pi为第i次随机变量向量[Y1, Y2, …, Yj, …, Yk]采样的概率,若m为均匀采样,则pi=1/m。
在此,给出随机不确定性分布参数Yj的随机区间数[yj, αi, yj, αi]生成过程。
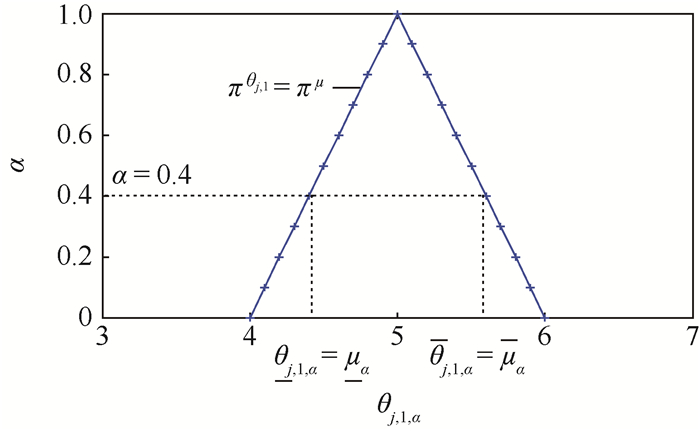
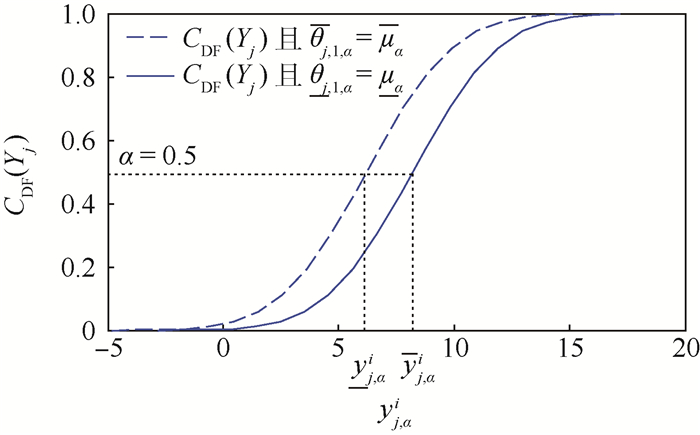
设定随机不确定性分布参数Yj服从正态分布,且分布参数为可能性分布θj=[θj, 1, θj, 2]=[μ, σ],均值μ=θj, 1服从模糊三角分布π(a, b, c), a=4, b=5, c=6,标准差为定值σ=θj, 2=4,按照上述计算流程,设α=0.4,μ=θj, 1对应的α-截集为[μα, μα]=[θj, 1, α, θj, 1, α]=[4.4, 5.6],如图 5所示。另外,由μα上下界[μα, μα]构建出随机不确定性分布参数Yj的累积分布函数FθjYj,如图 6所示,在内层循环中,假设随机抽样参数μji=0.5,采用双层蒙特卡罗模拟法计算出分布参数Yj的随机区间为
|
| 图 5 三角模糊分布函数μ=θj, 1α-截集 Fig. 5 α-cut of triangular fuzzy distribution function of μ=θj, 1 |
|
| 图 6 均值为[μα, μα]的Yj的累计分布函数曲线 Fig. 6 Curves of cumulative distribution function of Yj between mean value [μα, μα] |
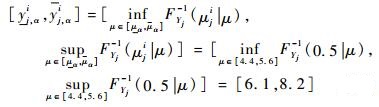
|
(25) |
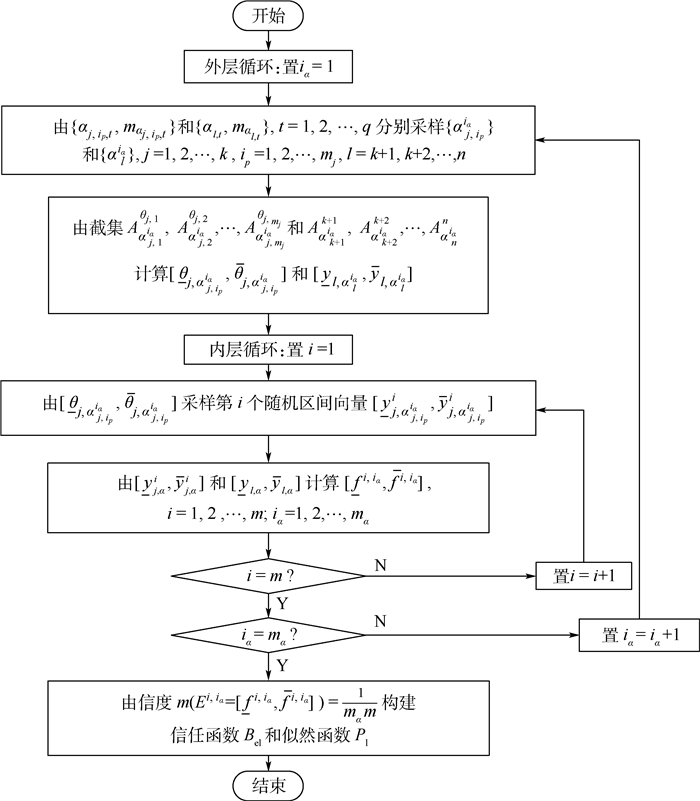
本节给出认知不确定性分布参数依赖性的一种特殊情况,当k=0时认知不确定性分布参数相互独立情形,由于认知不确定性分布参数的独立性,无法通过采用α-截集的处理方法进行双循环采样分析。在此,提出将模糊认知不确定性分布参数转化为证据信度空间进行处理,并引入随机集理论,实现随机采样达到处理随机不确定性的目的,具体流程如图 7所示。
|
| 图 7 参数独立时的混合不确定性传播流程 Fig. 7 Hybrid uncertainty propagation flowchart under dependent distribution parameters |
在给出认知不确定性分布参数独立传播流程之前,先定义模糊不确定性分布参数到证据空间的转换。
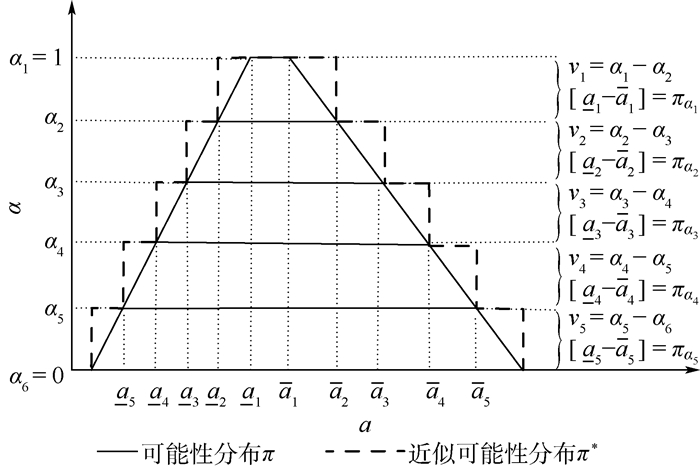
Y是模糊可能性变量,π描述Y的可能性分布,πα定义π的α-截集,α-截集对应Y的焦元(παj), j=1, 2, …, q,α1=1>α2>…>αq+1=α0=0,定义vj=αj-αj+1(j=1, 2, …, q)为焦元(παj)的信度分配。信度分配原理如图 8所示[1]。
|
| 图 8 可能性分布到信度空间的转换 Fig. 8 Transformation from possibility distribution to belief space |
风险模型同2.2节。
认知不确定性分布参数独立时算法步骤如下:
步骤1 iα=1, iα=1, 2, …, mα开始外层循环。
步骤2 由离散的证据识别框架{(αj, ip, t, mαj, ip, t):t=1, 2, …, q}随机抽取概率分布向量[Y1, Y2, …, Yk]的认知不确定性分布参数证据信度{αj, ipiα}, j=1, 2, …, k, ip=1, 2, …, mj;同理,随机抽取可能性分布向量[Yk+1, Yk+2, …, Yn]证据信度{αliα}, l=k+1, k+2, …, n;不同于蒙特卡罗-模糊扩展原则法对可能性分布参数获取相同的置信度水平α-截集,基于证据信度空间的随机集方法实现了认知不确定性分布参数的独立随机采样。
步骤3 由步骤2的证据信度{αj, ipiα}与{αliα},获取对应的随机焦集Aαj, 1iαθj, 1, Aαj, 2iαθj, 2, …, Aαj, mjiαθj, mj与Aαk+1iαk+1, Aαk+2iαk+2, …, Aαniαn;并由Aαj, 1iαθj, 1, Aαj, 2iαθj, 2, …, Aαj, mjiαθj, mj与Aαk+1iαk+1, Aαk+2iαk+2, …, Aαniαn计算[θj, αj, ipiα, θj, αj, ipiα]与[yl, αliα, yl, αliα]。
步骤4 i=1, i=1, 2, …, m,开始内层循环。
步骤5 由步骤3的[θj, αj, ipiα, θj, αj, ipiα]计算第i次抽样随机概率分布Y1, Y2, …, Yj, …, Yk的随机集[yj, αj, ipiαi, yj, αj, ipiαi]。
步骤6 由步骤3和步骤5计算随机集Ei, iα=[fi, iα, fi, iα],i=1, 2, …, m, iα=1, 2, …, mα。
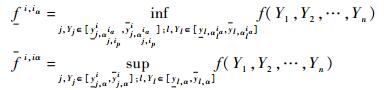
|
步骤7 如果i≠m,i=i+1并返回步骤5;否则继续步骤8。
步骤8 如果iα≠mα,iα=iα+1并返回步骤2;否则结束。
同理,假设集合A包含于风险模型Z的输出域UZ,则集合A的信度函数与似然函数分别为

|
(26) |
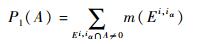
|
(27) |
式中:
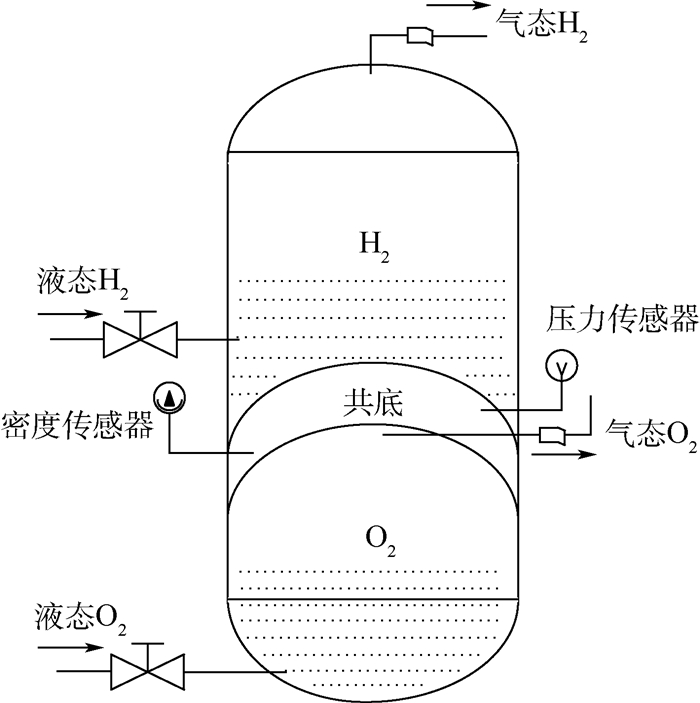
为了验证本文方法的可行性和有效性,以某型火箭低温液氢液氧发动机贮箱共底漏气率为风险分析对象进行说明,某型氢氧发动机燃料贮箱结构采用绝热复合材料设计,氢氧贮箱采用共底结构设计,共底层为真空密闭空间,将贮箱分成液氢箱和液氧箱2个独立部分,结构如图 9所示。
|
| 图 9 液氧液氢贮箱共底结构 Fig. 9 Co-bottom tank structure of liquid oxygen and liquid hydrogen |
为保证共底结构的密闭性绝热性,要求共底具有一定的真空度。同时为确保贮箱安全,安装有共底安全监测系统对共底进行压力、气体浓度以及真空度检测[23]。在贮箱存储液氢液氧期间,其主要技术指标为:12h漏气率应小于3×10-3 Pa·m3/s。
本文以12 h静态共底漏气率Q来表征氢氧贮箱共底安全性:
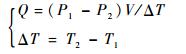
|
(28) |
式中:Q为共底漏气率,Pa·m3/s;P1为T1时刻共底压强检测值,Pa;P2为T2时刻压强检测值,Pa;V为共底容积,m3;ΔT为P1与P2检测时间差,s。输入变量P1、P2、V、T1与T2为不确定性变量。
3.2 共底漏气率模型不确定性分布参数由于测量、设计等系统误差的影响,精确的参数信息无法直接获得,需借助一定的专家知识,但是专家信息具有认知不确定性。因此,本文所给参数信息同时具有随机不确定性和认知不确定性。
已知参数P1~N(μP1, σP1)、P2~N(μP2, σP2),均值无法给出精确值,经领域专家给出认知不确定性描述:均值μP1、μP2服从模糊三角分布,标准差σP1、σP2为固定值。共底容积V~LN(μV, σV),参数μV、σV为认知不确定性变量,服从模糊三角分布;T1~N(μT1, σT1)、T2~N(μT2, σT2),μT1、σT1、μT2和σT2服从模糊三角分布,上述分布参数见表 1。
| 参数 | 数值 |
| μP1 | (6 500, 7 000, 7 500) |
| σP1 | 100 |
| μP2 | (3 300, 3 500, 3 400) |
| σP2 | 100 |
| μV | (0.49, 0.50, 0.51) |
| σV | (0.004 5, 0.005 0, 0.005 5) |
| μT1 | (0, 10, 5) |
| σT1 | (0.05, 0, 0.1) |
| μT2 | (43 100, 43 200, 43 300) |
| σT2 | (0, 100, 200) |
同时,由于专家主观偏好的影响,认知不确定性分布参数存在相互依赖性,其中,经领域专家判断,μP1、μP2、σP1、σP2、μT1、μT2存在依赖性,其余参数相互独立,表 2给出依赖性参数之间的依赖性系数。
| 参数1 | 参数2 | k |
| μP1 | μP2 | -0.5 |
| σP1 | σP2 | 0.3 |
| μT1 | μT2 | -1 |
| σT1 | σT2 | 0.7 |
3.3 结果分析
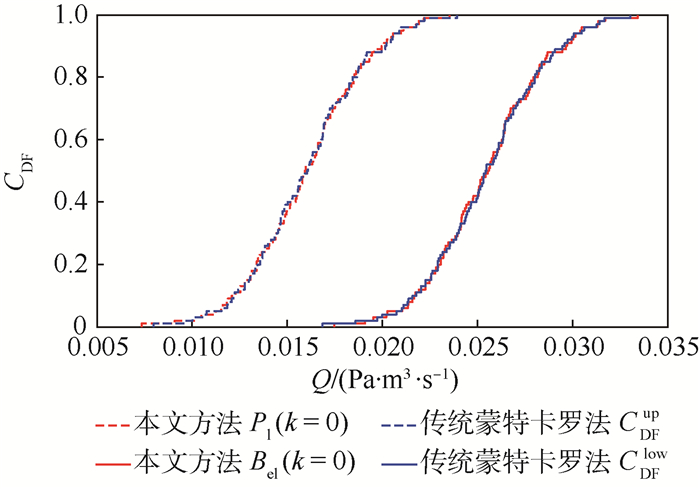
1) 为验证本文方法的有效性,在参数相互独立时与Baudrit等[11]所提的双层蒙特卡罗方法对比分析,结果如图 10所示。通过对比,本文所提混合不确定性传播方法与双层蒙特卡罗方法计算结果具有较好的一致性,上下界累积概率分布(CDF)与Bel、Pl分布一致,且有Bel(Q<0.03)=0.93,CDFlow(Q<0.03)=0.95。
|
| 图 10 认知不确定性分布参数独立时混合不确定性传播与双层蒙特卡罗不确定性传播曲线对比 Fig. 10 Compared curves of hybrid uncertainty propagation and two-level Monte Carlo uncertainty propagation with epistemic uncertainty distribution parameters independence |
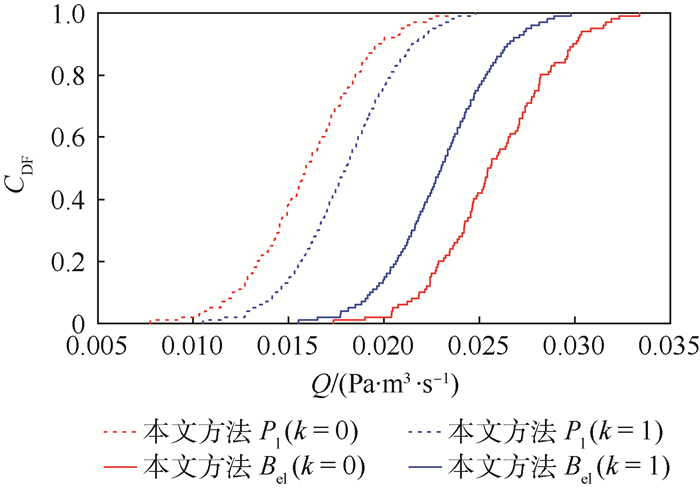
2) 为分析认知不确定性分布参数依赖性对混合不确定性传播结果的影响,在本实例中,以μP1与μP2为分析对象,其他参数服从表 1分布且不变,仅考虑当μP1与μP2独立k=0与完全依赖k=1时不确定性结果的分布,采用本文所提混合不确定性传播框架,计算结果如图 11所示。通过对比,当认知不确定性分布参数完全依赖时,Bel(k=1)与Pl(k=1)被Bel(k=0)与Pl(k=0)包络;另外,当认知不确定性分布参数独立时,风险不确定性结果相对保守。
|
| 图 11 认知不确定性分布参数依赖性、独立性的不确定性传播结果曲线对比 Fig. 11 Compared curves of uncertainty propagation with epistemic uncertainty distribution parameters dependency and independency |
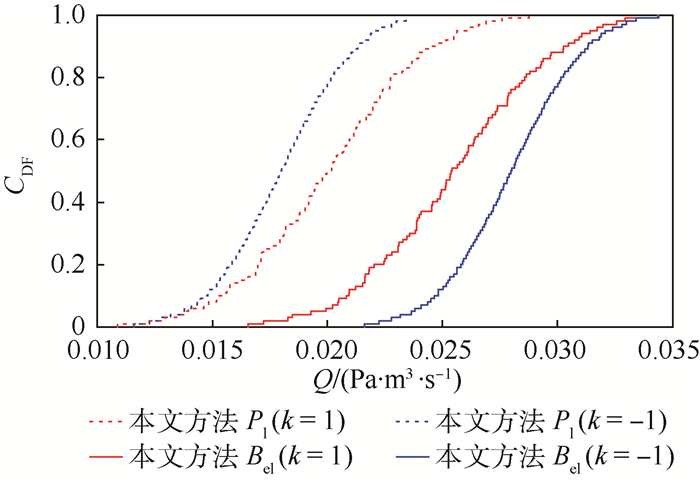
3) 在本文所提混合不确定性传播框架下,为分析认知不确定性分布参数完全正、负依赖情形下对风险模型输出不确定性结果的影响,以μP1与μP2相互依赖为分析对象,其他参数不变,k=-1与k=1情形下不确定性结果如图 12所示。通过对比,认知不确定性为可能性分布刻画时,参数完全正依赖时,输出不确定性区间小于参数完全负依赖时输出不确定性区间。依据Vose[24]对风险输出结果随机不确定性与认知不确定性的界定,由图 12计算结果得出,参数完全正依赖时产生的随机不确定性更大,相反,参数完全负依赖时产生的认知不确定性更大。
|
| 图 12 认知不确定性分布参数完全正、负依赖时的不确定性传播结果曲线对比 Fig. 12 Compared curves of uncertainty propagation of epistemic uncertainty distribution parameters with total dependence and independence |
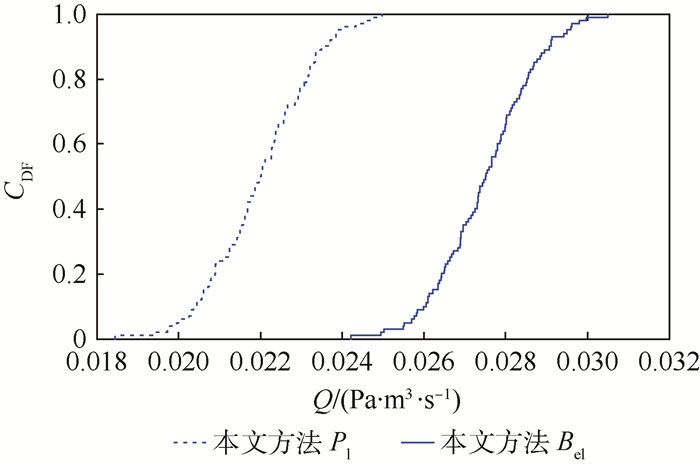
4) 在表 1和表 2参数下,利用本文所提混合不确定性传播框架,计算出氢氧共底漏气率不确定性包络曲线,如图 13所示。结果看出,Bel(Q<0.3)=0.995,评估结果满足设计安全要求。
|
| 图 13 共底漏气率不确定性结果 Fig. 13 Uncertainty of co-bottom gas leakage rate |
5) 在本算例中,为了验证本文方法的计算效率,将本文方法分别与蒙特卡罗法进行对比,不同方法计算结果如表 3所示。表 3中:Mpr为单一概率刻画下的双层蒙特卡罗混合不确定性分析方法;Mpo为概率-可能性刻画下的混合不确定性分析方法;NL1为本文方法内层循环次数;NL2为外层循环次数;tCPU为MATLAB获取的计算机CPU计算时间。由表 3看出,本文方法效率优于单一概率或者概率-可能性分布刻画下的混合不确定性传播方法,且认知不确定性分布参数所需采样次数明显减少。
| 方法 | NL1 | NL2 | tCPU/s |
| Mpr | 3×105 | 1×105 | 15.3 |
| Mpo | 2×102 | 1×103 | 7.5 |
| 本文方法 | 5×101 | 1×103 | 3.5 |
4 结论
在风险评估混合不确定性传播过程中,针对传统混合不确定性传播框架下认知不确定性分布参数完全相关的不足,本文提出了考虑认知不确定性分布参数依赖时统一的混合不确定性传播框架。
1) 构建的考虑认知不确定性分布参数依赖时的双层混合不确定性传播框架与双层蒙特卡罗不确定性传播框架对比,本文方法具有较小的不确定性输出结果,并通过认知不确定性分布参数独立时的实例验证了其可行性。
2) 分别给出了参数非独立、完全独立情形下的认知不确定性通用依赖性分析模型,特别针对参数独立时,提出了基于D-S证据理论与随机集相结合的混合不确定性传播方法,克服了单一概率刻画下的双层蒙特卡罗计算代价大的难题。
3) 在本文所提混合不确定分析框架下,当认知不确定性分布参数独立时风险输出不确定性最大。本文方法适用于认知不确定性分布参数精确概率分布无法获取情形时风险量化评估,风险计算结果相对保守。
4) 对比分析认知不确定性分布参数完全正依赖、完全负依赖情形下的风险不确定性结果。完全正依赖时,随机不确定性达到最大;完全负依赖时,认知不确定性达到最大。
5) 通过对氢氧贮箱共底漏气率算例分析,验证了本文方法的可行性与有效性,该方法还可以用于其他工程实际问题的风险与可靠性评估不确定性分析,具有一定的工程应用价值。
| [1] | ABDELLAOUI M, LUCE R D, MACHINA M J, et al.Uncertainty and risk:Mental, formal, experimental representations[M/OL].Berlin:Springer-Verlag, 2007:5-98[2017-09-30].http://www.springer.com/us/book/9783540489344. |
| [2] | HELTON J C, JOHNSON J D, OBERKAMPF W L, et al. Representation of analysis results involving aleatory and epistemic uncertainty[J]. International Journal of General Systems, 2010, 39 (6): 605–646. DOI:10.1080/03081079.2010.486664 |
| [3] | HELTON J C. Uncertainty and sensitivity analysis in the presence of stochastic and subjective uncertainty[J]. Journal of Statistical Computation and Simulation, 1997, 57 (1-4): 3–76. DOI:10.1080/00949659708811803 |
| [4] | GUYONNET D, BOURGINE B, DUBOIS D, et al. Hybrid approach for addressing uncertainty in risk assessments[J]. Journal of Environmental Engineering, 2003, 129 (1): 68–78. DOI:10.1061/(ASCE)0733-9372(2003)129:1(68) |
| [5] | MOENS D, HANSS M. Non-probabilistic finite element analysis for parametric uncertainty treatment in applied mechanics:Recent advances[J]. Finite Elements in Analysis & Design, 2011, 47 (1): 4–16. |
| [6] | ROHMER J, BAUDRIT C. The use of the possibility theory to investigate the epistemic uncertainties within scenario-based earthquake risk assessments[J]. Natural Hazards, 2011, 56 (3): 613–632. DOI:10.1007/s11069-010-9578-6 |
| [7] | AGARWAL H, RENAUD J E, PRESTON E L, et al. Uncertainty quantification using evidence theory in multidisciplinary design optimization[J]. Reliability Engineering & System Safety, 2004, 85 (1): 281–294. |
| [8] | SHAH H, HOSDER S, WINTER T. Quantification of margins and mixed uncertainties using evidence theory and stochastic expansions[J]. Reliability Engineering & System Safety, 2015, 138 : 59–72. |
| [9] | RAO K D, GOPIKA V, RAO V V S S, et al. Dynamic fault tree analysis using Monte Carlo simulation in probabilistic safety assessment[J]. Reliability Engineering & System Safety, 2009, 94 (4): 872–883. |
| [10] | BARALDI P, ZIO E. A combined Monte Carlo and possibilistic approach to uncertainty propagation in event tree analysis[J]. Risk Analysis, 2008, 28 (5): 1309–1326. DOI:10.1111/risk.2008.28.issue-5 |
| [11] | BAUDRIT C, DUBOIS D, GUYONNET D. Joint propagation and exploitation of probabilistic and possibilistic information in risk assessment[J]. IEEE Transactions on Fuzzy Systems, 2006, 14 (5): 593–608. DOI:10.1109/TFUZZ.2006.876720 |
| [12] | DEMPSTER A P. Upper and lower probabilities induced by a multivalued mapping[J]. Annals of Mathematical Statistics, 1967, 38 (2): 325–339. DOI:10.1214/aoms/1177698950 |
| [13] | SHAFER G. A mathematical theory of evidence[J]. Technometrics, 1978, 20 (1): 579–601. |
| [14] | KAY R U. Fundamentals of the Dempster-Shafer theory and its applications to system safety and reliability modelling[J]. Reliability:Theory & Applications, 2007, 2 : 173–185. |
| [15] | GUAN J W, BELL D A. Evidence theory and its applications.Vol.2[M]. New York: Elsevier Science, 1991: 37-53. |
| [16] | SADIQ R, NAJJARAN H, KLEINER Y. Investigating evidential reasoning for the interpretation of microbial water quality in a distribution network[J]. Stochastic Environmental Research and Risk Assessment, 2006, 21 (1): 63–73. DOI:10.1007/s00477-006-0044-7 |
| [17] | GRABISCH M. Dempster-Shafer and possibility theory[M]. Berlin: Springer, 2016: 377-437. |
| [18] | DUBOIS D, NGUYEN H T, PRADE H.Possibility theory, probability and fuzzy sets misunderstandings, bridges and gaps[M]//DUBOIS D, PRADE H.Fundamentals of fuzzy sets.Berlin:Springer, 2000:343-438. http://link.springer.com/10.1007/978-1-4615-4429-6_8 |
| [19] | ROSS T J. Fuzzy logic with engineering applications[M]. New York: John Wiley & Sons, 2009: 408-433. |
| [20] | DUBOIS D. Fuzzy sets and systems:Theory and applications[M]. Orlando: Academic Press, 1980: 9-146. |
| [21] | DUBOIS D. Possibility theory and statistical reasoning[J]. Computational Statistics & Data Analysis, 2006, 51 (1): 47–69. |
| [22] | PEDRONI N, ZIO E. Empirical comparison of methods for the hierarchical propagation of hybrid uncertainty in risk assessment, in presence of dependences[J]. International Journal of Uncertainty, Fuzziness and Knowledge-based Systems, 2012, 20 (4): 509–557. DOI:10.1142/S0218488512500250 |
| [23] |
王荣宗, 孙天辉. 低温贮箱共底真空性能分析及测试[J].
导弹与航天运载技术, 2002 (2): 47–51.
WANG R Z, SUN T H. Analysis and measure of vacuum character for the co-bulkhead of the cryogenic tanks[J]. Missiles and Space Vehicles, 2002 (2): 47–51. (in Chinese) |
| [24] | VOSE D. Risk analysis:A quantitative guide[M]. New York: John Wiley & Sons, 2007: 52-158. |



