2. 北京航空航天大学 自动化科学与电气工程学院, 北京 100083
2. School of Automation Science and Electrical Engineering, Beijing University of Aeronautics and Astronautics, Beijing 100083, China
飞艇飞行所需升力主要来自于气体浮力,不必为平衡自身重力而做相对运动,消耗能量小,续航时间长。与固定翼飞机、直升机和旋翼机相比,飞艇具有飞行速度低、姿态稳定、安全性高等特点。近年来,重载飞艇[1]、平流层飞艇[2]等受到世界各强国的广泛关注,而控制策略一直是飞艇研究的重要问题。
飞艇的体密度小,所受惯性力不可忽略,对操纵机构的响应慢、时滞较大;飞艇动力学特性相对复杂,艇体的柔性、弹性以及外界的随机扰动等,使得飞艇控制成为具有不确定性的问题[3]。常见的飞艇控制方法包括PID控制[4]、反步法[5-6]、动态逆[7]和滑模控制[8]等。其中,PID控制器的应用最为广泛,但是PID控制器需要对比例、积分、微分等相关参数进行人工调节,在模型参数和环境发生变化时,常常需要重新调整控制器参数。反步法、动态逆和滑模控制方法能够保证控制器在非线性系统中的鲁棒性和全局稳定性,但是其系统建模和参数辨识等工作依然较为复杂。
作为一种重要的非监督学习算法,增强学习通过“动作和回报”的机制[9],能够在缺少动力学模型的情况下实现控制器的自适应[10]。在飞行器控制领域,增强学习算法已经取得了许多成功的应用。Pearre[11]、Ragi[12]和Dunn[13]等以飞行航迹角为学习动作,分别选定能源消耗、飞行时间、避障避险等作为目标回报函数,灵活生成和优化飞行器的参考路径。Zhang等[14]设计了“几何增强学习”的方法,通过在非相邻状态之间进行转移,为方法提供更多的可用学习动作,从而获得更优的路径。Faust[15]以四旋翼模型的加速度为学习动作,研究了四旋翼吊挂重物的路径优化问题。以上文献主要是利用增强学习算法生成外环路径,其内环依然需要设计控制律来控制飞行器的姿态,未能充分利用算法的自学习能力。Ko等[16]将增强学习算法用于飞艇模型参数辨识,降低了控制器中模型相关参数的误差。Rottmann等[17]设计了基于Q-Learning算法的高度控制器,通过在线学习在数分钟内就实现了飞艇高度方向上的控制,获得了与PID控制器精度相当的控制效果。但是,在实际控制问题中,系统自由度多、状态空间维数大、算法学习效率不高,造成学习时间过长进而陷入所谓的“维数灾难”。利用随机过程、神经网络等理论对动作值函数进行泛化是解决这一问题的有效手段。小脑模型关节控制器(CMAC)神经网络在局部邻域内进行泛化,收敛速度快[18],适合对飞艇的实际运动进行拟合。
本文通过分析飞艇的运动特点,对飞艇运动状态空间进行了简化,设计了建立飞艇控制马尔可夫决策过程(MDP)模型的自适应方法;利用Q-Learning算法设计飞艇的航向控制器,直接以执行机构的动作为输入、飞艇的位置姿态变化为输出进行在线学习,同时利用CMAC神经网络对动作值函数进行泛化。这一策略对于无人船、水下机器人的控制也具有一定的参考意义。
1 飞艇观测模型飞艇经过放飞升空等过程后,逐渐稳定于设计高度。此时在纵向主要依靠升降舵、自重调节、浮力调节等装置实现高度的控制,在横航向则主要依靠螺旋桨、方向舵和矢量推力装置等实现水平位置和航向的控制。与飞机的运动相比,飞艇的滚转角较小,高度相对稳定,纵向运动和横航向运动耦合小,滚转运动对水平面运动的影响甚微[19]。借鉴既有文献[5, 19]的处理方式,在航向运动的控制中,不关注滚转运动产生的影响。
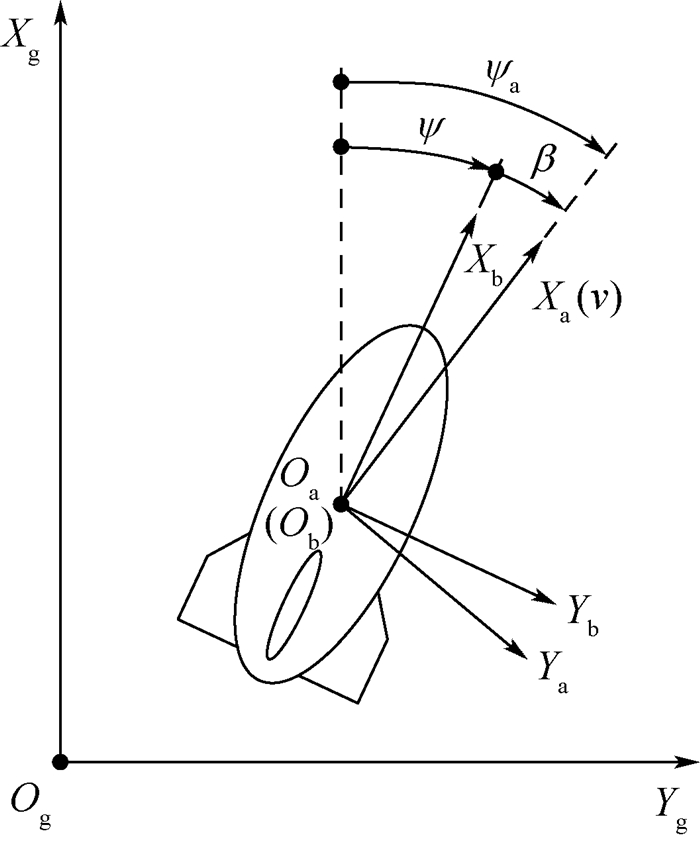
根据以上任务描述和分析,绘制飞艇观测坐标系的俯视图如图 1所示。设地面惯性坐标系为OgXgYgZg,气流坐标系为OaXaYaZa,艇体坐标系为ObXbYbZb,Oa和Ob在浮空器的体心。图 1中:ψ为偏航角; ψa为航向角; β为侧滑角; Xa的方向在风速为零时与飞行速度v的方向相同。
|
| 图 1 飞艇观测坐标系俯视图 Fig. 1 Vertical view of airship observation coordinate system |
MDP是增强学习算法的理论基础,本文首先把飞艇控制问题建模为离散的MDP。离散的MDP可以用五元数组{S, A, r, P, J}来表示,S为根据飞艇的位置、速度和姿态等参数划分而成的状态空间,A为浮空器的可用控制指令组成的动作空间,r为对应状态和行为的回报,P为状态之间的转移概率,J为控制决策的优化目标函数。离散的MDP具有如下特性:

|
(1) |
式中:pij(ak)称为在si状态,采取ak动作,转移到sj状态的概率;t为时间参数。通过合理选择构成状态空间S的状态参数,可以使浮空器控制问题模型近似满足这一性质。
2.1 状态空间参数S的确定在浮空器航向运动的控制过程中,易于观测到的状态参数包括目标点的位置xd、yd,飞艇的位置xg、yg,飞艇的航向角ψa等。为了控制状态空间的规模,可以采取相对坐标建模的方法,常见的做法是以目标点的位置为原点建立坐标系,设xr、yr为飞艇相对目标位置的坐标,有xr=xg-xd,yr=yg-yd,飞艇的位置和航向角就可以用(xr, yr, ψa)来表示。本文中,为了进一步压缩状态空间的规模,采取了类似极坐标系的建模方法来确定飞艇和目标的相对位置,如图 2所示。图中:lr为目标到飞艇的相对距离;ψd为飞艇和目标的连线与Xg轴的夹角;ψr为飞艇航向偏离目标的角度。飞艇和目标的相对位置可以用(lr, ψr)来描述,根据几何关系有

|
| 图 2 飞艇和目标相对位置坐标示意图 Fig. 2 Coordinate schematic diagram of relative position of airship and target |
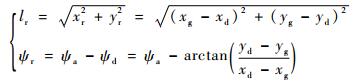
|
(2) |
利用增强学习算法设计的控制器,虽然不必获知飞艇的动力学模型,但是依然要确定MDP模型的参数。离散的MDP模型中,飞艇动力学模型的变化主要影响状态空间S离散参数的范围和精度,其参数选择的优劣将直接影响控制器的学习效果。如果状态空间离散参数范围过小,离散精度不足时,会造成学习不收敛,无法获得可行的控制指令;如果离散参数范围过大,离散精度过高时,会使实际学习时间过长,无法在有限时间内完成对控制器的训练。现有文献的通用做法是通过研究人员的观察进行试凑和调整,因此在系统动力学模型发生变化时,如果不能及时人工调整,控制器的效果就很可能大打折扣甚至失效。因此,本文力图通过对飞艇运动的分析,在真实运动数据的基础上,确定状态空间参数的范围和离散精度,以便在飞艇模型变化时进行自主调整。
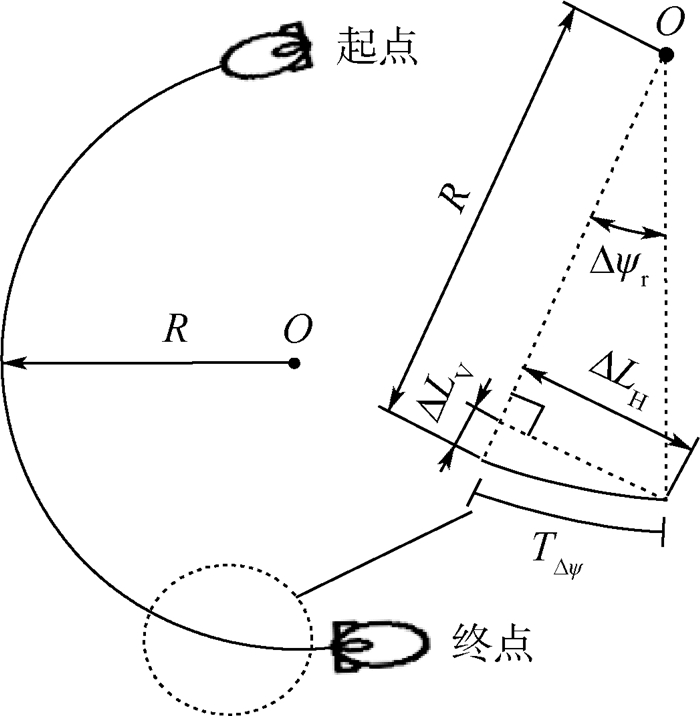
当采用(lr, ψr)坐标描述飞艇和目标的相对位置时,状态空间S的主要未知离散参数为lr、ψr的范围,lr、ψr的离散精度Δlr、Δψr以及控制指令执行的单位时间。定义控制指令执行的单位时间为控制步长Tstep。按照以下步骤进行真实运动:在飞艇的额定巡航速度下,将方向舵输入控制为最大偏角,记录飞艇飞行实时位置和姿态,直至飞艇的飞行轨迹近似为圆弧形。得到飞艇的航迹如图 3所示。图中:R为飞艇的转弯半径;Δψr为航向角的离散精度,由控制要求决定;TΔψ为转过Δψr角度所需的时间;ΔLV为飞艇在TΔψ时间位移垂直初速度方向的分量;ΔLH为位移沿初速度方向的分量。
|
| 图 3 飞艇圆弧形航迹 Fig. 3 Arc flight trajectory of airship |
由几何关系可知,ΔLV=R(1-cos Δψr),ΔLH=Rsin Δψr,航向角ψr的范围为[-π, +π]。控制步长Tstep必须足够小,以便飞艇在相邻的离散航向角间实现状态转移,因此有Tstep≤TΔψ,在本文中取Tstep≈TΔψ。在一个控制步长Tstep内,飞艇垂直初速度方向上的位移分量ΔLV远小于沿初速度方向上的位移分量ΔLH,lr的离散精度Δlr应当小到足以分辨ΔLV,因此有Δlr≤ΔLV,在本文中取Δlr≈ΔLV。状态空间的尺寸lr应当足够大以保证飞艇的自由运动,考虑到飞艇常见的原地掉头、八字等机动动作,有lr≥4R,在本文中取lr≈4R。
通过以上对飞艇运动的分析,飞艇控制MDP模型状态空间S的离散参数确定方法总结如表 1所示。
| 参数 | 取值规则 | 本文取值 |
| ψr | [-π, +π] | [-π, +π] |
| lr | ≥4R | 4R |
| Δψr | 控制要求决定 | π/9 |
| Δlr | ≤R(1-cos Δψr) | R(1-cos Δψr) |
| Tstep | ≤TΔψ | TΔψ |
2.2 参数A、r、P、J的确定
MDP模型五元数组的其余4个参数A、r、P、J主要根据任务目标构造。动作空间A由方向舵偏输入构造;回报函数r由障碍、能耗的负回报值和目标的正回报值等构造;转移概率P取决于动作执行后飞艇的真实运动结果;目标函数J设为总的回报值。设π为动作选择策略,J*为最优回报值,有
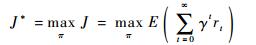
|
(3) |
式中:γ∈(0, 1)为回报折扣因子;rt为t时刻的回报值。
3 控制策略设计 3.1 Q-Learning算法增强学习算法通过与环境交互的方式进行学习,控制系统首先选择行动策略,随后外部环境给予回报(奖励或惩罚),而控制系统则利用实时回报重新评估行动策略的优劣,以最终实现累积回报的最大化。传统的监督学习方法利用已知样本进行训练,而增强学习算法则通过不断“试错”的方式对行动策略进行优化。基于这一理论框架,Q-Learning算法对MDP模型中不同状态下的动作值函数进行存储和估计,利用环境的反馈进行动作值函数的迭代更新,以求解具有延迟回报的序贯决策优化问题。飞艇的姿态相对稳定,控制动作在“试错”过程中的一时失误一般不会造成艇毁人亡的灾难性后果;其续航时间长、驻空能力强,有相对充裕的时间对算法中的动作值函数进行充分的迭代估计。因此,Q-Learning算法可用于飞艇控制的在线学习。设Q(s, a)为在状态s时a动作的值函数估计,有
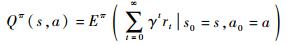
|
(4) |
式中:s0为初始状态;a0为初始动作。
根据运筹学相关理论,Q(s, a)满足如下的Bellman方程:
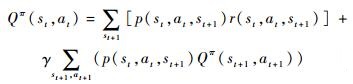
|
(5) |
式中:p(st, at, st+1)为在状态st下,采取at动作,转移到st+1状态的概率;r(st, at, st+1)为动作at和状态st转移到st+1的回报值。
对应式(3)的最优动作估计Qπ*(s, a)和最优策略π*(s)如下:
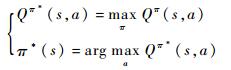
|
(6) |
利用直接梯度下降的方式对Qπ(s, a)进行估计,得到迭代公式为
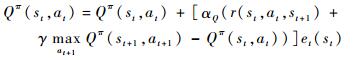
|
(7) |
式中:αQ∈(0, 1)为学习率;et为适合度参数,反映状态st的访问频繁程度:
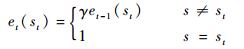
|
(8) |
神经网络可分为全局逼近神经网络和局部逼近神经网络。对于全局逼近神经网络(如BP网络),其每个权值都可能对输出产生影响,每个训练样本都会更新网络的所有权值,收敛速度慢,难以满足实时在线学习的要求。对于局部逼近神经网络(如CMAC网络),某个输入空间只有少数权值对输出产生影响,训练样本只对局部权值进行更新,可以快速逼近时变、非线性的函数。虽然全局逼近神经网络在飞艇控制领域有大量成功的应用,但本文的飞艇控制任务中,缺少足够的训练样本而只有有限的在线实时尝试结果,对收敛速度要求高;当飞艇处于不同的状态下,状态场景相近时其控制策略相似,状态场景变化大时控制策略可能完全不同(例如机动空间不足时应先采取远离迂回的策略),这一特性契合局部逼近神经网络的优势。CMAC神经网络通过表格查询的方式对非线性函数进行拟合,在局部邻域内进行权值更新,计算量小,便于在飞控计算机的嵌入式软件中实现,适合对飞艇控制的在线学习过程进行泛化加速。其典型的结构如图 4所示。图中:S为m个离散的状态空间;W为n个内存地址中储存的权值;ynet为网络输出。

|
| 图 4 CMAC神经网络结构 Fig. 4 Structure of CMAC neural network |
真实状态映射到状态空间S中,每个离散的状态si对应多个物理地址储存的权值W。状态之间相距越近,其物理地址重叠(图中的阴影部分)越多,而相距较远的状态则没有重叠。设
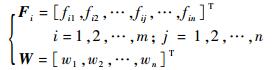
|
(9) |
式中:Fi为状态si对权值的激活状态,fij=1或0表示状态si对权值wj的激活状态。则输出为
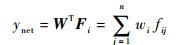
|
(10) |
利用直接梯度下降的方法,在状态st=si时,权值更新公式为
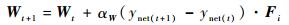
|
(11) |
式中:αW为权值学习率。
本文为每个动作的值函数估计建立一个CMAC神经网络,设st=si时第k个动作的函数值估计为Qk,其权值为Wk,激活状态为Fki,则结合式(7)和式(11),有

|
(12) |
本文利用控制动作的实时执行情况对控制器进行训练,通过学习持续改善控制效果。为了避免学习陷入局部最优,同时保证控制器的学习收敛速度,需要在在自由探索和贪心策略之间达到平衡。本文采用基于Boltzmann分布的随机动作选择方法,设可用动作集为A={ak}, k=1, 2, …,p(a|s)表示在状态s下选择动作a的概率,则动作选择策略π可以表示为

|
(13) |
式中:Ttemp为探索系数。类似于模拟退火方法的温度系数,通过逐渐降低Ttemp,能够保证初始情况下较高的探索率,并最终趋于贪心策略。
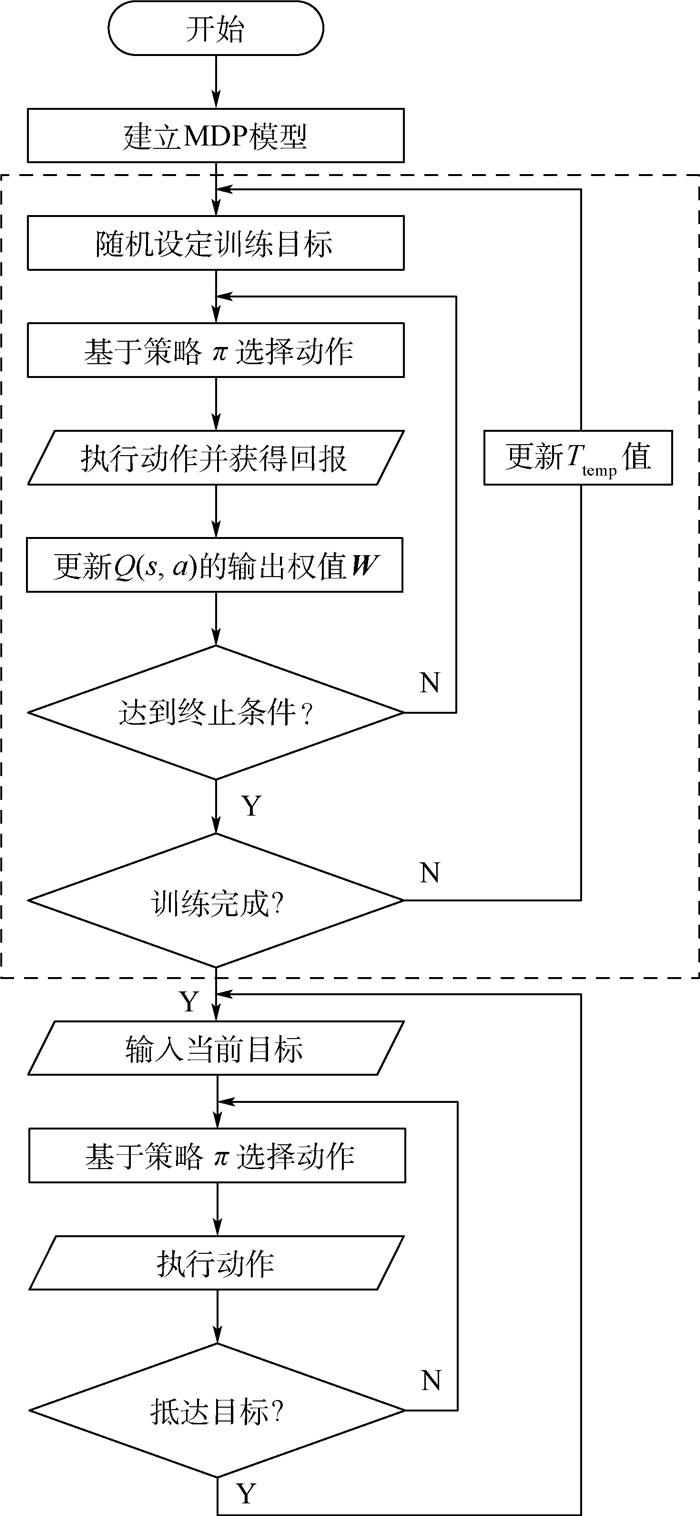
设计整个策略的流程如图 5所示,其中虚线框内部为控制器的在线学习过程,虚线框以下为实际任务中的控制过程。
|
| 图 5 控制策略流程 Fig. 5 Flow of control strategy |
为了验证控制策略的有效性,本文进行了模型仿真和对比分析。
参照已有文献[4, 19]的建模方法,建立了低空飞艇[20]的仿真模型,其中飞艇所受气动力和力矩可以表示为式(14):

|
(14) |
式中:Q∞=ρv2/2为来流动压,ρ为大气密度;α为飞艇的迎角;FaX、FaY、FaZ和La、Ma、Na分别为飞艇所受气动力和力矩;CX1~CN4为艇体气动力系数;δR为方向舵总偏角;δE为升降舵总偏角。
仿真模型主要外形和气动参数如表 2所示。
| 参数 | 数值 |
| m/kg | 100 |
| ▽/m3 | 79.0 |
| ρ/(kg·m-3) | 1.225 |
| Ix/(kg·m2) | 324 |
| Iy/(kg·m2) | 474 |
| Iz/(kg·m2) | 202 |
| k1 | 0.084 |
| k2 | 0.856 |
| k3/m2 | 5.543 |
| CX1 | -0.518 |
| CX2 | -5.629 |
| CY1 | -5.629 |
| CY2 | -10.798 |
| CY3 | -22.852 |
| CY4 | 2.336 |
| CZ1 | -5.629 |
| CZ2 | -10.798 |
| CZ3 | -21.622 |
| CZ4 | -2.336 |
| CL2 | 2.337 |
| CM1 | 36.364 |
| CM2 | -56.948 |
| CM3 | -42.655 |
| CM4 | -12.324 |
| CN1 | -36.364 |
| CN2 | 56.948 |
| CN3 | 42.655 |
| CN4 | -12.324 |
| 注:m—飞艇质量;▽—飞艇体积; Ix、Iy、Iz—转动惯量; k1、k2、k3—惯性因子。 | |
本文控制策略的算法主要参数如下:回报折扣因子γ=0.9;学习率αW=0.003;探索系数Ttemp=40;目标回报值rsuccess=+10,超差回报值rfail=-10;可用动作集为:{δR}={-π/3, -π/6, 0, +π/6, +π/3},单位为rad。
4.2 控制器训练对应图 5虚线框中的流程,在飞艇周围随机设定位置作为任务目标,反复对控制器进行训练。经过约3 h(10 000 s)的在线学习,飞艇完成任务的成功率稳定在100%,即完成训练。在本文的某控制器训练过程中,完成训练任务的成功率和平均耗时情况如图 6所示。

|
| 图 6 训练任务的成功率和平均耗时 Fig. 6 Success rate and time length in training tasks |
由图 6可看出,训练任务的成功率先迅速提高,而后稳步上升,最终稳定在100%,对应控制器的自主学习并逐渐收敛的过程;训练任务的平均耗时先增加后逐渐减少,对应学习过程中经历了从“很快碰壁”到“走弯路抵达目标”再到“直接抵达目标”3个阶段。
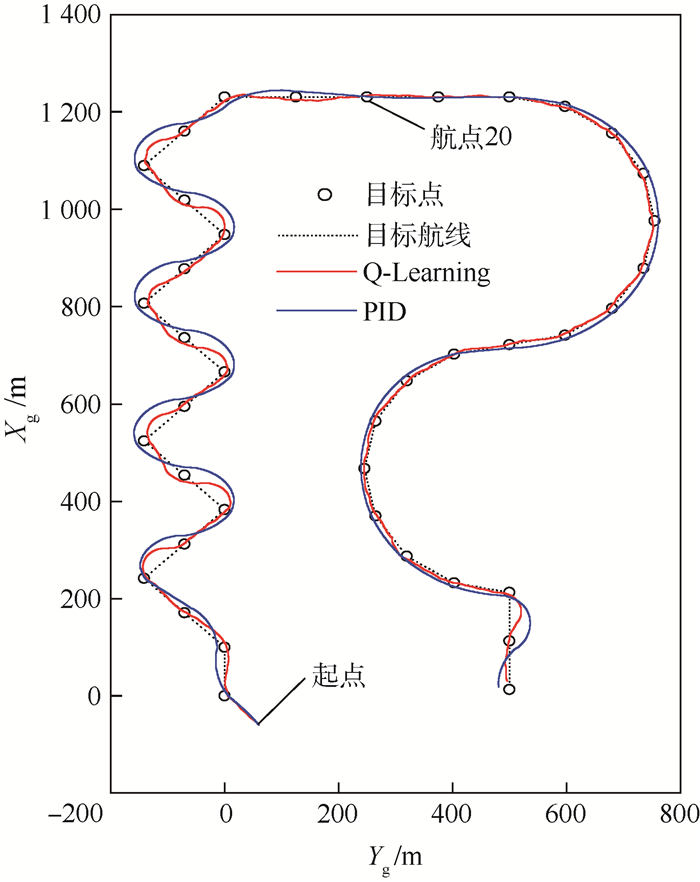
4.3 实际任务仿真对飞艇某典型控制任务进行仿真,如图 7所示。其中目标点间距为100 m,目标航线为目标点顺次连线而成,近似为连续转弯、直线和近似圆弧的组合。
|
| 图 7 典型任务执行情况 Fig. 7 Performance of typical tasks |
作为对比,本文参照文献[4]的处理方式,利用飞艇模型结构和气动力参数建立飞艇的非线性动力学方程,再经过小扰动线性化后获得飞艇的横向扰动方程,求得飞艇方向舵偏角δR到航向角ψa的传递函数。并以此为基础设计了PID内环控制器,利用MATLAB中的rltool工具分析传递函数的根轨迹,完成对增益参数的整定。在控制器外环,则采用视线制导(LOS)方法[21]。
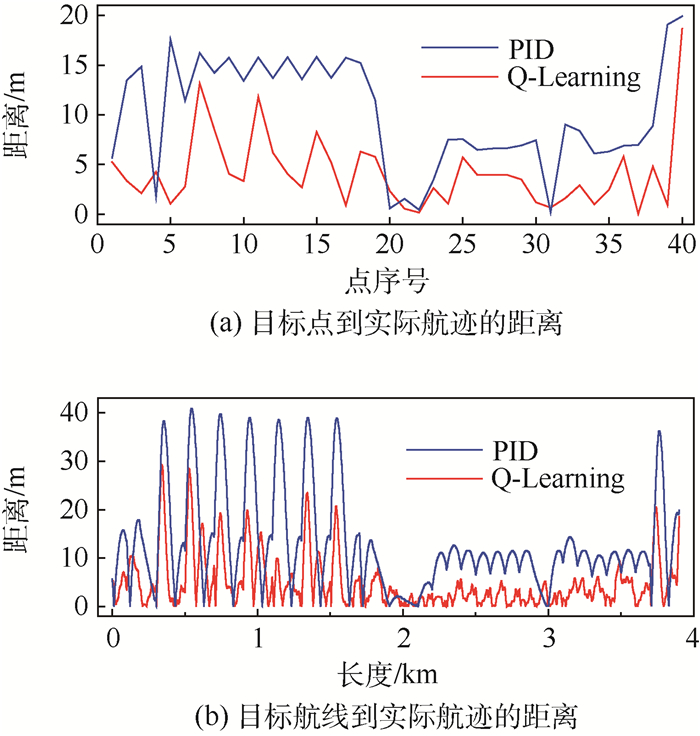
通过仿真得到PID控制器和Q-Learning控制器的实际航迹如图 7所示,目标点和目标航线到飞艇实际航迹的距离如图 8所示。其中只有直线航线阶段(第20航点附近,2 km位置处),2个控制器控制精度接近,此时Q-Learning控制器的控制精度主要受限于MDP模型的离散精度;其余的机动阶段,Q-Learning控制器均得到了略优于PID控制器的控制精度,这是因为Q-Learning控制器的输出不是由当前偏差而是由以往的总体回报情况决定的,在飞艇航向即将出现偏差和偏差较小时就能及时发现并处理控制超调的情况。
|
| 图 8 目标点和目标航线到实际航迹的距离 Fig. 8 Distances from target points and paths to actual trajectories |
飞艇的目标点和目标航线到实际航迹的距离情况以及完成整个任务的耗时情况如表 3所示。可知,Q-Learning控制器不仅在控制精度方面占优,而且任务全程耗时也较短。
| 控制器 | 目标点最大偏离/m | 目标点平均偏离/m | 目标航线最大偏离/m | 目标航线平均偏离/m | 任务全程耗时/s |
| PID | 17.55 | 10.06 | 40.89 | 19.92 | 443.7 |
| Q-Learning | 13.16 | 4.19 | 29.23 | 4.81 | 419.2 |
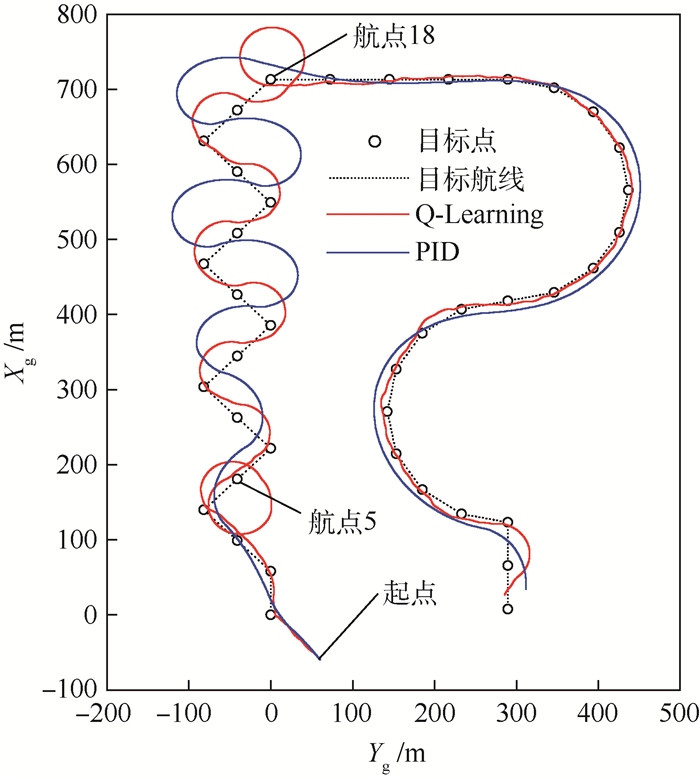
为了进一步考察Q-Learning控制器的控制能力,将目标点间距缩短至60 m,相当于转弯半径减小,仿真结果如图 9所示。此时由于飞艇的转弯能力有限,视线制导PID控制器不够智能,在连续转弯中非常容易陷入以目标点为圆心的无尽绕圈中而不能抵近目标,因此不得不扩大目标点的覆盖范围进而放宽任务要求。Q-Learning控制器则在训练阶段就已学习到迂回抵达目标的方法,在直接转弯无法抵近目标时(第5航点、第18航点),能够通过先远离再转弯的这种更为智能的方式完成任务。
|
| 图 9 缩小尺度后任务执行情况 Fig. 9 Performance of reduced-scale tasks |
本文结合Q-learning算法和CMAC神经网络,提出了一种基于自主建模和在线学习机制的控制方案,其优点如下:
1) 在真实运动数据的基础上建立飞艇控制的MDP模型,具有自适应性,飞艇模型改变后可以自主调整。
2) 合理简化飞艇控制模型,并利用神经网络对学习成果进行泛化,控制器学习速度较快,训练过程持续约3 h。
3) 不需要获取飞艇的动力学模型参数,能够达到与经过参数整定的PID控制器相近的控制精度,且更为智能。
| [1] | PRENTICE B E, KNOTTS R. Cargo airships:International competition[J]. Journal of Transportation Technologies, 2014, 4 : 187–195. DOI:10.4236/jtts.2014.43019 |
| [2] |
赵达, 刘东旭, 孙康文, 等. 平流层飞艇研制现状、技术难点及发展趋势[J].
航空学报, 2016, 37 (1): 45–56.
ZHAO D, LIU D X, SUN K W, et al. Research status, technical difficulties and development trend of stratospheric airship[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37 (1): 45–56. (in Chinese) |
| [3] |
郭虓. 平流层浮空器轨迹优化研究[D]. 北京: 北京航空航天大学, 2013: 29-36.
GUO X.Trajectory optimization research for stratospheric aerostat[D].Beijing:Beihang University, 2013:29-36(in Chinese). |
| [4] | KHOURY G A. Airship technology[M]. New York: Cambridge University Press, 2012: 34-40. |
| [5] | YANG Y, WU J, ZHENG W. Positioning control for an autonomous airship[J]. Journal of Aircraft, 2016, 53 (6): 1638–1646. DOI:10.2514/1.C033709 |
| [6] | ZHENG Z W, ZHU M, SHI D L, et al.Hovering control for a stratospheric airship in unknown wind:AIAA-2014-0973[R].Reston:AIAA, 2014. https://arc.aiaa.org/doi/abs/10.2514/6.2014-0973 |
| [7] | ZHENG Z, LIU L, ZHU M. Integrated guidance and control path following and dynamic control allocation for a stratospheric airship with redundant control systems[J]. Proceedings of the Institution of Mechanical Engineers, Part G:Journal of Aerospace Engineering, 2016, 230 (10): 1813–1826. DOI:10.1177/0954410015613738 |
| [8] | YANG Y, YAN Y, ZHU Z, et al. Positioning control for an unmanned airship using sliding mode control based on fuzzy approximation[J]. Proceedings of the Institution of Mechanical Engineers, Part G:Journal of Aerospace Engineering, 2014, 228 (14): 2627–2640. DOI:10.1177/0954410014523577 |
| [9] | ABBEEL P, COATES A, QUIGLEY M, et al.An application of reinforcement learning to aerobatic helicopter flight[C]//Advances in Neural Information Processing Systems, 2007:1-8. http://ieeexplore.ieee.org/document/6287086/ |
| [10] |
徐昕.
增强学习与近似动态规划[M]. 北京: 科学出版社, 2010: 18-27.
XU X. Reinforcement learning and approximate dynamic programing[M]. Beijing: Science Press, 2010: 18-27. (in Chinese) |
| [11] | PEARRE B, BROWN T X. Model-free trajectory optimization for unmanned aircraft serving as data ferries for widespread sensors[J]. Remote Sensing, 2012, 4 (10): 2971–3005. |
| [12] | RAGI S, CHONG E K P. UAV path planning in a dynamic environment via partially observable Markov decision process[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49 (4): 2397–2412. DOI:10.1109/TAES.2013.6621824 |
| [13] | DUNN C, VALASEK J, KIRKPATRICK K.Unmanned air system search and localization guidance using reinforcement learning:AIAA-2012-2589[R].Reston:AIAA, 2012. https://arc.aiaa.org/doi/abs/10.2514/6.2012-2589 |
| [14] | ZHANG B, MAO Z, LIU W, et al. Geometric reinforcement learning for path planning of UAVs[J]. Journal of Intelligent & Robotic Systems, 2015, 77 (2): 391–409. |
| [15] | FAUST A. Reinforcement learning and planning for preference balancing tasks[J]. AI Matters, 2015, 1 (3): 8–12. |
| [16] | KO J, KLEIN D J, FOX D, et al.Gaussian processes and reinforcement learning for identification and control of an autonomous blimp[C]//Proceedings 2007 IEEE International Conference on Robotics and Automation.Piscataway, NJ:IEEE Press, 2007:742-747. http://ieeexplore.ieee.org/document/4209179/ |
| [17] | ROTTMANN A, PLAGEMANN C, HILGERS P, et al.Autonomous blimp control using model-free reinforcement learning in a continuous state and action space[C]//2007 IEEE/RSJ International Conference on Intelligent Robots and Systems.Piscataway, NJ:IEEE Press, 2007:1895-1900. http://ieeexplore.ieee.org/document/4399531/ |
| [18] | LIN C M, PENG Y F. Adaptive CMAC-based supervisory control for uncertain nonlinear systems[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B(Cybernetics), 2004, 34 (2): 1248–1260. DOI:10.1109/TSMCB.2003.822281 |
| [19] | SCHMIDT D K. Modeling and near-space station keeping control of a large high-altitude airship[J]. Journal of Guidance, Control, and Dynamics, 2007, 30 (2): 540–547. DOI:10.2514/1.24865 |
| [20] | LS-S1200 UAV airship system overview parameters[EB/OL].[2017-12-18].http://www.lonsan.com.cn/english/Products_1.asp?oneclass=5&pid=13. |
| [21] | ATAEI M, YOUSEFI-KOMA A. Three-dimensional optimal path planning for waypoint guidance of an autonomous underwater vehicle[J]. Robotics and Autonomous Systems, 2015, 67 : 23–32. DOI:10.1016/j.robot.2014.10.007 |



