2. 北方工业大学 柔性变截面辊弯成形北京市工程技术研究中心, 北京 100144
2. Beijing Engineering Research Center of Flexible Roll Forming, North China University of Technology, Beijing 100144, China
与传统的串联机构相比,空间并联机构具有更高的刚度、精度和较强的承载能力等优点,广泛应用于虚拟轴机床、微动机器人等现代尖端技术的许多领域。并联机构位置正解就是根据并联机构驱动杆长来推算动平台相对静平台的位置和姿态,该问题是该机构速度、加速度、误差分析、工作空间分析、奇异位置分析、动力学分析等问题的理论基础[1]。因此,并联机构位置正解研究已成为机构学研究领域中的热点与难点之一。
空间3-RPS并联机构具有3个自由度,最早由Hunt[2]在1983年作为一种少自由度并联机构而提出,并引起了广泛关注与研究。Lee和Shah[3]采用数值方法对该机构的位置正解进行了研究并应用在微动机器人上。Nanua等[4]采用代数法经过复杂的数学推导证明了该机构位置正解最多为16。Fang和Huang[5]采用数值方法对上下平台皆为等边三角形的空间3-RPS并联机构(等边3-RPS机构)的速度和加速度进行了分析。李树军[6]和韩方元[7]等采用数值方法求解了等边3-RPS机构位置正解。王进戈等[8]应用Groebner基法获得了等边3-RPS机构位置正解封闭形式的解析解。目前各种常用的方法主要是经过繁琐的坐标变换和矩阵计算,建立多元非线性方程组数学模型,然后进行各具特点的复杂非线性方程组数值计算或代数消元求解。求解过程和最终获得的解都难以揭示机构结构参数与运动之间的几何关系[9]。
共形几何代数(CGA)是几何代数的一个分支,是建立在共形空间上的几何代数[10-11]。其优越的几何计算能力和时空表达能力,已被广泛应用于相对论物理学和计算机视觉等领域[12-13]。文献[14]将齐次变换矩阵改写成CGA形式,然后沿用目前传统的方法进行数学建模以及代数方程组求解,CGA内在的独特几何与运算优势没能得到体现。本文将CGA引入空间并联机构位置正解分析中,提出了一种空间3-RPS并联机构位置正解的新算法,只需经过简单的平方运算,可直接推导出该问题无增无漏的一元16次输入输出方程,进而获得了该机构全部16组解析解,求解过程简洁。
1 共形几何代数CGA包括内积、外积和几何积3种运算。对于矢量u和v有[12]
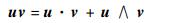
|
(1) |
式中:uv为矢量u和v的几何积;u·v为u和v的内积;u∧v为u和v的外积。
对于三维欧氏空间的一组规范正交基{e1, e2, e3, e0, e∞},有
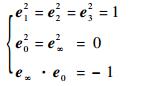
|
(2) |
式中:e0为原点;e∞为无穷远点。
CGA中,几何元素的表达式如表 1所示。INPS和OPNS分别为内积零空间和外积零空间[12]。
| 几何元素 | 表达式1 (IPNS) | 表达式2 (OPNS) |
| 点 | P=X+X2e∞/2+e0 | |
| 球 | S=P-r2e∞/2 | S*=X1∧X2∧X3∧X4 |
| 平面 | π=n+te∞ | π*=X1∧X2∧X3∧e∞ |
| 圆 | Z=S1∧S2 | Z*=X1∧X2∧X3 |
| 直线 | l=π1∧π2 | l*=X1∧X2∧e∞ |
| 点对 | PP=S1∧S2∧S3 | P*P=X1∧X2 |
表 1中,Si、πi、l和Xi分别为CGA中的球、平面、线和点,r为球半径,n为3维欧氏空间中平面的法向量,t为平面到原点的距离,X为3维欧氏空间的点
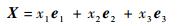
|
(3) |
式中:xi(i=1, 2, 3)为欧氏空间点的x、y、z坐标值。
由式(3)可得,点P的CGA表达式为
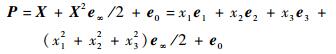
|
(4) |
在CGA中,2个点P与S的内积与距离的关系为
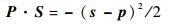
|
(5) |
式中:p=p1e1+p2e2+p3e3,s=s1e1+s2e2+s3e3,pi和si(i=1, 2, 3)为相应的坐标值。
已知表 1中点对PP的表达式,可以通过式(6)取出点对中的点为[12]
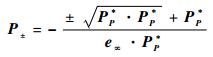
|
(6) |
几何元素o的刚体运动的CGA表示为[13]
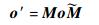
|
(7) |
式中:o′为几何体o变换后的几何体;M为运动变换算子,M=RT, R为旋转算子,R=cos(θ/2)-Lsin(θ/2),θ为旋转角度,L为旋转轴线,T为移动算子,T=1-te∞/2,t为平移向量,t=t1e1+t2e2+t3e3,ti(i=1, 2, 3)为相应的坐标值;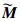
图 1为一种空间3-RPS并联机构,该机构由动平台P1P2P3和静平台B1B2B3以及3条RPS运动支链BiPi(i=1, 2, 3)连接而成,每条运动支链由1个转动副R、1个移动副P以及1个球副S组成,主动副为移动副P,其余运动副为被动副。下平台的铰接点以及各转动副的中心轴线在同一平面内任意分布。通过移动副P改变运动支链的杆长,控制动平台相对静平台的不同位置和姿态。

|
| 图 1 一种空间3-RPS并联机构 Fig. 1 A spatial 3-RPS parallel mechanism |
建立静坐标系O-xyz如图 1所示,平面xz与静平台B1B2B3平面重合,设静平台B1B2B3的3个铰接点在坐标系O-xyz中的坐标为B1(b1x, 0, b1z),B2(b2x, 0, b2z),B3(b3x, 0, b3z),动平台P1P2P3的3条边长为a12、a23、a13,静平台上的3条转动轴线矢量为u1、u2、u3且同在静平台平面上,3条运动支链的杆长分别为q1、q2、q3。空间3-RPS并联机构位置正解就是已知3条运动支链的长度,求动平台P1P2P3相对静平台B1B2B3的位置和姿态,即动平台P1P2P3的3个铰接点在静坐标系O-xyz中的坐标。
由于转动轴线矢量为u1、u2、u3且同在静平台平面上,由式(3)有
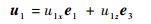
|
(8) |
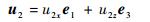
|
(9) |
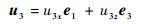
|
(10) |
设运动支链B1P1相对静平台平面的转角为θ1,由于运动支链B1P1绕转动副轴线u1转动,由式(7)可得动平台铰接点P1关于θ1的CGA表达式为
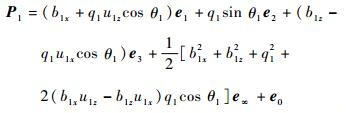
|
(11) |
由于运动支链B2P2绕转动副轴线u2转动,因此,点P2应始终在以轴线u2为法线且过点B2的平面π2内,由表 1可得平面π2的CGA表达式为
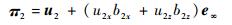
|
(12) |
由图 1知,点P2同时在以P1为球心、a12为半径的球S12和以B2为球心、q2为半径的球S22以及平面π2相交的点对Pp2上。由式(6)有
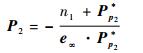
|
(13) |
式中:n12=Pp2*·P*p2,Pp2=S12∧S22∧π2,S12=P1-a122e∞/2,S22=B2-q22e∞/2。
同理有
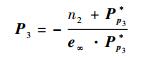
|
(14) |
式中:n22=P*p3·P*p3,Pp3=S13∧S33∧π3,S13=P1-a132e∞/2,π3=u3+(u3xb3x+u3zb3z)e∞,S33=B3-q32e∞/2。
已知动平台P1P2P3平面中铰接点P2和P3的距离为a23,由式(5)、式(13)和式(14)有
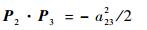
|
(15) |
展开式(15)可得
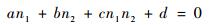
|
(16) |
式中:a、b、c、d为关于θ1的表达式中的系数。
对式(16)左边多项式进行二次平方后可得
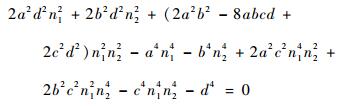
|
(17) |
将n12和n22代入式(17),展开可得关于cos θ1的一元十六次方程:
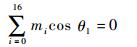
|
(18) |
式中:mi为关于参数B1、B2、B3,u1、u2、u3,a12、a23、a13以及q1、q2、q3的已知结构参数。
式(18)为所获得的单变量一种空间3-RPS并联机构位置正解输入输出方程。求解式(18)可获得θ1的16组解(0≤θ1≤π),代入式(11)、式(13)和式(14)即可确定动平台各顶点的坐标值。
4 实例验证如图 1所示一种空间3-RPS并联机构,进行实例计算。已知机构结构参数如下[15]:u1=e1,u2=-0.5e1-0.866e3,u3=-0.5e1+0.866e3;a12=2.0,a13=1.5,a23=2.0;B1=(0, 0, 2.0),B2=(1.5, 0, -1.0),B3=(-1.75, 0, -1.0)。3条运动支链的杆长分别为:q1=5,q2=5,q3=4.5。
采用第3节的方法,基于计算机代数系统Maple15编程,求解该空间机构的位置正解,可获得动平台3个铰接点在绝对坐标系的16组坐标解,其中实数解为6组,如表 2所示。所得结果与文献[15]中得到的结果完全相同,无增无漏。
| 组号 | P1 | P2 | P3 |
| 1 | (0, 4.115, -0.840) | (-1.320, 3.795, 0.628) | (0.650, 3.545, 0.386) |
| 2 | (0, 4.909, 1.051) | (-1.491, 3.616, 0.727) | (0.455, 3.710, 0.273) |
| 3 | (0, 3.688, -1.376) | (1.456, 5.000, -0.975) | (0.150, 3.929, 0.097) |
| 4 | (0, 4.833, 0.719) | (1.234, 4.991, -0.847) | (0.668, 3.529, 0.399) |
| 5 | (0, 3.566, -1.505) | (1.240, 4.991, -0.850) | (-0.548, 4.281, -0.306) |
| 6 | (0, 4.861, 0.830) | (1.153, 4.984, -0.799) | (-0.693, 4.331, -0.390) |
上述过程基于计算机代数计算系统Maple15编程,在操作系统为Microsoft Windows XP,频率为2.70 GHz,内存为2 GB的计算机中,占用内存47.49 MB,运算时间为22.94 s。
5 结论1) 将共形几何代数引入空间并联机构位置正解分析中,提出了一种空间3-RPS并联机构位置正解解析解新算法。
2) 通过构造空间球、平面等几何体的外积运算,只需要简单的距离公式即可得到关于该问题的一元十六次输入输出方程,进而获得了全部的16组解析解,求解过程没有传统并联机构运动学理论必须处理的复杂旋转角和矩阵运算以及多元高次非线性方程组求解,过程简洁明了。
| [1] |
黄真, 赵永生, 赵铁石, 等.
高等空间机构学[M]. 北京: 高等教育出版, 2006: 141-166.
HUANG Z, ZHAO Y S, ZHAO T S, et al. Advanced spatial mechanism[M]. Beijing: Higher Education Press, 2006: 141-166. (in Chinese) |
| [2] | HUNT K H. Structural kinematics of in-parallel-actuated robot-arms[J]. ASME Journal of Mechanisms Transmissions and Automation in Design, 1983, 105 (4): 705–712. DOI:10.1115/1.3258540 |
| [3] | LEE K M, SHAH D. Kinematic analysis of a three-degree-of-freedom in-parallel actuated manipulator[J]. IEEE Journal of Robotics and Automation, 1988, 4 (2): 354–360. |
| [4] | NANUA P, WALDRON K J, MURTHY V. Direct kinematic solution of a Stewart platform[J]. IEEE Journal of Robotics and Automation, 1990, 6 (4): 438–444. DOI:10.1109/70.59354 |
| [5] | FANG Y, HUANG Z. Kinematics of a three-degree-of-freedom in-parallel actuated manipulator mechanism[J]. Mechanism and Machine Theory, 1997, 32 (7): 789–796. DOI:10.1016/S0094-114X(97)00008-6 |
| [6] |
李树军, 王阴, 王晓光. 3-RPS并联机器人机构位置正解的杆长逼近法[J].
东北大学学报, 2001, 22 (3): 285–287.
LI S J, WANG Y, WANG X G. Forward position analysis of 3-RPS in-parallel manipulator using self-modified successive approximation method[J]. Journal of Northeastern University, 2001, 22 (3): 285–287. (in Chinese) |
| [7] |
韩方元, 赵丁选, 李天宇. 3-RPS并联机构正解快速数值算法[J].
农业机械学报, 2011, 42 (4): 229–233.
HAN F Y, ZHAO D X, LI T Y. A fast forward algorithm for 3-RPS parallel mechanism[J]. Transactions of the Chinese Society for Agricultural Machinery, 2011, 42 (4): 229–233. (in Chinese) |
| [8] |
王进戈, 范丽华, 徐礼钜. 3-RPS并联平台机构的位置正解与奇异构形分析的数值-符号解[J].
机械设计, 2005, 22 (5): 15–19.
WANG J G, FAN L H, XU L J. Positional forward solution and numeric-symbolic solution of singular configuration analysis for 3-RPS parallel platform mechanism[J]. Journal of Machine Design, 2005, 22 (5): 15–19. (in Chinese) |
| [9] | SCHADLBAUER J, WALTER D R, HUSTY M L. The 3-RPS parallel manipulator from an algebraic viewpoint[J]. Mechanism and Machine Theory, 2014, 75 : 161–176. DOI:10.1016/j.mechmachtheory.2013.12.007 |
| [10] | LI H, HESTENES D, ROCKWOOD A. Generalized homogeneous coordinates for computational geometry[M]. Berlin: Springer, 2001: 27-76. |
| [11] | LI H, HESTENES D, ROCKWOOD A. Spherical conformal geometry with geometric algebra[M]. Berlin: Springer, 2001: 61-76. |
| [12] | LEO D, DANIEL F, STEPHEN M. Geometric algebra for computer science, an object-oriented approach to geometry[M]. Burlington: Morgan Kaufmann, 2007: 15-30. |
| [13] | HESTENES D. New foundations for classical mechanics[M]. Dordrecht: Kluwer Academic Publishers, 2002: 53-96. |
| [14] |
倪振松, 廖启征, 魏世民, 等. 空间一般6R机械手位置反解的新方法[J].
北京邮电大学学报, 2009, 32 (2): 29–32.
NI Z S, LIAO Q Z, WEI S M, et al. New algorithm for inverse kinematics analysis of general 6R serial robot[J]. Journal of Beijing University of Posts and Telecommunications, 2009, 32 (2): 29–32. (in Chinese) |
| [15] | JAIME G, HPRACIO O, JOSE M R. Kinematics of 3-RPS parallel manipulators by means of screw theory[J]. International Journal Advance Manufacture Technology, 2008, 36 (5): 598–605. |



