气液两相流广泛存在于航空发动机等多种航空机械设备中,其流型状态对于设备的正常运行起着至关重要的作用[1-2]。例如,在应用于空间冷却的各项技术中,两相循环冷却技术应用了饱和工质吸热气化温度不变的特性已经被证明是最适合航天器在太空轨道运行时的热控技术之一[3]。以此设计的滑油系统是航空发动机的关键技术之一,用于润滑和冷却航空发动机各承力和传动部件,对发动机的工作可靠性起着决定性作用[4]。
自20世纪80年代后期, 美国普渡大学等校的许多学者开始研究气泡雾化喷嘴, 这种喷嘴中不同颗粒气泡形成的雾化效果, 对于飞机燃油的完全燃烧起着至关重要的作用[5]。气泡在喷嘴中相对于液体的位置不同,会使喷嘴内会呈现出不同的两相流态, 因此产生不同的雾化特性,雾化效果也不尽相同。因此,对航空飞行器各组件处的两相流态的可视化研究有着重要的意义。
电阻抗断层成像(Electrical Impedance Technology, EIT)技术[6]具有非侵入、成像实时性好以及成本低廉等优点,近年来已成为成像研究的热点,其原理是基于不同介质间电特性参数性质的差异,重建被测敏感场内电特性参数的分布以重建场域内的介质分布。该技术为航空气液两相流的可视化提供了新的思路[7]。
但是,已有的EIT算法成像空间分辨率不高,限制了其可应用的范围,目前已经提出的克服该问题的算法仍有提升空间。本文针对EIT技术中的FCM(fuzzy c-means)聚类算法的灵敏度系数信息缺失以及测量电压利用率低两方面问题提出优化算法,旨在提高算法的成像空间分辨率,从而提高其在可视化检测中的应用潜力。
1 研究背景及相关工作图像重构算法的设计与改进一直是电学成像研究中的重点。而电学成像问题的实质是被测场域的正问题和逆问题的求解过程。如图 1所示。其正问题可归结为对已知的传感器结构、激励/测量模式,设定敏感场内介质分布,施加边界条件,求解场域内电磁场的分布,最终获得场域的边界响应值与介质分布的对应关系,即灵敏度系数矩阵。逆问题为对敏感电极阵列和激励/测量策略所得的测量数据,根据正问题中求得的灵敏度系数矩阵反演场域内介质分布。图像重建即为逆问题的求解过程,是EIT技术的核心所在。首先由于EIT系统投影数据量远小于未知变量个数,造成图像重建的欠定性,其解不唯一;其次电场分布具有“软场”特性[8],电势分布受介质分布的影响,二者为非线性关系;最后,逆问题求解具有不稳定性,即边界信号的微小扰动将导致重构值的较大变化。因此,现有的灵敏度系数矩阵和边界测量电压值[9]的有效利用对重建图像的质量起到关键性的作用。

|
| 图 1 正问题/逆问题求解过程 Fig. 1 Solution procedure of forward/inverse problem |
不同于硬场的射线技术,电学层析成像的被测物场为“软场”,测量值与物场中电学特征参数之间具有高度的非线性特性,电场线的分布会随场域内介质的分布而发生改变。
对于存在“软场”效应的物场而言,在某一频率下测得的电学参数包括电容、电感、电阻等参数,是由灵敏度系数矩阵确定的。而灵敏度系数矩阵在一定程度上可以反映这种“软场”效应。
本文假设需要研究的物场为圆形场域,敷设16个电极。考虑到EIT可测量值的有限性,笔者将场域内的区域分为812个像素点,由这812个点的对应灵敏度系数构成灵敏度系数矩阵[10]。在EIT技术中,电极对j相对于电极对i的灵敏度系数可表示为
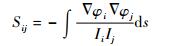
|
(1) |
式中:Sij为灵敏度系数矩阵S的元素; φi、φj分别为第i个电极对和第j个电极对分别以电流Ii、Ij激励时被测场域内的电势分布; s为面积。
1.2 EIT的FCM聚类算法FCM聚类算法是一种应用广泛的聚类算法,是图像处理中典型的图像划分算法。在文献[11-12]中,把FCM聚类算法成功应用于EIT成像中。结果表明,EIT中FCM聚类算法具有成像速度快,参数鲁棒性强等特点,可以用作实时监测。以下称该算法为FCM-EIT算法。该算法的具体说明如下:
1) 根据等势线反投影(LBP)算法[13]求得每个剖分单元16次激励后的电压均值,生成矩阵u(812×1)。
2) 根据每个剖分单元的位置信息将u矩阵转换为灰度共生矩阵G(32×32)。
3) 求得灰度共生矩阵G的方差矩阵d(812×1),则D=[u, d]作为FCM聚类算法的特征值进行聚类成像。
4) 求得隶属度矩阵U(812×2),则每个像素点的灰度值P(i)=max(U(i, :))。
但是,基于FCM-EIT算法没有充分考虑到软场效应的存在,忽略了灵敏度系数在成像过程中的影响,成像空间分辨率不高。
2 基于FCM-EIT的优化算法本节从灵敏度系数的应用和测量数据按照权系数处理2个角度优化FCM-EIT算法。
2.1 测量数据权系数计算以16电极EIT系统为例,在正问题的求解过程中可以得到208个空场边界电压数据Uk和208个满场边界电压数据Um。已有EIT算法中直接使用(Um-Uk)或(Um-Uk)/Um进行一次归一化后求解逆问题,数据的利用率低。使得成像结果分辨率不高,误差较大[14]。
为克服上述问题,本文将边界测量值按照权系数处理,计算过程是每当一对激励电极固定时,对相应测量得到的13个可应用测量值进行依次处理。即沿着边界以最小的测量值为起点,从低到高依次计算每个测量值在所有测量值之和中所占的权重。对于空场电压而言,其计算表达式为

|
(2) |
式中:Uemptyi为处理后的每个电极对的空场测量电压差;Uempi为原始空场测量电压差。相应地,对满场电压差Ufuli做相同的处理,得到处理后的每个电极对的满场测量电压差Ufulli为
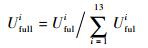
|
(3) |
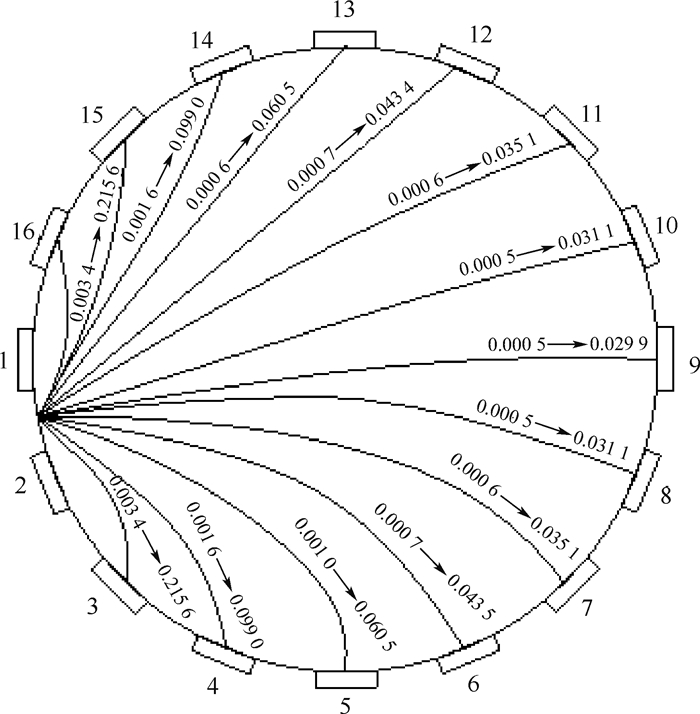
每一个原始的测量值经过式(2)和式(3)计算后作为新的测量值进行反投影,以空场测量值为例,如图 2所示,可见处理后电压差明显大于原始测量电压差(数据单位:V)。
|
| 图 2 测量数据权系数化说明 Fig. 2 Weight coefficient of measurement data |
将Uemptyi和Ufulli (i=1, 2, …, 208)依次对应,进行上述一次归一化,得到权系数处理后电压的2种不同形式:
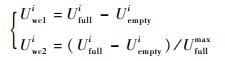
|
(4) |
式中:Ufullmax为满场电压中的最大值。
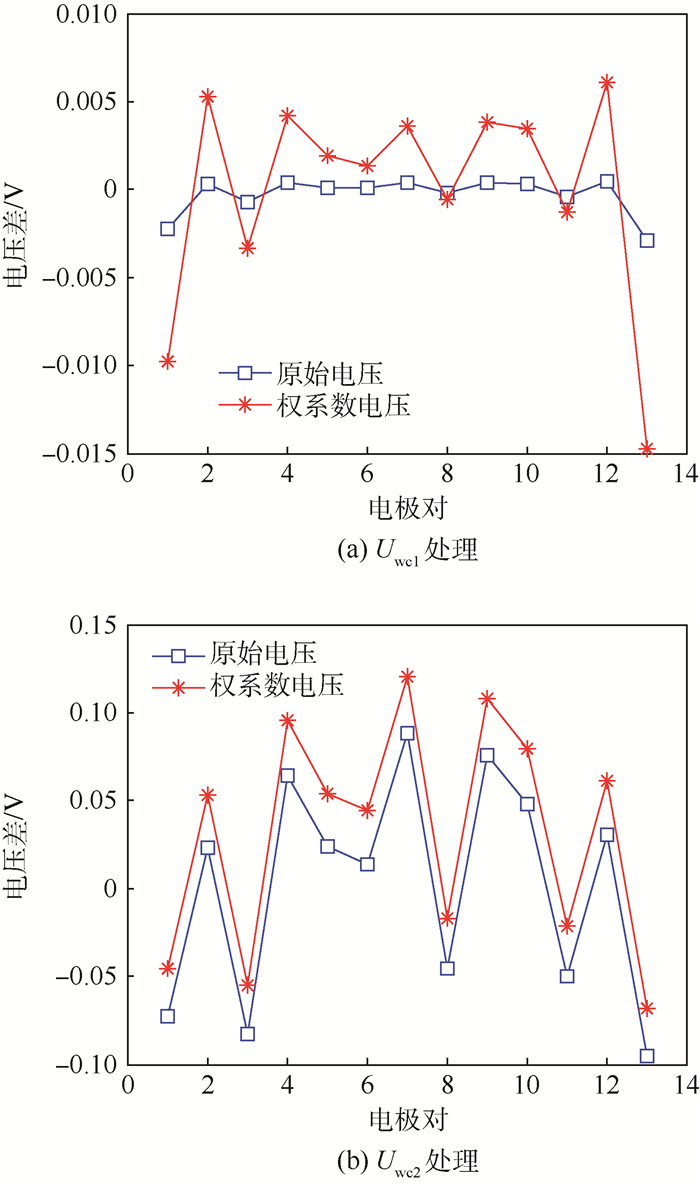
如图 3所示,图中表明在经权系数处理后2种计算方法得到的电压差整体趋势基本不变,但数值明显增大,即提高了数据的区分度,测量数据的对比效果更为明显。需要注意的是图 3(a)中原始电压差数量级在10-4左右,经比例放大10倍后对比效果更为直观。
|
| 图 3 权系数化前后的测量值 Fig. 3 Measured values before and after coefficient weighting |
假设b为边界测量电压矩阵,g为被测物场不同像素对应的待求电学特征参数分布矩阵,即灰度矩阵。
而原有的FCM-EIT算法并没有考虑灵敏度系数对于重建图像的影响。而事实上,灵敏度系数矩阵中含有剖分单元的位置信息,在目前大多数已有的电学层析算法中,灵敏度系数是重要的先验信息,对于成像的空间分辨率起重要的作用[15]。为此,本文提出了一种基于灵敏度系数的FCM-EIT的优化算法,在每次激励中,从S中选取剖分单元i的第j个灵敏度系数值Sji修正FCM-EIT算法中剖分单元i的测量值可表示为
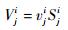
|
(5) |
式中:Vji构成V为计算后部分单元的电压,i为剖分单元序号,j为i所在的等位区号;vji构成v为剖分单元的电压。如此循环激励16次,i从第1到第812个剖分单元。
用S修正后所得的V矩阵计算的均值和方差作为输入特征值用于FCM-EIT算法的计算。
3 仿真实验和结果根据流动形态与界面尺度的关系,可将气液两相流分为几个典型的流型,即离散流(泡状流、液滴流、粒子流)、分层流(膜状流、环状流、水平分层流、喷射流)、混合流或瞬变流(气泡环状流、液滴环状流、气泡-液滴环状流、搅拌湍流、段塞流), 图 4所示为分层流和泡状流的真实分布。

|
| 图 4 流型分布 Fig. 4 Distribution of flow patterns |
采用16电极EIT系统模拟了4种不同的介质分布,在有限元软件COMSOL3.5a中采用自适应一阶三角网格用于正问题计算,采用相邻激励和相邻测量模式。
3.1.1 优化后FCM-EIT算法性能测试在FCM-EIT算法中加入电压权系数预处理方法以及灵敏度系数矩阵信息,重建图像如表 1所示。表中,第1列为模型序号,第2列为模拟的4种不同介质分布下的两相流模型,第4、第5列分别为FCM-EIT在优化前和优化后的图像结果,同时在第3列加入常用于流型识别的LBP算法进行比较,为了更好地评估改进后算法的优越性,在模型1和模型2中分别加入1%和3%的高斯白噪声。
| 模型序号 | 两相流模型 | LBP算法 | FCM-EIT算法 | 优化后FCM-EIT算法 |
| 1 |  |
 |
 |
 |
| 2 | ||||
| 3 | ||||
| 4 |
优化后算法重建时间与传统算法处于同一数量级。图像结果表明,优化后的FCM-EIT算法对气泡位置、大小检测以及对层流和环状流界面、内部分布均匀性的识别效果均高于优化前的算法,加入噪声后算法重建效果也好于传统FCM-EIT算法。
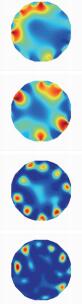
3.1.2 测量数据的权系数化对其他算法的作用为了验证测量数据预处理方法的可行性和普适性,笔者使用如下2种对泡状介质分布辨识度高的EIT经典图像重建算法进行仿真实验,如表 2所示。表中,对于泡状介质分布模型,分别应用普通Landweber[16-17]算法和Tikhonov[18-19]算法成像,以及应用笔者提出的测量数据权系数法处理后的Landweber和Tikhonov成像。其中Tikhonov使用Uwc1方式进行预处理, Landweber使用归一化方程Uwc2方式进行预处理。
| 泡状介质分布模型 | Landweber/Tikhonov算法成像 | 权系数法处理后成像 |
 |
 |
 |
实验结果表明,边界测量值权系数化处理后2种算法成像效果均好于之前的结果,目标伪影变小,用权系数化方法对电压进行预处理提高了空满场数据的变化量。以上2种算法虽然成像效果较好,但成像速度慢实时性较差。
3.2 评价参数为了更好地对优化后FCM-EIT算法对两相流流型监测的重建图像质量进行评价,选用相关系数和相对误差定量反映优化效果。
3.2.1 相关系数原始图像与重建图像的相关系数是评价重建图像质量和成像算法质量的一个重要因素[20]。
首先,计算原始图像和重建图像之间的相关系数:
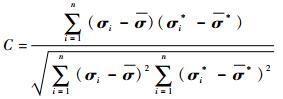
|
(6) |
式中:σ为计算的电特性参数值;σ*为模拟分布的实际电特性参数值;σi和σi*分别为σ和σ*的第i行元素;σ和σ*分别为σ和σ*的平均值;n为像素数量。
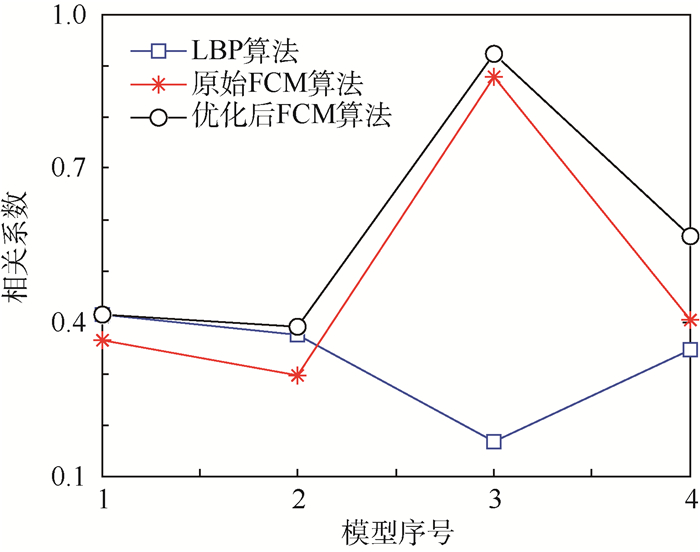
表 3列出了3种算法的相关系数。为便于比较,在图 5中给出了相应的折线示意图。
| 模型序号 | LBP算法 | 原始FCM算法 | 优化后FCM算法 |
| 1 | 0.414 1 | 0.364 7 | 0.415 4 |
| 2 | 0.373 8 | 0.295 9 | 0.390 2 |
| 3 | 0.166 9 | 0.877 7 | 0.922 2 |
| 4 | 0.345 5 | 0.405 1 | 0.568 4 |
|
| 图 5 LBP、原始图像和优化后图像的相关系数对比 Fig. 5 Comparison among correlation coefficient of LBP, original image and optimized image |
从表 3和图 5可以看出,相比于原始FCM算法,优化后的算法得到的重建图像的相关系数更大。在部分模型中相关系数也比LBP算法大。
3.2.2 相对误差评价成像算法的另一个因素是相对误差(R)。R反映原始图像与重建图像之间的误差。通过式(7)计算重建图像和原始图像之间的相对误差:
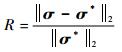
|
(7) |
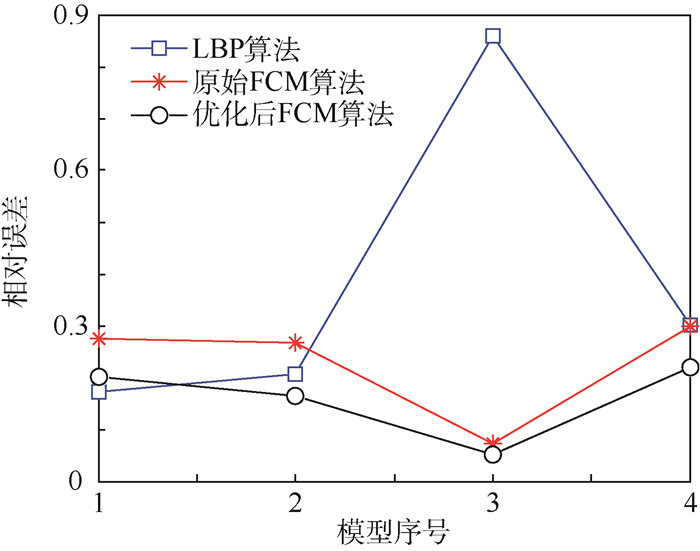
表 4给出了3种算法的相对误差。为了便于进行比较,图 6中给出了相应的折线示意图。
| 模型序号 | LBP算法 | 原始FCM算法 | 优化后FCM算法 |
| 1 | 0.173 4 | 0.276 3 | 0.201 1 |
| 2 | 0.207 7 | 0.267 8 | 0.163 9 |
| 3 | 0.859 8 | 0.072 8 | 0.050 5 |
| 4 | 0.301 2 | 0.297 8 | 0.219 5 |
|
| 图 6 LBP、原始图像、优化后图像的相对误差对比 Fig. 6 Comparison among relative errors of LBP, original image and optimized image |
从表 4和图 6中可见,相比于原始FCM算法,优化后的算法得到的重建图像比原重建图像的相对误差更小。
4 结论本文提出了一种用于EIT成像中的FCM聚类算法。该算法可以更为准确地监测到泡状流中气泡的大小及位置分布,对层状流和环状流的内部介质均匀性及界面的识别也更为准确。
1) 充分利用了灵敏度系数的信息以及对测量电压值进行更高效率的利用,提高了聚类算法的精度。图像相关系数提高了近5%~20%,相对误差降低了约5%~15%。数值仿真结果验证了优化后的算法在成像领域具有更好的性能。
2) 本文提出的边界电压权系数处理方法在其他成像算法中也进行了部分模型验证,均得到了较好的成像效果。
如何在现有的数据条件下发挥FCM聚类算法最好的性能,并将其运用到航空发动机中的两相流监测以及多样性的数据处理方法对于各种EIT成像算法的优化还有待于进一步的探索。
| [1] |
张文伟, 柯鹏. 流道弯曲度对微重力膜式水气分离性能的影响[J].
北京航空航天大学学报, 2016, 42 (8): 1639–1648.
ZHANG W W, KE P. Impact of channel curvature on microgravity membrane gas-liquid separation performance[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016, 42 (8): 1639–1648. (in Chinese) |
| [2] |
薛好, 谢永奇, 戴华, 等. 加速度场中环路热管温度波动现象分析[J].
北京航空航天大学学报, 2016, 42 (7): 1502–1508.
XUE H, XIE Y Q, DAI H, et al. Investigation of temperature fluctuation in loop heat pipe under acceleration fields[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016, 42 (7): 1502–1508. (in Chinese) |
| [3] |
杨晓军, 陶智, 丁水汀, 等. 旋转对气膜冷却覆盖区域的影响[J].
北京航空航天大学学报, 2007, 33 (12): 1383–1386.
YANG X J, TAO Z, DING S T, et al. Rotation effects on the film covering area[J]. Journal of Beijing University of Aeronautics and Astronautics, 2007, 33 (12): 1383–1386. DOI:10.3969/j.issn.1001-5965.2007.12.001 (in Chinese) |
| [4] |
陈云霞, 刘王佳. 考虑喷油润滑的附件机匣温度场分析[J].
北京航空航天大学学报, 2015, 41 (7): 1171–1176.
CHEN Y X, LIU W J. Accessory gearbox temperature field analysis considering fuel injection lubrication[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41 (7): 1171–1176. (in Chinese) |
| [5] |
梁雪萍, 郭志辉, 徐行, 等. 气泡雾化喷嘴水平喷射的雾化特性研究[J].
北京航空航天大学学报, 1998, 24 (1): 28–31.
LIANG X P, GUO Z H, XU X, et al. Influence of gas injector geometry on atomization performance of horizontally injecting effervescent atomizers[J]. Journal of Beijing University of Aeronautics and Astronautics, 1998, 24 (1): 28–31. (in Chinese) |
| [6] |
苌飞霸, 张和华, 颜乐先. 电阻抗断层成像技术研究[J].
中国医疗器械杂志, 2016, 40 (1): 52–54.
CHANG F B, ZHANG H H, YAN L X. Research on electrical impedance tomography[J]. Chinese Journal of Medical Instrumentation, 2016, 40 (1): 52–54. (in Chinese) |
| [7] |
董峰, 徐立军, 刘小平, 等. 用电阻层析成像技术实现两相流流型识别[J].
仪器仪表学报, 2010, 22 (3): 416–417.
DONG F, XU L J, LIU X P, et al. Identification of two phase flow regimes using electrical resistance tomography[J]. Chinese Journal of Science Instrument, 2010, 22 (3): 416–417. (in Chinese) |
| [8] | CAO Z, XU L J.Direct image reconstruction for ERT by using measurements on partial boundary[C]//2013 IEEE International Conference on Imaging Systems and Techniques.Piscataway, NJ:IEEE Press, 2013:377-380. http://ieeexplore.ieee.org/document/6729725/ |
| [9] | KIM B S, KIM S, KIM K Y. Image reconstruction with prior information in electrical resistance tomography[J]. Journal of the Korean Mathematical Society, 2014, 18 (1): 8–18. |
| [10] |
唐磊. 电阻抗断层成像算法研究及系统软件设计[D]. 天津: 天津大学, 2006.
TANG L.Research on image reconstruction algorithms and design of software for electrical impedance tomography system[D].Tianjin:Tianjin University, 2006(in Chinese). http://cdmd.cnki.com.cn/article/cdmd-10056-2007043071.htm |
| [11] | YUE S H, WANG J S, CHEN X, et al. Clustering mechanism for electric tomography imaging[J]. Science China Information Sciences, 2012, 55 (12): 2849–2864. DOI:10.1007/s11432-012-4748-7 |
| [12] | YUE S H, WANG J S, CHEN X, et al. An unsupervised grid-based approach for clustering analysis[J]. Science China Information Sciences, 2010, 53 (7): 1345–1357. DOI:10.1007/s11432-010-3112-z |
| [13] | WANG Q, WANG H X, ZHANG R H, et al. Image reconstruction based on L1 regularization and projection methods for electrical impedance tomography[J]. Review of Scientific Instruments, 2012, 83 (10): 104707. DOI:10.1063/1.4760253 |
| [14] |
范文茹. 生物电阻抗成像技术研究[D]. 天津: 天津大学, 2010.
FAN W R.Research on biological electrical impedance tomography[D].Tianjin:Tianjin University, 2010(in Chinese). http://cdmd.cnki.com.cn/article/cdmd-10056-1011278260.htm |
| [15] |
王化祥, 朱学明, 张立峰. 用于电容层析成像技术的共轭梯度算法[J].
天津大学学报(自然科学与工程技术版), 2005, 38 (1): 1–4.
WANG H X, ZHU X M, ZHANG L F. Conjugate gradient algorithm for electrical capacitance tomography[J]. Journal of Tianjin University(Science and Technology), 2005, 38 (1): 1–4. (in Chinese) |
| [16] |
肖理庆, 王化祥, 厉丹. 改进Landweber预迭代ERT图像重建算法[J].
中国电机工程学报, 2013, 33 (23): 118–125.
XIAO L Q, WANG H X, LI D. Improved Landweber pre-iteration algorithm for ERT image reconstruction[J]. Proceedings of the CSEE, 2013, 33 (23): 118–125. (in Chinese) |
| [17] | SONG X Z, XU Y B, DONG F. A spatially adaptive total variation regularization method for electrical resistance tomography[J]. Measurement Science & Technology, 2015, 26 (12): 125–401. |
| [18] | WANG C L, YUE S H.New selection methods of regularization parameter for electrical resistance tomography image reconstruction[C]//Proceedings of 2016 IEEE International Instrumentation and Measurement Technology Conference.Piscataway, NJ:IEEE Press, 2016:1-5. http://ieeexplore.ieee.org/abstract/document/7520352/ |
| [19] | CAO Z, WANG H X. Electromagnetic model and image reconstruction algorithms based on EIT system[J]. Transactions of Tianjin University, 2006, 12 (6): 420–424. |
| [20] | WANG B L, TAN W H, HUANG Z Y, et al. Image reconstruction algorithm for capacitively coupled electrical resistance tomography[J]. Flow Measurement & Instrumentation, 2014, 40 : 216–222. |



