医学影像成像方法是借助某种介质与人体组织之间的相互作用,通过成像的方法将人体组织、器官的密度、结构和状况以图像方式表现出来的技术。医生可通过经验结合影像成像结果对病人状况进行分析诊断,因此X射线断层成像(X-Ray Computed Tomography,X-CT)、磁共振成像(Magnetic Resonance Imaging,MRI)、正电子发射断层成像(Positron Emission Tomography,PET)、B型超声扫描(B-scan ultrasonography)、彩色多普勒血流显像(Color Doppler Flow Imaging,CDFI)等影像方法的出现使对疾病的诊断水平得到了很大提升。
磁感应层析成像(Magnetic Induction Tomography,MIT)是一种典型的非接触式检测技术,在工业检测和生物医学检测领域有广泛的潜在应用价值[1]。MIT应用在生物医学领域的研究始于20世纪60年代,Tarjan和McFee建立了非电极磁耦合阻抗测试系统,用于检测人体躯干和头部的电导率[2]。MIT基本原理是电磁感应原理,由分布在截面边界处的激励线圈在被测对象区域产生主磁场,由于被测对象的导电性和导磁性,被测对象内部产生涡流,涡流产生次级磁场,由分布在截面边界处的检测线圈获取磁场的变化,进而分离出被测区域的电导率σ和磁导率μ[3]。
2000年,Korjenevsky等设计了一个16通道MIT系统,测量对象具有与生物组织相同的电学特性,证明了MIT在生物医学应用中的适用性[4]。MIT临床应用优势包括:采用无接触的电磁场,而不是用射线和核素,对生物组织几乎没有电离和辐射效果护;穿透性较强,比较适合用于颅脑成像[5-6];系统结构简单,测量便捷,可以实现对患者长期的医学图像监护。从MIT开始出现以来,出现了各种模式的MIT系统:8线圈系统[7]、多激励模式系统[8]、平面系统[9]、无磁屏蔽系统[10]、圆环形系统[11]等。典型的MIT系统结构可以分为4部分:①传感器线圈阵列(包括激励线圈和检测线圈),在被测区域构建磁场,并提取有效测试信息;②激励信号产生模块,产生激励信号驱动传感器线圈产生磁场;③检测和调理模块,对检测到的信号进行放大、滤波、解调等处理;④图像重建与信息提取模块,通过检测到的边界感应电压值,利用图像重建算法对被测物场进行成像,进而获得被测物场的特征信息。
针对具有低电导率的生物组织介质的测试要求,Watson等设计出16通道MIT系统,实现电导率在10 S·m-1以下的介质分布成像[12];Wei和Soleimani采用模块化测试仪器搭建了一套能够实现电磁信号驱动、数据采集任务的MIT系统[13]。针对MIT系统采集的数据,Vauhkonen等采用基于时间谐波麦克斯韦方程式的图像重建算法,有较好的图像重建效果[14]。Smith等通过实验发现当生物组织发生病变时其电导率也会发生变化[15]。已有研究工作表明,采用MIT系统通过对生物组织电导率分布的图像重建,可以实现生物组织是否病变的判断。但已有的MIT系统多采用单一激励频率,需要生物组织未病变时的电导率分布信息。而在实际情况下,生物组织未病变的电导率分布信息很难得到,因此受到应用前提的限制。
由于生物组织电导率具有随频率变化的特点,MIT系统可采用不同的激励频率获取多种生物组织分布信息,进而实现图像重建,可有效突破传统的需获取病前先验信息的限制[16]。
为实现生物组织的多频磁感应层析成像,本文设计了一种基于CPCI(Compact Peripheral Component Interconnect)工业总线标准的多激励频率模式MIT测试系统,可以实现频率在100 kHz~4 MHz范围内可选的单频、扫频和混频3种激励频率的工作模式。通过对系统的性能进行测试,采用不同的激励频率可以准确提取被测物场介质电导率分布的信息。
1 系统设计 1.1 系统结构多激励频率模式MIT系统硬件部分由3部分构成:信号激励模块、检测模块、数据采集和预处理模块。系统可以在不同激励信号频率下工作,工作频率范围100 kHz~4 MHz,系统架构如图 1所示。
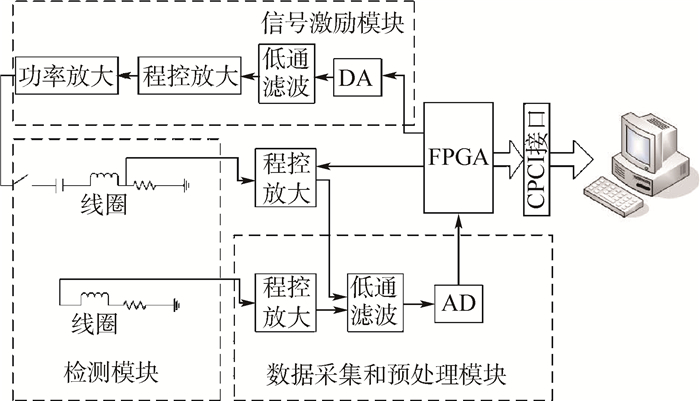
|
| 图 1 多激励频率模式MIT系统架构 Fig. 1 Architecture of multi-excitation frequency mode MIT system |
信号激励模块产生稳定的幅值、相位和频率可调的单频、扫频或者混频信号;激励信号进入传感器线圈,驱动激励线圈产生主磁场;检测线圈对物场边缘感应电压进行获取;通过多路复用器选择不同通道依次采集电压信号;获得的信号通过数据采集和预处理模块进行放大、滤波等预处理;处理后的信号通过AD芯片转换为数字信号;进入现场可编程门阵列(Field-Programmable Gate Array,FPGA)进行解调,解调后的数据通过CPCI总线接口传给主控计算机进行图像重建。
1.2 信号激励模块在MIT测试系统正常工作时,需要产生3种激励频率模式的激励信号:单频、扫频和混频模式的电压激励信号,信号激励模块流程图见图 2。

|
| 图 2 信号激励模块流程图 Fig. 2 Signal flow chart of excitation module |
FPGA通过已经存储在ROM表中的数据产生离散的正弦信号。在MIT系统激励源数字转换成模拟信号电路部分,采用一个14位精度的高速DAC芯片将正弦数字信号转换成模拟信号,芯片转换速率为125 MSPS。当fclk=50 MHz且fout < 5 MHz时,无杂散动态范围可以达到83 dBc,其中fclk为时钟频率,fout为输出信号频率。
初始的正弦激励信号通过二阶有源低通滤波模块滤除激励信号的高频杂波,并使用程控放大器放大激励信号幅值。因为线圈需要较大的功率驱动,调整后的信号需进入功率放大模块。功率放大模块选用高速低噪声电压反馈放大器,该放大器可以提供的最大激励电压值为±15 V,最大持续驱动电流为100 mA,有较低的无杂散动态范围和总谐波失真,可有效提高驱动激励线圈功率,增强信号的带载能力。信号通过功率放大模块后进入线圈产生磁场。
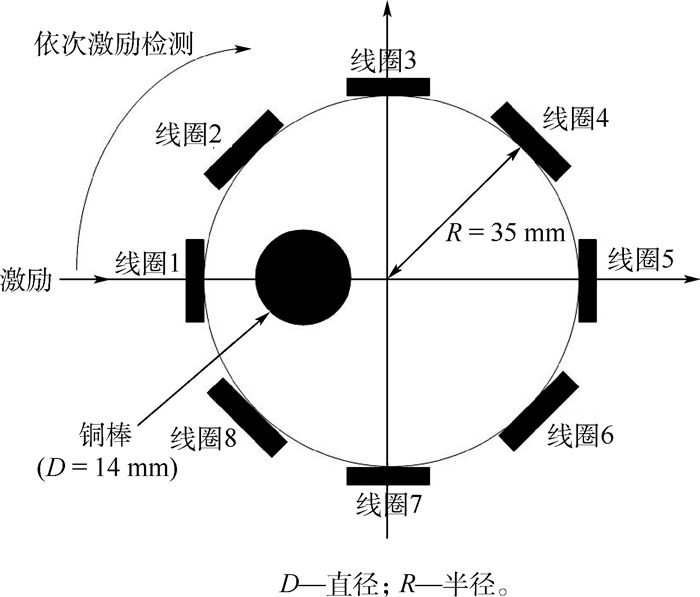
1.3 电磁线圈传感器传感器是检测的重要部分,直接影响测量的精度。磁感应层析成像系统有不同种类的传感器:空气线圈传感器、球形传感器、环形传感器等。由于铜线圈产生的磁场较强,选用铜线圈作为传感器材质。传感器线圈为8线圈环形结构,均匀地对称分布在被测物场的周围,传感器线圈的几何结构如图 3所示。

|
| 图 3 传感器线圈几何尺寸 Fig. 3 Geometric dimension of sensor coils |
传感器阵列采用单线圈激励模式,其工作原理明确、实现方法简单、技术相对成熟,已被很多MIT系统设计工作接受和采用。为保证各线圈的一致性,在线圈绕制的过程中,采用阻抗分析仪对线圈的阻抗进行测试,确保线圈绕制的精度。线圈的匝数选择与一定频率下的电感和输入阻抗有关,本设计中的传感器采用100匝线圈,在1 MHz频率下的线圈阻抗为400 Ω。
1.4 数据采集和预处理模块FPGA通过控制多路复用器不同通道的通断来获取不同线圈的检测值,提取有效磁场信号。由于提取到的有效信号幅值较小,首先要通过程控放大模块进行放大,再经过二阶有源滤波模块滤除信号杂波,得到较纯净的检测信号。在模拟信号转换为数字信号电路部分,采用一个12位精度的ADC芯片将检测到的模拟信号转换为数字信号,芯片的转换速率为40 MSPS,芯片采用多级微分线性结构并且有输出误差矫正逻辑设计保证数字信号的准确性,其信号噪声失调比为68.3 dB,无杂散动态范围是81 dBc。转换后的数字信号进入FPGA中进行数字解调。数据采集和预处理模块流程图如图 4所示。

|
| 图 4 数据采集和预处理模块流程图 Fig. 4 Signal flow chart of detection and conditioning module |
系统在FPGA中采用正交解调方法提取被测电磁信号的幅值信息和相位信息。正交解调方法有较强的谐波抑制能力,无直流漂移,且可以提高信号的信噪比。正交解调的基本原理如下:
设f1为输入信号的频率,fs为采样信号的频率,则两者之间的关系为:fs=Nf1,其中N≥2。对信号采样q个周期,则采样点的总个数为M=qN。
输入信号V1(k)、正弦参考序列V2(k)、余弦参考序列V3(k)的表达式分别为
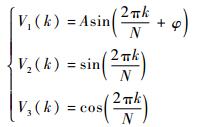
|
(1) |
式中:φ为采样开始时刻信号的相位。
则V1(k)与V2(k)的互相关系数R1, V1(k)与V3(k)的互相关系数R2分别为
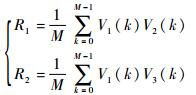
|
(2) |
由式(2)可得被测信号幅值A为
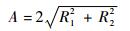
|
(3) |
由式(2)可知,耗时环节主要在乘法和累加过程,系统选用的FPGA有156个18位(18位的乘法器,保证了正交解调的速度。
2 系统实验测试 2.1 实验模型搭建为了验证所设计的MIT系统对被测物场介质分布信息获取的有效性,以及利用所获得测试数据进行图像重建的可行性。建立以空气为背景场、用铜棒模拟局部电导率分布变化的简化模拟实验模型,对MIT系统的性能进行测试,实验系统如图 5所示,传感器线圈的结构和检测模型如图 6所示。

|
| 图 5 多激励频率模式MIT系统 Fig. 5 Multi-excitation frequency mode MIT system |
|
| 图 6 传感器线圈的结构和检测模型 Fig. 6 Sensor coils' structure and detection model |
系统选择扫频激励频率模式,信号分别采用幅值为5 V的1 MHz和4 MHz正弦信号,每完成一帧数据的测量,改变一次激励频率。同时实验采用循环激励、循环测量的方式,选择其中1个传感器线圈为激励线圈,其他7个线圈依次为检测线圈,单截面数据的获取需要完成56次测量,每次测量采集40个周期的信号,AD采集速率均采用40 MSPS,在1 MHz和4 MHz的工作频率下,每周期分别采集40个点和10个点进行数字解调,得到对应的电压值,56个电压值为一帧数据。
2.2 系统信噪比采集n帧测量数据计算系统信噪比
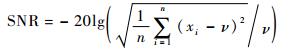
|
(4) |
式中:ν为检测数据的平均值,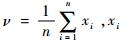
在1 MHz和4 MHz频率下,分别采集100帧背景场下的数据,即n=100,通过式(4)计算56个检测通道的信噪比,用所有信噪比的平均值来表示系统的信噪比,系统在1 MHz和4 MHz频率下的信噪比分别为48 dB和46 dB。
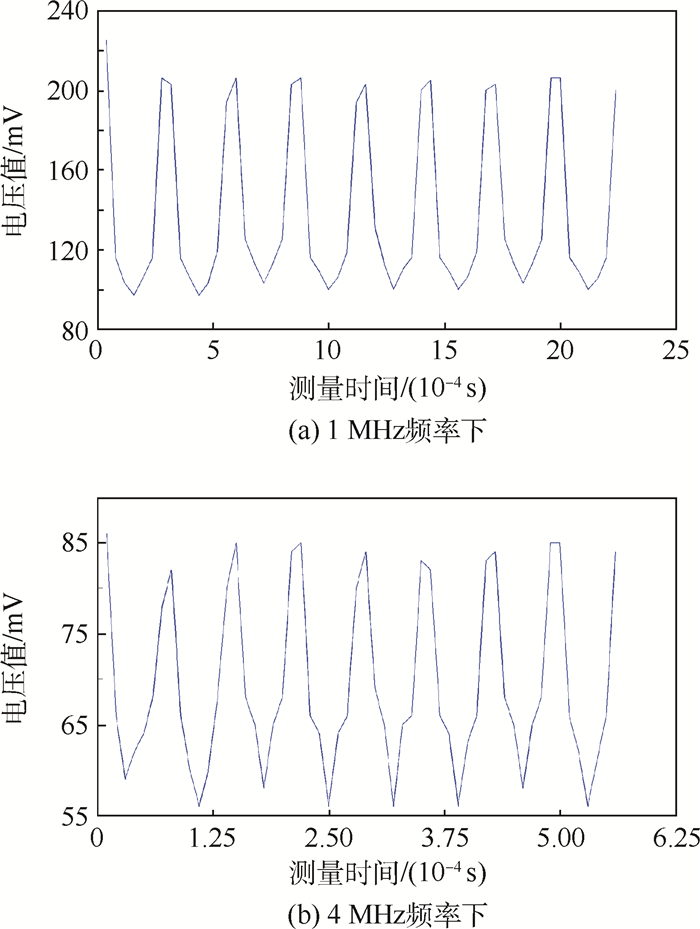
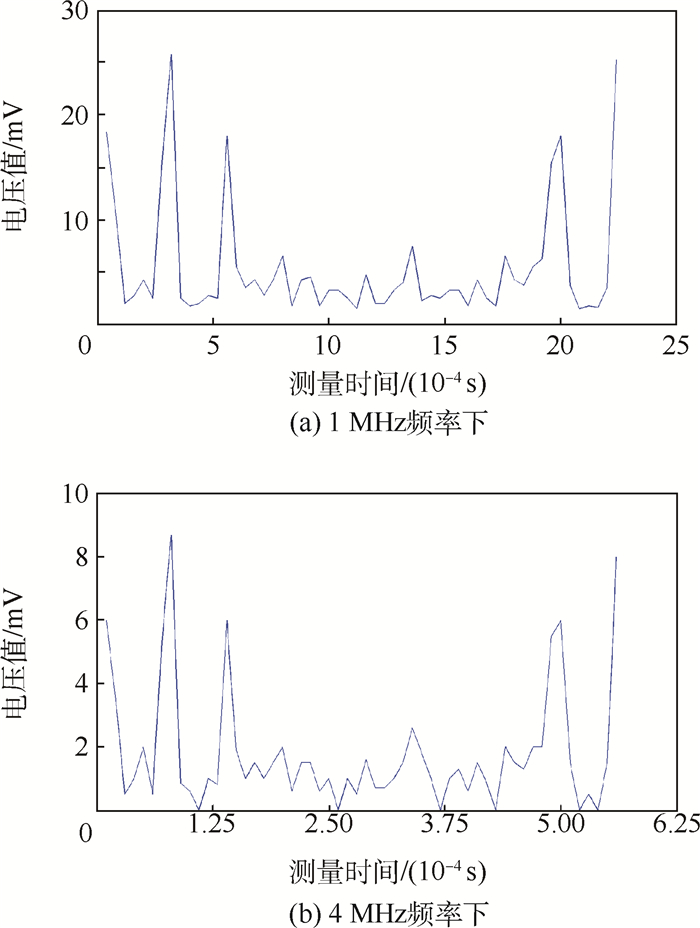
2.3 实验结果在1 MHz和4 MHz工作频率下,检测线圈在背景场条件下采集到的电压值分别如图 7(a)、图 7(b)所示。在局部电导率分布改变(有介质分布)条件下,采集到的电压值减去背景场时测得的电压值,为介质分布的有效信号,分别如图 8(a)、图 8(b)所示。该信号可用于对被测介质分布进行图像重建。
|
| 图 7 1 MHz和4MHz频率下的空场电压值 Fig. 7 Empty field voltage values at frequency of 1 MHz and 4 MHz |
|
| 图 8 1 MHz和4 MHz频率下的有效信号 Fig. 8 Effective signal at frequency of 1 MHz and 4 MHz |
从图 7可以看出,系统在1 MHz和4 MHz激励频率下的测量电压值曲线均为U型曲线。在1 MHz频率下的U型曲线较为理想,而在4 MHz频率下的U型曲线幅值降低,曲线最低点相对降低。是由于在4 MHz频率下线圈感抗增大,系统采用电压激励与测量的模式,驱动线圈产生的磁场强度减小造成的。
图 8中检测的峰值是由于被测对象在激励线圈附近时,靠近被测对象的检测线圈检测到的电压值形成的。从测量结果可以看出,系统可以较为准确地检测到有效信号,且靠近被测对象线圈的灵敏度较高。
图像重建选用Tikhonov正则化算法,通过检测到的电压值的变化ΔV计算出被测介质电导率分布,公式为[15]
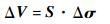
|
(5) |
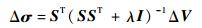
|
(6) |
式中:Δσ为电导率变化;S为灵敏度矩阵;I为单位正则化矩阵;λ为标量正则化参数。
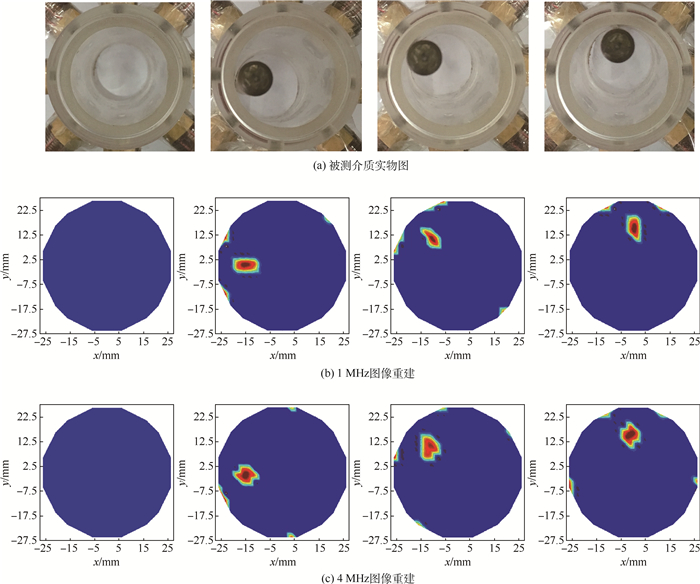
实验中,将f1=1 MHz和f2=4 MHz采集的数据代入式(5),进行图像重建。图像重建结果如图 9所示。
|
| 图 9 图像重建结果 Fig. 9 Image reconstruction results |
图 9(a)为被测介质实物图;图 9(b)和图 9(c)分别为激励频率在1 MHz条件下和4 MHz条件下的图像重建结果,其中第1列为背景场(无分布介质)条件下的图像重建结果,其余为物场(有分布介质)条件下的图像重建结果,被测介质分别放在被测区域的不同位置。
图像重建结果代表了被测物场电导率分布。图 9中图像重建结果被测介质的位置和大小与模拟实验中的被测实物基本一致,而且图像有较为清晰的边界,说明搭建的MIT系统能够较为准确地提取被测物场的电导率变化信息,可以实现图像重建功能。
3 结论1) 设计了一种多激励频率模式MIT系统,采用FPGA实现激励信号产生,控制多路开关选通,以及信号解调等功能。系统可以在3种激励频率模式下进行工作:单频、扫频和混频,在3种激励频率模式下系统都能够较为准确地提取被测物体的电导率信息。
2) 基于CPCI工业总线标准的集成化设计保证了系统的精度和稳定性,信噪比可保持在46 dB以上。
3) 系统的工作频率在100 kHz~4 MHz范围内可选,满足生物组织图像重建需求,通过两相介质分布的模拟实验,对于在被测区域内不同位置的介质,系统能够准确提取被测场域内介质电导率的分布信息,进而为在多频率磁场下生物组织成像提供测试信息,实现图像重建功能。
| [1] | GRIFFITHS H. Magnetic induction tomography[J]. Measurement Science & Technology, 2001, 12 (8): 1126–1131. |
| [2] | TARJAN P P, MCFEE R. Electrodeless measurements of the effective resistivity of the human torso and head by magnetic induction[J]. IEEE Transactions on Bio-medical Engineering, 1968, 15 (4): 266–278. |
| [3] |
徐征, 何为, 何传红, 等. 生物组织电导率磁感应测量原理及系统研究[J].
仪器仪表学报, 2008, 29 (9): 1878–1882.
XU Z, HE W, HE C H, et al. Study on the principles and system of measurement biological tissue conductivity with magnetic induction method[J]. Chinese Journal of Scientific Instrument, 2008, 29 (9): 1878–1882. (in Chinese) |
| [4] | KORJENEVSKY A, CHEREPENIN V, SAPETSKY S. Magnetic induction tomography:Experimental realization[J]. Physiological Measurement, 2000, 21 (1): 89–94. DOI:10.1088/0967-3334/21/1/311 |
| [5] |
王聪, 秦明新, 董秀珍, 等. 磁感应方式电导率测量基础研究[J].
中国医学物理学杂志, 2004, 21 (3): 182–185.
WANG C, QIN M X, DONG X Z, et al. The basic research of the measurement of conductivity in a magnetic induction way[J]. Chinese Journal of Medical Physics, 2004, 21 (3): 182–185. (in Chinese) |
| [6] | NETZ J, FORNER E, HAAGEMANN S. Contactless impedance measurement by magnetic induction-A possible method for investigation of brain impedance[J]. Physiological Measurement, 1993, 14 (4): 463–471. DOI:10.1088/0967-3334/14/4/007 |
| [7] |
刘浩仟. 电磁层析成像系统的软硬件设计[D]. 沈阳: 辽宁大学, 2015.
LIU H Q.Hardware and software design of electromagnetic tomography system[D].Shenyang:Liaoning University, 2015(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10140-1015417823.htm |
| [8] |
刘泽, 何敏, 徐苓安, 等. 多激励模式的电磁层析成像系统[J].
仪器仪表学报, 2001, 22 (6): 614–617.
LIU Z, HE M, XU L A, et al. Multi-mode excitation electromagnetic tomography system[J]. Chinese Journal of Scientific Instrument, 2001, 22 (6): 614–617. (in Chinese) |
| [9] | ROSELL-FERRER J, MERWA R, BRUNNER P, et al. A multifrequency magnetic induction tomography system using planar gradiometers:Data collection and calibration[J]. Physiological Measurement, 2006, 27 (5): S271–S280. DOI:10.1088/0967-3334/27/5/S23 |
| [10] | WANG C, ZHANG J Q, LI F W, et al. Design of a non-magnetic shielded and integrated electromagnetic tomography system[J]. Measurement Science and Technology, 2011, 22 (10): 1–10. |
| [11] | JIN G, SUN J, QIN M, et al. A new method for detecting cerebral hemorrhage in rabbits by magnetic inductive phase shift[J]. Biosensors and Bioelectronics, 2014, 52 : 374–378. DOI:10.1016/j.bios.2013.09.019 |
| [12] | WATSON S, WILLIAMS R J, GOUGH W, et al. A magnetic induction tomography system for samples with conductivities below 10 Sm-1[J]. Measurement Science & Technology, 2008, 19 (4): 88–91. |
| [13] | WEI H Y, SOLEIMANI M. Hardware and software design for a national instrument-based magnetic induction tomography system for prospective biomedical applications[J]. Physiological Measurement, 2012, 33 (5): 863–879. DOI:10.1088/0967-3334/33/5/863 |
| [14] | VAUHKONEN M, HAMSCH M, IGNEY C H. A measurement system and image reconstruction in magnetic induction tomography[J]. Physiological Measurement, 2008, 29 (6): S445–S454. DOI:10.1088/0967-3334/29/6/S37 |
| [15] | SMITH R W M, FREESTON I L, BROWN B H. A real-time electrical impedance tomography system for clinical use-design and preliminary results[J]. IEEE Transactions on Biomedical Engineering, 1995, 43 (2): 133–140. |
| [16] | ZOLGHARNI M, GRIFFITHS H, LEDGER P D. Frequency-difference MIT imaging of cerebral haemorrhage with a hemispherical coil array:Numerical modelling[J]. Physiological Measurement, 2010, 31 (8): S111–S125. DOI:10.1088/0967-3334/31/8/S09 |



