流速是描述流体流动现象的重要参数之一,流动现象广泛存在于工业、农业、医学、航空、国防等领域,如锅炉燃烧控制、血液流动监测及微流控芯片设计等与流场流速存在密切联系[1-4]。发展一种精确高效的流场流速测量技术尤为迫切。三维流速信息可视化是揭示各种复杂流动现象的重要手段之一。在各种可视化测量技术中,层析粒子图像测速(Tomo-PIV)技术由于具有较高的空间分辨率、非接触、瞬态、可获得三维空间三速度分量(3D-3C)的速度场等优点[5],已引起国内外学者的广泛关注。
Elsinga等[6]于2006年利用多相机在不同视角同时拍摄流场,首次将层析重建技术应用于流场流速的测量。Atkinson等[7-8]针对层析重建计算效率低的问题,对层析重建算法进行了改进及优化,提高了重建效率及精度。由于传统相机获取的图像丢失了光场的方向信息,使得Tomo-PIV技术需要同步控制器控制多台相机在多个方向上同时拍摄流场,同时每台相机的光轴需要严格相交于被测流场的某一位置,大大增加了Tomo-PIV技术的成本、复杂程度及计算量。Gao等[9]提出了一种单相机的Tomo-PIV技术,该技术将一块三棱面特效透镜置于相机镜头前,使单相机能同时获取3个不同视角的流场信息,但该方法是通过牺牲大量的CCD的面积来换取3个不同视角信息,限制了大尺寸流场的测量。不同于传统相机,光场成像能同时实现光场方向和位置信息的采集[10]。目前,国内外学者已逐步开展了光场PIV技术的研究。Auburn大学的Fahringer和Thurow[11]提出了基于传统光场相机的Tomo-PIV技术。上海交通大学的施圣贤课题组[12]也开展了基于传统光场相机的Tomo-PIV技术的研究,讨论了微透镜几何参数、像素尺寸等对层析重建质量的影响。目前,基于单光场相机的Tomo-PIV技术的应用并不成熟,主要表现在层析重建中像素对体素或体素对像素的贡献矩阵的计算上。如基于传统光场相机的Tomo-PIV技术不能利用传统Tomo-PIV技术的方法来计算贡献矩阵,目前所采用的方法是计算体素发出的每一根光线对像素的贡献,这种方法计算量巨大,往往需要12 h以上,降低了重建效率[13]。
针对基于传统光场相机的层析重建技术的问题,本文提出一种基于单聚焦光场相机的层析重建技术用于三维粒子场的重构。为了验证该方法的可行性,首先,利用几何光学建立三维粒子光场成像的数学模型,追迹示踪粒子产生的散射光线在聚焦光场相机中的成像过程,并获得光场图像;其次,建立基于单聚焦光场相机的层析重建模型,根据计算所得的光场图像,利用乘法代数重构技术(MART)重构流场中的三维粒子场信息;最后,分析了松弛因子、迭代次数对重建质量的影响。
1 聚焦光场相机的光线追迹 1.1 聚焦光场相机的结构及原理光场的概念是Gershun[14]在1939年首先提出的,用于表征光辐射在三维空间中的空间分布和方向分布。1992年,Adelson和Wang[15]设计了全光相机,采用一个中继镜头将微透镜阵列焦面上的像转接到探测器中,然而中继镜头的引入造成了严重的渐晕效应。2005年,Ng等[10]简化了全光相机的设计,在传统相机的CCD面前安装了一微透镜阵列,提出了光场相机1.0,但其空间分辨率低。针对此问题,Lumsdaine和Georgiev[16]在2008年提出了光场相机2.0(聚焦光场相机)。不同于光场相机1.0,聚焦光场相机的探测器像面关于微透镜的共轭面为主透镜后某个距离处的虚拟像面,提高了空间分辨率。
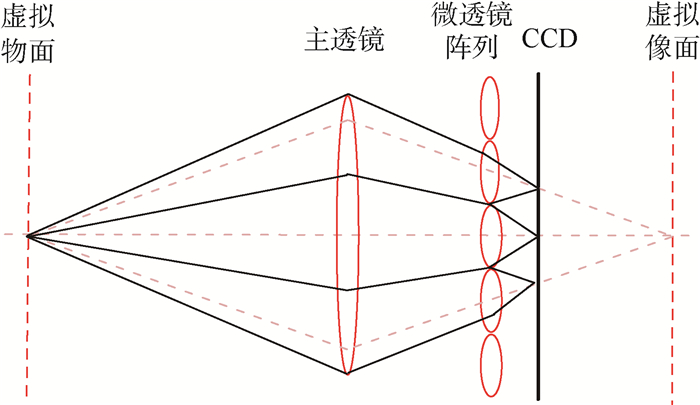
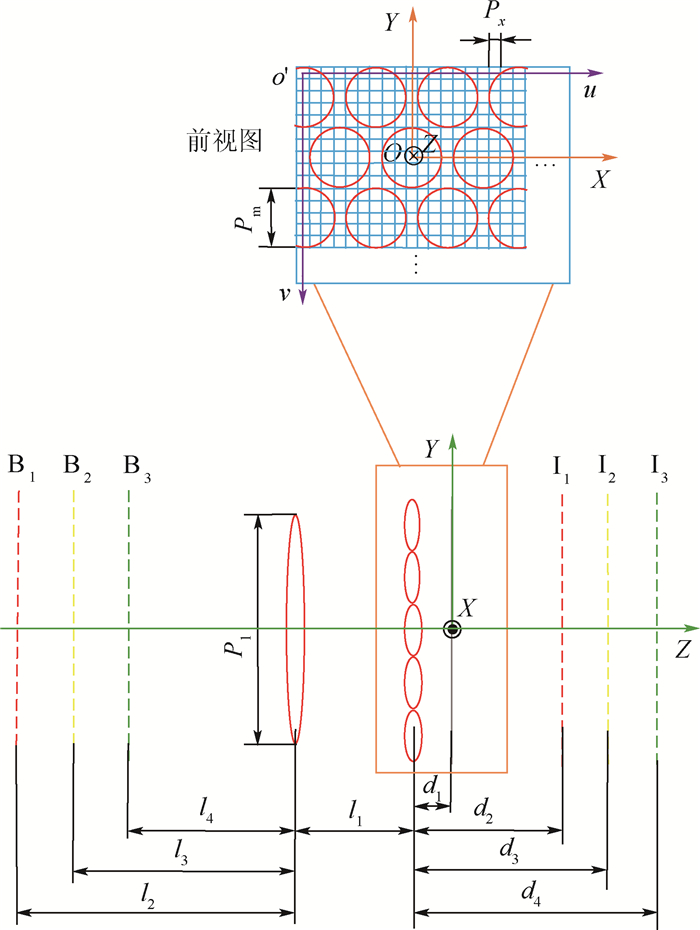
图 1为聚焦光场相机结构示意图。其结构从左向右依次为虚拟物面、主透镜、微透镜阵列、CCD及虚拟像面。虚拟像面位于CCD之后,虚拟像面关于主透镜的共轭面为虚拟物面,虚拟像面、CCD面关于微透镜共轭。由物面发出的光线经过主透镜成像在虚拟像面上,微透镜阵列将虚拟像面二次成像在CCD上。本文采用的聚焦光场相机由3种不同焦距的微透镜阵列组成,因此对应3个虚拟像面I1、I2、I3和3个虚拟物面B1、B2、B3。图 2为聚焦光场相机的坐标及参数定义,规定以下涉及的坐标都符合左手坐标系。令聚焦光场相机的CCD面的中心为世界坐标系XOY的原点O,OZ为光轴;uo′v为像素坐标,(u, v)表示第v行第u列的像素点。聚焦光场相机的主要参数见表 1。
|
| 图 1 聚焦光场相机结构示意图 Fig. 1 Schematic of structure of focused light field camera |
|
| 图 2 聚焦光场相机的坐标及参数定义 Fig. 2 Coordinate and parameter definition of focused light field camera |
| 参数 | 数值/mm |
| 主透镜焦距f | 100 |
| 主透镜与微透镜的距离l1 | 147.425 |
| 虚拟物面B1与主透镜的距离l2 | 300 |
| 虚拟物面B2与主透镜的距离l3 | 296.916 |
| 虚拟物面B3与主透镜的距离l4 | 290.164 |
| 微透镜与CCD的距离d1 | 0.592 |
| 微透镜与虚拟像面I1的距离d2 | 2.575 |
| 微透镜与虚拟像面I2的距离d3 | 3.358 1 |
| 微透镜与虚拟像面I3的距离d4 | 5.161 3 |
| 主透镜的入瞳直径Pl | 32.7 |
| 微透镜直径Pm | 0.170 5 |
| 微透镜焦距f1, f2, f3 | 0.768 7, 0.718 7, 0.668 7 |
| 像元尺寸Pp | 5.5×10-3 |
本文所用的聚焦光场相机存在以下共轭关系:
1) 3个虚拟物面、虚拟像面满足:
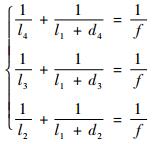
|
(1) |
2) 3个虚拟像面、CCD面满足:
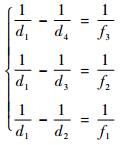
|
(2) |
不同深度位置的粒子光场成像的差异是评价基于单聚焦光场相机的三维粒子场重建的可行性的方法。因此,本文利用数值模拟计算了不同深度位置的粒子的光场成像。当利用一个双脉冲激光器照射待测流场中的示踪粒子时,示踪粒子会产生散射光并进入聚焦光场相机成像到CCD上。利用几何光学可以追迹某一场景中的光线通过均匀介质和各种光学元件路径到任意位置并成像[17]。根据几何光学,示踪粒子的尺寸远小于聚焦光场相机系统,因此在数值模拟计算过程中,单个示踪粒子可以被近似为点光源,将点光源发出的球面光代替实际粒子产生的散射光。利用几何光学可视化追迹这些光线在聚焦光场相机中传递及成像,从而获得三维粒子场的光场图像。
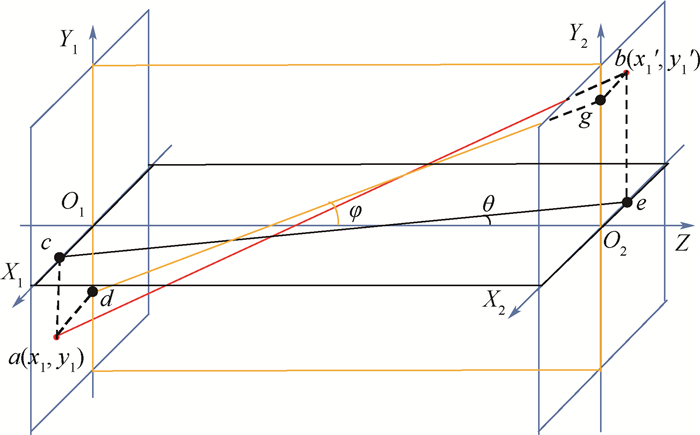
本文利用Georgeiv和Intwala[17]提出的改进的两平面参数化光线方法来表征三维空间光线,如图 3所示。在一均匀介质中,利用2个平面X1-O1-Y1、X2-O2-Y2与空间光线ab的交点a(x1, y1, θ1, φ1)、b(x′1, y′1, θ′1, φ′1)来表征空间光线。其中:x1、y1表示光线起点a与平面X1-O1-Y1的交点在坐标系X1O1Y1上的坐标;θ1、φ1表示方向坐标,定义为点a在坐标轴O1X1和O1Y1上的投影点c、d分别沿着Z轴正方向以θ、φ角度传播; 点b表示光线的起点a沿Z轴传播距离t后到达的点,点b的坐标定义与点a相同。
|
| 图 3 空间光线的表征 Fig. 3 Characterization of ray of light in space |
假设激光体光源沿X轴正方向入射到待测流场使其中的示踪粒子产生散射光,由聚焦光场相机采集散射光。根据光线通过聚焦光场相机里光学器件的顺序,散射光线追迹过程为:①光线经过自由空间传递到主透镜平面;②光线经主透镜后再经过一定的自由空间传递到微透镜平面;③光线经微透镜后传递一定自由空间,最后成像在CCD面上。相应的光线追迹模型如下[17]。
自由空间的追迹模型(包括物面光线→主透镜平面、主透镜平面→微透镜平面、微透镜平面→CCD面):
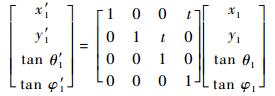
|
(3) |
式中:t和坐标(x1, y1, θ1, φ1)、(x′1, y′1, θ′1, φ′1)定义与图 3相同;当光线为近轴光线时,有θ1(θ′1)≈tan θ1(tan θ′1)。
经过主透镜的光线追迹模型:
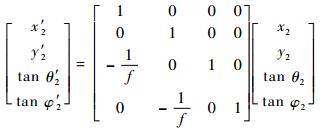
|
(4) |
式中:(x2, y2, θ2, φ2)为光线经过主透镜前的坐标;(x′2, y′2, θ′2, φ′2)为光线经过主透镜后的坐标;当光线为近轴光线时,有θ2(θ′2)≈tan θ2(tan θ′2)。
经过微透镜的光线追迹模型:
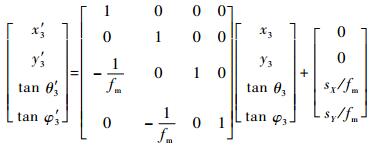
|
(5) |
式中:(x3, y3, θ3, φ3)为光线经过微透镜前的坐标;(x′3, y′3, θ′3, φ′3)为光线经过微透镜后的坐标;fm为微透镜的焦距;sX、sY为每个微透镜的中心相对于光轴Z的偏移;当光线为近轴光线时,有θ3(θ′3)≈tan θ3(tan θ′3)。
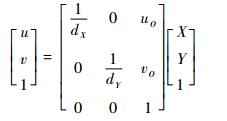
世界坐标XOY到像素坐标uo′v的转换模型:
|
(6) |
式中:dX、dY分别为每个像素点在X轴、Y轴方向上的物理尺寸;(uO, vO)为世界坐标系的原点O在像素坐标uo′v中的坐标。
1.3 单粒子及多粒子光场成像的模拟结果不考虑衍射的情况,利用式(3)~式(6)对物空间中不同位置的粒子进行追迹及成像。
图 4为单粒子在Y=0的子午面的可视化光线追迹示意图。粒子位于第3个虚拟物面B3的中心,所在世界坐标为(0, 0, -438.181) mm,根据表 1数据计算该粒子所在位置对应的虚拟像面、CCD面是关于焦距为f3=0.668 7 mm的微透镜共轭,f3=0.668 7 mm的微透镜将处于Z=-438.181mm处的粒子产生的散射光线聚焦于CCD平面上,而另2种微透镜对光线的成像处于离焦状态,像的离焦程度与微透镜阵列焦距及像素尺寸有关。从图 4可以看出,微透镜与CCD面之间的距离非常小,导致肉眼无法识别该距离。因此,将微透镜与CCD这一区域放大可以发现,由于主透镜入瞳直径大小的限制,导致某些微透镜接收的光线少,使该微透镜下的像素接收的光线较少。

|
| 图 4 单粒子的光线追迹示意图 Fig. 4 Schematic of ray tracing of a single particle |
图 5为单粒子在CCD面上成像的示意图。图 5(a)~(d)分别为位于坐标为(0, 0, -438.181) mm、(0, 0, -444.933) mm、(0, 0, -448.017) mm、(0, 0, -452.017) mm的粒子在CCD面上的成像,每个粒子发出的光线数均设为10 000。为方便识别,用绿、蓝、红圈划出光线分别在焦距为f1=0.768 7 mm、f2=0.718 7 mm、f3=0.668 7 mm的微透镜下的成像(子图像)。从图 5(a)中可以看出,不同焦距的微透镜阵列对散射光的聚集程度不同。当粒子位于虚拟物面B3的中心时,即坐标为(0, 0, -438.181) mm,产生的散射光经过焦距f3=0.668 7 mm的微透镜(红圈)时会被聚焦在一个像素点上,子图像为聚焦状态;散射光线经过焦距为f1=0.768 7 mm,f2=0.718 7 mm的微透镜时会被多个像素点接收,子图像为离焦状态。相对于图 5(a),当粒子向主透镜方向远离时(在一定距离内),子图像的数量呈现减少的趋势,如图 5(b)~(d)所示,且f3=0.668 7 mm的微透镜下的子图像从清晰成像到逐渐模糊。当粒子位于虚拟物面B2的中心时,即坐标为(0, 0, -444.933) mm,产生的散射光经过焦距为f2=0.718 7 mm的微透镜(蓝圈)时会被聚焦在一个像素点上,因此该微透镜下的子图像是清晰成像,另2种微透镜下的子图像都是模糊的,如图 5(b)所示;当粒子逐渐远离主透镜时,该微透镜下的子图像逐渐模糊,如图 5(c)、(d)所示。当粒子位于虚拟物面B1的中心时,即坐标为(0, 0, -448.017) mm,产生的散射光经过焦距为f1=0.768 7 mm的微透镜(绿圈)时会被聚焦在一个像素点上,该微透镜下的子图像是清晰成像,而另2种微透镜下的子图像都是模糊的,如图 5(c)所示;当粒子逐渐远离主透镜时,该微透镜下的子图像变模糊,如图 5(d)所示。从图 5中可以看出,相同焦距微透镜下的子图像强度不一致,这是由于主透镜入瞳直径大小的限制,使得一些微透镜接收的光线少于其他微透镜,导致这些微透镜下的像素灰度值小于其他微透镜下的像素灰度值。

|
| 图 5 单粒子成像示意图 Fig. 5 Schematic of imaging of a single particle |
考虑到粒子的尺寸及在物空间中强度分布的情况,假设物空间中粒子的光强E服从三维高斯Blob模型,此模型使颗粒的光强投影到所有方向均为衍射光斑,其表达式[18]为
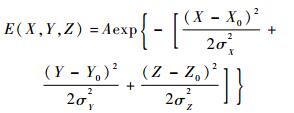
|
(7) |
式中:A为振幅;(X0, Y0, Z0)为粒子的中心坐标;σX、σY和σZ为标准差,用于表征粒子在X、Y和Z轴方向的宽度。
利用式(7)将粒子的光强映射到5×5×5的体素中,将每个体素看成一个点光源,利用几何光学追迹每一个体素发出的光线在聚焦光场相机中成像。图 6为物空间中20个随机位置的粒子在聚焦光场相机中的成像结果。可以看出,当粒子之间的距离较近时,粒子所成的像会出现叠加,空间中不同位置的粒子在聚焦光场相机中的成像不同,为单聚焦光场相机重建三维粒子场提供基础。

|
| 图 6 多粒子成像示意图 Fig. 6 Schematic of imaging of multiple particles |
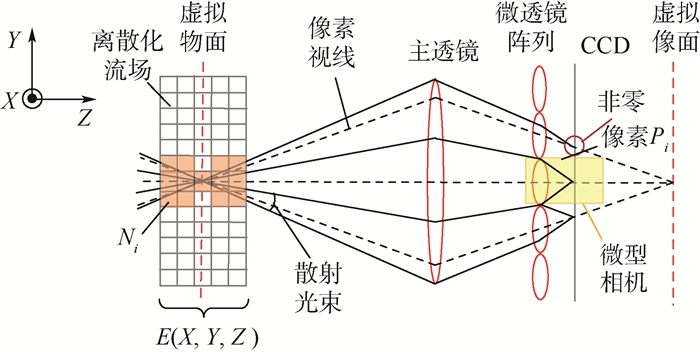
光学层析是一种降维的处理方式,是指将三维空间离散化成许多二维平面的过程,而层析重建便是光学层析的逆过程,已知多个视角的二维图像利用数学方法重建出三维体[19]。基于聚焦光场相机的层析重建原理如图 7所示,体光源沿X轴平行入射到流场中,根据Mie散射理论,粒子将产生散射光,位于Z轴上的聚焦光场相机采集到散射角约为90°的散射光。
|
| 图 7 基于聚焦光场相机的层析重建原理 Fig. 7 Theory of tomographic reconstruction based on focused light field camera |
聚焦光场相机每个微透镜记录了光场的方向信息,每个微透镜下的像素点记录了光场的位置信息[16]。对于聚焦光场相机的层析重建,聚焦光场相机可等效为多个以微透镜阵列为镜头的微型相机,每一个像素的强度是物空间中的体素发出某一角度的一束光线沿着该像素方向si的积分[8],即
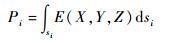
|
(8) |
式中:E(X, Y, Z)为三维空间中坐标为(X, Y, Z)的体素的强度;Pi为散射光沿着方向si投影到第i个像素的强度。
离散射化式(8)得
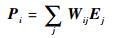
|
(9) |
式中:Wij为第j个体素沿着相应方向投影到第i个像素的贡献矩阵(权重矩阵),该值与相机的视角和体素的尺寸、形状有关,是一个非常稀疏的矩阵;Ej为第j个体素的强度。
粒子的三维强度分布的反演归结于线性方程式(9)的反演,本文利用MART算法对三维粒子场的光场图像进行反演计算,其表达式为
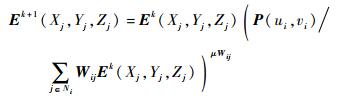
|
(10) |
式中:k为迭代次数;(Xj,Yj,Zj)为第j个体素所在的三维坐标;μ为松弛因子,取值范围为(0, 1];Ni为与像素视线相交的体素。
层析重建中,权重矩阵Wij的计算是获得三维粒子场的关键。传统光场Tomo-PIV计算权重矩阵是在正向光线追迹的过程中得到的,即设定每个体素发出许多光线,计算每根光线对微透镜阵列和像素的贡献,该方法计算时间在12 h以上且需要占用大量的计算机内存[20]。而对于聚焦光场相机的权重矩阵计算,本文利用后向投影技术来计算像素对体素的贡献。将聚焦光场相机的微透镜阵列等效成一系列针孔模型。从子图像里的非零像素中心发出一根光线(称为像素视线si),利用几何光学追迹这些光线到对应的微透镜中心,然后追迹光线经过镜头投影到重建体素上。将每个像素的视线近似为圆柱,每个体素近似为球体,则每个体素对应的像素的贡献被近似计算为体素与圆柱相交的体积与整个体素体积之比,或计算体素中心位置与光线的距离d,然后权重矩阵可以由一个高斯函数来表征:
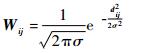
|
(11) |
式中:σ为标准差;dij为体素中心坐标与像素视线的距离。
2.2 单粒子及多粒子的层析重建结果为了验证聚焦光场相机重建三维粒子场的准确性,对单粒子的位置重建精度及多粒子重建质量进行了分析。设粒子直径为10 μm,由式(7)计算出单粒子场的理论分布,如图 8所示。从图 8(b)中可以看出,粒子由一层低能量的体素包围,导致无法观测粒子内部能量分布情况。因此,用一个Y=0的平面将粒子剖开便可观测到粒子内部能量分布情况,如图 8(a)所示,粒子能量分布非常均匀,能量最大值所在三维位置为粒子所在位置。
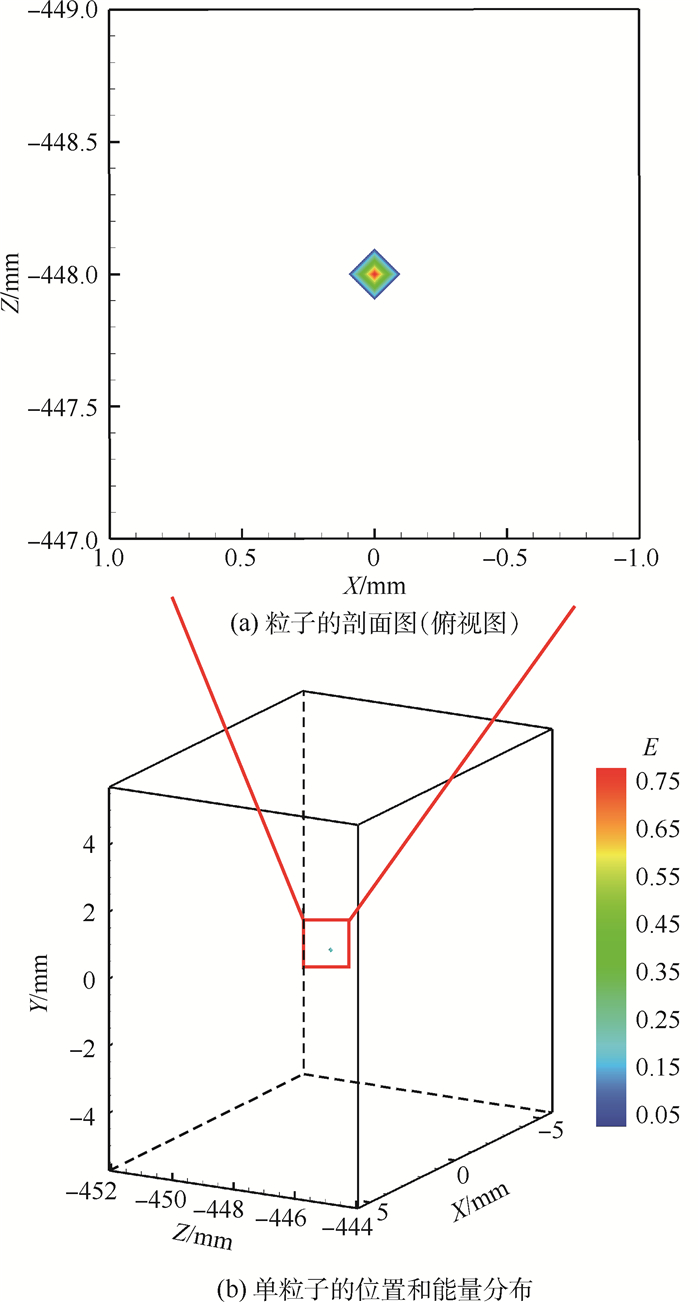
|
| 图 8 单粒子场理论分布 Fig. 8 Theoretical distribution of a single particle field |
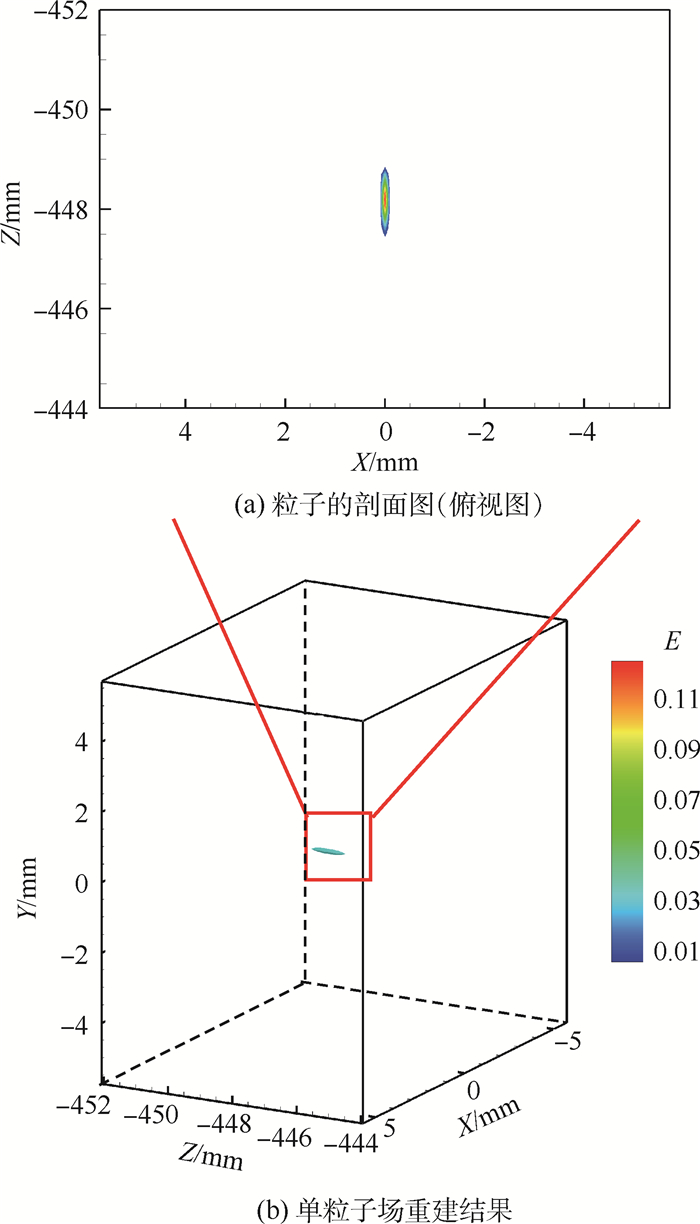
对该粒子分别进行正向光线追迹、层析重建,图 9为单粒子的层析重建结果及相应的剖面图。从图 9(a)中可以看出,粒子能量最大值位于粒子中心区域,能量大小沿粒子的径向方向逐渐减小;相比于理论分布,重建所得的能量分布出现沿Z轴方向的拉伸现象,但能量分布比较均匀,且能量最大值所在的三维位置为粒子所在位置。
|
| 图 9 单粒子重建结果 Fig. 9 Reconstruction results of a single particle |
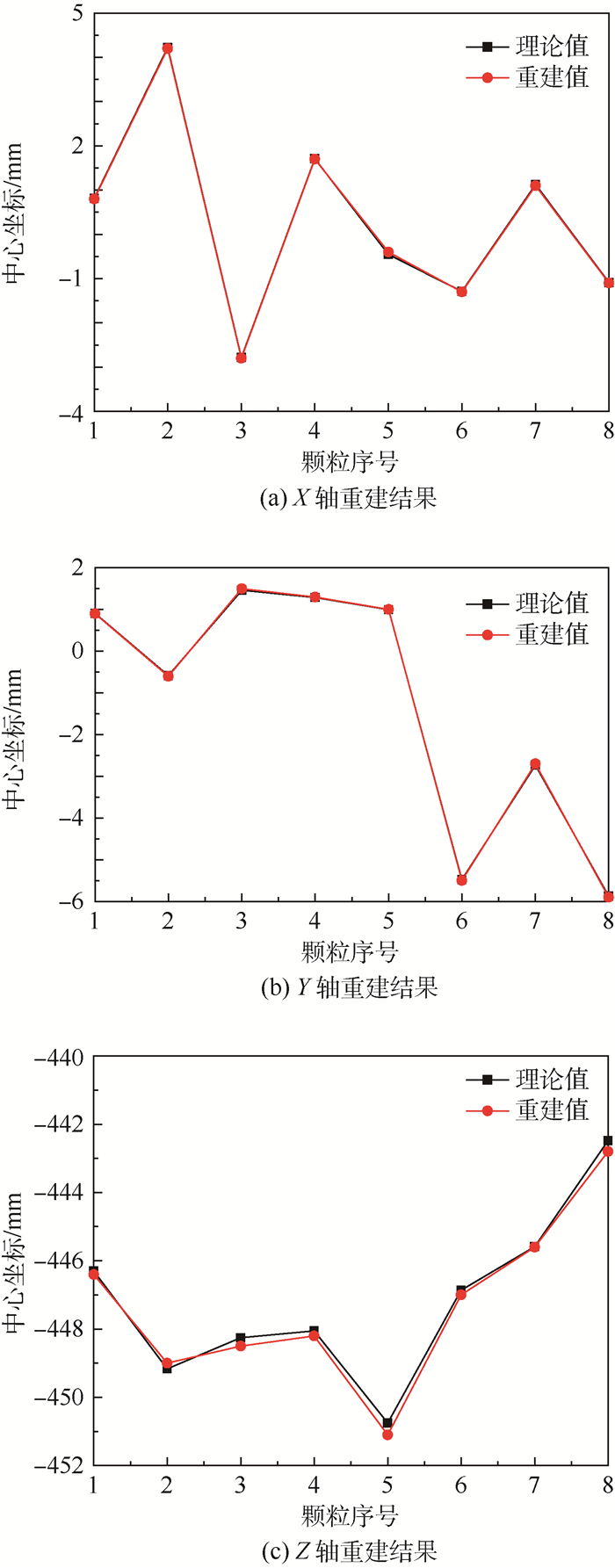
对流场中不同深度位置的单粒子重建情况进行分析和评价,在流场所在位置处随机产生8个粒子(8幅图片),依次进行光线追迹、层析重建。图 10为单粒子三维位置坐标的重建结果,通过计算重建所得粒子的三维位置坐标与理论三维位置坐标的绝对误差表明,X轴、Y轴的绝对误差在±0.05 mm以内,Z轴的绝对误差在±0.35 mm以内,在可以接受的范围内。对多粒子进行正向模拟和层析重建,为了节约计算量,对体积为10.5 mm(X轴)×10.5 mm(Y轴)×7.5 mm(Z轴)的流场进行计算,将流场划分为105×105×75个体素。在此体积范围内随机产生10个粒子,进行光线追迹和层析重建。
|
| 图 10 单粒子位置坐标重建结果 Fig. 10 Reconstruction results of position coordinate of a single particle |
为了评价重建结果的质量,本文采用Elsinga等[6]的方法来评价多粒子的重建质量,即求解重建的三维粒子强度分布和实际的三维粒子强度分布的归一化互相关系数Q,其表达式为
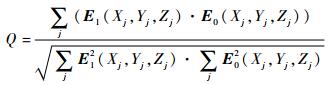
|
(12) |
式中:E1为实际的三维粒子强度分布;E0为重建所得的三维粒子强度分布。Q≤1且值越大,重建质量越好。式(12)可以很方便地对重建所得的多粒子的位置和能量分布进行整体评价。
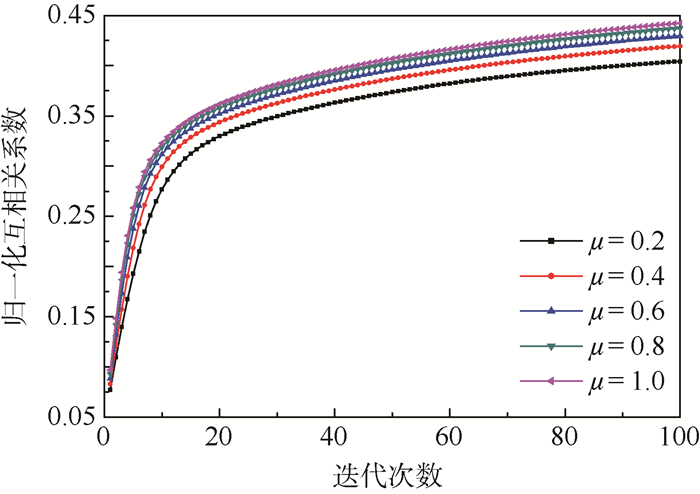
图 11为层析重建质量在不同松弛因子、迭代次数下的变化情况。可以看出,随着松弛因子的增大,MART算法重建结果的质量会逐渐增高,因此,松弛因子等于1.0时有利于MART算法的计算;随着MART算法迭代次数的增加,重建结果的质量先逐渐增高后会趋于稳定。
|
| 图 11 归一化互相关系数 Fig. 11 Normalized correlation coefficient |
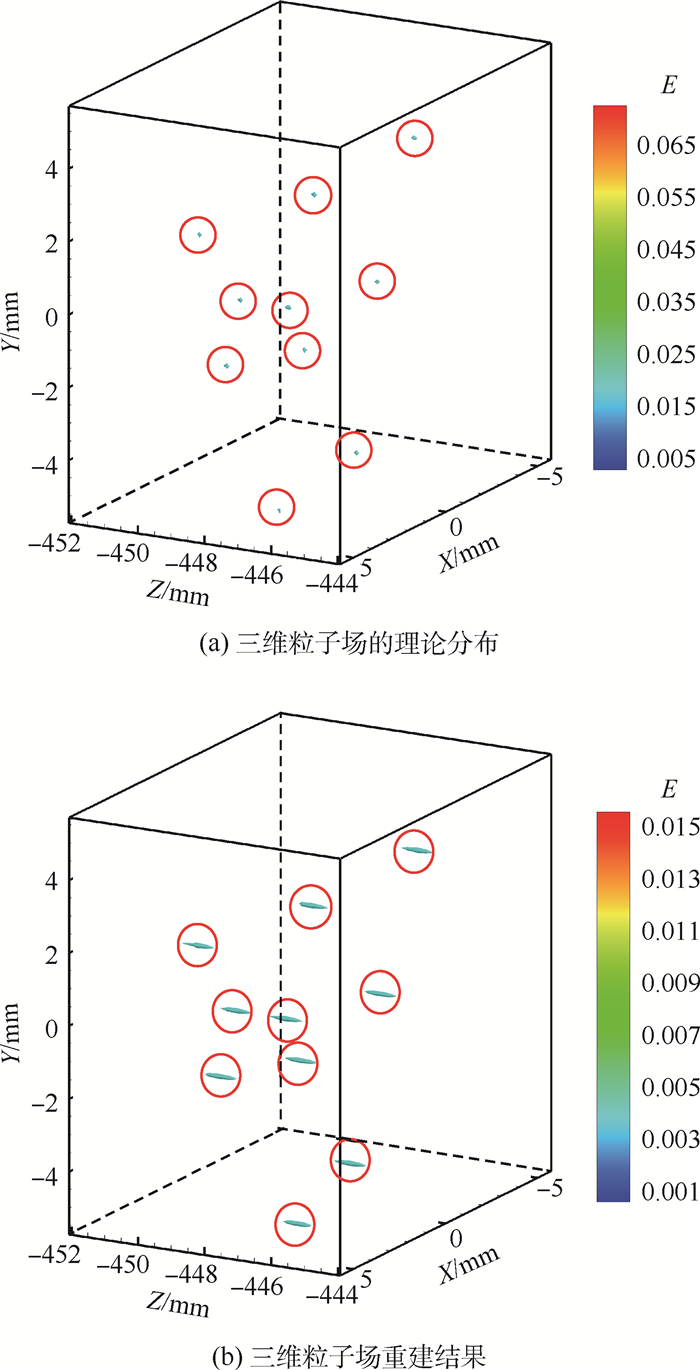
图 12(a)为三维粒子场的理论分布,图 12(b)为三维粒子场重建结果,松弛因子等于1.0,迭代次数为100次。可以看出,尽管粒子能量分布出现拉伸的情况,但每个粒子的能量分布一致,且对重建所得的粒子能量最大值所在位置的影响并不大,在可以接受的范围内,证明了聚焦光场相机能成功用于三维粒子场的重建。
|
| 图 12 多粒子重建结果 Fig. 12 Reconstruction results of multiple particles |
本文提出了一种基于单聚焦光场相机的层析重建技术。通过对粒子在聚焦光场相机中的成像计算、单粒子和多粒子的层析重建结果分析得到以下结论:
1) 通过对单粒子的光线追迹可知,不同焦距的微透镜阵列对散射光的聚焦程度不同;由于主透镜入瞳直径大小的限定,某些微透镜阵列接收的散射光线数量较少,导致这些微透镜阵列下的像素的灰度值比同类型微透镜阵列下的像素灰度值小。
2) 通过对单粒子的成像计算发现,不同深度位置的粒子在聚焦光场相机中的成像不同,当粒子向主透镜方向远离时(在一定距离内),子图像数量呈现减小的趋势;当粒子向主透镜方向靠近时,子图像数量呈现增加的趋势。
3) 对于单粒子的层析重建,重建所得粒子的X轴、Y轴位置的绝对误差在±0.05 mm以内,Z轴位置的绝对误差在±0.35 mm以内;对于多粒子的层析重建,当松弛因子等于1.0时,MART算法只需迭代若干次便能获得令人满意的重建结果。为后续的三维互相关计算及3D-3C速度矢量分布表征提供了基础,本文计算权重矩阵的速度远快于传统光场相机Tomo-PIV技术的计算速度。
| [1] | COGOTTI A. Evolution of performance of an automotive wind tunnel[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96 (6): 667–700. |
| [2] | TOKAREV M P, SHARABORIN D K, LOBASOV A S, et al. 3D velocity measurements in a premixed flame by tomographic PIV[J]. Measurement Science & Technology, 2015, 26 (6): 1–13. |
| [3] | PARK H, YEOM E, LEE S J. X-ray PIV measurement of blood flow in deep vessels of a rat:An in vivo feasibility study[J]. Scientific Reports, 2016, 6 : 1–8. DOI:10.1038/s41598-016-0001-8 |
| [4] | FILATOV N A, BELOUSOV K I, BUKATIN A S, et al. The study of mixing of reagents within a droplet in various designs of microfluidic chip[J]. Journal of Physics:Conference Series, 2016, 741 (1): 1–6. |
| [5] | GAO Q, WANG H P, SHEN G X. Review on development of volumetric particle image velocimetry[J]. Science Bulletin, 2013, 58 (36): 4541–4556. DOI:10.1007/s11434-013-6081-y |
| [6] | ELSINGA G E, SCARANO F, WIENEKE B, et al. Tomographic particle image velocimetry[J]. Experiments in Fluids, 2006, 41 (6): 933–947. DOI:10.1007/s00348-006-0212-z |
| [7] | ATKINSON C H, SORIA J.Algebraic reconstruction techniques for tomographic particle image velocimetry[C]//16th Australasian Fluid Mechanics Conference, 2007:191-198. https://www.researchgate.net/publication/43472385_Algebraic_Reconstruction_Techniques_for_Tomographic_Particle_Image_Velocimetry |
| [8] | ATKINSON C H, BUCHMANN N, STANISLAS M, et al.Adaptive MLOS-SMART improved accuracy tomographic PIV[C]//15th Sympoium on Applications of Laser Techniques to Fluid Mechanics, 2010:1-12. https://www.researchgate.net/publication/260085204_Adaptive_MLOS-SMART_improved_accuracy_tomographic_PIV |
| [9] | GAO Q, WANG H P, WANG J J. A single camera volumetric particle image velocimetry and its application[J]. Science China Technological Sciences, 2012, 55 (9): 2501–2510. DOI:10.1007/s11431-012-4921-7 |
| [10] | NG R, LEVOY M, BREDIF M, et al. Light field photography with a hand-held plenoptic camera[J]. Computer Science Technical Report, 2005, 2 (11): 1–11. |
| [11] | FAHRINGER T, THUROW B S.Tomographic reconstruction of a 3-D flow field using a plenoptic camera[C]//42nd AIAA Fluid Dynamics Conference and Exhibit.Reston:AIAA, 2012:1-13. http://arc.aiaa.org/doi/pdf/10.2514/6.2012-2826 |
| [12] | SHI S X, WANG J H, DING J F, et al. Parametric study on light field volumetric particle image velocimetry[J]. Flow Measurement and Instrumentation, 2016, 49 : 70–88. DOI:10.1016/j.flowmeasinst.2016.05.006 |
| [13] | THUROW B S, FAHRINGER T.Recent development of volumetric PIV with a plenoptic camera[C]//10th International Symposium on Particle Image Velocimetry, 2013:1-7. http://repository.tudelft.nl/view/conferencepapers/uuid:087ebcbc-b6fd-4db5-9e66-684eca0db20f |
| [14] | GERSHUN A. The light field[J]. Studies in Applied Mathematics, 1939, 18 (1-4): 51–151. |
| [15] | ADELSON E H, WANG J Y A. Single lens stereo with a plenoptic camera[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 1992, 14 (2): 99–106. |
| [16] | LUMSDAINE A, GEORGIEV T.Full resolution lightfield rendering[R].San Jose:Adobe Systems, Inc., Technical Report, 2008:1-12. http://www.researchgate.net/publication/228888002_Full_resolution_lightfield_rendering |
| [17] | GEORGIEV T, INTWALA C.Light field camera design for integral view photography[R].San Jose:Adobe System, Inc., Technical Report, 2006:1-13. https://www.researchgate.net/publication/242321329_Light_Field_Camera_Design_for_Integral_View_Photography |
| [18] | FAHRINGER T W, THUROW B S.3D particle position reconstruction accuracy in plenoptic PIV[C]//52nd Aerospace Sciences Meeting.Reston:AIAA, 2014:1-10. http://arc.aiaa.org/doi/abs/10.2514/6.2014-0398 |
| [19] | BAO Q, JIANG N. A simplified 3D reconstruction technique for tomographic particle image velocimetry[J]. Advanced Materials Research, 2013, 718 : 2184–2190. |
| [20] | LYNCH K, FAHRINGER T, THUROW B.Three-dimensional particle image velocimetry using a plenoptic camera[C]//50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition.Reston:AIAA, 2012:1-14. https://arc.aiaa.org/doi/abs/10.2514/6.2012-1056 |



