2. 天津市过程检测与控制重点实验室, 天津 300072;
3. 天津市计量监督检测科学研究院, 天津 300192
2. Tianjin Key Laboratory of Process Measurement and Control, Tianjin 300072, China;
3. Tianjin Institute of Metrological Supervision and Testing, Tianjin 300192, China
音速喷嘴因具有构造简单、性能稳定、精确度高等优点,被普遍应用于能源、化工、制药、航天等诸多领域[1]。由于喷嘴的测量对象多数含有水蒸气,而喷嘴内超音速流动会产生凝结、热阻塞以及激波现象[2],其变化规律以及对喷嘴流量计量精度的影响一直未得到很好的解释。
针对音速喷嘴凝结现象的问题,已有一些专家学者进行了探究。Aschenbrenner[3]针对该问题首先提出了不考虑凝结的混合气体湿度修正公式。在此研究基础上,多个国家研究人员各自提出了湿度修正公式,但无法形成统一标准[4-6]。Lim[7]、Chahine[8]等实验发现,湿度对流量的影响不容忽视,有可能是凝结现象造成的。Mickan和李春辉[9]曾研究音速喷嘴后方凝结对流量计量的影响,但并未涉及喷嘴内部的凝结流动。因此,凝结现象对喷嘴计量带来的影响值得加以重视并进行深入细致研究。Young[10]、Kane等[11]提出了水蒸气凝结液滴成核率模型。Wegener和Pouring[12]、蔡颐年和王乃宁[13]提出了液滴生长率模型。由于计算流体力学(CFD)的快速发展,数值仿真实验成为该领域复杂现象研究的技术手段。马庆芬[14]、Avetissian[15]、Dykas[16]、Wang[17]等分别建立了各自二维或三维CFD数值模型。凝结现象复杂多变,Wegener和Cagliostro[18]、Skilling[19]从实验中观察到存在非稳态的自激振荡现象。Adam[20]、吴晓明[21]等从实验角度研究自激振荡现象,并将其分为不同振荡模式进行分析。
以上成果为音速喷嘴凝结现象的研究提供了一定的参考和指导,但并未有较为成熟的实验和仿真数据。本文针对音速喷嘴的凝结特性展开研究,搭建一个凝结实验平台,并利用凝结流动Eulerian两相模型,通过大量实验研究,辅以数值模型的仿真实验,获得一定的凝结现象规律。
1 音速喷嘴凝结现象基本原理 1.1 音速喷嘴测量原理音速喷嘴的常用结构如图 1所示。喷嘴的背压比表示为出口压力p1与入口滞止压力p0的比值[22]。随着背压比的减小,喉部气体流速不断增大,流速最大时对应的背压比称为临界背压比bcr,此时喉部的气体速度为当地音速。
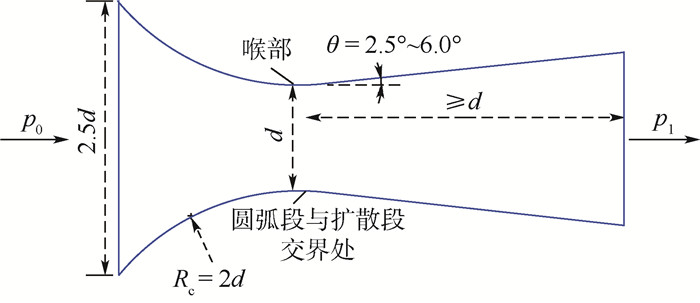
|
| 图 1 音速喷嘴结构 Fig. 1 Sonic nozzle structure |
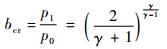
|
(1) |
式中:γ为比热容比。
此时通过喷嘴的质量流量为
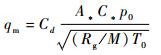
|
(2) |
式中:Cd为喷嘴流出系数;A*为喷嘴喉部截面积,m2;C*为临界流函数;Rg为通用气体常数,约为8.314 41 J/(mol·K);M为摩尔质量,kg/mol;T0为滞止温度,K。
1.2 高速气体自发凝结理论蒸汽或含湿气体在音速喷嘴内部是一个加速、降温膨胀流动的过程,当达到饱和状态后继续加速流动,气体会发生凝结现象。但当流过的是纯净的气体,且不与冷壁接触,则气体即使达到饱和状态也不会立即凝结,而是越过一个临界极限后才开始产生凝结。该临界极限称之为Wilson点,所有工况下的Wilson点连在一起称为Wilson线,如图 2所示。气体在喷嘴中降温膨胀的流动过程如图 3所示,随着喷嘴内部流动进行,温度和压力逐渐下降,在喉部之后达到饱和。此时气体并没有立即发生凝结现象,而是继续膨胀为过饱和气体,达到Wilson点时才开始突然产生凝结核,之后继续生长为液滴。
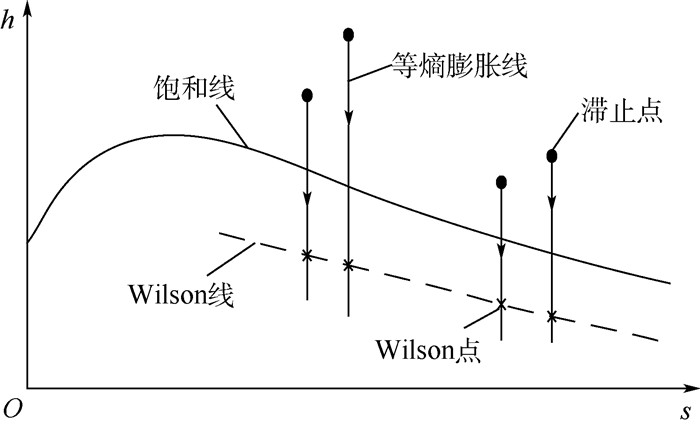
|
| 图 2 Wilson线在焓熵(h-s)图中的走势 Fig. 2 Tendency of Wilson line in an enthalpy-entropy(h-s) map |
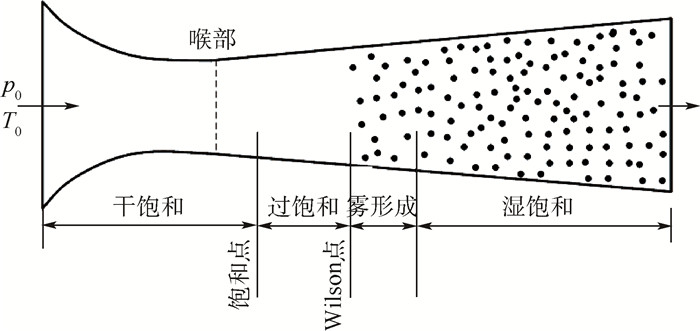
|
| 图 3 音速喷嘴中膨胀凝结过程 Fig. 3 Expansion and condensation process in sonic nozzle |
凝结过程中,由于释放了大量的潜热,对于凝结稳态流动的气体,突然间的膨胀过程导致一个压力突跃,即产生了凝结激波。气体在突跃之后继续膨胀,只要有够低的背压比,气体压力还会不断降低[23-24]。2014年,丁红兵[25]在其博士学位论文中提出了音速喷嘴在低压和高压条件下自发凝结流动的Wilson点解析表达式,只需知道喷嘴的几何尺寸、入口的温度、压力以及相对湿度,即可快速精确地计算出Wilson点位置及相应的状态。
1.3 非稳态自激振荡流动由于凝结会释放大量的潜热,加上气动激波的影响,可能会产生非稳态的自激振荡现象。凝结释放的潜热越来越大,气动激波的位置随之向前移动,甚至可能越过喉部,到达上游,从而导致凝结强度相应减弱。进而潜热释放量相应减小,激波减弱甚至消失,这样凝结发生区域的前方温度又变回低温状态,凝结再次增强,继而产生了新的激波。自激振荡按此周期循环往复进行。根据Wegener和Pouring[12]相关研究,湿空气在喷嘴中凝结自激振荡频率f与载气入口压力、温度、轴向梯度特征长度等参数有关。
2 实验平台与CFD模型 2.1 温湿度调节装置凝结实验平台如图 4所示,其核心在于温度、湿度的调节,主要组成是管道加热器、微雾发生装置和蒸发器。管道加热器设计功率为25 kW,运行压力为1.6 MPa,内嵌12根均匀分布的电加热丝,由可控硅的通断进行加热控制。
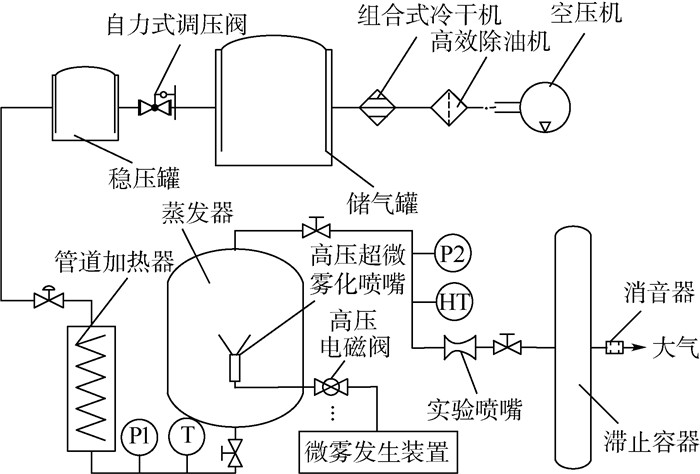
|
| 图 4 凝结实验平台结构 Fig. 4 Structure of experimental condensation apparatus |
为了达到更均匀的雾化效果,采用高压雾化的加湿方式。如图 5所示,本模块主要由变频器、液压隔膜计量泵、高压电磁阀组、单向止回阀组以及高压超微雾化喷嘴组成。利用稳定性高达0.32%的液压隔膜计量泵将水压提高到3~8 MPa,然后将加压后的水经高压管路输送至高压超微雾化喷嘴[26]将其雾化,以1~15 μm的超微雾粒喷射到蒸发器中,雾粒在空气中吸收热量,汽化、蒸发,从而改变环境的湿度。系统采用旋流式喷嘴和撞针式喷嘴组合使用的形式。旋流式喷嘴采用德国Lechler喷嘴,其喷嘴孔径为0.1 mm,喷雾角度为45°,流量为1.02~2.46 L/h(40~100 bar)。撞针式喷嘴采用意大利PNR喷嘴,其喷嘴孔径为0.18 mm,喷雾角度为50°,流量为3.3~8.7 L/h(10~70 bar)。蒸发器由整流器和气体分布器组成,可以有效增加水雾跟随气流上升的时间,促进气体与水雾的接触,提高蒸发的效率。
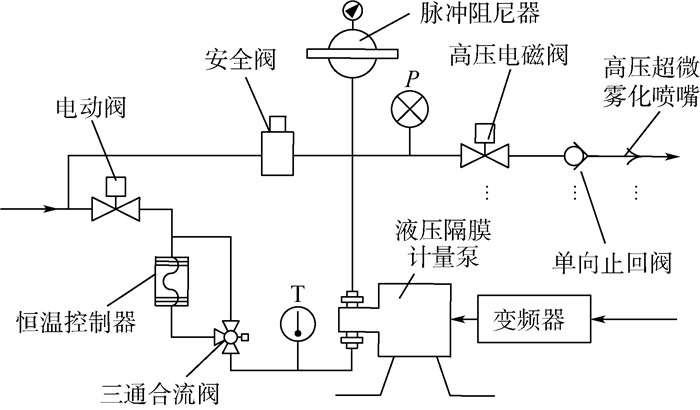
|
| 图 5 高压雾化装置 Fig. 5 High-pressure atomization generator |
为了测试实验平台的效果以及进一步展开分析音速喷嘴的凝结现象,采用轴对称喷嘴,如图 6所示,其喉部直径为10 mm。设计了一套沿程压力采集系统,如图 7所示。沿着喷嘴壁面分布设置13个直径1 mm的微型引压孔[27],用于测量时均压力和动态压力信号。时均压力传感器精度为0.2%,量程范围为0~800kPa,测量频率范围为0~20 kHz。动态压力传感器采用Kulite MEMS压力传感器,可实现快速响应,其精度为0.2% FS,固有频率为100 kHz,用于测量凝结自激振荡的动态压力。
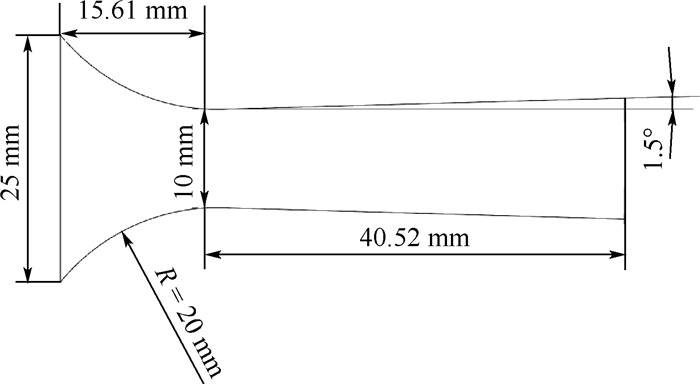
|
| 图 6 实验喷嘴结构和尺寸 Fig. 6 Structure and size of experimental nozzle |
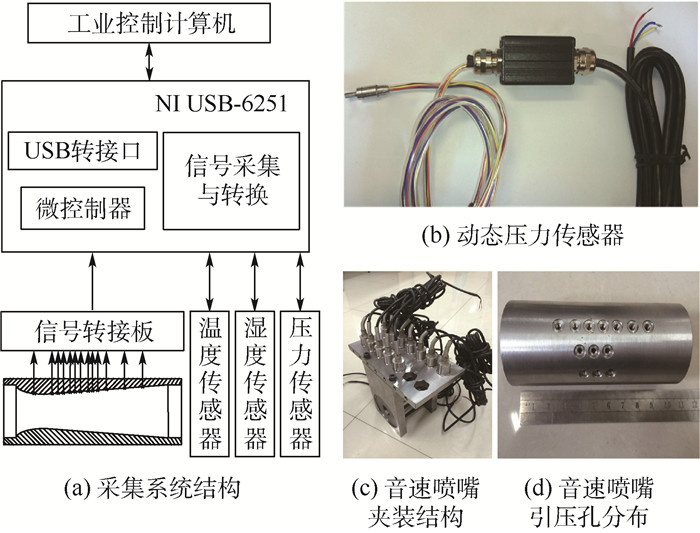
|
| 图 7 沿程压力采集系统 Fig. 7 Acquisition system of pressure distribution at nozzle wall |
建立适用于无外凝结核的自发凝结流动Eulerian两相模型[28],其质量、动量、能量守恒方程为
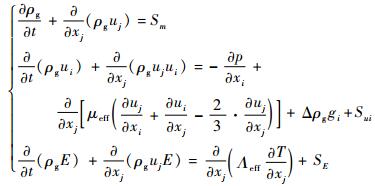
|
(3) |
式中:ρg为气体密度;u为速度;p为总压;Δρg为气体密度变化值;gi为i方向上的重力加速度;E为总能量;T为温度;μeff为等效动力黏度;Λeff为导热系数; SE=-ρwmv(E+pg/ρg-hfg),Sm=-ρwmv,Sui=-ρwmvui为方程的源项, ρw为水的密度, mv为凝结速率, pg为气体压力;hfg为水蒸气潜热。
混合气体中,组分s的组分质量守恒方程如下:
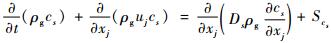
|
(4) |
式中:cs为组分s的体积浓度;Ds为组分扩散系数;当组分为水蒸气时,源项Scs=-ρwmv。
忽略气液两相间的速度滑移,液相只需给出水滴数密度、统计水滴半径以及蒸汽湿度的控制方程。式(5)~式(7)为自发凝结状态下的液相控制方程:
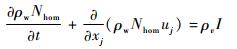
|
(5) |
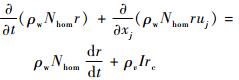
|
(6) |
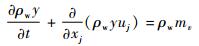
|
(7) |
式中:ρv为水蒸气密度;I为成核率;Nhom为均质的液滴密度;r为水滴半径;rc为临界成核半径。
3 实验结果与CFD分析 3.1 凝结稳态特性为了研究不同入口载气条件对凝结位置和强度的影响,进行了稳态压力实验。由时均压力传感器测量出音速喷嘴的沿程时均压力,记录气体压力p0、温度T0、相对湿度Φ0发生变化时的音速喷嘴沿程压力情况,以此分析凝结位置和强度的变化。
建立凝结稳态数值模型,采用标准k-ε模型和壁面函数法相结合的形式对二维旋转轴对称喷嘴进行模拟。数值方案方面,气液两相控制方程使用有限体积法三阶MUSCL格式进行离散化。时间离散化方法采用基于密度基的隐式格式。边界条件方面,使用压力入口和压力出口,且将喷嘴背压比控制在0.1以防止出现气动激波。网格方面,采用结构化四面体网格。经过网格独立性测试,结果如表 1所示,N1为轴向方向网格数,N2为径向方向网格数,独立性测试结果为900×120。
| 参数 | 网格 (N1×N2) |
质量流量/(kg·s-1) | 相对变化量/% |
| N1变化 N2=120 |
850×120 | 0.053 020 379 | |
| 900×120 | 0.053 027 642 | 0.013 7 | |
| 950×120 | 0.053 028 746 | 0.002 1 | |
| N1 = 900 N2变化 |
900×100 | 0.053 035 973 | |
| 900×120 | 0.053 027 642 | 0.015 7 | |
| 900×140 | 0.053 026 096 | 0.002 9 |
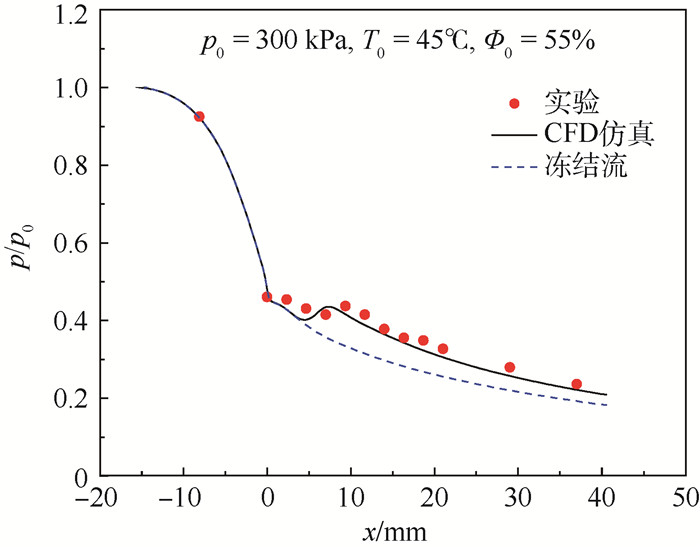
基于正压法音速喷嘴标准装置,由于实验条件限制,实验过程中喷嘴背压比均小于0.337。对实验平台的可靠性进行了测试,结果如图 8所示,其中实线表示CFD仿真的曲线,虚线表示气体在喷嘴内部等熵流动,散点表示不同条件下实验所得喷嘴壁面处沿程压力变化。结果表明,CFD仿真结果与实验数据较接近,实验平台是可靠的。
|
| 图 8 CFD仿真与实验数据对比 Fig. 8 Comparison between CFD simulation and experimental data |
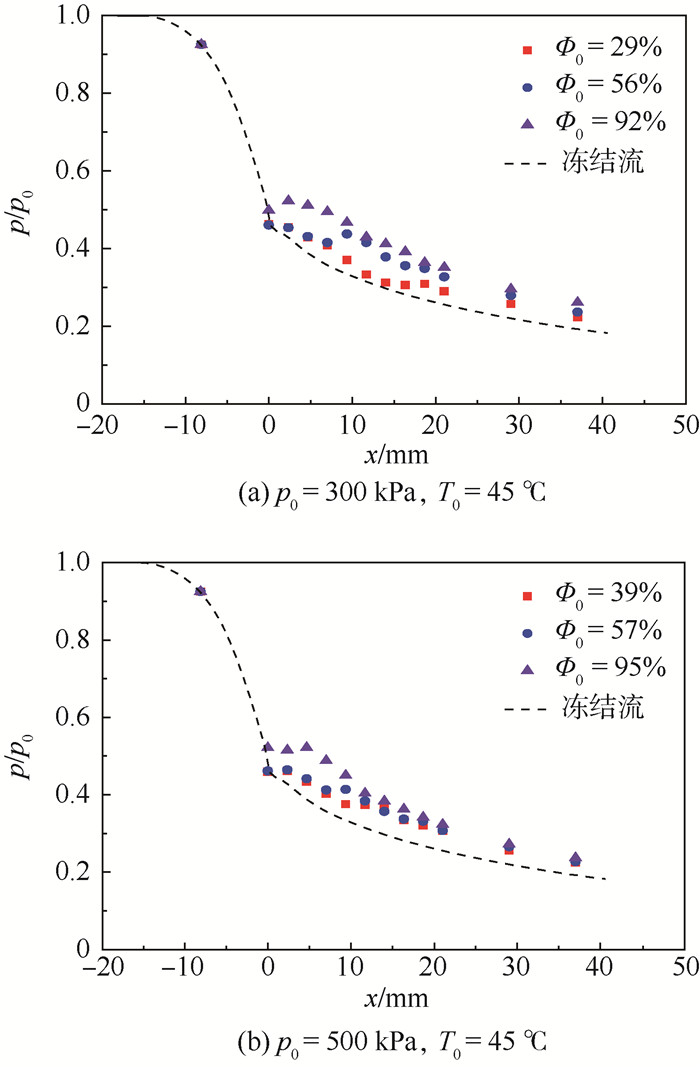
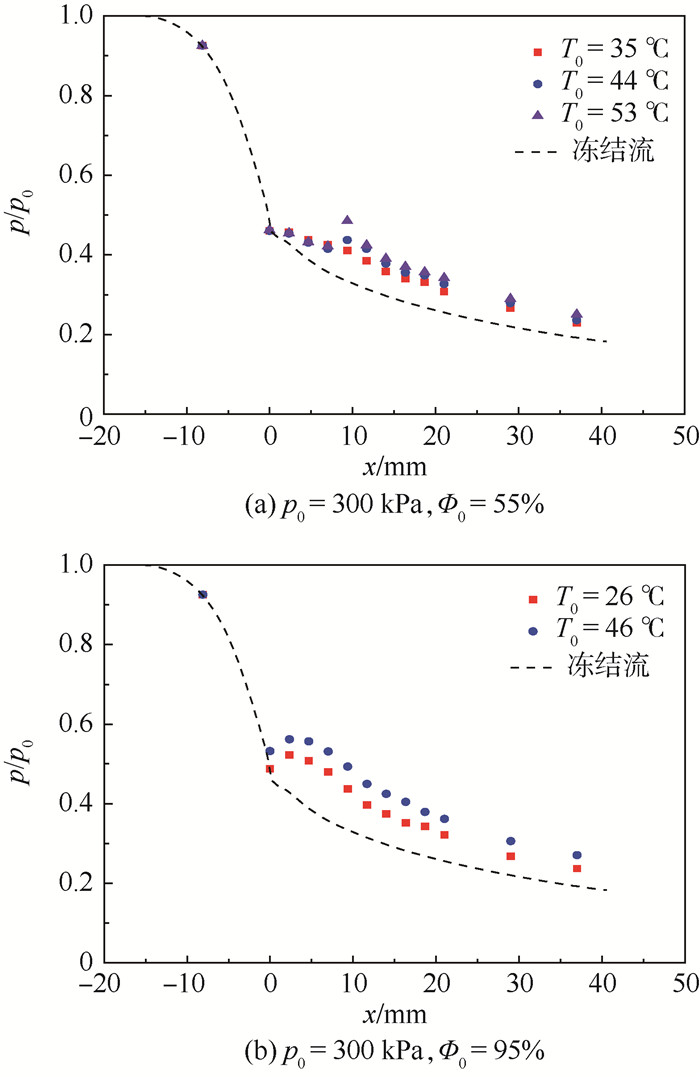
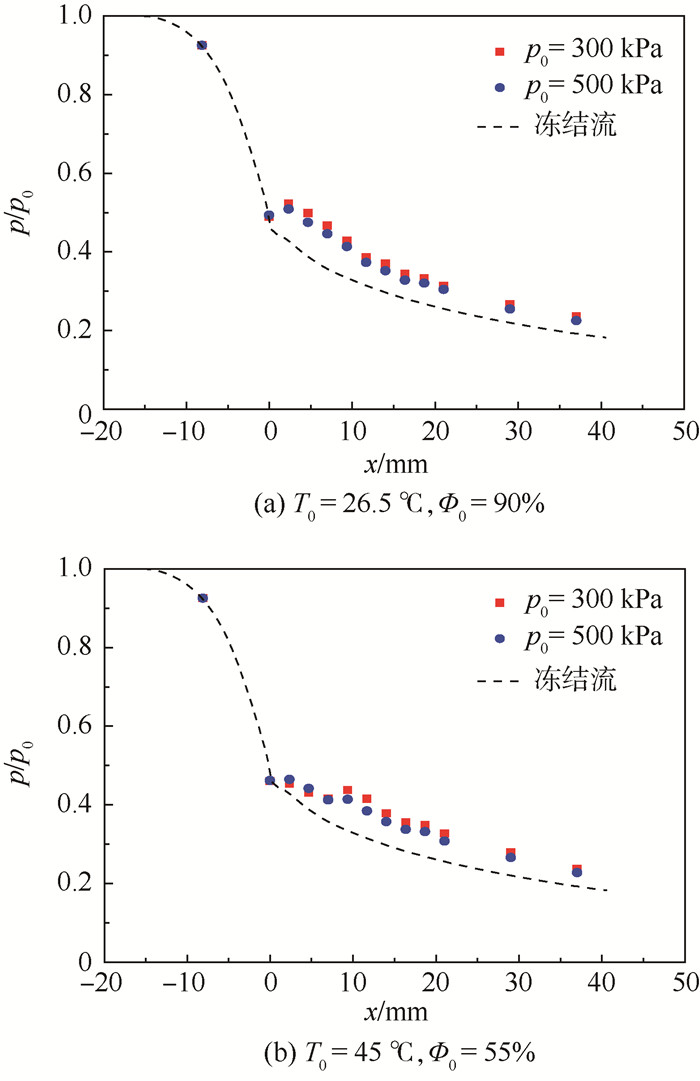
分别改变气体湿度、温度以及入口压力,进行3组对照实验, 实验记录如图 9~图 11所示。可知,凝结发生的位置会随着载气压力、湿度、温度的增大而向喉部方向移动,凝结的强度随着载气湿度和温度的增大而增强,但却随载气压力的增大而减弱。
|
| 图 9 不同入口湿度下喷嘴壁面压力分布 Fig. 9 Pressure distribution at nozzle wall with different inlet humidity |
|
| 图 10 不同入口温度下喷嘴壁面压力分布 Fig. 10 Pressure distribution at nozzle wall with different inlet temperatures |
|
| 图 11 不同入口压力下喷嘴壁面压力分布 Fig. 11 Pressure distribution at nozzle wall with different inlet pressure |
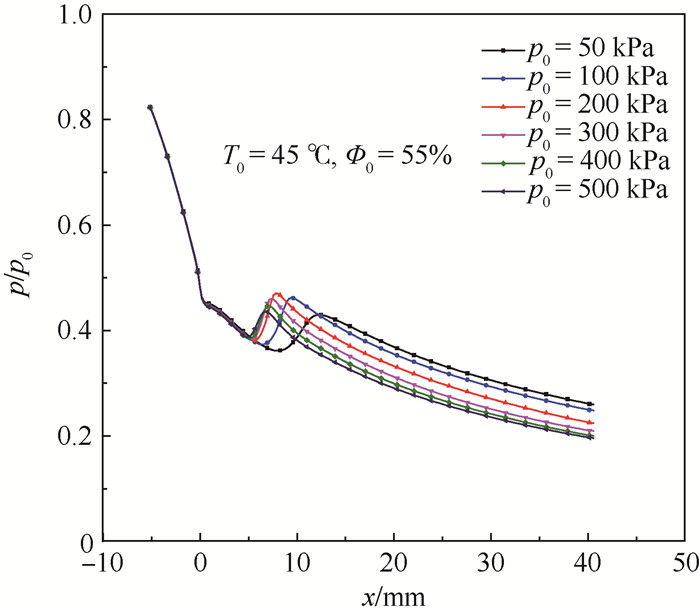
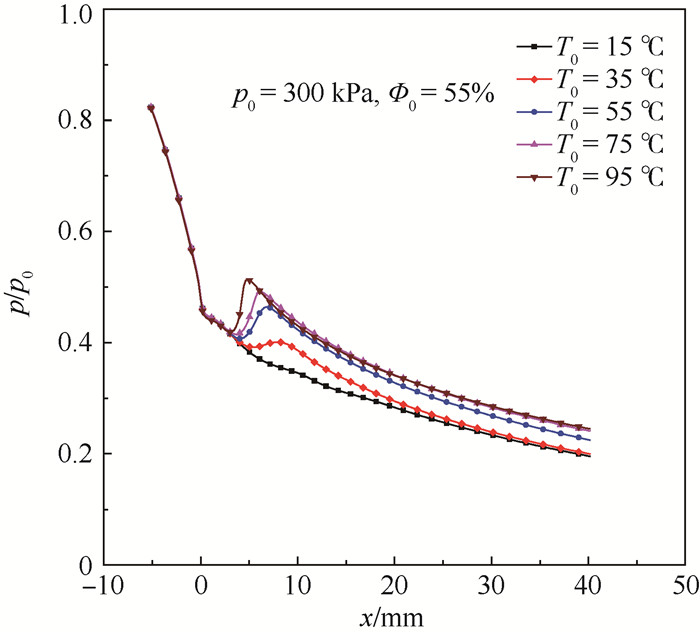
利用本文所述数学模型,对图 6所示喷嘴的凝结现象进行了CFD仿真研究。载气温度维持在45 ℃,相对湿度为55%,改变载气压力,喷嘴壁面处沿程压力分布如图 12所示。结果表明,随着载气压力的增大,凝结的位置向上游喉部靠近,而凝结强度先增大后有所降低。载气压力300 kPa、相对湿度55%维持不变,改变载气温度,则喷嘴壁面处沿程压力分布如图 13所示。结果表明,随着载气温度的增大,凝结的位置向上游喉部靠近,而凝结强度也有所增强,与实验结果一致。
|
| 图 12 不同入口压力下喷嘴壁面压力分布(CFD) Fig. 12 Pressure distribution at nozzle wall with different inlet pressure (CFD) |
|
| 图 13 不同入口温度下喷嘴壁面压力分布(CFD) Fig. 13 Pressure distribution at nozzle wall with different inlet temperatures (CFD) |
针对音速喷嘴凝结自激振荡现象,进行了动态压力的测量。分别改变入口载气湿度、温度、压力,记录自激振荡的频率f与幅度A的变化,将所测时域信号通过FFT变换转到频域分析,其结果如图 14所示。
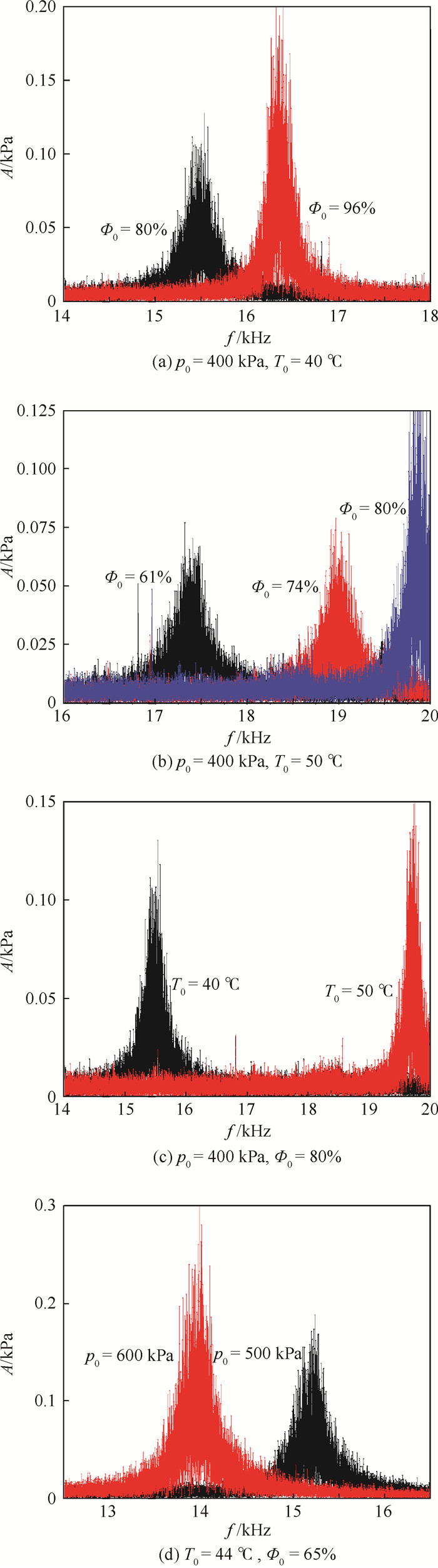
|
| 图 14 动态压力测试 Fig. 14 Dynamic pressure test |
由图 14(a)~(c)可知,当只改变湿度Φ0或者温度T0时,振荡频率f和振幅A与其呈正相关。图 14(d)表示,随着载气压力p0的增大,振幅A增大,振荡频率f却相应的降低了,这是由于音速喷嘴内部凝结的复杂性无法用单一的模型概括。此外,针对凝结自激振荡现象,在之前的研究中[29],获得了水蒸气下自激振荡频率、幅值与入口过冷度ΔT0的关系,如图 15所示。可知,在模式Ⅰ中,波动幅值A随ΔT0(Φ0)增大而先升高后降低,波动频率f则一直增大,实验数据与之吻合。后续将进一步深入研究音速喷嘴含湿气体凝结产生的自激振荡现象。
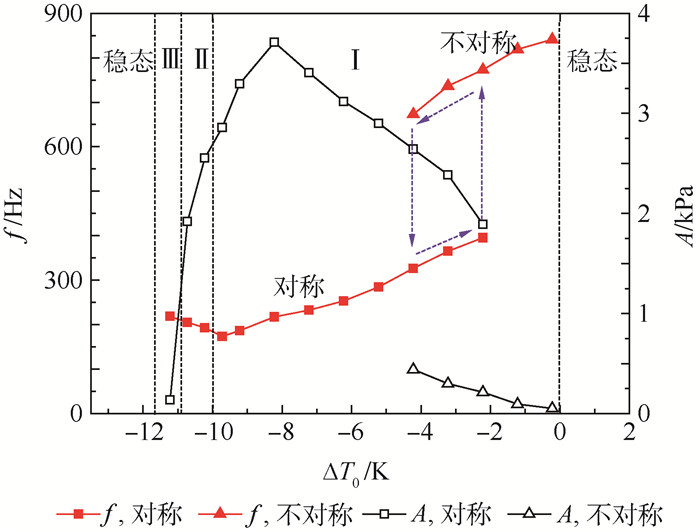
|
| 图 15 不同自激振荡模式下频率和幅值与过冷度关系 Fig. 15 Relationship between frequency and amplitude and degree of supercooling under different self-oscillation modes |
本文针对音速喷嘴内部凝结现象的影响规律进行了探究,建立了凝结流动的Eulerian两相模型,对音速喷嘴凝结现象进行了数值研究。并建立了参数可调节的凝结实验平台,准确捕获了凝结压力突跃现象。
1) 载气压力、温度以及相对湿度对凝结会产生较大影响。
2) 对于凝结稳态特性,在一定范围内,随着载气压力的增大,凝结位置向喉部方向移动,但凝结强度相对减弱;随着载气温度和相对湿度的增大,凝结位置均向前移并且强度也有所提高。
3) 对于凝结自激振荡压力波动特性,其波动频率与入口湿度、入口温度呈正相关,与入口压力呈负相关;凝结自激振荡的振幅与入口湿度、入口温度和入口压力呈正相关。
此外,本文仅对音速喷嘴内部凝结现象规律做了初步探究,凝结流动中还存在复杂的变化,包括流动分歧等现象,值得继续深入探究。
| [1] |
汪欢欢. 基于音速喷嘴的气体流量标准装置的研制[D]. 广州: 华南理工大学, 2013.
WANG H H.The development of gas flow standard device based on sonic nozzle[D].Guangzhou:South China University of Technology, 2013(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10561-1013319445.htm |
| [2] |
代钦, 魏润杰, 黄湛, 等. 超音速喷流DPIV瞬时速度场实验测量[J].
北京航空航天大学学报, 2001, 27 (6): 666–669.
DAI Q, WEI R J, HUANG Z, et al. Experimental study of supersonic jet flow using DPIV[J]. Journal of Beijing University of Aeronautics and Astronautics, 2001, 27 (6): 666–669. (in Chinese) |
| [3] | ASCHENBRENNER A.The influence of humidity on the flow-rate of air through critical flow nozzles[C]//Proceedings of the International Conference on Flow Measurement, 1983:71-74. |
| [4] |
李春辉, 王池. 通过音速喷嘴气体流量的湿度修正方法研究[J].
计量学报, 2007, 28 (3A): 160–164.
LI C H, WANG C. The humidity correction on the flow through sonic nozzle[J]. Acta Metrologica Sinica, 2007, 28 (3A): 160–164. (in Chinese) |
| [5] | BRITTON C L, CAZON R W, KEGEL K.The critical flow function, C, for humid air[C]//ASME Fluids Engineering Division Summer Meeting.New York:ASME, 1998:No.5309. |
| [6] | STEWART D G, WATSON J T R, VAIDYA A M.The effect of using atmospheric air in critical flow nozzles[C]//4th International Symposium on Fluid Flow Measurement, 1999:27-30. |
| [7] | LIM J M, YOON B H, OH Y K, et al. The humidity effect on air flow rates in a critical flow venture nozzle[J]. Flow Measurement and Instrumentation, 2011, 22 (5): 402–405. DOI:10.1016/j.flowmeasinst.2011.06.004 |
| [8] | CHAHINE K, BALLICO M.Evaluation of the effect of relative humidity of air on the coefficients of critical flow venturi nozzles[C]//16th International Flow Measurement Conference, 2013:24-26. |
| [9] | LI C H, MICKAN B.The humidity effect on the calibration of discharge coefficient of sonic nozzle by means of pVTt facility[C]//Proceedings of 8th International Symposium on Fluid Flow Measurement, 2012:No.302. |
| [10] | YOUNG J B. The spontaneous condensation of steam in supersonic nozzles[J]. Physico Chemical Hydrodynamics, 1982, 3 (1): 57–82. |
| [11] | KANE D, FISENKO S P, RUSYNIAK M. The effect of carrier gas pressure on vapor phase nucleation experiments using a thermal diffusion cloud chamber[J]. Journal of Chemical Physics, 1999, 111 (18): 8496–8502. DOI:10.1063/1.480190 |
| [12] | WEGENER P P, POURING A A. Experiments on condensation of water vapor by homogeneous nucleation in nozzles[J]. The Physics of Fluids, 1964, 7 (3): 352–361. DOI:10.1063/1.1711206 |
| [13] |
蔡颐年, 王乃宁.
湿蒸汽两相流[M]. 西安: 西安交通大学出版社, 1985.
CAI Y N, WANG N N. Wet steam two-phase flow[M]. Xi'an: Xi'an Jiaotong University Press, 1985. (in Chinese) |
| [14] |
马庆芬. 旋转超音速凝结流动及应用技术研究[D]. 大连: 大连理工大学, 2009.
MA Q F.Study on the rotating supersonic condensing flow and application technology[D].Dalian:Dalian University of Technology, 2009(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10141-2009116110.htm |
| [15] | AVETISSIAN A R, PHILIPPOV G A, ZAICHIK L I. Effects of turbulence and inlet moisture on two-phase spontaneously condensing flows in transonic nozzles[J]. International Journal of Heat and Mass Transfer, 2008, 51 (17): 4195–4203. |
| [16] | DYKAS S, WROBLEWSKI W. Numerical modelling of steam condensing flow in low and high-pressure nozzles[J]. International Journal of Heat and Mass Transfer, 2012, 55 (21): 6191–6199. |
| [17] | WANG C, WANG L, ZHAO H X, et al. Effects of superheated steam on non-equilibrium condensation in ejector primary nozzle[J]. International Journal of Refrigeration, 2016, 67 : 214–226. DOI:10.1016/j.ijrefrig.2016.02.022 |
| [18] | WEGENER P P, CAGLIOSTRO D J. Periodic nozzle flow with heat addition[J]. Combustion Science and Technology, 1973, 6 (5): 269–277. DOI:10.1080/00102207308952329 |
| [19] | SKILLING S A.An analysis of the condensation phenomena occurring in wet steam turbine[D].Birmingham:University of Birmingham, 1987. http://www.mysciencework.com/publication/show/analysis-condensation-phenomena-occurring-wet-steam-turbines-bbbf1d90 |
| [20] | ADAM S, SCHNERR G. Instabilities and bifurcation of non-equilibrium two-phase flows[J]. Journal of Fluid Mechanics, 1997, 348 (1): 1–28. |
| [21] |
吴晓明, 李国君, 李亮, 等. 湿蒸汽凝结流中自激振荡模式的数值模拟[J].
动力工程, 2009, 29 (8): 747–751.
WU X M, LI G J, LI L, et al. Numerical simulation of self-excited oscillation patterns in wet steam flow with condensation[J]. Journal of Power Engineering, 2009, 29 (8): 747–751. (in Chinese) |
| [22] | International Standard Organization. Measurement of gas flow by means of critical flow venturi nozzles:ISO9300-2005[S].Geneva:International Standard Organization, 2005. |
| [23] | WANG C, DING H B, ZHAO Y K, et al.Sensor system for unsteady flow characteristics in a sonic nozzle with vapor condensation[C]//2014 IEEE International Instrumentation and Measurement Technology Conference.Piscataway, NJ:IEEE Press, 2014, 5:772-775. http://ieeexplore.ieee.org/document/6860847/ |
| [24] | DING H B, WANG C, CHEN C. Experimental and numerical studies on self-excited periodic oscillation of vapor condensation in a sonic nozzle[J]. Experimental Thermal and Fluid Science, 2015, 68 : 288–299. DOI:10.1016/j.expthermflusci.2015.05.002 |
| [25] |
丁红兵. 音速喷嘴边界层发展及凝结现象研究[D]. 天津: 天津大学, 2014.
DING H B. Boundary layer development and vapor condensation in sonic nozzle[D].Tianjin:Tianjin University, 2014(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10056-1016183408.htm |
| [26] |
金如山. 喷嘴雾化研究[J].
北京航空航天大学学报, 1989 (3): 69–78.
JIN R S. Atomization study[J]. Journal of Beijing University of Aeronautics and Astronautics, 1989 (3): 69–78. (in Chinese) |
| [27] | WANG C, DING H B, LIU Q, et al.The dynamic compensation of temperature sensors in sonic nozzle airflow standard facilities based on method of positive pressure[C]//2012 IEEE International Instrumentation and Measurement Technology Conference. Piscataway, NJ:IEEE Press, 2012:2005-2009. The dynamic compensation of temperature sensors in sonic nozzle airflow standard facilities based on method of positive pressure |
| [28] |
孙铁志, 魏英杰, 王聪, 等. 通气位置对潜射航行流体动力特性影响分析[J].
北京航空航天大学学报, 2013, 39 (10): 1303–1308.
SUN T Z, WEI Y J, WANG C, et al. Analysis of the effect of ventilation positions on hydrodynamic characteristics of submarine-launched vehicle[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39 (10): 1303–1308. (in Chinese) |
| [29] |
王超, 王刚, 丁红兵. 音速喷嘴内水蒸汽自发凝结流动自激振荡和分歧现象研究[J].
天津大学学报(自然科学与工程技术版), 2016, 49 (11): 1113–1120.
WANG C, WANG G, DING H B. Research of spontaneous condensation steam flow with self-excited oscillation and bifurcation phenomenon in sonic nozzles[J]. Journal of Tianjin University(Science and Technology), 2016, 49 (11): 1113–1120. (in Chinese) |



