2. 北京航空航天大学 机械工程及自动化学院, 北京 100083
2. School of Mechanical Engineering and Automation, Beijing University of Aeronautics and Astronautics, Beijing 100083, China
配平是直升机飞行仿真的重要组成部分。配平是根据稳定飞行条件下来确定直升机的配平状态量,为直升机控制提供初始值,并使沿着机体坐标系每个轴的力和力矩之和达到零,同时观察独立变量的所有边界以及因变量的全部约束。直升机配平模型是初始值难以确定的且多次多变量非线性方程组,配平计算中需要同时求解的未知量数目很大,其配平算法和求解非常复杂。在飞行仿真中,这些精确的初始值可以为直升机操纵和飞行性能提供数据参考[1]。在飞行过程中保持直升机平衡对驾驶员来说并不困难,但是利用数值计算方法对高非线性方程组进行求解,结果可能不唯一,且仅有一个符合实际情况的最优解是配平飞行仿真数学模型的难题。针对直升机配平难题,需要寻求一种快速且大范围收敛的数学方法将直升机动力学微分方程转换为代数方程,进而得到稳定飞行状态下的配平结果。
飞行动力学模型传统的配平一般都着眼于研究飞机的操控品质。根据配平状态量构造目标函数代数式,求出目标函数对配平控制量的偏微分,基于梯度优化的方法找到目标函数的极小值,此时的控制量即为待求配平控制量[2]。由于直升机飞行动力学模型由机身、旋翼、尾桨、起落架和发动机/传动动力等多系统组成,这些系统模型由复杂的数学方程构成,并且各系统间相互耦合,显然,用传统解析方法求出目标函数对配平控制量的偏微分是非常困难的。国内外很多学者和工程技术人员从传统的数值方法中发展出很多配平算法,这些配平算法采用连续修正法[3-4]、梯度优化法[5-7]和拟牛顿法[8-10]。在求解过程中,连续修正法存在着独立的控制量会遇到非对角项的问题,需要很长时间才能收敛甚至不收敛。而梯度优化法为局部优化算法,收敛速度快,初始值的选取对于能否求得全局最优解至关重要。拟牛顿法是求解非线性方程组最常用的方法,局部收敛速度非常快,但该算法涉及大量的偏导数计算,计算效率低,同样依赖于初始值的设置。显然,这些算法并不适用于实时飞行仿真的配平计算,因为实时飞行仿真系统由飞行仿真数学模型、虚拟场景和操纵输入等复杂系统组成,求解状态量对操纵量的偏导数计算速度跟不上飞行状态。Subramanian等[11]将梯度优化法和拟牛顿法结合,综合两者的优点,形成一种对大范围内偏离精确解的任意初值均能收敛、且有一定收敛速度的组合迭代法。但该算法涉及大量多元多次函数的偏导数,计算效率较低。Burden和Faires[12]对牛顿法进行各种改进,降低了初始值的依赖,局部收敛速度很快,但很难实现大范围收敛。这些算法都存在大量偏导数计算且精度较低的缺陷,不适合实时飞行仿真,也有学者将几种算法结合使用但计算效率较低,弥补这些缺陷将是今后的研究重点。
近年迅速兴起的遗传算法(Genetic Algorithm,GA)已广泛应用于优化设计领域,为解决直升机非线性问题提供了新的思路。GA是基于生物遗传学和适者生存发展起来的一种进化算法,具有并行、高效、全局搜索的能力,并自适应地控制搜索过程,可以克服梯度优化方法的不足[13]。该算法以种群中的个体为操作对象,但如果种群较大时,此算法仍存在后续寻优速度较慢且精度较低的缺陷,鉴于此,大量学者将其算法与其他方法相结合应用在飞机配平计算中,并取得了很大成功。Zhang等[14]发展了将模式搜索与GA相结合的混合遗传算法,使用模式搜索对种群中精英个体进行再优化,并成功验证在倾斜跑道上的配平。文献[15]将GA与单纯形法相结合,通过分析飞机平衡状态的基本特性,提出了一种求解不同类型飞机多种平衡状态的通用方法。文献[16]在分析了定常状态的基本特性和相应约束条件的基础上,提出了基于“学习潜能”的混合遗传算法,利用状态参数进行计算,求解了定常水平/直飞和协调转弯状态下的配平结果。文献[17]将浮点GA和拟牛顿法相结合,计算了直升机定常直飞状态的最优配平解,该方法虽不依赖初始值,但容易收敛到非物理解。文献[18]将GA计算的全局较优解作为LM(Levenberg-Marquardt)算法的初值,计算了直升机平飞和协调转弯状态的配平解,但该方法在解算过程中可能出现矩阵不可逆现象,需增加系数阻尼矩阵,计算复杂。文献[19]建立了基于GA/拟牛顿法的高效混合迭代算法,计算了旋翼操纵配平控制量,为模拟地面效应作用下的旋翼拉力增益、功率变化奠定基础。以上研究都是对地面、平飞和协调转弯飞行状态进行配平,而对前推/后拉飞行配平计算却少有研究。
本文针对复杂的直升机动力学微分方程,介绍了一种可以用于任何稳态飞行状态的直升机飞行仿真配平算法,使目标函数达到极小值而得到最佳配平解。首先,引入直升机各系统动力学数学模型以及全机动力学模型,其中旋翼配平模型考虑了实际飞行条件下桨叶的挥舞运动、旋翼流场和非定常气动特性三者之间的动态平衡。然后,详细推导了直升机在前推/后拉情况下的约束方程和配平控制量,构造目标函数,将GA和拟牛顿法相结合,建立出了一种具有全局和局部快速收敛特点的混合遗传优化配平算法。最后,通过对UH-60A直升机在前推/后拉飞行仿真进行配平计算,计算结果与飞行试验结果进行对比分析,验证了配平算法的可行性和有效性,弥补了直升机在前推/后拉飞行状态的配平。
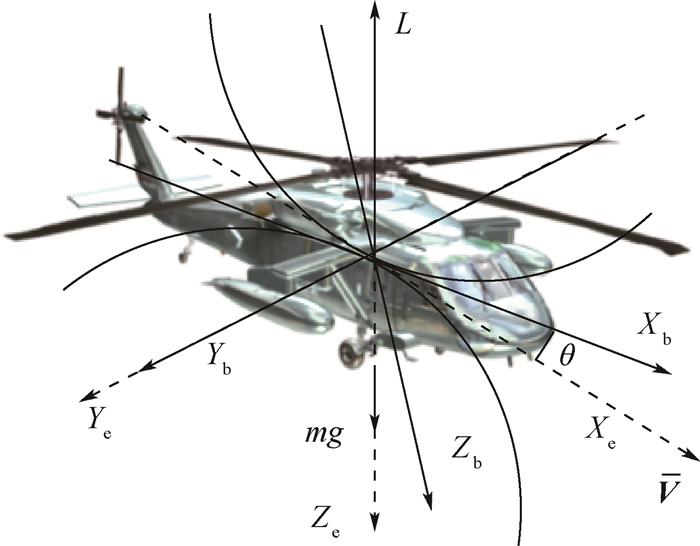
1 数学模型 1.1 坐标系为了描述直升机的6个自由度运动,本文涉及4个坐标系:地球惯性坐标系(NED)、机体坐标系、速度坐标系和稳定坐标系,这4个坐标系原点都位于直升机质心上,如图 1所示为前推/后拉状态的部分坐标系。NED坐标系Xe轴指向正北(north)方向,Ye轴指向正东(east)方向,Ze轴指向地心(down)方向。机体坐标系Xb轴沿着机身指向机头前方(纵轴方向),Yb轴指向机头方向的右侧(横轴方向),垂直于直升机纵剖面,Zb轴在直升机纵剖面上垂直于Xb轴并指向下方。机体坐标系与NED坐标系之间的关系用Euler角来确定。速度坐标系Xa轴沿直升机空速矢量方向,Za轴在其对称平面内并指向机体下方,Ya轴垂直于XaZa平面指向右方。稳定坐标系由机体坐标系绕其Yb轴旋转迎角α得到,Xs轴在空速矢量V和Yb确定的平面内且在直升机的对称平面内,Xs轴和空速矢量V的夹角为侧滑角β。L为Zs方向总的气动力,m为机身质量,g为重力加速度,θ为俯仰角。
|
| 图 1 前推/后拉的配平状态 Fig. 1 Trim attitude of push-forward/pull-backward |
旋翼模型包括桨叶气动载荷计算模型和桨叶挥舞动力学模型。前者由于操纵、非定常来流以及旋翼诱导速度,使桨叶气动载荷具有非定常特性。后者由于机体和旋翼的耦合运动,引起桨叶的挥舞运动。本文建立旋翼气动力数学模型的过程中,做出一些假设:① 空气是无黏、不可压的理想气体;② 桨叶为刚性且无后掠,线性扭转,桨叶弦长和质量特性沿展向不变;③ 不考虑桨叶的摆振运动,仅考虑挥舞和变距运动,且挥舞和变距铰位置重合,旋翼挥舞运动只取一次谐波量;④ 桨叶剖面的气动力和力矩计算基于剖面气动中心处的入流速度。
由挥舞铰力矩平衡得到旋翼挥舞动力学方程[20]:
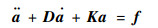
|
(1) |
式中:D和K分别为阻尼和刚度矩阵;a为挥舞运动一阶向量;f为桨叶气动力向量,同时又是机体角速度ωb、角加速度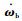
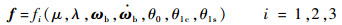
|
(2) |
关于桨叶气动模型,本文采用叶素法。计算每一叶素上的气动力和力矩,沿翼展方向和方位角进行积分,得到旋翼空气动力在机体坐标系下的力和力矩:
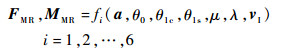
|
(3) |
式中:vI为旋翼诱导速度。入流比λ和旋翼诱导速度vI又是操纵输入的函数:
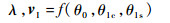
|
(4) |
本文诱导速度模型采用Pitt-Peters动态入流模型,采用一阶谐波形式表示成旋翼径向位置r和方位角Ψ的函数[21]:

|
(5) |
式中:vI0、vIs和vIc分别为时均、一阶纵向和横向入流分量,具体计算方法参见文献[21]。
1.3 尾桨模型尾桨模型计算方法与旋翼类似,没有周期变距操纵,尾桨入流模型采用均匀入流模型。机体坐标系下尾桨的气动力和力矩表示为
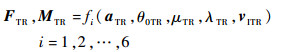
|
(6) |
式中:aTR、θ0TR、μTR、λTR和vITR分别为尾桨挥舞运动向量、脚蹬、尾桨前进比、入流比和尾桨诱导速度。λTR和vITR是θ0TR的函数:
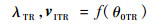
|
(7) |
机身、平尾及垂尾模型采用估算公式得到。计入旋翼诱导速度的影响确定气动参考点处的入流速度,然后根据入流速度确定气动参考点迎角α、侧滑角β和动压q后通过数值插值方法得到气动载荷系数,最后根据估算公式计算各气动部件气动力和力矩。
1.5 起落架模型起落架的轮胎模型等效于弹簧-阻尼系统,直升机在与地面接触时计算起落架对机身的力和力矩表示为
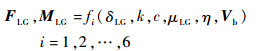
|
(8) |
式中:δLG为弹簧压缩量;k和c分别为弹簧刚度系数和阻尼系数;μLG为轮胎滑动摩擦系数;η为刹车效率;Vb=[u, v, w]T为线速度,u、v、w分别为3个机体轴分线速度。
1.6 全机重力模型全机重力作用点本身就是质心,不存在力矩。将全机重力投影到机体坐标系下可得全机重力为
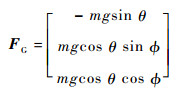
|
(9) |
式中:φ为滚转角。
1.7 全机动力学模型机体坐标系下的全机动力学方程为

|
(10) |
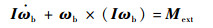
|
(11) |
式中:ωb=[p, q, r]T为角速度,p、q、r分别为3个机体轴分角速度;Fext和Mext分别为机体所受的合外力和合外力矩;I为惯性矩阵。
全机运动学方程为
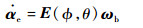
|
(12) |
式中:Euler角αe=[ϕ, θ, ψ]T,ψ为偏航角;E(ϕ, θ)为机体角速度到Euler速度的转换矩阵,其表达式为
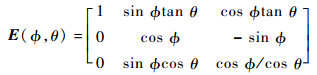
|
(13) |
将式(10)~式(12) 非线性方程表示为隐式方程形式:
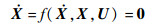
|
(14) |
式中:X=[XdT, XkT]T为状态向量,Xd=[u, v, w, p, q, r]T为动力学向量,Xk=[x, y, z, ϕ, θ, ψ]T为运动学向量;U=[θ0, θ1c, θ1s, θ0TR]T为操纵输入。在飞行仿真配平中,稳态拉起/推倒时的动力学向量Xd需为常数或0,运动学向量Xk则不需满足此条件,而所有加速度都为0。隐式方程(14) 包含12个非线性方程,而待求变量包含16个变量(12个状态量和4个操纵量),配平问题必须规定足够的约束和可用的配平控制变量,以便得到唯一确定物理解,需给定4个已知约束条件或附加4个约束方程。
2 配平算法 2.1 配平过程在无风的情况下,速度坐标系相对于NED坐标系的姿态由姿态角ϕs、θs、ψs表示。在NED坐标系中唯一的非零偏航角ψ作为可自由调整的参数,假设某时刻ψ=ψs=0,θ=θs=0,ϕ=ϕs=0,此时机体坐标系、速度坐标系与稳定坐标系三者重合。在稳定坐标系Zs方向定义载荷系数为
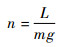
|
(15) |
式中:n>1为拉起操纵,n < 1为推倒操纵。由稳定坐标系Zs轴力的边界条件:

|
(16) |
其中:V为空速矢量。
可得到附加约束方程:
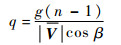
|
(17) |
对于直升机稳态拉起/推倒的配平问题,当n为某一确定值,侧滑角β为定值或0,约束条件:

|
(18) |
配平控制变量为

|
(19) |
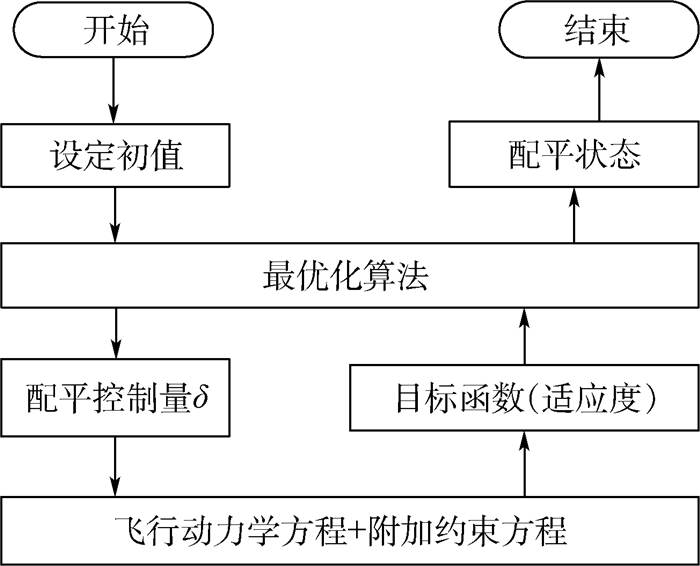
在飞行仿真配平计算中,计算机在配平算法的控制下,依据配平初始值和约束方程重复进行计算,直到得到满足所给飞行条件下的配平结果。如图 2所示为配平过程。
|
| 图 2 配平过程 Fig. 2 Trim process |
前推/后拉配平计算中步骤如下:① 飞行状态量V、n、β和4个控制量赋初值;② 根据式(14) 和式(17) 满足约束条件式(18);③ 求解式(17) 中的未知量。
为了寻找配平控制量,通过已知飞行条件和某些状态量,使用最优化算法使目标函最小化。对式(14) 构造目标函数:

|
(20) |
当g(X)=0时,{X}为式(14) 的精确解。
目标函数与飞行状态和操纵输入相关,由于一部分飞行状态量在配平过程中是常值,而变化的只有配平控制量δ,在不同飞行情况下配平控制量是不同的,约束条件也不同。最优化算法调整控制变量δ,使目标函数值为零,当满足条件之后,仿真运算结束并输出最优结果。本文提供的配平计算程序中通过判断不同的飞行条件,提供不同的边界条件和约束方程。
与传统的数值算法不同,GA是模拟生物在自然环境中的遗传和进化过程而形成的一种自适应全局优化概率搜索算法。进化过程中,利用编码方法通过有限个被称为染色体随机群体中所有个体为操作对象,通过个体之间的交叉和变异来完成搜索操作,以找到群体中的最优个体,最优个体所对应的适应度值就是该问题的最优解。虽然随着群体的进化过程会产生越来越多的优良个体,但由于选择、交叉、变异等遗传操作的随机性,可能会破坏当前群体中适应度最好的个体,为了让适应度最好的个体尽可能地保留在下一代群体中,本文使用最先保存策略进化模型(elitist model)进行优胜劣汰操作。提高运算效率,本文在求解非线性方程组过程中,采用浮点编码形式,即将个体的染色体基因值用一个浮点数表示。GA的交叉操作采用算术交叉(arithmetic crossover)技术通过序列{X}中2个个体x1和x2之间的线性组合产生出2个新的个体:

|
(21) |
参数k为
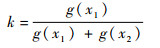
|
(22) |
k越小,新个体x1*就越接近旧个体x1,适应度低的个体既是最优个体,适应度高的个体遗传到下一代继续进行迭代计算。变异操作采用均匀变异(uniform mutation)来完成个体基因值的变异。
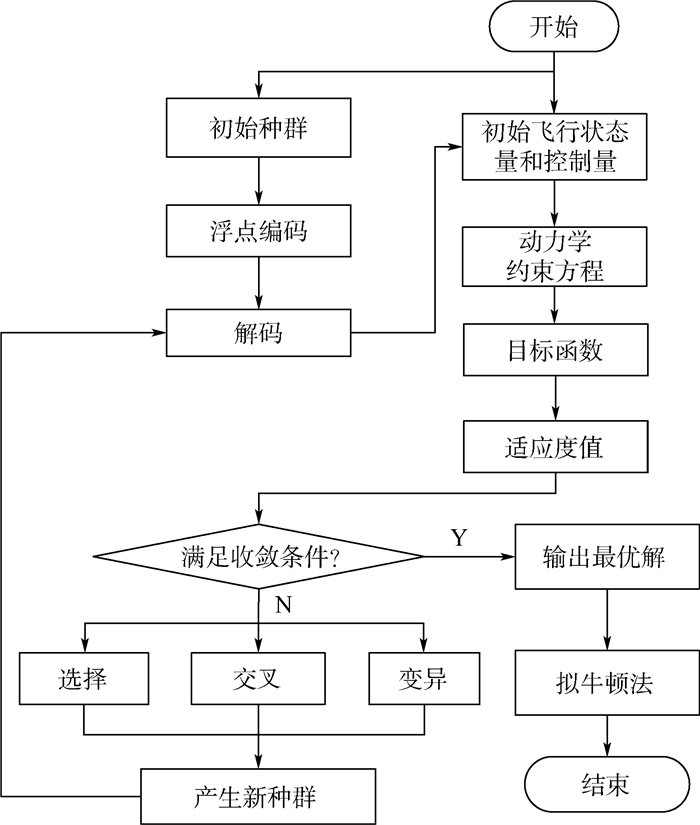
在优化算法中,拟牛顿法属于局部收敛算法,依赖于初值,在远离精确解的时候,它是发散的,而在越接近精确解的时候,其收敛速度越快[22]。对多变量多约束的直升机非线性方程来说,这种依赖初始值的单一算法无法满足计算要求。本文结合拟牛顿法在收敛域内收敛速度快和GA全局搜索优点,发展了一种混合遗传算法。具体计算流程如图 3所示。
|
| 图 3 混合遗传算法流程图 Fig. 3 Flowchart of hybrid genetic algorithm |
首先,给直升机飞行状态量和控制量赋初值并初始化动力学模型和约束方程,配平算法向计算机飞行仿真系统随机产生N个种群个体所代表的配平控制量进行迭代计算,将式(20) 作为适用度函数,采用轮盘算法选择适应度值,计算当前群体平均适应度ξavg及最佳适应度ξbes,本文既是目标函数值。当满足ξavg≤ξξbes条件,ξ为系数,则结束GA迭代,记录寻优结果,将适应度优的个体作为拟牛顿法的初值,得到方程组的最优解。若不满足给定条件,则对GA的选择、交叉、变异等算法进行迭代,在迭代的新种群中找出30个最优个体注入原种群,新种群的平均适应度ξavg将会得到提升。最后,在达到GA的终止条件后,输出最佳配平解。
3 实例验证前推/后拉是直升机比较特殊的配平问题。文献[23]描述UH-60A前推/后拉时的配平操纵和飞行姿态。为了验证本文提出的配平算法,选用UH-60A直升机作为研究对象,在前推/后拉状态下进行配平计算。桨叶翼型以SC-1095翼型为主,转速为27 rad/s,全机、旋翼、尾桨和尾翼的气动数据取自文献[23]。为了避免收敛到非物理配平解并提高收敛速度,本文缩小配平初始值范围[24]:
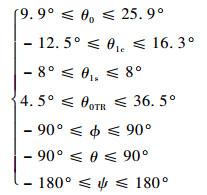
|
(23) |
根据本文建立的全机数学模型,在飞行仿真平台中,将整个配平算法封装为一个函数类,在装有Intel(R) Xeon(R) CPU E5-1607的Del工作站上完成飞行仿真配平计算。将4个操纵量转换为操纵杆位置[24],以51.44 m/s速度前飞的UH-60 A为例,瞬间以3×10-3 ft/min爬升率稳定拉起(1 ft= 0.304 8 m),设置α=β=0°。设定种群数N=100,交叉概率η1=0.9,变异概率η2=0.1,遗传迭代次数为100,设定适应度比值ξ=1.1。配平操纵量和Euler角的初始值为:① 总距操纵杆在最低位置;② 周期变距杆和脚蹬在中间位置;③ 滚转角和偏航角为0°[25]。在俯仰角为0°时设置操纵量和Euler角初始值为
δ=[0°, 0°, 10.4°, 2.1°, 0°, 20.5°]
由表达式(14)、式(17) 和式(18) 得到配平解:
δ′=[0.2°, -0.5°, 8.5°, 1.9°, -0.64°, 22.06°]
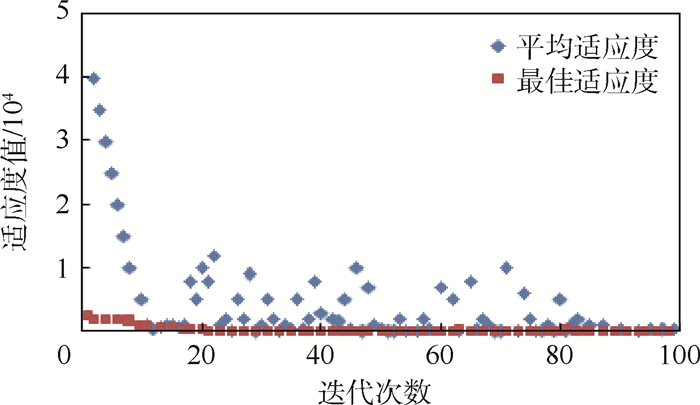
图 4为随机一次混合遗传算法的快速收敛迭代曲线。在初始迭代阶段寻优速度非常高,当其平均适应度ξavg快接近最佳适应度ξbes的时候,其寻优速度逐渐变慢,但寻优精度较高,此时适应度值为0.034。每次迭代计算时间在0.214~0.219 s之间,满足实时飞行仿真要求。
|
| 图 4 目标函数迭代曲线 Fig. 4 Iterative curves of objective function |
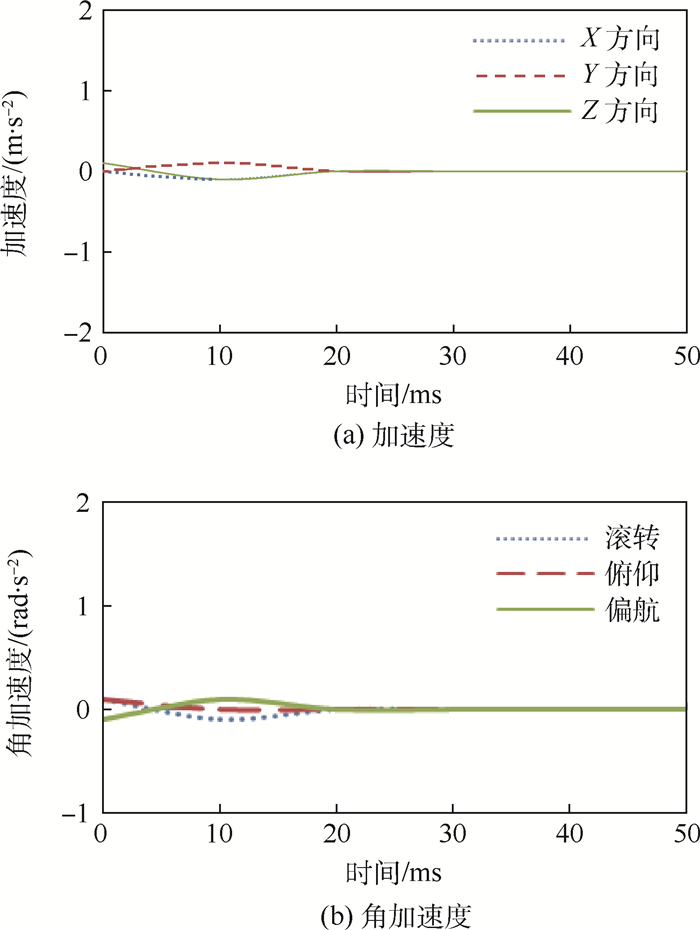
直升机由平飞状态瞬间转换为拉起飞行,总距和纵向周期变距操纵瞬间变化致使旋翼气动非定常特性增大,旋翼对机体的力和力矩不平衡导致线加速度和角加速度的微小波动,配平算法程序启动及时平衡飞行状态,配平后的线加速度和角加速度如图 5所示。加速度微小波动对飞行仿真影响不大,20 ms后加速度趋于稳定并等于0,满足约束条件式(18)。
|
| 图 5 加速度和角加速度配平结果(机体坐标系) Fig. 5 Trim results of acceleration and angular acceleration in body coordinate system |
调整总距杆和纵向周期变距杆位置,驱动垂直方向(Zb轴)力为零,同时,调整脚蹬位置尽量保持直升机的0°角航向姿态,使UH-60A直升机以51.44 m/s速度尽量保持平飞,小幅度操纵纵向周期变距杆分别以±3×10-3 、±2×10-3 、±1×10-3 和0ft/min保持恒定爬升率作前推/后拉配平仿真,在某一恒定爬升率情况下,配平计算记录5次,取平均值。
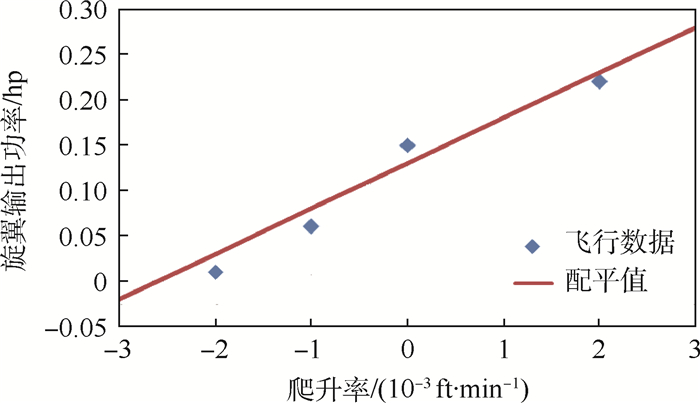
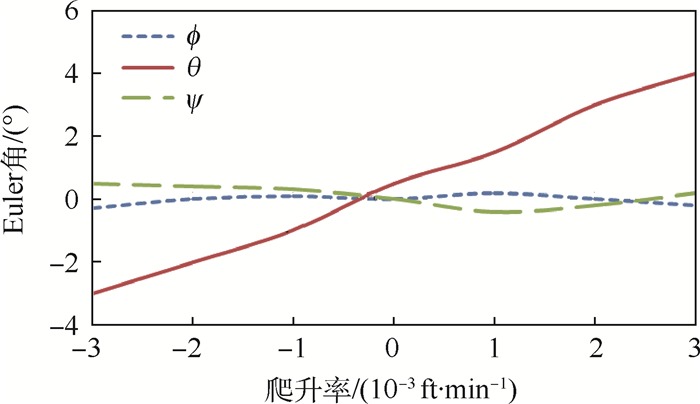
由于没有公开旋翼载荷系数nZ实测值可比对,本算例中以已有可比对的旋翼功率形式输出。从图 6中的旋翼功率(1 hp=745.699 9 W)对比可知,旋翼输出功率线性增加,即nZ在恒定爬升率情况下仍能保持稳定,且随爬升率增大而线性增大,与飞行数据[22]基本一致。在整个配平过程中,Euler配平结果如图 7所示。滚转角ϕ和偏航角ψ趋于平稳,俯仰角θ线性增大且对称,配平结果满足稳定前推/后拉飞行条件。
|
| 图 6 旋翼功率配平结果 Fig. 6 Trim results of rotor power |
|
| 图 7 Euler配平结果(地球惯性坐标系) Fig. 7 Trim results of Euler angles in earth inertial coordinate system |
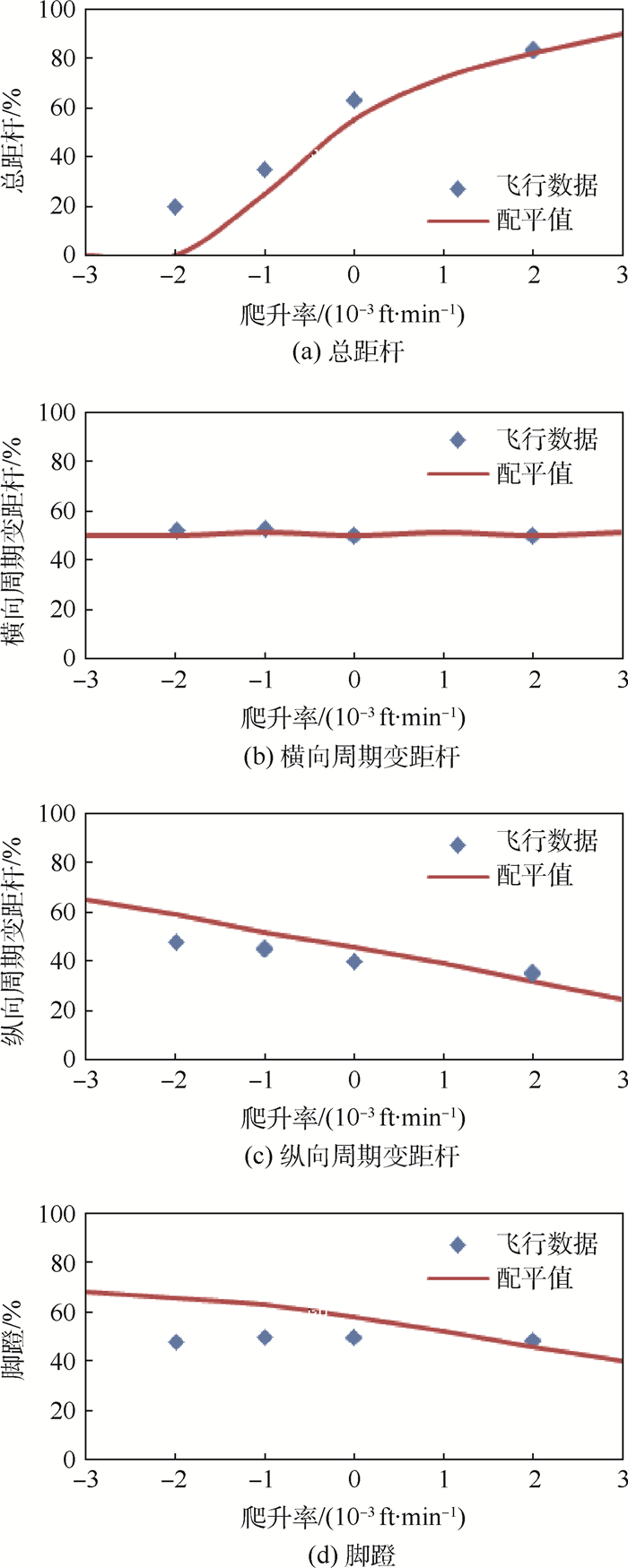
控制变量配平结果如图 8所示。为了进一步研究配平计算值和飞行数据之间的相关性,分析误差产生的原因,将操纵动作分为2个阶段:前推(爬升率小于0) 和后拉(爬升率大于0)。在稳定前推阶段,机体做低头运动,俯仰角及俯仰角速度由正值变成负值,桨叶迎角减小,桨叶失速范围增大,旋翼气动速度迅速减小,旋翼拉力随之快速减小,旋翼非定常特性增大,此时虽然增加总距,但来不及抵消旋翼拉力减小值,导致总距(见图 8(a))配平结果与飞行测试结果存在误差,爬升率越大,误差越大;而此时旋翼扭矩在急速增大,导致偏航力矩增大,脚蹬来不及补偿偏航力矩,造成脚蹬(见图 8(d))配平值与飞行数据存在误差。在稳定拉起阶段,机体做抬头运动,桨叶迎角增大,桨叶部分区域会失速但范围不大,旋翼气动速度增大,旋翼拉力逐渐增大而扭矩逐渐减小,旋翼非定常特性变化不突出,此时调整脚蹬位置平衡直升机航向并使偏航角保持为0°,配平计算的4个操纵量与飞行测试值吻合较好。在前推和后拉阶段,脚蹬也会产生滚转力矩,本文设置横向周期变距杆为自动调整滚转力矩使直升机重新回到平衡状态。由于实际飞行测试中很难保证机身迎角α和侧滑角β初始值同时都为0°,尤其是在俯仰过程中受迎角影响最大,因此在受迎角影响明显的纵向方向上,纵向操纵变距杆(见图 8(c))配平结果与飞行测试结果存在较小偏差。本文设置风速为0,而实际飞行实测数据很难保证无风,这也是引起误差的原因。总体而言,本文配平结果与飞行数据吻合较好,变化趋势一致,能够真实反映前推/后拉飞行条件下的飞行姿态和配平控制量。
|
| 图 8 总距杆、横向周期变距杆、纵向周期变距杆及脚蹬配平结果 Fig. 8 Trim results of collective stick, lateral cycle stick, longitudinal cycle stick and pedal |
本文在直升机动力学方程基础上,详细推导了前推/后拉状态的附加约束方程,得出配平控制量,应用混合遗传算法得出了UH-60A直升机前推/后拉配平计算并与飞行数据对比分析,得到以下结论:
1) 建立的混合遗传算法能够快速、准确捕捉到直升机全机的配平最优解,满足直升机稳定前推/后拉飞行的约束条件。
2) 在前推阶段,突出的旋翼非定常特性是引起总距和脚蹬配平计算误差的主要原因;在后拉阶段,配平结果与飞行数据吻合较好。
3) 本文的配平算法通用性强,只要改变边界条件、约束方程和配平控制量,能够适用于不同飞行条件下的直升机配平仿真工作。
| [1] | DE MARCO A, DUKE E L, BERNDT J S.A general solution to the aircraft trim problem[C]//AIAA Modeling and Simulation Technologies Conference and Exhibit.Reston:AIAA, 2007:3. |
| [2] |
张镭. 飞行模拟器飞行仿真系统建模与软件实现[D]. 哈尔滨: 哈尔滨工业大学, 2009: 62-69.
ZHANG L.Flight simulation modeling and software development for flight simulator[D].Harbin:Harbin Institute of Technology, 2009:62-69(in Chinese). |
| [3] | PADFIELD G D. Helicopter flight dynamics:The theory and application of flying qualities and simulation modeling[M]. Oxford: Blackwell Publishing Ltd, 2007: 192-204. |
| [4] | SEKULA M K, GANDHI F. Effects of auxiliary lift and propulsion on helicopter vibration reduction and trim[J]. Journal of Aircraft, 2004, 41 (3): 645–656. DOI:10.2514/1.496 |
| [5] | STEIJL R, BARAKOS G, BADCOCK K. A framework for CFD analysis of helicopter rotors in hover and flight[J]. Intermational Journal of Numerical Methods in Fluids, 2006, 51 (8): 819–847. DOI:10.1002/(ISSN)1097-0363 |
| [6] |
杨超, 洪冠新. 求解非线性代数方程组的一种建议方法[J].
飞行力学, 1997, 15 (2): 42–46.
YANG C, HONG G X. A suggested method of solving the nonlinear algebraic equations[J]. Flight Dynamics, 1997, 15 (2): 42–46. (in Chinese) |
| [7] | SUBRAMANIAN S, VENKATARATNAM S, GAON-KAR G H. Parallel fast-floquet analysis of trim and stability for large helicopter models[J]. Mathematical and Computer Modeling, 2001, 33 (10-11): 1155–1176. DOI:10.1016/S0895-7177(00)00305-8 |
| [8] | SCHANK T C.Optimal aeroelastic trim for rotorcraft with constrained non-unique trim solutions[D].Atlanta:Georgia Institute of Technology, 2008:87-90. |
| [9] | YAMASHITA N, FUKUSHIMA M. Modified Newton methods for solving a semi smooth reformlation of mono-tone complementarity problems[J]. Math Program, 1997, 76 (3): 469–491. DOI:10.1007/BF02614394 |
| [10] |
孙传伟, 黄一敏, 高正. 直升机飞行品质评估数学建模研究[J].
飞行力学, 2001, 19 (1): 10–12.
SUN C W, HUANG Y M, GAO Z. Investigation of helicopter mathematical model appropriate for flying quality evaluation[J]. Flight Dynamics, 2001, 19 (1): 10–12. (in Chinese) |
| [11] | SUBRAMANIAN S, GAONKAR G H, MAIER T H.A theoretical and experimental investigation of hingeless-rotor stability and trim[C]//Twenty-Third European Rotorcraft Forum.Dresdoen:ERF, 1997:10-18. |
| [12] | BURDEN R L, FAIRES J D. Numerical analysis[M]. 7th ed Boston: Prindle, Weber & Schmidt,, 2001: 851-865. |
| [13] |
刘国强. 基于遗传算法的直升机旋翼桨叶气动外形优化设计[D]. 南京: 南京航空航天大学, 2011: 11-12.
LIU G Q.Aerodynamic shape optimization design for helicopter rotor blades based on the genetic algorithm[D].Nanjing:Nanjing University of Aeronautics and Astronautics, 2011:11-12(in Chinese). |
| [14] | ZHANG L, HUANG Q T, JIANG H Z. Trimming aircraft on the ground based on the hybrid genetic algorithm[J]. The Japan Society for Aeronautical and Space Sciences, 2009, 52 (177): 117–224. |
| [15] |
王海涛, 高金源. 基于混合遗传算法求解飞机平衡状态[J].
航空学报, 2005, 26 (4): 470–475.
WANG H T, GAO J Y. Solving the equilibrium states of aircraft based on mixture genetic algorithm[J]. Acta Aeronautica et Astronautica Sinica, 2005, 26 (4): 470–475. (in Chinese) |
| [16] |
栾志博, 郑淑涛, 李洪人. 基于混合遗传算法求解飞机定常状态[J].
吉林大学学报(工学版), 2011, 41 (1): 165–170.
LUAN Z B, ZHENG S T, LI H R. Solution of steady state of aircraft based on mixture genetic algorithm[J]. Journal of Jilin University(Engineering and Technology Edition), 2011, 41 (1): 165–170. (in Chinese) |
| [17] | DAI J Y.Robust flight controller design for helicopters based on genetic algorithms[C]//Proceedings of 15th Triennial World Congress of IFAC.Barcelona:IFAC, 2002:68-75. |
| [18] |
吴超, 谭剑锋, 王浩文, 等. 基于GA/LM混合优化的直升机全机配平算法[J].
飞行力学, 2014, 32 (1): 5–9.
WU C, TAN J F, WANG H W, et al. Optimal trim for helicopter based on GA and LM hybrid algorithm[J]. Flight Dynamics, 2014, 32 (1): 5–9. (in Chinese) |
| [19] |
朱明勇, 招启军, 王博. 基于CFD和混合配平算法的直升机旋翼地面效应模拟[J].
航空学报, 2016, 37 (8): 2539–2551.
ZHU M Y, ZHAO Q J, WANG B. The simulation of helicopter rotor in-ground-effect based on CFD method and hybrid trim algorithm[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37 (8): 2539–2551. (in Chinese) |
| [20] | TALBOT P D, TINLING B E, DECKER W A, et al.Mathematical model of a single main rotor helicopter for piloted simulation:NASA-TM-84281[R].Washington, D.C.:NASA, 1982. |
| [21] | PITT D M, PETERS D A. Theoretical prediction of dynamic inflow derivatives[J]. Vertica, 1981, 5 (1): 21–34. |
| [22] |
代冀阳, 吴国辉, 朱国民. 适于直升机配平计算的混合遗传算法[J].
飞行力学, 2010, 28 (1): 24–27.
DAI J Y, WU G H, ZHU G M. Equilibrium computation of helicopters used by hybrid genetic algorithm[J]. Flight Dynamics, 2010, 28 (1): 24–27. (in Chinese) |
| [23] | BALLINM G.Validation of a real-time engineering simulation of the UH-60A helicopter:NASA-TM-88360[R].Washington, D.C.:NASA, 1987. |
| [24] | HOWLETT J J.UH-60A black hawk engineering simulation program:VolumeⅠ-Mathematical model:NASA CR-166309[R].Washington, D.C.:NASA, 1981. |
| [25] | DREIER M E. Introduction to helicopter and tiltrotor flight simulation[M]. Reston: AIAA, 2007: 328. |



