2. 海军航空工程学院 飞行器工程系, 烟台 264001
2. Department of Airborne Vehicle Engineering, Naval Aeronautical and Astronautical University, Yantai 264001, China
无人机具有重量轻、成本低和适应性强等特点,已成为世界许多国家的研究热点[1]。在无人机的相关研究中,航迹跟踪是无人机安全飞行、完成飞行任务的基础。在航迹跟踪的过程中,必须综合考虑无人机的跟踪精度与自身稳定性,以保证无人机的安全性和追踪的可靠性[2-3]。
无人机飞行控制系统作为无人机的“大脑”,是机上设备进行操纵指令传递、舵面运动控制的所有装置和部件的总和[4]。目前对飞行器控制系统的研究,主要有2种实现方式:一类实现方式将飞行器控制系统进行分解,分为外环制导与内环控制2个回路;另一类实现方式将整个控制系统统一求解,是一种综合式的方式。综合各种因素,目前采用较多的仍然是第1类实现方式[5]。
在分层设计的飞行控制系统结构中,针对外环的制导回路,目前主要的几种航迹跟踪算法包括:基于比例、微分、积分(PID)控制的跟踪算法、视场制导算法、纯视场跟踪(PLOS)算法、向量场算法以及非线性制导方法等。其中,文献[6]将PID控制器与微分几何制导算法相结合,设计了一套完整的控制系统,并通过仿真实验进行了验证; 文献[7]在经典PID控制器的基础上,研究了融合反向传播(BP)神经网络PID控制算法,提高了无人机的自适应能力; 文献[8]介绍的视场制导算法可以用于航迹跟踪,却无法有效消除航迹侧偏距; 文献[9]讨论了PLOS算法的抗外界扰动能力(重点是抗风能力);文献[10-11]介绍的向量场算法具有很高的跟踪精度,但因涉及的参数较多,调试较复杂,实用性一般;文献[12-13]中讨论的非线性制导方法是利用期望航迹上的虚拟目标点以及虚拟目标点与无人机实际位置之间的“虚拟距离”作引导的跟踪算法;文献[14]对非线性制导方法可跟踪的航迹进行了分析,证明了其通用性;文献[15]在非线性制导方法的基础上,考虑制导回路计算所得的期望侧向加速度指令与无人机实际状态之间存在的偏差,并为了补偿该偏差,在制导回路加入了反馈项,通过仿真证明了该算法能有效提高跟踪精度。
为了满足各种实时飞行任务的需求,本文以基于航迹引导点的非线性制导算法为基础,提出一种引导长度自适应的航迹跟踪方法。其思想是根据无人机的实际位置与航向,实时解算出利于飞机平稳飞行且能够高精度跟踪期望航迹的引导长度,从而提高非线性制导方法在航迹跟踪过程中的灵活性和实用性。
1 非线性制导方法 1.1 无人机运动方程无人机运动方程包括动力学方程和运动学方程,前者体现无人机系统的动力学特性,主要在内回路中考虑,后者体现无人机的运动学特性,主要在外回路中考虑。针对本文所研究的航迹跟踪问题,重点研究外回路产生控制指令的过程。
为描述无人机在空间里的飞行状态,在本文中采用三自由度点质量模型,在满足算法设计的要求下近似地表示无人机的运动特性[16]。
在本文中主要考虑平面内的航迹跟踪问题,假设无人机保持平飞的状态,以稳定的高度飞行,v表示无人机的实际飞行速度,并忽略转弯过程中侧滑角的影响,则运动方程为
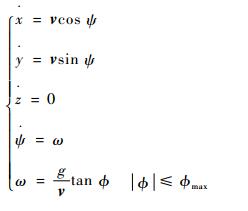
|
(1) |
式中:x、y、z表示无人机在地球轴线(等同于经度、纬度、海拔)中的重心坐标;ψ为航向角;ω为航向角速度,它通过飞机的滚转角输入进行计算;ϕ为滚转角;ϕmax为飞机所能达到的最大滚转角;g为当地的重力加速度。
1.2 基于航迹引导点的非线性制导方法运用基于航迹引导点的非线性制导方法来进行无人机航迹跟踪,其原理是通过期望航迹上的引导点以及无人机实时的位置信息,计算无人机的侧向加速度指令,再通过滚转角及副翼控制内回路,保证无人机对航迹的跟踪。
考虑如图 1所示的无人机平飞过程中与期望航迹的二维关系图。

|
| 图 1 非线性制导方法几何示意图 Fig. 1 Geometric drawing of nonlinear guidance method |
图 1中,R为预测航迹半径。假设无人机在某时刻与期望航迹存在一定的侧偏距dcr,需要通过侧向指令使无人机趋近期望航迹。设航迹引导点与无人机之间的直线距离用d表示,引导长度为L,期望的侧向加速度as,期望航迹(desired path)与无人机速度矢量的夹角为α,无人机与引导点连线方向与无人机速度矢量方向的夹角为η,则p点的选择必须满足以下几个约束:
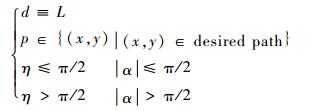
|
(2) |
在每个控制周期内,利用圆周运动近似无人机飞向引导点的预测轨迹,进而根据牛顿第二定律与图 1所示的几何关系,求出期望的侧向加速度as:

|
(3) |
根据飞行动力学原理,当飞行器以滚转角ϕ飞行时,其受力分析如图 2所示。图中:FL为升力; m为飞机质量。
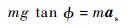
|
(4) |

|
| 图 2 无人机滚转时重力与升力的平衡关系 Fig. 2 Equilibrium relationship between weight and lift on rolling of UAV |
联立式(3) 和式(4),最终得到期望滚转角指令:
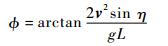
|
(5) |
解算出滚转角指令以后,将其传输给内回路,内回路运用经典PID控制理论可实现良好的控制效果,本文中不再详细展开。
通过式(5) 可以看出,在飞行速度基本不变的情况下,滚转角主要受引导长度L和η这2个变量的影响,而后者的大小又直接由L值所决定。因此,L的取值直接影响到滚转角指令的大小,并进而影响实际的跟踪效果。
1.3 引导长度对跟踪效果的影响引导长度是无人机当前位置与当前引导点连线的距离,目前相关的文献没有对非线性制导方法中的引导长度设计进行讨论。
下面通过某次飞行试验的实际数据,分析引导长度对跟踪效果的影响。
试验飞机翼展2.4 m,机身长度1.6 m,起飞重量6.4 kg,采用无刷电机驱动螺旋桨产生拉力。飞机采用后三点、上单翼常规式布局,翼型较厚,低速性能优异,起飞降落较为容易,对场地要求不高,飞行试验用无人机如图 3所示。

|
| 图 3 飞行试验用无人机 Fig. 3 UAV for flight experiment |
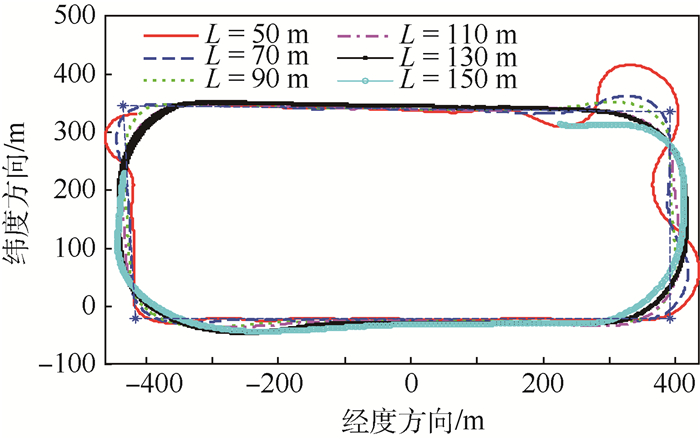
飞行试验时,有大约4 m/s的偏南风,设定期望空速恒为15 m/s,拟跟踪一个四边形航迹(4个航路点在图 4中用*点表示)。初始状态将引导长度L设为50 m,每飞行一圈增加20 m,直到150 m,飞行轨迹如图 4所示。
|
| 图 4 不同引导长度下的航迹 Fig. 4 Flight track with different guidance lengths |
从图 4可以看出,当L较小(如L=50 m和L=70 m)转弯时,由于受到滚转角幅值与变化速率的限制以及环境因素的影响,控制需要一个渐近收敛的过程。在收敛的过程中,飞行轨迹与期望航迹可能出现较大的偏差,特别是顺风的情况下,地速较大,超调现象会尤为明显(如由东南方的航路点飞向东北方的航路点过程)。
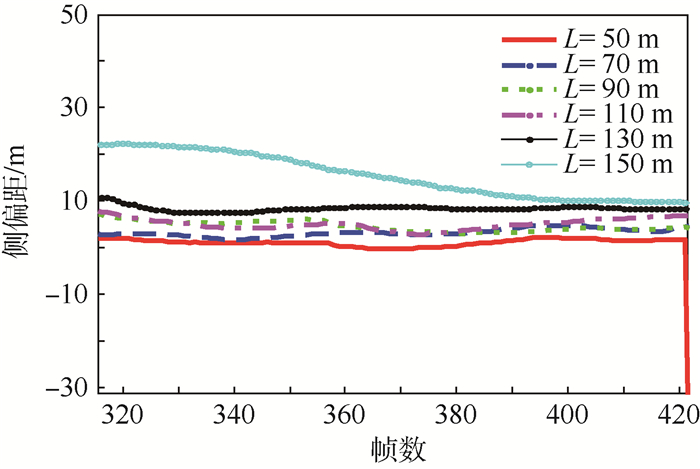
分析稳定跟踪直线段时的侧偏距,得到图 5所示的结果。
|
| 图 5 稳定跟踪过程的侧偏距 Fig. 5 Cross track error of stable tracking process |
计算上述算法在稳定段跟踪过程中侧偏距的均方根,结果如表 1所示。
| L/m | 侧偏距的均方根/m |
| 50 | 1.148 2 |
| 70 | 3.740 0 |
| 90 | 4.674 5 |
| 110 | 5.361 7 |
| 130 | 8.245 1 |
| 150 | 9.243 7 |
从表 1中可以看出,在稳态跟踪直线的情况下,L越小,跟踪精度越高,在L=50 m的情况下,控制精度能收敛到1 m的范围内。
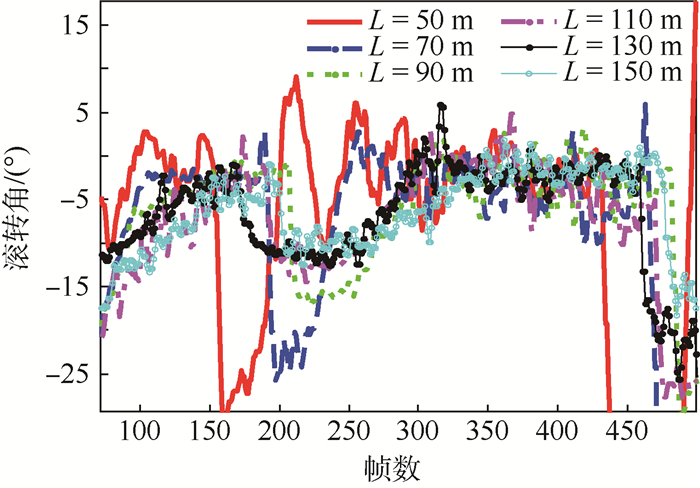
飞机滚转角的变化情况,能体现出飞机飞行的稳定性与安全性,在飞行试验时设定滚转角限幅为30°,截取一段从拐弯到稳定跟踪的过程,对滚转角进行分析,如图 6所示。
|
| 图 6 不同引导长度下的滚转角变化 Fig. 6 Variation of roll angle under different guidance lengths |
从图 6中可以看出:L越小,滚转角变化越剧烈。L=50 m时,滚转角接近限幅,出现震荡现象。L达到90 m以上时,滚转角曲线保持较平稳的状态。
通过飞行试验和相关的仿真结果,可以得到引导长度与跟踪性能之间的关系:
1) 在飞行速度范围内,相同的引导长度下,随着飞机地速的增加,紧密跟踪航迹的能力变差,直接体现在飞机稳定跟踪上期望轨迹的时间较长,同时拐弯段震荡超调明显。
2) 在曲率变化较小的稳定跟踪段,飞行速度恒定时,引导长度越短,跟踪精度越高。
3) 引导长度越短,滚转角变化越剧烈,由于无人机在实际飞行中存在滚转角幅值和速率限幅,引导长度过短很可能会导致飞机失稳。
综上,从飞行稳定性和安全性角度考虑,合理选取引导长度也有着很重要的意义,以防止出现振荡的现象。因此要实现更佳的航迹跟踪效果,有必要对每一时刻下的引导长度进行优化。
2 引导长度自适应的原理 2.1 引导长度范围的确定假设无人机的飞行速度范围为(vmin, vmax),由于受到各种外界扰动的影响,无人机的实际飞行速度(即地速)为v(v∈(vmin, vmax))。
文献[17]推导了利用非线性制导方法跟踪航迹的近似线性模型,并得到了非线性制导律的带宽ωguidance,其值由无人机的速度v的大小与引导长度L的比来确定,即
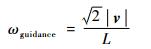
|
(6) |
从制导律的动态特性与无人机飞行控制系统的动态特性约束角度考虑,根据香农采样定理,应保证制导律带宽小于无人机飞行控制系统的带宽ωUAV的一半,即
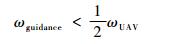
|
(7) |
联立式(6) 和式(7),得到L的下限为
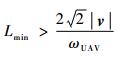
|
(8) |
由式(8) 可以看出,速度v下的引导长度变化范围,由无人机飞行控制系统的带宽ωUAV所决定。根据非线性制导方法及后续的滚转角控制回路,ωUAV可近似用无人机横向滚转通道的闭环控制带宽ωH表示。
求解ωUAV的问题进而转换成求解滚转通道的传递函数H(s)的问题。首先要求出以副翼偏转增量Δδa为控制输入,滚转角增量Δϕ为输出的传递函数G(s)(主要考虑副翼控制实现无人机滚转)。
建立无人机的横侧向线性小扰动运动方程,状态向量包括侧滑角增量Δβ、滚转角速度变化量Δp、偏航角速度变化量Δr和滚转角增量Δϕ,控制输入向量包括副翼偏转增量Δδa以及方向舵变化量Δδr,写成矩阵的形式如下[18]:
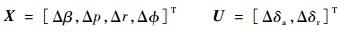
|
Ẋ=AX+BU为横侧向线性状态方程的标准式,其中矩阵A、B由量纲导数及其一导数组成,具体如式(9)~式(11)。

|
(9) |
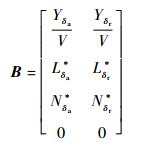
|
(10) |
式中:
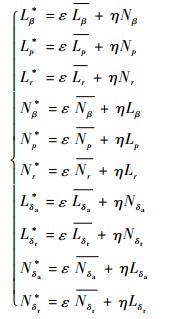
|
(11) |
其中:横侧向的量纲导数及其相对应的量纲一导数详见文献[18]。由此列出特征行列式|sI-A|。
根据克莱姆法则,利用特征行列式和控制矩阵B,可求出所需要的传递函数。
本文选取水平飞行状态作为基准运动,此时航迹倾角μe=0,便于对其进行理论分析。另外再考虑到由于副翼偏转所产生的侧力和偏航力矩的效应相对较小,即Yδa/V和Nδa*可以忽略,又有Yr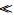
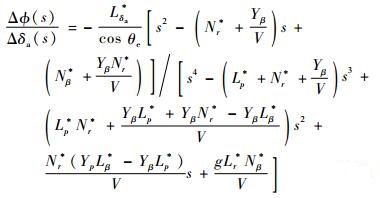
|
(12) |
通过AVL(Athena Vortex Lattice)估算出所研究飞机的各部分气动导数,文献[19]具体阐述了试验所用无人机的气动导数求解过程,并进而得到横侧向的量纲导数[18]。经过系统辨识的反复校正,得到副翼-滚转角通道的低阶近似传递函数:

|
(13) |
辨识传递函数的仿真结果与原辨识数据进行对比,如图 7所示。
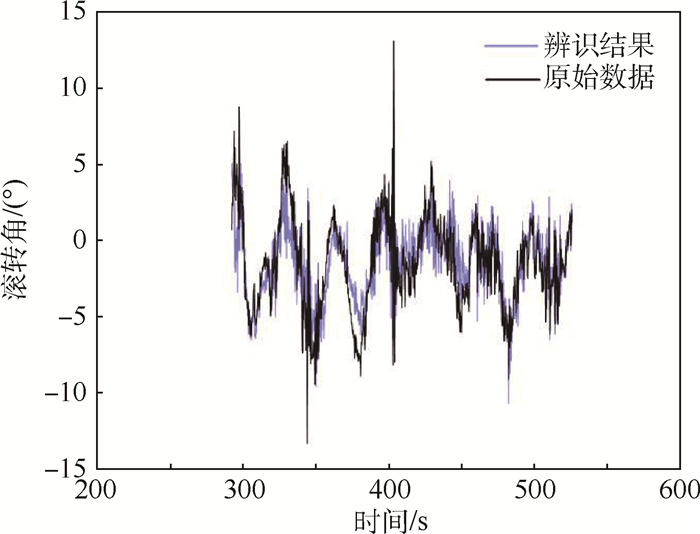
|
| 图 7 辨识结果与原始数据对比 Fig. 7 Comparison between identification results and initial data |
从图 7可以看出,辨识出的传递函数能较好地还原原始数据。在求得G(s)的基础上,设飞行系统的滚转角输入指令为ϕc,输出量为ϕa,两者偏差e为

|
(14) |
采用测速反馈控制进行滚转角回路的控制[20],可以解算出副翼偏转增量Δδa,并进而利用G(s)可得到滚转角通道的闭环控制传递函数H(s),系统结构如图 8所示。
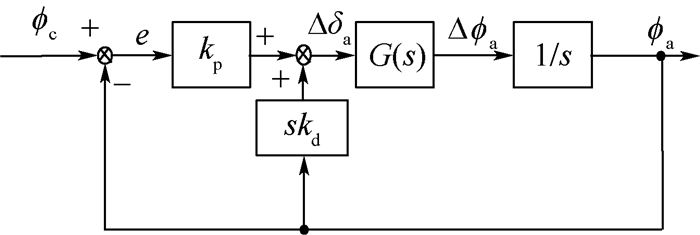
|
| 图 8 滚转通道闭环传递函数的框图 Fig. 8 Block diagram of roll channel closed-loop transfer function |
具体计算如下:

|
(15) |
代入相关参数,得
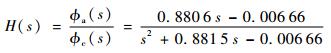
|
(16) |
H(s)的伯德图如图 9所示。从图 9得出控制带宽ωUAV大约是0.9,从而根据式(8) 可以求出速度v下的引导长度下限。
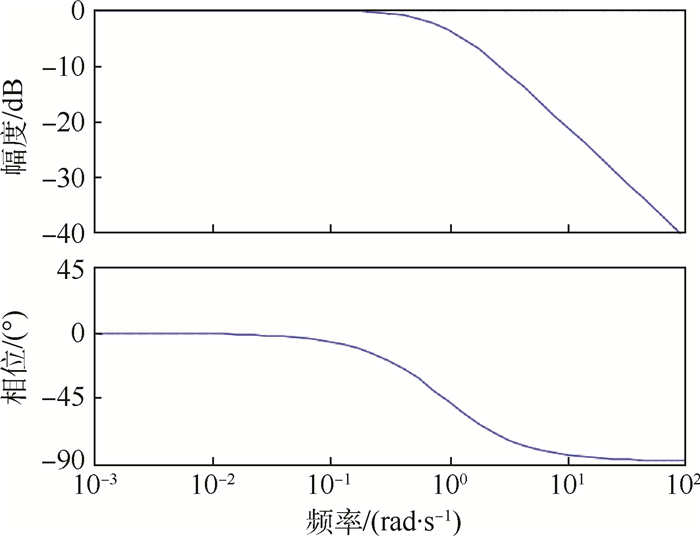
|
| 图 9 滚转通道闭环传递函数的伯德图 Fig. 9 Bode diagram of roll channel closed-loop transfer function |
为保证航迹跟踪的实时性,设无人机每个控制周期允许的引导长度计算时间为ta,以上述计算得到的引导长度下限为初始值,不断增加引导长度进行优化,直至计算时间大于ta时停止。根据仿真结果,对于试验所用的低速飞机(15~30 m/s),L的范围上限一般在下限以上的80 m左右范围内,因此在确定引导长度的范围时可以综合考虑计算时间和经验值。
2.2 引导长度的评价准则设飞机当前位置坐标为f(xe, ye),引导长度L下的引导点坐标为(xref, yref),由飞机当前位置到引导点之间的预测航迹用圆弧近似表示,预测航迹的圆心坐标为(x0, y0),自适应引导长度的航迹跟踪方法原理图如图 10所示。

|
| 图 10 自适应引导长度的航迹跟踪方法原理图 Fig. 10 Illustrative diagram of path following method with adaptive guidance length |
为了对引导长度进行优化,在这里主要采用预测航迹与期望航迹之间的偏差评价引导长度的合理性。借鉴PLOS[5]的航迹跟踪方法,在这里采用预测航迹与期望航迹之间的最大的距离偏差dmax及引导点处的航向偏差Δθ作为评价准则,评价函数P可以表示为
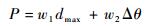
|
(17) |
式中:w1和w2分别为距离偏差和航向偏差的权重,且w1=1-w2。
w1的值随着侧偏距的变化而变化,可通过式(18) 进行计算:

|
(18) |
式中:Lmin、n0分别为飞行试验和理论仿真得到的经验值,通常n0取10~15。
根据上述评价准则,设计如下的引导长度自适应计算方法:
1) 当引导长度为L时,对预测航迹和期望航迹分别进行等间距离散采样,得到L个采样点。分别为(x01, y01),(x02, y02),…,(x0n, y0n)和(x′01, y′01),(x′02, y′02),…,(x′0n, y′0n),其中1≤n≤L。
2) 分别计算期望航迹与预测航迹上采样点的坐标:对于期望航迹上的采样点坐标计算,首先计算出飞机当前位置在期望轨迹上的投影点(x00, y00)。计算过程如式(19):

|
(19) |
式中:dcr_i为飞机当前点到期望轨迹上某点pi的距离;N为离散采样点个数。
根据(x00, y00)与引导点的坐标,易得期望轨迹上的采样点的坐标。对于预测航迹上的采样点坐标计算,首先应求解出预测轨迹的圆心(x0, y0)的坐标值。利用图 10所示的几何关系,可得
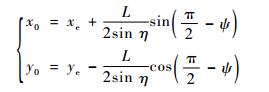
|
(20) |
在此基础上,类似于式(21) 的逆过程,可得到预测轨迹上相对应的采样点坐标,如下:
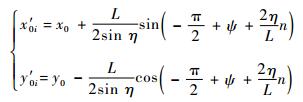
|
(21) |
3) 计算期望航迹与预测航迹的距离偏差。根据对应采样点的坐标,通过迭代搜索,计算出预测航迹与期望航迹的最大距离偏差dmax,过程如下:

|
(22) |
式中:dn为预测航迹与期望航迹对应采样点之间的距离。
4) 计算期望航迹与预测航迹在引导点处的角度偏差:其中期望航迹的航向θ1可通过式(23) 求得
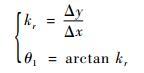
|
(23) |
式中:Δx、Δy分别为期望轨迹在引导点附近沿x轴、y轴的微小变化量; kr为期望航迹在引导点处的切线斜率。
预测航迹在引导点处与x轴正方向的夹角θ2可以通过η和ψ求得
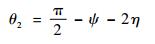
|
(24) |
从而得出角度偏差Δθ:
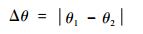
|
(25) |
5) 通过对不同的引导长度进行评价得到最优的引导长度Lbest,过程如下:
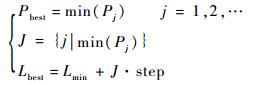
|
(26) |
式中:j为当前控制周期对引导长度的离散采样数;Pj为不同引导长度下的评价函数值;Pbest为最优评价函数值;J为对应最优评价函数值的采样周期数;step为引导长度的采样步长。
3 仿真验证 3.1 复杂航迹跟踪效果验证设无人机当前位置为(0, 0),初始航向角30°,飞行速度v=20 m/s。现要分别跟踪y1、y22条曲线航迹, 其表达式如下:

|
(27) |
根据已知条件,首先确定引导长度的范围。将已知条件代入式(8),可得引导长度下限Lmin=60 m。内回路的控制频率为50 Hz,即ta=0.01 s,以较好地保证控制的实时性。设引导长度的采样步长step=5,n0=5,引导长度的上限和权重值由算法的实时性自动确定。利用自适应引导长度的方法进行航迹跟踪,得到如图 11~图 16所示结果。
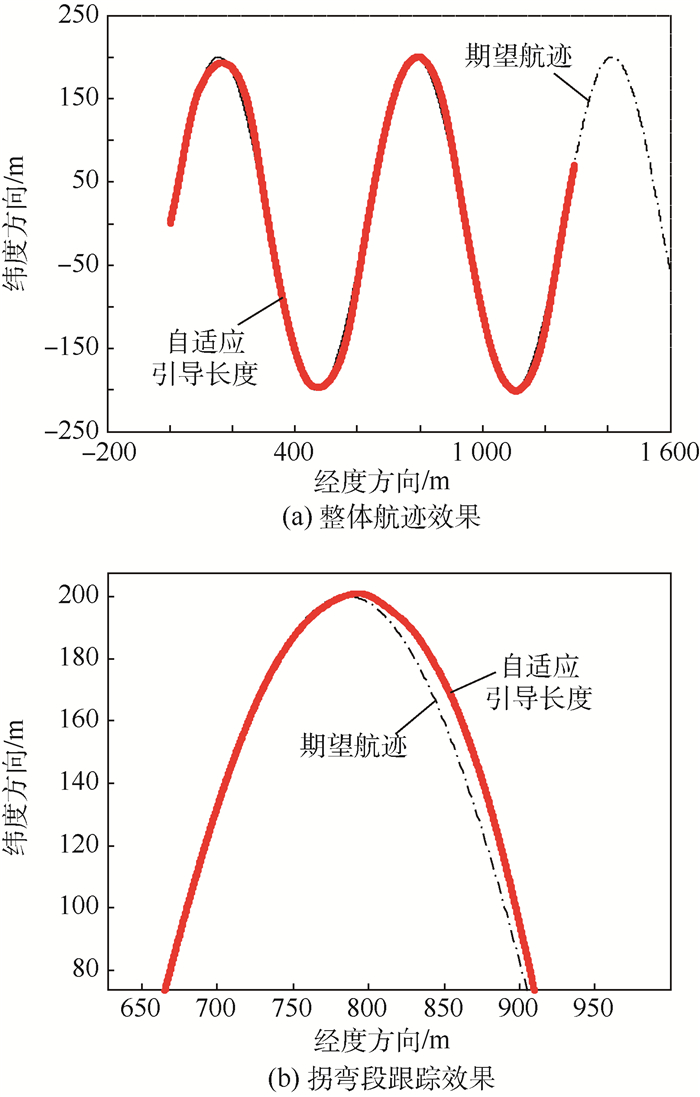
|
| 图 11 跟踪曲线y1时航迹示意图 Fig. 11 Schematic of flight track when tracking curve y1 |

|
| 图 12 跟踪曲线y1时滚转角示意图 Fig. 12 Schematic of roll angle when tracking curve y1 |
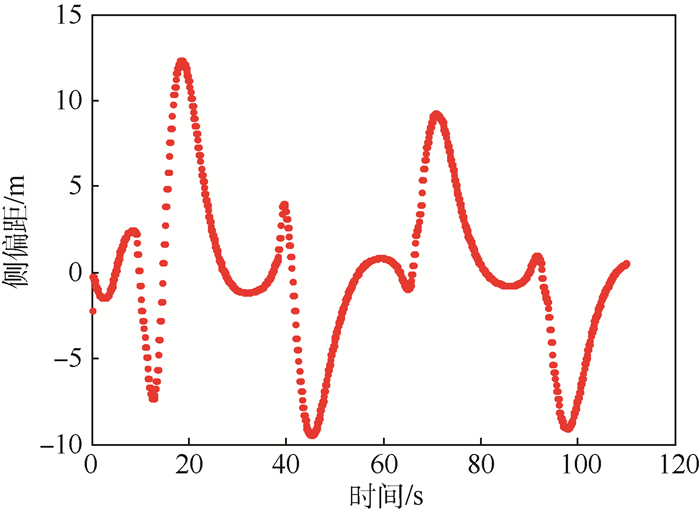
|
| 图 13 跟踪曲线y1时侧偏距示意图 Fig. 13 Schematic of cross track error when tracking curve y1 |

|
| 图 14 跟踪曲线y2时航迹示意图 Fig. 14 Schematic of flight track when tracking curve y2 |
|
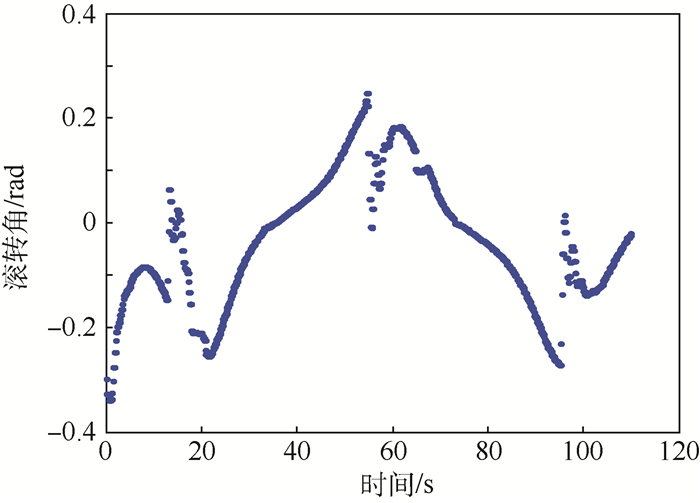
| 图 15 跟踪曲线y2时滚转角示意图 Fig. 15 Schematic of roll angle when tracking curve y2 |
|
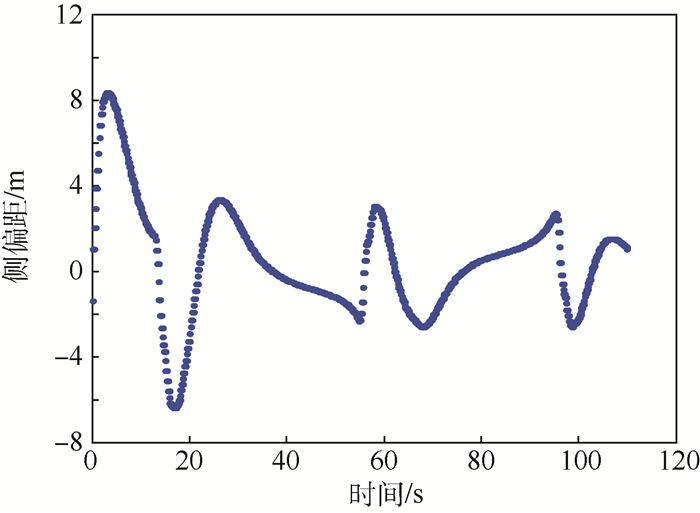
| 图 16 跟踪曲线y2时侧偏距示意图 Fig. 16 Schematic of cross track error when tracking curve y2 |
由图 11、图 14的航迹图可以看出,自适应引导长度方法对正弦轨迹有较好的跟踪效果,结合侧偏距变化图可以看出,只有在跟踪曲线y1的峰值处会有较大误差,其余精度达到2 m以内。
对拐弯处出现较大侧偏距的原因进行分析,从图 12的35~45 s可以看出,无人机的滚转角在追踪y1峰值时接近最大限幅0.6rad,而当周期增大1倍、峰值处曲率变化较平缓时(如图 14曲线y2),如图 15的50~70 s所示,在满足无人机的静态约束要求的情况下(滚转角约0.2 rad),拐弯段可以达到较高的追踪精度(2 m以内)。因此图 13所示的峰值处误差是无人机自身转弯半径的限制所致。
3.2 方法改进前后对比设无人机当前位置为(-100, 100) m,航向角45°,期望无人机沿着y3=x的直线飞往位于(600, 600) m的大本营,飞行速度大小v=25 m/s。在飞向大本营的过程中,突然发现目标点处有敌情,要求无人机迅速改到以大本营为圆心,200 m为半径的圆形航线上对敌情进行监视。
针对该实际问题,与3.1节类似,先确定引导长度下限,由式(8) 求出Lmin=80 m,其他参数与3.1节保持不变,将基于定引导长度(下限)飞行的效果与改进后方法进行对比,得到如图 17~图 20所示结果。
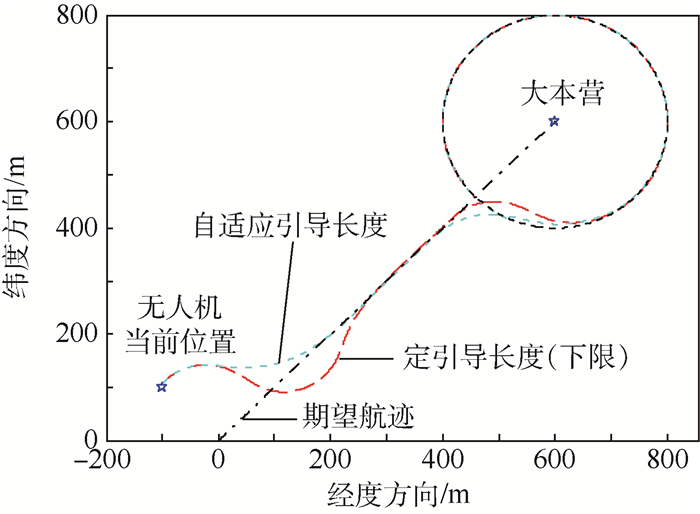
|
| 图 17 定引导长度与自适应引导长度航迹对比 Fig. 17 Comparison of flight track between fixed guidance length and adaptive guidance length |
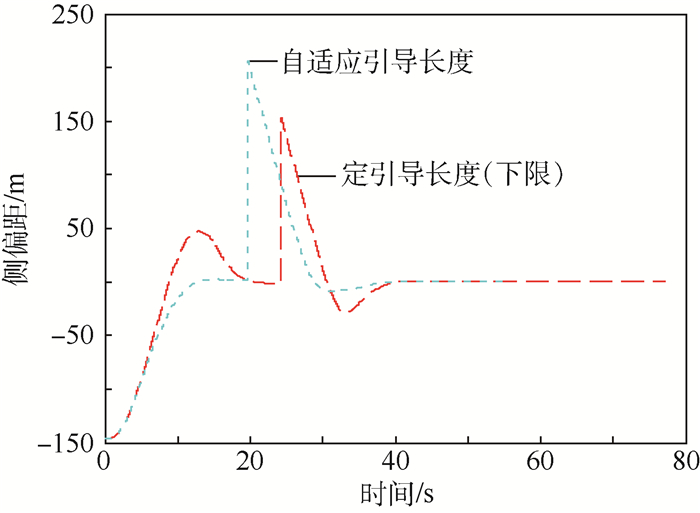
|
| 图 18 侧偏距对比 Fig. 18 Comparison of cross track error |
|
| 图 19 滚转角对比 Fig. 19 Comparison of roll angle |
|
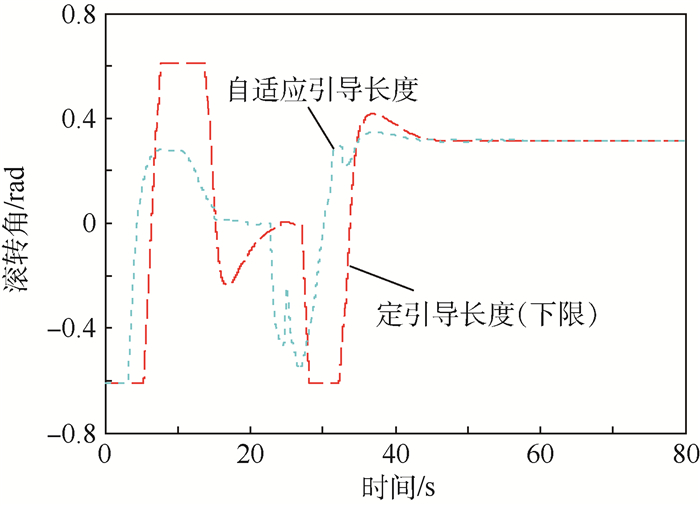
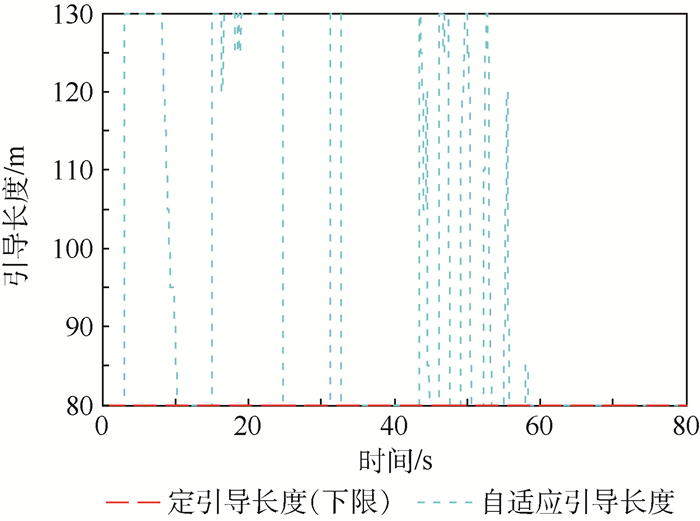
| 图 20 引导长度变化对比 Fig. 20 Comparison of guidance length variation |
通过图 17和图 18可以看出,自适应引导长度的航迹跟踪方法与定引导长度的算法相比,在跟踪精度及飞行的稳定性上有一定的优势,特别是在消除较大的初始偏差和航路点切换方面。
在较大初始偏差的情况下,基于自适应引导长度的航迹跟踪方法,仅利用12 s的时间就收敛到期望航迹,实现了对直线段的高精度(侧偏距5 m以内)稳定跟踪,而基于定引导长度(引导长度下限)的航迹跟踪方法,则需要20 s的时间,在切换到圆形航线的过程中也存在着类似的规律。结合图 19、图 20进行分析,当无人机当前位置与期望航迹有较大偏差时,无人机以合适的引导长度进行飞行,既保证滚转角较小,飞机平稳飞行,又能快速收敛到期望航迹。当侧偏距减小到一定范围时,自动地选择较短的引导长度飞行,可迅速减小跟踪误差并避免振荡现象。在无人机稳定跟踪阶段,2种方法的跟踪精度都较高,且均能保持平稳的飞行。
综上,与定引导长度的航迹跟踪方法相比,自适应引导长度的航迹跟踪方法能根据实时状态,自动选择合适的引导长度,既保证飞机安全平稳地飞行,又能保证高精度的航迹跟踪,较好地实现了稳定性与航迹跟踪精度地统一。
4 结论本文基于航迹引导点的非线性制导方法,对无人机的航迹跟踪问题进行了研究。分析和仿真的结果表明:
1) 在大的尺度下,飞行速度越高,引导长度越长,两者之间必须保证满足飞行器的动态特性;在小的尺度下,引导长度影响航迹跟踪的精度与飞机的稳定性。
2) 引导长度的搜索范围受无人机飞行控制系统带宽的影响,后者可近似用无人机横向滚转通道的闭环控制带宽计算。
3) 引导长度自适应的航迹跟踪方法能较好地跟踪各种复杂航迹,除受无人机自身转弯半径限制的飞行段以外,跟踪精度能达到2 m以内。
4) 引导长度自适应的航迹跟踪方法可以较好地解决较大的初始偏差情况下及航路点切换过程中易出现的超调严重、滚转角过大、无人机飞行不稳定等问题。
将提出的方法拓展到三维空间、考虑风场的影响是下一步值得研究的内容。
| [1] | TAKESHI Y, KEISUKE E, HIROYUKI T.Advanced pure pursuit guidance via sliding mode approach for chase UAV[C]//AIAA Guidance, Navigation, and Control Conference.Reston: AIAA, 2009:6298-6304. |
| [2] | SUJIT P B, SRIKANTH S, JOAO B S.An evaluation of UAV path following algorithms[C]//European Control Conference.Piscataway, NJ:IEEE Press, 2013:3332-3337. |
| [3] | HECHT C.Homing guidance using angular acceleration of the line of sight[R].Reston: AIAA, 1976: 2701-2706. |
| [4] | SUN M, ZHU R, YANG X.UAV path generation path following and gimbal control[C]// IEEE International Conference of Networking, Sensing and Control.Piscataway, NJ:IEEE Press, 2008:870-873. |
| [5] | RHEE I, PARK S, RYOO C K.A tight path following algorithm of an UAS based on PID control[C]//SICE Annual Conference, IEEE.Piscataway, NJ:IEEE Press, 2010:1270-1273. |
| [6] | LI C Y, JING W X. Application of PID controller to 2d differential geometric guidance problem[J]. Journal of Control Theory and Applications, 2007, 5 (3): 285–290. DOI:10.1007/s11768-006-6109-9 |
| [7] |
吴国强. 无人机航迹跟踪控制方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2010: 24-48.
WU G Q.The study of UAV flight path tracking control method[D].Harbin:Harbin Engineering University, 2010:24-48(in Chinese). http: //cdmd. cnki. com. cn/Article/CDMD-10217-1011019691. htm |
| [8] | RYSDYK R.UAV path following for constant line-of-sight[C]//AIAA"Unmanned Unlimited" Systems Technologies & Operations Aerospace Land & Sea Conference.Reston: AIAA, 2003:6626-6636. |
| [9] | OTHARI M, POSTLETHWAITE L, GU D W. UAV path following in windy urban environments[J]. Journal of Intelligent & Robotic Systens, 2014, 74 (3-4): 1013–1028. |
| [10] | DALE A L, ERIC W F, WILLIAM J P. Lyapunov vector fields for autonomous UAV flight control[J]. Journal of Guidance, Control, and Dynamics, 2008, 31 (5): 1220–1229. DOI:10.2514/1.34896 |
| [11] | NELSON D R, BARBER D B, MCLAIN T W, et al. Vector field path following for miniature air vehicles[J]. IEEE Transactions on Robotics, 2007, 23 (3): 519–529. DOI:10.1109/TRO.2007.898976 |
| [12] | SANGHYUK P, JOHN D, JONATHAN P H.A new nonlinear guidance logic for trajectory tracking[C]//AIAA Guidance, Navigation, and Control Conference and Exhibit.Reston:AIAA, 2004:1-16. |
| [13] | SANGHYUK P, JOHN D, JONATHAN P H. Performance and Lyapunov stability of a nonlinear path-following guidance method[J]. Journal of Guidance, Control, and Dynamics, 2007, 30 (6): 1718–1728. DOI:10.2514/1.28957 |
| [14] | OSBOME J, RYSDYK R.Waypoint guidance for small UAVs in wind[C]//AIAA Infotech, Aerospace Conference, Arlington.Reston:AIAA, 2005:459-470. |
| [15] | MAO Y H, CHEN Q Y, HOU Z X, et al.An improved nonlinear guidance law for unmanned aerial vehicles path following[C]//Proceedings of the 34th Chinese Control Conference.Piscataway, NJ:IEEE Press, 2015:5271-5276. |
| [16] |
方振平, 陈万春, 张曙光.
航空飞行器飞行动力学[M]. 北京: 北京航空航天大学出版社, 2005: 20-32.
FANG Z P, CHEN W C, ZHANG S G. Flight dynamics for aircraft[M]. Beijing: Beihang University Press, 2005: 20-32. (in Chinese) |
| [17] |
董芳. 无人机航迹跟踪技术的研究[D]. 南京: 南京航空航天大学, 2010: 37-42.
DONG F.Research on path tracking technology of UAV[D].Nanjing:Nanjing University of Aeronautics and Astronautics, 2010:37-42(in Chinese). http: //d. wanfangdata. com. cn/Thesis/Y1811068 |
| [18] |
吴森堂, 费玉华.
飞行控制系统[M]. 北京: 北京航空航天大学出版社, 2006: 75-100.
WU S T, FEI Y H. Flight control system[M]. Beijing: Beihang University Press, 2006: 75-100. (in Chinese) |
| [19] |
关键. 低速无人机动态气动特性数值模拟及布局研究[D]. 长沙: 国防科学技术大学, 2013: 40-62.
GUAN J.The numerical research on transient aerodynamic performances and configurations of low speed UAVs[D].Changsha:National University of Defense Technology, 2013:40-62(in Chinese). http: //cdmd. cnki. com. cn/Article/CDMD-90002-1015958195. htm |
| [20] |
胡寿松.
自动控制原理[M]. 北京: 科学出版社, 2013: 56-70.
HU S S. Automatic control principle[M]. Beijing: Science Press, 2013: 56-70. (in Chinese) |



