在航空航天、核反应堆控制、汽轮机械等工程领域,系统的安全性能越来越受到工程技术人员的关注。与此同时,系统设计也日趋大型化和复杂化。这些都对系统的可靠性设计分析提出了更高的要求。
系统由多个元器件按照特定关系连接构成,系统工作状态与元器件工作状态密切相关。一般情况下,元器件失效率为定值。然而,系统设备中广泛存在着各种不确定性因素。目前将这些不确定性因素归结为2类[1-4]:偶然不确定性和认知不确定性。偶然不确定性是因外界环境的改变等因素引起,它是随机的,而且不可提前预知。认知不确定性则是由于人们知识的缺乏、对系统设备和物理过程不了解等人为因素引起的。Zio等[5]指出,在实际工程系统中,这2种不确定性因素是普遍存在的。因此,在系统可靠性分析中,元器件的失效率一般不为定值,而将其设定为随机变量更符合实际情况[6-7]。当元器件失效率为随机变量时,系统失效概率函数为系统工作时间和元器件失效率的多元函数。
为了分析元器件失效率的不确定性对系统输出特征的影响,本文将从两方面来进行研究。一方面,当给定某一系统正常工作时间要求时,系统的失效概率只受元器件失效率的影响,因此,可以求解当元器件失效率具有不确定性时系统失效概率的概率密度函数,并可以预测分析在给定某一系统正常工作时间要求时,系统失效概率受元器件失效率不确定性的影响程度。另一方面,当给定某一系统失效概率阈值时,系统的正常工作时间只受元器件失效率的影响。此时,可以求解当元器件失效率具有不确定性时系统正常工作时间的概率密度函数,并预测分析在给定系统失效概率阈值时,系统正常工作时间受元器件失效率不确定性的影响程度。
重要性测度分析主要研究输入随机变量对结构系统输出响应的不确定性影响[8],其主要任务是对影响结构系统输出响应不确定性的输入随机变量进行重要性排序。分析输入随机变量的重要性排序结果,对重要性程度大的基本变量重点考虑,忽略重要性程度低的基本变量,从而对结构系统工程设计和优化提供理论指导。基于这些原因,很多学者提出了许多重要性测度指标和相应的求解方法。一般可将重要性测度分为3类:基于非参数的方法[9]、基于方差的方法[10]和矩独立方法[8]。基于方差的方法能简单有效地反映输入对输出不确定性的影响程度,因而应用最为广泛。本文将采用基于方差的重要性测度分析方法,建立2种新的重要性测度指标,定量分析当给定系统工作时间要求和给定系统失效概率阈值时,元器件失效率的不确定性对系统输出性能的影响程度。
在对系统输出特征(本文中指的是给定工作时间要求时系统的失效概率特征,以及给定失效概率要求时系统的正常工作时间特征)不确定性分析以及重要性分析中,主要任务是求解得到系统输出特征的概率密度函数以及求解输出特征的统计矩。可以采用蒙特卡罗模拟构建求解算法,然而该方法计算量太大,效率很低,不能被工程技术人员所接受。为此,本文将进一步采用基于分数矩的极大熵方法来进行输出特征的概率密度函数求解。分数矩通常可以包含大量整数矩的信息,因此,基于分数矩的极大熵方法将可以很精确地估计出变量的概率密度函数,尤其是尾部分布[11-13]。对于重要性分析中的各种统计矩的计算,本文则主要采用乘法降维的方法进行求解,将高维积分降成一维积分后,可以采用一维高斯积分来高效求得重要性分析中的各种统计矩。
本文首先简单介绍确定性动态系统失效的分析流程,然后提出一种新的动态系统失效的不确定性分析理论,并对给定条件下的系统元器件失效率进行重要性测度分析。引入基于分数矩的极大熵方法和乘法降维方法,并结合高斯积分的思想,对所提理论方法和指标进行求解。最后,通过2个工程算例,验证了所提方法理论的可行性和算法的高效性。
1 确定性失效率下系统失效分析假设某一系统含有n个元器件,其失效率为λ=[λ1 λ2 … λn]。一般元器件的失效时间服从指数分布,则第i个元器件的失效概率可表示为

|
(1) |
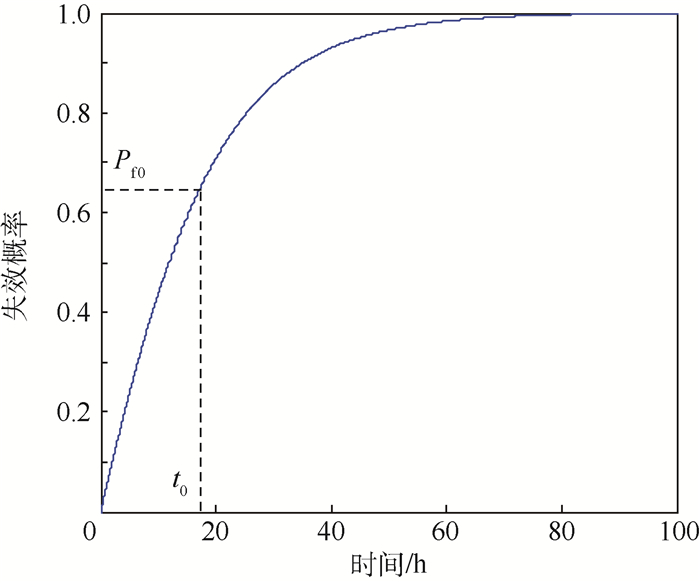
由系统中元器件的连接方式,可以得到系统的失效概率函数为Pf=G(t, λ),它是系统工作时间t和元器件失效率λ的函数。当元器件失效率λ为固定值时,系统失效概率Pf只与系统工作时间t有关。此时可以得到系统失效概率随系统工作时间变化的函数曲线如图 1所示。
|
| 图 1 系统失效概率随系统工作时间变化曲线 Fig. 1 Variation of system failure probability with system function time |
由图 1中可知,当给定某一系统正常工作时间要求t0时,就可以求得此时系统的失效概率值Pf0;同时若给定某一系统失效概率阈值Pf0时,也可以求得系统失效概率达到此阈值时,系统的正常工作时间t0。
2 不确定性失效率下系统失效分析Zio等[5]指出,由于受外界环境和人为的一些不可控因素影响,系统元器件的失效率一般并不是定值,将它处理为一个随机变量更为合理。在考虑不确定性因素的影响时,元器件的失效率一般设定为服从正态分布[6]、三角分布[6]和对数正态分布[7]等分布的随机变量。根据实际问题,本文中将元器件的失效率设定为服从对数正态分布的随机变量,则它的概率密度函数为
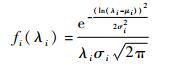
|
(2) |
式中:μi为失效率的均值;σi为失效率的标准差。
2.1 满足工作时间要求t0的失效概率预测分析当元器件失效率λ为随机变量时,系统失效概率函数Pf为系统工作时间t和元器件失效率λ的多变量函数。若给定某一系统工作时间要求t0,系统失效概率函数Pf变为元器件失效率λ的多变量函数Pf=G(λ),此时可采用以下蒙特卡罗模拟方法求解当系统工作时间达到t0时,系统的失效概率值Pf的分布特征。
1) 根据元器件失效率的概率分布特征,抽取失效率λ的N组样本点A(N×n):
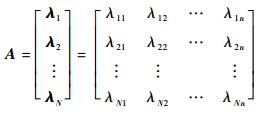
|
(3) |
2) 从样本矩阵A(N×n)任意抽取一组失效率样本点λk=[λk1 λk2 … λkn](k=1, 2, …, N),代入系统失效概率函数Pf=G(t, λ)中,那么就可以得到在给定系统工作时间要求t0时,系统的失效概率值Pfk=G(t0, λk)。
3) 重复步骤2),遍历元器件失效率样本A(N×n)中的所有样本点,求得失效率样本A(N×n)在给定系统工作时间要求为t0时,对应的系统失效概率样本[Pf1 Pf2 … PfN]。
4) 根据求得的[Pf1 Pf2 … PfN],采用核密度估计[14]等方法就可以得到系统失效概率的概率密度函数曲线,同时可以求出它的均值μPf、标准差σPf,以及满足某一置信度q要求的系统失效概率置信区间[Pf(t0, q), Pf(t0, q)]。
2.2 满足失效概率约束Pf0的正常工作时间预测分析当元器件失效率λ为随机变量时,系统失效概率函数Pf为系统工作时间t和元器件失效率λ的多变量函数。若给定某一系统失效概率阈值Pf0,也可以采用蒙特卡罗模拟方法求解当系统满足失效概率约束阈值Pf0要求时系统正常工作时间t的分布特征,其分析步骤如下:
1) 根据元器件失效率的概率分布特征,抽取失效率λ的N组样本点A(N×n)。
2) 从样本A(N×n)任意抽取一组失效率样本点λk=[λk1 λk2 … λkn](k=1, 2, …, N),代入系统失效概率函数Pf=G(t, λ)中,此时Pf仅为系统工作时间的单变量函数,即Pfk=G(t, λk)。由第1节所述,可以求得系统失效概率随系统工作时间的变化曲线。
3) 当设定系统失效概率阈值为Pf0时,由上述曲线可得对应的系统工作时间tk=G-1(Pfk, λk)。
4) 重复步骤2) 和步骤3),遍历元器件失效率样本A(N×n)中的所有样本点,求得失效率样本A(N×n)在满足系统失效概率阈值Pf0要求时,对应的系统工作时间样本[t1 t2 … tN]。
5) 根据求得的[t1 t2 … tN],采用核密度估计[14]等方法就可以得到系统正常工作时间t的概率密度函数曲线,同时可以求出它的均值μt和标准差σt,以及满足某一置信度q要求前提下的系统正常工作时间的置信区间[t(Pf0, q), t(Pf0, q)]。
3 元器件失效率重要性测度分析元器件失效率的不确定性会影响系统输出的不确定性。由第2节分析可知,当元器件失效率为随机变量时,系统输出特征的不确定性将由元器件失效率的不确定性来决定。本节的重要性测度分析研究元器件失效率对系统失效概率和正常工作时间不确定性的影响程度,可以区分出对系统失效概率和正常工作时间影响较大的关键元件,从而对这些关键元器件重点考虑,优化系统结构。
3.1 给定系统工作时间要求t0时元器件失效率对系统失效概率的影响分析假设给定系统工作时间要求t0,当元器件失效率λ按其分布规律取值时,由2.1节所述方法可求得此时系统失效概率Pf的分布规律。为了合理衡量系统元器件失效率λ对系统失效概率Pf的影响程度,可定义如式(4) 所示的基于系统失效概率方差的重要性测度指标:
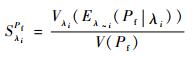
|
(4) |
式中:SλiPf为在给定系统工作时间要求t0时,第i个元器件失效率的重要性测度指标;V(Pf)为系统失效概率的无条件方差;Eλ~i(Pf|λi)为系统失效概率的条件均值;Vλi(Eλ~i(Pf|λi))为系统失效概率条件均值的方差。
3.2 给定系统失效概率阈值Pf0时元器件失效率对系统正常工作时间的影响分析假设给定系统失效概率阈值为Pf0,当元器件失效率λ按其分布规律取值时,由2.2节所述方法可求得此时系统正常工作时间t的分布规律。为了合理衡量系统元器件失效率λ对系统正常工作时间t的影响程度,定义如式(5) 所述基于系统正常工作时间方差的重要性测度指标:
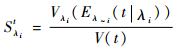
|
(5) |
式中:Sλit为在给定系统失效概率阈值Pf0时,第i个元器件失效率的重要性测度指标;V(t)为系统正常工作时间的无条件方差;Eλ~i(t|λi)为系统正常工作时间的条件均值;Vλi(Eλ~i(t|λi))为系统正常工作时间条件均值的方差。
4 高效求解算法本节采用文献[15]中基于分数矩的极大熵方法来求解第2节所述系统失效概率和正常工作时间的概率密度函数。对于第3节提出的重要性测度指标,采用基于乘法降维的方法来求解内层条件均值,然后用高斯积分求解外层条件方差,以下给出所提方法的基本原理和具体求解流程。
4.1 基于分数矩的极大熵方法求解概率密度函数结构系统输出响应Y的概率密度函数为fY(y),则求解fY(y)的极大熵准则模型为
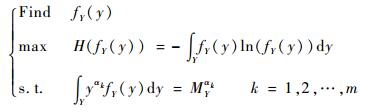
|
(6) |
式中:H(fY(y))为输出响应Y的信息熵;MYαk为输出响应Y的αk阶分数矩。
在输出响应Y的分数矩约束下,使得输出响应Y的信息熵H(fY(y))达到最大就可得fY(y)的近似估计函数

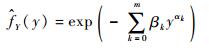
|
(7) |
式中:α=[α0 α1 … αm]T, α0=0;β=[β0 β1 … βm]T为拉格朗日乘子,且有β0= 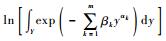
α和β的求解,根据文献[16]所述,引入K-L交叉熵(Kullback-Leibler cross-entropy),fY(y)与
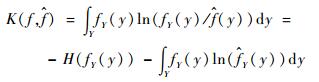
|
(8) |
由于H(fY(y))是Y的真正密度对应的熵,因此它独立于α和β。将式(7) 中
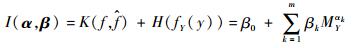
|
(9) |
根据定义,fY(y)与
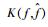


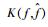
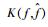

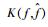
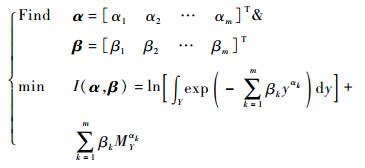
|
(10) |
式中:嵌套的分数矩MYαk可采用文献[13]所述乘法降维的方法进行高效求解。至此,输出响应Y的概率密度函数
假设结构系统输出响应功能函数Y=G(X),其中X=[X1 X2 … Xn]T(n为输入变量维数)。文献[13]给出的输出响应Y的α阶分数矩的乘法降维求解公式为
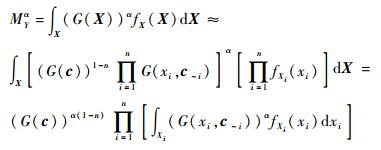
|
(11) |
式中:fX(X)为输入变量X的联合概率密度函数,fXi(xi)为输入变量Xi的边缘概率密度函数,输入变量X均值向量c=[c1 c2 … cn]T,c~i=[c1 c2 … ci-1 ci+1 … cn]T为除Xi的输入变量X的均值向量。
由式(11) 可看出,输出响应Y的α阶分数矩的n元积分问题可以由n个一元函数积分的乘积近似计算获得,而一元积分可以采用高斯积分来完成。常用分布类型的高斯积分表达式、高斯积分点及对应权重系数可查阅文献[13]。显然此公式也可以用来求解整数阶矩,例如输出响应Y的均值和方差。
4.3 系统失效概率和正常工作时间的概率密度函数高效求解流程1) 满足工作时间要求t0的系统失效概率的概率密度函数求解。
步骤1 由元器件失效率的分布特征,获取失效率λ的高斯积分点及对应权重。
步骤2 根据系统失效概率函数Pf=G(t, λ),由4.2节所述,求取系统失效概率Pf的各阶分数矩。
步骤3 采用4.1节所述极大熵方法估计系统失效概率的概率密度函数。
2) 满足系统失效概率阈值Pf0的系统正常工作时间的概率密度函数求解。
步骤1 由元器件失效率的分布特征,获取失效率λ的高斯积分点及对应权重。
步骤2 根据系统正常工作时间t=G-1(Pf, λ),由4.2节所述,求取满足条件的系统正常工作时间t的各阶分数矩。
步骤3 采用4.1节所述极大熵方法估计系统正常工作时间的概率密度函数。
4.4 重要性测度指标的高效求解流程本文第3节给出了2种重要性测度指标,以式(4) 为例,采用基于乘法降维和高斯积分相结合的方法来进行重要性测度指标的高效求解。
步骤1 根据输入变量λi的概率分布特征,得到对应的K点的高斯积分节点pk和对应权重系数wk(k=1, 2, …, K)。
步骤2 固定输入变量λi在点pk(k=1, 2, …, K)时,由4.2节所述乘法降维方法,求得式(4) 中的V(Pf)和Eλ~i(Pf|pk)。
步骤3 式(4) 中的外层条件方差则可以采用K点高斯积分求解得到:
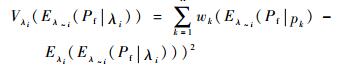
|
(12) |
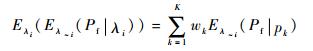
|
(13) |
至此,式(4) 中所有量均已求出。式(5) 的求解也可按照类似方法求解,这里不再赘述。
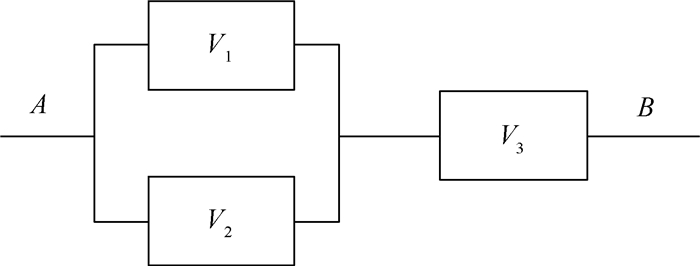
5 算例分析 5.1 阀门控制系统图 2所示为一个阀门控制系统[17],系统由V1、V2、V3 3个部件组成,系统功能定义为从A到B流体通道畅通,阀门正常状态为“通”,失效状态为“断”。3个部件的失效率服从对数正态分布,其参数如表 1所示。系统的失效概率函数为:Pf=Pf1Pf2+Pf3-Pf1Pf2Pf3,其中Pf1、Pf2、Pf3分别为部件1、2、3的失效概率。
| λi | 均值/10-2 | 方差/10-5 |
| λ1 | 4 | 2 |
| λ2 | 2 | 1 |
| λ3 | 1 | 0.5 |
1) 给定阀门控制系统工作时间要求为t0=30 h,预测分析系统失效概率Pf的取值规律及元器件失效率λi的重要性测度指标。
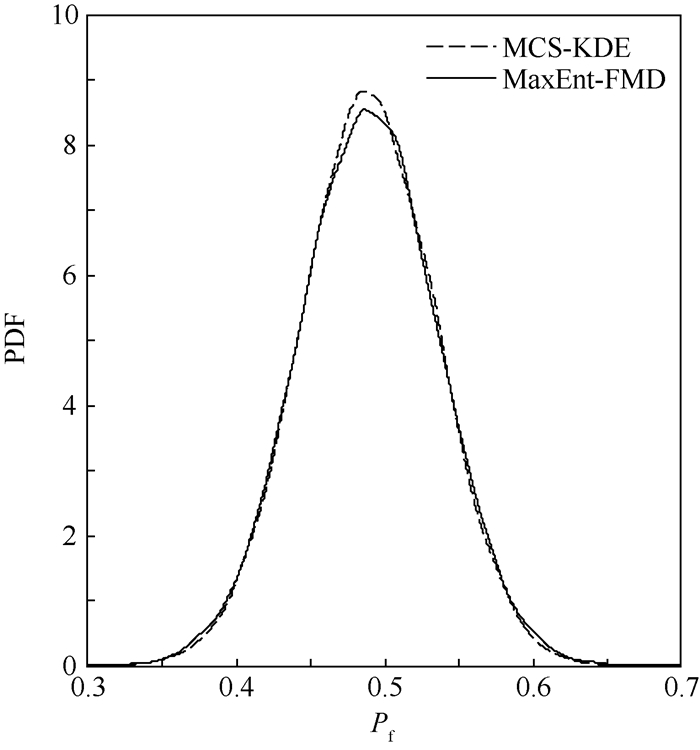
采用基于蒙特卡罗的核密度估计(MCS-KDE)方法和本文建立的基于分数矩的极大熵(MaxEnt-FMD)方法求解得到此时系统失效概率(Pf)的概率密度函数(PDF)曲线如图 3所示。
|
| 图 3 阀门控制系统失效概率的概率密度曲线 Fig. 3 Probability density curves of failure probability of valve control system |
表 2中给出了分别采用2种方法求解得到系统失效概率的概率密度函数的均值、标准差、95%置信度条件下的系统失效概率置信区间和计算量。综合图 3和表 2可以看出,MaxEnt-FMD方法和MCS-KDE方法求得的阀门控制系统失效概率的概率密度曲线基本一致,其均值和标准差也十分接近,满足精度要求。MaxEnt-FMD功能函数调用次数仅为16,计算效率优于MCS-KDE方法。
| 方法 | μPf | σPf | 置信区间(95%) | 计算量 |
| MCS-KDE | 0.489 3 | 0.045 1 | [0.401 2, 0.578 0] | 1×103 |
| MaxEnt-FMD | 0.489 4 | 0.045 6 | [0.400 0, 0.578 8] | 16 |
本文第3节给出了在给定系统工作时间要求时,元器件失效率重要性测度的计算公式。分别采用蒙特卡罗模拟(MCS)方法和本文建立的高斯积分结合基于乘法降维的方法来进行求解,计算结果如表 3所示。
| 方法 | λ1 | λ2 | λ3 | 计算量 |
| MCS | 0.090 2 | 0.353 1 | 0.569 0 | 4×106 |
| 本文方法 | 0.089 8 | 0.354 0 | 0.567 1 | 181 |
表 3中给出了2种方法求解得到的指标结果和调用功能函数的计算量。从表 3中可以看出,MCS方法作为对比参照解,在满足精度要求的前提下,本文所提方法能高效地求得指标结果,计算量很少。2种方法所得在此条件下的元器件失效率排序相同,均为λ3>λ2>λ1。表明在此阀门控制系统中,系统的失效概率受元器件V3失效率的影响最大。在实际操作时,应重点关注元器件V3的工作状况,以保证系统正常运行。
2) 给定阀门控制系统失效概率阈值为Pf0=0.2,预测分析系统正常工作时间t的取值规律及元器件失效率λi的重要性测度指标。
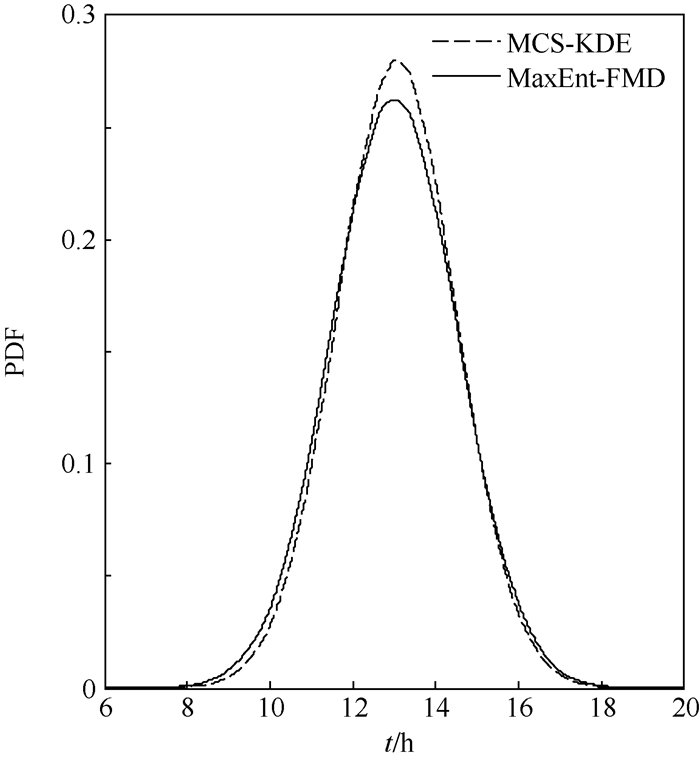
图 4所示为采用MCS-KDE方法和MaxEnt-FMD方法求解得到的此时系统正常工作时间概率密度曲线。表 4中给出了此概率密度曲线对应的均值、标准差和95%置信度要求的系统正常工作时间的置信区间,同时也给出了2种方法计算功能函数的总次数。
|
| 图 4 阀门控制系统工作时间的概率密度曲线 Fig. 4 Probability density curves of function time of valve control system |
| 方法 | μt | σt | 置信区间(95%) | 计算量 |
| MCS-KDE | 13.058 6 | 1.424 8 | [10.266 0, 15.851 2] | 142 172 |
| MaxEnt-FMD | 13.010 3 | 1.511 5 | [10.047 8, 15.972 8] | 2 279 |
从图 4中可以看出,2种方法计算得到的系统正常工作时间概率密度曲线近似相同。由表 4可知MCS-KDE方法和MaxEnt-FMD方法计算的概率密度函数分布参数也近似相等,满足精度要求,而MaxEnt-FMD方法的计算次数小于MCS-KDE方法的计算总次数,效率很高。
表 5所示为采用MCS方法和本文所提方法计算得到的在给定系统失效概率阈值时,元器件失效率的重要性测度指标结果。从表中数据可以看出,在满足精度要求的前提下,采用2种方法得到的计算结果近似相同;同时,本文所提方法的总计算次数很少,很大程度上提高了该重要性测度指标的求解效率。2种方法所得该条件下元器件失效率的重要性排序相同:λ3>λ2>λ1。这说明在此工作条件下,阀门控制系统元器件V3的失效率对系统正常工作时间影响最大,应重点关注。
| 方法 | λ1 | λ2 | λ3 | 计算量 |
| MCS | 0.060 2 | 0.201 2 | 0.786 5 | 2.36×108 |
| 本文方法 | 0.067 9 | 0.189 9 | 0.780 3 | 26 656 |
5.2 民用飞机电液舵机系统
相比于军用飞机,大型民用飞机结构复杂,功用较多,而且对可靠性的要求更高。本文选取文献[18]中的国外民用飞机舵面所采用的电液舵机系统进行分析验证。
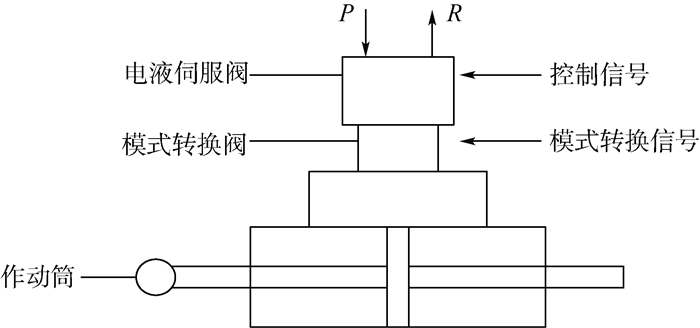
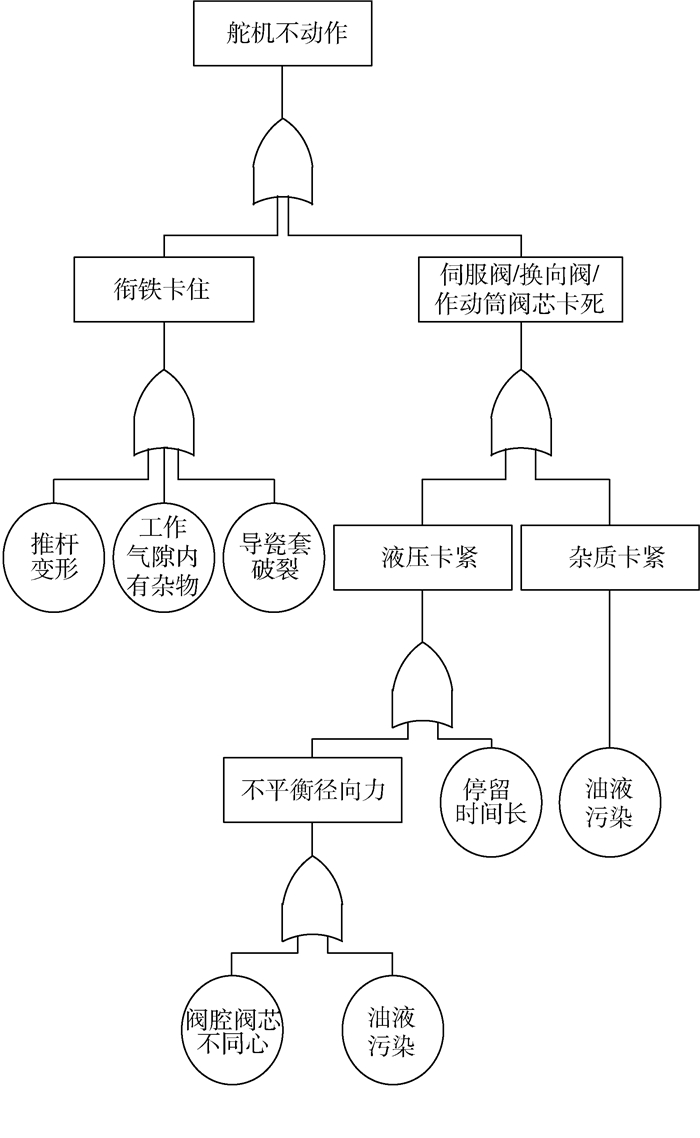
空客A系列飞机主控制面舵机的基本结构如图 5所示[18]。电液舵机系统常见的故障形式有:衔铁卡住(导瓷套破裂、工作气隙内有杂物、推杆变形等)、伺服阀/换向阀/作动筒阀芯卡死(杂质卡紧、液压卡紧)等。根据电液舵机系统的组成和工作原理,以“舵机不动作”为系统失效事件,构建系统故障树如图 6所示[18],可求得系统的失效概率函数Pf(t, λ)。表 6给出了构成系统的各个底事件的失效率分布参数,均服从对数正态分布。其中,λi(i=1, 2, …, 6) 分别代表以下底事件的失效率:“1推杆变形”、“2工作气隙内有杂物”、“3导瓷套破裂”、“ 4阀腔阀芯不同心”、“5油液污染”、“6停留时间长”。
| λi | 均值/10-7 | 方差/10-14 |
| λ1 | 3.5 | 2 |
| λ2 | 2 | 1 |
| λ3 | 3 | 1.5 |
| λ4 | 10 | 5 |
| λ5 | 6 | 5 |
| λ6 | 2.5 | 1 |
1) 给定飞机电液舵机系统工作时间要求为t0=5 000 h,预测分析系统失效概率Pf的取值规律及底事件失效率λi的重要性测度指标。
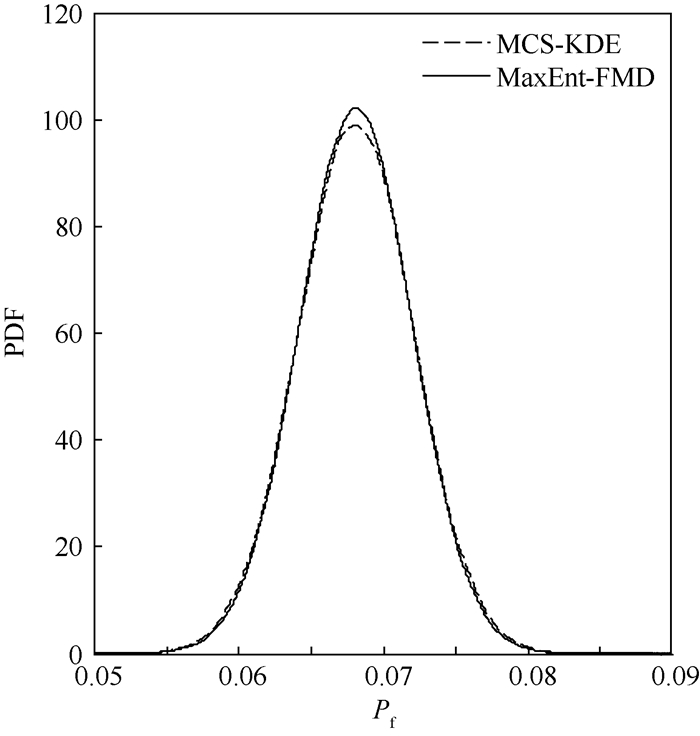
采用MCS-KDE方法和MaxEnt-FMD方法计算得到此时系统失效概率的概率密度函数如图 7所示。从图中可以看出2种方法求得的概率密度曲线基本相同。表 7给出了2种方法计算得到的该曲线分布参数和95%置信度要求的系统失效概率的置信区间,结果也十分接近。表中最后一列为调用功能函数总次数,MCS-KDE方法计算次数为1×105,而MaxEnt-FMD方法的计算次数仅为31,计算效率得到很大提高。
|
| 图 7 飞机电液舵机系统失效概率的概率密度曲线 Fig. 7 Probability density curves of failure probability of aircraft electro-hydraulic actuator system |
| 方法 | μPf | σPf | 置信区间(95%) | 计算量 |
| MCS-KDE | 0.068 1 | 0.004 0 | [0.060 3, 0.075 9] | 1×105 |
| MaxEnt-FMD | 0.068 1 | 0.003 9 | [0.060 5, 0.075 7] | 31 |
表 8为给定飞机电液舵机系统工作时间要求为t0=5 000 h时,采用MCS和本文所提方法计算得到的系统底事件失效率重要性测度指标。在给定精度要求的前提下,2种方法所得结果近似相同。由表 8最后一列功能函数的总次数(计算量)可知,本文所提方法的计算效率高于MCS方法。2种方法计算得到的底事件失效率排序均相同,其中λ4、λ5的重要性指标值较大。即对此飞机电液舵机系统油液污染和阀腔阀芯不同心对系统的失效概率影响较大,应及时清理系统中的油液污染问题,检查阀腔阀芯的安装工况,保证飞机电液舵机系统的正常运转。
| 方法 | λ1 | λ2 | λ3 | λ4 | λ5 | λ6 | 计算量 |
| MCS | 0.068 2 | 0.032 3 | 0.050 2 | 0.165 2 | 0.655 1 | 0.031 5 | 7×107 |
| 本文方法 | 0.065 2 | 0.032 6 | 0.048 9 | 0.162 9 | 0.651 7 | 0.032 0 | 811 |
2) 给定飞机电液舵机系统失效概率阈值为Pf0=0.01,预测分析系统正常工作时间t的取值规律和底事件失效率λi的重要性测度指标。
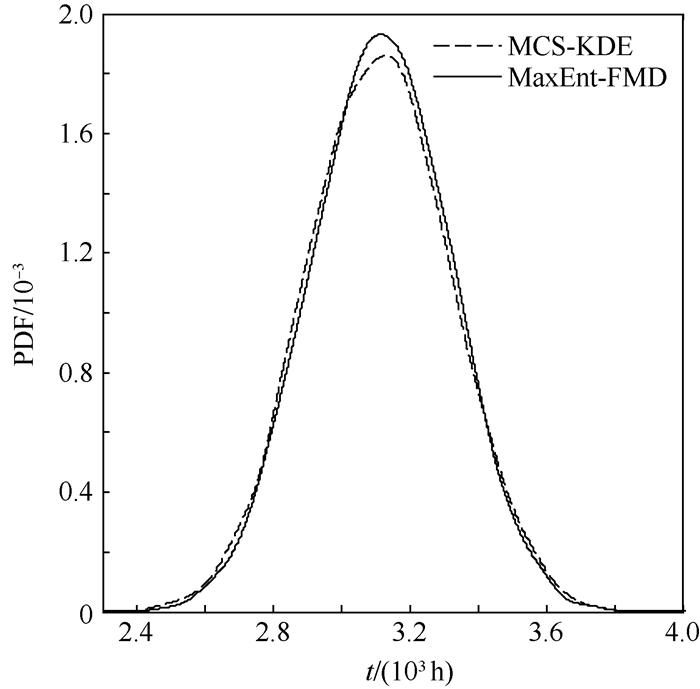
采用MCS-KDE和MaxEnt-FMD求解得到此时系统正常工作时间的概率密度曲线如图 8所示。表 9中给出了分别采用2种方法求解得到系统正常工作时间的概率密度函数的分布参数、95%置信度要求下的系统正常工作时间的置信区间和功能函数计算量。综合图 8和表 9可以看出,MaxEnt-FMD方法和MCS-KDE方法求得的飞机电液舵机系统正常工作时间的概率密度曲线基本一致,其均值和标准差也十分接近,满足精度要求。相比较,ManEnt-FMD方法的计算效率高于MCS-KDE方法。
|
| 图 8 飞机电液舵机系统工作时间的概率密度曲线 Fig. 8 Probability density curves of function time of aircraft electro-hydraulic actuator system |
| 方法 | μt | σt | 置信区间(95%) | 计算次数 |
| MCS-KDE | 3 111.78 | 207.21 | [2 705.65, 3 517.91] | 132 178 |
| MaxEnt-FMD | 3 115.26 | 203.46 | [2 716.48, 3 514.04] | 5 894 |
在给定系统失效概率阈值时,底事件失效率的重要性测度指标计算结果如表 10所示。从表中数据可知,在满足精度要求的前提下,2种方法计算得到的结果近似相同,而本文所提方法计算功能函数的总次数很少,计算效率高于MCS方法。MCS方法和本文所提方法计算所得底事件的重要性排序相同,可以发现该电液舵机系统的油液污染问题对系统正常工作时间的影响最大,应重点关注,及时清理油污。同时,阀腔阀芯不同心对系统正常工作时间也有较大影响,应及时检查阀腔阀芯的安装工况。
| 方法 | λ1 | λ2 | λ3 | λ4 | λ5 | λ6 | 计算量 |
| MCS | 0.040 8 | 0.031 2 | 0.059 2 | 0.145 2 | 0.621 1 | 0.031 5 | 5.97×109 |
| 本文方法 | 0.043 8 | 0.029 6 | 0.058 6 | 0.147 1 | 0.614 4 | 0.029 7 | 42 851 |
6 结论
1) 鉴于系统在实际工程应用中存在的各种不确定性问题,本文将系统元器件的失效率处理成含有不确定性的随机变量,在考虑失效率不确定性条件下,系统失效概率函数为失效率和系统工作时间的多变量函数。提出了一种新的系统失效性能(包括给定失效概率约束的正常工作时间和给定工作时间要求的失效概率)预测分析理论和2种新的元器件失效率重要性测度指标。本文提出的新理论方法能够合理预测系统失效概率和系统正常工作时间受系统元器件失效率不确定性的影响情况,为工程实际提供理论指导。
2) 为了能够高效求解所提性能和指标,引入基于分数矩的极大熵方法来求解概率密度函数,采用高斯积分和乘法降维求解2种新的重要性测度指标。所提方法的优势在于直接继承了极大熵方法和乘法降维的优越性,在很大程度上减少了调用功能函数的次数。
| [1] | PARRY G W, WINTER P W. Characterization and evaluation of uncertainty in probabilistic risk analysis[J]. Nuclear Safety, 1981, 22 (1): 251–263. |
| [2] | HOFFMAN F O, HAMMONDS J S. Propagation of uncertainty in risk assessments:The need to distinguish between uncertainty due to lack of knowledge and uncertainty due to variability[J]. Risk Analysis, 1994, 14 (5): 707–712. DOI:10.1111/risk.1994.14.issue-5 |
| [3] | ELDRED M S, SWILER L P, TANG G. Mixed aleatory-epistemic uncertainty quantification with stochastic expansions and optimization-based interval estimation[J]. Reliability Engineering & System Safety, 2011, 96 (9): 1092–1113. |
| [4] | KELLY E J, CAMPBELL K. Separating variability and uncertainty in environmental risk assessment—Making choices[J]. Human and Ecological Risk Assessment, 2000, 6 (1): 1–13. DOI:10.1080/10807030091124419 |
| [5] | BARALDI P, ZIO E, COMPARE M. A method for ranking components importance in presence of epistemic uncertainties[J]. Journal of Loss Prevention in the Process Industries, 2009, 22 (5): 582–592. DOI:10.1016/j.jlp.2009.02.013 |
| [6] | ZAFIROPOULO E P, DIALYNAS E N. Reliability and cost optimization of electronic devices considering the component failure rate uncertainty[J]. Reliability Engineering & System Safety, 2004, 84 (3): 271–284. |
| [7] | BLANKS H S. Arrhenius and the temperature dependence of non-constant failure rate[J]. Quality and Reliability Engineering International, 1990, 6 (4): 259–265. DOI:10.1002/(ISSN)1099-1638 |
| [8] | BORGONOVO E. A new uncertainty importance measure[J]. Reliability Engineering & System Safety, 2007, 92 (6): 771–784. |
| [9] | SALTELLI A, MARIVOET J. Non-parametric statistics in sensitivity analysis for model output:A comparison of selected techniques[J]. Reliability Engineering & System Safety, 1990, 28 (2): 229–253. |
| [10] | SOBOL I M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates[J]. Mathematics and Computers in Simulation, 2001, 55 (1): 271–280. |
| [11] | NOVI INVERARDI P L, TAGLIANI A. Maximum entropy density estimation from fractional moments[J]. Communications in Statistics-Theory and Methods, 2003, 32 (2): 327–345. DOI:10.1081/STA-120018189 |
| [12] | DENG J, PANDEY M D. Estimation of the maximum entropy quantile function using fractional probability weighted moments[J]. Structural Safety, 2008, 30 (4): 307–319. DOI:10.1016/j.strusafe.2007.05.005 |
| [13] | ZHANG X, PANDEY M D. Structural reliability analysis based on the concepts of entropy, fractional moment and dimensional reduction method[J]. Structural Safety, 2013, 43 (9): 28–40. |
| [14] | CREMERS D, OSHER S J, SOATTO S. Kernel density estimation and intrinsic alignment for shape priors in level set segmentation[J]. International Journal of Computer Vision, 2015, 69 (3): 335–351. |
| [15] |
张磊刚, 吕震宙, 陈军. 基于失效概率的矩独立重要性测度的高效算法[J].
航空学报, 2014, 35 (8): 2199–2206.
ZHANG L G, LYU Z Z, CHEN J. An efficient method for failure probability-based moment-independent importance measure[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35 (8): 2199–2206. (in Chinese) |
| [16] | LEIBLER R A, KULLBACK S. On information and sufficiency[J]. Annals of Mathematical Statistics, 1951, 22 (1): 79–86. DOI:10.1214/aoms/1177729694 |
| [17] |
尹晓伟, 钱文学, 谢里阳. 系统可靠性的贝叶斯网络评估方法[J].
航空学报, 2008, 29 (6): 1482–1489.
YIN X W, QIAN W X, XIE L Y. A method for system reliability assessment based on bayesian networks[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29 (6): 1482–1489. (in Chinese) |
| [18] |
袁朝辉, 崔华阳, 侯晨光. 民用飞机电液舵机故障树分析[J].
机床与液压, 2006 (11): 221–223.
YUAN C H, CUI H Y, HOU C G. Fault tree analysis of civil aircraft electro-hydraulic actuator[J]. Machine Tool & Hydraulics, 2006 (11): 221–223. DOI:10.3969/j.issn.1001-3881.2006.11.075 (in Chinese) |