空战态势评估是决策的前提,是智能空战中必不可少的一个环节。随着众多信息化空空武器列装部队,战场信息量剧增,态势环境复杂,数据的搜集、整理、学习和理解越来越重要。当前,空战模式越来越多,但电子干扰等技术的发展,削弱了战机的探测和跟踪能力,如果在超视距范围内无法发现和歼灭敌方,双方将不可避免地进入近距空战,近距空战将是自卫和消灭对手的最后有效手段。
近距空战态势评估方法大致可以分为2类:非参量法[1]和参量法。
非参量法主要是将空战中参战双方的态势信息进行定量化判断,充分体现空战态势特征的信息和便于进行量化分析的态势因素。李望西等[2]从交战双方几何位置出发,分析交战双方的角度、速度、能量等因素,构造优势函数,建立态势函数进行评估。吴文海[3]和顾佼佼[4]等将导弹发射区和导弹命中概率引入优势函数中,使模型更符合实战。但非参量法态势函数定义可移植性差,各因素权值的确定主观性强。
参量法也称为不确定性理论方法,包括动态贝叶斯网络、神经网络和支持向量机等方法,是运用统计学习理论,刻画评估指标间的关系。胡云安[5]和史建国[6]等提出动态贝叶斯网络算法,引入区间概率,增加评估的动态性。王向华等[7]利用径向基神经网络学习空战样本,避免了人工权值的主观性。郭辉[8]和张文忠[9]等基于回归型的支持向量机,借鉴传统评估指标对目标威胁进行评估。传统参量法在处理当前大规模数据方面存在模型输入少、特征提取能力不足的问题。
近年来,以深度学习为代表的人工智能取得了巨大突破,并且成功应用在围棋方面,研制出AlphaGo,击败人类,标志着深度学习理论已经成功转化为技术应用。深度学习有两大经典模型[10]:深度置信网络(Deep Belief Network,DBN)与卷积神经网络(Convolutional Neural Network,CNN)。其中深度置信网络具有特征提取能力强、精度高的优点。其半监督学习的训练方法,适合于空战态势评估中标准数据库规模小的现状。
基于此,本文使用密度峰值聚类对空战数据进行聚类分析,并结合态势函数和专家判读方法构建空战态势样本库,提出基于时间段数据特征的态势分类。在构建DBN模型过程中,提出有效的拓扑结构和最优参数确定方法。尝试从数据内部挖掘特征关系,从新的视角解决态势评估问题。
1 近距空战态势样本库的建立构建深度置信网络需要一定量训练样本,参考典型态势评估模型,确定4类典型近距空战态势,通过密度峰值算法对空战训练中积累的客观数据进行聚类分析,结合传统算法和专家判读,建立空战态势样本库。
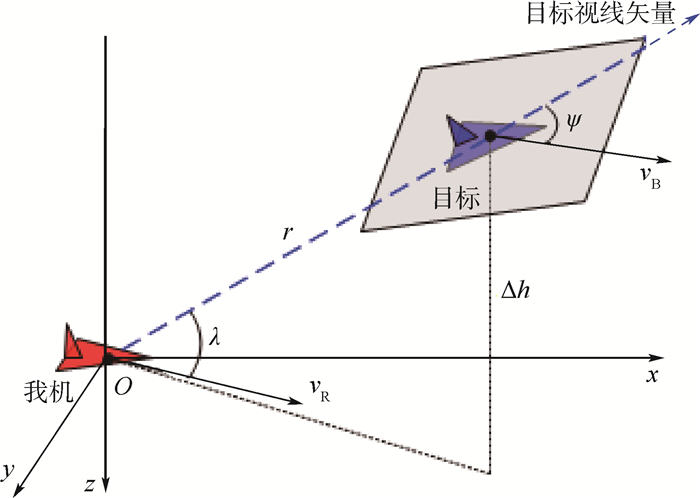
1.1 空战态势的描述 1.1.1 评估参数选取近距空战中,对抗双方的几何关系[11]如图 1所示。机体坐标系的原点O为飞机的重心, x轴与飞机的纵轴一致指向机头方向, y轴垂直于飞机的对称面并指向右方, z轴在飞机对称面内并且垂直纵轴指向下方。目标视线与本机速度(vR)方向的夹角为目标方位角λ,目标视线延长线与目标机速度(vB)方向的夹角为目标进入角ψ。两机速度矢量的夹角为η,两机距离和高度差分别为r和Δh。
|
| 图 1 空战双方位置关系 Fig. 1 Position relationship between two sides in air combat |
交战双方进行视距内作战,以近距格斗弹为武器,对雷达的性能要求不高,对双方相对角度要求较高。马耀飞等[12]提出描述近距空战的一组评估参数,主要考察高度、速度、距离和角度等因素。在此基础上,本文提出一组评估参数,如表 1所示。
| 参数 | 值域 |
| 目标方位角λ/rad | [0, π] |
| 目标进入角ψ/rad | [0, π] |
| 速度矢量夹角η/rad | [0, π] |
| 两机距离r/km | [0, 10] |
| 两机速度平方差Δv2 | |
| 我机速度vR | |
| 两机高度差Δh/m | [0, 18 000] |
| 我机高度h/m | [0, 18 000] |
1.1.2 态势空间划分
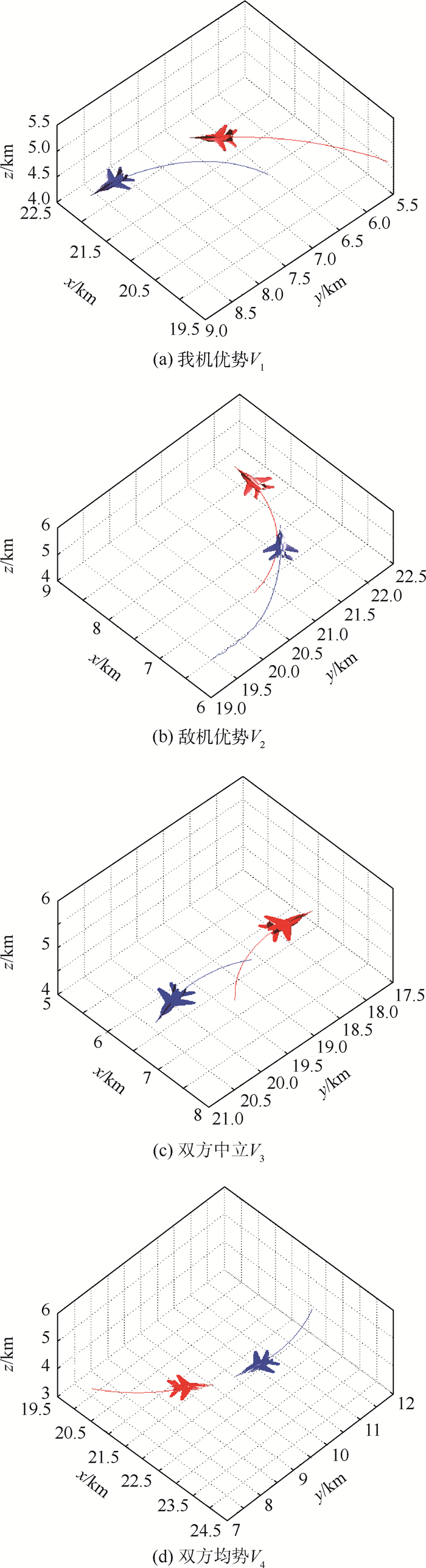
根据空战双方的参数关系,将空战态势分为我机优势V1、敌机优势V2、双方中立V3和双方均势V4 4种态势, 如图 2所示。
|
| 图 2 4种典型空战态势 Fig. 2 Four kinds of typical air combat situations |
红方为我方战机,蓝方为敌方战机。态势V1为我机处于优势,目标方位角小,目标进入角小,两机距离小,我机速度和高度大,我机达到攻击敌机条件;态势V2为我机处于劣势,目标方位角大,目标进入角大,两机距离小,敌机速度和高度大,敌机达到攻击条件;态势V3为两机中立,两机距离大,目标方位角大,目标进入角小,距离大于8 km,均不利于攻击;V4两机均势,距离小,目标方位角小,目标进入角大,速度和高度基本相同,双方均达到攻击对方条件。
1.2 典型态势优势函数构建近距态势评估主要考虑战机的作战能力和空战场态势2个方面因素。根据朱建益[13]的模型,作战能力方面,建立空战能力优势函数Tc:
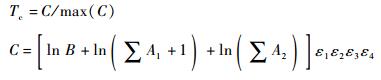
|
(1) |
式中:C为作战能力; B为机动参数; A1为火力参数; A2为探测参数; ε1为操纵系数; ε2为生存系数; ε3为航程系数; ε4为电子对抗系数。
空战态势方面,建立角度优势函数Ta、距离优势函数Td、速度优势函数Tv和高度优势函数Th。将5个优势函数加权合成近距空战综合态势优势函数T,利用模糊层次分析法计算权重系数:

|
(2) |
式中: k1、k2、k3、k4、k5表示空战能力优势、角度优势、距离优势、速度优势和高度优势权重。
1.3 基于密度峰值法的聚类分析由1.1节可知,4种典型空战态势特征数据值有明显差异,因此假设,每一类态势对应的特征在多维空间中是聚集的,同种态势的数据之间的距离比不同种数据的之间的相似度大。基于此,引入密度峰值聚类算法[14]进行分析。
密度峰值算法,对于每一个数据点i,计算2个特征:① 该点处数据分布的密度ρi;② 该点到比它密度大点的最小距离δi。2个特征都只由数据点之间的欧式距离dij确定。密度定义为
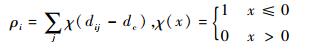
|
(3) |
式中:dc定义为截断距离; ρi的值是与该点距离小于dc的点的个数。
特征δi是通过计算点i和所有比它密度高的点的最小距离,其数学定义为
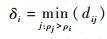
|
(4) |
δi反映密度较大点之间的距离。对于密度最高的点,将它的δi定义为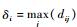
聚类中心点应被密度较低的点包围,且与具有更高密度的其他数据点有相对较大的距离。因此只有当数据点的ρi和δi均大于一定阈值时才可认为它是聚类的中心点。
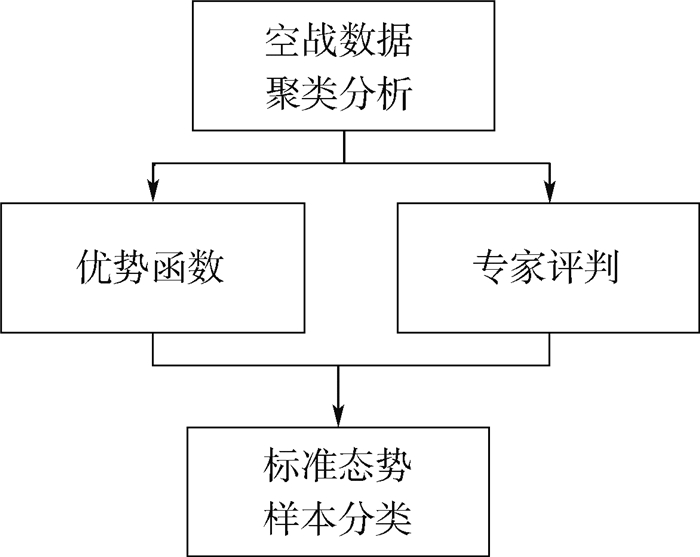
1.4 态势样本库的构建从客观数据中提取聚类分析所需的特征数据,进行聚类分析,得出每组数据的态势样本分类。然后结合优势函数和专家评判,对分类结果进行修正。具体流程如图 3所示。
|
| 图 3 样本库构建流程图 Fig. 3 Flowchart for constructing sample library |
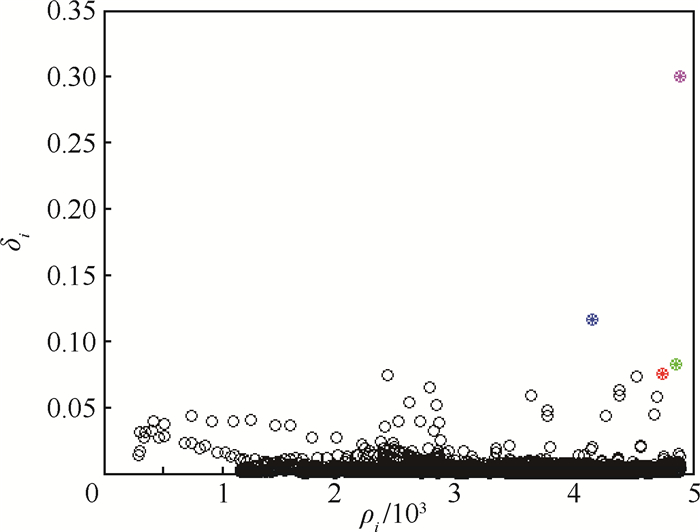
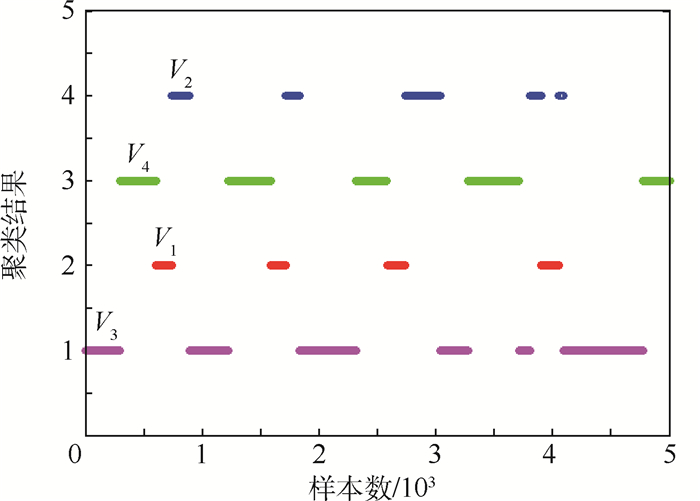
空战数据聚类方面,对每个空战时刻,选用表 1中的8类特征数据,分别归一化,接着进行密度峰值计算,考虑计算效率,每一批数据规模为5 000组。实验结果如图 4所示。图中品红、蓝、绿、红4个点代表ρi和δi最大的4个时刻,将其定义为4类态势的中心点,通过数据特性找到这4个中心点的对应态势类型,从4个中心点分别取一定距离为分类半径对其余4 996组数据进行分类,若出现分类区域重叠,则根据到中心点距离进行分类。其结果如图 5所示,其中,横轴代表参与聚类的5 000组数据,纵轴代表 4种态势类型。
|
| 图 4 密度峰值算法结果 Fig. 4 Results of density peaks algorithm |
|
| 图 5 4类空战态势聚类结果 Fig. 5 Clustering results of four kinds of air combat situations |
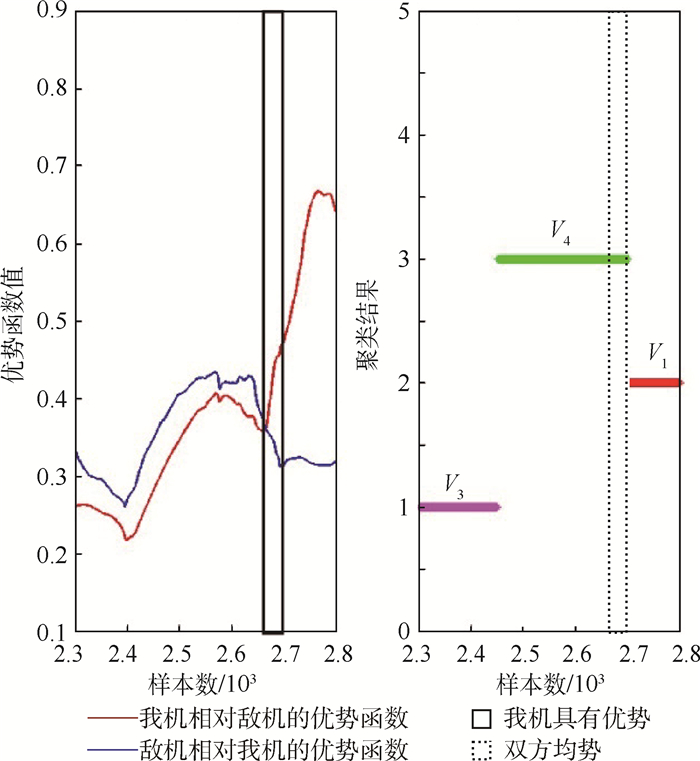
根据式(2),计算4类数据的优势函数值,确定其对应分类,其中品红为态势V3,红色为态势V1,绿色为态势V4,蓝色为态势V2。对比优势函数和聚类分析2种方法的结果,具有较强的一致性,但态势结果仍存在一定差异,如图 6所示。
|
| 图 6 2种方法结果对比 Fig. 6 Result comparison of two algorithms |
由图 6可知,差异均处于态势变化的临界状态附近,说明这些时刻数据变化具有连续性。
由此可知,空战态势变化是连续的过程,态势评估的目标应该选择时间段数据。每组数据选取连续的25个时刻作为输入,每个时刻对应表 1中的8类特征数据,按时间顺序排列,输入维度为25×8。每个时刻均通过聚类算法得出其态势类型,若一组输入中所有时刻类型一致,则该样本对应这种态势类型,若该输入内各时间点分类存在差异,则通过专家判读和传统态势函数方法,对已聚类好的数据进行修正,确定其对应态势类型。
依照上述流程,运行3轮,得到了数据量为15 000组的空战态势样本库。由于选取数据取自多次完整训练,样本数据和实际情况同分布,因此具备应用价值。
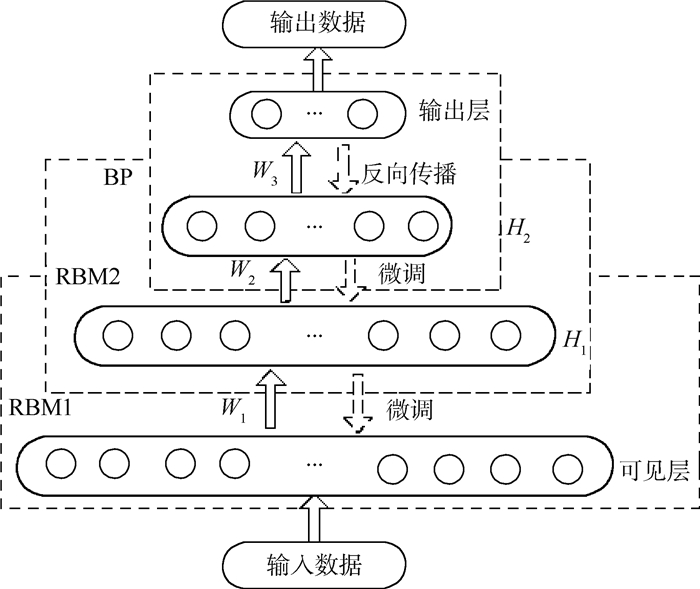
2 基于DBN的空战态势分类 2.1 DBN模型DBN结合了无监督学习和有监督学习,是由一系列叠加的受限玻尔兹曼机(RBM)和一层BP网络构成的深层神经网络。其结构如图 7所示。可见层的输入为训练样本集, H1、H2分别为第一、第二隐含层,Wi为相邻两层神经元之间的权值,相邻两层神经元构成一个玻尔兹曼机。
|
| 图 7 DBN结构 Fig. 7 Structure of DBN |
DBN采用“逐层贪婪[15]”的训练方法,过程可以分为两步:首先,使用无监督学习方法训练每一层RBM,且上一层RBM的输出为下一层RBM的输入,每一层RBM参数单独训练,确保特征向量在逐层映射时,能尽量保留特征信息;然后,使用最后一层的BP网络接收最后一个RBM的输出,用有监督的方式训练整个网络,通过反向传播对全网络参数进行微调。
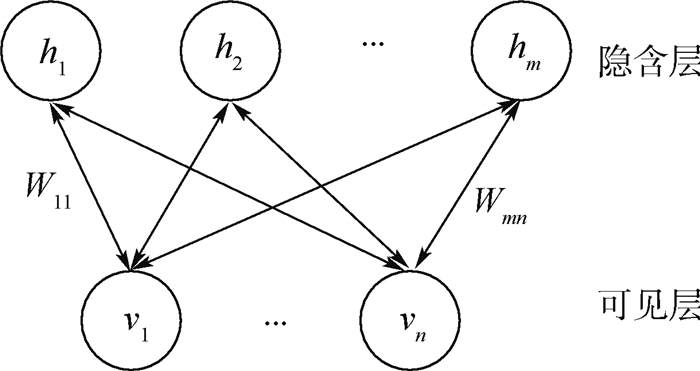
RBM是DBN的核心组件之一,它由一个可见层和一个隐含层组成,层间的节点两两相连,层内的节点不相连,其结构如图 8所示。其中:vi和hj分别表示可见层和隐含层的节点值;Wij为可见层和隐含层之间的权值。RBM训练为无监督训练方式,主流学习方法采用对比散度法[16]。
|
| 图 8 RBM网络结构图 Fig. 8 Structure of RBM network |
RBM的重构特征与原始数据的误差用“重构误差”表示,是以训练数据为初始状态,经过RBM的分布进行一次Gibbs采样后得到的新特征与原数据的差异,即
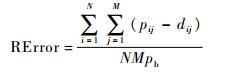
|
(5) |
式中:N为样本个数;M为样本维度;p为经过Gibbs采样重构的新特征;d为训练数据;pb为取值个数或范围。重构误差能在一定程度上反映RBM对输入数据的似然度。
2.2 模型建立和参数训练 2.2.1 样本的选取从获得空战态势样本库中选取样本,构建模型的训练样本集(Xtrain, Ytrain)与测试样本集(Xtest, Ytest),其中:Xtrain为样本库中随机抽取的10 000组数据,Xtest为样本库中另外5 000组数据,Ytrain和Ytest分别为每组数据对应的态势。
2.2.2 网络拓扑结构的确定DBN已成功应用于多个领域,但模型拓扑结构的确定,缺乏权威的方法,一直是研究的热点问题。黄海波等[17]基于经验和试错的方式确定网络结构,误差较大,易造成计算成本较高。潘广源等[18]证明重构误差和网络能量正相关关系,提出以网络的重构误差为标准确定网络深度,是对于模型规模确定的有效尝试。在此基础上,本节提出重构误差和测试错误率双重标准的模型规模确定方法,以最小训练代价求出网络拓扑结构。
2.2.2.1 隐含层深度要确定DBN模型的隐含层层数,需要先确定每层的隐含节点个数,一般将每个隐含层的隐含节点数设置为固定值,再通过增加隐含层的层数来确定模型最优深度。
当前研究成果表明,DBN深度和该网络重构误差与模型精度之间存在以下规律:
1) 随着DBN模型深度的增加,对输入数据的抽象描述能力越来越高[19]。
2) 重构误差反应模型对原始数据的描述能力,重构误差越小,说明网络各节点组成的状态空间更接近原始数据。
3) DBN中,反向微调的梯度下降法会导致训练误差逐层扩大,因此层数增大会导致训练误差的增大。
4) 随着网络深度的增大,训练和使用网络所消耗的成本会急剧增大。
因此在解决实际问题时,选择合适深度的网络,既能满足精度的要求,又能最大程度地节约成本。基于此,引入重构误差RError和测试错误率Error 2种参量,测试错误率Error为模型反向微调后,从态势样本库中抽取一定量样本进行测试,模型判别错误样本的个数占总测试样本数的比率,模型深度确定规则为
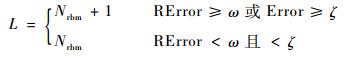
|
(6) |
式中:ω为目标重构误差预设值;ζ为目标精度误差预设值;L为隐含层个数;Nrbm为RBM层数。网络通过无监督学习后,如果重构误差大于预设值,则网络层数加1,继续训练。如果满足预设值,则对其进行有监督的反向微调和数据测试。若测试错误率高于预设值,则网络层数加1,并继续进行RBM训练,若满足预设值则训练结束。网络训练流程如图 9所示。

|
| 图 9 DBN深度确定流程图 Fig. 9 Flowchart for determining depth of DBN |
在(Xtrain, Ytrain)中选取5 000组样本用于无监督学习,1 000组样本用于监督学习,1 000组样本用于错误率测试。5 000组无监督学习样本分50批,每批100个样本,每层默认神经元100个,重构误差条件设定为RError≤0.15,模型错误率Error≤8.5%。通过实验,结果如图 10和表 2所示。
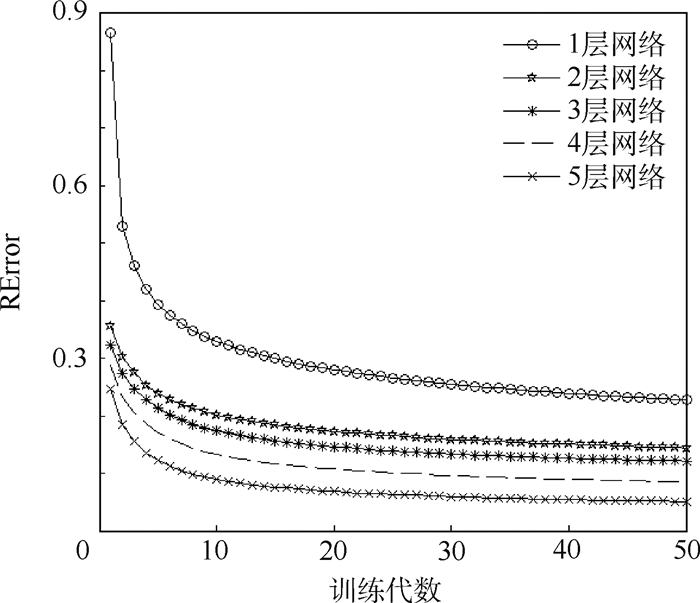
|
| 图 10 不同深度DBN重构误差 Fig. 10 Reconstruction error of different depth of DBN |
| 网络深度 | 测试错误率/% | 训练时间/s |
| 1 | 10.12 | 266.758 7 |
| 2 | 9.46 | 431.971 7 |
| 3 | 8.72 | 578.341 0 |
| 4 | 8.40 | 933.181 1 |
| 5 | 9.88 | 1 269.745 0 |
由图 10可见,网络重构误差随着深度的增加而减小。
由表 2可知,网络在隐含层达到4时停止增加,说明这时网络深度已经满足要求。为了进行进一步讨论,计算了5层网络的情况。运算时间随深度增大而增大,这符合预期效果。测试错误率先随着深度增大而减小,在深度为4时达到最小,然后又出现增大的情况。这说明层数的增大导致反向梯度下降算法的误差累加过大。也就是模型深度并不是越大越好。
2.2.2.2 隐含层节点数对于隐含层神经元个数的选取尚无理论上的指导,没有统一的经验公式。根据样本数据将可见层神经元个数取为nv=200,输出层神经元个数no=4, 最优隐含层深度为4。根据大量模型的参数设置经验,每个隐含层又是原始样本的另一种表达,因此通过逐层减少隐含层神经元个数,将数据中态势信息的主要特征信息逐步提取出来。因此将隐含层设置为nh1=180,nh2=150,nh3=100。最后一层隐含层直接关系到模型最终的准确率,因此nh4的取值在步长为5的区间(20, 95) 中,通过重构误差和测试错误率标准进行搜索,得到最优的取值,如图 11和图 12所示。图中横轴代表最后一层节点数,纵坐标分别代表对应隐含层节点数的网络重构误差和测试错误率。由图可知,当最后一层隐含层节点数达到45时模型效果最优。
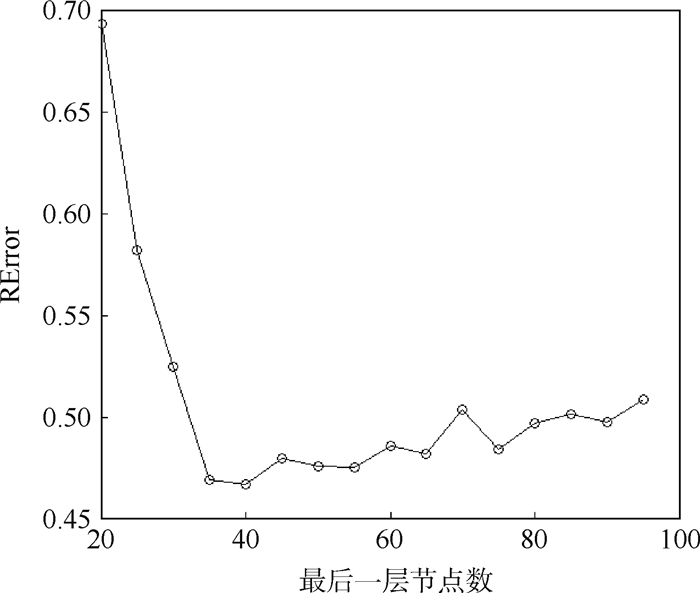
|
| 图 11 最后一层隐含层训练重构误差 Fig. 11 Training reconstruction error of last hidden layer |
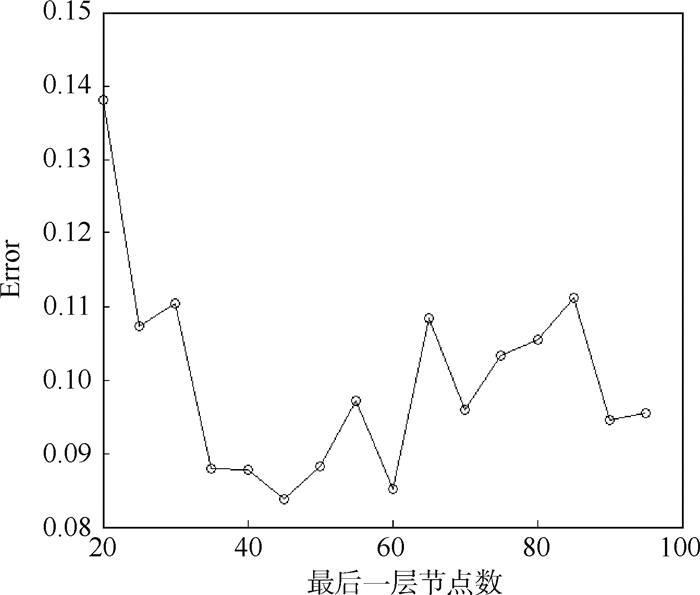
|
| 图 12 最后一层隐含层测试错误率 Fig. 12 Test error rate of last hidden layer |
综上所述,最终建立的DBN拓扑结构为200-180-150-100-45-4。
2.2.3 DBN参数设置在进行模型训练之前,需要对模型各参数进行初始化,DBN的主要可调参数[20]如下:
1) RBM学习率
学习率一般取(0.005, 0.200) 之间,令权重学习率lw=0.050,可见层偏置学习率lbv=0.100,隐含层偏置学习率lbh=0.100。为动态调整学习率,引入了动量项[16-17],该项可使本次参数更新的方向不完全由当前的梯度方向决定,避免算法早期陷入局部极值。更新公式为
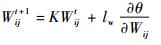
|
(7) |
其中:K为动量项,开始时令K=0.5,中后期令K=0.9;θ为网络参数集;t为迭代次数。
2) RBM初始权重与偏置
连接权重可初始化为正态分布N~(0, 0.1) 上的随机数,可见层单元偏置和隐含层单元偏置初始化为0。
3) 小批量数据容量
对权重和偏置的更新,若每次都基于全部训练样本进行,计算量将非常大。为减少运算量,将训练集事先分成包含100样本的小批量数据。
4) 微调次数
微调次数决定模型精度,因此求出不同微调次数对应的测试错误率,找到该模型最优的微调次数。如图 13所示,微调次数达到447时测试错误率达到要求,并且趋于稳定。因此微调次数取450次。
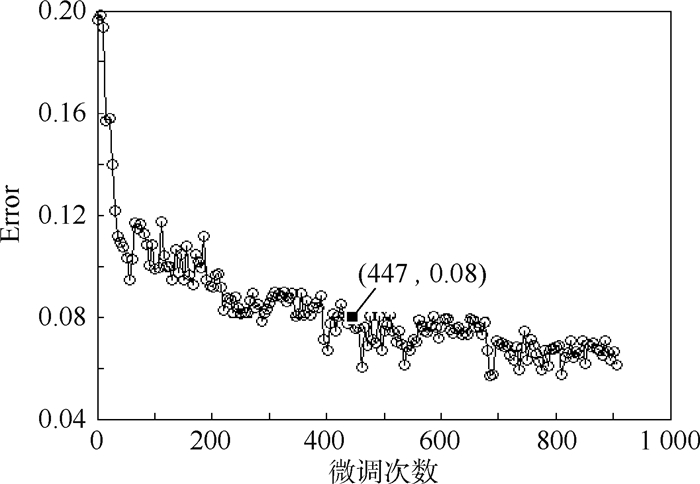
|
| 图 13 微调次数与测试错误率 Fig. 13 Fine-tuning times and test error rate |
训练完毕,逐层提取出原始数据经过网络后的参数值,得到逐层的特征提取线,如图 14所示。
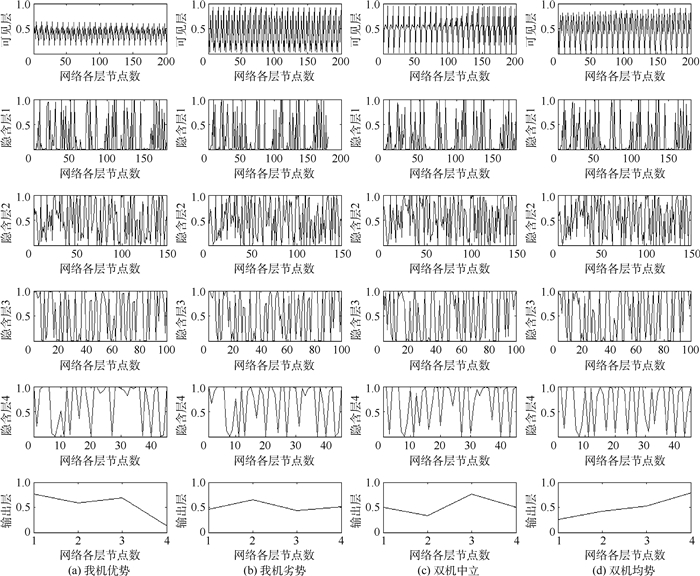
|
| 图 14 4类空战态势逐层特征提取线 Fig. 14 Feature extraction lines per layer of four kinds of air combat situations |
由图 14可知:① 由原始数据的曲线形态可知,4种不同态势的特征具有明显区别的;② 随着隐含层深度增加,态势的特征越来越抽象,但特征数量越来越少,说明深度网络能将数据主要特征逐层提取出来;③ 从隐含层4的特征提取线看出,我机优势和我机劣势曲线波动频率较低,而双方均势和双方中立的波动频率高,说明后者的参数变化剧烈,两机的态势胶着,符合实际情况。
2.3.2 模型效果对比实验采用的硬件平台为Intel(R) Xeon(R) CPU E5-2643, 主频3.50 GHz,内存8 GB。软件配置为Microsoft Windows 7旗舰版32位操作系统,Python 2.70运行环境。样本按照2.2.1节定义的训练样本集和测试样本集来选取。
为进行效果对比,使用BP神经网络(模型结构200-200-4) 和支持向量机(RBF核函数,惩罚因子c取4,核函数参数g取2.5) 算法进行测试,结果如表 3所示。
| 算法 | 训练集正确率/%(正确样本/训练样本) | 测试集正确率/%(正确样本/测试样本) | 运行总时间/s | 单组数据运行时间/s | 内存占用率峰值/% |
| BP神经网络 | 87.88 | 86.5 | 21.553 7 | 0.010 4 | 1.62 |
| 支持向量机 | 89.50 | 89.1 | 15.482 9 | 0.004 1 | 0.82 |
| DBN | 93.01 | 92.7 | 23.105 9 | 0.011 5 | 1.99 |
由表 3可知,本文DBN模型正确率高于BP神经网络和支持向量机模型。主要原因是,模型输入的维数高,实际采集数据含有大量的噪声,2种方法均难以提取出态势的主要特征信息,导致分类正确率不高。而BP神经网络规模小,特征提取能力差,较大的数据量也使支持向量机训练成本急剧增加,噪声的影响使惩罚因子等参数难以确定。而DBN通过深层的网络结构,能良好地建立从原始输入到抽象特征的映射关系,从而有效地对空战态势进行分类。
对比3种算法处理10 000组测试数据的运行时间和内存占用率峰值,支持向量机所需时间最短,内存占用率最小,BP神经网络和DBN由于隐含层较多,所以运行时间和内存占用率相对较大。但是测试DBN单组数据运行时间为0.011 5 s,满足实时数据传输频率的计算要求,内存占用率对硬件要求较低,具有实用性。
2.3.3 实例评估将两机实际数据进行处理,提取相关参数,作为输入,经过训练好的DBN网络模型运算,对每个时段两机的态势进行分类,并结合实际飞行状况进行对比分析。具体输出结果如图 15所示。
|
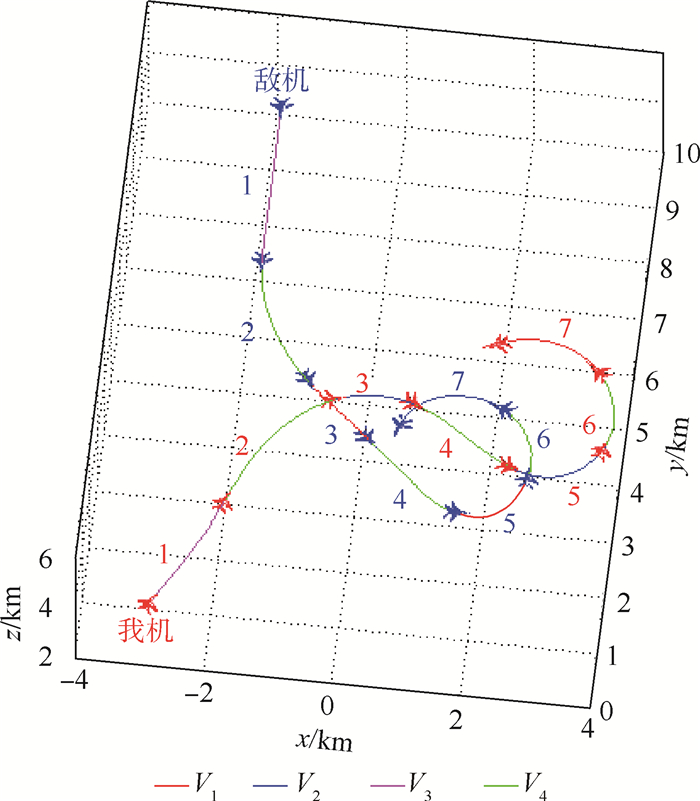
| 图 15 两机空战对抗实例 Fig. 15 Example of 1 versus 1 in air combat |
模型将实例中的对抗划分为7个过程。过程1对应态势V3,此时处于空战进入阶段,两机距离较远,均未达到攻击条件;过程2对应态势V4,此时双方开始做机动,进入对抗区域,互相均有威胁;过程3对于我机对应态势V2,此时敌机位于我机侧后方,我机处于劣势;过程4对应态势V4,敌机角度虽略优于我机,但我机有高度占优,因此模型判断为均势;过程5对于我机对应态势V2,敌机做大机动,将角度优势扩大,并缩小了高度差距,此时我机处于劣势;过程6对应态势V4,此时双方均可做机动,从而攻击对方;过程7对应态势V1,我机通过过程5、6占据了高度和角度上的优势,对敌形成尾后攻击的态势,模型判定为我机优势。
通过对抗过程的分析,模型输出的结果和实际态势一致性较强,验证了模型的有效性。
3 结论本文构建深度置信网络模型,对客观数据进行特征分析,克服传统方法在线计算优势函数的局限,为解决近距空战态势评估提供新视角:
1) 模型态势评估正确率高,运算时间和硬件要求较低,具有较强应用性。
2) 多种方法联合构建的态势样本库,解决空战态势样本库缺失的问题。
3) 总结和提出一套可行的深度置信网络参数整定方法,提高了训练效率和模型精度。
4) 具有较强移植性,通过丰富空战态势样本库,可以实现多种机型、多种作战模式下的态势评估。
本文重点讨论了深度置信网络在空战态势评估中的有效性,在态势分类上只引入了4类经典态势分类,因此结合更多要素,细化态势分类将是本文改进的方向。
| [1] |
孙永芹, 世文荣, 彭海军, 等. 基于改进非参量法的现代空战威胁评估研究[J].
火控雷达技术, 2013, 42 (3): 28–33.
SUN Y Q, SHI W R, PENG H J, et al. Study on improved non-parameter model based threat assessment in modern air combat[J]. Fire Control Radar Technology, 2013, 42 (3): 28–33. (in Chinese) |
| [2] |
李望西, 黄长强, 王勇, 等. 三维空间空战态势评估角度优势建模与仿真[J].
电光与控制, 2012, 19 (2): 21–25.
LI W X, HUANG C Q, WANG Y, et al. Modeling and simulation of air combat situation assessment's angle superiority in three dimensional space[J]. Electronics Optics and Control, 2012, 19 (2): 21–25. (in Chinese) |
| [3] |
吴文海, 周思羽, 高丽, 等. 基于导弹攻击区的超视距空战态势评估改进[J].
系统工程与电子技术, 2011, 33 (12): 2679–2685.
WU W H, ZHOU S Y, GAO L, et al. Improvements of situation assessment for beyond-visual-range air combat based on missile launching envelope analysis[J]. Systems Engineering and Electronics, 2011, 33 (12): 2679–2685. DOI:10.3969/j.issn.1001-506X.2011.12.20 (in Chinese) |
| [4] |
顾佼佼, 刘卫华, 姜文志. 基于攻击区和杀伤概率的视距内空战态势评估[J].
系统工程与电子技术, 2015, 37 (6): 1306–1312.
GU J J, LIU W H, JIANG W Z. WVR air combat situation assessment model based on weapon engagement zone and kill probability[J]. Systems Engineering and Electronics, 2015, 37 (6): 1306–1312. DOI:10.3969/j.issn.1001-506X.2015.06.13 (in Chinese) |
| [5] |
胡云安, 刘振, 史建国. 态势评估的变结构区间概率动态贝叶斯网络方法[J].
系统工程与电子技术, 2013, 35 (9): 1891–1897.
HU Y A, LIU Z, SHI J G. Situation assessment using variable structure interval probability dynamic Bayesian network[J]. Systems Engineering and Electronics, 2013, 35 (9): 1891–1897. (in Chinese) |
| [6] |
史建国, 高晓光, 李相民. 基于离散模糊动态贝叶斯网络的空战态势评估及仿真[J].
系统仿真学报, 2006, 18 (5): 1093–1097.
SHI J G, GAO X G, LI X M. Modeling air combat situation assessment by using fuzzy dynamic Bayesian network[J]. Journal of System Simulation, 2006, 18 (5): 1093–1097. (in Chinese) |
| [7] |
王向华, 覃征, 刘宇, 等. 径向基神经网络解决威胁排序问题[J].
系统仿真学报, 2004, 16 (7): 1576–1579.
WANG X H, QIN Z, LIU Y, et al. RBF neural network for threat sequencing[J]. Journal of System Simulation, 2004, 16 (7): 1576–1579. (in Chinese) |
| [8] |
郭辉, 徐浩军, 刘凌. 基于回归型支持向量机的空战目标威胁评估[J].
北京航空航天大学学报, 2010, 36 (1): 123–126.
GUO H, XU H J, LIU L. Target threat assessment of air combat based on support vector machines for regression[J]. Journal of Beijing University of Aeronautics and Astronautics, 2010, 36 (1): 123–126. (in Chinese) |
| [9] |
张文忠, 孙永芹, 杨洪立, 等. 基于Rough集和回归型SVM的超视距空战威胁评估[J].
四川兵工学报, 2013, 34 (7): 14–18.
ZHANG W Z, SUN Y Q, YANG H L, et al. Threat assessment based on rough set and support vector machines for regression in beyond-visual-range air combat[J]. Journal of Sichuan Ordnance, 2013, 34 (7): 14–18. (in Chinese) |
| [10] |
尹宝才, 王文通, 王立春. 深度学习研究综述[J].
北京工业大学学报, 2015, 41 (1): 48–59.
YIN B C, WANG W T, WANG L C. Review of deep learning[J]. Journal of Beijing University of Technology, 2015, 41 (1): 48–59. (in Chinese) |
| [11] |
左家亮, 杨任农, 张滢, 等. 基于模糊聚类的近距空战决策过程重构与评估[J].
航空学报, 2015, 36 (5): 1650–1660.
ZUO J L, YANG R N, ZHANG Y, et al. Reconstruction and evaluation of close air combat decision making process based on fuzzy clustering[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36 (5): 1650–1660. (in Chinese) |
| [12] |
马耀飞, 龚光红, 彭晓媛. 基于强化学习的航空兵认知行为模型[J].
北京航空航天大学学报, 2010, 36 (4): 379–383.
MA Y F, GONG G H, PENG X Y. Cognition behavior model for air combat based on reinforcement learning[J]. Journal of Beijing University of Aeronautics and Astronautics, 2010, 36 (4): 379–383. (in Chinese) |
| [13] |
朱建益. 空战中的威胁评估与态势评估研究[D]. 西安: 西安电子科技大学, 2013: 1-22.
ZHU J Y.A study of threat and situation assessment in air combat[D].Xi'an:Xidian University, 2013:1-22(in Chinese). http: //cdmd. cnki. com. cn/Article/CDMD-10701-1013295653. htm |
| [14] | ALEX R, ALESSANDRO L. Clustering by fast search and find of density peaks[J]. Science, 2014, 344 (6191): 1492–1496. DOI:10.1126/science.1242072 |
| [15] | HINTON G E, SALAKHUDINOV R R. Reducing the dimensionality of data with neural network[J]. Science, 2006, 313 (5786): 504–507. DOI:10.1126/science.1127647 |
| [16] |
张春霞, 姬楠楠, 王冠伟. 受限波尔兹曼机[J].
工程数学学报, 2015, 32 (2): 159–173.
ZHANG C X, JI N N, WANG G W. Restricted Boltzmann machines[J]. Chinese Journal of Engineering Mathematics, 2015, 32 (2): 159–173. (in Chinese) |
| [17] |
黄海波, 李人宪, 杨琪, 等. 基于DBN的车辆悬架减振器异响鉴别方法[J].
西南交通大学学报, 2015, 50 (5): 776–782.
HUANG H B, LI R X, YANG Q, et al. Identifying abnormal noise of vehicle suspension shock absorber based on deep belief networks[J]. Journal of Southwest Jiaotong University, 2015, 50 (5): 776–782. (in Chinese) |
| [18] |
潘广源, 柴伟, 乔俊飞. DBN网络的深度确定方法[J].
控制与决策, 2015, 30 (2): 256–260.
PAN G Y, CHAI W, QIAO J F. Calculation for depth of deep belief network[J]. Control and Decision, 2015, 30 (2): 256–260. (in Chinese) |
| [19] | BENGIO Y. Learning deep architectures for AI[J]. Foundations and Trends in Machine Learning, 2009, 2 (1): 1–127. DOI:10.1561/2200000006 |
| [20] |
周树森. 基于深度置信网络的分类方法[D]. 哈尔滨: 哈尔滨工业大学, 2012: 5-25.
ZHOU S S.Deep belief networks based classification methods[D].Harbin:Harbin Institute of Technology, 2012:5-25(in Chinese). http: //d. wanfangdata. com. cn/Thesis/D419897 |



