航空科技的持续快速进步,促进了机载作动系统的迅速革新,北京航空航天大学王占林和付永领教授一直致力于研究集成作动系统[1-2]。电静液作动器(Electro-Hydrostatic Actuator,EHA)作为集成作动系统的典型代表,具有集成化程度高、轻量化和安全性好等优点,其先进性已经在F-18、F-35等战斗机和A380、B787等飞机上得到了验证。EHA是飞机操纵与控制系统的关键组成部分,对飞机飞行姿态和飞行轨迹控制起决定性作用,其稳健性和可靠性直接影响飞机的安全性,美国空军飞机曾经发生过多起由于作动系统故障导致的严重事故,因此研究EHA的可靠性对降低飞机飞行故障率和提升飞行安全性具有重大意义。而EHA是一个多状态、有时序、多反馈、状态随时间变化的复杂机电液控集成一体化系统,其可靠性分析具有挑战性,故需寻求一种有效且准确的EHA可靠性分析方法。
在系统可靠性分析中,故障树分析(FTA)是一种最常用的有效方法。然而,FTA有一定的局限性,对复杂系统的建树相当困难,特别是对有多重状态、有信号反馈和有时序功能变化的系统,FTA可能变得更为复杂[3]。GO法是一种几乎与FTA同时产生的可靠性分析方法,对于多状态、有时序的系统,尤其是有实际物流的系统更为合适,但不易处理有多重状态改变和有复杂时序的系统[4]。在GO法的基础上,日本Matsuoka和Kobayashi两位学者开发了一种新的系统可靠性分析方法——GO-FLOW法[5],不仅解决了FTA建树困难的问题,而且相比于GO法,计算复杂度降低,更适用于有时序、有阶段性任务和状态随时间变化的复杂系统[6]。金霞和段富海[7]应用GO法分析了飞机EHA的可靠性;Hashim等[8]应用GO-FLOW法分析了压水堆AP1000冷却系统的可靠性;武光江等[9]应用GO-FLOW法分析了可维修系统的可靠性。
本文应用GO-FLOW法分析飞机EHA的可靠性。按照EHA结构原理图建立GO-FLOW模型,针对GO-FLOW图不允许存在循环的难题,采用一种新的解决方案,即用布尔代数求解描述反馈环的布尔方程,准确表示EHA系统的反馈信号。通过MATLAB运算和曲线拟合,得到系统在各时间点的可靠度以及随时间的变化规律。
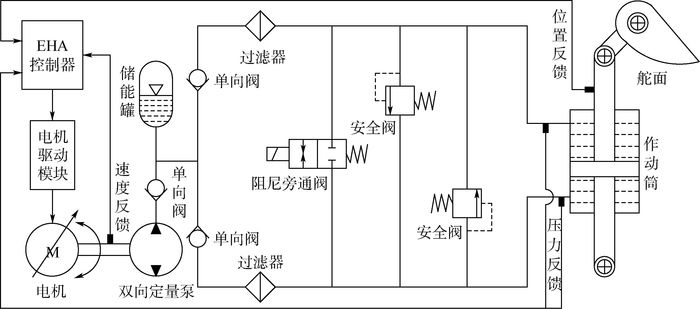
1 EHA系统分析EHA系统通常由控制器、电机驱动模块、270 V直流无刷电机、双向定量泵、储能罐及辅助液压阀组、作动筒等组成[10],结构原理如图 1所示。
EHA工作过程中,控制器和伺服驱动模块接受上位机的指令,驱动直流无刷电机转动,电机带动双向定量泵作旋转运动,继而控制泵输出到作动筒的高压油的流量,以容积调速方式完成对作动筒的控制。储能罐通过单向阀为系统进行补油增压,保持系统的最低压力,并防止油液中发生气穴现象,定量泵通过单向阀回油到储能罐。过滤器用来过滤液压油中的杂质,保证系统液压管道和其他设备的正常运行。
阻尼旁通阀起故障安全隔离的作用,安全阀防止作动筒的两腔内压力过高。速度、压力和位移传感器将系统的相关参数反馈给控制器,形成闭环回路,用于对系统的实时控制和监测[11]。
2 GO-FLOW法分析EHA可靠性GO-FLOW法的主要分析过程包括建立GO-FLOW模型和完成定量计算。作动杆部件按照控制指令要求输出相应位移代表EHA系统成功工作,结合模型图和运算规则计算系统成功工作的概率,即系统的可靠度。
2.1 求解EHA反馈环在EHA系统结构图中,闭环反馈回路为系统提供了实时准确的监测和控制。但是GO-FLOW图不允许有循环,若不能合理地求解反馈环,就不能准确地评估系统的可靠性,因此不能保证充分或最佳使用系统性能。通常,采用信号发生器简单替代反馈信号,但该方法必然会带来误差,影响可靠性分析精度。到目前为止,在求解反馈回路方面已经做了很多尝试,Matsuoka [12]提出了一个打破GO-FLOW分析逻辑回路的方法,Vaurio [13]也提出了一种递归的方法,但对于反馈回路的一般解决方法还没有给出明确的表示。本文采用布尔代数求解描述反馈环的布尔方程[14],准确表示EHA系统的反馈信号,提高了可靠性分析精度。
EHA带有反馈环的部分系统结构如图 2所示。
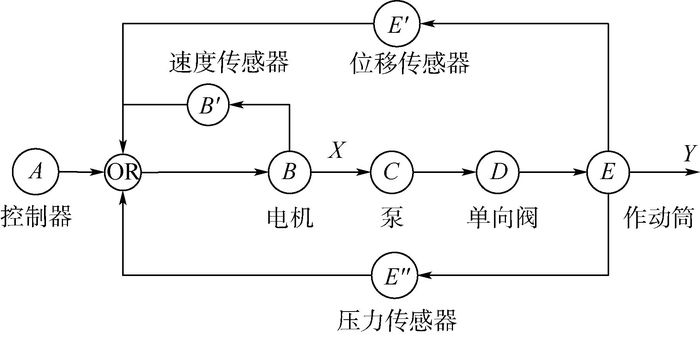
|
| 图 2 EHA带有反馈环的结构图 Fig. 2 EHA structure diagram with feedback loops |
以A部件为例,将t时刻成功输出的事件集合表示为AqAs,其中Aq代表A部件成功起动的事件集合,As代表A部件的全部状态集合,其余部件的表示方法同A部件。X(=Bout)和Y(=Eout)分别表示B和E部件的成功输出事件集合,那么布尔关系式可表示为
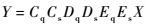
|
(1) |
已知,X为B′部件的输入信号,Y为E′和E″部件的输入信号。同时,A、B′、E′、E″部件的输出信号是或门(OR)的输入信号,所以或门的输出信号经过B部件后得到X的表达式为
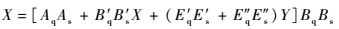
|
(2) |
整理式(1) 和式(2) 得
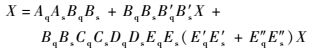
|
(3) |
基于布尔代数AsAs=As,1+As=1的运算思想,解式(3) 布尔方程得到
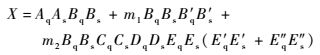
|
(4) |
式中:m1和m2是任意布尔元素。
GO-FLOW法以成功为导向,系统所有部件在t时刻成功起动,因此As=Bs=Cs=Ds=Es=B′s=E′s=E″s=1.0,即

|
(5) |
由图 2可推导出在建立反馈环后,E部件成功输出的事件集合X的表达式为
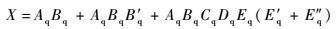
|
(6) |
比较式(5) 和式(6),可得到m1和m2的表达式:m1=Aq,m2=Aq。因此获得X(=Bout)和Y(=Eout)的表达式分别为
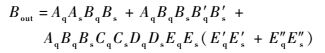
|
(7) |
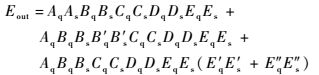
|
(8) |
式中:第1部分代表主路作用;第2部分代表B-B′环结构作用;第3部分代表B-C-D-E-E′和B-C-D-E-E″环结构作用,翻译成GO-FLOW模型如图 3所示。
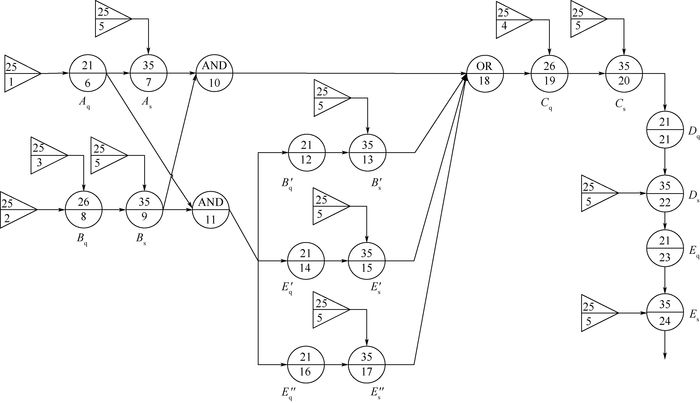
|
| 图 3 求解反馈环的GO-FLOW图 Fig. 3 GO-FLOW chart of solving feedback loops |
GO-FLOW模型主要由操作符和信号流两部分组成[15]。结合EHA结构模型图 1和求解反馈环模型图 3,在单元功能合理划分的基础上,建立EHA系统GO-FLOW模型如图 4所示。
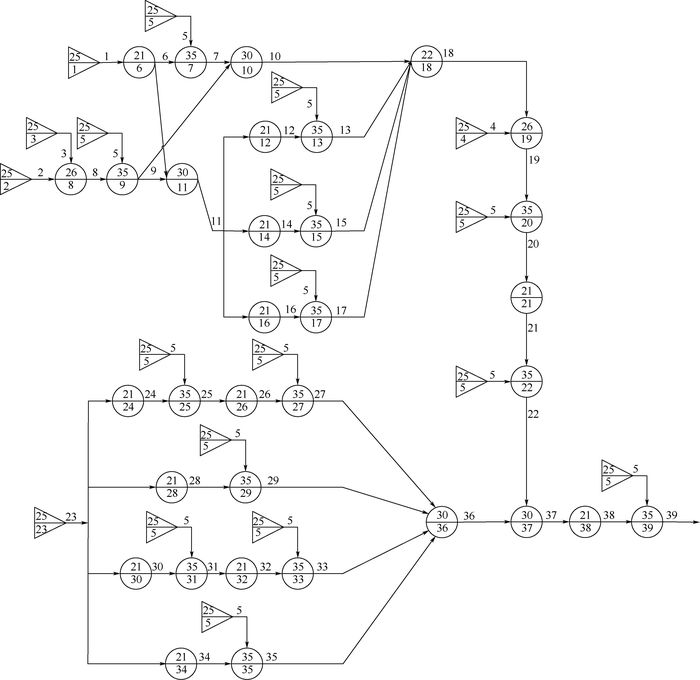
|
| 图 4 EHA系统的GO-FLOW图 Fig. 4 GO-FLOW chart of EHA system |
电源信号、控制信号和油液进入信号可用类型25信号发生器操作符输出。电机和定量泵都是有激励信号才能让输入信号导通的部件,可用类型26操作符表示,导通信号可用类型25操作符输出,同时考虑部件会随着运行而失效,因此增加类型35操作符表示失效概率随时间的变化,工作时间间隔信号也用类型25操作符输出。控制器、传感器、单向阀、过滤器、安全阀和作动筒都可看作两状态元件,所以可用类型21两状态操作符和类型35随时间失效操作符表示。图 4中操作符符号水平线上的数字表示操作符的类型,水平线下的数字表示操作符的编号,信号线上的数字表示信号流的编号。图中,信号39是系统的最终输出信号。
为能更好地说明GO-FLOW法在处理阶段性任务的应用,定义EHA系统中4个时间点:
时间点1是系统初始时间点,即系统尚未开始任何动作。
时间点2是控制器信号控制电机,电机开始工作,是实际时间的0时刻。
时间点3是电机驱动泵运转的时刻,与时间点2相差无几,这里可以忽略,系统开始工作。
时间点4是时间点3之后的300 h。
表 1列出了各操作符类型、参数和含义[7],其中:R(t)为t时刻操作符的输出信号;Pp为部件提前起动的概率;Pg为部件正常工作的概率;λ为部件运行失效的概率。
2.3 GO-FLOW可靠性运算GO-FLOW法在确定成功准则和定义时间点后,从信号发生器开始,沿信号线序列,按运算规则,逐个对操作符计算,直到得到最终输出信号在各时间点的“强度”,即系统的可靠性。图 4中关键信号流的表达式如下,其中Ii(t)表示信号i在时间点t的强度。
1) 信号流18:或门
首先,由于信号13、15、17都是在信号11存在的条件下才存在,它们的强度计算式中都包含信号11的强度,信号11是它们的共有信号,对共有信号进行修正后[16],得到信号13、15、17或门运算强度I′11(t)为
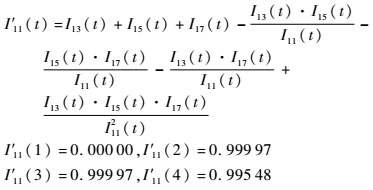
|
(9) |
再将信号10与信号13、15、17或门运算结果进行或门运算,信号6和9是它们的共有信号,因此信号流18的强度为
| 编号 | 类型 | 参数 | 含义 |
| 1 | 25 | R(1)=0, R(t)=1(t≠1) | 电源信号 |
| 2 | 25 | R(1)=0, R(t)=1(t≠1) | 控制指令信号 |
| 3 | 25 | R(2)=1, R(t)=0(t≠2) | 电机运行信号 |
| 4 | 25 | R(3)=1, R(t)=0(t≠3) | 泵运转信号 |
| 5 | 25 | R(4)=300 h, R(t)=0(t≠4) | 时间间隔信号 |
| 23 | 25 | R(1)=0, R(t)=1(t≠1) | 油液信号 |
| 6, 7 | 21, 35 | Pg=0.999 997 9, λ=2.1×10-6/h |
控制器 |
| 8, 9 | 26, 35 | Pp=12.0×10-6, Pg=0.999 973 0, λ=15.0×10-6/h |
电机 |
| 10, 11 | 30 | 与门 | |
| 12, 13 | 21, 35 | Pg=0.999 999 5, λ=0.5×10-6/h |
速度传感器 |
| 14, 15 | 21, 35 | Pg=0.999 999 5, λ=0.5×10-6/h |
位移传感器 |
| 16, 17 | 21, 35 | Pg=0.999 999 5, λ=0.5×10-6/h |
压力传感器 |
| 18 | 22 | 或门 | |
| 19, 20 | 26, 35 | Pp=0.0, Pg=0.999 988 0, λ=12.0×10-6/h |
泵 |
| 21, 24, 30 | 21 | Pg=0.999 998 8 | 单向阀 |
| 22, 25, 31 | 35 | λ=1.27×10-6/h | 单向阀 |
| 26, 32 | 21 | Pg=0.999 992 0 | 过滤器 |
| 27, 33 | 35 | λ=8.0×10-6/h | 过滤器 |
| 28, 34 | 21 | Pg=0.999 996 2 | 安全阀 |
| 29, 35 | 35 | λ=3.8×10-6/h | 安全阀 |
| 36, 37 | 30 | 与门 | |
| 38, 39 | 21, 35 | Pg=0.999 999 6, λ=0.4×10-6/h |
作动筒 |
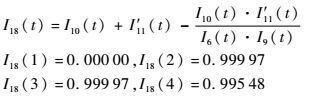
|
(10) |
2) 信号流36:与门
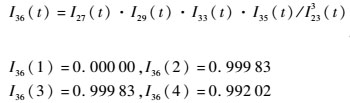
|
(11) |
3) 信号流38
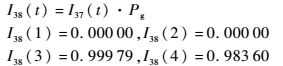
|
(12) |
4) 信号流39
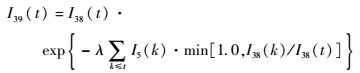
|
(13) |
因为I5(1)=I5(2)=I5(3)=0.0,得到
I39(1)=I38(1)=0.000 00
I39(2)=I38(2)=0.000 00
I39(3)=I38(3)=0.999 79
因为I5(4)=300.0,得到
I39(4)=I38(4)·exp(-λI5(4)×1.0)=0.983 48
所有操作符计算完成后,得到了EHA系统输出信号流22、36、39在所有时间点的强度,如表 2所示。
| 操作符 编号 |
操作符 类型 |
输出信号在各时间点的强度 | |||
| 1 | 2 | 3 | 4 | ||
| 22 | 35 | 0.000 00 | 0.000 00 | 0.999 96 | 0.991 51 |
| 36 | 30 | 0.000 00 | 0.999 83 | 0.999 83 | 0.992 02 |
| 39 | 35 | 0.000 00 | 0.000 00 | 0.999 79 | 0.983 48 |
3 与GO法比较
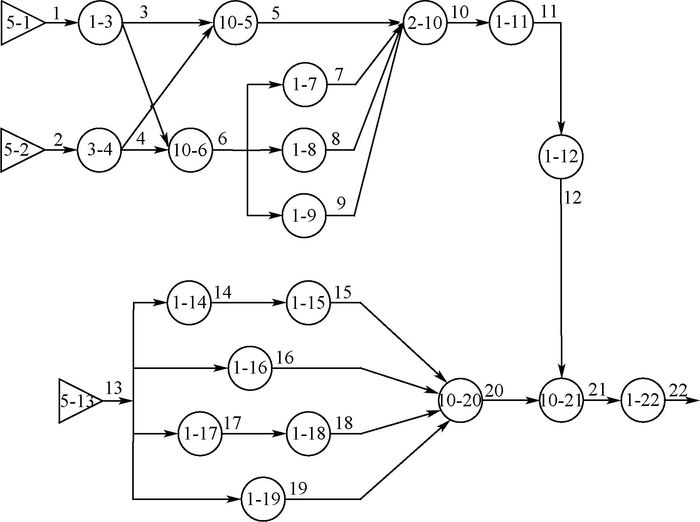
利用GO法分析上述EHA系统,同样地,根据系统原理图,用GO法相应操作符表示系统部件,用GO法信号流表示系统的输入和输出以及部件之间的关联,并应用2.1节求解反馈环的方法,建立系统GO模型如图 5所示。
|
| 图 5 EHA系统GO图 Fig. 5 GO chart of EHA system |
系统有3个状态:提前状态、成功状态和故障状态。根据表 1所列的状态概率,所有操作符按照GO法运算规则计算完成后,得到了EHA系统输出信号流22各个状态的概率,提前状态概率Pp=0.000 00,成功状态概率P=0.999 787 315 8,故障状态概率λ=1-Pp-P=2.126 842×10-4。
由表 2列出的GO-FLOW法分析结果可知,系统在开始工作时刻的可靠度为0.999 787 316 1,由于系统部件会随时间失效,所以随着时间的推移,系统可靠度降低,在工作300 h后的可靠度为0.983 482 232 9。根据GO法分析结果可知,系统处于成功状态的概率,即系统的可靠度为0.999 787 315 8。由于本文GO法的分析过程未考虑系统部件状态的变化,所以GO法可靠度计算结果等同于GO-FLOW法开始工作时刻的可靠度,可见两种方法的计算结果差异非常小,基本吻合。GO法已经成熟,其可行性已得到充分验证,因此,GO-FLOW可靠性分析方法是可行的,其结果是准确的,并且相比于GO法,GO-FLOW法只需一次运算,就可得到系统在各时间点的可靠度。而两种方法的计算结果又不完全相等,因为两种方法的基本概念和算法有差异,所以导致两种方法的计算结果有一定的差别。
4 系统可靠度的变化规律为了能更直观地了解EHA系统工作时可靠度的变化规律,在时间点3和时间点4之间以50 h为间隔插入5个时间点,因时间点2是实际时间的0时刻,而时间点3与时间点2相差无几,这里可以忽略,因此将时间点3看成0时刻,计算从0开始到300 h各时间点操作符22、36、39的输出信号强度,如表 3所示。
| 时间/h | 信号强度 | ||
| 操作符22 | 操作符36 | 操作符39 | |
| 0 | 0.999 96 | 0.999 83 | 0.999 79 |
| 50 | 0.998 55 | 0.998 52 | 0.997 05 |
| 100 | 0.997 13 | 0.997 22 | 0.994 32 |
| 150 | 0.995 73 | 0.995 92 | 0.991 60 |
| 200 | 0.994 32 | 0.994 62 | 0.988 89 |
| 250 | 0.992 92 | 0.993 32 | 0.986 18 |
| 300 | 0.991 51 | 0.992 02 | 0.983 48 |
由表 3可直观得到EHA系统从开始工作后每隔50 h各信号强度的变化规律,随着系统各部件的顺序动作和时间的推移,系统的信号强度随时间降低。为了更形象地描述这个规律,运用MATLAB对表中信号流39的强度进行线性拟合,得到系统可靠度变化规律如图 6所示。
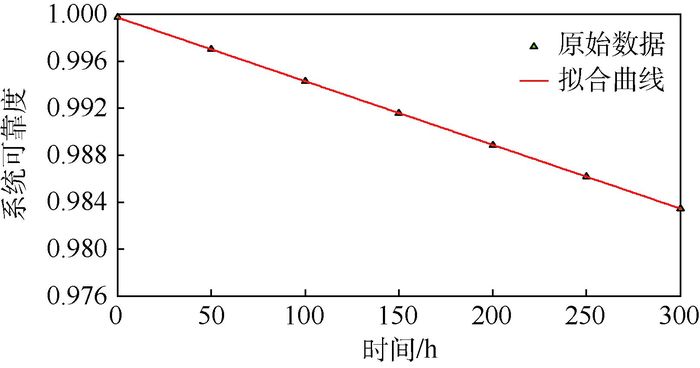
|
| 图 6 EHA系统可靠度变化规律 Fig. 6 System reliability changing rule of EHA |
MATLAB拟合得到曲线的函数表达式为R(t)=-5.435 70×10-5t+0.999 77。由该表达式可以快速而准确地计算出EHA系统在任意时刻的工作可靠度,以便及时对系统进行检修和维护。
5 结论1) 研究了GO-FLOW法在EHA系统可靠性分析中的应用。采用布尔代数求解描述反馈环的布尔方程,解决了模型中不允许存在循环的难题,并将计算结果与GO法的结果相比较,验证了GO-FLOW法的可行性与准确性,得到了系统在各时间点的可靠度以及随时间的变化规律,便于及时对系统进行检修和维护。
2) 充分挖掘了GO-FLOW法分析系统可靠性的优势,只需进行一次运算,就可得到系统最终信号在所有时间点的强度,完成对有复杂运行时序且状态随时间变化的系统可靠性分析。若采用GO法对大型的复杂系统进行分析计算,由于需要庞大的内存支持,往往难以获取最终信号存在概率的精确值。因此,GO-FLOW法能凭借其独特的优势为可靠性工程的深入研究提供重要支持。
| [1] |
李军, 付永领, 王占林. 机载电静液作动系统的发展现状与关键技术研究[J].
航空制造技术, 2005(11): 73–77.
LI J, FU Y L, WANG Z L. Present development status and key technology research of airborne electro-hydrostatic actuation system[J]. Aeronautical Manufacturing Technology, 2005(11): 73–77. DOI:10.3969/j.issn.1671-833X.2005.11.015(in Chinese) |
| [2] |
付永领, 邵云滨, 齐海涛, 等. 集成电动静液作动系统理论与技术[J].
液压与气动, 2015(5): 1–9.
FU Y L, SHAO Y B, QI H T, et al. Integrated electro-hydrostatic actuator system:Theory and technology[J]. Chinese Hydraulics & Pneumatics, 2015(5): 1–9. (in Chinese) |
| [3] | WANG Y Y, ZHOU J J, CHEN W G. Assessment method for the reliability of power transformer based on fault-tree analysis[J]. High Voltage Engineering, 2009, 35(3): 514–520. |
| [4] |
沈祖培, 黄祥瑞.
GO法原理及应用[M].北京: 清华大学出版社, 2004: 57-168.
SHEN Z P, HUANG X R. Principle and application of GO methodology[M].Beijing: Tsinghua University Press, 2004: 57-168. (in Chinese) |
| [5] | MATSUOKA T, KOBAYASHI M. GO-FLOW:A new reliability analysis methodology[J]. Nuclear Science & Engineering the Journal of the American Nuclear Society, 1988, 98(1): 64–78. |
| [6] |
林洁. GO-FLOW原理及其计算机辅助技术[D]. 长沙: 国防科学技术大学, 2003: 9-35.
LIN J.Research on the principles and the computer aided technology of the GO-FLOW[D].Changsha:National University of Defense Technology, 2003:9-35(in Chinese). |
| [7] |
金霞, 段富海. 基于GO法的电动静液作动器可靠性分析[J].
大连理工大学学报, 2013, 53(6): 846–850.
JIN X, DUAN F H. Reliability analysis on electro hydrostatic actuator based on GO methodology[J]. Journal of Dalian University of Technology, 2013, 53(6): 846–850. DOI:10.7511/dllgxb.2013.6.010(in Chinese) |
| [8] | HASHIM M, YOSHIKAWA H, MATSUOKA T, et al. Quantitative dynamic reliability evaluation of AP1000 passive safety systems by using FMEA and GO-FLOW methodology[J]. Journal of Nuclear Science & Technology, 2014, 54(4): 526–542. |
| [9] |
武光江, 王勇, 尚彦龙, 等. 基于GO-FLOW方法的可维修系统可靠性分析[J].
核动力工程, 2012, 33(2): 25–29.
WU G J, WANG Y, SHANG Y L, et al. Reliability analysis of repairable system based on GO-FLOW methodology[J]. Nuclear Power Engineering, 2012, 33(2): 25–29. (in Chinese) |
| [10] | KANG R, JIAO Z, WANG S, et al. Design and simulation of electro -hydrostatic actuator with a built-in power regulator[J]. Chinese Journal of Aeronautics, 2009, 22(6): 700–706. DOI:10.1016/S1000-9361(08)60161-2 |
| [11] |
赵静静. 基于GO法的电静液作动器可靠性研究[D]. 大连: 大连理工大学, 2014: 3-4.
ZHAO J J.Reliability analysis on electro hydrostatic actuator based on GO methodology[D].Dalian:Dalian University of Technology, 2014:3-4(in Chinese). |
| [12] | MATSUOKA T. A method to solve logical loops in the GO-FLOW methodology[C]//Proceedings of PSAM-V, International Conference on Probabilistic Safety Assessment and Management, Osaka, 2000, the International Association for PSAM.London:Springer, 2000:1461-1465. |
| [13] | VAURIO J K. A recursive method for breaking complex logic loops in Boolean system models[J]. Reliability Engineering and System Safety, 2007, 92(10): 1473–1475. DOI:10.1016/j.ress.2006.09.020 |
| [14] | MATSUOKA T. An exact method for solving logical loops in reliability analysis[J]. Reliability Engineering and System Safety, 2009, 94(8): 1282–1288. DOI:10.1016/j.ress.2009.01.007 |
| [15] | YU J, YU S, SONG Y M, et al. Application of GO-FLOW methodology to the reliability evaluation in CNC machine tools[J]. Advanced Materials Research, 2013, 694-697: 1833–1837. DOI:10.4028/www.scientific.net/AMR.694-697 |
| [16] |
林洁, 颜兆林, 龚时雨, 等. GO-FLOW方法及其改进的精确算法[J].
系统工程与电子技术, 2005, 27(1): 193–196.
LIN J, YAN Z L, GONG S Y, et al. GO-FLOW methodology and improved exact algorithm[J]. Systems Engineering and Electronics, 2005, 27(1): 193–196. (in Chinese) |