为了有效打击敌方弹道导弹、隐身飞机和卫星等低可观测[1]军用目标,要求探测系统能够对其进行远距离发现、跟踪、捕获和截击,而传统的多源跟踪算法无法满足作战需求。当探测系统跟踪低可观测编队目标[2]时,受制于测量设备角度分辨力、距离分辨力、威力及测量精度等因素,编队目标常存在3种状态:完全可辨、部分可辨、不可辩。随着探测系统性能的提高,如何利用部分可辨编队的信息来改善跟踪效果,成为目前国内外学者研究的热点。稳态编队[3]的概念相对于机动编队,主要指编队成员个数不变、拓扑结构变化缓慢、整体运动态势较为稳健的编队状态。在机群完成某个战术目的的整个过程中,稳态编队占据了绝大部分的时间,因此,对部分可辨条件下稳态编队的研究在空间目标监视、弹道导弹防御、要地防空等方面将有广泛的应用前景及重要的科学和实际意义。
现有研究部分可辨时编队跟踪的文献大多还是集中于解决编队整体[4-7]的状态估计、机动处理等问题,从位置、方向、航迹历史等方面理清编队分裂、合并及交叉的逻辑关系,然后基于动态网络[8]、概率数据互联(Probability Data Association, PDA)[9]、模式空间[10]、马尔可夫链蒙特卡罗(Markov Chain Monte-Carlo, MCMC)粒子滤波[11]、序贯蒙特卡罗概率假设密度滤波器(Sequential Monte-Carlo-Probability Hypothesis Density Filter, SMC-PHDF)[12]等方法完成编队的机动处理,可总体上仍着眼于编队整体,没有考虑编队内目标的具体运动轨迹,对编队内目标的航迹跟踪研究较少,特别是编队部分可辨时成员的状态估计需要改善。文献[13]研究了测量起源模糊时的群结构及状态估计问题;文献[14]基于随机集对部分可辨群目标及扩展目标的数据互联和航迹维持问题进行了分析;文献[15]提出了一种基于SMC-PHDF的部分可分辨的群目标跟踪算法,可直接获得群的个数、质心状态及形状,但这些算法均无法获得部分可辨时编队内目标的精确航迹。在一些实际应用中,往往更关心编队内个体目标的情况。例如,航天器在轨爆炸后所产生的空间碎片会形成一个编队目标,这个编队目标将会严重威胁太空安全,为消除太空安全隐患,必须精确掌握每一个碎片的运动轨迹,简单跟踪编队整体已无法满足工程实际需求;再如,当面对敌方编队飞机突防时,为更好地进行战术拦截和打击,要求在探测系统只能部分分辨飞机编队的条件下,尽可能精确地估计出编队中飞机的个数及各架飞机的运动轨迹,以便为后续的作战决策提供精确的信息支持。为数不多的关注编队内目标航迹的算法[16-19]推导环境又过于简单,难以适用于编队部分可辨的情况。
为了解决部分可辨条件下稳态编队目标的精细跟踪问题,本文针对该问题的各个技术环节,有针对性地采用迭代就近点(Iterative Closest Point,ICP)算法[20-21]、漏观测航迹填补等技术,提出了基于ICP的精细跟踪算法,并采用仿真数据对该算法的效能进行了验证。
1 ICP基本思想设模型数据点集A=[a1, a2, …, am]T和待匹配数据点集B=[b1, b2, …, bu]T,其中m和u分别表示A与B中数据点的个数。为了获取A与B之间的旋转和平移刚体变换参数,通过不断的迭代方式来逼近有效值。
设在l-1步时获得的旋转与平移估计分别为
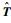

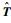

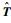

|
(1) |
式中: ║ ║表示欧氏统计距离。
由上述可知,在第l步时点集Al在B中寻找了每个相对应的点SB(ali),即对于每个ali∈Al,都有SB(ali)∈B与之对应。定义SB(Al)为满足式(1) 最近邻条件的所有点构成的新点集,即
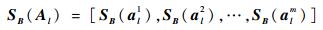
|
(2) |
为了衡量旋转与平移参数使Al与SB(Al)的贴合效果,定义代价函数,即第l步点集变换后的不相似度为
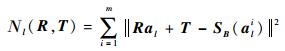
|
(3) |
通过最小化代价函数Νl(R, T),来获得刚体变换参数R和T的最优估计为
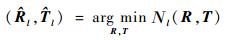
|
(4) |
也表示了在参数
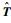
通过上述可以看出,ICP算法的实质是将模型数据点集A通过重复地进行“图形刚体变换、映射比对、获取最优估计”,一步步地逼近待匹配数据点集B,直到满足正确匹配的收敛准则为止,其实质是一种基于最小二乘准则的点集最优匹配方法。
对于稳态的编队目标,其队形结构的形状拓扑变换缓慢,因此相邻时刻的队形拓扑的位置变换可采用刚体图形匹配表示,有利于成员航迹的关联。因此,在进行编队精细跟踪时,将ICP算法应用于编队成员的精细点航数据关联可起到理想的效果。
2 基于ICP的编队成员关联编队目标在稳态条件下,成员之间的距离较近,且拓扑结构变换缓慢,相邻时刻的编队结构变换甚微,各成员运动速度的大小、方向相近,采用传统的多目标关联算法易造成航迹交叉、航迹模糊[5]等误关联问题。因此,需要采用针对编队特征的关联算法将回波点划分对应于已跟踪航迹,才能有效地对编队进行精细跟踪。
2.1 点航映射关联设某重点关注编队在经过编队精细起始以及跟踪滤波后的航迹,在k时刻的位置状态估计记为{Xik}i=1n,其中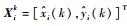
1) p<n,则编队目标存在漏观测。
2) p=n,不确定关系。
3) p>n,则量测中一定存在杂波。
在理想情况下,k时刻与k+1时刻编队目标拓扑存在旋转量为φ,平移量为(Tx, Ty)的刚体变换关系,即
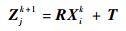
|
(5) |
式中: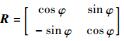
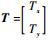
设在第l步时,已经获得的第l-1步迭代的旋转与平移估计为
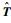

|
(6) |
为了使k时刻刚体变换后的航迹与k+1时刻的量测在对比关联时具有一定的容错能力,以适应部分可辨条件所带来的漏观测难题,这里采用双门限思想[22]进行对比关联。
设定粗关联波门(第一门限)的距离阈值为Dmax,在量测集{Zjk+1}中搜索对应于{Xi, lk}中每一个元素的集合
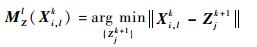
|
(7) |
且满足条件

|
(8) |
式中:DX, Zl=║Xi, lk-Zjk+1║。同时满足式(7) 和式(8) 的量测点,被确定为Xi, lk的最近邻点。
设定计数器λl与计数门限值λmin(第二门限),λmin取值跟目标发现概率和容错率有关,通常情况下,取λmin=n-1或n-2。变量i的值取1~n,当Xi, lk能搜索到对应的最近邻点时,则λl=λl+1。
完成搜索后,若满足

|
(9) |
判断为关联成功,则在各条航迹在后续滤波时取对应的k+1时刻的量测,若某个航迹没有关联到对应量测,则借鉴概率最近邻[5]的思想,取滤波预测值代替。若λl<λmin,则判断为关联失败,继续进行第l+1步迭代。
2.2 旋转与平移参数估计若第l步关联失败,需要进行第l+1步迭代,则需要获得第l步关联后的{Xi, lk}与{MZl(Xi, lk)}之间的旋转与平移参数估计值(
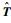
为简化表达方式,2个点迹集合表示为

|
(10) |
式中:ZiX=MZl(Xi, lk)。
计算2个集合的重心为

|
(11) |
因此,代价函数可表示为

|
(12) |
设

|
(13) |
则式(12) 可表示为

|
(14) |
将其展开,可得
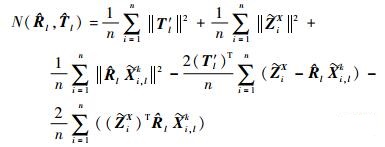
|
(15) |
当Tl′=0时,即

|
(16) |
则式(15) 等号右边中第1项为0;同时,第4项也为0;第3项满足旋转关系:
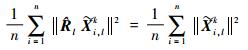
|
(17) |
因此第3项与旋转变量无关;同理第2项也与旋转变量无关。
至此,为了最小化代价函数N(
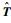

|
(18) |
式中:xiZ(k)、yiZ(k)分别表示第l步时Xi, lk对应MZl(Xi, lk)的x、y轴坐标;Λxx、Λyy、Λyx和Λxy分别为等号前()中各对应项的简写表示。
为使式(18) 取极大值,可取第l步的φl估计值为

|
(19) |
获得

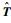
综上,基于ICP的关联算法流程可大致分为如下几个步骤。
步骤1 初始化:设定一组初始的旋转与平移量(
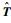
步骤2 点航映射:基于第l-1步的旋转与平移估计量(
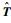
步骤3 最近邻关联:针对每个状态估计点Xi, lk,利用最近邻法,在量测集{Zjk+1}中搜索满足式(7) 条件的对应点,组成新的集合{MZl(Xi, lk)}。
步骤4 更新旋转与平移量:采用2.2节所述方法求取{Xi, lk}与{MZl(Xi, lk)}之间能使代价函数N(
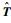
步骤5 终止与迭代:采用双门限准则,若满足式(8) 与式(9) 条件,则终止迭代,确定{Xik}i=1n中每个元素在{Zjk+1}j=1p中的对应量测(关联成功);若不能满足条件,则取l=l+1,跳转至步骤2,迭代更新。
为了防止在特殊情况下出现无限循环情况,若在某步迭代更新后,{MZl-1(Xi, l-1k)}与{MZl(Xi, lk)}相同,则终止迭代,取仅满足式(8) 条件的{Xik}i=1n的对应量测。
若算法在第L步迭代终止,则k时刻的位置状态估计{Xik}i=1n与k+1时刻量测集{Zjk+1}j=1p之间最终的旋转角与平移量估计为
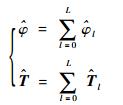
|
(20) |
由于量测条件为部分可辨,因此该关联算法的处理结果易出现漏关联情况(即未能对{Xik}i=1n中每个元素关联到对应量测)。出现这种情况是正常的,会在本文算法的后续过程中对其进行针对处理。
3 编队成员航迹的状态更新 3.1 漏关联量测填补经过编队内点航关联后,可获得k+1时刻量测与k时刻n条航迹不完全一一对应的关系。部分可辨条件下的编队回波特征为目标发现概率低,即目标的航迹时有时无,航迹信息不完全,因此在量测集中不一定存在与成型航迹相对应的目标回波。为了解决这个问题,需要对没有回波的目标进行量测填补,从而用于后续的状态更新滤波。
这里借鉴概率最近邻[5]的思想,未关联到对应量测的航迹,采用k+1时刻的状态预测作为其更新值,即

|
(21) |
对应的误差协方差为
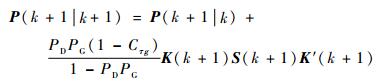
|
(22) |
式中: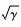
为了防止对航迹过度填补而形成的虚假航迹,这里需要对同一条航迹的填补频次加以制约。采用滑窗α/β逻辑[5]准则对单个成员航迹进行逐点判断。在窗口长度为β的时间滑窗内,若填补量测的个数大于β-α,则认为该条航迹为不可信任,将该航迹终结;若填补个数不大于β-α,则认为该航迹在填补量测后仍然为可信任航迹,维持并更新该航迹。
3.2 基于多模型的滤波更新编队目标在稳态条件下,各成员目标的运动状态相似,且编队拓扑结构变化缓慢。因此,每个编队成员的运动状态为匀速直线运动或加速度较小的大半径转弯。采用单一的滤波模型不能较好地对航迹进行滤波贴合,因此本节采用多模型[5]算法对编队成员航迹滤波。
设置3个过程噪声级,给每个过程噪声级建立一个滤波器,根据似然函数计算各个模型的贴合度,然后求它们的加权和。由于目标运动的机动幅度不大,因此在过程噪声级设置时采用较小的过程噪声协方差系数。这里不再赘述多模型滤波的具体流程,但需要注意的是,由于编队具有稳态特征,可以通过监视各成员与3个模型之间的贴合系数,判断编队拓扑结构是否改变。
设某时刻编队成员对于各噪声模型的贴合度集合为{Μwσ}w=1n,w为编队成员序号,σ取值{1, 2, 3},表示对应3个过程噪声模型。则该时刻编队的模型平均值和成员模型平均值分别为
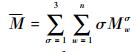
|
(23) |
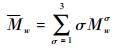
|
(24) |
设定阈值系数κΜ,若
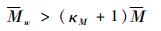
|
(25) |
则认为成员w在编队内的相对移动幅度较大,将改变编队的拓扑结构。需要注意的是,由于成员w在编队内的相对移动幅度较大,可能产生编队内的交叉航迹,因此出现该情况时,编队成员关联可能出现MZl(Xi, lk)=MZl(Xj, lk)(即2条航迹关联到同一个量测点),这里采用非抢占式的滤波更新,即2条航迹均将采用该量测做滤波更新。由于航迹的速度矢量不同,因此在后续关联滤波中航迹可自动分离。
4 算法仿真验证与分析为了验证本文算法的性能及有效性,本文采用1 000次Monte-Carlo仿真对本文提出的基于ICP的稳态编队精细跟踪算法(本节后文中简称ICP算法)与基于模版匹配的编队目标跟踪算法(TM算法)[19]、传统多目标跟踪算法中性能优越的多假设算法(MHT算法)[5]在多场景下对已起始的航迹进行跟踪,并对跟踪结果进行性能比较与分析。
4.1 仿真环境设雷达的采样周期T=1 s。为了多角度比较分析各算法的航迹跟踪性能,设置了以下3种经典仿真环境。
环境1 模拟杂波条件下稳态稀疏编队与稳态密集编队的目标环境。稀疏编队目标环境下,编队成员之间距离一般为[600, 1 000]m;密集编队目标环境下,距离一般为[100, 300]m。设在雷达视域内,存在2个稳态编队。第1个为稀疏编队,做小机动参数的大半径转弯,由5个成员组成,各成员的初始位置为(10 000, 15 000) m、(9 000, 15 400) m、(9 000, 14 600) m、(10 000, 15 800) m、(10 000, 14 200) m, 初始速度为(-392, 0) m/s;第2个为密集编队,做匀速直线运动,由4个成员组成,各成员的初始位置为(5 000, -4 200) m、(5 200, -4 150) m、(5 350, -4 100) m、(5 550, -4 170) m,初始速度为(0, 300) m/s。
仿真中设置雷达视域范围为x∈[-16 000 12 000]m,y∈[-10 000 26 000]m,雷达位于坐标原点(0, 0)。雷达的测向误差σθ=0.2°、测距误差σρ=20 m。设置雷达对目标的发现概率为Pd=0.83。杂波的产生方式为,在雷达视域范围内,每时刻随机均匀产生1 000个杂波。
环境2 模拟杂波条件下稳态编队成员的相对位置发生缓慢变化(即编队拓扑结构变化)条件下的目标环境。设雷达视域内存在一个编队,由5个成员组成,各成员初始位置为(10 900, -4 100) m、(10 450, -4 550) m、(10 000, -5 000) m、(9 550, -5 450) m、(9 100, -5 900) m, 初始速度为(-200, 300) m/s。在16~31 s间,成员2与成员3做小机动交错飞行;在41~71 s间,成员2、成员4、成员5同时做小机动交错飞行,机动参数略。其他雷达与杂波等参数同环境1。
环境3 为了验证各个算法时间复杂度在实际运行速度上的差别,在环境1的条件下,针对稀疏编队和密集编队,分别对各个算法的处理时间进行对比。对该条件下的处理过程进行1 000次Monte-Carlo仿真,记录运行时间并取平均值。
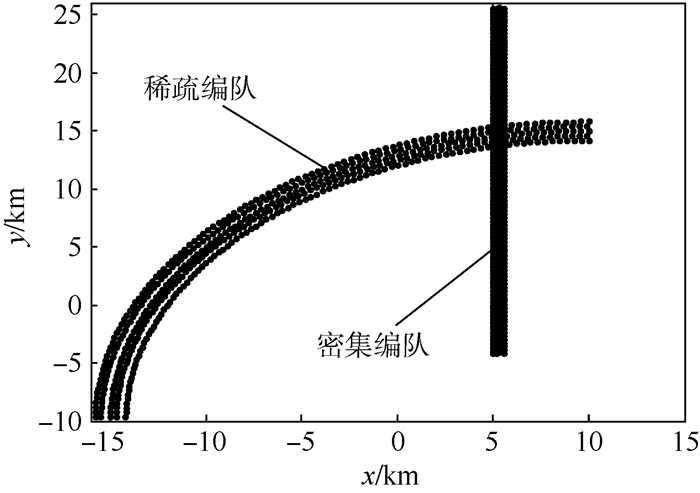
4.2 仿真结果与分析1) 在仿真环境1中,雷达视域内共存在2个编队合计9批目标,所有目标的真实运动态势如图 1所示。
|
| 图 1 目标整体态势(环境1) Fig. 1 Overall situation of targets (Environment 1) |
由于编队目标成员距离较近,因此跟踪过程中极易出现航迹模糊现象(2条或多条航迹合并为一条航迹,从而另一条航迹丢失)与航迹错误交叉等误跟踪问题。为了对算法性能进行有效评估,结合工程中对数据准确率的要求,这里只对可行航迹[5](即航迹批号始终对应正确的起始航迹批号)进行衡量统计。为了有效评价航迹跟踪的可靠性,这里定义平均可行航迹批数为
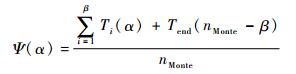
|
(26) |
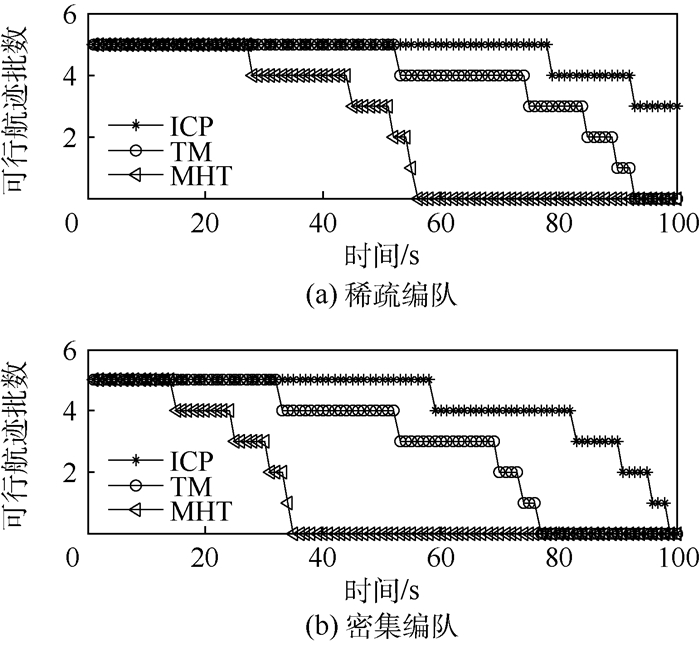
式中:α为可行航迹批数;Ti(α)为在第i次仿真中出现α批可行航迹的时刻;nMonte为Monte-Carlo仿真次数;β为nMonte次Monte-Carlo仿真中出现α批可行航迹的次数;Tend为仿真中总时刻数。在本文仿真中,α∈{1, 2, 3, 4, 5},nMonte=1 000,Tend=100。因此在环境1条件下,仿真后3种算法对稀疏编队与密集编队的处理结果中平均可行航迹的批数如图 2所示。
|
| 图 2 平均可行航迹批数比较(环境1) Fig. 2 Comparison of average number of feasible track (Environment 1) |
从图 2可以看出,ICP算法对2种编队条件的跟踪处理,平均可行航迹批数均显著优于其他2种算法,这说明ICP算法对部分可辨条件下的编队跟踪具有更高的可靠性。对比图 2(a)与图 2(b),密集编队条件下,各算法的可行航迹批数有所下降,特别是MHT算法。通过对算法理论分析可知,MHT算法没有对编队整体拓扑的关联,因此在多目标同速同向运动时,极易出现错误关联,从而降低跟踪的正确率。而当编队成员较密集时,该现象尤为显著。对于ICP算法及TM算法,当可行航迹批数小于3时,则曲线迅速会降至0。通过分析可知,由于ICP算法与TM算法均对编队整体拓扑进行了关联,但是可行航迹批数小于3时,编队整体的拓扑对准受到了严重的影响,关联错误率大大上升,因此导致该现象的发生。另外,由于ICP算法针对目标低可观测条件,采用了漏关联量测填补技术,可进一步提高ICP算法的正确关联率,因此,ICP算法具有较高的跟踪可靠性。
为了衡量各算法的跟踪精度,对跟踪时可行航迹的位置与速度精度进行统计。由于在密集编队条件下,MHT算法的可行航迹太少,Monte-Carlo仿真时没有成功跟踪到一条完整的可行航迹。因此这里仅对稀疏编队条件下的跟踪精度进行统计。各算法跟踪航迹的y轴位置、速度的均方根误差比较图分别如图 3所示。

|
| 图 3 y轴位置、速度的均方根误差比较(环境1) Fig. 3 Comparison of position and speed root mean square error at y axes (Environment 1) |
从图 3(a)中可以看出,ICP算法的位置均方根误差曲线显著低于其他2种算法,具有较高的位置跟踪精度。ICP算法的平均y轴位置RMSE为21.4 m,TM算法的为27.6 m,MHT算法的为53.7 m,因此较高的跟踪精度也是跟踪可靠性的保证。在图 3(b)中,ICP算法的速度均方根误差曲线也显著低于其他2种算法。
从环境1的仿真结果可以看出,ICP算法在跟踪可靠性、位置精度和速度精度上都显著优于TM算法与MHT算法,算法有效性显著。
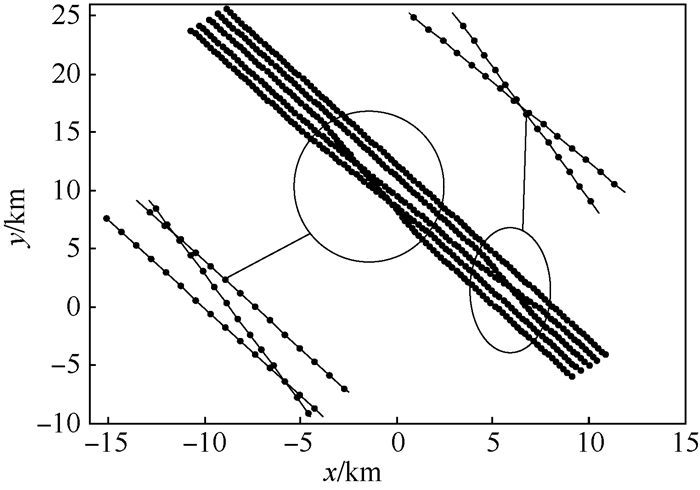
2) 在仿真环境2中,雷达视域内共存在一个编队合计5批目标,所有目标的真实运动态势如图 4所示。
|
| 图 4 目标整体态势(环境2) Fig. 4 Overall situation of targets (Environment 2) |
从图 4中可以看到,该编队经历过2次编队拓扑变化:第1次为成员2与成员3互换位置,第2次为成员2与成员4一并与成员5互换位置。在这种情况下,编队的精细跟踪极易出现错误。为了验证算法在该环境下的跟踪能力,鉴于在环境1的仿真中已经验证过算法的可靠性与跟踪精度,这里仅验证成员航迹交错时的正确跟踪率(即航迹与批号正确对应),如表 1所示。
| % | ||
| 算法 | 第1次拓扑变化 | 第2次拓扑变化 |
| ICP | 88.5 | 63.4 |
| TM | 81.2 | 45.5 |
| MHT | 84.9 | 50.7 |
在表 1中需要说明的是,当第1次拓扑改变正确跟踪的前提下,才对第2次拓扑改变进行正确跟踪率统计。ICP算法在2次拓扑改变时的正确跟踪率均为最高,对于整个航迹的跟踪率,本文算法的正确跟踪率为56.1%(88.5%×63.4%),远高于TM算法的36.9%和MHT算法的43.0%,说明本文算法在编队拓扑缓慢改变时比现有算法具有较高的跟踪可靠性。从表 1中还可看出,TM算法的正确跟踪率不如MHT算法,分析算法里可知,在低发现概率条件下,点航关联在航迹交错时易出现多航迹对应同一量测点,MT算法的模版建立在区域矩形划分的基础上,匹配模糊性较大;而MHT多假设全临最优思路可使关联跟踪的正确性增大。但这2种算法在应对低发现概率的编队目标精细跟踪时,在关联与滤波的各个环节均不如ICP算法有针对性,因此,ICP算法在该背景下具有最优的跟踪效能。
3) 在仿真环境3中,各算法对稀疏编队与密集编队的平均处理时间如表 2所示。
| ms | ||
| 算法 | 稀疏编队 | 密集编队 |
| ICP | 0.516 | 0.477 |
| TM | 0.438 | 0.401 |
| MHT | 0.985 | 0.794 |
从表 2可以看出,MHT算法在对2种编队的处理时间上显著高于ICP算法与TM算法,ICP算法略高于TM算法,但也相差不到0.1 ms,因此ICP算法的处理效率略低于TM算法,但远优于MHT算法,具有较高算法实时性,可应用于实时性要求较高的工程背景中。
5 结论为解决部分可辨条件下稳态编队的精细跟踪难题,本文提出了一种基于ICP的稳态部分可辨编队精细跟踪算法,该算法的优势与特点如下:
1) 采用循环迭代方式实现点航关联的最优匹配,提高了编队成员关联的准确性。
2) 在编队成员航迹的状态更新中采用滑窗α/β逻辑的漏关联量测填补技术,有效提高了在部分可辨条件下的航迹维持问题。
3) 采用非抢占式的多模型滤波更新方法,有效提高了编队内对交叉航迹的正确跟踪率。
4) 经过仿真验证,ICP算法对稳态部分可辨编队具有较高的跟踪可靠性与跟踪精度,且在编队出现交叉航迹时仍具有较高的有效性。
5) 具有较高的处理效率,算法实时性较好。
综上,ICP算法在稳态部分可辨编队条件下的精细跟踪中,具有优越的性能优势及可靠性,为实际工程应用提供了新的技术途径。
| [1] |
黄天俊. 低可观测目标的检测跟踪算法[D]. 西安: 西安电子科技大学, 2012: 1-3.
HUANG T J.The algorithm of detection and tracking for low-observable target[D].Xi'an:Xidian University, 2012:1-3(in Chinese). |
| [2] | GVAN K, FGAN F. MHT extraction and track maintenance of a target formation[J]. IEEE Transactions on Aerospace and Electronic System, 2002, 38(1): 288–294. DOI:10.1109/7.993248 |
| [3] |
张昌芳. 阵群目标信息相关技术研究[D]. 长沙: 国防科学技术大学, 2009: 1-10.
ZHANG C F.Research on data association method of group data[D].Changsha:National University of Defense Technology, 2009:1-10(in Chinese). |
| [4] |
赵志超, 饶彬, 王雪松, 等. 基于概率网格Hough变换的多雷达航迹起始算法[J].
航空学报, 2010, 31(11): 2209–2215.
ZHAO Z C, RAO B, WANG X S, et al. Multi-radar track initiation algorithm based on probabilistic Hough transform[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(11): 2209–2215. (in Chinese) |
| [5] |
何友, 修建娟, 张晶炜, 等.
雷达数据处理及应用[M].2版.北京: 电子工业出版社, 2009: 121-293.
HE Y, XIU J J, ZHANG J W, et al. Radar data processing with applications[M].2nd ed. Beijing: Publishing House of Electronics Industry Press, 2009: 121-293. (in Chinese) |
| [6] | WANG H L, WANG D S, TIAN L S.A new algorithm for group tracking[C]//2011 CIE International Conference on Radar.Xi'an:[s.n.], 2011:1159-1163. |
| [7] |
何友, 王海鹏, 熊伟, 等. 基于相对位置矢量的灰色精细航迹起始算法[J].
航空学报, 2012, 33(10): 1850–1863.
HE Y, WANG H P, XIONG W, et al. Refined gray track initiation algorithm of group targets based on relative position vectors[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(10): 1850–1863. (in Chinese) |
| [8] |
邢凤勇, 熊伟, 王海鹏. 基于聚类和Hough变换的多编队航迹起始算法[J].
海军航空工程学院学报, 2010, 25(6): 624–629.
XING F Y, XIONG W, WANG H P. A formation target track initiation algorithm based on clustering and Hough transform[J]. Journal of Naval Aeronautical and Astronautical University, 2010, 25(6): 624–629. (in Chinese) |
| [9] |
耿文东. 基于PDA的群目标合并与分离方法研究[J].
无线电工程, 2007, 37(2): 24–26.
GENG W D. A study on group target merging and splitting method based on PDA[J]. Radio Engineering, 2007, 37(2): 24–26. (in Chinese) |
| [10] |
刘红, 耿文东. 基于模式空间的群目标合并与分离方法研究[J].
无线电工程, 2010, 40(2): 53–56.
LIU H, GENG W D. A study of merging and splitting methods for group targets based on pattern space[J]. Radio Engineering, 2010, 40(2): 53–56. (in Chinese) |
| [11] | FRANCOIS S, SZE K P. Tracking of coordinated groups using marginalized MCMC-based particle algorithm[J]. IEEE Transactions on Automatic Control, 2009, 31(2): 1–11. |
| [12] |
连峰, 韩崇昭, 刘伟峰, 等. 基于SMC-PHDF的部分可分辨的群目标跟踪算法[J].
自动化学报, 2010, 36(5): 731–741.
LIAN F, HAN C Z, LIU W F, et al. Tracking partly resolvable group targets using SMC-PHDF[J]. Acta Automatica Sinica, 2010, 36(5): 731–741. (in Chinese) |
| [13] | MIHAYLOVA L, GNING A.Group object structure and state estimation in the presence of measurement origin uncertainty[C]//2009 IEEE/SP 15th Workshop on Statistical Signal Processing.Piscatawey, NJ:IEEE Press, 2009:473-476. |
| [14] | FELDMANN M, FRANKEN D.Advances on tracking of extended objects and group targets using random matrices[C]//2009 12th International Conference on Information Fusion.Piscatawey, NJ:IEEE Press, 2009:1029-1036. |
| [15] | LIAN F, HAN C Z, LIU W F. Sequential monte carlo implementation and state extraction of the group probability hypothsis density filter for partly unresolvable group targets-tracking problem[J]. IET Radar, Sonar and Navigation, 2010, 4(5): 685–702. DOI:10.1049/iet-rsn.2009.0109 |
| [16] |
王海鹏, 熊伟, 何友, 等. 集中式多传感器群目标灰色精细航迹起始算法[J].
系统工程与电子技术, 2012, 34(11): 2249–2255.
WANG H P, XIONG W, HE Y, et al. Gray refined track initiation algorithm for centralized multi-sensor group targets[J]. System Engineering and Electronics, 2012, 34(11): 2249–2255. DOI:10.3969/j.issn.1001-506X.2012.11.11(in Chinese) |
| [17] |
王海鹏, 董云龙, 熊伟, 等. 运动状态下多传感器群目标精细航迹起始算法[J].
宇航学报, 2012, 33(11): 1690–1698.
WANG H P, DONG Y L, XIONG W, et al. Multi-sensor group target refined track initiation algorithm based on moving state[J]. Journal of Astronautics, 2012, 33(11): 1690–1698. DOI:10.3873/j.issn.1000-1328.2012.11.019(in Chinese) |
| [18] | PANG S K, LI J, GODSILL S J. Detection and tracking of coordinated groups[J]. IEEE Transcations on Aerospace and Electronic Systems, 2011, 47(1): 472–502. DOI:10.1109/TAES.2011.5705687 |
| [19] |
王海鹏. 多传感器编队目标跟踪算法研究[D]. 烟台: 海军航空工程学院, 2012: 71-85.
WANG H P.Study of multi-sensor group targets tracking algorithm[D].Yantai:Naval Aeronautical and Astronautical University, 2012:71-85(in Chinese). |
| [20] |
祝继华, 郑南宁, 袁泽剑, 等. 基于ICP算法和粒子滤波的未知环境地图创建[J].
自动化学报, 2009, 35(8): 1107–1113.
ZHU J H, ZHENG N N, YUAN Z J, et al. A SLAM approach by combibing ICP algorithm and particle filter[J]. Acta Automatica Sinica, 2009, 35(8): 1107–1113. (in Chinese) |
| [21] |
宋强. 目标航迹对准关联与传感器系统误差估计技术研究[D]. 烟台: 海军航空工程学院, 2010: 33-39.
SONG Q.Target track alignment-correlation and sensor bias estimation technique research[D].Yantai:Naval Aeronautical and Astronautical University, 2010:33-39(in Chinese). |
| [22] |
何友, 王国宏, 关欣.
信息融合理论及应用[M].北京: 电子工业出版社, 2010: 189-193.
HE Y, WANG G H, GUAN X. Information fusion theory with applications[M].Beijing: Publishing House of Electronics Industry, 2010: 189-193. (in Chinese) |



