2. 上海航天控制技术研究所 研发中心, 上海 201109;
3. 上海市空间智能控制技术重点实验室, 上海 201109
2. Research and Development Centre, Shanghai Institute of Spaceflight Control Technology, Shanghai 201109, China;
3. Shanghai Key Laboratory of Aerospace Intelligent Control Technology, Shanghai 201109, China
常值推力下面内轨道转移是指航天器在大小恒定、方向可调的轨控推力下,实现面内轨道转移的轨道机动方式,在逃逸飞行、轨道交会、空间碎片离轨操作等领域有广泛应用[1-3]。已有文献主要研究航天器在诸如切向、周向、径向等特定推力方向下的轨道运动特性及应用[4-6]。特定推力方向下航天器轨道机动控制规律简单,但多数情况下不能达到入轨条件或转移轨道的优化要求,实际轨道转移过程中,需要通过调节推力方向以实现精准高效的优化转移。尽管已有学者针对连续常值推力下的轨道优化问题进行了研究[7-8],但是当推力方向角调节能力受限时,相关研究较少。在某些情况下,航天器的推力方向只能通过调整姿态实现,而航天器姿态机动能力非常有限,尤其是绳系卫星[9-11]。在绳系卫星轨道机动过程中,为了保持绳系卫星稳定,轨控推力应沿系绳连线方向施加,所以绳系卫星在做最优轨道转移时需要不断调整姿态以适应最优推力方向,但是由于绳系卫星庞大的转动惯量,其姿态调节能力非常有限。所以在设计最优转移轨道时,应该考虑到姿态调节能力的限制。因此,研究推力方向角调节能力受限的常值推力下航天器面内转移轨道优化方法对未来多任务航天器灵活机动的在轨操作非常重要。
实质上轨道优化问题是最优控制问题,其求解方法通常可分为直接法和间接法2种。直接法将具有连续状态量和控制量的最优控制问题离散化后转为非线性规划问题进行求解,其不同方法在计算量、收敛性等方面各有差异[12],最具代表性的方法是由Benson[13]和Huntington[14]提出的Gauss伪谱法,其求解平滑型最优控制问题时收敛性好,被广泛应用于飞行器轨迹优化[15-17]。但是离散化造成信息损失,限制了直接法的求解精度,且在状态量或控制量变化剧烈时算法难以收敛。间接法利用Pontryagin极值原理,将最优控制问题转化为常微分方程的两点边值问题后,采用打靶法等数值方法进行求解。由于具有完整的数学模型,间接法解的最优性和高精度易得到保证。但是打靶法求解微分方程的两点边值问题时,需要给出变量的一组初值,而不恰当的初值会导致数值发散。所以,如何给定一组与最优轨迹尽可能接近的变量初值是间接法成功与否以及能否快速收敛的关键,而协态变量无实际物理意义,初值范围、量级很难确定,如何确定协态变量的初值范围是间接法求解的难点。各国学者针对具体问题,提出了各自实用的确定协态变量初值范围的方法[18-19],但是尚无一种简单通用的方法。
本文针对常值推力下航天器面内轨道转移燃耗最省的轨道优化问题,首先利用Pontryagin极值原理导出协态变量微分方程和含协态变量的初始控制方程;然后将初始控制方程代入协态变量微分方程得到一个不含协态变量的控制方程;最后结合动力学方程提出一种求解航天器面内最优转移轨道改进间接法,及其在推力方向角调节能力受限条件下的应用方法。本文方法与传统间接法相比不需求解协态变量微分方程,初值猜测难度和计算量更低;与Gauss伪谱法相比具有更高的精度和更好的数值光滑性。
1 轨道优化模型航天器在中心引力场和常值推力作用下做面内轨道转移,不考虑任何扰动,极坐标下轨道动力学方程为
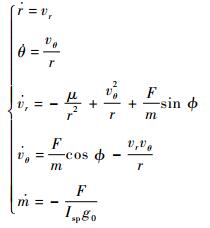
|
(1) |
式中:r、θ、vr、vθ、m、ϕ、F、μ、Isp和g0分别为轨道极坐标下的极径、极角、径向速度大小、切向速度大小、航天器质量、推力方向角、推力大小、地球引力常量、发动机比冲和海平面重力加速度。
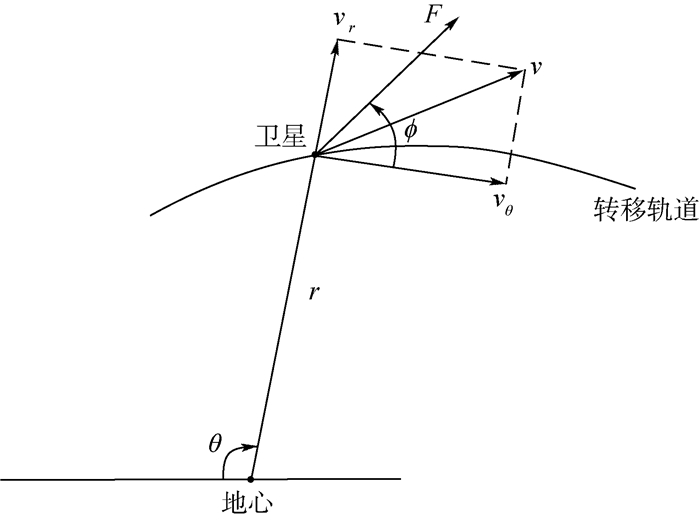
推力方向角ϕ定义为推力矢量与切向速度之间的夹角,如图 1所示。在轨道机动过程中,推力大小F和发动机比冲Isp恒定,因此质量流量恒定,燃耗最省问题等价于时间最短问题,而燃耗等于航天器变轨前质量m0与航天器变轨后质量mf之差,所以目标函数可定义为
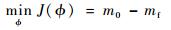
|
(2) |
|
| 图 1 变量示意图 Fig. 1 Illustration of variables |
推力方向角ϕ为控制变量,在轨道机动过程中动态调节。当航天器配置确定后,航天器面内转动惯量I和俯仰调姿力矩T确定,推力方向角的二阶导数ϕ″满足约束:
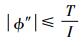
|
(3) |
本文以GEO轨道废星离轨过程为研究对象,太空拖船拖曳废星由GEO轨道转移至GEO轨道上方几百公里的坟墓轨道,因此初始状态r0、θ0、vr0、vθ0和m0给定,边界约束设为:末端轨道近地点高度rpf达到期望高度h。

|
(4) |
由Kepler轨道性质得
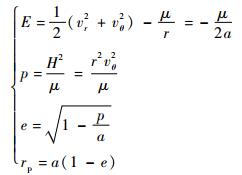
|
(5) |
式中:E、a、p、H、e和rp分别为轨道能量、椭圆轨道半长轴、椭圆轨道半通径、轨道动量矩、轨道偏心率和椭圆轨道近地点高度。
所以
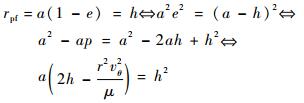
|
(6) |
再将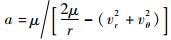
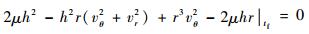
|
(7) |
所以,该轨道优化问题最终转化为5个状态量、1个控制量、1个终端约束、初始状态已知、终止时间tf自由的最优控制问题。
2 最优控制模型不考虑推力方向角的二阶导数ϕ″受限,ϕ为任意连续函数,根据最优控制理论的变分原理,该最优控制问题的哈密顿函数为
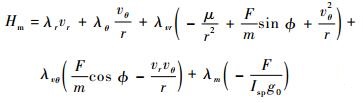
|
(8) |
式中:λr、λθ、λvr、λvθ和λm为各状态量微分约束的拉格朗日系数,称为协态变量。
由变分法得到协态变量微分方程为
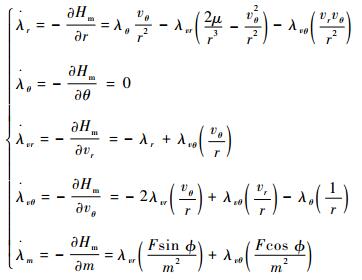
|
(9) |
最优控制条件为

|
(10) |
则控制方程为
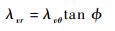
|
(11) |
根据末端横截条件可得
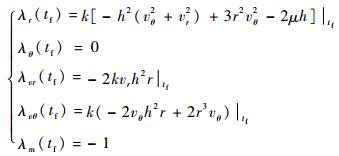
|
(12) |
式中:k为边界约束等式(7) 的拉格朗日系数。
根据末端时间最优条件可得
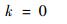
|
(13) |
由此横截条件结合式(9) 可以得出λθ≡0,将其代入式(9) 整理化简得
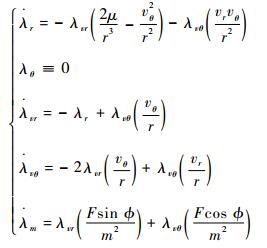
|
(14) |
根据化简后的式(14) 和式(11) 可以求出推力方向角的微分方程,将式(11) 代入式(14) 的第4个等式整理得
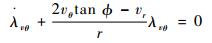
|
(15) |
令
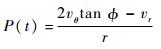
|
(16) |
则可得
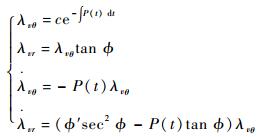
|
(17) |
式中:c为待定积分常数。
将式(17) 代入式(14) 的第3个等式可得
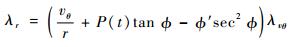
|
(18) |
再设
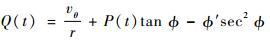
|
(19) |
则
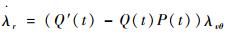
|
(20) |
设式(14) 中第1个等式右边为
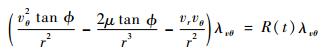
|
(21) |
则根据等式(14) 有
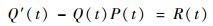
|
(22) |
将式(16)、式(19) 和式(14) 中的第1个等式代入化简整理得
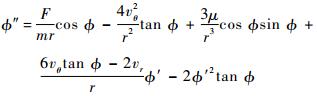
|
(23) |
式(23) 描述了常值推力下航天器面内轨道转移,燃耗最省(时间最短)转移轨道推力方向角应满足的控制微分方程。
由推导过程知,虽然式(23) 是在特定的边界条件和目标函数下给出的,但推导过程仅用到横截条件λθ(tf)=0,而只要末端约束和目标函数中不显含极角θ,则λθ(tf)=0均成立。所以式(23) 在求解常值推力面内转移轨道优化问题中有一定的通用性。
3 数值求解传统间接法通过求解状态微分方程式(1) 和协态微分方程式(9) 组成的方程组获得最优解,但由于初始状态量r0、θ0、vr0、vθ0和m0已知,而横截条件给定了协态变量的末端值λr(tf)、λθ(tf)、λvr(tf)、λvθ(tf)和λm(tf),该问题为典型的微分方程两点边值问题。利用打靶法求解时需给出协态变量的初值猜测,而协态变量无实际物理意义,初值范围、量级很难确定是传统间接法求解的难点。
本文利用推导出的控制微分方程式(23) 与状态微分方程式(1) 建立一种改进间接法,通过求解式(23) 与式(1) 组成的微分方程组获得最优解,由于初始状态量r0、θ0、vr0、vθ0和m0已知,最优解由ϕ0、ϕ′0唯一确定,利用打靶法优化ϕ0、ϕ′0即可得到最优解。该方法不引入协态变量,初值猜测只需给出有物理意义的初值ϕ0、ϕ′0,大大降低了初值猜测的难度;同时该方法将传统间接法迭代10个微分方程、优化5个初值变量,降低为迭代7个微分方程、优化2个初值变量,降低了打靶法求解的计算量。
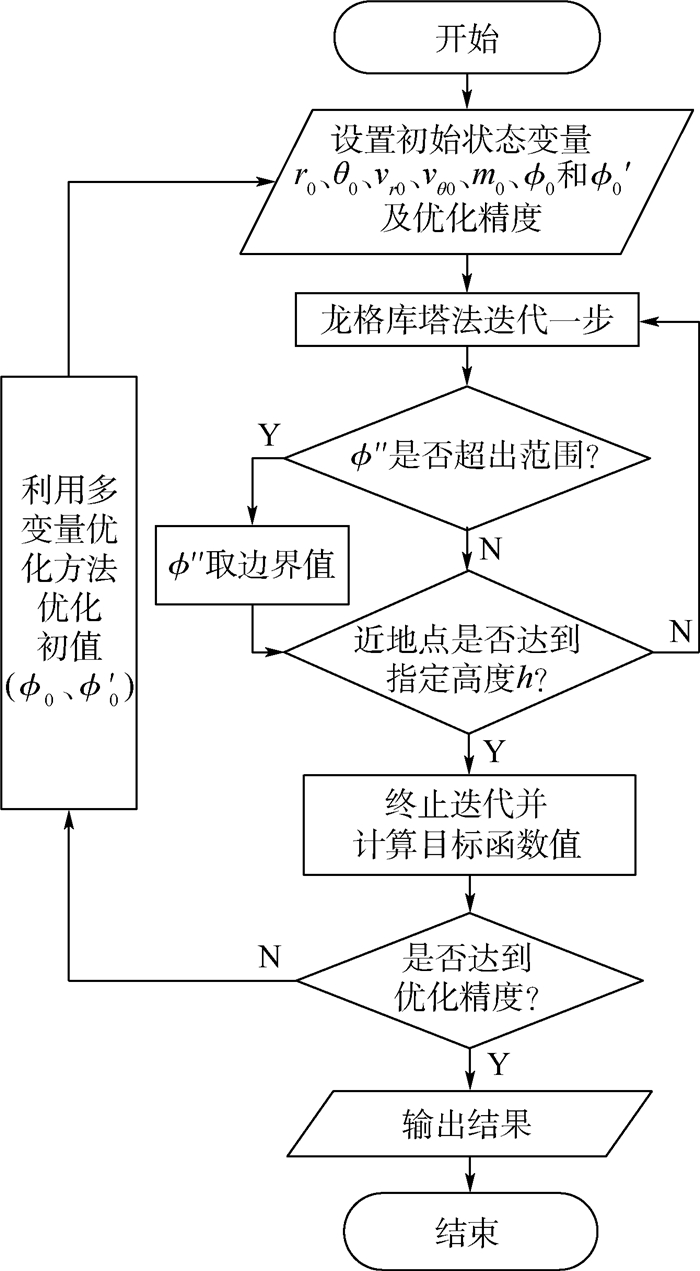
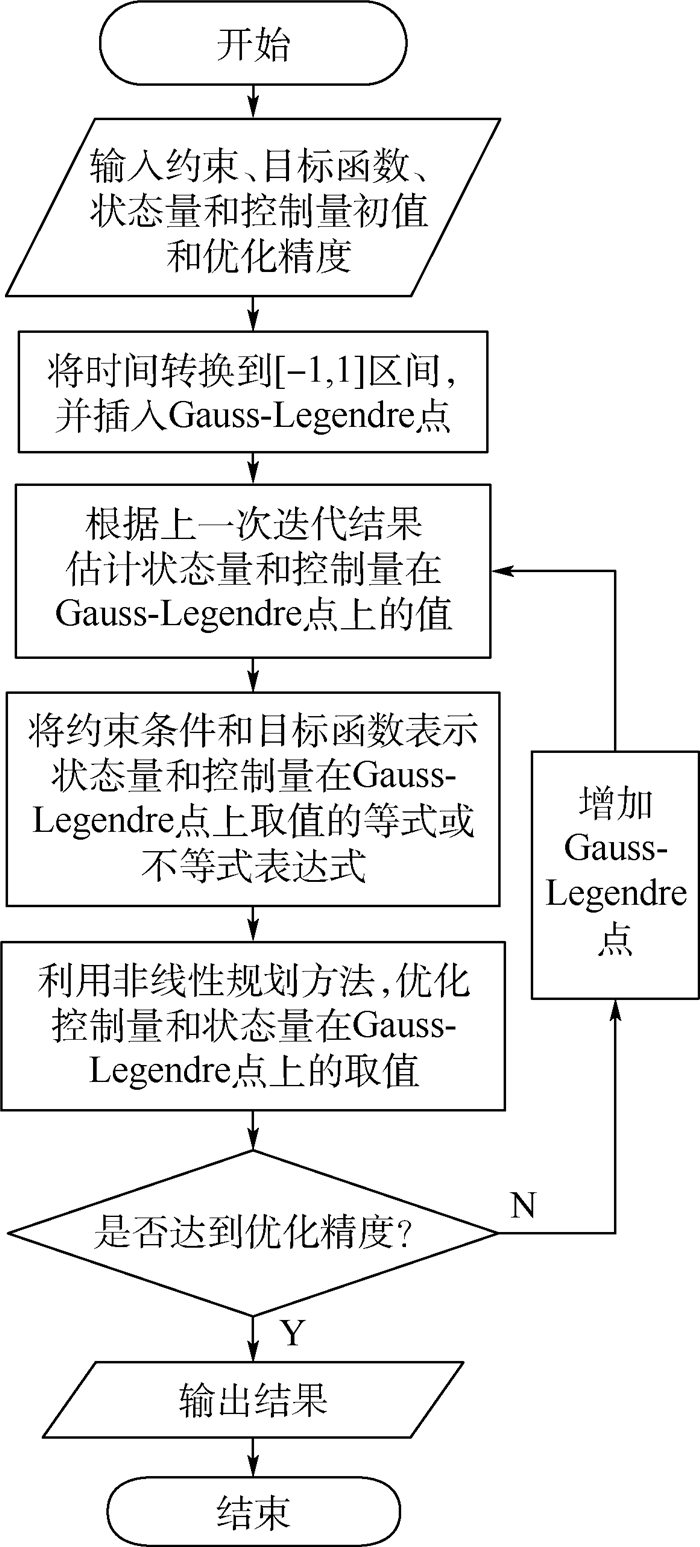
改进间接法求解时,末端边界条件只有式(7),两点边值问题缺少一个末端边界条件,因为文中的最优控制问题中终止时间tf自由,广义目标函数应满足终止时间最优条件,但在最优控制模型推导中尚未使用该条件,该条件可在打靶法求解过程中使用。由第1节分析可知,文中的燃耗最省问题等价于时间最短问题,在打靶法求解时,式(7) 作为龙格库塔迭代终止条件,燃耗最省作为优化目标用于优化初值ϕ0、ϕ′0。同时提出一种推力方向角调节能力受限条件下的求解方法。当推力方向角的二阶导数ϕ″受限时,如果ϕ″超过限制范围,ϕ″则取边界值,其求解流程如图 2所示。为了验证改进间接法的正确性,用Gauss伪谱法独立求解以做对比,Gauss伪谱法求解流程如图 3所示。
|
| 图 2 改进间接法求解流程 Fig. 2 Flowchart of improved indirect method |
|
| 图 3 Gauss伪谱法求解流程 Fig. 3 Flowchart of Gauss pseudospectral method |
为了使求解结果不受限于航天器质量和发动机比冲,以下仿真计算中以推力加速度f和速度变化量Δv分别代替推力F和燃耗Δm,转化公式如下:
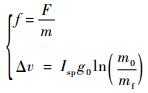
|
(24) |
式中:推力F为常值;推力加速度f随着航天器燃料消耗质量减少而略有变化,下文f值均由航天器初始质量计算得出。
GEO废星离轨过程轨道优化问题的实际参数为:航天器质量为5t,初始轨道为GEO轨道,在连续常值推力作用下近地点升高Δh=350km。
4.1 ϕ″不受限的轨道优化首先不考虑推力方向角调节能力受限,ϕ为任意连续函数,设计燃耗最省的转移轨道。用改进间接法和Gauss伪谱法分别求解。
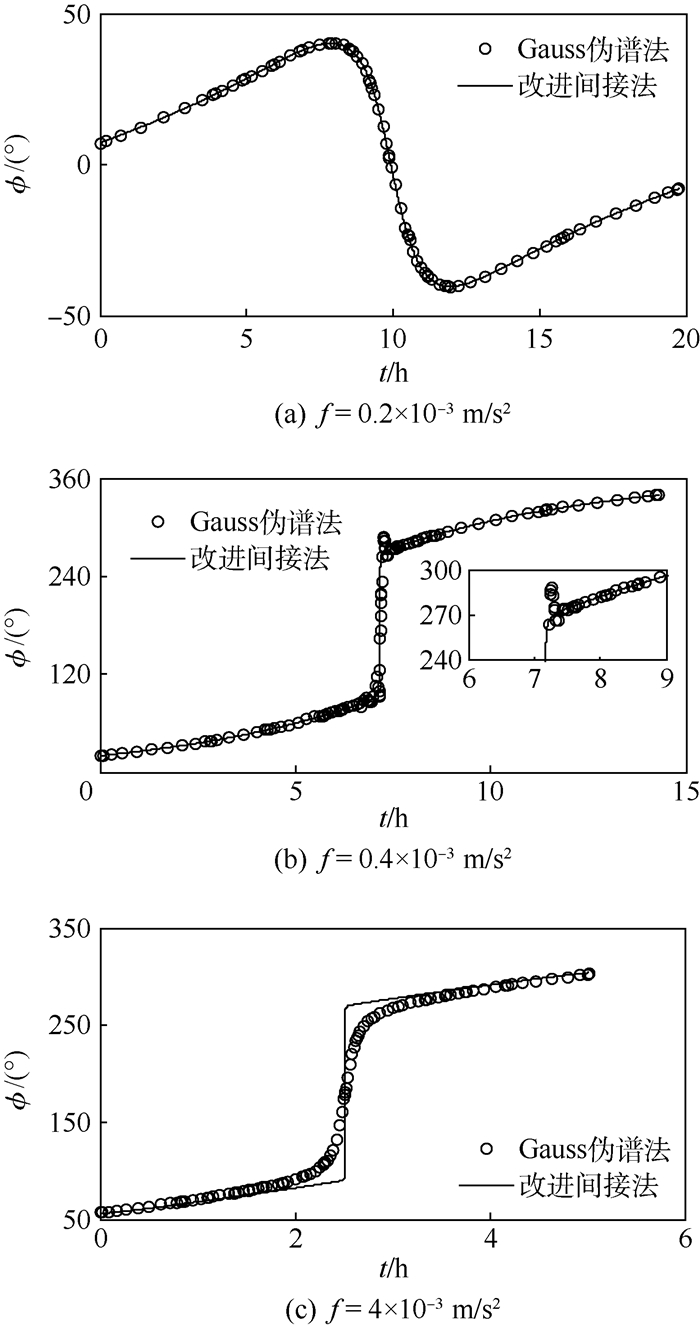
图 4为3种不同推力加速度下,燃耗最省转移轨道推力方向角ϕ变化曲线。可以看出:① 推力加速度较小时,推力方向角呈现一次往复摆动,变化范围在[-90°, 90°]之间,其变化规律如图 4(a)所示,变化过程较平缓;推力加速度较大时,推力方向角旋转一周,变化范围在[0°, 360°]之间,变化规律如图 4(b)和图 4(c)所示,由90°~270°时变化较剧烈。② 推力方向角变化平滑时,改进间接法与Gauss伪谱法求解结果非常吻合;推力方向角变化剧烈时,Gauss伪谱法在变化剧烈处作了圆滑处理并且容易出现局部波动,准确性与数值光滑性不如改进间接法。
|
| 图 4 不同推力加速度下推力方向角变化曲线 Fig. 4 Thrust angle vs time under different thrust acceleration |
由第4.1节知,当推力方向角的二阶导数自由时,随推力加速度增加推力方向角变化范围增加到[0°, 360°],此时推力方向角ϕ存在由90°~270°的突变,推力方向角变化率ϕ′及推力方向角的二阶导数ϕ″均存在变化峰值,如图 5所示,并且此峰值随着推力加速度增加更加明显,当推力加速度f=10×10-3m/s2时,推力方向角的二阶导数峰值达到50 (°)/s2。
|
| 图 5 ϕ″不受限时推力方向角变化规律 Fig. 5 Change law of thrust angle when ϕ″ is free |
实际工程中,推力方向角的二阶导数调节能力有限,上述最优控制规律难以实现。本节以绳系卫星为参考,考虑推力方向角的二阶导数|ϕ″|≤0.008 (°)/s2时,燃耗最省转移轨道的控制规律,用改进间接法和Gauss伪谱法分别求解。
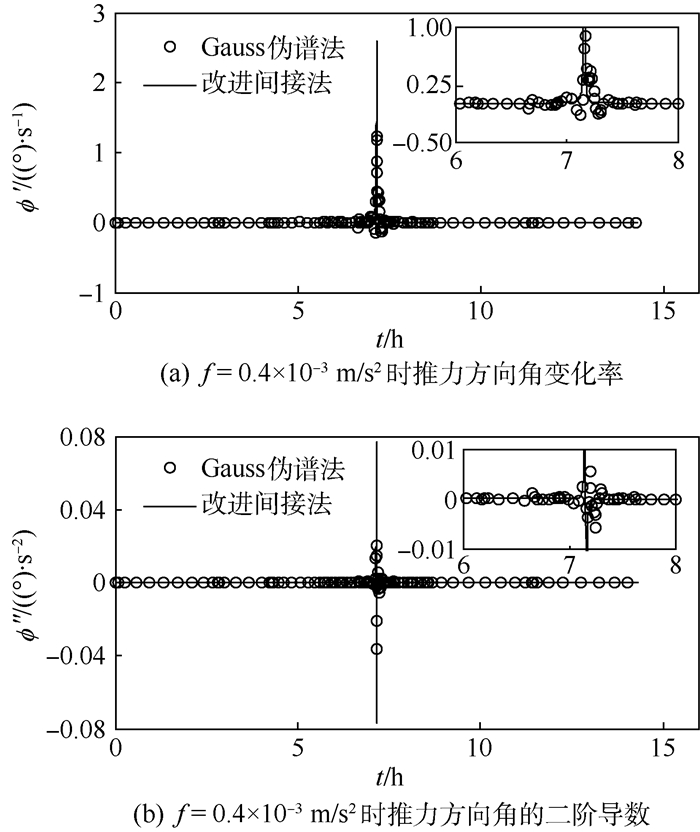
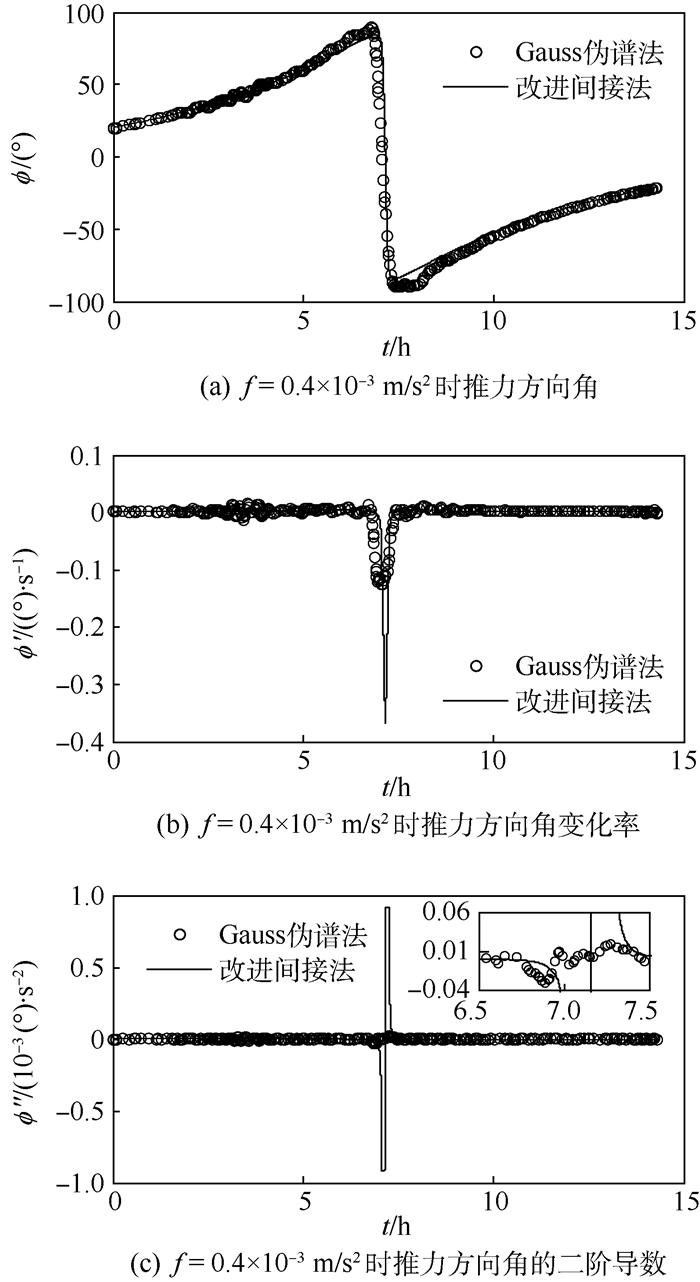
图 6为f=0.4×10-3m/s2, |ϕ″|≤0.008 (°)/s2时,改进间接法与Gauss伪谱法求解的燃耗最省转移轨道推力方向角、推力方向角变化率、推力方向角的二阶导数变化曲线。可以看出:① 对推力方向角二阶导数的限制改变了推力方向角的变化规律,使其由旋转一周转变为一次往复运动,减小了姿态机动的范围及变化速率,增加了飞船的稳定性。② 尽管改进间接法在推力方向角的二阶导数超出约束边界时作了近似处理,但是与Gauss伪谱法求解的最优控制律基本一致,燃耗也相同(见表 1)。当推力方向角的二阶导数受限时,Gauss伪谱法由于数值精度不能达到边界值,但改进间接法能够准确地达到边界值,并且改进间接法求解结果的数值光滑性优于Gauss伪谱法的求解结果。
|
| 图 6 |ϕ″|≤0.008 (°)/s2时推力方向角变化规律 Fig. 6 Change law of thrust angle when |ϕ″|≤0.008 (°)/s2 |
| 推力加速度/ (10-3m·s-2) |
速度变化量/(m·s-1) | ||||
| 切向推力转移轨道 | 优化轨道 | ||||
| Gauss伪谱法求解不限ϕ″ | Gauss伪谱法求解|ϕ″|≤0.008 (°)/s2 | 改进间接法求解不限ϕ″ | 改进间接法求解|ϕ″|≤0.008 (°)/s2 | ||
| 0.02 | 13.205 | 12.757 | 12.757 | 12.757 | 12.757 |
| 0.10 | 14.862 | 14.005 | 14.007 | 14.005 | 14.005 |
| 0.15 | 12.858 | 12.713 | 12.713 | 12.713 | 12.713 |
| 0.20 | 14.995 | 14.254 | 14.257 | 14.254 | 14.254 |
| 0.40 | 22.588 | 20.645 | 20.722 | 20.645 | 20.670 |
| 1.00 | 40.315 | 34.428 | 34.447 | 34.309 | 34.421 |
| 4.00 | 100.270 | 72.974 | 73.007 | 72.856 | 72.937 |
| 10.00 | 185.780 | 117.660 | 117.770 | 117.560 | 117.690 |
4.3 燃耗分析
表 1列出了不同条件下优化轨道燃耗与切向推力转移轨道燃耗。
由表 1可以看出:① 推力加速度越大燃耗越多,当推力加速度f=0.15×10-3 m/s2时,燃耗达到局部极小值,此时推力大小满足由GEO轨道到GEO上方350km圆轨的转移条件——圆轨到圆轨转移条件[3]。② 推力加速度较小时,最优转移轨道燃耗与切向推力转移轨道燃耗相差较小;推力加速度较大时,最优转移轨道比切向推力转移轨道显著节省燃耗,当f=10.00×10-3 m/s2时,最优转移轨道省燃料达36.7%,所以在大推力场合,更适合选用优化方法计算转轨方案。
5 结论本文研究了常值推力作用下燃耗最省的面内轨道最优转移过程。
1) 所提出的改进间接法由于避免了协态变量微分方程组的求解,相对于传统间接法降低了初值猜测的难度和计算量; 与Gauss伪谱法相比,改进间接法求解精度更高;在推力方向角调节能力受限时,所提出的近似优化方法求解结果与Gauss伪谱法求解结果一致并且精度更高,有工程应用价值。
2) 推力方向角的二阶导数受限能够改变推力方向角变化规律,降低推力方向角变化范围(姿态机动范围)和变化速率,增加航天器的稳定性。
3) 总体上推力加速度越大燃耗越多,当推力加速度较小时,最优转移轨道燃耗与切向推力转移轨道燃耗相差很小;当推力加速度较大时,最优转移轨道比切向推力转移轨道显著节省燃耗,所以在大推力场合,更适合选用优化方法计算转轨方案。
| [1] | MENGALI G, QUARTA A. Escape from elliptic orbit using constant radial thrust[J]. Journal of Guidance, Control, and Dynamics, 2009, 32 (3): 1018–1022. DOI:10.2514/1.43382 |
| [2] | QI Y Q, JIA Y M. Constant thrust fuel-optimal control for spacecraft rendezvous[J]. Advances in Space Research, 2012, 49 (7): 1140–1150. DOI:10.1016/j.asr.2012.01.002 |
| [3] |
朱仁璋, 王晓光. 连续常值推力机动分析与应用[J].
中国空间科学技术, 2008, 28 (3): 22–28.
ZHU R Z, WANG X G. Analyses and applications of continuous constant thrust maneuver[J]. Chinese Space Science & Technology, 2008, 28 (3): 22–28. (in Chinese) |
| [4] |
张皓, 师鹏, 赵育善, 等. 常值径向推力下的航天器运动轨迹[J].
北京航空航天大学学报, 2012, 38 (4): 551–556.
ZHANG H, SHI P, ZHAO Y S, et al. Trajectory of a spacecraft with constant radial thrust[J]. Journal of Beijing University of Aeronautics and Astronautics, 2012, 38 (4): 551–556. (in Chinese) |
| [5] | BOMBARDELLI C, BAÙ G, PELÁEZ J. Asymptotic solution for the two-body problem with constant tangential thrust acceleration[J]. Celestial Mechanics and Dynamical Astronomy, 2011, 110 (3): 239–256. DOI:10.1007/s10569-011-9353-3 |
| [6] | PRUSSING J E, CARROLL V C. Constant radial thrust acceleration redux[J]. Journal of Guidance, Control, and Dynamics, 1998, 21 (3): 516–518. |
| [7] |
王明春, 荆武兴, 杨涤, 等. 能量最省有限推力同平面轨道转移[J].
宇航学报, 1992, 13 (3): 24–31.
WANG M C, JING W X, YANG D, et al. Minimum fuel orbit coplanar transfers with finite thrust[J]. Journal of Astronautics, 1992, 13 (3): 24–31. (in Chinese) |
| [8] | JEZEWSKI D J, STOOLZ J M. A closed-form solution for minimum-fuel, constant-thrust trajectories[J]. AIAA Journal, 1970, 8 (7): 1229–1234. DOI:10.2514/3.5877 |
| [9] | ZHAO G W, SUN L, HUANG H. Thrust control of tethered satellite with a short constant tether in orbital maneuvering[J]. Proceedings of the Institution of Mechanical Engineers, Part G:Journal of Aerospace Engineering, 2014, 228 (14): 2569–2586. DOI:10.1177/0954410014521151 |
| [10] | ZHAO G W, SUN L, TAN S P, et al. Librational characteristics of a dumbbell modeled tethered satellite under small, continuous, constant thrust[J]. Proceedings of the Institution of Mechanical Engineers, Part G:Journal of Aerospace Engineering, 2013, 227 (5): 857–872. DOI:10.1177/0954410012445845 |
| [11] | SUN L, ZHAO G W, HUANG H. Stability and control of tethered satellite with chemical propulsion in orbital plane[J]. Nonlinear Dynamics, 2013, 74 (4): 1113–1131. DOI:10.1007/s11071-013-1028-z |
| [12] | RAO A V. A survey of numerical methods for optimal control[J]. Advances in the Astronautical Sciences, 2009, 135 (1): 497–528. |
| [13] | BENSON D.A Gauss pseudospectral transcription for optimal control[D]. Cambridge:Massachusetts Institute of Technology, 2005. |
| [14] | HUNTINGTON G T.Advancement and analysis of Gauss pseudospectral transcription for optimal control problems[D]. Cambridge:Massachusetts Institute of Technology, 2007. |
| [15] |
李亦楠, 杨凌宇, 申功璋. 基于操纵面故障影响估计的安全飞行轨迹优化[J].
北京航空航天大学学报, 2012, 38 (12): 1601–1605.
LI Y N, YANG L Y, SHEN G Z. Safe trajectory optimization with control failure effects estimation[J]. Journal of Beijing University of Aeronautics and Astronautics, 2012, 38 (12): 1601–1605. (in Chinese) |
| [16] |
孟少华, 向锦武, 罗漳平, 等. 微小型无人直升机避障最优轨迹规划[J].
北京航空航天大学学报, 2014, 40 (2): 246–251.
MENG S H, XIANG J W, LUO Z P, et al. Optimal trajectory planning for small-scale unmanned helicopter obstacle avoidance[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40 (2): 246–251. (in Chinese) |
| [17] |
邵龙飞, 师鹏, 赵育善. 电磁航天器编队动力学建模与运动规划方法[J].
北京航空航天大学学报, 2015, 41 (4): 737–743.
SHAO L F, SHI P, ZHAO Y S. Dynamics modeling and motion programming for eletromagnetic formation flight[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41 (4): 737–743. (in Chinese) |
| [18] | THORNE J D, HALL C D. Approximate initial Lagrange costates for continuous-thrust spacecraft[J]. Journal of Guidance, Control, and Dynamics, 1996, 19 (2): 283–288. DOI:10.2514/3.21616 |
| [19] | LEE D, BANG H. Efficient initial costates estimation for optimal spiral orbit transfer trajectories design[J]. Journal of Guidance, Control, and Dynamics, 2009, 32 (6): 1943–1947. DOI:10.2514/1.44550 |



