2. 中国空间技术研究院 载人航天总体部, 北京 100094
2. General Department of Manned Spacecraft, China Academy of Space Technology, Beijing 100094, China
线性二阶上风格式在激波附近总会产生非物理振荡,因此,必须设法构造无振荡的二阶格式使其能精确地捕捉激波和接触间断。在满足总变差衰减 (TVD)[1]条件和熵条件的前提下,提高一阶精度限制的有效途径是引入非线性成分。这个概念是Leer[2]以“限制器 (limiters)”的形式提出的。目前针对几种高精度计算格式,如TVD格式、ENO格式[3]、WENO格式[4]的研究从未停止,对新型限制器的开发、限制器性能对比以及基于限制思想的高阶计算格式的开发和设计都是计算流体力学 (CFD) 的热点问题。Sweby[5]基于标量守恒分析提出了TVD限制区间,但仅适用于二阶精度。Venkatakrishman[6]针对限制器对计算精度和收敛性的影响开展研究,并设计了一种阈值函数,使限制器函数在流场光滑区域或微弱振荡区域自动关闭。进入21世纪以来,限制技术成为发展高精度、无振荡、低耗散计算格式的核心。虽然已经进行了很多基于限制思想的CFD技术的研究[7-10],但限制函数分辨率和耗散性一直没得到良好的权衡。Kim等[11]提出了一种基于TVD插值的三阶精度限制器,在提高计算精度的同时,具有较好的收敛特性。本文将其与3种传统TVD限制器进行对比研究,并研究其在高超声速数值模拟中的性能表现。发现其有如下优点:在激波间断处数值耗散小同时保持三阶精度;能有效抑制振荡,鲁棒性好;在高超声速复杂流动模拟中能较为准确刻画激波;构造简单,容易实现。
1 计算方法 1.1 控制方程无热源、无体积力的非定常三维可压缩Navier-Stokes方程,在直角坐标系 (x, y, z) 下向量形式为[12]
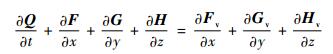
|
(1) |
式中:F、G、H分别为x, y, z 3个方向上的无黏通量矢量;Q为守恒变量矢量;Fv、Gv、Hv分别为x, y, z 3个方向上的黏性通量矢量。
1.2 二阶TVD限制器的一般形式由原始变量q=(ρ, u, p)T (ρ为密度;u为速度;p为压强。) 构成的限制器的一般表达式可写为
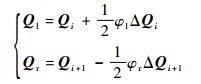
|
(2) |
式中:ΔQi=Qi-Qi-1; 下标r和l分别表示变量是自单元界面的右边和左边插值得来;φl、φr为限制函数,其一般形式为

|
(3) |
式中: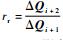
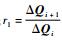
minmod限制器:
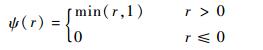
|
(4) |
superbee限制器:
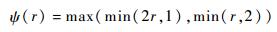
|
(5) |
double minmod限制器:
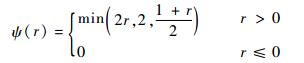
|
(6) |
三阶TVD限制器 (为方便引用,本文将其简称为T-3限制器) 的构造原理如下[11]。
首先进行三阶插值:
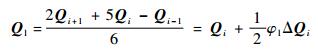
|
(7) |
式中: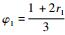
再加入double minmod限制器对插值坡度进行限制:
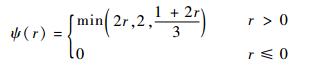
|
(8) |
因此,T-3限制器的表达式可写为
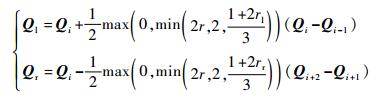
|
为分析验证该T-3限制器的性能,采用3个算例进行数值模拟实验,并与经典二阶TVD限制器superbee、minmod和double minmod的计算结果对比。
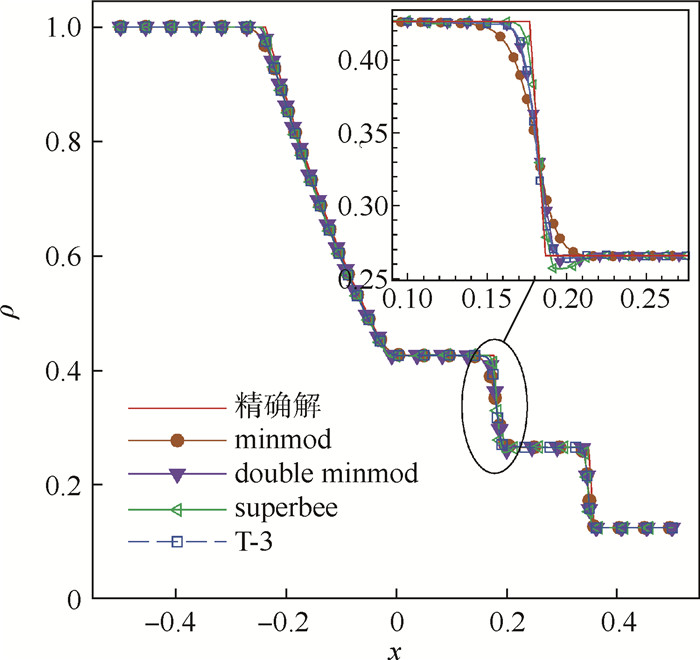
2.1 Sod问题计算域为[0, 1],计算推进到t=0.2 s时停止,此时流场中包含一个激波,一个接触间断,一个膨胀波[13]。时间格式采用三阶Runge-Kutta,方向240个网格单元,初始条件为

|
(9) |
如图 1为密度分布与精确解的结果对比图,由图知,T-3与superbee具有较高间断分辨率,double minmod次之,minmod耗散较大。
|
| 图 1 密度分布曲线 Fig. 1 Density distribution curves |
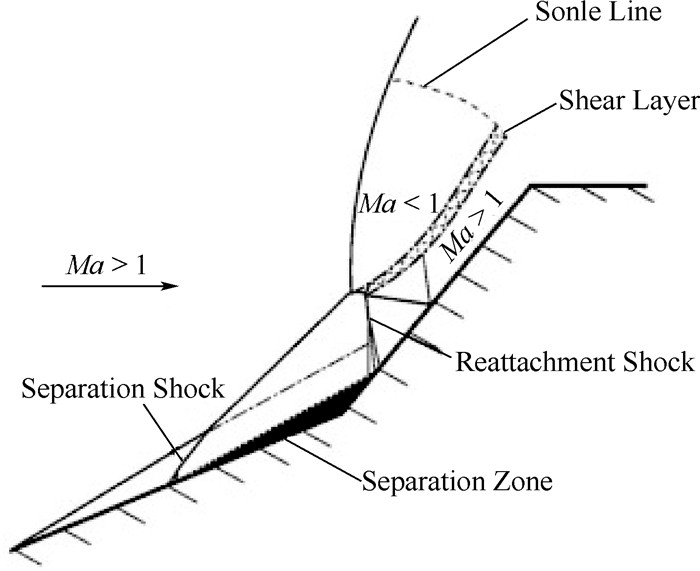
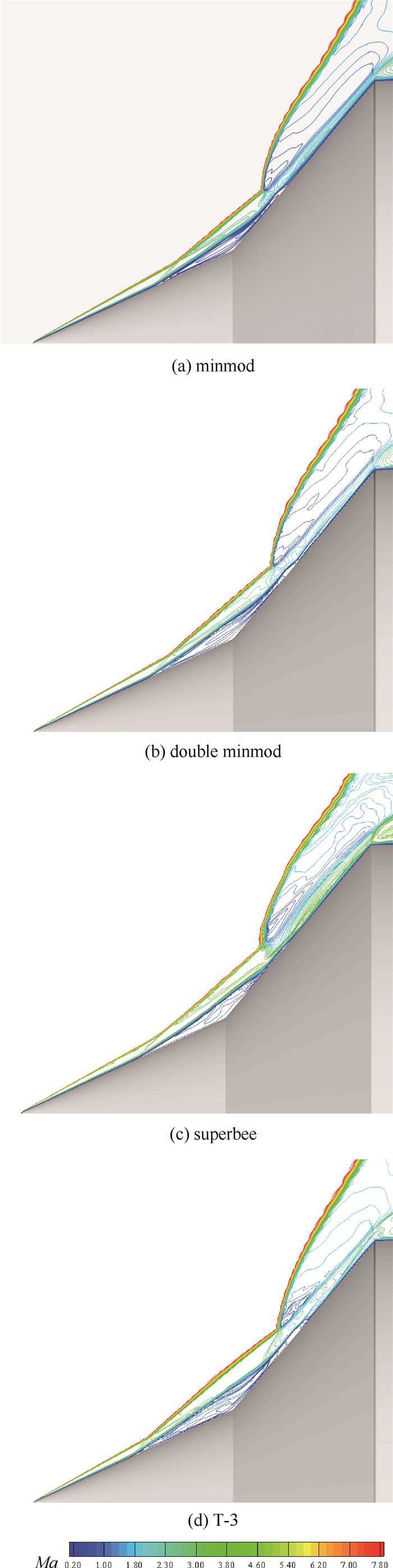
高超声速双锥绕流具有许多复杂的流动现象,流场结构如图 2所示[14]。选取25°/50°双锥,计算条件为:来流马赫数Ma=8,来流压强p∞=3.51 MPa,来流温度T∞=788 K,来流雷诺数Re∞=2.7×105,壁温Tw=590 K。时间格式采用无条件稳定的LUSGS。1/4双锥网格总量为2 850 000,法向第一层网格的高度为0.0005 m。图 3给出了不同限制器计算得到的对称面马赫数等值线图。
|
| 图 3 对称面等马赫线分布 Fig. 3 Mach contours in symmetry plane |
由图 3可知,4种限制器都较好地分辨出了流场结构并且superbee和T-3能刻画出滑移线由于剪切失稳拖起的涡,但在细节流动结构的刻画上存在明显差异。分离区的大小对于该流场流动结构的形成及分布产生了重要影响,由于分离起始位置不同所导致的分离激波差别明显,进而影响到二次三波点 (流动至第二锥处,弓形激波、斜激波与λ激波的交点) 及再附点位置。
图 4给出了不同限制器壁面压强沿母线的分布与实验结果的对比曲线。其中,横坐标代表沿锥面母线与顶点之间的距离,并且采用第一锥面的长度L作归一化,纵坐标压强系数表示为当地压强与远方来流压强的比值,即p/p∞。从图 3和图 4可以看出,不同限制器计算结果差异主要集中在3个方面,即分离点起始位置、分离区大小以及再附点后压强峰值强度。为了便于定量比较,表 1给出了分离点、再附点的具体位置以及分离区的长度,表 2则给出了各限制器计算得到的再附点后壁面压强峰值及所在位置,并与实验结果进行对比,给出其误差范围。

|
| 图 4 壁面压强沿母线分布曲线 Fig. 4 Distribution curves of wall surface pressure along generating line |
| 限制器 | x/L | ||
| 分离点 | 再附点 | 分离区长度 | |
| minmod | 0.597 5 | 1.103 5 | 0.506 |
| double minmod | 0.565 8 | 1.164 1 | 0.598 |
| superbee | 0.505 0 | 1.151 1 | 0.646 |
| T-3 | 0.449 1 | 1.095 0 | 0.646 |
| 限制器 | 峰值位置 (x/L) | 位置误差/% | 压强峰值 (p/p∞) | 峰值误差/% |
| 实验 | 1.424 5 | 104.698 | ||
| minmod | 1.358 5 | 4.633 0 | 94.307 | 9.925 |
| double minmod | 1.429 6 | 0.358 0 | 94.689 | 9.560 |
| superbee | 1.437 5 | 0.913 0 | 107.886 | 3.045 |
| T-3 | 1.498 5 | 1.825 0 | 102.831 | 1.783 |
T-3与superbee限制器对双锥绕流流场结构计算最为准确。但superbee由于耗散小,导致振荡大,流场结构不够清晰。T-3不仅得到的对称面等马赫线流场结构清晰,而且子午线的压强分布与实验值误差最小。
2.3 X-33外形飞行器
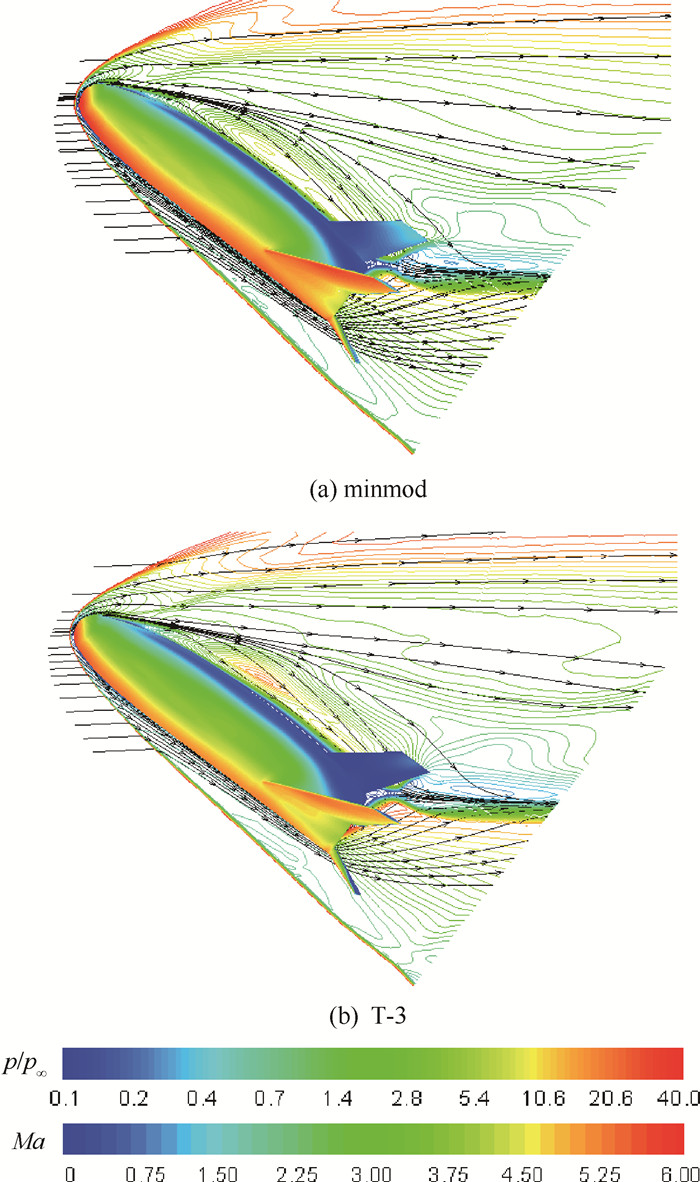
根据文献中的风洞试验状态[15-16],计算条件取:Ma=5.99,ρ∞=0.062 8 kg/m3,T∞=62.1 K,Tw=300 K,边界条件为无滑移固壁,计算迎角α=40°。湍流模型为SST两方程湍流模型。半模网格总量3 500 000。选取minmod与T-3进行对比分析。图 5给出该模型40°迎角时对称面等马赫线图和壁面压强云图。
|
| 图 5 40°迎角下对称面等马赫线图和壁面压强云图 Fig. 5 Mach contours in symmetry plane and wall surface pressure contours at α=40° |
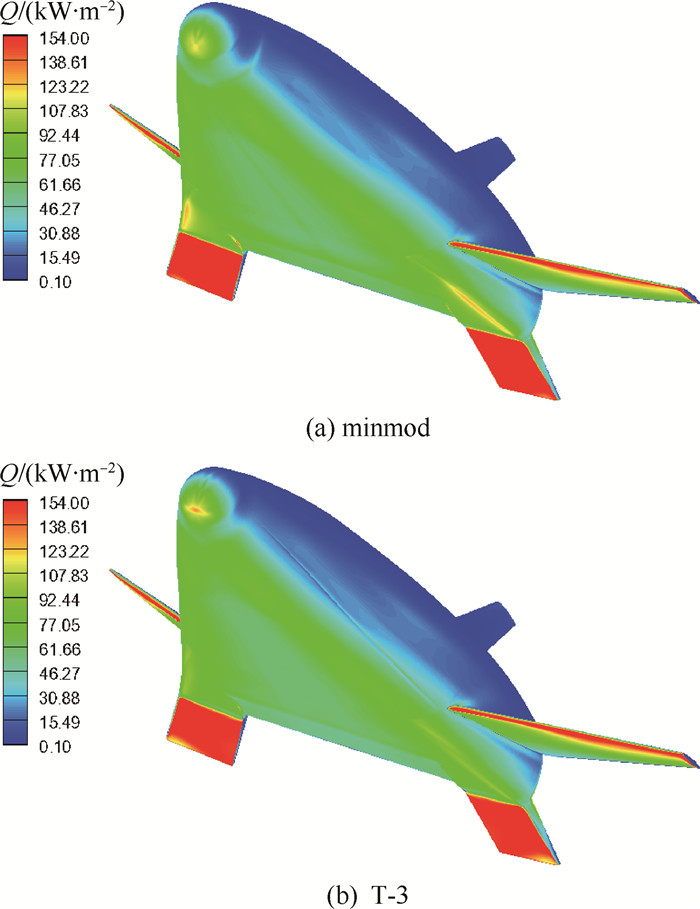
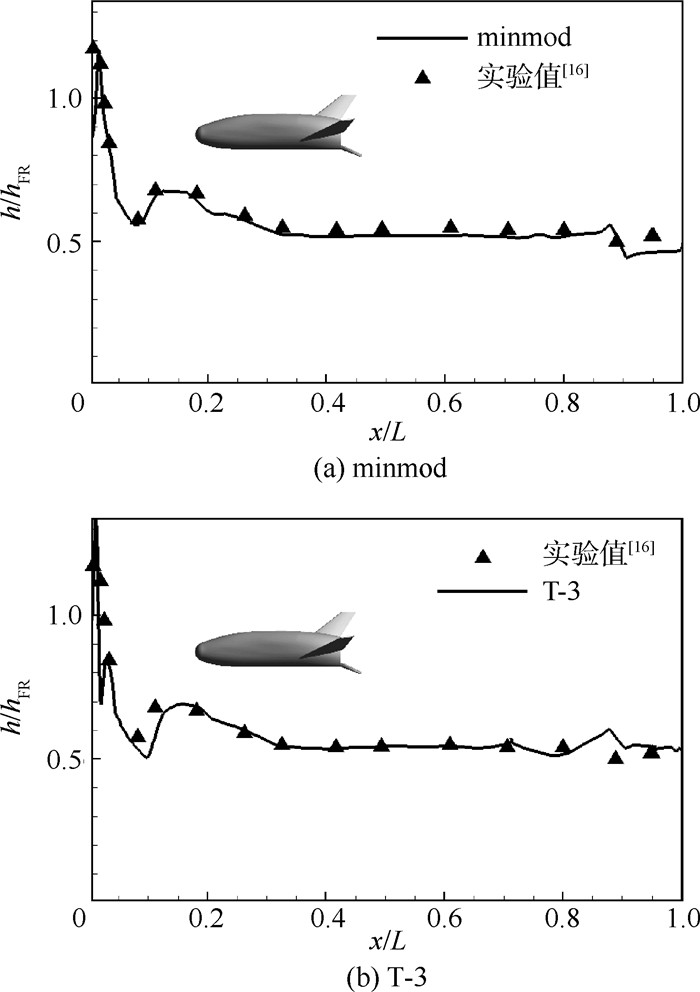
由图 5可知,2种限制器刻画的流场流动结构与壁面压强分布基本一致,显示出了一致的性能。在同等网格条件下,minmod限制器捕捉的头部脱体弓形激波相对较弱,说明其在此复杂流动中对激波的分辨率低于T-3。接下来重点对比气动热的刻画能力,图 6给出计算的热流 (Q) 分布云图。图 7为迎风区子午线上的热流分布与实验对比结果图。图中:h=q/(Haw-Hw),h为热传导系数,q为热流,Hw为壁面焓,Haw为自由来流总焓。焓的计算公式为H=cpT,cp为定压比热比,T为温度。图中的hFR为相同尺度的球形利用Fay-Riddell算法预估的驻点参考热流结果:hFR=0.539 (kg/m2)/s。
|
| 图 6 40°迎角下热流云图 Fig. 6 Contours of heat transfer at α=40° |
|
| 图 7 迎风区子午线热流分布与实验值的对比 Fig. 7 Comparison between windward centerline heat flow distribution and experimental data |
由图 7可知,热流在头部驻点处到达峰值,在过膨胀区有明显的下降现象。T-3与minmod限制器计算结果均与实验值[16]较为匹配,能较为准确刻画出驻点位置,并且T-3在x/L>0.2区域的热流值更接近实验数据。由此可见,T-3限制器表现出了较好的高超声速流动适用性及气动热预测能力,能较为准确刻画壁面的热流分布。
3 结论本文主要研究了一种新型三阶TVD限制器的性能并将其与传统限制器进行对比分析,经数值实验表明:
1) 限制器的选取需要兼顾分辨率和计算稳定性2个方面,T-3限制器与superbee相比,数值色散小,具有良好的稳定性和收敛性以避免非物理解的产生。与double minmod相比,构造原理相同,但计算精度更高。与minmod相比,具有好的间断分辨率且通过限制函数避免了过多的数值耗散。
2) 一维Sod激波管算例表明,T-3、minmod、superbee和double minmod均能较为准确捕捉激波、接触间断和膨胀波等结构。
3) 双锥绕流算例表明,对于复杂流动,T-3限制器性能较为优越。T-3分辨率与superbee相当,且由于耗散比superbee大,得到的流场结构更加稳定清晰。
4) 对X-33外形的热流计算表明,T-3限制器能合理预测驻点位置,较为准确地刻画热流分布的规律,表现出了较好的高超声速流动适用性及气动热预测能力。
| [1] | HARTEN A. High resolution schemes for hyperbolic conservation laws[J]. Journal of Computational Physics, 1983, 49 (3): 357–393. DOI:10.1016/0021-9991(83)90136-5 |
| [2] | LEER B V. Towards the ultimate conservative difference scheme V:A second-order sequal to Godunov's method[J]. Journal of Computational Physics, 1979, 32 (1): 101–136. DOI:10.1016/0021-9991(79)90145-1 |
| [3] | HARTEN A, ENGQUIST B, OSHER S, et al. Unifomrly high-order accurate essentially non-oscillatory schemes[J]. Journal of Computational Physics, 1987, 71 (2): 231–303. DOI:10.1016/0021-9991(87)90031-3 |
| [4] | LIU X D, OSHER S, TONY C. Weighted essentially non-oscillatory schemes[J]. Journal of Computational Physics, 1994, 115 (1): 200–212. DOI:10.1006/jcph.1994.1187 |
| [5] | SWEBY P K. High resolution schemes using flux limiters for hyperbolic conservational laws[J]. SIAM Journal of Numerical Analysis, 1984, 21 (5): 995–1011. DOI:10.1137/0721062 |
| [6] | VENKATAKRISHMAN V. Convergence to steady state solutions of the Euler equations on unstructured grids with limiters[J]. Journal of Computational Physics, 1995, 118 (1): 120–130. DOI:10.1006/jcph.1995.1084 |
| [7] |
屈峰, 阎超, 于剑, 等. 高精度激波捕捉格式的性能分析[J].
北京航空航天大学学报, 2014, 40 (8): 1085–1089.
QU F, YAN C, YU J, et al. Assessment of shock capturing methods for numerical simulations of compressible turbulence with shock waves[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40 (8): 1085–1089. (in Chinese) |
| [8] | YEE H C, KLOPFER G H, MINTAGNE J L. High resolution shock capturing schemes for inviscid and viscous hypersonic flows[J]. Journal Computational Physics, 1990, 83 (1): 31–61. |
| [9] | SPEKREIJSE S. Multigrid solution of monotone second order discretization of hypersonic conservation laws[J]. Mathematics of Computational, 1987, 49 (179): 135–155. DOI:10.1090/S0025-5718-1987-0890258-9 |
| [10] | YOON S H, KIM K H, KIM C. Multi-dimensional limiting process for the three-dimensional flow physics analyses[J]. Journal of Computational Physics, 2008, 227 (12): 6001–6043. DOI:10.1016/j.jcp.2008.02.012 |
| [11] | KIM K H, KIM C. Accurate, efficient and monotonic numetical methods for multi-dimensional compressible flows, Part Ⅱ:Multi-dimensional limiting process[J]. Journal of Computational Physics, 2005, 208 (2): 570–615. DOI:10.1016/j.jcp.2005.02.022 |
| [12] |
阎超.
计算流体力学方法及应用[M]. 北京: 北京航空航天大学出版社, 2006: 123-127.
YAN C. Computational fluid dynamic's methods and applications[M]. Beijing: Beihang University Press, 2006: 123-127. (in Chinese) |
| [13] |
孙迪, 阎超, 于剑, 等. 高精度多维限制器的性能分析[J].
北京航空航天大学学报, 2015, 41 (3): 437–442.
SUN D, YAN C, YU J, et al. Performance analysis of high accurate multi-dimensional limiting process[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41 (3): 437–442. (in Chinese) |
| [14] | WRIGHT M J, SINHA K, OLEJNICZAK J, et al. Numerical and experimental investigation of double-cone shock interactions[J]. AIAA Journal, 2000, 38 (12): 2268–2276. DOI:10.2514/2.918 |
| [15] | BRIAN R H, THOMAS J H, SCOTT A B, et al. X-33 computational aeroheating predictions and comparisons with experimental data[J]. Journal of Spacecraft and Rockets, 1999, 38 (5): 658–669. |
| [16] | BERRY S A, HORVATH T J, HOLLIS B R, et al. X-33 hypersonic boundary-layer transition[J]. Journal of Spacecraft and Rockets, 2001, 38 (5): 646–657. DOI:10.2514/2.3750 |