2. 上海航天控制技术研究所, 上海 20023;
3. 上海市空间智能控制技术重点实验室, 上海 200233
2. Shanghai Aerospace Control Technology Institute, Shanghai 20023;
3. Shanghai Key Laboratory of Aerospace Intelligent Control Technology, Shanghai 200233, China
随着人类航天活动的发展,空间机械臂在航天器在轨维护、空间站在轨装配和空间目标捕获等复杂任务中发挥着越来越重要的作用[1-3]。为节约燃料消耗并提高任务可靠性,空间机械臂的最佳工作模式是基座的位置和姿态均不受控的自由漂浮空间机器人 (Free-Floating Space Robot, FFSR) 模式[4]。但是,FFSR基座的不受控将导致基座和机械臂的运动之间存在复杂的耦合关系:当机械臂运动时,基座的位置和姿态均会产生相应的反向运动。与FFSR的运行轨道半径相比,位置耦合运动幅度很小,且通常对任务不产生本质影响,是可以忽略不计的;相比之下,姿态耦合运动则不能忽略,为了保证基座上通信天线、太阳能帆板等有指向要求部件的正常工作,要求基座始终维持比较稳定的姿态。因此,鉴于机械臂操作过程中基座恒定姿态的重要性,本文将对全程恒定基座姿态零扰动的FFSR末端位姿轨迹规划问题展开研究。
为了解决FFSR轨迹规划中的基座姿态扰动问题,Vafa[5]和Zappa[6]等提出了扰动图方法和增强扰动图方法,该类方法是第1类方法,其针对较少自由度的机械臂,在关节空间有限个离散点上计算出使基座姿态扰动最大和最小的关节运动方向和幅值,进而构成扰动图。扰动图可以定性地辅助基座姿态小扰动的路径设计,但并不能精确地给出全过程最优的小扰动或无扰动路径。第2类基座姿态小扰动设计方法针对具有运动学冗余的机械臂系统,该类方法利用运动学冗余自由度可以设计出全程恒定基座姿态零扰动的关节角轨迹。例如,Yoshida等[7]和Nenchev[8]指出当机械臂存在3个以上冗余自由度时,可实现三维空间中基座姿态恒定零扰动的轨迹规划;黄攀峰[9]和Patolia[10]等则针对2副机械臂的情况,提出利用其中1个机械臂的运动来补偿另1个臂对基座的扰动,从而实现基座全程零扰动。但从工程实践的角度来看,冗余自由度增加了FFSR系统的硬件成本以及发射和运营维护成本。当FFSR系统没有运动学冗余自由度时,同时考虑基座姿态和机械臂末端位姿的协同轨迹规划问题本质上是一个欠驱动的非完整运动规划问题,这正是FFSR轨迹规划问题的难点所在。
尽管如此,目前针对该非完整运动规划问题也已经有了一系列经典的解决方法,这类方法可视为考虑基座姿态扰动的FFSR轨迹规划的第3类方法,主要有Vafa和Dubowsky[5]提出的闭环自校正法、Nakamura和Mukherjee[11]提出的双向搜索法、Fernandes等[12]提出的基于控制函数参数化的最优控制方法、徐文福等[13]提出的基于关节函数参数化的最优化方法等。然而,这些方法只是保证基座姿态在运动的终点返回到期望的初始状态,即与初始状态相比不出现扰动,但在运动的中间过程中,由于对基座姿态没有做特别的约束,它会偏离期望的恒定指向,甚至出现偏离过大的情况,如偏差最大达到约10°[11]或25°[13]。
鉴于上述原因,第4类方法[14-15]在以终点基座姿态作为边界约束的前提下,同时以全过程中基座姿态所受的总扰动作为待优化性能指标,利用最优控制或最优化方法进行求解。如此,不但保证了第3类方法所能达到的非完整运动规划的基本结果,而且较好地约束了基座姿态在运动过程中与期望稳定指向的偏离程度。然而,由于此类方法是通过对关节角或控制函数作有限维参数化实现的,导致设计变量并非在原始的完整Hilbert函数空间内进行逼近,因此,其结果只能是次优而非全局最优。从仿真结果可以发现,采用该类次优方法,基座姿态在中间过程中的扰动虽然与第3类方法相比显著减小,但仍存在非零扰动,因此,该类方法无法解决完整Hilbert空间中的全局优化问题,即无法使无冗余自由度的FFSR如第2类方法中的冗余自由度机器人那样得到全过程彻底零扰动的轨迹规划。
第5类方法对于无运动学冗余自由度FFSR则通过减少被控量维数得到全程恒定基座姿态零扰动的轨迹规划结果。付宜利等[16-17]对无运动学冗余自由度的FFSR首次提出了确保末端位姿轨迹规划,同时全程恒定基座姿态零扰动的工作模式,并推导了该模式下新的广义雅可比矩阵。但文献[16]只是在形式上通过雅可比矩阵给出了系统方程,并没有证明该系统是否可控,即没有证明该工作模式是否可行。而其在文献[17]中给出的一种具体的基座姿态恒定零扰动轨迹规划方法,不仅设计方法复杂,规划任务能否实现不可预测,且最关键的是其全程恒定基座姿态零扰动是以忽略末端姿态轨迹,而仅规划末端位置轨迹为代价的。忽略末端姿态轨迹的降维规划不但不能实现末端位姿同时抓捕的任务要求,而且其本质上已被简化为普通的全驱动问题而非原始的欠驱动问题,全驱动系统的轨迹规划问题通过驱动变换等一般方法即可解决。徐文福等[18]也根据这一降维思路规划了全程恒定基座姿态零扰动的末端位置轨迹,或末端姿态轨迹,但同样不能在基座姿态恒定零扰动时实现末端位置和姿态的同时规划。廖一寰等[19]以基座姿态零扰动的系统平移运动为基础提出了另一种轨迹规划方法,但也只规划了末端位置轨迹而没有考虑末端姿态轨迹。
此外,第6类方法是Carpenter[20]、贾英宏[21]等提出的以角动量交换装置代替关节电机驱动机械臂关节的新型空间机器人,并指出这种新型空间机器人一般不能完全消除全过程中的基座姿态扰动,但是对于相同的机械臂运动,其基座姿态扰动将小于以电机作关节驱动的情况。
综上可知,对于空间机器人基座姿态扰动问题的研究,不能实现全程恒定的零扰动,如第1类、第3类、第4类和第6类方法;或需要借助冗余关节来解决,如第2类方法;或不能规划全部的末端位置和姿态轨迹,从而不能实现完整位姿抓捕的典型任务要求,如第5类方法。因此,当FFSR没有运动学冗余自由度时,其全程恒定基座姿态零扰动的末端“位置+姿态”的轨迹规划仍然是一个尚未解决的问题。另一方面,当空间机器人处在机械臂作在轨装配、目标抓捕等轨迹规划任务的关键飞行模式时,基座航天器的持续稳定指向要求使该工作模式对于工程实践又有着明显的实际意义。因此,本文将对这一轨迹规划问题进行研究,给出此种规划问题可行性的基本结论,并提出一种实现全程恒定基座姿态零扰动的末端位置和姿态同时作轨迹规划的新方法。
本文以平面三自由度FFSR为例,首先,推导末端位姿和关节角之间的状态变换关系。然后,引出以基座姿态和关节角为状态量的系统方程;根据该系统方程,给出全程恒定基座姿态零扰动的末端位姿全状态轨迹规划问题的可行性结论及其证明,并设计一种具体的全程恒定基座姿态零扰动的全状态轨迹规划方法。最后,通过数值仿真,验证了结论的正确性和设计方法的有效性。
1 运动学模型本文研究对象为无运动学冗余的单臂FFSR,其典型模型是三维空间中的六自由度机械臂系统,是三维空间中的全自由度系统。但本文为了尽量简化计算而突出方法本身,选取无运动学冗余的平面全自由度系统进行设计。无运动学冗余的平面全自由度系统和三维空间全自由度系统在轨迹规划方法设计上具有很好的可类比性,区别主要是后者的计算和推导更为复杂。
无冗余平面全自由度FFSR模型为如图 1所示的三自由度平面机器人。设其平面运动自由度为沿惯性坐标系∑I的XI-YI平面上的平动和XI-YI平面内的转动,即绕ZI轴方向的转动。记FFSR基座为B0,质心为C0,C0处固连有基座本体系∑0,其z轴方向z0与ZI方向一致,基座质量和绕z0轴的转动惯量分别为m0和I0;机械臂各杆件为Bj (j=1, 2, 3),质心为Cj,各Cj处固连有杆件本体系∑j,其z轴方向zj与ZI方向一致,各杆件质量和绕自身本体系zj轴转动惯量分别为mj和Ij,杆长为lj,内侧关节为Jj;系统总质量为M,系统质心为CM。假设各杆件质心均位于其两侧关节的连线上,cj1和cj2分别为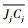
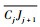
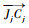
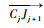

|
| 图 1 三自由度平面FFSR一般模型 Fig. 1 Three-degree-of-freedom planar FFSR general model |
1) 在此FFSR系统中,基座和所有杆件均为刚体,相邻杆件间具有一个可控的旋转自由度,由一个力矩控制器控制,但是载体的位姿不受控。
2) 没有任何外力和外力矩作用在系统上, 因此在运动过程中, 系统满足动量守恒和角动量守恒定律。
3) 系统的初始状态是已知的。
基座姿态零扰动轨迹规划的原始待规划量为基座姿态角φ0及末端位置re=(xe ye)T 和姿态φe,即Z=(φ0 xe ye φe)T,同时记末端位姿为q=(xe ye φe)T。当作如下状态变换后,设计过程将更加简明:

|
(1) |
式中:θ=(θ1 θ2 θ3)T 为各关节角。两组状态变量之间的不同分量有3个,为了实现该变换需要有3个几何约束关系,下面对其进行推导。
对于末端姿态,容易得到
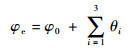
|
(2) |
各刚体质心Cj (j=0, 1, 2, 3) 及末端作用器E在惯性坐标系∑I中的位置矢量分别为
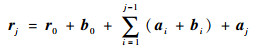
|
(3) |
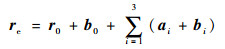
|
(4) |
由于系统动量守恒,因此系统质心位置不变,于是有
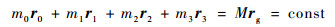
|
(5) |
式中:rg为系统质心CM在惯性坐标系∑I中的位置矢量。
从式 (5) 中解出r0,代入式 (4),可得

|
(6) |
综合式 (2)、式 (6),即为实现状态变换式 (1) 的约束关系:

|
(7) |
需要指出的是,根据机器人逆运动学可知,当给定的末端位姿 (xe ye φe)T 位于基座姿态固定为φ0的固定基座机器人的位姿工作空间内时,该状态转换的解总是存在的,但是三角函数的多值性和逆运动解的固有多值性导致由式 (7) 得到的解不是唯一的[22]。仅从数学角度上看,其任意一组解都是可行的,但是从实际角度出发,应该根据各关节位移的容许范围进行检查,去掉超出关节运动范围的解,再在剩下的有效解中根据其他可能的工程约束选取一组优化解。
以X=(φ0 θ1 θ2 θ3)T 为状态量及各关节角速度为控制量进行轨迹规划的系统模型为[23]
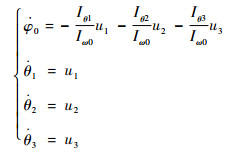
|
(8) |
式中:Iω0、Iθ1、Iθ2和Iθ3分别为Bj (j=0, 1, 2, 3) 的等效转动惯量,它们是关于状态量X的时变函数;同时选定了以各关节角速度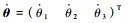
从形式上看,系统式 (8) 是以三维控制量控制四维状态量的欠驱动控制系统,且其中的基座姿态分量要求实现全过程的稳定控制,而各关节角分量则仅要求实现起点到终点的点到点规划。该问题是否有解并不是直观的,因此下面给出其结论及相应证明。
命题1 对于FFSR系统式 (7)、式 (8),其全程恒定基座姿态零扰动的末端“位置+姿态”的全规划问题是可行的,即对于末端位姿工作空间中的任意点q0=(xe0 ye0 φe0)T 和qf=(xef yef φef)T,存在时间T > 0和[0, T]上的控制u=(u1 u2 u3)T,使得系统式 (7)、式 (8) 满足:
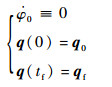
|
(9) |
证明 首先证明全程恒定基座姿态零扰动的关节角轨迹规划是可行的,即对于关节角空间中的任意点θ0=(θ10 θ20 θ30)T 和θf=(θ1f θ2f θ3f)T,存在时间T > 0和[0, T]上的控制u=(u1 u2 u3)T,使得系统式 (8) 满足:
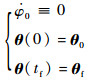
|
(10) |
基座姿态恒定零扰动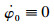

|
(11) |
取与零扰动基座姿态维数γ相等的部分控制分量作为被动控制量,用该部分控制量保证全程恒定基座姿态零扰动关系的成立。在平面FFSR模型式 (8) 中,γ=1,取u=(u1 u2 u3)T 的任何一维分量作被动控制量均可,此处选取u1为被动控制量,其保证基座姿态恒定零扰动的控制为
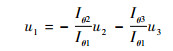
|
(12) |
剩下部分的控制量作为主动控制量,用于实现所有关节角从初始状态到终端状态的点到点规划,相应的降维子系统为
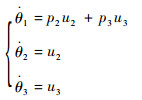
|
(13) |
式中:p2=-Iθ2/Iθ1;p3=-Iθ3/Iθ1。所有表示其基本可行运动方向的向量场为
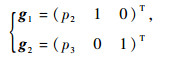
|
(14) |
根据Chow的非线性系统可控性判定定理[24],检验由{g1, g2}在李括号作用下所生成分布

|
(15) |
的秩rank (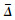
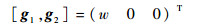
|
(16) |
式中: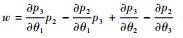

|
(17) |
于是

|
(18) |
因此
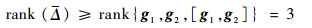
|
(19) |
另一方面,该子系统状态的维数为n1=3,而rank (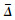
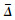

|
(20) |
综合式 (19)、式 (20) 可知
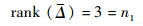
|
(21) |
即分布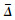
最后,由全程恒定基座姿态零扰动的关节角轨迹规划的可行性,结合Z=(φ0 xe ye φe)T 与X=(φ0 θ1 θ2 θ3)T 之间的状态变换关系式 (7) 可知,全程恒定基座姿态零扰动的末端“位置+姿态”的全规划问题是可行的。 证毕
3 全程恒定基座姿态零扰动轨迹规划方法设计 3.1 设计过程全程恒定基座姿态零扰动的末端位姿轨迹规划问题描述如下:
1) 系统在初始时刻t0的基座姿态为φ00,关节角为θ0=(θ10 θ20 θ30)T,末端位姿为 (xe0 ye0 φe0)T。
2) 系统的终点时刻为tf,在保持全程基座姿态恒定零扰动,即φ0 (t)≡φ00的前提下,期望的终点时刻末端位姿为 (xed yed φed)T。
本文给出一种基于最优控制的全程恒定基座姿态零扰动轨迹规划方法。将路径规划问题转换为最优控制问题,人为地强化了其内部约束,即在系统动力学模型和已有基本约束条件的基础上再引入一个性能指标,要求可行解使该指标最优。强化后的最优控制问题初看起来应该比原问题更加难于求解,但实际上,各种强大的最优控制方法和工具的出现,却使其成为更易求解的方式。
详细规划方法按照如下步骤依次进行:
1) 状态转换
规划的第1步是状态转换。对于期望的以末端位姿表示的终点状态 (φ00 xed yed φed)T,通过求解非线性方程组可得到其对应的以关节角表示的终点状态 (φ00 θ1d θ2d θ3d)T。
2) 被动控制量设计
与可控性证明中所述相同,选取u1为被动控制量,并使其取如下控制律以保证恒定零扰动的基座姿态: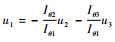
3) 主动控制量设计
设计ua=(u2 u3)T 使子系统式 (13) 的关节角状态由初态θ0=(θ10 θ20 θ30)T 运动至终态θd=(θ1d θ2d θ3d)T。这是一个欠驱动的点到点规划问题,且已有若干较通用的设计方法,参数化方法即为其中应用最广泛的一种。下面用基于控制函数参数化和改进牛顿迭代法的“基算法”[12]进行设计。
对于子系统式 (13),取主动控制关节的耗散能为性能指标函数,即
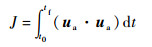
|
(22) |
由于各控制量均为Hilbert空间中的可测函数,因此可以用其任一组正交基进行逼近,或称为函数参数化。此处取傅里叶基{ei}作参数化:

|
(23) |
式中:αj=(αj1 αj2 … αj∞)T 为uj在基{ei}上的投影,并记

|
(24) |
实际计算时,考虑有限维情况,取
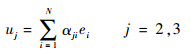
|
(25) |
此时有
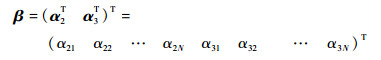
|
(26) |
注意到傅里叶基向量的正交性,并以罚函数方法引入罚因子λ处理关节角终端约束,于是目标函数式 (22) 成为

|
(27) |
式中:θ (tf) 为子系统式 (13) 在给定控制输入ua=(u2 u3)T 时在t=tf时的状态。显然,θ (tf) 是β的函数,设θ (tf)=f (β),当N和λ给定时,式 (27) 可写为
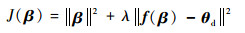
|
(28) |
因此,原最优控制问题转换为寻找参数向量β使目标函数式 (28) 为最小值的最优化问题。根据文献[12],该最优化问题可通过改进的牛顿迭代法予以求解,得到的迭代公式为
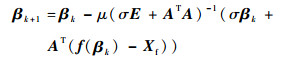
|
(29) |
式中:A=∂f/∂β可通过数值求导计算得到;E为2N×2N维单位阵;σ=1/λ;μ∈(0, 1) 为迭代系数。当β离最优值较远,即迭代收敛速度较快时,μ可取较小值; 而当β逐渐接近于收敛值时,μ应取较大值。
4) 设计结果综合
最终,综合上述过程,可得全部控制量为
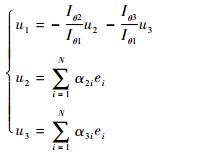
|
(30) |
特别值得指出的是,任何机械臂系统都具有由其机构几何参数所决定的运动学奇异特性,而FFSR更是具有不但与机构几何参数有关,同时还与系统的质量和惯量等动力学参数有关的复杂动力学奇异特性[25]。在FFSR的笛卡儿空间轨迹规划方法中,由于需要使用从笛卡儿空间的末端位姿到关节空间的关节角之间的逆运动学转换,即需要对雅可比矩阵进行求逆,因此必须专门对系统的运动学奇异和动力学奇异问题进行避奇异处理[25-26]。但在本文设计方法中,可以看出除了第1步需要对初始状态和末端状态作逆运动学状态转换外,中间规划过程完全在关节空间中进行,不需要进行逆运动学计算,从而避免了奇异问题的出现;而初始状态和末端状态是否奇异则是由初始任务设定而决定的,不是轨迹规划所能解决也不是其所需要面对的问题。因此,本文的轨迹规划方法是没有奇异性的。
4 数值仿真本节对本文提出的全程恒定基座姿态零扰动的末端位姿全状态轨迹规划方法进行仿真验证。
三自由度FFSR的质量惯量及各结构参数如表 1所示。
| 部件 | mj/kg | Ij/(kg·m2) | lj/m |
| B0 | 500.0 | 62.5 | 0.5 |
| B1 | 100.0 | 33.3 | 2.0 |
| B2 | 100.0 | 75.0 | 3.0 |
| B3 | 100.0 | 200.0 | 4.0 |
质心位置参数为cji=0.5 (j=1, 2, 3; i=1, 2)。
轨迹规划任务如表 2所示。根据表 2中的期望终端基座姿态和末端位姿,利用状态变换关系式 (7),可得到相应的期望关节角为θd=(15.0°-35.0° -45.0°)T。
| 状态 | 时刻/s | 基座姿态/(°) | 末端位置/m | 末端姿态/(°) | 关节角/(°) |
| 初始状态 | 0 | 5.0 | (4.0066; -5.0158) | 76.5 | (2.5;-54.0; -30.0) |
| 终端状态 | 16.0 | 5.0 | (5.5877; -3.2883) | -60.0 |
设计过程中的控制参数为迭代更新公式 (27) 中的迭代系数σ和μ。σ取为0.05。μ则根据收敛速度分段取值,当收敛较快,在本仿真中设为相邻两步的性能指标之差大于1.0时,μ取较小值0.1;否则取较大值0.5。仿真中,对于u2和u3分别选取如下7个傅里叶正交基向量:
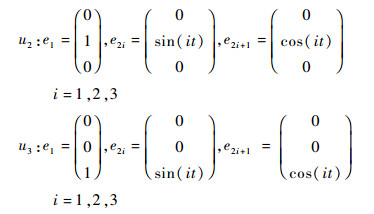
|
通过改进的牛顿迭代法迭代求解基向量对应的系数参数β=(α2T α3T)T,其设置的迭代初值和迭代计算得到的终值如表 3所示。
| 变量 | 取值 |
| α2迭代初值 | (0.05, -0.05, 0.05, -0.05, 0.05, -0.05, 0.05) |
| α3迭代初值 | (0.05, -0.05, 0.05, -0.05, 0.05, -0.05, 0.05) |
| α2迭代终值 | (-0.0505, -0.2734, 0.3977, -0.3145, 0.0181, -0.0292, -0.0859) |
| α3迭代终值 | (0.1600, -0.4040, -0.1294, -0.0958, -0.0993, 0.0242, -0.0011) |
迭代收敛过程如图 2 (a) 所示。在第19次迭代时性能指标发生了一个跳变,这是由于从此时开始相邻两步的性能指标之差开始小于设定的阈值1.0,μ取值由0.1变为0.5,从而使前后两部分的性能指标计算表达式不一致,等效为μ取恒定值0.1的迭代收敛过程如图 2 (b) 所示。

|
| 图 2 迭代收敛过程 Fig. 2 Iterative convergence process |
|
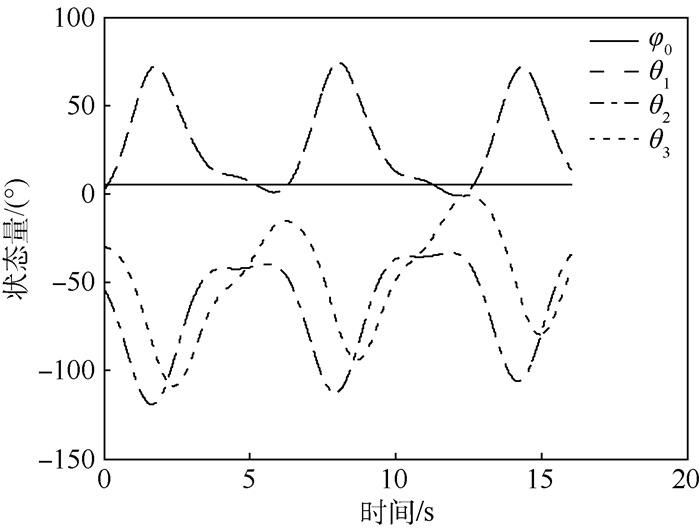
| 图 3 系统状态量 Fig. 3 State variables of system |
|
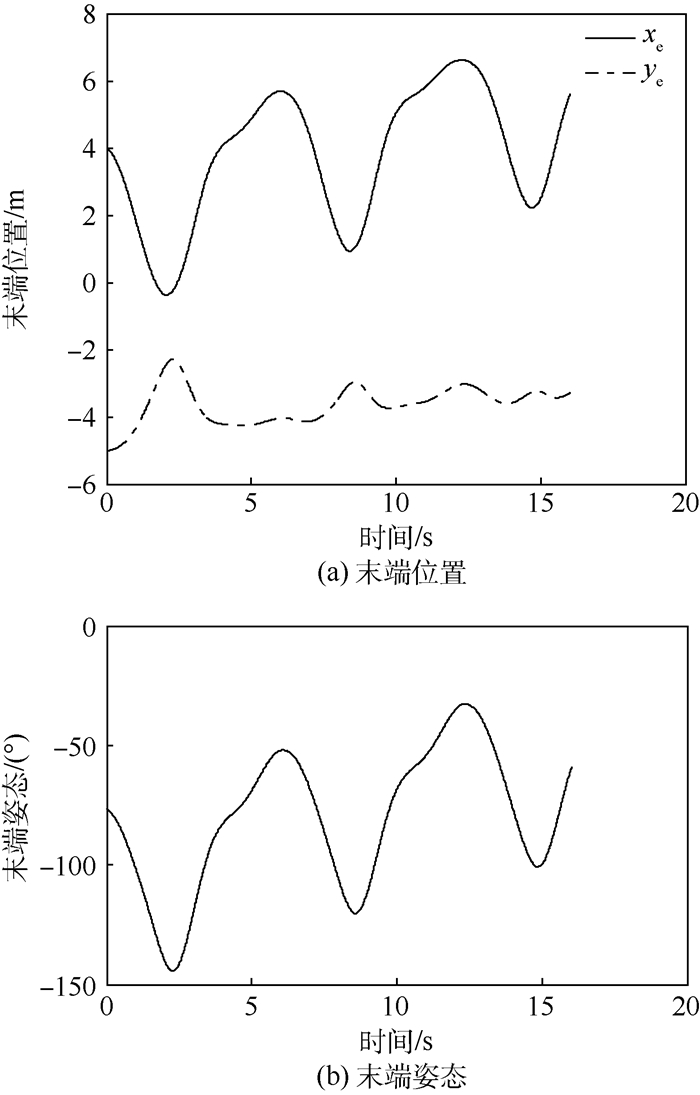
| 图 4 机械臂末端位姿 Fig. 4 Position and attitude of end effector of manipulator |
|
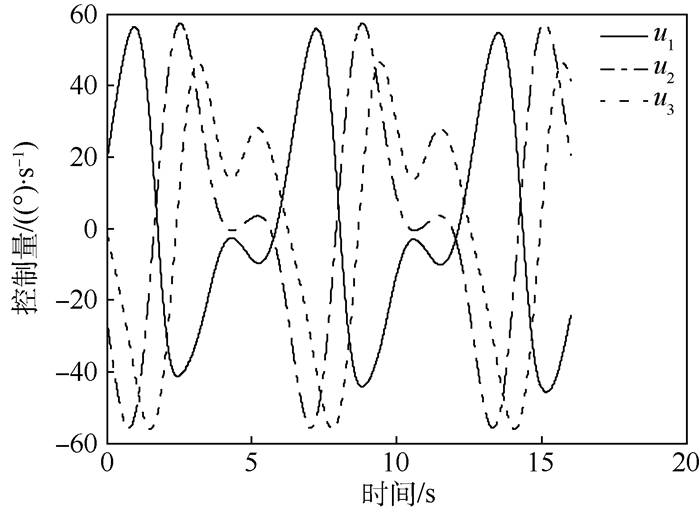
| 图 5 系统控制量 Fig. 5 Control variables of system |
图 3显示了整个轨迹规划过程中的状态量曲线,包括基座姿态角和关节角。可以看出,基座姿态角在整个过程中始终保持为恒定的5.0°。与基于系统动力学的控制器设计不同,在基于运动学的轨迹规划过程中,由于并不考虑除机械臂对基座姿态作用之外的任何其他扰动或误差因素,如空间环境力矩的扰动作用和状态测量误差等,所以在本文的全程恒定基座姿态零扰动的设计方法下,基座姿态在整个规划过程中与期望的恒定指向姿态是精确吻合而没有任何偏离的,这也是本文所设计方法与已有各种基座小扰动研究或仅终端零扰动研究相比的最大创新点。此外还可看到,图 3中所示各关节角从初始状态运动到期望末端状态,整个过程平滑而不超过基本合理的关节角运动范围。
图 4显示了末端位姿从指定的初始状态 (xe0 ye0 φe0)T=(4.0066 m -5.0158 m 76.5°) 在tf=16 s时成功地运动到末端状态 (xed yed φed)T=(5.5877 m -3.2883 m -60°),且整个运动过程平滑。
图 5显示了整个过程的控制量作用,3个关节的控制量,即各关节角速度均平滑有界,符合工程实际的一般要求。
类似的,进行多组其他指定基座姿态和灵巧工作空间内的末端目标位姿的仿真,结果显示出同样能实现全程恒定基座姿态不动、而末端位姿在终点时刻到达指定状态的预期结果。由于篇幅所限,不再作过多分析。
总的来看,本仿真中全程恒定基座姿态零扰动轨迹规划任务的实现也以实例的方式验证了第3节中给出的该轨迹规划可行性结论的正确性。
5 结论1) 证明了无运动学冗余的三自由度平面FFSR在实现全程恒定基座姿态零扰动的前提下,其末端位置和姿态同时作轨迹规划是可行的。
2) 为无运动学冗余的三自由度平面FFSR设计了一种全程恒定基座姿态零扰动的末端位姿轨迹规划方法,数值仿真验证了其有效性。
3) 所设计轨迹规划方法在关节空间中进行,不存在奇异问题。
4) 为了计算的简易性,选取平面三自由度机械臂进行研究,工程实践中的更一般系统是三维空间中的六自由度机械臂,后者除了计算复杂度更大外,在本文所研究的问题上,两者是可完全类推的,本文所提出的全程恒定基座姿态零扰动可行性结论和轨迹规划设计方法对于六自由度机械臂仍然是适用的。
| [1] | FRIEND R B.Orbital express program summary and mission overview[C]//Proceeding of SPIE 6958, Sensors and Systems for Space Applications Ⅱ.Orlando:SPIE, 2008, 4:695803.1-695803.11. |
| [2] | DEBUS T J, DOUGHERTY S P.Overview and performance of the front-end robotics enabling near-term demonstration (FREND) robotic arm:AIAA-2009-1870[R].Reston:AIAA, 2009. |
| [3] | FLORES-ABAD A, MA O, PHAM K, et al. A review of space robotics technologies for on-orbit servicing[J]. Progress in Aerospace Sciences, 2014, 68 (1): 1–26. |
| [4] | MOOSAVIAN S A A, PAPADOPOULOS E. Free-flying robots in space:An overview of dynamics modeling, planning and control[J]. Robotica, 2007, 25 (5): 537–547. |
| [5] | VAFA Z, DUBOWSKY S. On the dynamics of space manipulator using the virtual manipulator with application to path planning[J]. The Journal of the Astronautical Sciences, 1990, 38 (4): 441–472. |
| [6] | ZAPPA B, LEGNANI G, ADAMINI R. Path planning of free-flying space manipulators:An exact solution for polar robots[J]. Mechanism and Machine Theory, 2005, 40 (7): 806–820. DOI:10.1016/j.mechmachtheory.2004.12.009 |
| [7] | YOSHIDA K, HASHIZUME K, ABIKO S.Zero reaction maneuver:Flight validation with ETS-Ⅶ space robot and extension to kinematically redundant arm[C]//Proceeding of the IEEE International Conference on Robotics and Automation.Piscataway, NJ:IEEE Press, 2001:441-446. |
| [8] | NENCHEV D N. Reaction null space of a multibody system with applications in robotics[J]. Mechanical Sciences, 2013, 4 (1): 97–112. DOI:10.5194/ms-4-97-2013 |
| [9] | HUANG P F, XU Y S, LIANG B.Balance control of multi-arm free-floating space robots during capture operation[C]//Proceeding of the IEEE International Conference on Robotics and Biomimetics.Piscataway, NJ:IEEE Press, 2005:398-403. |
| [10] | PATOLIA H, PATHAK P M, JAIN S C. Trajectory control of a dual-arm planar space robot with little attitude disturbance[J]. Simulation, 2011, 87 (3): 188–204. DOI:10.1177/0037549710381654 |
| [11] | NAKAMURA Y, MUKHERJEE R.Nonholonomic motion planning of free-flying space robots via a bi-directional approach[M]//XU Y S, KANADE T.Space robotics:Dynamics and control.New York:Springer, 1993:101-130. |
| [12] | FERNANDES C, GURVITS L, LI Z X.Attitude control of space platform/manipulator system using internal motion[M]//XU Y S, KANADE T.Space robotics:Dynamics and control.New York:Springer, 1993:131-163. |
| [13] | XU W F, LI C, WANG X, et al. Study on non-holonomic cartesian path planning of free-floating space robotic system[J]. Advanced Robotics, 2009, 23 (1-2): 113–143. DOI:10.1163/156855308X392708 |
| [14] | KAIGOM E G, JUNG T J, ROSSMANN J.Optimal motion planning of a space robot with base disturbance minimization[C]//11th Symposium on Advanced Space Technologies in Robotics and Automation.Noordwijk:ESA/ESTEC, 2011, 4:1-6. |
| [15] | WU J, SHI S, WANG B, et al.Path planning for minimizing base reaction of space robot and its ground experimental study[C]//Proceeding of the IEEE International Conference on Mechatronics and Automation.Piscataway, NJ:IEEE Press, 2009:4627-4632. |
| [16] | 付宜利, 张福海, 王树国, 等. 载体姿态无扰的自由漂浮空间机器人运动学特性研究[J]. 宇航学报, 2008, 29 (6): 1858–1864. FU Y L, ZHANG F H, WANG S G, et al. Research on kinematic characteristic of free floating space robot with zero-disturbance spacecraft attitude[J]. Journal of Astronautics, 2008, 29 (6): 1858–1864. (in Chinese) |
| [17] | ZHANG F H, FU Y L, HUA L, et al.Point-to-point planning for free-floating space manipulator with zero-disturbance spacecraft attitude[C]//Proceeding of the IEEE International Conference on Information and Automation.Piscataway, NJ:IEEE Press, 2012:142-147. |
| [18] | 徐文福, 刘宇, 强文义, 等. 自由漂浮空间机器人的笛卡尔空间连续路径规划[J]. 控制与决策, 2008, 23 (3): 278–282. XU W F, LIU Y, QIANG W Y, et al. Cartesian continuous-path planning for free-floating space robot[J]. Control and Decision, 2008, 23 (3): 278–282. (in Chinese) |
| [19] | LIAO Y H, LI D K, TANG G J. Translational zero-disturbance curve and its application to zero-disturbance motion planning of space manipulator system[J]. Science China-Technological Sciences, 2011, 54 (5): 1234–1239. DOI:10.1007/s11431-010-4248-1 |
| [20] | CARPENTER M D, PECK M. Reducing base reactions with gyroscopic actuation of space-robotic systems[J]. IEEE Transactions on Robotics, 2009, 25 (6): 1262–1270. DOI:10.1109/TRO.2009.2032953 |
| [21] | 贾英宏, 赵楠, 徐世杰. 控制力矩陀螺驱动的空间机器人轨迹跟踪控制[J]. 北京航空航天大学学报, 2014, 40 (3): 285–291. JIA Y H, ZHAO N, XU S J. Trajectory tracking control of space robot actuated by control moment gyroscopes[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40 (3): 285–291. (in Chinese) |
| [22] | 孙增圻, 严隽薇, 钱宗华. 机器人智能控制[M]. 太原: 山西教育出版社, 1995: 58-73. SUN Z Q, YAN J W, QIAN Z H. Robot intelligent control[M]. Taiyuan: Shanxi Educational Press, 1995: 58-73. (in Chinese) |
| [23] | HUANG X H, XU S J. Free floating space robot kinematic modeling and analysis[J]. Advances in the Astronautical Sciences, 2014, 150 (1): 2067–2077. |
| [24] | CHENG D Z, HU X M, SHEN T L. Analysis and design of nonlinear control systems[M]. New York: Springer, 2010: 121-146. |
| [25] | PAPADOPOULOS E, DUBOWSKY S. Dynamic singularities in free-floating space manipulators[J]. Journal of Dynamic Systems, Measurement, and Control, 1993, 115 (1): 44–52. DOI:10.1115/1.2897406 |
| [26] | 徐文福. 空间机器人目标捕获的路径规划与实验研究[D]. 哈尔滨: 哈尔滨工业大学, 2007: 68-104. XU W F.Path planning and experiment study of space robot for target capturing[D].Harbin:Harbin Institute of Technology, 2007:68-104(in Chinese). |



