2. 北京航空航天大学 机械工程及自动化学院, 北京 10008;
3. 北京航空航天大学 先进航空发动机协同创新中心, 北京 100083
2. School of Mechanical Engineering and Automation, Beijing University of Aeronautics and Astronautics, Beijing 10008;
3. The Collaborative Innovation Center for Advanced Aero-Engine (CICAAE), Beijing University of Aeronautics and Astronautics, Beijing 100083, China
近年来,SiCp/Al复合材料以其优异的物理性能和机械性能,如:低密度、高比强度、高比刚度、低热膨胀系数和高导热系数等[1-2],在航空航天领域逐渐得到广泛应用,已作为结构材料应用于航空航天结构件、直升机旋翼连接件、飞机腹鳍、导流叶片和支撑结构件等[3-4]。因其物理、机械性能与飞行器性能和安全可靠性紧密相关,因此必须严格控制此类材料和构件的制造质量[1-2, 4]。
最新研究表明[1-3],SiCp颗粒分布是影响SiCp/Al复合材料机械性能的一个关键因素。但是,SiCp/Al材料在制备过程中,受粉末冶金或铸锭冶金工艺影响,会导致SiCp颗粒分布不均匀,使材料性能显著下降、构件机械性能降低,严重影响飞行器性能和安全可靠性。针对这一问题,目前虽然已严格控制生产工艺,但仍无法保证SiCp颗粒完全均匀分布,必须采用有效、可靠的无损检测方法准确检测材料均匀性[2, 5-7],以保证构件的机械性能满足应用要求。
在各种无损检测方法中,超声检测是SiCp/Al复合材料检测采用的主要方法[5, 7-9]。高翌飞等[5]、魏勤和尤建飞[9]采用超声C扫描方法对SiCp/Al复合材料进行成像检测,观测到毫米级的SiCp颗粒团聚。为更准确地检测SiCp/Al材料均匀性,魏勤和张迎元[7]采用实验方法分析了超声衰减与SiCp体积分数间的关系,表明可通过超声衰减成像分析SiCp颗粒分布均匀性;周正干等[6]通过实验研究了超声波的声速与SiCp体积分数和SiCp/Al材料弹性模量间的关系;高翌飞等[5]采用厚度无关声反射板法对SiCp/Al材料进行声速成像检测,表明可根据声速变化反映材料中SiCp颗粒分布均匀性。但是,目前在SiCp颗粒分布均匀性超声衰减及声速成像方法的准确度和适用范围等方面缺少必要的分析与验证。
因此,本文研究SiCp/Al复合材料SiCp增强颗粒分布均匀性的超声成像方法,分析、验证其准确度和适用范围,为提高SiCp/Al复合材料均匀性的超声评价准确度提供方法。
1 试样制备及实验装置 1.1 试样制备采用粉末冶金工艺和标准的SiCp含量控制方法[3, 5-7],制备5件SiCp增强颗粒含量不同的SiCp/Al复合材料试样,其中SiCp增强颗粒尺寸约在3~20 μm范围,Al基体颗粒尺寸约在20~40 μm范围。制备的5件试样的SiCp体积分数分别为10%、15%、20%、25%和30%,表面光洁度一致,试样实物如图 1所示。

|
| 图 1 不同SiCp增强颗粒含量的SiCp/Al复合材料试样 Fig. 1 SiCp/Al composite specimens with different contents of SiCp reinforced particle |
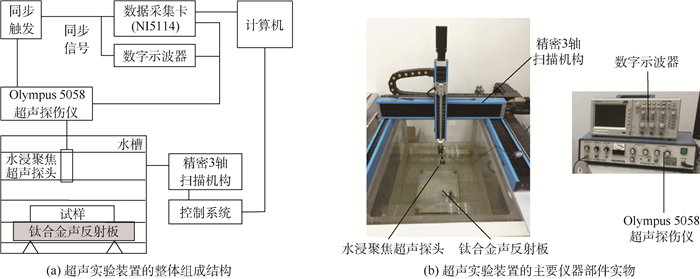
采用的超声实验装置主要包括:泛美V309-SU水浸聚焦超声探头 (中心频率5 MHz、焦距101.6 mm)、Olympus 5058超声探伤仪、NI5114数据采集卡、Olympus信号线及电磁屏蔽环、精密3轴扫描机构及控制系统、声反射板、水槽、超声测量和扫描成像程序。超声实验装置的整体组成结构和主要仪器部件实物如图 2所示。
|
| 图 2 超声实验装置整体组成结构及主要仪器部件 Fig. 2 Overall structure and main equipment parts of ultrasonic experimental facility |
根据超声传播理论,超声波在材料中传播时导致衰减的因素包括吸收衰减、散射衰减和扩散衰减[10-11],其中吸收衰减和散射衰减与材料特性紧密相关,而扩散衰减取决于声源产生的波型和声束性质,与材料性质无关[11]。因此,在选定超声探头的条件下,利用超声衰减原理成像时,主要通过分析材料对声波的吸收衰减和散射衰减变化进而表征材料性质变化[12-13]。
对于SiCp/Al材料中声波的吸收衰减,由于材料对声波的吸收机制涉及材料黏滞性、热传导和各种弛豫过程,具有较高复杂度,通常将材料对声波的吸收衰减简化表示为[7, 11]
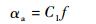
|
(1) |
式中:αa为吸收衰减系数;C1为与材料晶粒大小和各向异性无关的常数;f为声波频率。
对于SiCp/Al材料中声波的散射衰减,由于实验装置中超声探头的中心频率为5 MHz,材料中SiCp颗粒尺寸远小于声波波长,根据超声散射理论,SiCp颗粒作为散射体可近似为半径为a的小球,对声波的散射衰减可表示为[11]

|
(2) |
式中:αs为散射衰减系数;C2为常数;k为波数;n0为单位体积介质中散射体小球的个数。
分析式 (1) 和式 (2) 得出,材料对声波的吸收衰减主要与声波频率相关;在选定超声探头频率的条件下,声波的散射衰减与材料中SiCp颗粒尺寸和分布均匀性紧密相关,通过测量由散射衰减变化导致的声波衰减系数的相对变化可以表征材料中SiCp颗粒的分布特征。
通过上述分析,采用相对测量方法定义声波的相对衰减系数为
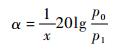
|
(3) |
式中:α为声波的相对衰减系数,dB/mm;x为声波传播距离;p0和p1分别为第1次和第2次材料底面回波幅度。
采用式 (3) 定义的声波相对衰减系数,利用超声实验装置对5件不同SiCp体积分数的SiCp/Al试样进行基于声波相对衰减系数的超声C扫描成像,主要实验参数为超声探头中心频率5 MHz、探头焦距101.6 mm、采样频率250 MHz、扫描分辨率100 μm,得到5件SiCp/Al试样的声波相对衰减系数图像如图 3所示。

|
| 图 3 不同SiCp体积分数的SiCp/Al试样的超声衰减成像 Fig. 3 Ultrasonic attenuation image of SiCp/Al specimens with different volumn fractions of SiCp |
分析图 3得出,SiCp/Al复合材料中SiCp体积分数由10%增加至30%过程中,声波相对衰减系数随SiCp体积分数增加而增大,主要原因是SiCp体积分数增加后声波散射衰减增强,使得声波相对衰减系数增大;不同SiCp体积分数下声波相对衰减系数变化范围为0.25~0.40 dB/mm;SiCp体积分数达到25%和30%时,从图像中观测到试样局部区域明显存在声波相对衰减系数变化,表征SiCp颗粒的突变式非均匀分布特征。
定义声波相对衰减系数的变化率为
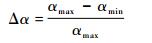
|
(4) |
式中:αmax和αmin分别为衰减系数最大值和最小值。
根据SiCp/Al试样的声波相对衰减系数的变化范围得出,不同SiCp体积分数下声波相对衰减系数的变化率为37.5%,这使得试样的相对衰减系数图像颜色变化显著,局部颜色呈突变特征。但是,声波相对衰减系数变化幅度与SiCp颗粒分布非均匀程度的关联性和一致性需要与声速成像方法和金相法作对比分析和验证。
3 声速成像SiCp/Al复合材料中SiCp体积分数会影响材料硬度和弹性模量等力学性能参量,进而导致材料声速产生变化[14-15],可以通过测量材料声速变化反映材料中SiCp颗粒分布特征。
对于声速测量,从微观层面分析,SiCp/Al材料声速与SiCp颗粒体积分数、脱黏率和基体孔隙率等参量紧密相关[7, 16],理论计算得到声速的误差较大。因此,采用实验方法测量SiCp/Al材料中超声纵波声速与SiCp体积分数关系,为SiCp颗粒分布特征的声速成像建立映射关系。
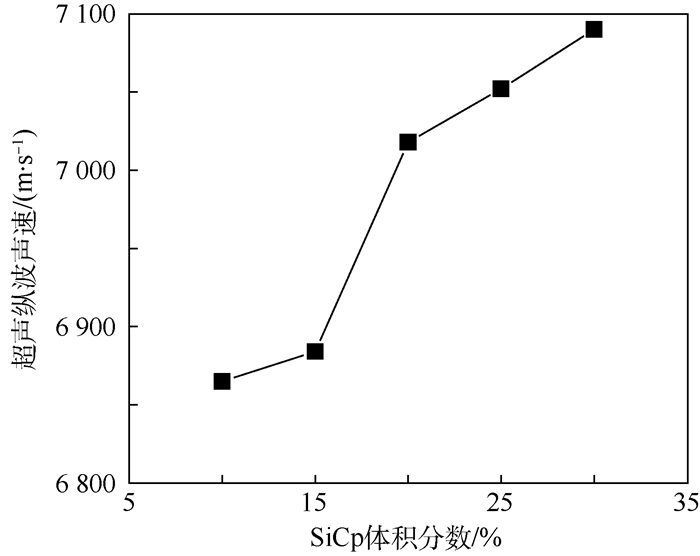
采用制备的5件SiCp/Al复合材料试样和超声实验装置,根据材料声速测量方法[5-6],测得不同SiCp含量下的超声纵波声速如表 1所示,超声纵波声速随SiCp体积分数增加的变化关系如图 4所示,其中每一个声速值均为在试样中取10处测量点测得的声速均值,以减小实验方法和材料非均匀性导致的声速测量误差。
| 试样编号 | Z-55 | Z-51 | Z-53 | Z-52 | Z-54 |
| SiCp体积分数/% | 10 | 15 | 20 | 25 | 30 |
| 超声纵波声速/(m·s-1) | 6 865 | 6 884 | 7 018 | 7 052 | 7 090 |
|
| 图 4 超声纵波声速随SiC体积分数增加的变化关系 Fig. 4 Relationship of ultrasonic velocity of longitudinal wave with increase of volumn fractions of SiCp |
分析图 4得出,SiCp/Al复合材料中超声纵波声速随SiCp体积分数增加而增大,通过测量材料不同位置的超声纵波声速可以反映材料局部SiCp含量,进而表征SiCp颗粒分布特征。
采用基于纵波声速的双次扫描TIRP法[5]对制备的5件不同SiCp体积分数的SiCp/Al试样进行声速成像,主要实验参数为超声探头中心频率5 MHz、探头焦距101.6 mm、采样频率250 MHz、扫描分辨率100 μm,得到5件SiCp/Al试样的声速图像如图 5所示。

|
| 图 5 不同SiCp体积分数的SiCp/Al试样的声速成像 Fig. 5 Velocity image of SiCp/Al specimens with different volumn frations of SiCp |
分析图 5得出,不同SiCp体积分数下SiCp/Al试样的声速图像整体颜色值随SiCp体积分数增加而逐渐增大,即超声纵波声速增大;不同SiCp体积分数下超声纵波声速变化范围约为6 800~7 100;单一SiCp体积分数试样 (如为25%的SiCp试样) 的声速图像存在局部颜色渐变现象,即局部声速变化,表征材料局部SiCp颗粒的渐变式非均匀分布特征。
定义材料声速的变化率为
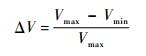
|
(5) |
式中:Vmax和Vmin分别为声速最大值和最小值。
根据SiCp/Al试样的超声纵波声速变化范围得出,不同SiCp体积分数下超声纵波声速的变化率约为4.2%;与超声衰减分析结果对比得出,不同SiCp体积分数下超声纵波声速变化率仅约为声波相对衰减系数变化率的1/9,这使得试样的声速图像具有颜色渐变、平滑过渡的特征,与超声衰减成像结果差异显著。因此,需要采用金相法作对比分析,验证2种成像方法的准确度,分析其适用范围。
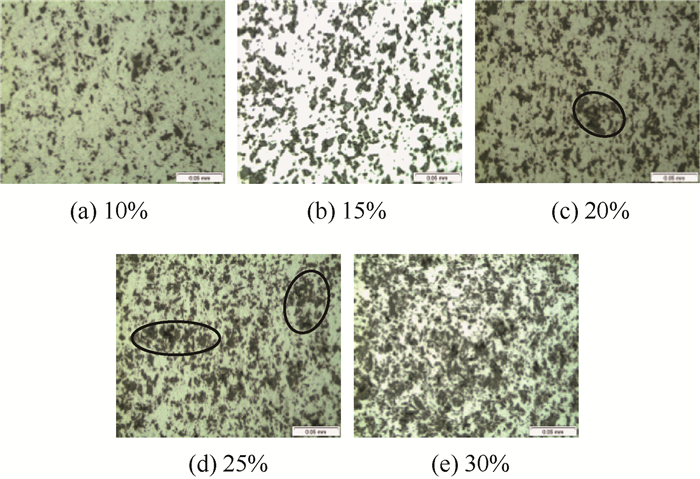
4 金相分析与验证根据超声衰减和声速成像 (见图 3和图 5) 反映的SiCp/Al试样中SiCp颗粒非均匀分布特征,选取试样不同部位横向解剖、提取部分材料制作显微分析试样,采用卡尔·蔡司Axio Lab.A1 MAT型金相显微镜对不同SiCp体积分数的SiCp/Al显微分析试样进行金相实验,得到5种SiCp体积分数下典型的细观SiCp颗粒分布特征如图 6所示。
|
| 图 6 不同SiCp体积分数下SiCp/Al试样的金相图 Fig. 6 Metallographic image of SiCp/Al specimens with different volumn frations of SiCp |
分析图 6得出,SiCp/Al试样中SiCp颗粒 (呈深颜色) 分布密集度随SiCp体积分数增加而增大,表现为金相图深颜色区域增加;SiCp体积分数为10%和15%时SiCp颗粒分布相对均匀;SiCp体积分数为20%和25%时局部SiCp颗粒分布相对密集,导致试样局部SiCp颗粒呈渐变式非均匀分布特征,而不具有突变特征;SiCp体积分数为30%时SiCp颗粒呈相对均匀的连续聚集型分布特征。
受金相法限制,虽然金相图仅表征出材料局部细观SiCp颗粒分布特征,而无法表征材料整体特征,但是通过高密度采样、显微分析不同位置得出,在材料内部不含宏观缺陷条件下,图 6所示不同SiCp体积分数下SiCp颗粒分布特征对材料整体具有一般性。
对比图 6和图 3、图 5分析结果得出,采用声速成像方法得到的SiCp颗粒的渐变式非均匀分布特征与金相分析结果具有更高一致性,表明声速成像方法具有更高准确度,适用于SiCp颗粒分布均匀性的定量表征;采用超声衰减成像方法得到的SiCp颗粒的突变式非均匀分布特征误差较大,适用于SiCp颗粒分布均匀性的定性表征;当SiCp体积分数较高 (如为30%) 时,局部连续聚集的SiCp颗粒对声波散射衰减显著增强,超声衰减成像的突变特征加剧、表征误差增大,需要采用声速成像方法更准确地表征SiCp颗粒分布均匀性。
5 误差分析根据超声衰减和声速成像原理[7, 11],导致SiCp/Al复合材料SiCp颗粒分布均匀性超声成像误差的因素包括材料特征、声学原理、成像方法和实验装置4个方面。
1) 从材料特征和声学原理角度分析
在超声衰减成像方面,SiCp/Al材料中的SiCp颗粒会对声波产生散射作用,导致声波衰减。由于声波散射衰减系数与SiCp颗粒近似小球半径的6次方和小球数量正相关 (式 (2)),当SiCp颗粒出现局部密集分布时声波散射衰减显著增强,实测声波衰减系数的变化率达到37.5%(SiCp体积分数为10%~30%),导致超声衰减图像呈突变特征,与实际的SiCp颗粒渐变式非均匀分布特征存在较大误差。
在声速成像方面,SiCp/Al材料中超声纵波声速随SiCp体积分数增加而增大 (SiCp体积分数为10%~30%),但实测声速变化率仅为4.2%,声速图像呈渐变特征,与实际的SiCp颗粒分布特征具有更高一致性,尤其是SiCp体积分数大于25%时声速成像方法的表征误差相对较小。
分析表明,当SiCp/Al材料中SiCp体积分数较高 (如体积分数大于25%) 并且需要定量表征SiCp颗粒分布均匀性时,可采用声速成像方法以减小由材料特征和声学原理导致的表征误差,达到更高准确度;当SiCp体积分数较低 (如体积分数小于20%) 且仅需定性表征SiCp颗粒分布均匀性时,可采用超声衰减成像方法。
2) 从成像方法和实验装置角度分析
在超声衰减成像方面,采用基于声波相对衰减系数的超声C扫描方法时,需要测量第1次和第2次材料底面回波幅度峰值,采用式 (2) 计算得出各测量点的声波相对衰减系数,映射建立声衰减系数图像。这种方法在测量过程中受材料几何特征、表面光洁度、相对位置、耦合介质纯净度和机械扫描装置精度等因素影响会产生测量误差,为减小误差,在材料表面光洁度一致的条件下,可采用高纯净度耦合介质、精密调节机构和机械扫描装置 (重复定位精度 < ±5 μm),精确调节材料表面、底面与超声探头距离及角度使其相对恒定。
在声速成像方面,采用基于纵波声速的双次扫描TIRP法[5]成像时,根据成像方法[5]需要测量3个关键参量:耦合介质声速、一次和二次材料底面回波时间差及放置材料前后声反射板表面反射回波时间差。其中,耦合介质声速的测量主要受耦合介质纯净度和温度影响,可采用高纯净度耦合介质并实测介质温度修正声速值以减小测量误差;材料底面回波时间差的测量主要受材料几何特征、相对位置和实验装置噪声影响,材料几何特征和相对位置的微小变化会使超声回波信号波形和回波峰值时间位置产生变化进而导致测量和计算误差,实验装置的噪声信号会使超声信号波形变化进而导致回波时间测量失准,为减小误差,可根据超声回波信号波形、噪声校正超声系统使信噪比达标且保持相对稳定,精密调节材料表面、底面与超声探头和声反射板间距离、角度使其相对恒定;放置材料前后声反射板表面反射回波时间差的测量主要受2次扫描时各测量点2次采样位置一致性影响,可采用高重复定位精度扫描装置以减小误差。
与超声衰减成像方法相比,由于不同SiCp体积分数下纵波声速变化率远小于声波相对衰减系数变化率,采用声速成像法时,测量误差导致的微小声速变化会显著影响SiCp颗粒分布均匀性的定量表征,实验过程中需要更为精确地控制导致声速测量误差的各项参量,以达到相对较高的定量表征准确度。
6 结论1) 不同SiCp体积分数下声波相对衰减系数变化率达到37.5%,超声衰减图像呈突变特征,与金相分析结果差异较大,超声衰减成像方法适用于SiCp颗粒分布均匀性的定性表征。
2) 不同SiCp体积分数下声速变化率为4.2%,声速图像呈渐变特征,与金相分析结果具有更高一致性,声速成像方法具有更高准确度,适用于SiCp颗粒分布均匀性的定量表征。
3) 当SiCp体积分数较高 (如大于25%) 且需定量表征SiCp颗粒分布均匀性时,采用声速成像方法;当SiCp体积分数较低 (如小于20%) 且仅需定性表征时,采用超声衰减成像方法。
4) 采用声速成像方法时,测量误差导致的微小声速变化会显著影响定量表征准确度,需要更为精确地控制超声系统噪声、机械精度、试件位置和耦合条件等主要误差因素。
| [1] | 凌杰, 辛志杰. SiCp/Al复合材料的高速铣削试验与表面缺陷研究[J]. 科学技术与工程, 2015, 15 (2): 217–221. LING J, XIN Z J. High-speed milling experiment and surface indefects of SiCp/Al composites[J]. Science Technology and Engineering, 2015, 15 (2): 217–221. (in Chinese) |
| [2] | 王唱舟, 周丽, 王洋, 等. 数值模拟SiCp/Al复合材料的微观结构对力学性能的影响[J]. 材料科学与工程学报, 2015, 33 (1): 122–126. WANG C Z, ZHOU L, WANG Y, et al. Simulation of microstructure-based effects on mechanical properties of SiCp/Al composites[J]. Journal of Materials Science & Engineering, 2015, 33 (1): 122–126. (in Chinese) |
| [3] | 蓝永庭, 秦亮, 张克实, 等. SiCp/Al复合材料增强颗粒尺寸效应的细观分析[J]. 应用力学学报, 2014, 31 (1): 20–25. LAN Y T, QIN L, ZHANG K S, et al. Meso analysis on size effect of SiCp/Al MMCs[J]. Chinese Journal of Applied Mechanics, 2014, 31 (1): 20–25. (in Chinese) |
| [4] | 樊建中, 肖伯律, 徐骏, 等. SiCp/Al复合材料在航空航天领域的应用与发展[J]. 材料导报, 2007, 21 (10): 98–101. FAN J Z, XIAO B L, XU J, et al. Development and application of SiCp/Al composites in aerospace field[J]. Materials Review, 2007, 21 (10): 98–101. (in Chinese) |
| [5] | 高翌飞, 周正干, 何方成. 基于TIRP法的铝基复合材料均匀性检测[J]. 北京航空航天大学学报, 2009, 35 (8): 1031–1034. GAO Y F, ZHOU Z G, HE F C. Homogeneity testing of aluminum metal matrix composites by TIRP method[J]. Journal of Beijing University of Aeronautics and Astronautics, 2009, 35 (8): 1031–1034. (in Chinese) |
| [6] | 周正干, 高翌飞, 吕炎, 等. 碳化硅颗粒增强铝基复合材料弹性常数测量[J]. 北京航空航天大学学报, 2009, 35 (2): 162–165. ZHOU Z G, GAO Y F, LV Y, et al. Elastic constant matrix measurement of SiCp reinforced aluminum metal matrix composites[J]. Journal of Beijing University of Aeronautics and Astronautics, 2009, 35 (2): 162–165. (in Chinese) |
| [7] | 魏勤, 张迎元. SiCp/Al复合材料中增强体SiC含量的测定方法研究[J]. 华东船舶工业学院学报 (自然科学版), 2005, 19 (4): 86–89. WEI Q, ZHANG Y Y. Research on volume fraction mensuration of SiC reinforce in SiCp/Al composites[J]. Journal of East China Shipbuilding Institute (Natural Science Edition), 2005, 19 (4): 86–89. (in Chinese) |
| [8] | 刘斯明, 彭地, 赵翰学, 等. SiCp颗粒增强铝基复合材料非共线非线性响应试验观察[J]. 机械工程学报, 2012, 48 (22): 21–26. LIU S M, PENG D, ZHAO H X, et al. Experimental observation of nonlinear response of SiCp aluminum-matrix composites using non-colinear technique[J]. Journal of Mechanical Engineering, 2012, 48 (22): 21–26. DOI:10.3901/JME.2012.22.021 (in Chinese) |
| [9] | 魏勤, 尤建飞. 超声C扫描系统在颗粒增强型金属基复合材料无损检测中的应用[J]. 华东船舶工业学院学报 (自然科学版), 2003, 17 (3): 66–69. WEI Q, YOU J F. Application of ultrasonic C-scanning system in nondestructive testing of particulate reinforced metal matrix composites[J]. Journal of East China Shipbuilding Institute (Natural Science Edition), 2003, 17 (3): 66–69. (in Chinese) |
| [10] | 罗斯J L. 固体中的超声波[M]. 何存富, 吴斌, 王秀彦, 译. 北京: 科学出版社, 2004: 67-71. ROSE J L.Ultrasonic waves in solid media[M]. HE C F, WU B, WANG X Y, translated. Beijing:Science Press, 2004:67-71(in Chinese). |
| [11] | 冯若. 超声手册[M]. 南京: 南京大学出版社, 1999: 26-27. FENG R. Ultrasonic handbook[M]. Nanjing: Nanjing University Press, 1999: 26-27. (in Chinese) |
| [12] | HSU D K. Simultaneous velocity and thickness imaging by ultrasonic scan[J]. Review of Progress in Quantitive Nondestructive Evaluation, 2001, 20B : 695–702. |
| [13] | AARON F, DONAL B D. 3D ultrasound imaging:A review[J]. IEEE Engineering in Medicine and Biology, 1996, 15 (6): 41–51. DOI:10.1109/51.544511 |
| [14] | JEONG H, HSU D K, SHANNON R, et al. Characterization of anisotropic elastic constants of silicon-carbide particulate reinforced aluminum metal matrix composites:Part I. Experiment[J]. Metallurgical and Materials Transactions A, 1994, 25 (4): 799–809. DOI:10.1007/BF02665456 |
| [15] | BURGHOLZER P, HOFER C, REITINGER B, et al. Non-contact determination of elastic moduli of continuous fiber reinforced metals[J]. Composites Science and Technology, 2005, 65 (2): 301–306. DOI:10.1016/j.compscitech.2004.07.011 |
| [16] | BINDUMADHAVAN P N, WAH H K, PRABHAKAR O. Assessment of particle-matrix debonding in particulate metal matrix composites using ultrasonic velocity measurements[J]. Materials Science and Engineering:A, 2002, 323 (1-2): 42–51. DOI:10.1016/S0921-5093(01)01399-5 |



