2. 洛阳电子设备试验中心, 洛阳 471000
2. Luoyang Electronics Equipment Test Center, Luoyang 471000
对于复杂多态系统,为有效的减少维修资源消耗,降低系统故障带来的运行风险,需要对其进行视情维修。视情维修(condition-based maintenance) 是从系统或部件状态性能的角度,发现其具有失效征兆时而进行的有针对性维修[1]。此外对系统内部件进行维修分析时,还需要考虑部件间的经济相关性,经济相关性是指系统内各部件同时维修要比各自单独维修节省费用,即系统每次停机检修都会带来较高的固定维修费用[2-3]。因此,考虑部件间经济相关性的同时,对多部件系统的视情维修更换决策进行研究具有重要意义。
当前,有关系统部件的维修更换决策研究主要分为2个方面。一方面是不考虑部件间的相关性,对部件的维修更换决策进行研究。以色列的Levitin教授和Lisnianski教授[4]首先采用多态系统相关理论对系统的维修决策问题进行研究;文献[5]以系统单位时间内期望报酬最大为决策目标,在完好维修策略下对基于部件状态的多态系统视情更换维修策略进行研究;成国庆等[6]在仅考虑部件间失效独立的情况下,对2个不同部件构成的串联多态系统的最优维修更换策略进行研究;黄傲林等[7]以长期运行费用率为评估指标,研究了劣化系统的周期预防性维修策略;孙志礼等[8]针对复杂可修系统,通过定义系统寿命周期,建立了工作时间和维修时间的联合概率密度函数,并对其预防性维修时间的确定方法进行研究。另一方面是考虑部件间的经济相关性,对部件的维修更换决策进行研究。机会维修(opportunistic maintenance) 策略是考虑部件经济相关性的重要维修策略,机会维修是指当系统内的某个部件发生失效时,通常会利用对失效部件维修的机会,对系统中短期内还需要维修的其他部件,进行提前预防性维修,此做法可以大大减小系统的非计划维修比例,降低停机时间和维修费用[9]。文献[10-11]对多态串并联系统的选择性维修更换策略进行研究;葛小凯等[12]以“部件二态假设为基础”,对考虑依赖性的多部件系统仿真建模和优化方法进行研究;张卓琦等[13]通过更新过程理论建立了期望维修成本率解析模型,并以系统期望成本率最低为优化目标,对考虑故障相关的2部件系统的机会维修策略进行研究;赵洪山等[14]以风电机组系统的维修费用最小为目标,提出了基于关键部件可靠度的机会更换维修决策方法,这一维修策略虽能有效地节约系统的维修资源,但对部件进行可靠性建模时仅考虑了服役时间与可靠度函数间的关系,并没有考虑部件状态性能参数动态变化对维修决策的影响;文献[15]采用比例失效模型来描述风电机组各部件的衰退过程,对典型的串联多部件系统的状态-机会维修策略进行分析,但其仅对较为简单的串联多部件系统的维修决策进行研究,对于结构更为复杂的多部件系统的维修决策并不适用。
对于多态部件构成的复杂多态系统,对系统内部件进行维修时,需要对系统进行停机、拆卸及测试。频繁的停机维修一定程度上增加了系统内部件的维修成本,增加了系统的失效风险。此外,以部件可靠度为基础的维修更换决策,实际上仍是基于部件“二态假设”,部件失效阈值的确定,可能使得部件的可靠性分析结果存在一定偏差。为此根据系统内部件的状态性能变化,如何调整不同部件的维修时机,将尽可能多的部件级维修组合起来,在保证系统可靠度的前提下降低维修费用,成为部件更换维修决策研究的难点。而机会维修策略和多态系统部件的维修更换策略的结合可以有效地解决该问题,基于此,以机会维修策略为基础,从“部件级更换的角度”出发,根据部件的状态性能变化,对多态系统的视情更换维修决策进行研究,并通过实例对所提决策方法进行分析。
1 Markov模型描述假设部件的衰退过程可用Markov模型进行表征,通过Markov模型描述部件的状态变化规律,并求解部件对应状态的状态概率。
假设部件在t时刻的状态为k,则在Δt时刻后其状态为k′的概率表示为[16]
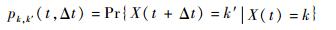
|
(1) |
该概率被称为状态转移概率。
令k=k′, 则有pk, k′(t, Δt)=Pr{X(t+Δt)=k∣X(t)=k′}, 它表示Δt时刻内部件驻留在状态k的概率,且有
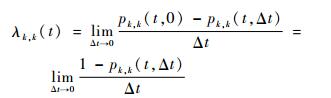
|
(2) |
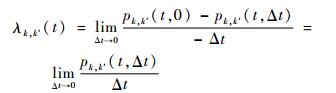
|
(3) |
式中:λk, k(t) 和λk, k'(t) 分别表示部件在t时刻离开状态k的转移概率和从状态k到k′的转移率。
由于环境因素或者其他未知条件的影响,部件通常会遭受各种冲击损伤和性能退化。因此,对于多态部件,其性能往往由性能高的状态向性能低的状态演变或者由性能高的状态直接跳转至性能低的状态,也可能由性能较高状态直接跳转到失效状态。基于此,假设多态部件i具有Mi个可能的状态,采用Markov模型描述过程具体如图 1所示。
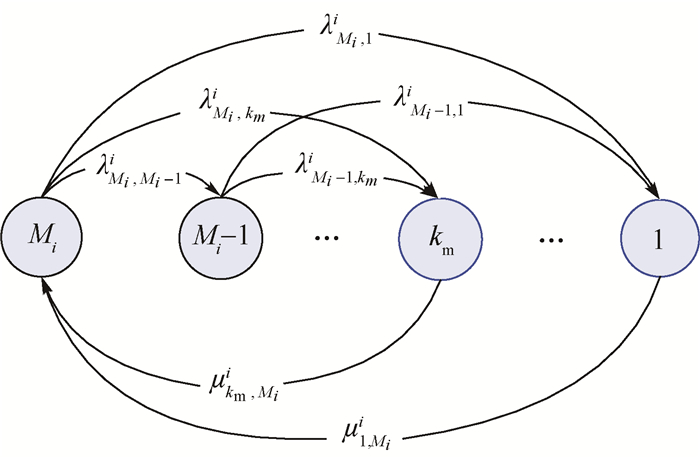
|
| 图 1 部件的Markov模型 Fig. 1 Component Markov model |
图 1中,Mi为部件i的性能最佳状态,1为部件i完全失效状态,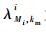

为了直观地对图 1进行描述,假定km=3,Mi=5,部件i的状态转移率矩阵表示为
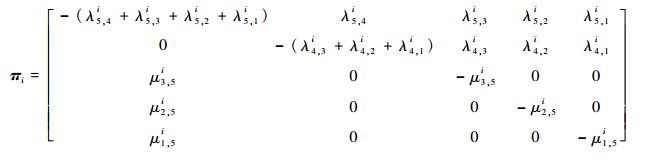
|
式中: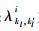
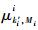
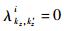
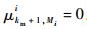
在任意t时刻,部件i在各个状态的概率分布可通过Kolmogorov微分方程组得到[16-17]:
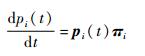
|
(4) |
式中:
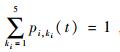
在对部件进行状态划分之前首先对部件的状态进行定义,其次根据系统的最小性能需求对部件的状态进行划分,对于一些功能复杂系统,很难直接通过系统的最小性能需求对部件状态进行划分,可以结合专家知识进行状态划分,此处重点对前者进行分析说明[18]。
首先假定部件i在状态ki时的状态性能为gi, ki,用于表示部件i处于不同性能参数水平时对整个系统正常工作性能的贡献比率,在此本文用百分比表示。通常结合系统结构函数与部件的性能参数进行定义,可分为以下2种情况:
1) 当部件i单独构成分系统l,且分系统l可以与其他分系统近似的认为是串联结构时,则有: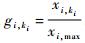
2) 当n′个部件i构成分系统l,且分系统l的性能输出为n′个部件i的性能输出和,同时分系统l可以与其他分系统近似的认为是串联结构时,则有: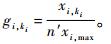
最后根据系统的最小任务性能需求与系统结构函数确定分配给部件的近似最小任务性能为wx,并在该区域附近尽量将其细化,便于系统状态与系统的最小任务性能需求进行区分。
2.2 通用生成函数定义
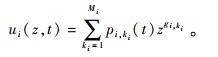
|
(5) |
式中:gi, ki和pi, ki(t) 分别为部件i在任意时刻t的状态性能和状态概率,i=1, 2, …, n,ki=1, 2, …, Mi。
2.3 通用生成函数运算法则系统的通用生成函数可通过如下运算获得:
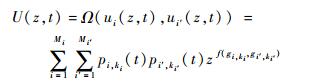
|
(6) |
式中:Ω(·) 为结构函数;ui(z, t) 为部件i的通用生成函数;ui′(z, t) 为部件i′的通用生成函数:
根据系统结构特点定义如下运算符。
1) 当gks为gi, ki与gi′, ki′的和时,定义δ1运算符:

|
2) 当gks为gi, ki与gi′, ki′的乘积时,定义δ2运算符:
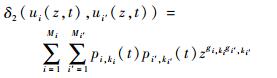
|
3) 当gks为gi, ki与gi′, ki′的最小值时,定义δ3运算符:
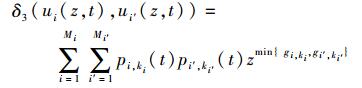
|
采用Markov模型得到部件的状态概率之后,根据系统的结构函数,采用通用生成函数(UGF) 方法对系统的可靠性指标进行分析。
3.1 多态系统可靠性分析根据第2.3节运算法则的分析,可得多态系统的通用生成函数为

|
(7) |
式中:gks为系统在第ks个状态的状态性能;pks(t) 为t时刻系统在第ks个状态的状态概率,ks∈{1, 2, …, Ms},Ms为系统的状态个数。
定义多态系统的最小任务性能需求为w,则系统的可靠度为
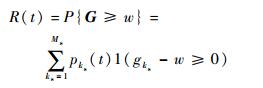
|
(8) |
式中:1(gks-w≥0) 为示性函数,当gks-w≥0时,1(gks-w≥0)=1,当gks-w < 0时,1(gks-w≥0)=0;G={gMs, …, gks, …, g2, g1}。
3.2 多态系统平均瞬态性能分析为了提高雷达功率放大系统的任务保障能力,可通过系统状态性能的高低来反映其满足任务需求能力的大小。因此对系统的平均瞬态性能分析具有重要意义,在此,采用状态性能的期望来描述多态系统的平均瞬态性能,具体如下:
定义多态系统在t时刻的平均瞬态性能大小为
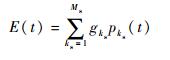
|
(9) |
多态部件的更换维修决策中,主要从2个方面进行考虑:一是构成系统的部件之间的经济相关性,即采用机会维修策略来解决部件之间存在的经济相关性问题;另一个方面是构成系统的部件之间的性能相关性,决策者通过优化决策,确定部件的更换阈值,使得系统在有限的服役期内的净效益最大。即当部件i的状态跳转到更换阈值状态θi及以下时,立即对部件i进行更换。综合上述2个方面,先根据部件之间的性能相关性确定部件的最佳更换阈值,而后,采用机会维修策略确定最佳更换时间阈值ΔT*。为了得到系统在有限服役期内的最大期望效益,则需要确定系统中各部件的最佳更换阈值状态θ*={θ1*, θ2*, …, θn*}和采用机会维修策略更换维修部件时的最佳更换时间阈值ΔT*。
4.1 基于部件状态的更换维修模型 4.1.1 模型假设对基于部件状态的更换维修模型分析之前,先做如下假设:
1) 假定系统可以由n个多态部件以串并联结构方式连接。
2) 假定构成系统的多态部件的状态转移过程可以用Markov模型进行描述。
3) 假定对系统内某一部件进行更换维修时,对其他部件的性能没有影响。
4) 系统在服役期间只有“工作”和“维修”2种状态,且对部件的任意次维修更换均需对系统进行停机。
5) 系统在运行过程中,可通过在线测试手段,实现对部件状态的准确监测。
6) 部件之间的维修费用具有一定经济相关性,即系统每次停机维修都会有较高的固定维修费用(如系统拆装、维修设备调试等)。
4.1.2 更换维修模型1) 若部件i跳转至更换阈值状态θi及以下时,将立即更换,从维修效果角度来讲为“修复如新”。
2) 为了减少系统停机维修更换次数,增强系统的任务执行能力,引入机会维修决策的观念。若部件i跳转至更换阈值状态θi及以下状态时,且在经过ΔT时间后,部件j将跳转至更换阈值状态θj,则在更换部件i的同时,将部件j一并更换,其中j=1, 2, …, n,且j≠i。
3) 对部件进行机会维修更换可节省对其维修时所需的一些固定费用,降低系统的运行风险。
4.2 更换决策目标由于电子装备系统的特殊性,在执行任务能力方面,通常认为系统不间断正常工作的时间越长越好。如若不能满足正常任务需求时,可通过经济补偿的观点,来反映其特殊性。则多态系统在有限服役时间内的净效益为
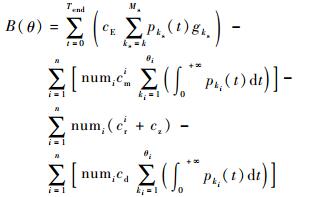
|
(10) |
式中:θ={θ1, θ2, …, θn}为各部件的更换阈值;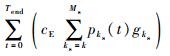
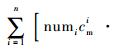
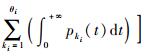
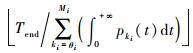
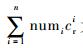
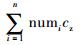
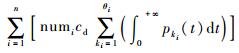
通过优化如下问题得到系统中各部件的最佳更换阈值状态:
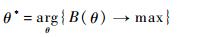
|
(11) |
对于式(11) 的求解问题,目前求解方法比较成熟,可采用传统枚举式方法进行求解,也可采用蚁群算法[5]、粒子群算法[19]和遗传算法[20]等智能算法来求解,此处不再赘述。
通过式(11) 得到系统内各部件的最佳更换阈值后,充分考虑雷达功率放大系统的特殊性,引入机会维修的观念,在式(11) 的基础上,对部件的更换决策模型做进一步改进。
为保证多态系统在有限服役时间内的期望报酬最大,可通过求解如下优化问题得到系统中各部件的最佳更换阈值:
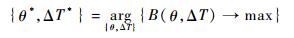
|
(12) |
通过第4.2节更换决策目标的分析可知,通过搜索最佳{θ*, ΔT*}可使系统在有限寿命周期内的净效益最大,即决策变量为系统内各部件的预防性(视情) 更换阈值θ1*, θ2*, …, θn*,和机会更换决策阈值ΔT*。
4.4 基于机会维修策略的部件更换决策分析基于上述分析,给出如下基于机会维修的部件更换维修决策分析步骤:
步骤1 根据第2.1节部件状态划分规则得到部件的状态性能,同时根据式(4) 求解部件的状态概率,并用通用生成函数方法对部件的状态概率分布进行表示。
步骤2 在得到部件的通用生成函数后,根据第2.3节定义的通用生成函数运算法则,求得分系统、系统关于通用生成函数的状态概率分布表示。
步骤3 根据第3.2节多态系统平均瞬态性能分析方法,求得系统平均瞬态性能。
步骤4 采用由部件1的阈值θ1至部件n的阈值θn的顺序,对部件的失效阈值θi逐次搜寻,直至满足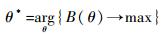
步骤5 在步骤4的基础上,采用机会维修的观点对部件的维修更换决策进行改进。
1) 根据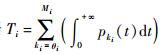
2) 根据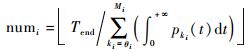
3) 令Ti, zi={Ti, 2Ti, …, numiTi}表示部件i在有限的服役时间内可能出现的更换时刻,其中0≤zi≤numi。
4) 从时间坐标轴上,根据构成系统部件可能出现的更换时刻进行逐次维修,假定在t时刻对部件i进行第一次更换,然而引入机会维修概念后,若在t+ΔT时刻后部件j的状态退化到θj及以下,那么在对部件i更换的同时,对部件j进行第一次机会维修更换,则对部件j第一次维修的时刻变为Tj, 2=Ti, 1+Tj, 1,同时对部件j的更换时刻集合Tj, zj进行更新,变为Tj, zj={Tj, Ti+Tj+Tmj, …, (numi-1)Ti+Tj+Tmj},依次逐渐对各部件的维修时刻进行更新,直至到达系统的最高服役年限,其中j∈{1, 2, …, n}且j≠i,Tmj为对部件j维修更换所需的时间,0≤ΔT≤min{T1, T2, …, Tn}。
步骤6 重复步骤5,对净效益B(θ, ΔT) 进行寻优, 直至将所有ΔT∈[0, min{T1, T2, …, Tn}]可能取值搜索完毕,进而得到最佳更换变量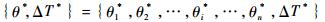
将本文所提的更换决策模型应用到某型雷达功率放大系统的更换维修决策问题中。该系统主要由4个分系统构成,包含5个性能退化部件、2个二态部件,如图 2所示。分系统1为性能退化部件预放大器组件;分系统2为二态部件1:4功率分配器;分系统3为性能退化部件功率放大组件1~4;分系统4为二态部件4:1功率合成器。根据部件处于不同性能水平时对整个雷达放大系统正常工作性能的贡献比率划分部件的状态水平,系统的最小性能需求为w=75%。
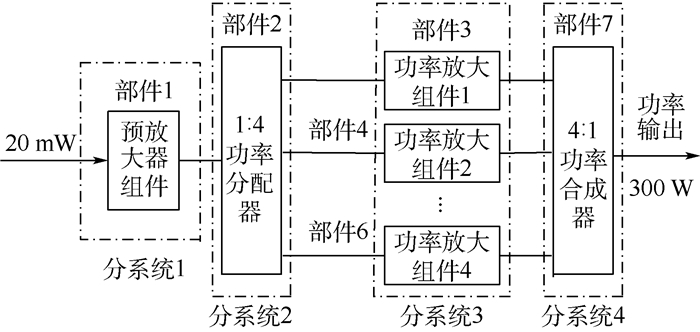
|
| 图 2 某型雷达功率放大系统 Fig. 2 A certain type of radar power amplifying system |
表 1为系统内部件与维修费用相关的参数。假定cE=5,cz=2,由于电子装备系统的特殊性,如若不能满足正常任务需求时,需要进行经济补偿,则cd=10。
| 部件编号 | cr/(万元·a-1) | cm/(万元·a-1) |
| 1 | 5 | 2 |
| 2 | 3 | 1 |
| 3 | 4 | 2 |
| 4 | 4.4 | 2.2 |
| 5 | 4.8 | 2.4 |
| 6 | 5 | 2.6 |
| 7 | 3 | 1.5 |
5.1 部件的状态和概率分析
根据第2.1节部件状态划分规则对系统中多态部件的状态进行划分,由于分系统1与分系统3状态性能之间存在一定的相关性,满足gsub1-3=gsub1gsub3。在二态部件1:4功率分配器和4:1功率合成器正常工作时,分系统1和分系统3构成的分系统1~3的性能满足gsub1-3≥w时整个功率放大系统正常工作。下面对分系统1和分系统3部件的状态进行分析。
1) 当分系统3的状态性能处于完好工作状态gsub3=100%时,分系统1部件此时所需的状态性能最小为gsub1=75%。
2) 当分系统1的状态性能处于完好工作状态gsub1=100%时,分系统3所需的状态性能最小为gsub3=75%。
3) 当分系统1和分系统3均处于不完全工作状态且2个分系统的性能相同时,此时2个分系统所需的最低性能为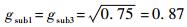
4) 为了增大系统状态与最小性能需求之间的区分度,将系统的状态性能在最小性能需求区域附近尽量将其细化,当部件具有5个状态时,结合本节1)~3) 分析,将分系统1的状态性能分别定义为{0, 81%, 87%, 93.5%, 100%},同理将分系统3的状态定义为{0, 81%, 87%, 100%},因分系统3的性能为各部件性能之和,将其内各部件状态定义为{0, 20.25%, 21.75%, 25%}。
假定部件的状态转移率和更换率如表 2所示。
| 部件编号 | 性能水平/% | 状态转移率/a-1 | 更换率/a-1 |
| 1 | g51=100 | λ5, 41=0.12, λ5, 31=0.135 λ5, 21=0.145, λ5, 11=0.25 |
μ4, 51=180 |
| μ3, 51=150 | |||
| μ2, 51=120 | |||
| μ1, 51=100 | |||
| g41=93.5 | λ4, 31=0.30, λ4, 21=0.35 | ||
| λ4, 11=0.40 | |||
| g31=87 | λ3, 21=0.50, λ3, 11=0.65 | ||
| g21=81 | λ2, 11=0.85 | ||
| g11=0 | |||
| 2 | g22=100 | λ2, 12=0.145 | μ1, 22=100 |
| g12=0 | |||
| 3 | g43=25 | λ4, 33=0.105, λ4, 23=0.15 λ4, 13=0.20 |
μ3, 43=200 |
| μ2, 43=150 | |||
| μ1, 43=100 | |||
| g33=21.75 | λ3, 23=0.30, λ3, 13=0.40 | ||
| g23=20.25 | λ2, 13=0.50 | ||
| g13=0 | |||
| 4 | g43=25 | λ4, 34=0.115, λ4, 24=0.15 λ4, 14=0.20 |
μ3, 44=200 |
| μ2, 44=150 | |||
| μ1, 44=100 | |||
| g33=21.75 | λ3, 24=0.30, λ3, 14=0.40 | ||
| g23=20.25 | λ2, 14=0.50 | ||
| g13=0 | |||
| 5 | g43=25 | λ4, 35=0.125, λ4, 25=0.15 λ4, 15=0.20 |
μ3, 45=200 |
| μ2, 45=150 | |||
| μ1, 45=100 | |||
| g33=21.75 | λ3, 25=0.30, λ3, 15=0.40 | ||
| g23=20.25 | λ2, 15=0.50 | ||
| g13=0 | |||
| 6 | g43=25 | λ4, 36=0.135, λ4, 26=0.15 λ4, 16=0.20 |
μ3, 46=200 |
| μ2, 46=150 | |||
| μ1, 46=100 | |||
| g33=21.75 | λ3, 26=0.30, λ3, 16=0.40 | ||
| g23=20.25 | λ2, 16=0.50 | ||
| g13=0 | |||
| 7 | g27=100 | λ2, 17=0.165 | μ1, 27=100 |
| g17=0 |
在完成对系统内部件状态划分之后,根据表 2给出的部件状态转移参数,通过求解式(5),可得各部件的状态概率随时间的变化关系,并采用通用生成函数方法得到各部件的状态性能概率分布。
5.2 基于部件状态的功率放大系统更换决策假定系统的有限服役周期Tend=8 a时,对式(11) 和式(12) 进行求解。

|
采用传统的枚举式搜索的方法,可得系统净效益的最大值为B(θ)=185.02万元,其对应的部件的更换阈值状态为θ*={4, 1, 1, 1, 1, 1, 1}。进一步考虑系统部件间的经济相关性和性能相关性,根据第4.3节基于机会维修策略的部件更换决策分析方法,可得系统内部件的更换阈值状态分别为θ*={4, 1, 1, 1, 1, 1, 1}、机会更换决策阈值ΔT*=0.8 a时,系统的净效益最大,即在整个雷达功率放大系统内,预防大器组件的更换阈值为93.5%,1:4功率分配器的更换阈值为0,功率放大器组件1~4的更换阈值为0,4 :1功率合成器的更换阈值为0,且系统内部件的机会更换决策时间阈值ΔT*=0.8 a时,该雷达功率放大系统获得最大净效益值为B(θ, ΔT*)=205.02万元,系统的净效益增加了20万元。
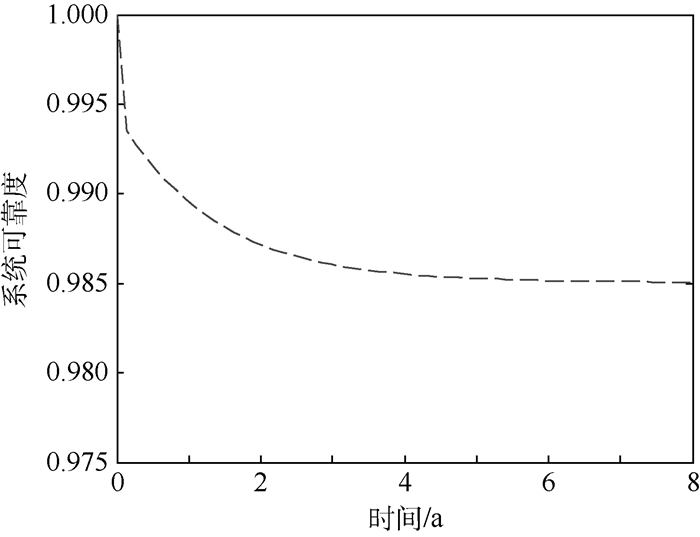
5.3 更换决策下功率放大系统可靠性分析通过第5.2节基于部件状态的功率放大系统更换决策的分析,说明该方法可以有效地节约维修资源,增加系统的净效益,然后该决策方法对系统在有限服役周期Tend=8 a内的可靠度影响,仍需探究,作为电子装备时刻保持着较高的可靠度是其任务属性所要求的,基于此,根据式(10),当系统内各部件更换阈值状态分别为θ*={4, 1, 1, 1, 1, 1, 1}、机会更换决策阈值ΔT*=0.8 a时对其可靠性进行分析,可得其随时间的变化关系如图 3所示。
|
| 图 3 系统可靠度与时间的关系 Fig. 3 Relationship between system reliability and time |
通过图 3可知,在没有维修费用限制的情况下,通过对系统内各部件按更换阈值状态和机会维修策略阈值进行视情更换,随着时间的推移系统的可靠度逐渐趋于稳定,即系统的可靠度不低于0.985。因此本文所提维修决策方法,通过尽可能多的部件级维修组合起来,在保证系统处于较高可靠度的前提下降低维修费用。
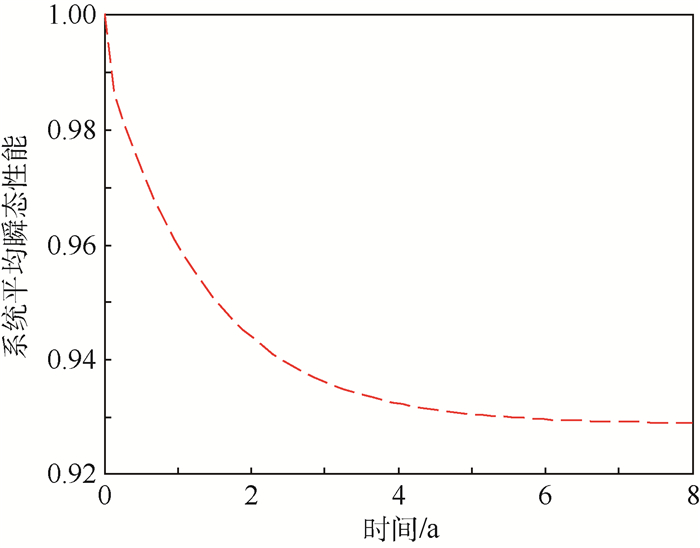
5.4 更换决策下功率放大系统平均性能分析雷达功率放大系统的任务保r障能力,主要通过系统的性能进行反应,因此对其平均瞬态性能的分析和研究具有重要意义。基于此,在有限服役周期Tend=8 a内,根据式(10),当系统内各部件更换阈值状态分别为θ*={4, 1, 1, 1, 1, 1, 1}和机会更换决策阈值ΔT*=0.8 a时,对其平均瞬态性能进行分析,可得其随时间的变化关系如图 4所示。
|
| 图 4 系统平均瞬态性能与时间的关系 Fig. 4 Relationship between system mean instantaneous performance and time |
通过图 4可知,在没有维修费用限制的情况下,通过对系统内各部件按更换阈值状态和机会维修更换决策阈值进行视情更换,随着时间的推移系统的平均瞬态性能逐渐趋于稳定,即系统的平均瞬态性能不低于92.5%。
6 结论为提高雷达功率放大系统的任务执行能力,提出了一种基于机会维修策略的雷达功率放大系统视情更换决策方法。
1) 采用本文所提基于机会维修的多态部件更换决策研究方法,通过尽可能多的将部件级维修组合起来,在保证系统处于较高可靠度的前提下降低了维修费用。
2) 充分结合机会维修和部件状态性能维修的优势,制定更加高效合理的维修决策方案,提高了雷达功率放大系统的任务执行能力。
| [1] | 任淑红.民航发动机性能可靠性评估与在翼寿命预测方法研究[D].南京:南京航空航天大学, 2010:88-90. REN S H.Research on methods of performance reliability assessments and life on wing prediction for civil aero engine[D].Nanjing:Nanjing University of Aeronautics and Astronautics, 2010:88-90(in Chinese). |
| [2] | 程志君, 杨征, 谭林. 基于机会策略的复杂系统视情维修决策模型[J]. 机械工程学报, 2012, 48 (6): 168–174. CHENG Z J, YANG Z, TAN L. Condition-based maintenance model of deteriorating complex system based on opportunistic policy[J]. Chinese Journal of Mechanical Engineering, 2012, 48 (6): 168–174. DOI:10.3901/JME.2012.06.168 (in Chinese) |
| [3] | 蔡景, 左洪福, 王华伟. 多部件系统的预防性维修优化模型研究[J]. 系统工程理论与实践, 2007, 27 (2): 133–138. CAI J, ZUO H F, WANG H W. A study on preventive maintenance optimization model for multi-unit system[J]. Systems Engineering-Theory & Practice, 2007, 27 (2): 133–138. (in Chinese) |
| [4] | LEVITIN G, LISNIANSKI A. Joint redundancy and maintenance optimization for multistate series-parallel systems[J]. Reliability Engineering & System Safety, 1999, 64 (1): 33–42. |
| [5] | 刘宇.多状态复杂系统可靠性建模及维修决策[D].成都:电子科技大学, 2011:69-79. LIU Y.Multi-state complex system reliability modeling and maintenance decision[D].Chengdu:University of Electronic Science and Technology of China, 2011:69-79(in Chinese). |
| [6] | 成国庆, 李玲, 唐应辉. 多态退化串联可修系统的最优维修更换策略[J]. 系统工程理论与实践, 2012, 32 (5): 1118–1123. CHENG G Q, LI L, TANG Y H. Optimal replacement policy for a deteriorating series repairable system with multi-state[J]. Systems Engineering-Theory & Practice, 2012, 32 (5): 1118–1123. (in Chinese) |
| [7] | 黄傲林, 李庆民, 黎铁冰, 等. 劣化系统周期预防性维修策略的优化[J]. 系统工程与电子技术, 2014, 36 (6): 1103–1107. HUANG A L, LI Q M, LI T B, et al. Optimization of periodic preventive maintenance policies for deteriorating repairable system[J]. Systems Engineering and Electronics, 2014, 36 (6): 1103–1107. (in Chinese) |
| [8] | 孙志礼, 王健, 印明昂, 等. 可修系统预防性维修时间的确定[J]. 东北大学学报(自然科学版), 2014, 35 (1): 84–87. SUN Z L, WANG J, YIN M A, et al. Determination about preventive maintenance time of the repairable system[J]. Journal of Northeastern University (Natural Science), 2014, 35 (1): 84–87. (in Chinese) |
| [9] | 狄鹏, 黎放, 杨元. 基于机会维修策略的预防性维修优化模型研究[J]. 工程设计学报, 2012, 19 (4): 263–267. DI P, LI F, YANG Y. Optimal preventive maintenance model based on opportunistic maintenance policy[J]. Chinese Journal of Engineering Design, 2012, 19 (4): 263–267. (in Chinese) |
| [10] | ZHOU Y, ZHANG Z, LIN T R, et al. Maintenance optimisation of a multi-state series-parallel system considering economic dependence and state-dependent inspection intervals[J]. Reliability Engineering & System Safety, 2013, 111 : 248–259. |
| [11] | CUONG D D, MING J Z, MAYANK P. Selective maintenance for multi-state series-parallel systems under economic dependence[J]. Reliability Engineering & System Safety, 2014, 121 : 240–249. |
| [12] | 葛小凯, 胡剑波, 张博锋. 考虑依赖性的多部件系统状态维修优化仿真建模[J]. 航空学报, 2013, 34 (8): 1854–1863. GE X K, HU J B, ZHANG B F. Simulation modeling for condition based maintenance optimization of multi-component systems with system with dependencies[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34 (8): 1854–1863. (in Chinese) |
| [13] | 张卓琦, 吴甦, 李斌锋. 考虑故障相关的两部件系统机会维修策略[J]. 清华大学学报(自然科学版), 2012, 52 (1): 122–127. ZhANG Z Q, WU S, LI B F. Opportunistic maintenance policy for a two-unit system with failure interactions[J]. Journal of Tsinghua University (Science and Technology), 2012, 52 (1): 122–127. (in Chinese) |
| [14] | 赵洪山, 鄢盛腾, 张小田. 风电机组确定性机会更换维修策略的研究[J]. 太阳能学报, 2014, 35 (4): 568–575. ZHAO H S, YAN S T, ZHANG X T. Deterministic opportunistic replacement maintenance strategy for wind turbine[J]. Acta Energiae Solaris Sinica, 2014, 35 (4): 568–575. (in Chinese) |
| [15] | 赵洪山, 张健平, 高夺, 等. 风电机组的状态-机会维修策略[J]. 中国电机工程学报, 2015, 35 (15): 3851–3858. ZHAO H S, ZHANG J P, GAO D, et al. A condition based opportunistic maintenance strategy for wind turbine[J]. Proceedings of the CSEE, 2015, 35 (15): 3851–3858. (in Chinese) |
| [16] | LIANIANSKI A, LEVITIN G. Multi-state system reliability:Assessment, optimization and applications[M]. Toh Tuck Link: World Scientific, 2003: 92-94. |
| [17] | LIANIANSKI A, FRENKEL I, DING Y. Multi-state system reliability analysis and optimization for engineers and industrial managers[M]. London: Springer, 2010: 40-45. |
| [18] | 潘刚, 尚朝轩, 梁玉英, 等. 考虑认知不确定的雷达功率放大系统可靠性评估[J]. 北京航空航天大学学报, 2016, 42 (6): 1185–1194. PAN G, SHANG C X, LIANG Y Y, et al. Reliability evaluation of radar power amplification system considering epistemic uncertainty[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016, 42 (6): 1185–1194. (in Chinese) |
| [19] | 章恩泽, 陈庆伟. 不确定可靠性优化问题的多目标粒子群优化算法[J]. 控制与决策, 2015, 30 (9): 1701–1705. ZHANG E Z, CHEN Q W. Multi-objective particle swarm optimization for uncertain reliability optimization problems[J]. Control and Decision, 2015, 30 (9): 1701–1705. (in Chinese) |
| [20] | 李春洋.基于多态系统理论的可靠性分析与优化设计方法研究[D].长沙:国防科学技术大学, 2010:92-114.LI C Y. Research on reliability analysis and optimization based on the multi-state system theory[D].Changsha:National University of Defense Technology, 2010:92-114(in Chinese). |



