转动副(R副)作为典型的传动关节,广泛应用于机构设计之中[1-3]。多个R副相互配合,或与其他运动副配合可设计出多种复合运动副[1]:具有2个转动自由度的虎克铰是由2个轴线垂直相交的R副组成;具有3个转动自由度的复合铰是由3个轴线相互垂直相交的R副组成;一种增大运动空间的新型球铰是由1个球副(S副)和1个R副组成[4]。绝大多数S副采用滑动配合,当结构空间受限时,R副也要采用滑动配合。
滑动配合的使用条件使得R副受到摩擦和间隙的影响,目前针对R副的研究主要集中在铰链间隙及摩擦对连杆机构动力学的影响,其中曲柄滑块机构及平面四连杆机构作为典型的应用背景得到了充分的讨论[5-8],考虑铰链间隙的机构运动学模型建立对本文有一定的参考意义,如Reis等[5]建立了考虑R副间隙和接触变形的曲柄滑块机构动力学模型。此外,考察R副精度及摩擦的研究有:Payandeh和Faraz[9]综合考虑了受载时铰链的接触变形和应力分布,对R副及S副的静摩擦力矩求解进行了分析,给出了滑动铰链静摩擦力矩同接触角及摩擦系数的数学模型;李新友等[10]对一种3-RPS并联机构进行了精度分析与综合; Khan和Chen[11]对包含R副的5轴叶片磨床进行了全面的几何精度分析,表明了R副对空间机构的几何精度亦有着重要影响。由上述研究可以看出,针对R副的研究大多独立讨论摩擦和间隙对机构精度的影响,综合考虑二者影响的静力学相关研究尚未得到充分开展。
临界角的存在将影响到运动副所在连杆机构的输出精度,因此对于R副的临界角计算可为连杆机构运动学模型的精确建立打下基础。本文以考虑接触变形和不考虑接触变形2种情况对R副的临界角进行了讨论,并以一平面四连杆机构为例进行了考虑R副临界角的机构精度分析,综合对比了铰链间隙、接触变形和摩擦因素对机构整体的影响程度。
1 临界角计算方法及R副结构 1.1 临界角计算方法接触面间有摩擦力f作用时,支撑面与平衡物体之间存在一摩擦角φf,如图 1(a)所示,当作用于物体上的主动力F作用线与接触点法线之间所成夹角θ小于摩擦角φf时,物体均可保持在支撑面上不滑动[12]。同时,当主动力作用延长线与接触区域相交时,如图 1(a)中所示情况,物体可保证不发生翻转;若力的作用线方向与接触区域不相交,则物体将发生翻转,作用力方向相对被施力物体发生角度变化,如图 1(b)所示。同时满足不滑动和不翻转2个条件的物体可实现自锁,本文借助物理学中临界角的概念,定义满足物体自锁的最大θ值为临界角,用θmax表示。有摩擦条件下,临界角取为上述实现自锁2个条件中较小的夹角值。此计算条件对应于与R副相连的连杆另一端为摩擦可忽略的理想运动副的应用情况。
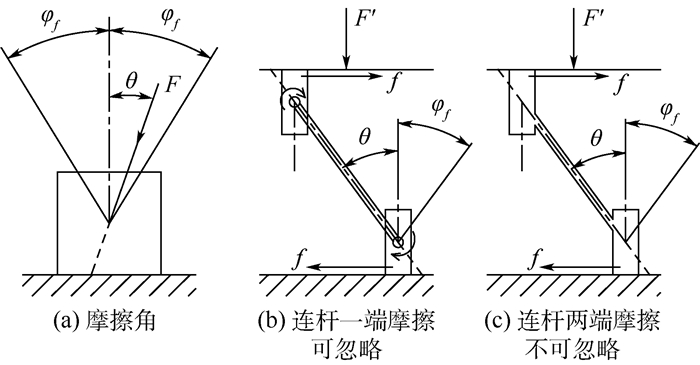
|
| 图 1 临界角成立条件 Fig. 1 Conditions for critical angle |
若物体因受到作用力的方向约束而不可独立翻转(例如并联机构中球铰球头与连杆相固连,球头不可绕连杆转动),简化为如图 1(c)所示情况,则物体只需满足摩擦角限制条件即可实现自锁,此时临界角等于摩擦角。此计算条件对应于连杆两端同时为摩擦不可忽略运动副的应用情况。
1.2 R副结构R副结构如图 2(a)所示。以运动副截面进行观察,可使用如图 2(b)所示的简化结构表示,主要包括底座、转动体以及与转动体相固连的连杆三部分。由于间隙和接触面间摩擦的共同作用,R副存在一个临界角,使得转动体在任意临界角范围内的载荷条件下可实现自锁。
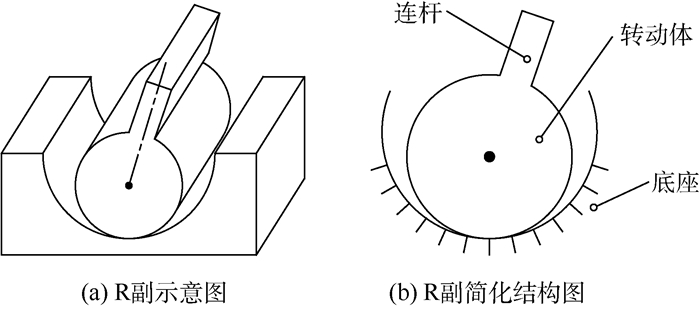
|
| 图 2 R副结构示意图 Fig. 2 Schematic diagram of structure of revolute pair |
R副的临界角也应同时满足使得转动体在底座内表面不滑动和不翻转2个条件。以下将分别从不考虑接触变形和考虑接触变形2种情况进行讨论。
2 R副临界角计算方法 2.1 不考虑接触变形条件假设运动副有间隙,转动体与底座均为刚体,转动体截面圆心位于连杆轴线上,当机构达到平衡状态时,沿连杆方向的作用力F必然通过转动体圆心,如图 3(a)所示。不考虑零件接触变形,截面内观察到的零件接触状态为点接触。
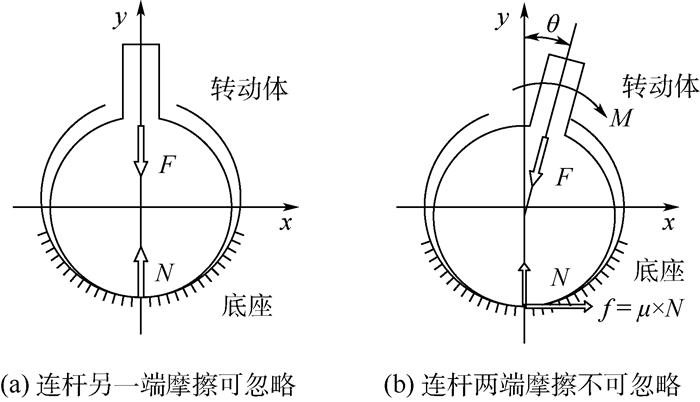
|
| 图 3 不考虑接触变形的R副临界角分析示意图 Fig. 3 Schematic diagrams of critical angle for revolute pair without contact deformation |
1)当与运动副相连的连杆另一端为摩擦可忽略的理想运动副时,连杆为二力杆不承受弯矩作用,连杆方向可随转动体发生自由摆转。则转动体所受作用力F方向亦随连杆的摆动而变化,因此当转动体达到静力平衡时接触点必然位于力F作用线与底座的交点处,支撑反力N与作用力F相平衡:

|
(1) |
此时临界角大小为0。
2)当连杆另一端同为摩擦不可忽略运动副时,连杆两端运动副可为连杆提供一弯矩M,使得连杆及转动体的平衡受力状态满足图 3(b),此时转动体受到连杆约束无法沿底座内表面滚动,夹角θ小于摩擦角φf时接触面间将无相对滑动。此时临界角大小为

|
(2) |
式中:μ为接触面间的滑动摩擦系数。
2.2 考虑接触变形条件如1.1节中的分析,连杆两端均为有摩擦R副时,接触变形对临界角大小无影响,临界角等于摩擦角。而连杆另一端为摩擦可忽略的理想运动副条件下,转动体与底座的接触变形区域将会进一步限制临界角大小。其中转动体与底座的接触区域及应力分布可通过赫兹应力分布公式得到[13]。
对于R副,转动体与底座可视为如图 4所示的圆柱体接触,根据赫兹接触理论求得的接触宽度2a、接触正应力σr分布公式如下[13]:
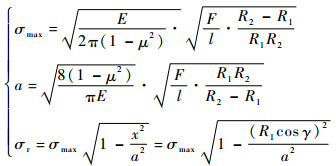
|
(3) |

|
| 图 4 两圆柱体接触应力分布示意图 Fig. 4 Schematic diagram of distribution of contact stress between two cylinders |
式中:E为材料的弹性模量;R1为转动体半径;R2为底座半径;l为转动体轴长;F为转动体承受的全部负载;γ为接触区边缘和水平方向的夹角。
两圆柱半径较为接近时,应力σr的分布方向可近似视为接触区域的法线方向,如图 4(c)所示。当施加在转动体上的负载P与竖直方向有一偏角θ时,σr与P的关系满足:
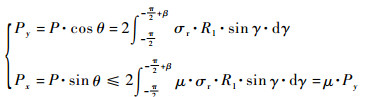
|
(4) |
式中:β为接触区域圆弧对应圆心角的1/2。
当转动体处于自锁状态时,载荷方向与接触区域中心法线方向夹角θ应满足以下条件:
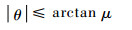
|
(5) |
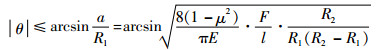
|
(6) |
条件式(5)保证转动体不滑动;条件式(6)保证转动体不滚动。当R1与R2相差很小时,R2/R1约等于1,临界角θmax取为
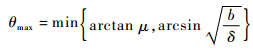
|
(7) |
式中:δ为R副间隙,δ=R2-R1;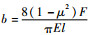
当铰链各个角度的间隙大小相同且受载后弹性变形量相等时,铰链的间隙误差可视为引入一虚拟连杆。仅考虑1个非理想球铰的四连杆机构可简化为一个五连杆机构,如图 5所示。
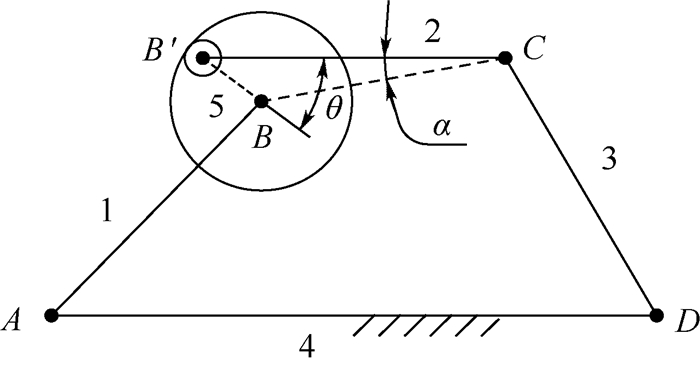
|
| 图 5 引入一个虚拟连杆的四连杆机构示意图 Fig. 5 Schematic diagram of a four-bar mechanism with one virtual link |
连杆L5(LBB′)为由于间隙等因素而引入的虚拟连杆,其长度包括:铰链初始间隙δ和接触变形所引入的转动体圆心位移ε两部分。即
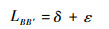
|
(8) |
LBC为确定连杆机构位姿的实际连杆长度,已知长度的初始连杆L2(LB′C)与实际连杆LBC之间的夹角α(∠B′CB)即为连杆的摆角误差。考虑摩擦因素的影响,最终平衡状态连杆L2与L5间夹角θ位于上述分析所得到的临界角θmax范围之内,即连杆将在以LBC为对称轴、以2θmax为圆心角的扇形区域内保持稳定,这使得最终计算出的实际连杆长度LBC在一定范围内具有随机性。LBC的数值范围为
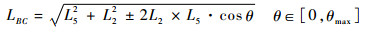
|
(9) |
考虑连杆L2的弹性变形时有
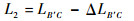
|
(10) |
式中:ΔLB′C为使用材料力学计算出的连杆受力弹性变形量。
综合式(8)~式(10)可求得摩擦所产生的夹角误差为
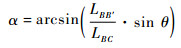
|
(11) |
由于同一连杆两端铰链均有间隙,引入2个虚拟连杆L5(LBB′)和L6(LCC′)。根据驱动杆的运动方向及负载方向,机构最终的平衡状态不同,且具有一定随机性,几种典型的连杆平衡状态如图 6所示。连杆L2(LB′C′)与两铰链接触点的法线方向夹角始终应满足θ < θmax,且两端铰链接触点的法线的方向向量数量积为负,即
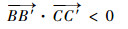
|
(12) |
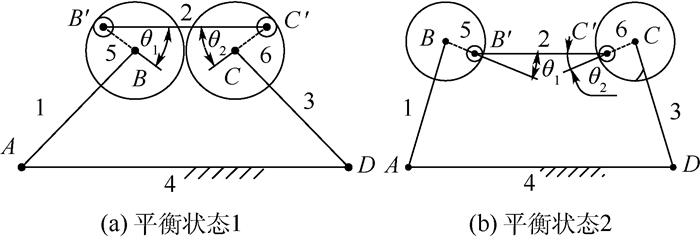
|
| 图 6 有2个非理想铰链的四连杆机构的2种典型平衡状态 Fig. 6 Two typically balanced states of four-bar mechanism with two non-ideal links |
通过连杆L2、L5之间夹角θ1以及L2、L6之间夹角θ2,可计算出LBC的变化范围:
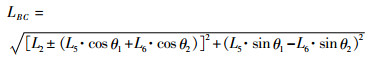
|
(13) |
式中:θ1∈[0, θmax1];θ2∈[0, θmax2],θmax1和θmax2为连杆两端铰链各自的临界角。
虚拟连杆L5和L6的长度为
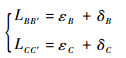
|
(14) |
考虑杆L2的弹性变形时有
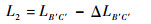
|
(15) |
连杆的倾角误差α表示为
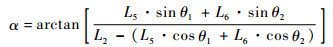
|
(16) |
式(13)中:“+”、“-”符号代表驱动连杆运动使实际连杆长度产生变化的方向。例如图 6(a)为LBC<LB′C′情况,计算中取“-”;图 6(b)为LBC < LB′C′情况,计算中取“+”。
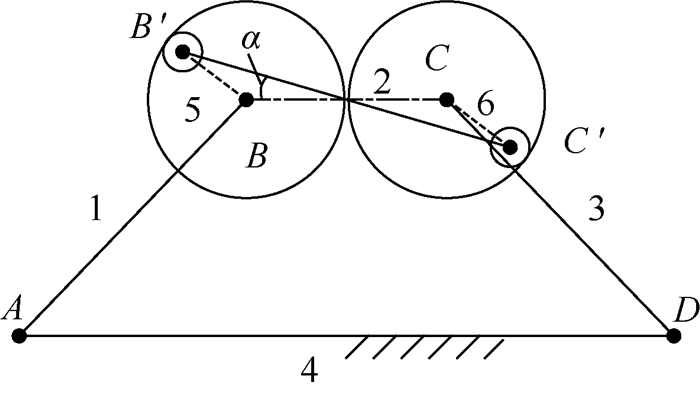
3.3 算例分析以具有2个非理想铰链的一个四连杆机构进行计算,机构示意图如图 7所示。
|
| 图 7 算例分析四连杆机构示意图 Fig. 7 Schematic diagram of four-bar mechanism in case study |
假设两铰链有摩擦且性能相同,取机构参数如表 1所示,材料属性E=2.06×105 MPa。
可求得
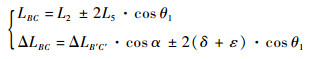
|
(17) |
| 参数类型 | 数值 |
| 四连杆机构 参数条件 | LAB=LB′C′=LCD=50 mm LAD=100 mm A杆=6.25π mm2 |
| 圆柱铰链 参数条件 | RB=RC,RB′=RC′(θmax1=θmax2=θmax, L5=L6) l柱销=10 mm |
| 变量 | 铰链间隙δ 连杆压力F 接触表面滑动摩擦系数μ |

|
(18) |
式中:连杆变形量由材料力学公式给出[14]:
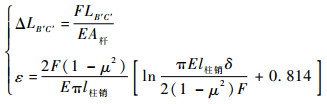
|
(19) |
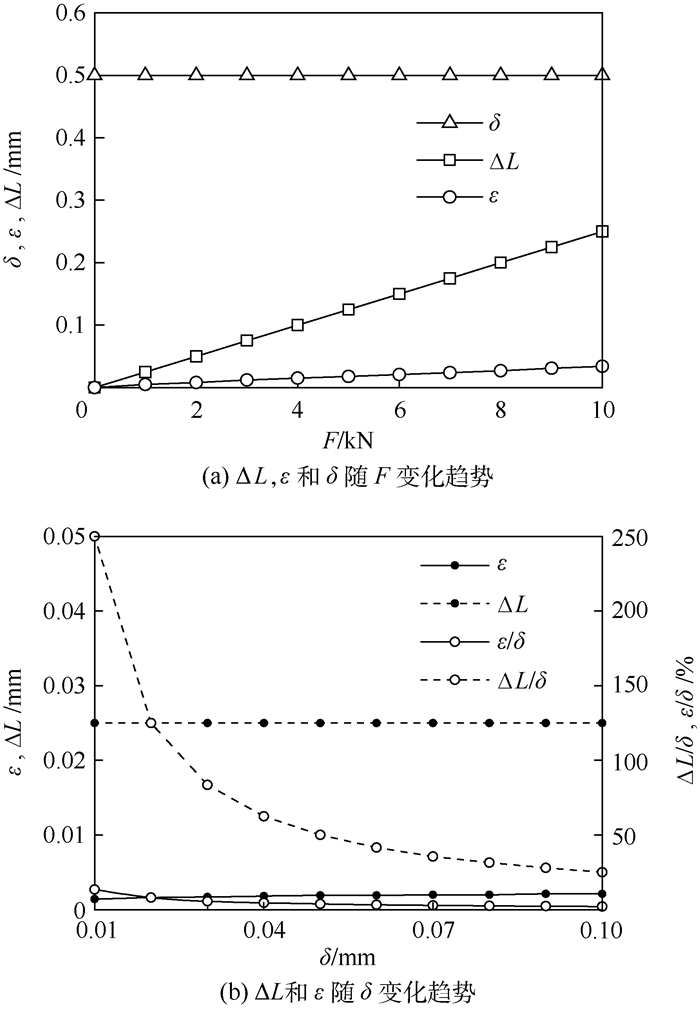
改变连杆LBC上的载荷F和铰链间隙值δ的大小,对比δ、ΔL(指代ΔLBC)、ε这3个误差项的量级。δ=0.5 mm时,误差项ΔL及ε随外力F变化的趋势如图 8(a)所示;F=100 N时,ΔL及ε随铰链间隙δ的变化趋势如图 8(b)所示。
|
| 图 8 ΔL、ε和δ随F及ΔL和ε随δ的变化示意图 Fig. 8 Variation of ΔL, ε and δ with F and variation of ΔL, ε with δ |
图 8(a)中直线ΔL和ε随载荷的变化率分别为25 μm/kN和3.4 μm/kN,而图 8(b)中代表ΔL和ε的直线斜率为零,可见上述两误差项均对外载荷变化比较敏感,而对铰链的设计间隙变化不敏感。图 8(a)中直线斜率代表零件刚度,直线ΔL的斜率约为ε斜率的7倍,表明连杆刚度约为R副刚度的1/7。ΔL只与载荷有关,ε随δ的变化值非常小,δ由铰链的设计及制造误差决定,因此可认为3个变量相互独立。
在无外载荷或载荷值较小的条件下,铰链的间隙值δ相对较大,为连杆的主要误差分量;ΔL与载荷F成正比,当载荷值足够大时,连杆误差将以杆长的弹性变形量ΔL为主。ε值同时与外载荷F及铰链间隙δ正相关,但数值与ΔL、δ两项相比较小(图 8(b)中ε/δ值约等于0),在载荷较大或间隙值较大时可忽略;在小载荷需精确求解的机构中引入可提高计算精度。
在设计中适当增加R副转动体长度以增加铰链内部接触面积,控制R副间隙大小均有助于减小接触变形引入的误差。
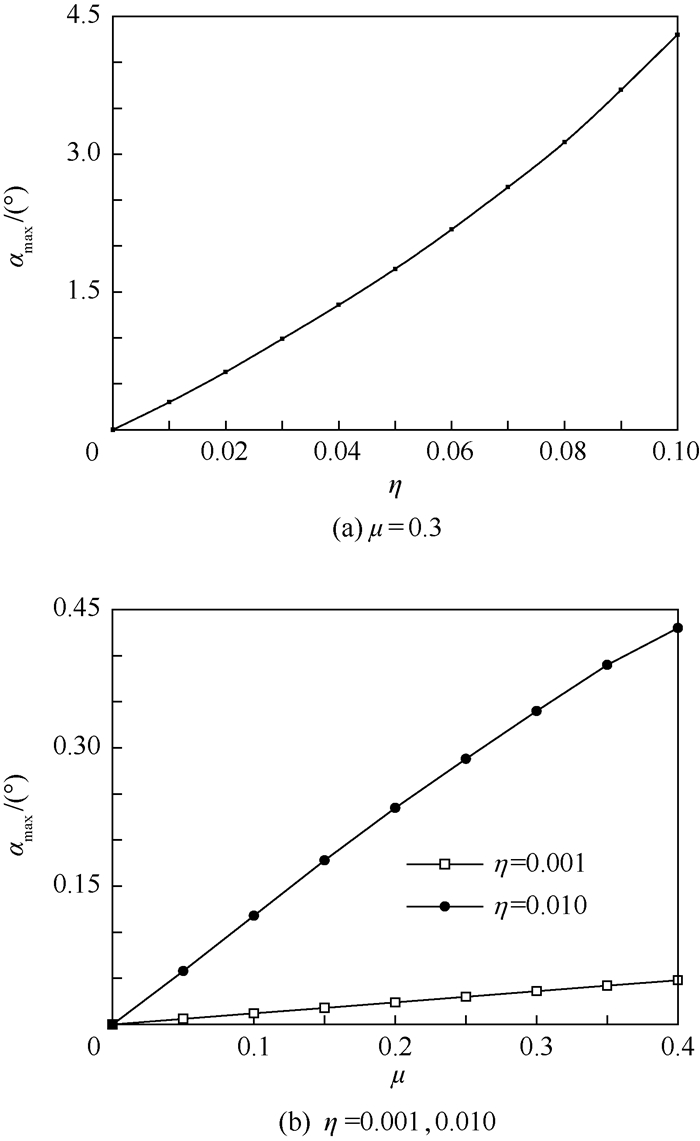
3.3.2 对αmax的讨论由式(18)可知,在摩擦系数一定的条件下,临界角θmax值一定,铰链间隙大小δ与所在连杆长度的比值(L5/L2)将影响到机构平衡时连杆的摆角误差范围。
设η=L5/L2,则αmax随η的变化趋势如图 9所示,其中图 9(a)为摩擦系数取为μ=0.3时αmax随η的变化关系,图 9(b)为在2种比值η条件下,αmax随摩擦系数μ的变化关系。
|
| 图 9 αmax随μ和η的变化趋势 Fig. 9 Variation trend of αmax with μandη |
从图 9中可以观察到,机构最终的连杆摆角误差最大值与比值η和摩擦系数μ正相关。由于连杆的最终位置与理想位置的夹角具有不确定性,减小并限制摆角边界αmax的值有利于机构最终位置精度的改善。减小比值η和摩擦系数μ可以有效减小摆角误差的边界值αmax,例如图 9(b)中η减小一个量级后αmax随μ的变化率亦减小为原变化率的10%,因此同时具有小的滑动摩擦系数和小的铰链间隙是最为理想的滑动铰链。
其中摩擦系数μ与铰链自身的材料属性及润滑条件有关,使用减摩材料和改善润滑条件在增加铰链运行流畅度的同时也可以提高连杆机构的整体精度。而在铰链性能一定的情况下,适当增加连杆长度可降低铰链间隙与杆长的比值η,以此实现连杆的输出位置精度改善。
但在其他条件不变的应用条件下,增加连杆长度时连杆受力变形量将有所增加,因此应当综合考虑连杆的摆角误差α与连杆长度误差的权重,结合机构的使用要求进行优化设计。
4 结论本文讨论了R副临界角计算方法,并给出了不考虑零件接触变形及考虑零件接触变形2种条件下临界角的表达式,结合四连杆算例分析得到以下结论:
1)铰链摩擦角的存在使得连杆在机构平衡状态下同时具有长度和偏角两项误差,连杆在此偏角范围内均可达到受力平衡状态并具有随机性,但可通过已知参数的计算确定其平衡范围。
2)当连杆两端均为有摩擦R副时,不考虑接触变形条件下临界角为0,考虑接触变形条件下临界角取值为
3)在四连杆算例分析中可得出,相比于连杆变形量和R副间隙大小,相同受力条件下R副的接触变形量可忽略,有利于简化复杂连杆机构的精度分析。
4)连杆摆角误差的最大值αmax与滑动摩擦系数μ及连杆长度比值η正相关,通过改善铰链的润滑条件、优化连杆长度可以有效降低临界角对机构的精度影响。
| [1] | 邹慧君, 高峰. 现代机构学进展[M]. 北京: 高等教育出版社, 2007 : 93 -94. ZOU H J, GAO F. The progress of modern organizations[M]. Beijing: Higher Education Press, 2007 : 93 -94. (in Chinese) |
| [2] | 郭卫东. 机械原理[M]. 北京: 科学出版社, 2010 : 168 . GUO W D. Mechanical principle[M]. Beijing: Science Press, 2010 : 168 . (in Chinese) |
| [3] | 黄昔光, 廖启征. 空间6R串联机器人机构位置逆解新算法[J]. 北京航空航天大学学报, 2010, 36 (3) : 295 –298. HUANG X G, LIAO Q Z. A new algorithm position inverse solution of 6-R serial robot mechanism[J]. Journal of Beijing University of Aeronautics and Astronautics, 2010, 36 (3) : 295 –298. (in Chinese) |
| [4] | 尚国强, 陈五一, 韩先国, 等. 并联机床的球铰链设计与分析[J]. 机械技术史及机械设计, 2008 : 286 –290. SHANG G Q, CHEN W Y, HAN X G, et al. Spherical hinge design and analysis of parallel machine tool[J]. Mechanical Technology and Mechanical Design, 2008 : 286 –290. (in Chinese) |
| [5] | REIS V L, DANIEL G B, CAVALCA K L. Dynamic analysis of a lubricated planar slider-crank mechanism considering friction and Hertz contact effects[J]. Mechanism and Machine Theory, 2014, 74 : 257 –273. DOI:10.1016/j.mechmachtheory.2013.11.009 |
| [6] | ZHANG X C, ZHANG X M, CHEN Z. Dynamic analysis of a 3-RRR parallel mechanism with multiple clearance joints[J]. Mechanism and Machine Theory, 2014, 78 : 105 –115. DOI:10.1016/j.mechmachtheory.2014.03.005 |
| [7] | BAI Z F, ZHAO Y. A hybrid contact force model of revolute joint with clearance for planar mechanical systems[J]. International Journal of Non-Linear Mechanics, 2013, 48 : 15 –36. DOI:10.1016/j.ijnonlinmec.2012.07.003 |
| [8] | JUNG K. Dynamic response of a revolute joint with clearance[J]. Mechanism and Machine Theory, 1995, 31 (1) : 121 –134. |
| [9] | PAYANDEH S, FARAZ A. Towards approximate models of coulomb frictional moments in:(I) revolute pin joints and (Ⅱ) spherical-socket ball joints[J]. Journal of Engineering Mathematics, 2001, 35 (403) : 283 –296. |
| [10] | 李新友, 陈五一, 韩先国. 基于正交设计的3-RPS并联机构精度分析与综合[J]. 北京航空航天大学学报, 2011, 37 (8) : 979 –984. LI X Y, CHEN W Y, HAN X G. 3-RPS parallel mechanism based on orthogonal design precision analysis and synthesis[J]. Journal of Beijing University of Aeronautics and Astronautics, 2011, 37 (8) : 979 –984. (in Chinese) |
| [11] | KHAN A W, CHEN W Y. Systematic geometric error modeling for workspace volumetric calibration of a 5-axis turbine blade grinding machine[J]. Chinese Journal of Aeronautics, 2010, 23 (5) : 604 –615. DOI:10.1016/S1000-9361(09)60261-2 |
| [12] | 瓦伦丁·L·波波夫.接触力学与摩擦学的原理及其应用[M].李强, 等, 译.北京:清华大学出版社, 2011:169-170. VALENTIN L P.Contact mechanics and tribology principle application[M].LI Q, et al, translated.Beijing:Tsinghua University Press, 2011:169-170(in Chinese). |
| [13] | 王元淳, 沃国纬. 弹性力学[M]. 上海: 上海交通大学出版社, 1998 : 133 -135. WANG Y C, WO G W. Elastic mechanics[M]. Shanghai: Shanghai Jiao Tong University Press, 1998 : 133 -135. (in Chinese) |
| [14] | 刘鸿文. 材料力学[M]. 北京: 高等教育出版社, 2005 : 34 . LIU H W. Material mechanics[M]. Beijing: Higher Education Press, 2005 : 34 . (in Chinese) |



