磁致伸缩材料(GMM)作为一种先进智能材料因其具有能量转换效率高、磁致伸缩应变量大、居里温度高、高频动态特性好和能量密度高等优点在很多领域得到了广泛的应用[1-2]。目前该材料数学模型主要有基于迟滞理论通过纯数学手段描述的Preisach模型[3]、神经网络磁滞模型[4]和基于磁畴理论的Jiles-Atherton (J-A)模型[5]、自由能模型[6]4种方式。J-A模型是据磁化机理建立起来的数学模型,能够较好地反映材料的迟滞特性,物理思想清晰,相对较稳定、准确,而且磁滞回线特性与模型参数紧密相关,因此得到了广泛的应用和发展[7-8]。GMM作为一种典型的铁磁性材料输入输出之间存在明显的迟滞非线性,并且易受温度、压力等环境因素的干扰,Ladjimi[9]和Nouicer[10]等通过对J-A模型参数修正得到了吻合性较强的模型,这就大大增强J-A模型的可拓展性和适应性。当GMM工作在不饱和小回线区域时,采用经典J-A模型常常会出现不对称及不饱和的现象[11],采用经典的J-A模型仿真和实验数据会存在一定的偏差[12-14],这就为开展超磁致伸缩作动器(GMA)非线性动力学行为特性及控制策略的研究带来极大的障碍。因此,本文针对不饱和小回线采用模型参数修正的方法,在改进J-A动态模型的基础上通过分析仿真与实验波形之间的偏离特性建立了动态小回线数学模型,并通过实验验证该模型的正确性。
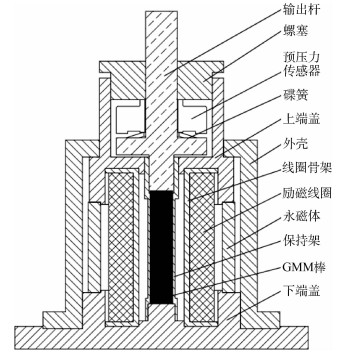
1 GMA结构及工作原理GMA的结构如图 1所示,其工作原理为GMM棒在励磁线圈产生动态驱动磁场的作用下产生伸缩位移,通过输出杆驱动其他装置运动。由于GMM自身的性能特点需要通过预压弹簧施加预应力来提高其磁致伸缩系数。采用环形外套式永磁体产生偏置磁场,一方面可以消除GMM自身的“倍频”特性实现双向位移输出,尽可能利用材料磁滞回线偏置磁场附近线性度较好的区域,降低材料自身非线性因素的影响,另一方面可提供较大的偏置磁场、能耗低、发热量小。在研究其中高频输出特性时,材料及结构的惯性、刚度和阻尼对位移输出产生一定的影响。
|
| 图 1 GMA工作原理 Fig. 1 Working principle of GMA |
J-A模型是基于铁磁材料的磁畴理论建立起来描述材料内部特性的数学模型,认为材料中非磁性夹杂、晶界和内应力等牵制点的存在使畴壁取代的磁化过程受阻而导致磁滞。因此,将磁畴运动分为可逆和不可逆壁移和壁转运动,将磁化强度可分为可逆磁化强度和不可逆磁化强度[15]。

|
(1) |
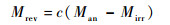
|
(2) |
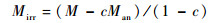
|
(3) |
式中:M为磁化强度;Mrev为可逆磁化强度;Mirr为不可逆可磁化强度;c为可逆损耗系数;Man为无磁滞磁化强度。采用改进的Langevin等式拟合各向同性材料得到无磁滞磁化曲线[16]。
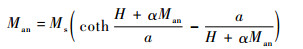
|
(4) |
式中:Ms为饱和磁化强度;H为磁场强度;a为无磁滞磁化强度形状参数;α为磁畴内部耦合的平均场参数。
Bertotti损耗统计理论[17]认为铁磁性材料的能量损耗主要是由磁滞损耗Ehysteresis、涡流损耗Eeddy和异常损耗Eanomalous三部分组成,因此在动态环境下J-A模型的能量守恒方程为
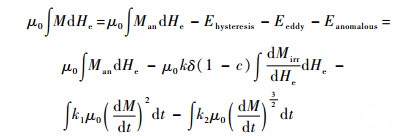
|
(5) |
式中:μ0为真空磁导系统; k为不可逆损耗系数;k1为涡流损耗因子;k2为异常损耗因子;He为有效磁场强度;δ为方向系数;当dH/dt>0时δ=1,当dH/dt < 0时δ=-1。
涡流损耗是由于材料的涡流效应而产生的损耗,在假设GMM磁化均匀且不考虑集肤效应时,根据Maxwell方程∇×E=-dB/dt可以求解得到涡流损耗方程式(6)[16]。异常损耗是指由于磁畴的往复磁化而消耗的能量,文献[7]对其进行了修正得到单位体积内的瞬间能量损耗(见式(7))。
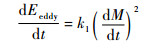
|
(6) |
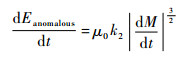
|
(7) |
将恒等式dM=(dM/dHe) dHe代入式(5)并对公式两端进行微分可得
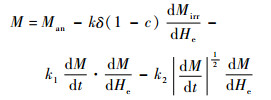
|
(8) |
GMA在中高频工作时,激励磁场的动态输入导致GMM棒处于快速伸缩状态,其输出特性受材料自身惯性、刚度和阻尼的影响较大。因此,本文在考虑材料自身特性的基础上结合GMA非线性动力学方程建立以励磁电流为输入、应变为输出的磁滞非线性动态模型。
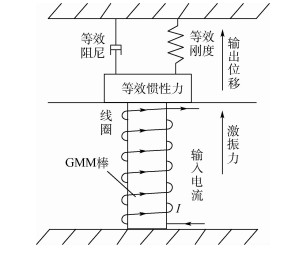
将GMA看作是一个轴向单自由度弹性阻尼系统,根据GMA的工作原理可以得到等效力学模型如图 2所示。当偏置磁场为Hbias,预压力为σ0A时,在材料输出应变[18]的基础上结合GMA牛顿第二定律建立了包含自身质量、刚度和阻尼的输出应变ε为
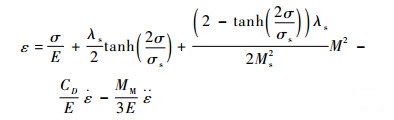
|
(9) |
|
| 图 2 GMA等效力学模型 Fig. 2 Equivalent mechanical model of GMA |
式中:E为GMM棒的弹性模量;CD为GMM棒Kelvin-Voigt阻尼系数;MM为GMM棒质量,根据GMA的动能拉格朗日函数可知GMM棒的等效质量为其自身的1/3[19];λs为饱和磁致伸缩系数;σs为饱和预压应力;σ为GMM材料受到的压应力,其定义为
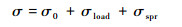
|
(10) |
式中:σ0为预压应力;σload为负载产生的压应力;σspr=ksprε为弹性应变ε产生的应力, kspr为GMA的等效刚度。
根据安培环路定理同时考虑漏磁的影响[20],当偏置磁场为Hbias时,则驱动磁场强度H为
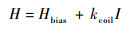
|
(11) |
式中:kcoil为励磁线圈产生的磁场系数。
因此联合式(1)~式(11)可以得到GMA的动态J-A模型。
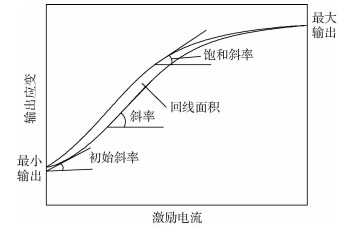
2.2 模型参数特性分析为了研究J-A模型参数对GMA磁滞回线特性的影响规律,本文引入初始斜率、斜率、饱和斜率、最大输出应变、最小输出应变和回线面积6个参量作为磁滞回线特征参数(如图 3所示),以J-A模型中某一参数为变量,其余参数不变来研究该参数对磁滞回线特征参数的影响规律。
|
| 图 3 磁滞回线特征参数 Fig. 3 Characteristic parameters of hysteresis loop |
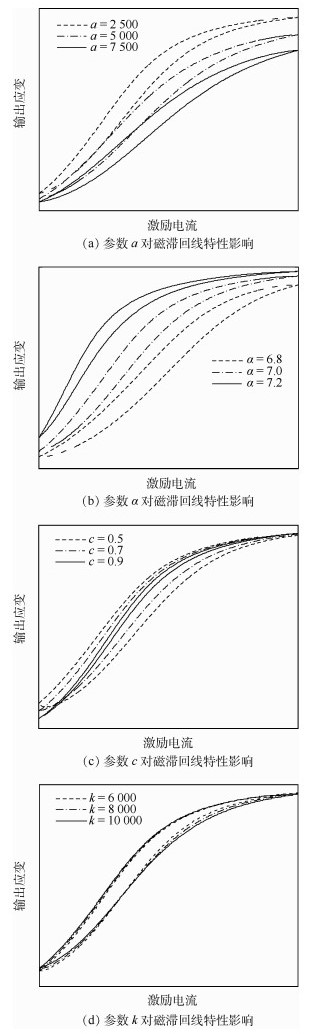
由J-A动态模型中各个参数的物理意义可知,无磁滞磁化强度形状参数a,磁畴内部耦合的平均场参数α,可逆损耗系数c和不可逆损耗系数k与磁滞回线的形状特性紧密相关,而且在不同工作环境下对J-A模型的改进也主要是对这4个参数进行修正[12-14],因此可得到各个参数对磁滞回线的影响规律如图 4所示。
|
| 图 4 J-A模型参数对磁滞回线特性影响 Fig. 4 Influence of J-A model parameters on hysteresis loop properties |
由图 4可以得出J-A模型参数对磁滞回线特征参数的影响规律,如表 1所示。从表 1中可以得出如下结论:参数a明显的与初始斜率、斜率、饱和斜率、最大输出和最小输出成反比,对回线面积的影响不大;参数α与初始斜率、斜率、最大输出和最小输出成正比,与回线面积成反比,对饱和斜率的影响不大;参数c可显著地改变回线面积并与其成反比, 与初始斜率和斜率成正比,与最小输出和回线面积成反比,对饱和斜率和最大输出的影响不大;参数k与最小输出和初始斜率成正比,与饱和斜率成反比,对斜率、最大输出和回线面积影响不大。
| 参数 | 初始斜率 | 斜率 | 饱和斜率 | 最大输出 | 最小输出 | 回线面积 |
| a↑ | ↓ | ↓ | ↓ | ↓ | ↓ | - |
| α↑ | ↑ | ↑ | - | ↑ | ↑ | ↓ |
| c↑ | ↑ | ↑ | - | - | ↓ | ↓ |
| k↑ | ↑ | - | ↓ | - | ↑ | - |
| 注:↑表示该变量增大;↓表示该变量减小;-表示该变量保持基本不变的状态。 | ||||||
2.3 不饱和小回线模型参数修正
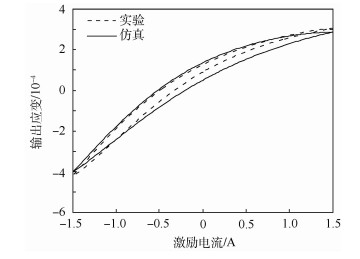
从图 5可以看出,当J-A模型用来仿真不饱和小回线时与实现数据存在严重的失真。从其磁滞回线特性分析可知,实验数据波形相对于仿真数据波形初始斜率、斜率、最大输出变大,最小输出和回线面积变小,饱和斜率基本上没有变化。
|
| 图 5 J-A小回线实验与仿真波形 Fig. 5 J-A minor loop experiment and simulation waveform |
根据J-A模型参数的性能特点及其对磁滞回线特性的影响规律并结合不饱和小回线模型中仿真和实验波形存在的差异特性,通过对J-A模型中参数a、α、c和k进行修正可以得到不饱和小回线J-A模型。
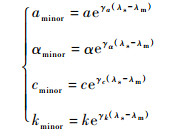
|
(12) |
式中:γa、γα、γc和γk分别为a、α、c和k的局部修正系数;kminor、aminor、cminor和αminor为小回线修正后参数;λm为小回线的最大磁致伸缩系数。
由式(12)可知,当λm=λs时,不饱和小回线的模型参数和饱和模型参数相同。由图 5实验与仿真波形对比可知初始斜率、斜率、饱和斜率、最大输出增大,最小输出和回线面积减小。由表 1可知,增大初始斜率、斜率、饱和斜率和最大输出可以通过减小a、k增大α、c实现,减小最小输出可以通过增大c减小k来实现,减小回线面积可以通过增大α和c来实现。因此,通过增大α和c,减小a和k对模型进行修正得到小回线J-A模型。
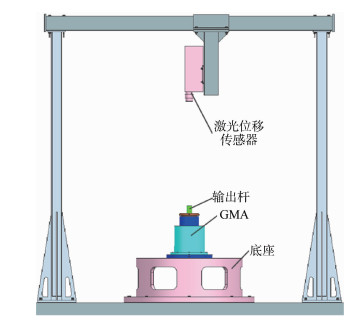
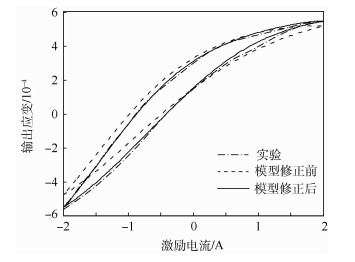
3 实验验证GMA实验台主要是由GMA、激光位移传感器以及测控实验台组成(如图 6所示),采用RTX为下位机、LabWindows为上位机的测控系统,采样周期为1 ms。选用日本电子技研工业(DENSHIGIKEN)株式会社生产的V100-MS激光位移传感器,可实现对位移、速度以及加速度的实时监测,位移测量精度高达5 μm/V。选用桂林风得控公司生产的ISF20DA250电流伺服驱动器,可实现电流反馈闭环控制,驱动频率高达15 kHz,幅值可达10 A。首先通过旋转螺塞压缩碟簧将初始预压力调整为6 MPa,工作台附近应保持安静的工作环境,防止周边的环境噪声对信号采集产生干扰。一切准备就绪之后给电流伺服驱动器下发激励电流幅值为2 A、频率为10 Hz的正弦信号指令,同时利用激光位移传感器采集GMA输出位移,并将采集信号记录保存。此组测试完成之后需将GMM棒取出放置在无磁环境中静置2 h方可重新进行实验,此组实验需重复3次取平均值方可得到激励电流幅值为2 A、频率为10 Hz时GMA输出位移波形曲线。J-A模型修正前后与实验波对比波形和磁滞回线特征参数分别如图 7和表 2所示,由此可以看出修正后模型磁滞回线的特征参数与实验数据比较接近,大大优于修正前模型,从而证明了该小回线模型的正确性。
|
| 图 6 GMA实验台 Fig. 6 GMA test bed |
|
| 图 7 J-A模型修正前后和实验对比 Fig. 7 Comparison between J-A model before and after modification and experiment loop |
| 参数 | 数值 | ||
| 实验 | 模型修正前 | 模型修正后 | |
| 初始斜率/(10-4A-1) | 2.08 | 1.00 | 2.00 |
| 斜率/(10-4A-1) | 3.4 | 2.8 | 3.4 |
| 饱和斜率/(10-4 A-1) | 1.0 | 0.7 | 1.0 |
| 最大输出应变/10-4 | 5.2 | 4.7 | 5.2 |
| 最小输出应变/10-4 | -5.54 | -5.4 | -5.5 |
4 结论
1) 在综合考虑GMA材料和结构动力学特性的基础上结合安培环路定理提出以励磁电流为输入、应变为输出的动态J-A模型。
2) 引入磁滞回线特性参数得出J-A模型参数对磁滞回线特性影响规律。
3) 根据不饱和小回线仿真与实验波形的偏离特性,通过增大参数α、c减小参数a、k来实现对J-A模型修正得到不饱和小回线动态J-A模型。
| [1] | GORAN E. Handbook of giant magnetostrictive materials[M]. Sa Diego: Academic Press, 2000 : 1 -13. |
| [2] | OHMATA K, ZAIKE M, KOH T. Three-link arm type vibration control device using magnetostrictive actuators[J]. Journal of Alloys and Compounds, 1997, 258 (1) : 74 –78. |
| [3] | TALEBIA S, HOJJA Y, GHODSI M. A combined Preisach-hyperbolic tangent model for magnetic hysteresis of Terfenol-D[J]. Journal of Magnetism and Magnetic Materials, 2015, 396 : 38 –47. DOI:10.1016/j.jmmm.2015.08.006 |
| [4] | 孙英.超磁致伸缩致动器的神经网络控制与动态模型及实验研究[D].天津:河北工业大学, 2007:26-45. SUN Y.Neural network control and dynamic model as well as experiment for giant magnetostrictive actuator[D].Tianjin:Hebei University of Technology, 2007:26-45(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10080-2008156848.htm |
| [5] | SABLIK M J, JILES D C. Coupled magnetoelastic theory of magnetic and magnetostrictive hysteresis[J]. IEEE Transactions on Magnetics, 1993, 29 (3) : 2113 –2123. |
| [6] | 田春.超磁致伸缩执行器的本征非线性研究及其补偿控制[D].上海:上海交通大学, 2007:18-32. TIAN C.Research and compensation control on constitutive nonlinear of giant magnetostrictive actuators[J].Shanghai:Shanghai Jiao Tong University, 2007:18-32(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10497-2008110000.htm |
| [7] | DU R, ROBERTSON P. Dynamic Jiles-Atherton model for determining the magnetic power loss at high frequency in permanent magnet machines[J]. IEEE Transactions on Magnetics, 2014, 51 (6) : 1 –10. |
| [8] | JILES D C, THOELKE J B. Theory of ferromagnetic hysteresis:Determination of model parameters from experimental hysteresis loops[J]. IEEE Transactions on Magnetics, 1989, 25 (5) : 3928 –3930. DOI:10.1109/20.42480 |
| [9] | LADJIMI O, SIXDENIER F, MORAL L. Temperature dependent extension of the Jiles-Atherton model:Study of the variation of microstructural hysteresis parameters[J]. IEEE Transactions on Magnetics, 2012, 48 (10) : 2567 –2572. DOI:10.1109/TMAG.2012.2201735 |
| [10] | NOUICER A, NOUICER E, FELIACH M. A neural network for incorporating the thermal effect on the magnetic hysteresis of the3F3material using the Jiles-Atherton model[J]. Journal of Magnetism and Magnetic Materials, 2015, 373 : 240 –243. DOI:10.1016/j.jmmm.2014.03.051 |
| [11] | IZYDORCZYK J. A new algorithm for extraction of parameters of Jiles and Atherton hysteresis model[J]. IEEE Transactions on Magnetics, 2006, 42 (10) : 3132 –3134. DOI:10.1109/TMAG.2006.880094 |
| [12] | HAMIMID M, MIMOUNE S, FELIACHI M. Minor hysteresis loops model based on exponential parameters scaling of the modified Jiles-Atherton model[J]. Physica B:Condensed Matter, 2012, 407 (13) : 2438 –2441. DOI:10.1016/j.physb.2012.03.042 |
| [13] | CHWASTEK K. Modelling offset minor hysteresis loops with the modified Jiles-Atherton description[J]. Journal of Physics D-Applied Physics, 2009, 42 (16) : 1 –5. |
| [14] | 李超, 徐启峰. J-A模型误差修正和温度特性仿真[J]. 电工技术学报, 2014, 29 (9) : 232 –238. LI C, XU Q F. Error modification and temperature simulation of J-A model[J]. Transactions of China Electrotechnical Society, 2014, 29 (9) : 232 –238. (in Chinese) |
| [15] | JILES D C, ATHERTON D L. Theory of ferromagnetic hysteresis[J]. Journal of Applied Physics, 1984, 55 (6) : 2115 –2120. DOI:10.1063/1.333582 |
| [16] | JILES D C. Frequency dependence of hysteresis curves inconducting magnetic materials[J]. Journal of Applied Physics, 1994, 76 (10) : 5849 –5855. DOI:10.1063/1.358399 |
| [17] | BERTOTTI G. Physical interpretation of eddy current losses in ferromagnetic materials[J]. Journal of Applied Physics, 1985, 57 (6) : 2110 –2126. DOI:10.1063/1.334404 |
| [18] | ZHENG X J, LIU X E. A nonlinear constitutive model for Terfenol-D rods[J]. Journal of Applied Physics, 2005, 97 (5) : 1 –8. |
| [19] | STORN R, PRICE K. Differential evolution-a simple and efficient heuristic for global optimization over continuous space[J]. Journal of Global Optimization, 1997, 11 (4) : 341 –359. DOI:10.1023/A:1008202821328 |
| [20] | 贾振元, 王晓煜, 王福吉. 超磁致伸缩执行器的动力学参数及磁滞模型参数的辨识方法[J]. 机械工程学报, 2007, 43 (10) : 9 –13. JIA Z Y, WANG X Y, WANG F J. Identification method of giant magnetostrictive actuator dynamics and model parameters[J]. Chinese Journal of Mechanical Engineering, 2007, 43 (10) : 9 –13. DOI:10.3901/JME.2007.10.009 (in Chinese) |



