2. 空间物理重点实验室, 北京 100076
2. Science and Technology on Space Physics Laboratory, Beijing 100076, China
不同于传统轴对称再入飞行器,升力体飞行器通常为面对称外形,具备较高的升阻比,其中,美国通用空天飞行器(CAV)[1-2]就是典型的高升阻比升力体飞行器。升力体飞行器在返回大气层内时,相比传统惯性轨迹,其利用高升阻比气动特性可进行大范围的倾斜转弯机动飞行,从而适应飞行器再入后返场点的灵活选择。飞行器在大气层内飞行过程中通过气动升力的倾斜实现转弯机动,受到气动阻力的作用持续减速,而当返场点确定的情况下,需调整飞行器的速度方向指向返场点,随后直线飞行完成返场任务,因此,飞行器通过倾斜机动使得速度方向指向返场点时对应的速度最大即倾斜转弯过程中能量损失最小是判断能否完成返场任务的关键点,规划满足驻点热流、过载及动压等多约束条件下能量最优的倾斜转弯飞行轨迹非常有意义。
针对倾斜转弯过程中能量损失最小问题,文献[3]在考虑动压、过载及热流密度等过程约束下,采用常值升阻比假设,获得了倾斜转弯转(BTT)弯半径等运动参数的解析关系,文献[4]分析了倾斜转弯的基本原理和控制特性;文献[5-11]分别采用遗传算法、直接法加序列二次规划法、高斯伪谱法对升力式飞行器再入机动轨迹进行了优化,为本文选择高斯伪谱法作为最优控制问题的优化求解方法提供了参考;文献[12]提出几何控制方案来解决再入飞行器的倾斜机动飞行问题。基于以上研究基础,从倾斜转弯的基本原理出发,推导给出能量最优的转弯机动策略,进一步采用优化算法进行仿真验证。
本文选取CAV为研究对象,考虑力、热等飞行过程约束,建立了飞行器动力学模型和高度-速度飞行走廊模型;基于升力体飞行器倾斜转弯基本原理和准平衡滑翔假设,推导获得了倾斜转弯终端速度与升阻比、倾侧角及终端弹道偏角的解析关系,提出了能量近似最优的倾斜转弯机动飞行策略;最后,建立了能量最优的非线性轨迹优化问题模型,采用高斯伪谱法获得了终端能量最优轨迹。仿真结果表明本文所提飞行策略与优化方法获得的结果高度一致,并且具有更高的计算效率。
1 数学模型 1.1 动力学模型为研究升力体飞行器大气层内再入倾斜转弯的弹道特性和规律,假设地球为均质无旋圆球,飞行器采用倾斜转弯飞行控制方式,因此,飞行器在空间内的再入运动方程可表述为
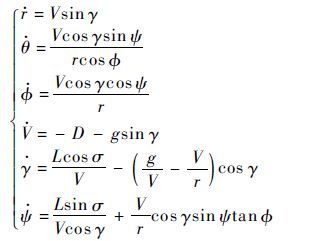
|
(1) |
式中:r、θ、Φ、V、γ、ψ分别为飞行器质心到地心的距离、经度、纬度、飞行器相对地球速度、弹道倾角及航向角;D、L分别为飞行器阻力加速度和升力加速度;σ为飞行倾侧角;g为引力加速度。
1.2 气动模型本文选择洛马公司的通用航空飞行器CAV-H[13]升力飞行器作为研究对象,该飞行器最大升阻比可达3.2。基于马赫数无关原理,当飞行马赫数大于8时,飞行器气动升力系数CL、气动阻力系数CD可拟合为攻角α相关的表达式[14]:
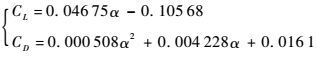
|
(2) |
飞行器在大气层内飞行约束主要包括过程约束和终端约束。其中,过程约束包括热流峰值约束、过载约束、动压约束以及控制量约束等[15],终端约束包括位置、速度以及航向角约束等。
1) 热流峰值约束

|
(3) |
式中:Rd为飞行器端头半径;C1为与飞行器特性相关的常数;ρ为飞行高度的大气密度; $\dot{Q}$max为驻点热流密度约束值。取C1/$\sqrt{\frac{R}{d}}$=5.188×10-8。
大气密度可采用如下指数函数近似计算:
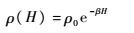
|
(4) |
式中:H为飞行高度;$\beta =\frac{1}{{{H}_{MCP}}}$,HMCP=7.11 km为大气刻度系数;ρ0=1.225 kg/m3为海拔0 km密度。
由于热流峰值仅与高度、速度相关,可进一步转化为飞行高度的下边界约束:
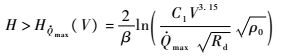
|
(5) |
由式(5)可知,热流约束仅与飞行高度及速度相关,与飞行攻角无关。
2) 动压约束
将大气密度公式代入动压计算公式并转换为高度和速度的关系式,得
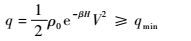
|
(6) |
进一步转化为飞行高度的上边界约束:
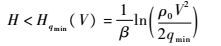
|
(7) |
由式(7)可知,动压约束仅与飞行高度及速度相关,与飞行攻角无关。
3) 过载约束
飞行器升力加速度及阻力加速度计算公式为

|
(8) |
过载约束可表述为
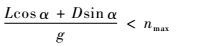
|
(9) |
进一步转化为飞行高度的下边界约束:
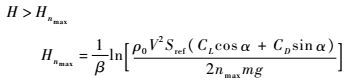
|
(10) |
由式(10)可知,过载的约束与飞行高度、速度及飞行攻角相关。
4) 控制量约束
飞行器在大气层内飞行时,主要控制量为飞行攻角α和倾侧角σ。对应控制量约束如下:

|
(11) |
5) 终端约束
飞行器在大气层内倾斜转弯的幅度可通过航向角ψ的变化量来描述。为研究能量最优的倾斜转弯策略,考虑终端航向角约束,可表述为
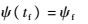
|
(12) |
式中:ψf为终端航向角约束值。
2 飞行器倾斜转弯基本原理飞行器在大气层内飞行的受力主要包括重力、气动升力及气动阻力,气动升力和气动阻力的改变实现纵向平面内飞行轨迹的控制,气动升力大小及方向的改变实现倾斜转弯机动。飞行器在倾斜转弯机动过程中,其对应的运动学方程为
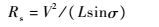
|
(13) |
式中:Rs对应为飞行器倾斜转弯机动过程中的转弯半径;L=ρ(H)V2SrefCL/(2m),当飞行器飞行速度V≠0,则可得
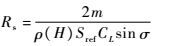
|
(14) |
由式(14)可知,在飞行器质量一定的情况下,飞行转弯半径Rs与飞行高度H、升力系数CL及倾侧角σ相关。
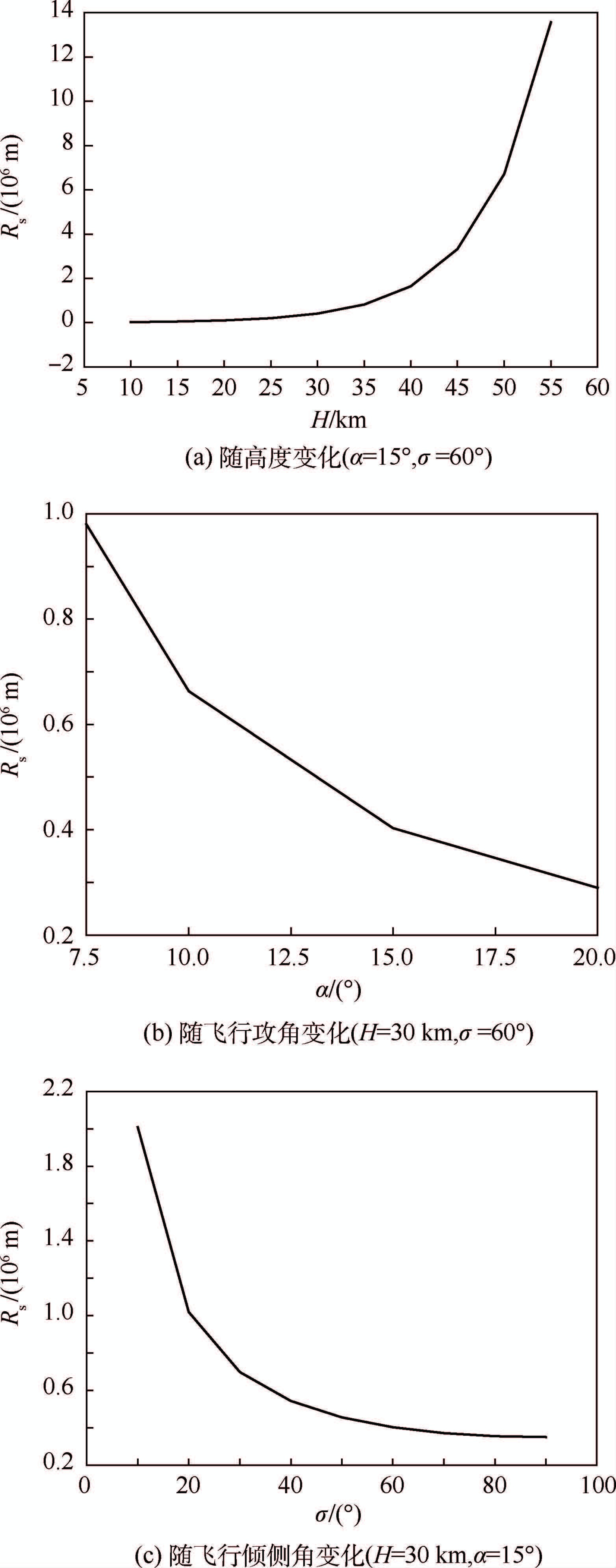
以CAV-H飞行器为例,对应的飞行器倾斜转弯机动的转弯半径特性曲线如图 1所示。
|
| 图 1 转弯半径特性曲线 Fig. 1 Characteristic curves of bank-to-turn radius |
由图 1可知:
1) 飞行高度越低,对应飞行器倾斜转弯半径越小。
2) 飞行倾侧角不为0时,飞行攻角越大,对应升力系数越大,则倾斜转弯半径越小。
3) 倾斜转弯机动过程中,飞行倾侧角对应的侧向升力分量越大,则倾斜转弯半径越小。
飞行高度、攻角及倾侧角的匹配关系决定了飞行器倾斜转弯机动过程中的转弯半径,同时,一定飞行速度的条件下,飞行器实际飞行过程中还需考虑驻点热流、动压及法向过载等约束条件。在飞行攻角确定的条件下,可将飞行约束转化为飞行高度约束条件,如表述为式(5)、式(7)及式(10)。
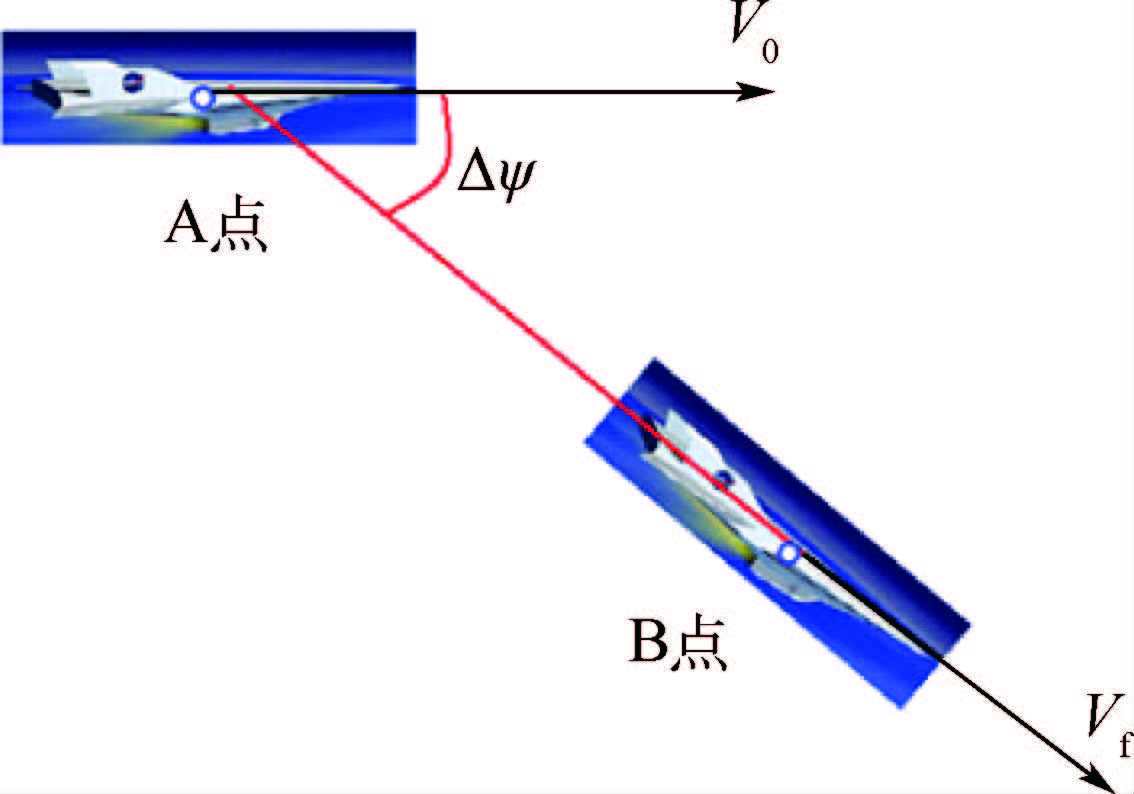
3 能量近似最优倾斜转弯飞行策略如图 2所示,飞行器倾斜转弯机动飞行过程中,飞行速度由初始速度V0变化为终端速度Vf,在速度方向偏转角度Δψ一定的条件下,如何使得终端速度Vf最大是以下分析的重点。
|
| 图 2 倾斜转弯示意图 Fig. 2 Schematic diagram of bank-to-turn |
飞行器在倾斜转弯过程中弹道倾角较小,则γ≈0,则动力学模型式(1)中速度对时间的导数表示为
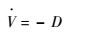
|
(15) |
式(1)中航向角表达式右边第一项Lsin σ/(Vcos γ)为气动升力在当地水平面的分量对航向角变化率的影响,第二项Vcos γ sin ψtan Φ/r为地球曲率对航向角变化率的影响。可以发现,纬度Φ越低,第二项对航向角变化率影响越小,当Φ→0,则tan Φ→0。为研究气动力对航向角改变能力的客观规律,定义以下变量
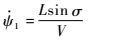
|
(16) |
式(15)反映了飞行器速度大小变化与受力关系;式(16)反映了飞行器在水平面速度方向变化与受力关系。由式(15)和式(16)可得
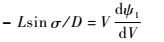
|
(17) |
假设飞行器飞行过程中升阻比为KLD,其中KLD=L/D。则可得
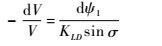
|
(18) |
对式(18)进行积分,则表达式可得
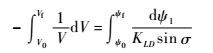
|
(19) |
假设飞行过程中KLD、倾侧角σ为常值,由式(19)可得出
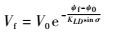
|
(20) |
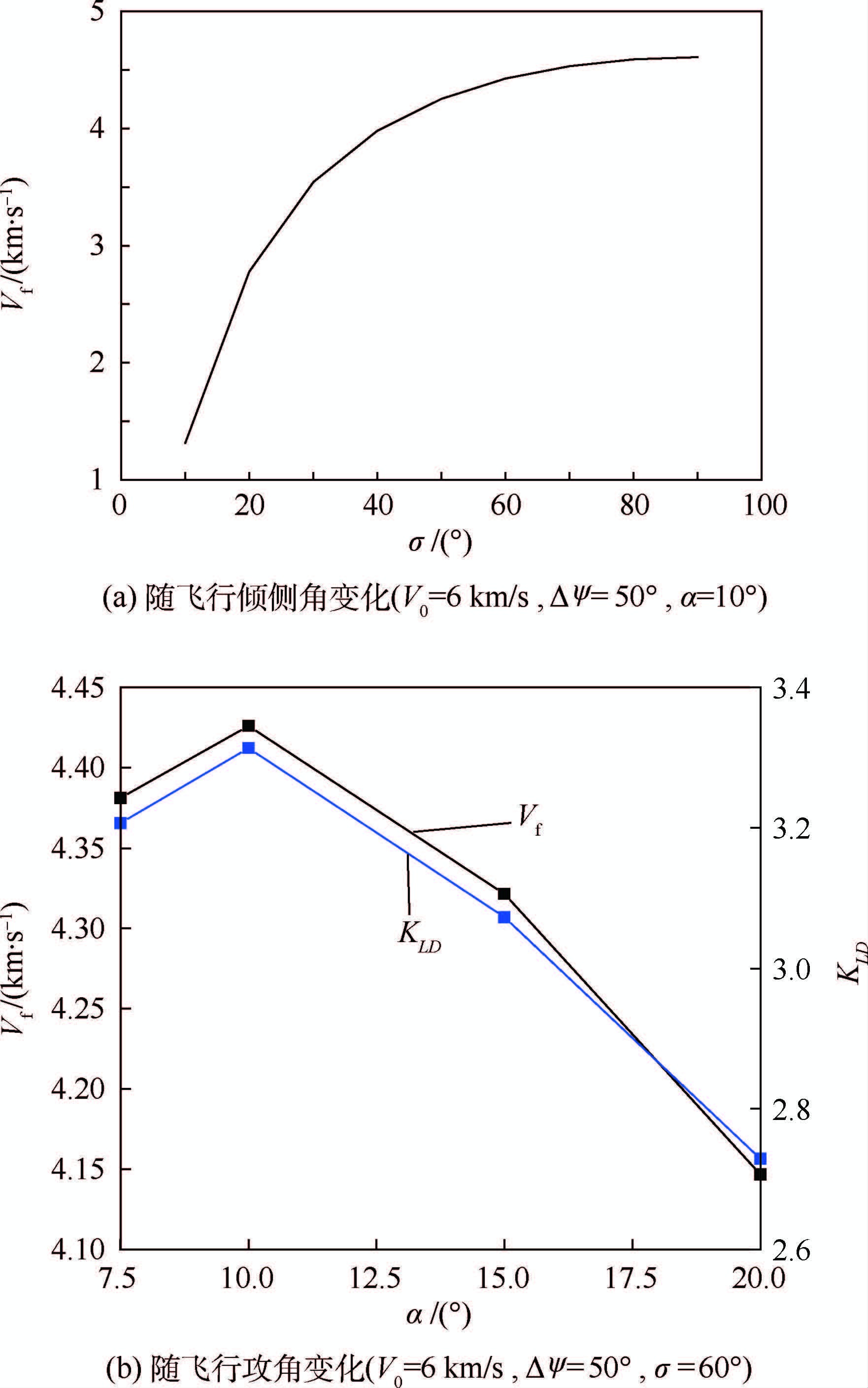
由式(20)可以看出,在V0及Δψ(Δψ=ψf-ψ0)一定的情况下,飞行器转弯结束点的速度仅与飞行过程中的KLD和σ相关。以CAV-H飞行器为例,对应飞行器倾斜转弯终端速度的特性曲线如图 3所示。
|
| 图 3 倾斜转弯终端速度的特性曲线 Fig. 3 Characteristic curves of bank-to-turnterminal velocity |
为使得倾斜转弯的终端速度最大,飞行器在飞行过程中的升阻比KLD及倾侧角σ的选取需尽可能大。
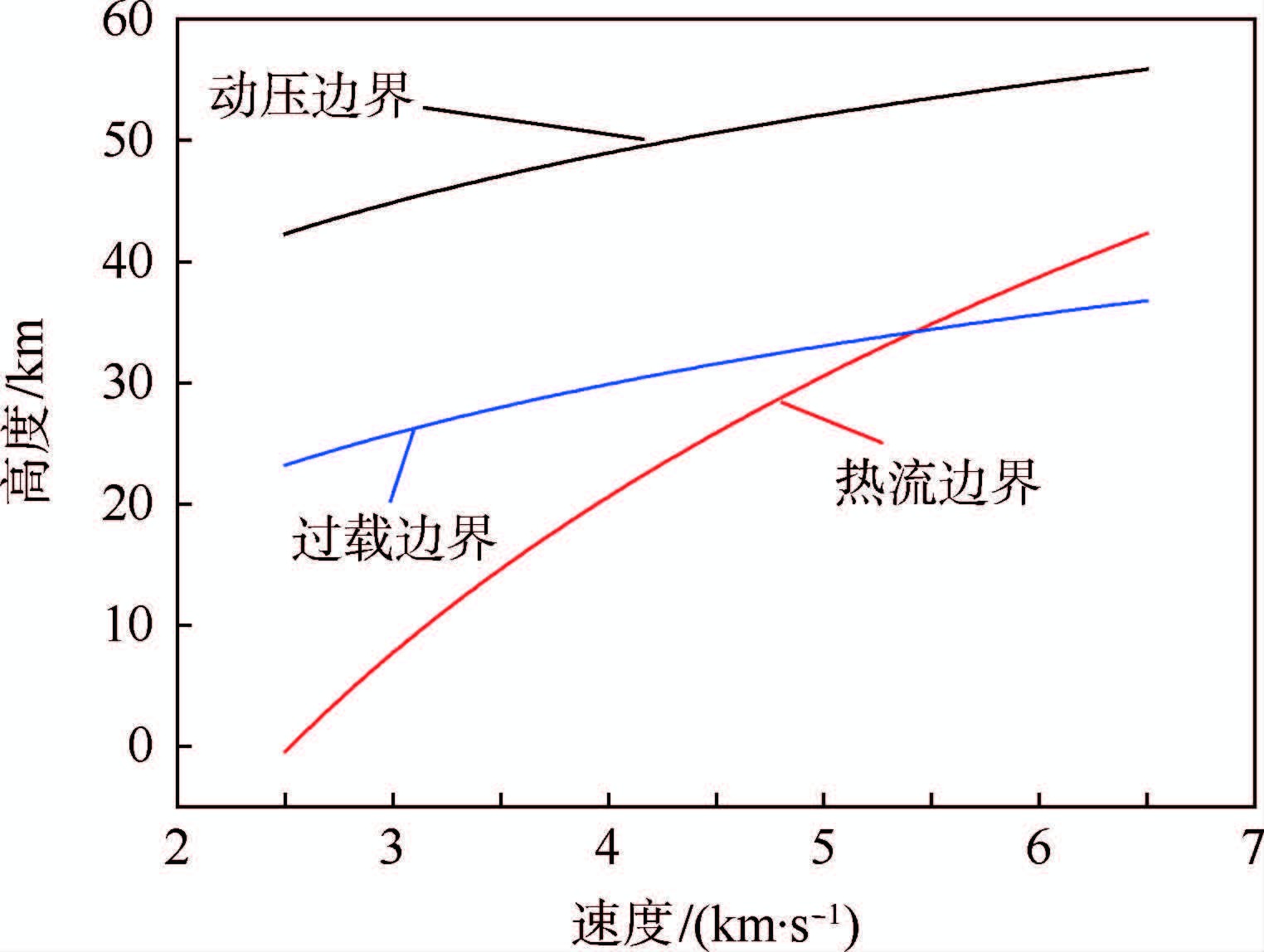
考虑飞行器飞行过程中的热流、动压及法向过载约束,对应的飞行高度-速度(H-V)约束边界如图 4所示。
|
| 图 4 高度-速度走廊边界示意图 Fig. 4 Schematic diagram of H-V corridor boundary |
由图 4可知,在飞行速度较大时,飞行边界由热流约束决定,随着飞行速度降低,飞行边界由过载约束决定。
由以上理论推导及弹道特性分析结果可知飞行器能量近似最优的倾斜转弯飞行策略如下:
1) 基于最优升阻比攻角-速度飞行剖面及飞行过程约束,规划高度-速度飞行走廊。
2) 基于高度-速度飞行走廊下边界获得倾斜机动能量最优高度-速度飞行剖面。
3) 纵向基于高度-速度及攻角-速度剖面、横向通过攻角及高度实时求解倾侧角,获得能量近似最优倾斜转弯轨迹。
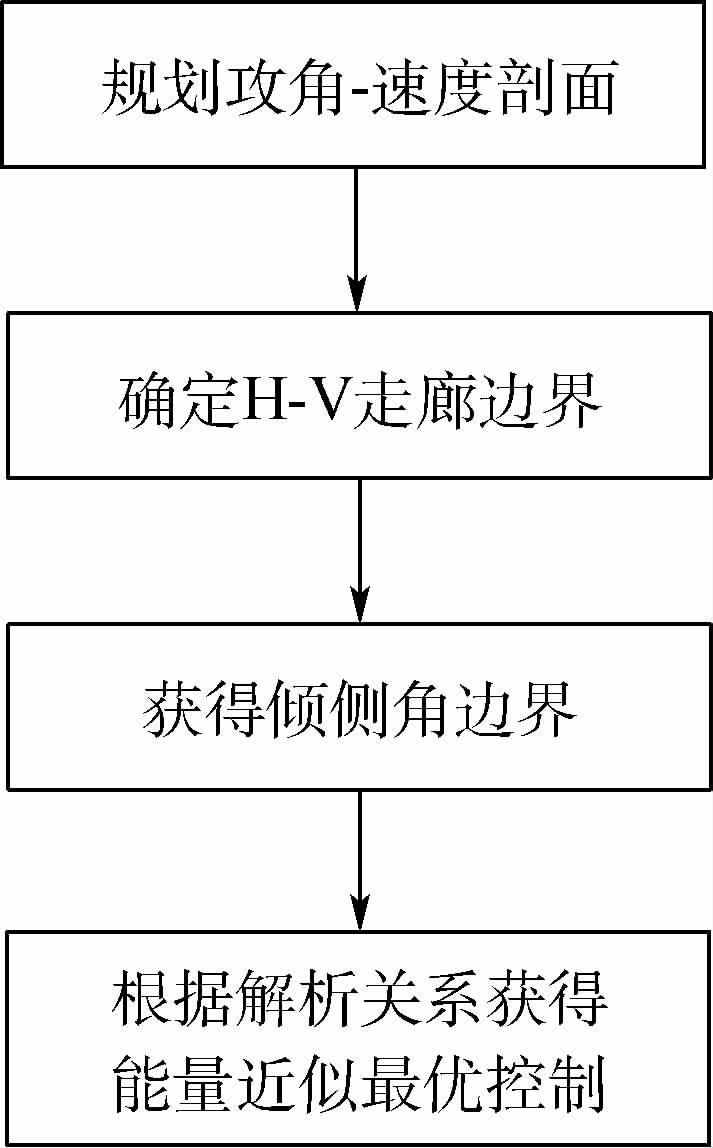
能量近似最优倾斜转弯机动策略的流程图如图 5所示。
|
| 图 5 能量近似最优飞行策略流程图 Fig. 5 Flowchart of energy suboptimal flight strategy |
为获取倾斜转弯能量最优的轨迹,可以通过间接法和直接法求解建立的相应最优控制问题。考虑到间接法求解多点边值问题时对初值估计精度要求高且对于过程约束问题求解困难,本文采用直接法对性能指标进行寻优,其基本思路是,通过对控制变量和状态变量进行参数化离散,从而将轨迹优化这一连续的最优控制问题转换成有限维的非线性规划(NLP)问题,并采用成熟的非线性规划求解工具进行求解。直接法应用时具有不需要推导一阶最优性条件、对初值估计精度要求不高以及通用性好等优点。
离散后的轨迹优化问题如下。
状态变量:
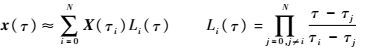
|
(21) |
式中:τi为配点,τi∈(-1,1),取自N 阶Legendre多项式PK(τ)的根。
控制变量:
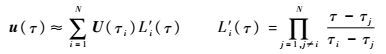
|
(22) |
运动方程约束:
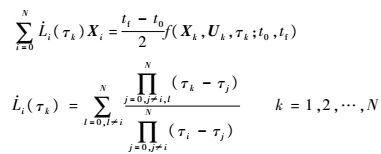
|
(23) |
终端状态约束:
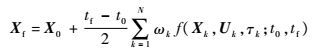
|
(24) |
式中:ωk为高斯积分权重系数。
过程约束和端点约束:
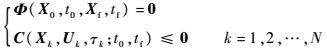
|
(25) |
目标函数:
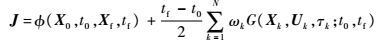
|
(26) |
经过上述转化后,将连续最优控制问题转化为NLP问题,然后可采用NLP方法进行求解。
为获取能量最优的倾斜转弯轨迹,建立能量最优的轨迹优化问题。
1) 性能指标选取
为了验证最优飞行策略的最优性,选择终端速度最大作为性能指标。
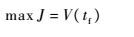
|
(27) |
2) 控制方程
满足非线性动力学方程式(1)。
3) 过程约束
满足热流峰值、动压及过载等过程约束方程式(3)、式(6)、式(9),满足控制量约束方程式(11)。
4) 终端约束
满足终端约束方程式(12)。
通过求解该最优控制问题,即可获得能量最优的轨迹。
5 仿真算例本文选择CAV-H作为研究对象,飞行器质量907 kg,飞行过程中最大热流峰值、最小动压及最大过载约束分别为3 000 kW/m2、10 kPa及3g。计算机环境为Windows XP 2.5 GHz,仿真软件基于VC++6.0。基于能量最优的倾斜转弯飞行策略及高斯伪谱法分别求解飞行轨迹,仿真计算初始条件如表 1所示,计算算例如表 2所示。
| 初始条件 | 高度/km | 速度/(m·s-1) | 弹道倾角/(°) | 经度/(°) | 纬度/(°) | 弹道偏角/(°) |
| 数值 | 50 | 6 000 | 0 | 0 | 0 | 0 |
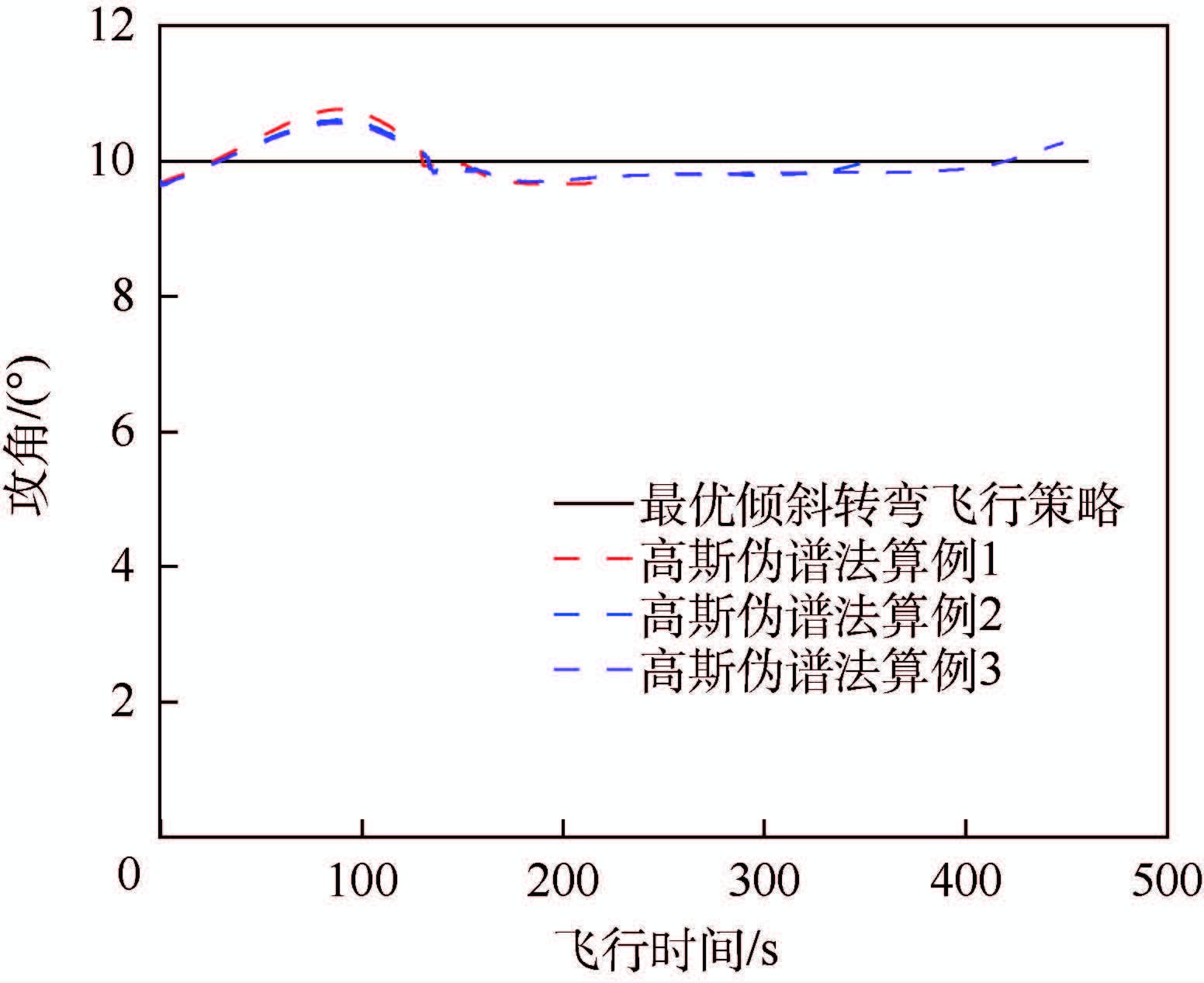
|
| 图 6 攻角随飞行时间变化 Fig. 6 Angle of attack changes with flight time |
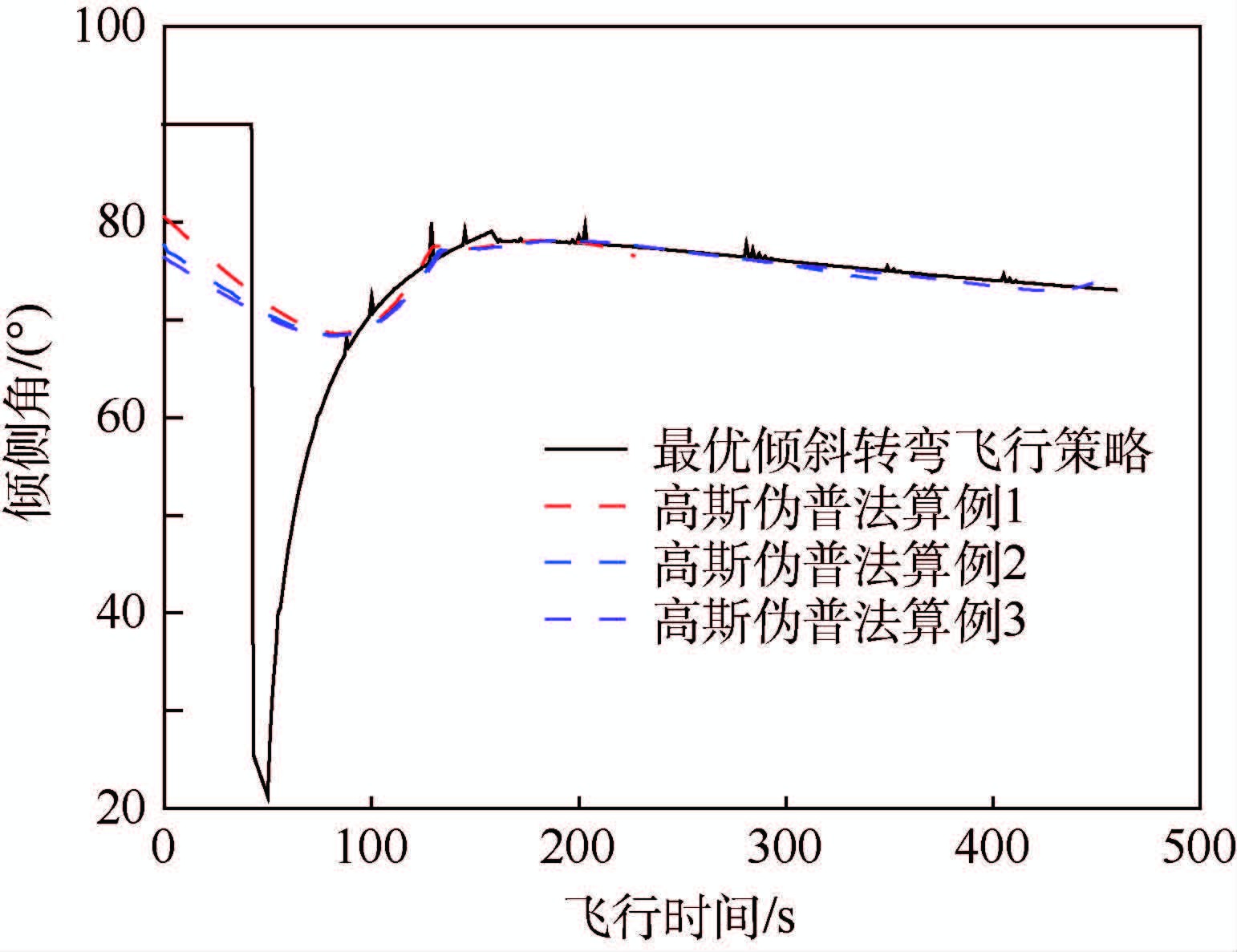
|
| 图 7 倾侧角随飞行时间变化 Fig. 7 Bank angle changes with flight time |
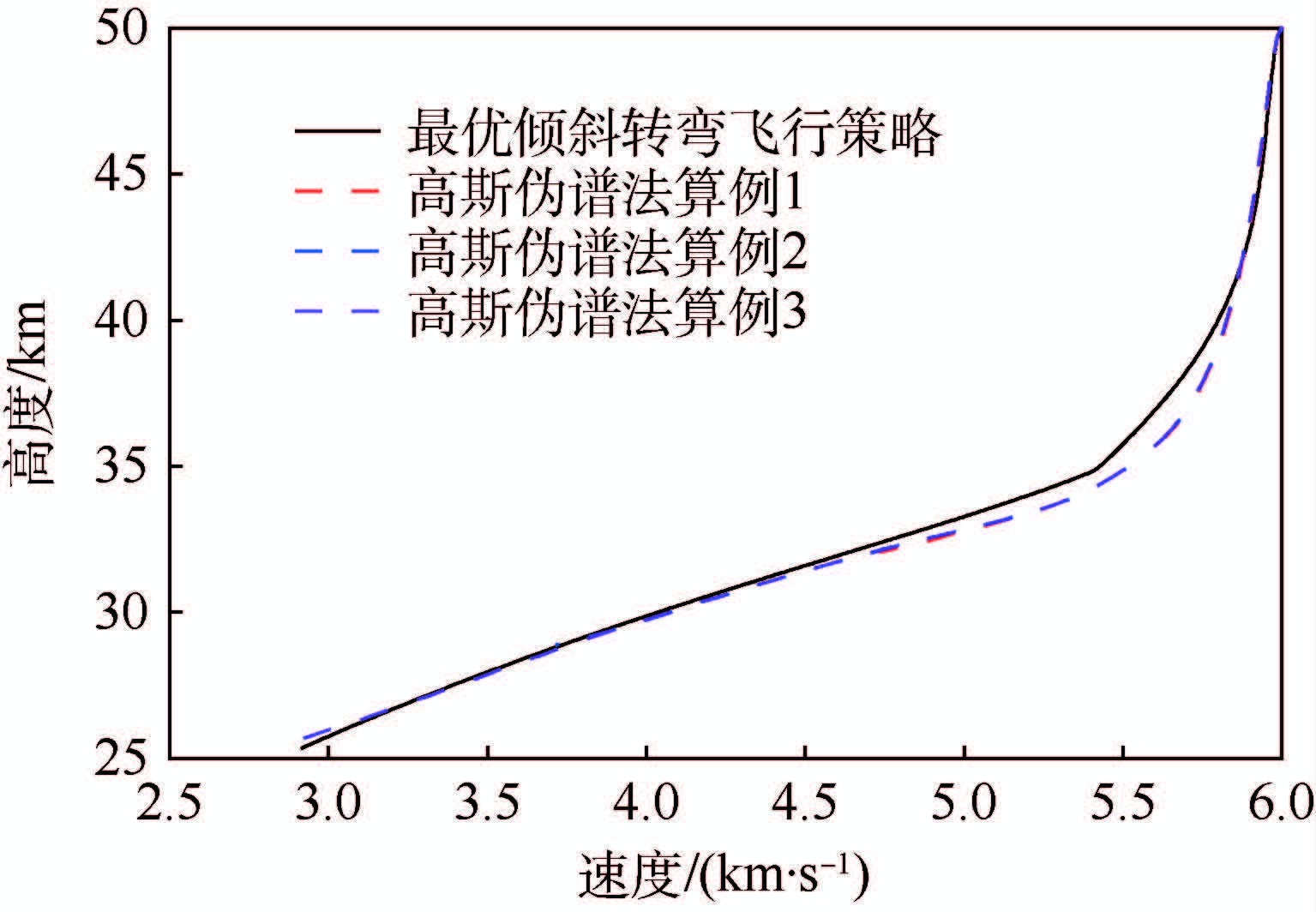
|
| 图 8 高度随速度变化关系 Fig. 8 Altitude changes with velocity |
|
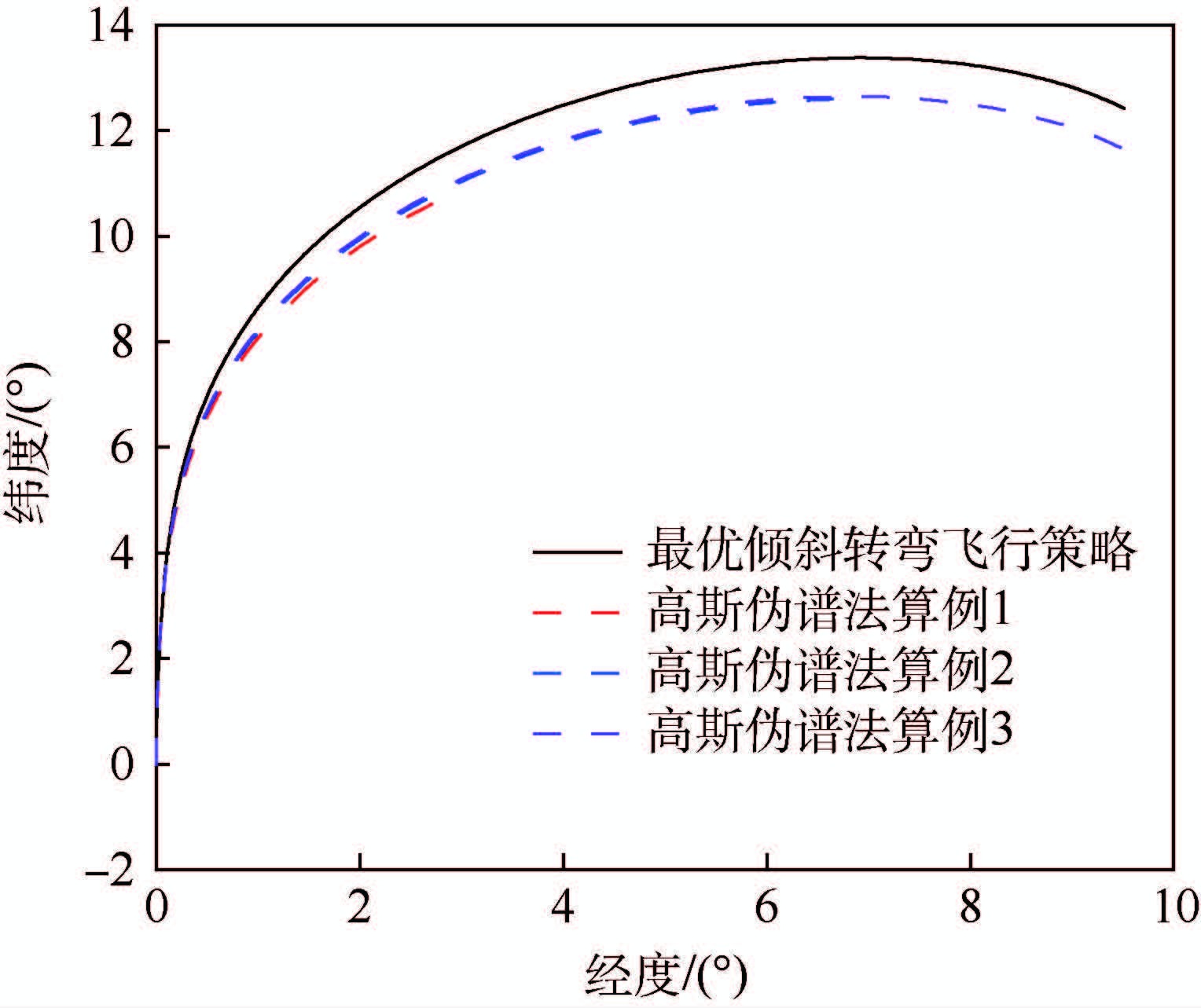
| 图 9 地面轨迹 Fig. 9 Ground track |
|
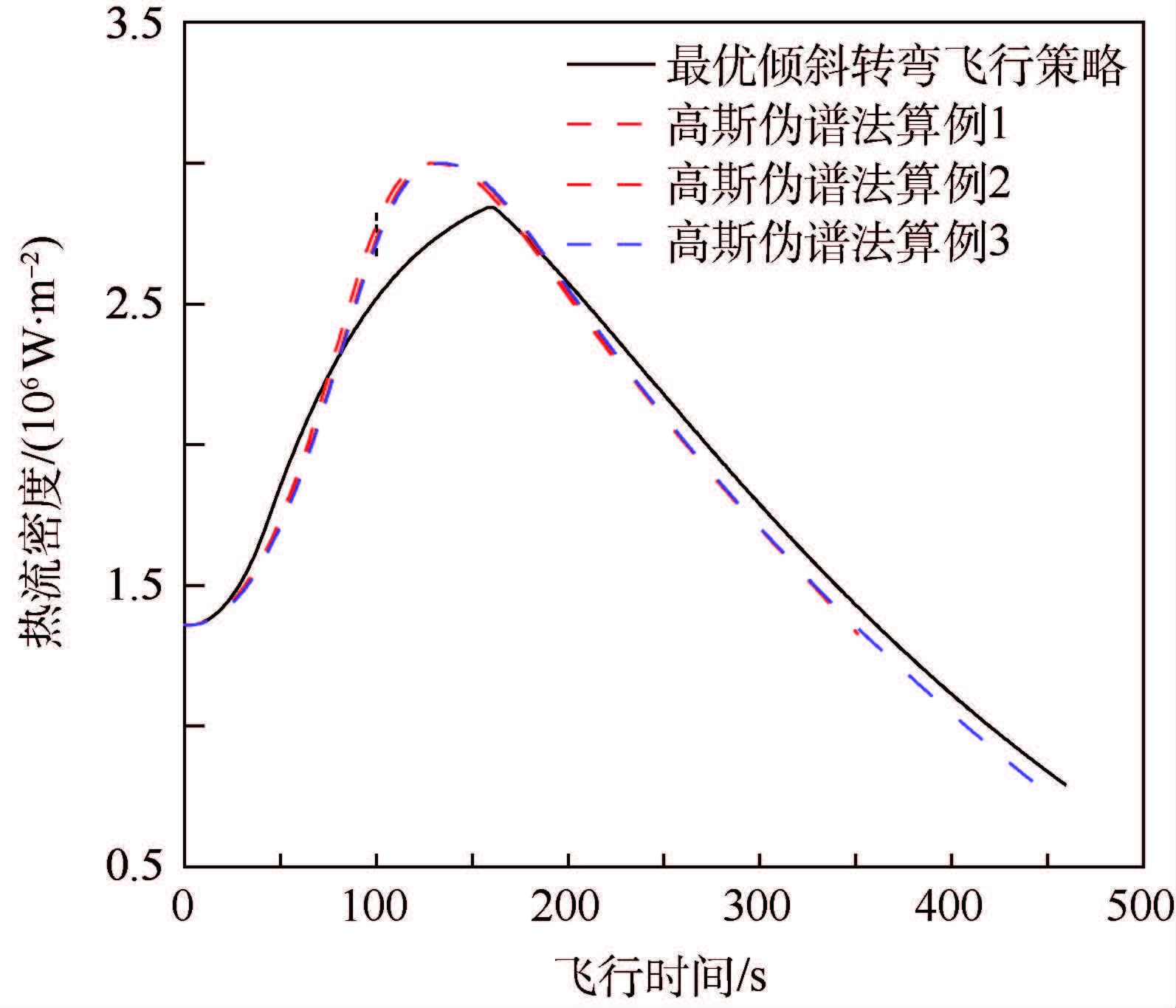
| 图 10 热流密度随飞行时间变化 Fig. 10 Heating rate changes with flight time |

|
| 图 11 法向过载随飞行时间变化 Fig. 11 Normal load factor changes with flight time |
针对3个典型算例进行了仿真,轨迹优化结果如表 3所示。由表 3可以看出,基于能量近似最优倾斜转弯飞行策略对应的终端速度与高斯伪谱法的优化结果相比,飞行热流密度、法向过载等均在过程约束范围内,终端速度偏差小于20 m/s,高度小于0.4 km。同时,基于高斯伪谱法直接寻优的攻角、倾侧角控制量与能量近似最优转弯策略对应的攻角、倾侧角飞行策略是一致的。
轨迹优化所需时间如表 4所示,可以看出,基于能量最优倾斜转弯飞行策略计算最优轨迹所需时间均小于1 s,高斯伪谱法优化轨迹所需时间均大于600 s。在优化结果性能一致的情况下,本文提出的能量最优倾斜转弯机动飞行策略具有更高的计算效率。
| 状态 | 终端弹道偏角/(°) | 终端速度Vf/(m·s-1) | 终端高度Hf/km | ||
| 近似最优倾斜转弯飞行策略 | 高斯伪谱法 | 近似最优转弯飞行策略 | 高斯伪谱法 | ||
| 算例1 | 45 | 4 702 | 4 720 | 32.3 | 32.1 |
| 算例2 | 90 | 3 712 | 3 726 | 28.8 | 28.9 |
| 算例3 | 135 | 2 917 | 2 926 | 25.3 | 25.7 |
| s | ||
| 状态 | 近似最优倾斜转弯飞行策略计算时间 | 高斯伪谱法计算时间 |
| 算例1 | <1 | 630 |
| 算例2 | <1 | 972 |
| 算例3 | <1 | 1 316 |
6 结 论
升力体外形飞行器大气层内能量最优的倾斜转弯轨迹优化问题是一个较为复杂的最优控制问题。本文基于飞行器倾斜转弯的基本原理和准平衡滑翔假设,从动力学模型出发,推导获得了倾斜转弯终端速度与升阻比、倾侧角及终端弹道偏角相关的解析解,提出了能量最优的倾斜转弯机动飞行策略,并与高斯伪谱法的优化轨迹进行了对比,结果表明最优轨迹高度一致,验证了该方法的最优性。并且,该方法的计算效率可大幅度提高,1 s之内可完成多约束条件下的最优倾侧转弯轨迹规划,具有较强的工程实际应用价值。
| [1] | 童雄辉. 美国未来全球快速精确打击体系预测分析[J]. 导弹与航天运载技术, 2008 (5) : 57 –61. TONG X H. Forecast and analysis of USA's future conventional prompt global strike system[J]. Missile and Space Vehicle, 2008 (5) : 57 –61. (in Chinese) |
| [2] | 康开华, 才满瑞, 伍赣湘, 等. 美国高超声速技术飞行器[J]. 航天制造技术, 2010 (5) : 7 –11. KANG K H, CAI M R, WU G X, et al. U.S.hypersonic technology vehicle[J]. Aerospace Manufacturing Technology, 2010 (5) : 7 –11. (in Chinese) |
| [3] | 李广华, 张洪波, 汤国建. 高超声速滑翔飞行器典型弹道特性分析[J]. 宇航学报, 2015, 36 (4) : 397 –403. LI G H, ZHANG H B, TANG G J. Typical trajectory characteristics of hypersonic glide vehicle[J]. Journal of Astronautics, 2015, 36 (4) : 397 –403. (in Chinese) |
| [4] | 陈小庆, 侯中喜, 刘建霞. 高超声速滑翔飞行器倾斜转弯分析及控制系统设计[J]. 国防科技大学学报, 2012, 34 (3) : 17 –23. CHEN X Q, HOU Z X, LIU J X. Analysis and controller design of bank-to-turn system for hypersonic gliding vehicle[J]. Journal of National University of Defense Technology, 2012, 34 (3) : 17 –23. (in Chinese) |
| [5] | 张忠峰, 高云峰, 宝音贺西. 高超声速飞行器机动航迹优化[J]. 弹箭与制导学报, 2009, 29 (3) : 164 –172. ZHANG Z F, GAO Y F, BAOYIN H X. Optimization of maneuvering flight path of hypersonic vehicle[J]. Journal of Projectiles,Rockets,Missiles and Guidance, 2009, 29 (3) : 164 –172. (in Chinese) |
| [6] | 黄育秋, 何麟书. 升力式再入飞行器多约束多阶段弹道优化设计[J]. 哈尔滨工业大学学报, 2011, 43 (7) : 144 –148. HUANG Y Q, HE L S. Multi-constraints and multi-phases trajectory optimization of lift reentry vehicle[J]. Journal of Harbin Institute of Technology, 2011, 43 (7) : 144 –148. (in Chinese) |
| [7] | 周文雅, 杨涤, 李顺利. 利用高斯伪谱法求解升力航天器最优再入轨迹[J]. 南京理工大学学报, 2010, 34 (1) : 85 –90. ZHOU W Y, YANG D, LI S L. Using Gauss pseudospectral method to solve optimal reentry trajectory for lifting vehicle[J]. Journal of Nanjing University of Science and Technology, 2010, 34 (1) : 85 –90. (in Chinese) |
| [8] | 周浩, 陈万春. 基于拟平衡滑翔的横程最大轨迹研[J]. 飞行力学, 2010, 28 (3) : 64 –68. ZHOU H, CHEN W C. Maximum cross range trajectory optimization based on quasi-equilibrium glide conditions[J]. Flight Dynamics, 2010, 28 (3) : 64 –68. (in Chinese) |
| [9] | 张红文, 张科南, 陈万春. 带静态参数的高超声速飞行器轨迹优化算法[J]. 北京航空航天大学学报, 2014, 40 (2) : 141 –147. ZHANG H W, ZHANG K N, CHEN W C. Indirect method for trajectory optimization of hypersonic vehicle with static parameters[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40 (2) : 141 –147. (in Chinese) |
| [10] | 李瑜, 杨志红, 崔乃刚. 助推-滑翔导弹最大射程优化[J]. 弹道学报, 2008, 20 (4) : 53 –56. LI Y, YANG Z H, CUI N G. Optimization of maximum range for boost-glide missile[J]. Journal of Ballistics, 2008, 20 (4) : 53 –56. (in Chinese) |
| [11] | ZHANG K N,CHEN W C.Reentry vehicle constrained trajectory optimization[C]//17th AIAA International Space Planes and Hypersonic Systems and Technologies Conference 2011.Reston:AIAA,2011. |
| [12] | ZHAO Z G.A rapid reentry trajectory planning method for CAV[C]//2010 3rd International Symposium on Systems and Control in Aeronautics and Astronautics.Piscataway NJ:IEEE Press,2010:1255-1260. |
| [13] | VINH N X. Flight mechanics of high-performance aircraft[M]. Cambridge: Cambridge University Press, 1993 : 374 . |
| [14] | TERRY H P.A common aero vehicle model,description,and employment guidance[R].Arlington:Schafer Corporation for AFRL and AFSPC,2003. |
| [15] | 汪朝群. 航天飞机的再入飞行走廊及再入飞行轨迹[J]. 航天控制, 1990 (1) : 1 –10. WANG C Q. On entry flight corridor and entry trajectory for space shuttle reentry[J]. Aerospace Control, 1990 (1) : 1 –10. (in Chinese) |



