近年来无人机被广泛运用于边界巡逻、目标跟踪及灾难救援等多个领域[1-2],而执行侦察任务也是无人机目前的一个主要应用领域[3]。
无人机执行任务时为有效监控并获得目标信息,应该使目标持续处于侦察传感器的监控范围内,并保持一段时间,即满足一定的持续侦察时间要求。文献[4]利用遗传算法(GA)实现无视线遮挡情况下的最短侦察路径规划;田菁和沈林成[5]针对时敏目标,以最小化未被侦察目标数目和侦察代价为性能目标,采用Pareto最优实现侦察序列优化;文献[6]中以单位时间内侦察目标数量作为侦察效能评估指标。上述文章虽充分考虑侦察任务中的各种侦察性能要求,但是却没有考虑侦察任务中对于指定侦察任务存在持续侦察时间的约束,也并未考虑侦察任务重叠的情况。虽然文献[7]中通过设定采样路标的方法来考虑侦察任务重叠的情况,但并未考虑同时完成多个侦察任务。
无人机执行侦察任务可以归结为旅行商问题,旅行商问题是一个著名的NP难问题,只能采用启发式算法近似求解,遗传算法[8]、蚁群算法[9]及粒子群[10]等算法都可求解旅行商问题。也有很多改进方法如将贪婪算法和遗传算法相结合,通过自适应调节遗传参数实现TSP问题求解[11];利用互信息对蚁群算法中的概率算子增加新的影响因子,实现旅行商问题求解[12]。而多机协同侦察可以归结为多旅行商问题,Yu等[13]采用两层混合算法求解多旅行商问题,利用k-means聚类和改进遗传算法将问题转化为单旅行商问题求解;而利用局部搜索[14]解决多基地多旅行商问题也获得了很好的效果。
本文假设各个侦察点的侦察进入方向由相邻侦察点确定,当侦察进入方向确定后,需要在相邻两个侦察点之间进行航路规划。Dubins[15]证明Dubins曲线是满足最大曲率约束和两点航向约束的最短可能路径,并且Dubins曲线在目标拦截路径规划[16]、最短时间集结[17]及障碍环境下的最短路径规划[18]等领域中都取得了很好的效果。
本文针对存在至多3个重叠侦察任务的情况,通过几何分析,明确提出了多侦察点同时侦察方法;基于相邻2个侦察点的位置信息确定当前侦察点的侦察进入方向,并利用Dubins曲线完成相邻两个侦察点之间的航路规划。本文将精英机制引入到文献[19]提出的混合粒子群优化(Hybird Particle Swarm Optimization, HPSO)算法,形成具有精英机制的混合粒子群优化(Elite HPSO, EHPSO)算法。利用随机搜索方法初始化粒子群,以最小化侦察路径长度为目标,获取最优侦察任务序列,实现具有持续侦察时间约束的协同航路规划。
1 侦察任务描述 1.1 无人机侦察传感器模型侦察传感器通常安置在机载万向节上。如图 1所示,万向节系统是一个可三自由度转动的系统,最常采用的是十字轴式,它由两个相交为十字的轴连接而成。设传感器系统万向节两转动轴之间的最大夹角为θ,不考虑无人机姿态角的变化,传感器在距离地面高度h处的探测范围就是以传感器在地平面的投影为圆心、h·tanθ为半径的圆。图中阴影部分为机载传感器可探测区域称为侦察圆,Reff=h·tanθ称为有效侦察半径。
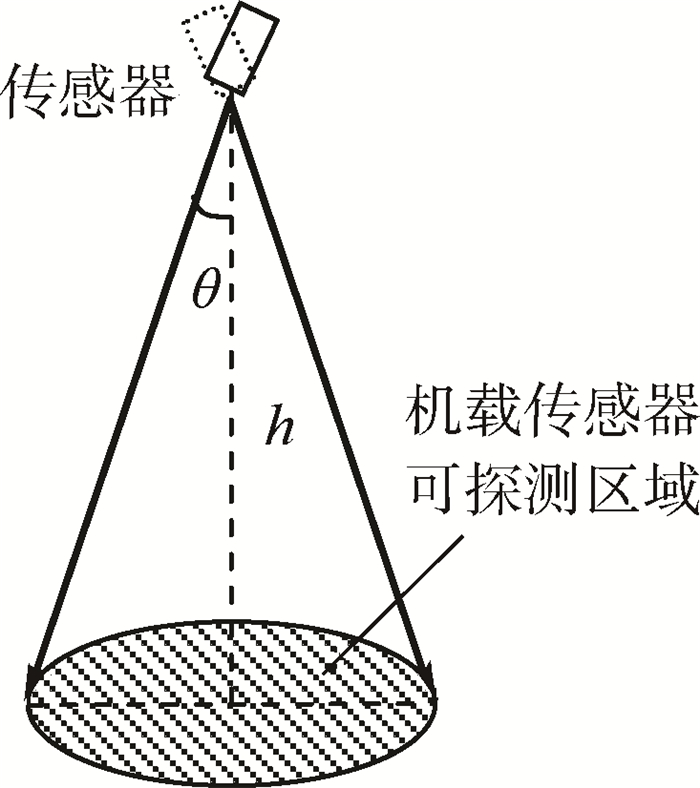
|
| 图 1 机载传感器侦察模型 Fig. 1 Airborne sensor reconnaissance model |
本文假设无人机定高常速飞行,在探测过程中为保证探测传感器稳定,要求执行侦察任务过程中无人机保持定直平飞。由于不同侦察点的属性和价值不同,因而需要的持续侦察时间也不同,需满足如下持续侦察时间约束:
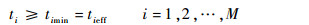
|
(1) |
式中:ti、timin和tieff分别为第i个侦察点的持续侦察时间、所需要的最短持续侦察时间和有效持续侦察时间;M为待侦察的侦察点数目。
由于假设无人机以常速v0定速飞行,式(1)可以转换为如下距离公式:
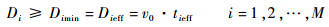
|
(2) |
式中:Di、Dimin和Dieff分别为第i个侦察点有效侦察距离、所需要的最小有效侦察距离和有效侦察距离。如图 2所示O为待侦察点位置,Reff为有效侦察半径,沿图上路径Deff的侦察进入方向,即可满足最短持续侦察时间tmin要求,且R′为此侦察过程中距离目标的最近距离。由于同一侦察点有效侦察距离Deff不唯一,需做如下假设:

|
| 图 2 有效侦察距离 Fig. 2 Effective reconnaissance distance |
1)任一侦察点最短持续侦察时间满足约束:tmin≤2Reff/v0
2)有效侦察路径Deff的进入方向由相邻两个侦察点相对位置确定。对第i个侦察点进行侦察,Deff进入方向由第i-1和第i+1个侦察点确定,侦察进入方向与第i-1指向第i+1个侦察点的方向一致,且Deff位于靠近相邻侦察点的一侧。
1.3 侦察任务重叠情况下的同时侦察方案如图 3所示,任务点1、2的有效持续侦察时间要求分别为t1eff、t2eff,对应的有效侦察距离为D1eff、D2eff。由于存在侦察任务重叠,可寻找满足式(3)的有效侦察距离Deff实现对两个侦察点同时侦察。无人机沿着Deff进行侦察时,可以在D′1eff完成对O1的侦察,在D′2eff完成对O2的侦察,同时侦察可以有效缩短持续侦察任务时间。
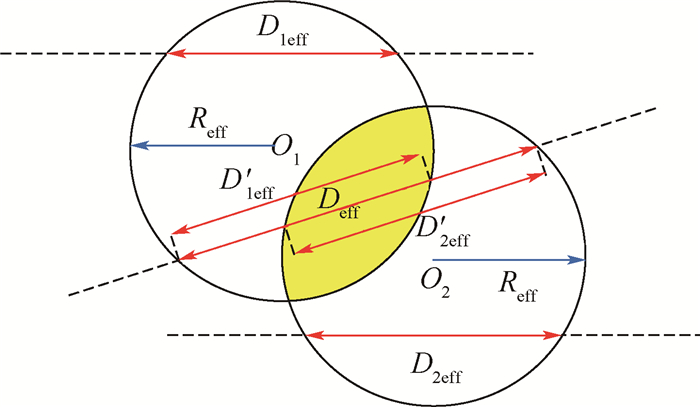
|
| 图 3 2个侦察任务重叠示意图 Fig. 3 Two overlapping reconnaissance missions's schematic diagram |

|
(3) |
由于任意M个侦察点随机分布可能存在侦察任务重叠的情况,需进行聚类分析。以各个侦察点的欧式距离为聚类原则,假设任意M个侦察点会分成M′个类,分类结果应满足如下约束:
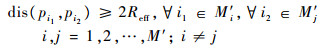
|
(4) |
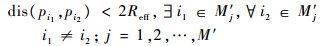
|
(5) |
式(4)表明任意两个不同类的侦察点之间的距离必定大于2倍有效侦察半径;式(5)表明相同类中的任一侦察点肯定存在至少一个侦察点与它的距离小于2倍有效侦察半径。
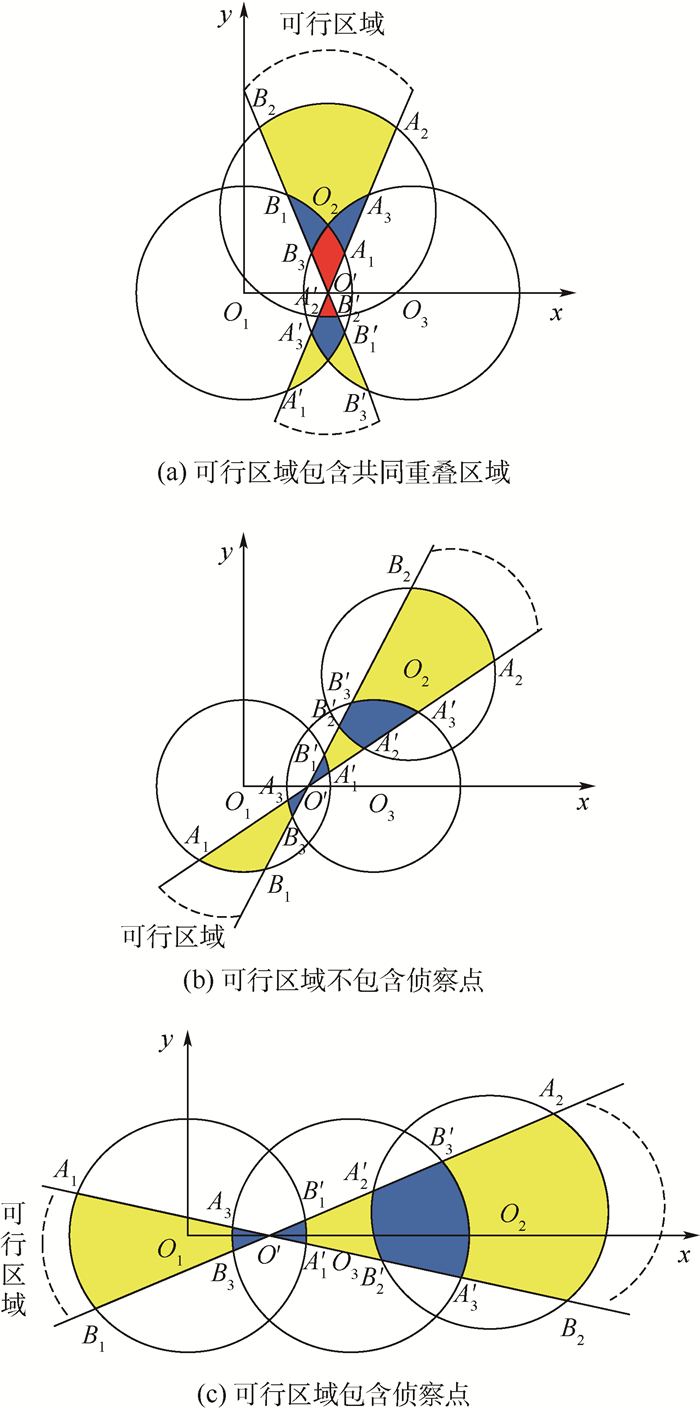
为确保能够同时对多个重叠侦察点进行侦察,需同时满足各自的持续侦察时间约束。如图 4所示,本文针对最多3个重叠侦察任务(当超过3个侦察点时会出现链式结构,而定直平飞无法穿过所有侦察圆,此时的解决方法是选择尽可能多的重叠侦察任务进行侦察),采用几何分析,提出多侦察任务重叠时同时侦察路径选择方案如下:
|
| 图 4 3个侦察任务重叠示意图 Fig. 4 Three overlapping reconnaissance missions's schematic diagram |
记侦察圆圆心O1、O3连线的中点为O′。3个侦察圆存在共同重叠区域的情况经坐标旋转如图 4(a)所示,设侦察点O2具有3个侦察点中最大持续侦察时间t2min;如图 4(b)和图 4(c)所示,针对3个侦察圆不存在共同重叠区域的情况,设侦察点O2的持续侦察时间t2min大于侦察点O1的持续侦察时间t1min,侦察点O3的持续侦察时间为t3min。过O′分别做满足与O2侦察圆的相交弦长等于有效侦察距离D2eff=v0·t2min的两条直线,与O2分别交于点A2、A′2、B2、B′2,直线O′A2、O′B2分别与圆O1、O3交于点A1、A′1、B1、B′1、A3、A′3、B3、B′3。图中带颜色区域为同时完成侦察任务的可能区域,红色区域为3个侦察圆的共同重叠区域,蓝色区域为两个侦察圆的共同重叠区域,黄色区域代表单个侦察圆存在的可行区域。由于要求无人机在执行侦察任务时定直平飞,可以得到如下结论:
结论1 如图 4(a)三侦察点存在共同可行侦察区域,若满足max(D1eff, D3eff)≤max(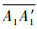
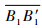
结论2 如图 4(b)所示,若3个侦察任务不存在共同可行侦察区域,且可行区域不含侦察点O1和O3,若满足max(D1eff, D3eff)≤max(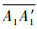
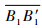
结论3 如图 4(c)所示,侦察可行区域包含侦察点O1和O3,则一定存在满足同时侦察的可行路径。
结论1和2证明:O′为圆O1、O3对应的圆心连线的中点,有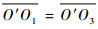
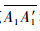
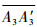
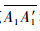
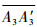
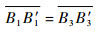
如图 4(a)和图 4(b)所示,在满足O2持续侦察时间后,可行区域不含有过侦察点O1、O3的直线。由图上绕O′将弦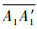
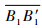
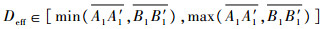
|
所以当max(D1eff, D3eff)≤max(A1A′1, B1B′1)时,就一定存在满足同时侦察的可行路径。 证毕
结论3证明:基于结论1和2的证明,且可行区域包含侦察点O1、O3。当侦察路径穿过侦察点O1、O3,其有效持续侦察距离为2Reff,可知O1、O3可行侦察区域内的有效持续侦察距离如下:
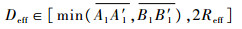
|
故一定存在满足同时侦察的可行路径。而存在共同重叠区域的3个侦察圆当可行区域包含侦察点的情况是结论3的特例,由于篇幅不再证明。
若基于上述方法无法找到满足要求的同时侦察路径,则选取其中两个侦察点进行同时侦察,并对剩余侦察点进行单独侦察。
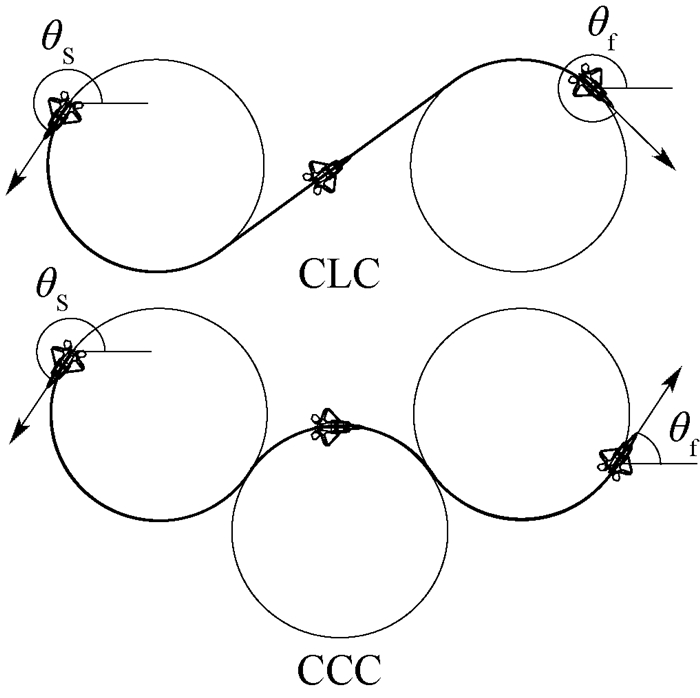
1.4 相邻侦察任务点间的航路规划由于侦察进入点位置和方向依据侦察任务序列确定,对应侦察离开方向也唯一确定。所以相邻侦察点之间的航路规划是一个具有起始角度θs和终端角度θf约束的路径规划问题。如图 5所示,文献[15]已证明Dubins曲线是满足最大曲率约束和航向约束的两点之间最短路径。Dubins曲线由直线段和弧线段构成,最短Dubins曲线必然是曲线集{LSL, RSR, RSL, LSR, RLR, LRL}中的一种(其中:L表示左圆弧;R表示右圆弧;S表示直线段),并能够准确获得Dubins曲线形式和长度。因此本文采用Dubins曲线实现相邻侦察点之间的航路规划。
|
| 图 5 Dubins路径模型 Fig. 5 Dubins path model |
设共有M个侦察点,N架无人机。每个侦察点满足持续侦察时间约束:
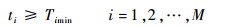
|
由于侦察进入点的确定,并尽可能缩短持续侦察时间,将上述约束改为
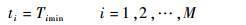
|
(6) |
设每架飞机的初始位置分别为(xi0, yi0),i=1, 2,…, N。
本文对应含有持续侦察时间约束的协同航路规划问题构建模型如下:
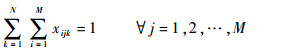
|
(7) |
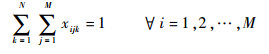
|
(8) |
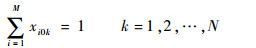
|
(9) |
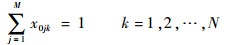
|
(10) |
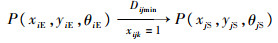
|
(11) |
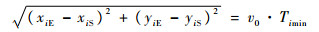
|
(12) |
设xijk∈{0, 1}为决策变量,当xijk=1表明第k架无人机执行从第i个侦察点到第j个侦察点的侦察任务,设xk={xijk}(M+1)×(M+1)为第k架无人机的决策变量矩阵,Ω为当前无人机所有可能决策变量矩阵集合,代表所有可能的侦察任务序列。对应第k架无人机的侦察航路长度为
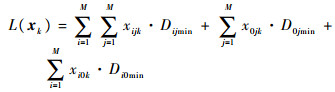
|
(13) |
无人机在执行任务过程中,考虑最大飞行距离约束如下:
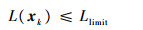
|
(14) |
式(7)和式(8)表示每个侦察点仅能被一架无人机侦察一次;式(9)和式(10)表示每架无人机初始和结束都要返回各自初始位置;式(11)表示第k架无人机从第i个侦察结束位置(xiE, yiE, θiE)到第j个侦察初始位置(xjS, yjS, θjS)采用Dubins曲线获得长度为Dijmin的最短侦察路径;式(12)表示对应第i个侦察点侦察过程中满足相应持续侦察时间约束;式(13)计算第k
参考文献[20]以最小化侦察路径长度为设计目标,考虑典型的3种协同航路规划性能指标:
1) MinSum以最小化所有无人机侦察路径长度之和为目标,其性能指标如式(15)所示:
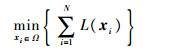
|
(15) |
2) MinMax以最小化所有无人机侦察路径长度中的最大值为目标,其性能指标如式(16)所示:
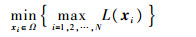
|
(16) |
3) MinAvg以最小化所有无人机侦察路径长度差值为目标,其性能指标如式(17)所示:
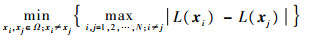
|
(17) |
参考文献[19]中所提出的混合粒子群优化算法,采用随机搜索的方法初始化粒子群,并引入精英机制对算法进行改进。实现对具有持续侦察时间约束的多无人机协同航路规划问题求解。
3.1 编码设共有M个侦察点,按照顺序对M个侦察点进行编号,对应为1, 2,…, M。设共有N架无人机,对应序号依次为1, 2,…, N,修改无人机的编码对应为M+1, M+2,…, M+N。采用单一编码对粒子进行编码。假设共有8个侦察点,2架无人机,则随机生成一个粒子的编码如下:

|
通常进化算法都是通过随机生成形成初始种群,初始种群的适应度可能会较差,而这也会对收敛速度造成一定的影响。本文为提高初始粒子适应值,采用随机搜索的方法,初始化粒子群。
首先为各架无人机随机选择一组不重复的侦察点,形成当前侦察点集{P1, P2, …, PN},然后在剩余的侦察点中选择各自距当前侦察点距离最近的点,形成最近侦察点集合{P′1, P′2, …, P′N},从最近点集合中选取使距离值增加最少的侦察点对应添加到相应无人机侦察序列中,并对应修正当前侦察点集,直到所有的侦察点都添加到侦察序列中,即利用随机搜索方法生成一个初始化粒子。
3.3 交叉传统粒子群算法依据个体和群体极值对粒子进行更新,在求解旅行商问题时通过对速度算式重建,通过交换子和交换序实现粒子更新。混合粒子群主要引入遗传算法中的交叉思想,通过当前粒子与个体极值和群体极值分别进行交叉,替代交换子和交换序。选择侦察航路长度的倒数作为粒子适应值,当交叉后的粒子适应值有所改善时,替换原有粒子。具体交叉方法如下。
当前个体粒子信息为:

|
当前个体最优粒子信息为:

|
随机生成交叉位为:4和7,对应取出个体最优粒子的待交叉片段如下:

|
相应替换当前粒子对应片段,生成新粒子:

|
考虑待交叉片段中可能包含重复侦察点,需用未包含侦察点对应替换,修正交叉后粒子如下:

|
当交叉后粒子的适应值优于原粒子的适应值时,对应替换原粒子,实现粒子更新。
3.4 变异随机生成两个自然数,作为变异位置点,若变异位置点分别为4和7,具体的变异操作如下。
当前个体粒子信息为:

|
变异后的粒子信息为:

|
当变异后的粒子适应值优于原粒子时对应替换原粒子,实现粒子更新。
3.5 精英机制在很多优化算法中,都会保留精英个体以替代交叉变异后群体中适应值最差的个体,以确保适应值高的精英个体可以得到保留和延续。
当求解空间很复杂并存在多个局部最优解时,基本的粒子群算法很容易收敛到局部最优而无法找到全局最优。基于精英机制[21]的启发,可能部分适应值排在前列的粒子比单一最优粒子具有更好的学习优势,可以提高粒子多样性。引入精英机制是为每一个粒子创建一个个体最优团体,为群体最优粒子创建一个群体最优团体。在每一次迭代循环过程中,精英机制主要体现在交叉过程中。当前粒子分别与个体最优团体中的粒子分别进行交叉,再与群体最优团体中的粒子分别进行交叉,当适应值有所改善时,替换原有粒子,实现粒子更新。引入精英机制可以有效增加粒子多样性,避免过早收敛到局部最优。
3.6 算法结构如图 6所示,具有精英机制的混合粒子群算法的基本流程如下:

|
| 图 6 引入精英机制的混合粒子群优化算法流程 Fig. 6 EHPSO algorithm flow |
采用随机搜索方法,添加最近侦察点形成初始侦察序列,实现粒子群信息初始化。
在每个迭代周期,将当前粒子分别与个体和群体最优团体中的粒子进行交叉,并进行个体变异,当适应值有所改善时完成粒子更新。
当满足迭代周期时,获得最优侦察序列信息,实现具有持续侦察时间约束的协同航路规划。
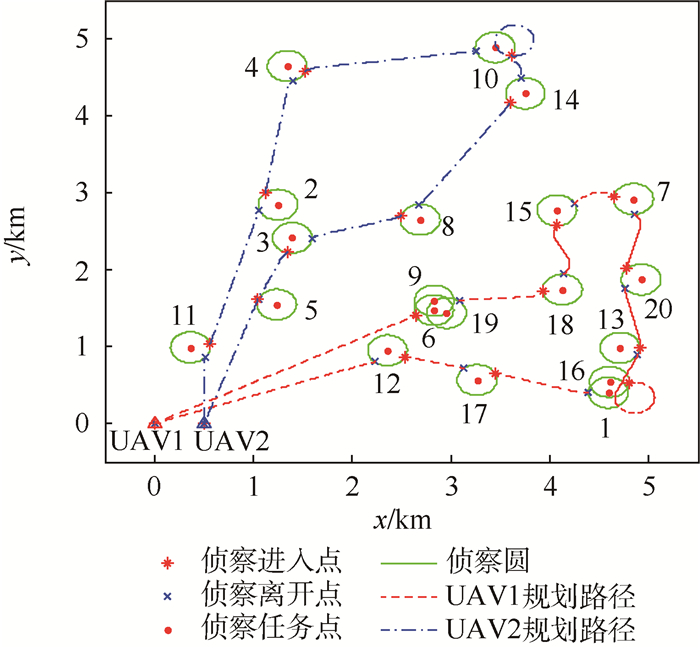
4 仿真对比仿真实验中,设定一个5 000 m×5 000 m的侦察区域,随机生成具有侦察任务重叠的20个侦察点位置和对应持续侦察时间,分别考虑MinSum、MinMax和MinAvg 3种性能指标,利用两架初始位置分别为(0 m, 0 m), (500 m, 0 m)的无人机对全部侦察点进行侦察,利用引入精英机制的混合粒子群算法对具有持续侦察时间约束的协同航路规划问题求解。以MinMax作为性能指标,并与混合粒子群算法和遗传算法进行对比,具体仿真结果如图 7~图 10所示,具体仿真参数如表 1所示。
|
| 图 7 3个重叠侦察任务航路规划 Fig. 7 Three overlapping reconnaissance missions' path planning |
|
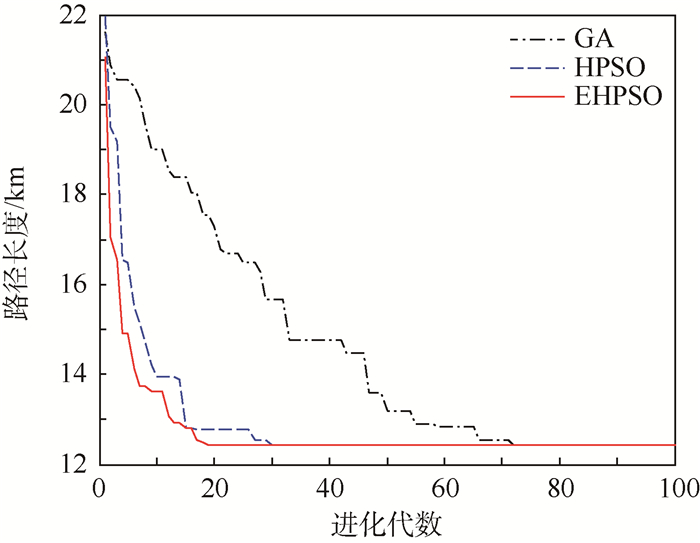
| 图 8 3个重叠侦察任务收敛曲线对比 Fig. 8 Three overlapping reconnaissance missions' convergence curves comparison |

|
| 图 9 2个重叠侦察任务航路规划 Fig. 9 Two overlapping reconnaissance missions' path planning |
|
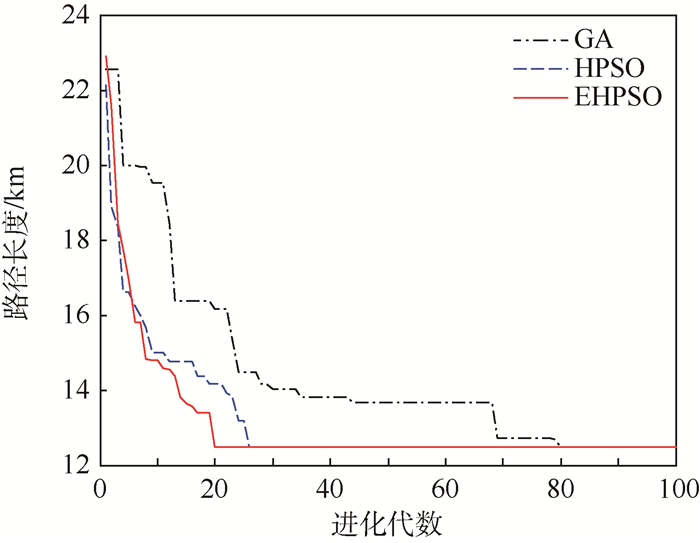
| 图 10 2个重叠侦察任务收敛曲线对比 Fig. 10 Two overlapping reconnaissance missions' convergence curves comparison |
| 参数 | 数值 |
| 无人机数量 | 2 |
| 无人机有效侦察半径Reff/m | 200 |
| 无人机最小转弯半径Rmin/m | 200 |
| 巡航速度v0/(m·s-1) | 20 |
| 最大侦察路径长度Llimit/km | 15 |
| 迭代步数 | 50 |
| 种群数量NP | 1 000 |
| 个体最优团体粒子数NEp | 3 |
| 群体最优团体粒子数NEg | 2 |
| 遗传算法变异概率Pv | 0.05 |
| 遗传算法交叉概率Pm | 0.9 |
具有精英机制的混合粒子群算法的其余参数设置与混合粒子群一致,参见文献[19]。
4.1 MinMax性能指标下的协同航路规划结果由图 7~图 10可以看出,无人机在侦察过程中,由侦察进入点进入,保持定直平飞实现目标持续侦察。当存在3个或2个侦察任务重叠时,利用本文提出算法能够实现对重叠侦察任务同时侦察。图 7中侦察点6、9、19 3个侦察任务重叠,侦察点19具有最大持续侦察时间为15.897 3 s,对应持续侦察距离为317.946 m。而在可行侦察区域选择侦察进入方向时,考虑相邻侦察点位置信息,最终确定的有效持续侦察距离为346.782 5 m,其他2个侦察任务也都满足结论1的条件,可以同时完成3个重叠侦察任务。相比分别对每个侦察点进行侦察,同时侦察能有效缩短侦察时间。
当相邻侦察点距离很近时为确保获得侦察进入方向,Dubins曲线会存在一段圆弧确保进入航向,如图 7的侦察点10所示。对应调整无人机最小转弯半径,则对应规划路径也会相应发生变化。
图 8和图 10为分别采用EHPSO、HPSO和GA求解问题时对应的收敛曲线。可以看出, 利用随机搜索生成初始化粒子群,采用精英机制对交叉操作进行改进,EHPSO算法的收敛性和粒子的多样性较比HPSO和GA都有一定的改善,证明EHPSO对本文问题求解的有效性。
4.2 3种性能指标仿真对比为验证本文算法的有效性,针对MinMax、MinSum和MinAvg 3种不同的典型协同航路规划性能指标进行仿真对比,具体的结果如表 2所示。
| 情景 | 性能指标 | 附加约束 | 侦察路径长度/km | |
| UAV1 | UAV2 | |||
| 2个侦察任务重叠 | MinMax | 1,2 | 12.397 | 12.497 |
| 2 | 14.686 | 14.921 | ||
| MinSum | 1 | 0 | 18.681 | |
| 1,2 | 13.674 | 95.206 | ||
| MinAvg | 1 | 30.459 | 30.459 | |
| 1,2 | 14.953 | 14.950 | ||
| 3个侦察任务重叠 | MinMax | 1,2 | 12.108 | 12.419 |
| 2 | 13.584 | 13.597 | ||
| MinSum | 1 | 0 | 20.249 | |
| 1,2 | 12.763 | 11.039 | ||
| MinAvg | 1 | 29.405 | 29.405 | |
| 1,2 | 14.848 | 14.848 | ||
| 注:附加约束1是指考虑侦察任务重叠同时侦察;附加约束2是指考虑无人机侦察最大飞行距离。 | ||||
由表 2可以看出,采用同时侦察方案较比依次对重叠侦察任务进行分别侦察可有效缩短侦察路径,证明本文提出的同时侦察方案的有效性。针对MinSum性能指标,不考虑侦察最大飞行距离时均为一架无人机完成所有侦察任务,造成侦察任务分配不均衡;此时考虑侦察最大飞行距离,则对应两架飞机侦察任务分配较为均衡,以加和最短完成侦察任务;针对MinAvg性能指标,若不考虑最大飞行距离,其结果严重依赖初始粒子,随机性很大; 考虑最大飞行距离约束,则两架飞机在满足最大飞行距离约束前提下, 侦察规划路径长度尽可能接近。针对不同性能指标和附加约束,利用本文提出的EHPSO可获得各种性能指标下满意的规划结果,也验证本文提出算法的有效性。
采用EHPSO求解本文问题,可能会获得近似最优解,为验证本文提出EHPSO算法的有效性,以MinMax作为性能指标对以上两组案例分别做10组重复试验,具体结果如表 3和表 4所示。
| 算法 | 最短 距离/km |
最长 距离/km |
平均 距离/km |
平均收敛 步数 |
| GA | 12.473 | 13.460 | 12.882 | 79.3 |
| HPSO | 12.473 | 13.409 | 12.792 | 27.6 |
| EHPSO | 12.473 | 12.970 | 12.644 | 25.5 |
| 算法 | 最短 距离/km |
最长 距离/km |
平均 距离/km |
平均收敛 步数 |
| GA | 12.419 | 13.733 | 12.669 | 77.3 |
| HPSO | 12.419 | 13.223 | 12.657 | 24.6 |
| EHPSO | 12.419 | 12.830 | 12.495 | 21.2 |
由统计结果可以看出:采用随机搜索初始化粒子群,可以有效提高初始粒子适应值,加快收敛速度;利用精英最优团体取代单个个体和群体最优,与个体粒子分别进行交叉操作,可有效提高粒子多样性,提高算法收敛速度和寻优能力。
5 结论主要针对具有持续侦察时间约束的多机协同路径规划问题进行研究。结论如下:
1) 提出3个以下重叠侦察任务的同时侦察方案,能有效缩短侦察路径长度。基于Dubins曲线和侦察点有效侦察路径,完成具有持续侦察时间约束的协同航路规划。
2) 采用具有精英机制的改进混合粒子群算法实现侦察序列优化,通过随机搜索初始化粒子群,采用精英机制改进粒子交叉操作,可有效增加粒子多样性,提高算法的收敛速度和寻优能力。
考虑侦察过程中的地形遮挡、三维地形侦察也是作者未来的研究方向。
| [1] | YANG K, KANG Y, SUKKARIEH S. Adaptive nonlinear model predictive path-following control for a fixed-wing unmanned aerial vehicle[J]. International Journal of Control Automation & Systems, 2013, 11 (1) : 65 –74. |
| [2] | CETIN O, ZAGLI I. Continuous airborne communication relay approach using unmanned aerial vehicles[J]. Journal of Intelligent & Robotic Systems, 2012, 65 (1-4) : 549 –562. |
| [3] | GENG L, ZHANG Y F, WANG P F, et al.UAV surveillance mission planning with gimbaled sensors[C]// Control & Automation (ICCA).Piscataway, NJ:IEEE Press, 2014:320-325. |
| [4] | OBERMEYER K J.Path planning for a UAV performing reconnaissance of static ground targets in terrain[C]//AIAA Guidance, Navigation, and Control Conference and Exhibit.Reston:AIAA, 2009. |
| [5] | 田菁, 沈林成. 多基地多无人机协同侦察问题研究[J]. 航空学报, 2007, 28 (4) : 913 –921. TIAN J, SHEN L C. Research on multi-base multi-UAV cooperative reconnaissance problem[J]. Acta Aeronautica et Astronautica Sinica, 2007, 28 (4) : 913 –921. (in Chinese) |
| [6] | 李响, 邢清华, 董涛. 无人机编队协同侦察效能研究[J]. 火力与指挥控制, 2013, 38 (10) : 103 –110. LI X, XING Q H, DONG T. Research on cooperative reconnaissance effectiveness of UAV formation[J]. Fire Control & Command Control, 2013, 38 (10) : 103 –110. (in Chinese) |
| [7] | OBERMEYER K J, OBERLIN P, DARBHA S. Sampling-based path planning for a visual reconnaissance unmanned air vehicle[J]. Journal of Guidance, Control, and Dynamics, 2012, 35 (2) : 619 –631. DOI:10.2514/1.48949 |
| [8] | 王剑文, 戴光明, 谢柏桥, 等. 求解TSP问题算法综述[J]. 计算机工程与科学, 2008, 30 (2) : 72 –74. WANG J W, DAI G M, XIE B Q, et al. A survey of solving the traveling salesman problem[J]. Computer Engineering & Science, 2008, 30 (2) : 72 –74. (in Chinese) |
| [9] | 宗德才, 王康康, 丁勇. 蚁群算法求解旅行商问题综述[J]. 计算机与数字工程, 2014, 42 (11) : 2004 –2013. ZONG D C, WANG K K, DING Y. Review of ant colony algorithm for solving traveling salesman problem[J]. Computer & Digital Engineering, 2014, 42 (11) : 2004 –2013. (in Chinese) |
| [10] | 黄岚, 王康平, 周春光, 等. 粒子群优化算法求解旅行商问题[J]. 吉林大学学报(理学版), 2003, 41 (4) : 477 –480. HUANG L, WANG K P, ZHOU C G, et al. Particle swarm optimization for traveling salesman problems[J]. Journal of Jilin University(Science Edition), 2003, 41 (4) : 477 –480. (in Chinese) |
| [11] | 于莹莹, 陈燕, 李桃迎. 改进的遗传算法求解旅行商问题[J]. 控制与决策, 2014, 29 (8) : 1483 –1488. YU Y Y, CHEN Y, LI T Y. Improved genetic algorithm for solving TSP[J]. Control and Decision, 2014, 29 (8) : 1483 –1488. (in Chinese) |
| [12] | 杜占玮, 杨永健, 孙永雄, 等. 基于互信息的混合蚁群算法及其在旅行商问题上的应用[J]. 东南大学学报(自然科学版), 2011, 41 (3) : 478 –481. DU Z W, YANG Y J, SUN Y X, et al. Hybrid ant colony algorithm based on mutual information and its application to traveling salesman problem[J]. Journal of Southeast University(Natural Science Edition), 2011, 41 (3) : 478 –481. (in Chinese) |
| [13] | YU Q S, WANG D, LIN D M, et al.A novel two-level hybrid algorithm for multiple traveling salesman problems[C]// 3rd International Conference on Swarm Intelligence, ICSI 2012.Heidelberg: Springer Verlag, 2012:497-503.. |
| [14] | LEVIN A, YOVEl U. Local search algorithms for multiple-depot vehicle routing and for multiple traveling salesman problems with proved performance guarantees[J]. Journal of Combinatorial Optimization, 2014, 28 (4) : 726 –747. DOI:10.1007/s10878-012-9580-x |
| [15] | DUBINS L E. On curves of minimal length with a constraint on average curvature, and with prescribed initial and terminal positions and tangents[J]. American Journal of Mathematics, 1957, 79 (3) : 497 –516. DOI:10.2307/2372560 |
| [16] | MEYER Y, ISAIAH P, SHIMA T. On Dubins paths to intercept a moving target[J]. Automatica, 2015, 53 : 256 –263. DOI:10.1016/j.automatica.2014.12.039 |
| [17] | BHATIA A, FRAZZOLI E.Decentralized algorithm for minimum-time rendezvous of Dubins vehicles[C]//American Control Conference.Piscataway:IEEE Press, 2008:1343-1349. |
| [18] | WANG Z, LI Y.A target visiting path planning algorithm for the fixed-wing UAV in obstacle environment[C]//6th IEEE Chinese Guidance, Navigation and Control Conference, CGNCC 2014.Piscataway:IEEE Press, 2014:2774-2778. |
| [19] | 史峰. MATLAB智能算法30个案例分析[M]. 北京: 北京航空航天大学出版社, 2011 : 144 -149. SHI F. Analysis of intelligent algorithm in 30 MATLAB cases[M]. Beijing: Beihang University Press, 2011 : 144 -149. (in Chinese) |
| [20] | SEGUI-GASCO P, SHIN H S, TSOURDOS A, et al.A combinatorial auction framework for decentralised task allocation[C]// 2014 IEEE Globecom Workshops, GC Wkshps 2014.Piscataway, NJ:IEEE Press, 2014:1445-1450. |
| [21] | CHEN P H. Two-level hierarchical approach to unit commitment using expert system and elite PSO[J]. IEEE Transactions on Power Systems, 2012, 27 (2) : 780 –789. DOI:10.1109/TPWRS.2011.2171197 |



