2. 空军预警学院 雷达技术系, 武汉 430019;
3. 火箭军指挥学院 指挥系, 武汉 430013
2. Department of Radar Technology, Academy of Air Force Early Warning, Wuhan 430019 ;
3. Department of Command, Rocket Army Command Academy, Wuhan 430012
时域有限差分(FDTD)方法自1966年Yee[1]提出后,经过几十年的发展,已成为一种成熟的数值方法被广泛应用于辐射天线分析、散射和雷达截面计算和周期结构分析等多个方面。但是,随着大规模精细电磁计算需求的不断发展,经典的理论和方法遇到前所未有的挑战,特别是在确定复杂电大尺寸目标的电磁辐射和散射特性、建立精确通用的电磁理论模型和数值模型、复杂平台环境下的散射和传播机理等方面存在困难。为此,国内外研究者着眼于FDTD 3个关键性技术,即高效计算网格建立技术、FDTD大规模并行计算中的效率提升和拓扑结构技术、求解区域协同计算适应性改进技术开展大量的开创性工作。
在FDTD大规模并行计算中的效率提升和拓扑结构技术、求解区域协同计算适应性改进技术方面,2004年Su等[2]提出了MPI与OpenMP结合的方式在SGI Origin2000并行系统上实现了FDTD并行计算;2005年余文华等[3]研究了FDTD并行算法实现、边界数据交换方式、并行效率等问题,使用200个以上处理器达到90%以上的并行效率;2004年Krakiwsky[4]、2007年Adams[5]等分别开展了单核图形处理单元(GPU)与Intel、AMD处理器的比对测试;2009年Du等[6]开展了基于CUDA平台的三维FDTD程序测试,该程序用C程序编写,在CPU系统下测试,实现了10倍的加速比;2008年刘瑜等[7]结合了Su[2]和余文华[3]等的工作,在Pentium4 CPU组成的PC集群系统上实现了超线程下的并行方案;2010年Komatitsch等[8]在GPU集群上(192颗)模拟地震波传播,比CPU版性能提升几十倍;2010年Jacobsen等[9]在Lincoln系统上取得8线程CPU版本130*的性能;2012年Nagaoka和Watanabe[10]运用3个节点(一共21块NVIDIA TESLA C2070 GPU)提高30%的并行效率;2011年Yang等[11]在由Tesla C1060和Tesla S1070组成的服务器上成功加速了冒泡排序、矩阵乘法等程序;2012年Kim和Park[12]做了GPU测试,获得GPU的Kernel函数理论计算效率; 2013年Xu等[13]使用64块NVIDIA Tesla K20m(GPU)做了三维FDTD测试,得到67.5%的并行效率和3.1的加速比(相对于Intel XEON E5-2670 CPU);Yang等[11]在GPU集群上(5颗)研究OpenMP+CUDA混合编程模型,发现其性能与MPI+CUDA类似。从前人的工作中发现:早些年PC系统价格过于昂贵、集群性的测试并没有得到广泛使用,计算单元的数量也急剧增加,模型和算法的并行效率又亟待提高,PC之间的网络速度成为瓶颈,计算单元间的负载平衡也成为重要问题之一;普通的PC机支持的GPU个数有限且显存大小受限,达不到解决数据规模非常巨大的任务需求,GPU和集群的计算能力亟待整合,以拓宽基于GPU通用计算的范围并使得并行计算性能得到更大的提升;需要通过计算复杂电大尺寸平台,以检验算法的并行效率和加速效果。
本文基于分布式平台开展一种新的FDTD并行算法研究,利用上海交通大学高性能计算中心GPU集群、上海超级计算机中心的“魔方”商用超级计算机以及国家超级计算济南中心的“神威蓝光”国产超级计算机平台开展测试。实验平台包括NVIDIA Tesla M2070(GPU)、NVIDIA Tesla K20m(GPU),机群使用MellanoxInfiniband FDR交换机、Intel Xeon E5-2670等计算设备。
1 FDTD 算法简介 1.1 三维FDTD基本方程FDTD算法将Maxwell旋度方程组进行时间和空间的离散,得到递推的差分方程,用差分方程的解近似代替原方程的解。在求解过程中,需要保证方程组解的收敛性和稳定性。研究无耗背景空间σ=0,σm=0(σ为介质的电损耗,σm为介质的磁损耗),则Maxwell转化为6个标量方程:
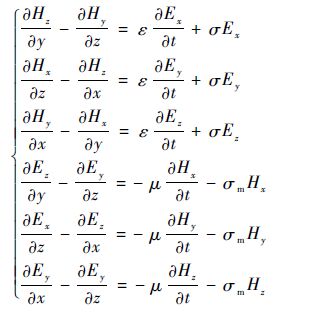
|
(1) |
式中:E(Ex,Ey,Ez)为电场强度;H(Hx,Hy,Hz)为磁场强度;μ和ε分别为媒质的磁导率和介电常数。
根据Yee提出的元胞原理,将式(1)离散得到[14]
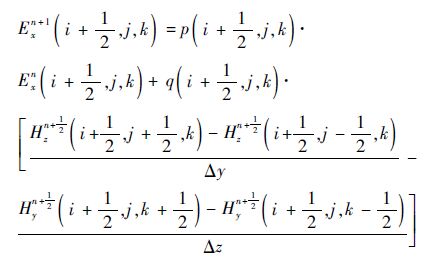
|
(2) |
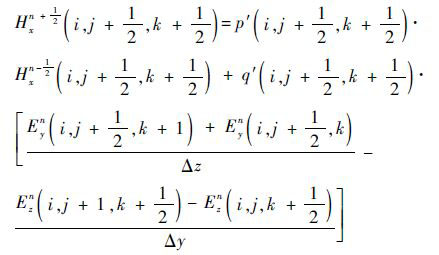
|
(3) |
式中:

|
Δx、Δy和Δz为空间步长;Δt为时间步长。同样可以得到Eyn+1、Hyn+ 1 2 、Ezn+1和Hzn+ 1 2 方程,形成三维场分量的FDTD差分方程组。任意时间步长值取决于前一时刻空间步长和时间步长电场和磁场的值。
1.2 数值稳定性和色散FDTD差分方程组只有离散才能求解,离散后需要确保方程组的解是收敛和稳定的,即Δx、Δy、Δz和Δt满足一定的条件[15],其中
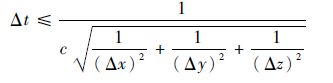
|
(4) |
式中:c为真空中的光速。该条件是FDTD算法的Courant稳定条件,也是Δt的最基本约束条件。如果Δx=Δy=Δz=δ(δ设定为立方体元胞边长)时,则得到
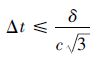
|
(5) |
从式(5)可以看出,时间变化量应该不大于光波过Yee元胞对角线长度的1/3的时间。
1.3 吸收边界条件本文采用Mur吸收边界以模拟电磁波无反射地通过截断边界,确保有限空间与无限空间等效,使得向边界面行进的波在边界处保持“外向行进”的特征向无限远处传播。Mur吸收边界是对Engquist-Majda吸收边界的一种近似。在三维Cartisian坐标系下,Mur吸收边界的迭代公式为(以Ez为例)[16]

|
(6) |
对其离散,设Δx=Δy=Δz=σ,得到
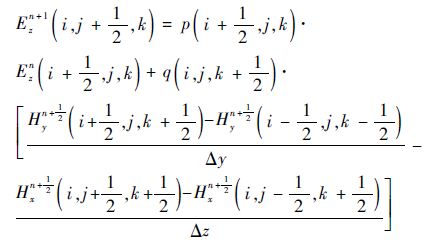
|
(7) |
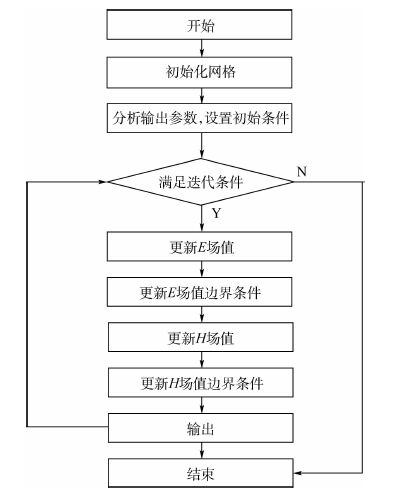
其余3条边界也可以做类似处理。当某一时刻的场值计算结束后,迭代程序就可以得到随时间变化的电磁场场值的分布情况,计算流程见图 1。
|
| 图 1 FDTD算法流程 Fig. 1 FDTD algorithm flow |
基于多GPU的计算平台,CUDA可实现对每个GPU的控制,即纹理的绑定、Kernel的执行、显存的分配与复制。CUDA5.0的平台规定多个主机线程可对一个设备进行操作,一个主机线程控制一个设备。为实现FDTD的多GPU并行递推及GPU之间的数据传输,考虑到GPU之间不能直接交换数据,只是与内存交换数据,所以只需要为边界的数据通信分配CPU内存,且在数据通信时考虑数据是否准备完毕以及选择交换的时机,同时考虑GPU与内存数据通信的特性,本文研究并提出两种数据通信方案,即同步数据传输方案和异步数据传输方案(见图 2)。在对两种方案的研究中发现:同步数据传输要求数据的传输均在GPU处理完所有Yee网格场值的递推后进行,每一次边界数据的传输都需要在所有区域的H(或者E)场值的更新完成后进行,同样在进行E(或者H)场值的更新前也需要等待传输数据的完成,要求数据的传输从GPU到CPU,再从CPU到另外一个GPU,从而影响整体的计算效率; 异步数据传输方案实现了GPU内部的多个核心并行及多个GPU并行计算,实现了计算与数据传输的并行,即实现了计算与任务分配的两级并行,虽然较同步数据传输方案更为复杂,但有效地减少了数据传输所占的时间比例,提高了并行效率。所以,本文选择使用异步数据传输方案。考虑到FDTD场值的更新仅仅需要其周围有限的几个场分量,所以边界数据的通信可以和不相邻区域的场值计算同步进行,使用CUDA中的流(Stream)控制机制和异步内存复制函数进行管理。

|
| 图 2 异步数据传输及计算方案 Fig. 2 Asynchronous data transmission andcomputing solutions |
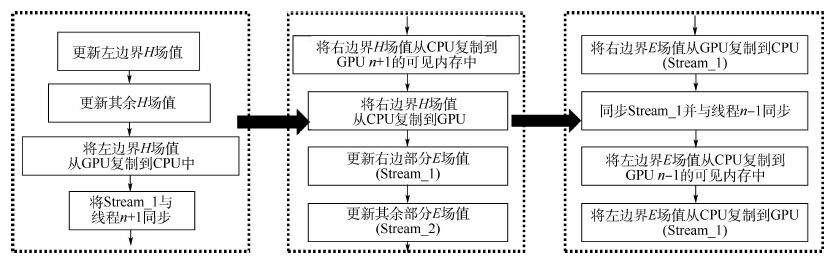
Stream按照顺序执行一系列操作,程序运行中可以有很多的Stream并发,一个Stream可以与其余的Stream乱序执行操作,也可以顺序或者同时执行操作,即一个Stream的计算与其余的Stream通信传输并发进行,提高了GPU中资源的使用率。Stream通过创建一个CudaStream_t对象来定义,在启动Kernel和进行内存复制后将该对象传入,不同的对象输入对应不同的Stream。本文利用多个Stream进行任务并行操作,选取其中的两个Stream解释其原理。令其中一个Stream为Stream_1,另外一个Stream为Stream_2。Stream_1负责部分边界场值的更新与数据通信传输,其中的数据通信传输部分使用CudaMemcpy2DAsync函数执行。Stream_1的更新考虑了计算资源的充分利用,避免网格数量过少,同时保证与其余Stream负载的平衡以及GPU的运算能力。Stream_1数据通信传输部分和Stream_2的计算部分可以同时进行。但是,异步复制函数中所用的内存必须页面锁定(page-locked),即当前的GPU可见,所以将右边界H场值从CPU内存复制到GPU n+1的可见内存区域以及将左边界E场值从CPU内存复制到GPU n-1的可见内存区域是必要的。详细流程见图 3。
|
| 图 3 异步数据传输及计算流程 Fig. 3 Asynchronous data transmission and computing flows |
假设一个时间步的通信需要的时间为
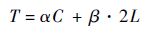
|
(8) |
式中:α为通信延迟时间;C为通信次数;β为传输速率;L为E/H通信数据量。各个参数的计算方式为
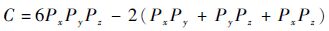
|
(9) |
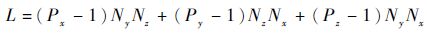
|
(10) |
式中:Px、Py和Pz分别为x、y和z方向上的拓扑值;Nx、Ny和Nz分别为x、y和z方向上的网格数。
由式(8)和式(9)可以看出,当通信数据量L一样时,不同的拓扑分布,可能会导致通信次数C的不同,以至总时间T的不同。
以曙光5000A为例,α=1.8~2.5 μs,β=1/1.656 3 Gb/s,如果网格数为1 000×1 000×1 000,总核数为1 000,那么通信响应时间(9.72 ms)比通信时间(121 ms)大约小一个量级,在这个核数规模下的通信响应时间为次要因素。单个进程的通信量为
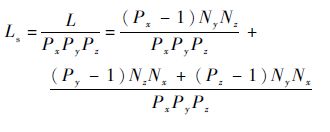
|
(11) |
式(11)除以常数Nx、Ny、Nz,得到

|
(12) |
由式(12)可知,当且仅当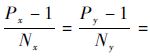

一般而言,节点内的进程间通信时间较节点间的通信时间要小,即节点内和节点间的字节通信时间因β不同。故而,当两种虚拟拓扑的C和L都相等时,就要考虑跨节点间进程的通信量的大小。本文通过3种优化虚拟拓扑策略获得并行FDTD算法高效率,方法如下:①选择拓扑使得总通信数据量L最小,即式(10)最小;②通信数据量相当的情况下,选择跨节点通信少的拓扑结构;③跨节点通信量相当时,选择通信负载较为均衡的拓扑。
2.3 GPU并行实现GPU运算具有高度并行的多Stream程序架构。为了实现FDTD运算加速,必须采用与CPU运算迭代更新不同的方式。该方式既可实现多重网格的同步迭代更新,还可配合GPU完成指令集的执行机制,从而实现对Stream的高效使用,同时隐藏其与设备内存的读写延时。
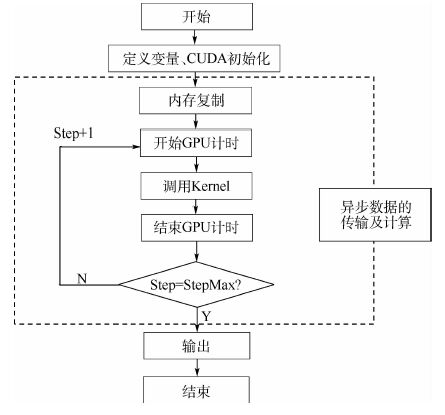
在GPU上实现FDTD加速算法思路(见图 4):整个加速过程可以分为三部分,即初始化部分、异步数据的传输及计算部分、输出(二次处理)部分。CUDA初始化将线程与每个数据形成一一对应的映射,从而将FDTD三维网格简化为一个二维工作组。一个工作组对应一个一维的工作项,利用工作项(localID)和工作组(groupID)确定数据在缓存中的位置,实现计算时场值的定位。异步数据的传输及计算部分为了实现工作项之间的数据共享、计算单元内存空间的异步/同步操作共享、需要限制Yee元胞(单个或多个)与工作组的数据交换,从而减少了对内存的消耗,加快了对数据的访问时间。该部分包含GPU与CPU之间的内存复制、调用Kernel(E-Kernel和H-Kernel)以及计算部分,是并行实现的核心部分。
|
| 图 4 GPU加速流程 Fig. 4 GPU acceleration flow |
本文算法将GPU核作为协同计算处理器,CPU核作为主处理器,开展两种核的协同并行工作。考虑到CPU核善于处理逻辑性强的事务、GPU核善于执行高度线程化的并行的特点,开展任务的分配和调度。CUDA的线程已经完成了透明扩展,即可以保证将一个编译任务分配在不同核数、不同硬件上开展运算。其Kernel按照线程网格(Grid)、线程块(Block)和线程(thread)三级模式组织。Grid是一系列block执行指令的集合,每个block之间是并行的关系,可以被同时执行,但是它们之间不能通信。
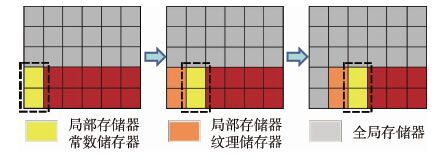
CPU核的每个计算单元在任务分配后都要读/写相应的全局内存数,以实现代码运行中每次循环的变量更新。OpenCL的并行方案采用内建矢量的方法,保证每次读入内存的3个变量能够选择储存到较快的局部存储器。为此,需要对逐单元的访存进行修改,变成逐数据块访存。改进后的存储方式实现了数据与线程一一对应的关系。这种方式也被引入到对Kernel内部内建矢量的优化处理。局部存储器和私有寄存器实现每个线程的操作,在CUDA的Grid中实现了多线程对相同全局存储器的访问,同时也可以访问只读存储器:纹理和常数存储器,见图 5。
|
| 图 5 局部存储器和内建矢量 Fig. 5 Local memory and built-in vector |
FDTD程序基于上海交通大学高性能计算中心GPU集群开展测试。实验平台包括NVIDIA Tesla M2070(GPU)、NVIDIA Tesla K20m(GPU),机群使用MellanoxInfiniband FDR交换机、Intel Xeon E5-2670(CPU,8核,2.6 GHz主频,2G缓存),中心有50个GPU计算节点,每个节点有两块NVIDIA Tesla K20m,同时配有两块Intel Xeon E5-2670。软件的编程基于MPI通信平台,使用Intel MPI 4.1.0库,Intel icpc 13.0.1编译器和CUDA5.0平台。FDTD程序的CPU部分基于上海超级计算机中心的“魔方”商用超级计算机(可以实现1万CPU核的计算)以及国家超级计算济南中心的“神威蓝光”国产超级计算机平台(并行规模可以突破1万CPU核)开展测试。
3.1 CPU测试 3.1.1 运行时间测试FDTD的CPU算法中,串行执行时,一次运算仅仅能得到一个点的场值。为了得到所有网格的值,需采用三重循环的方式。大部分时间消耗在电场向量 E 和磁场向量 H 修正计算的多重循环上(见表 1),实验数据的规模为256×256×256。随着计算机核数的增加,更新E场域、更新E场域边界、更新H场域、更新H场域边界运算的时间比例有所增加,而更新等效原理(huygens)和其他过程运算时间比较有所减少。主要是因为在CPU算法中,多核的运算过程核与核之间有任务的分配和等待的时间,通信耗费了一些时间。不过由于在计算过程中多核的并行运行减少了计算时间,所以最终总的时间耗费比例并没有太大的变化,总的耗费时间是在减少。
| 名称 | 运行时间比例/% | |||||
| 更新E 场域 |
更新E 场域边界 |
更新H 场域 |
更新H 场域边界 |
更新等 效原理 |
其他 过程 |
|
| 1核 | 17.1 | 7.5 | 16.8 | 10.2 | 25.5 | 22.0 |
| 4核 | 17.2 | 7.5 | 17.1 | 10.3 | 24.9 | 21.6 |
| 8核 | 17.4 | 7.6 | 17.2 | 10.4 | 24.6 | 21.5 |
| 16核 | 17.5 | 7.6 | 17.4 | 10.5 | 24.4 | 21.3 |
| 32核 | 17.7 | 7.8 | 17.9 | 10.6 | 24.0 | 20.8 |
| 64核 | 17.9 | 8.1 | 18.2 | 10.9 | 23.4 | 20.5 |
3.1.2 准确性测试
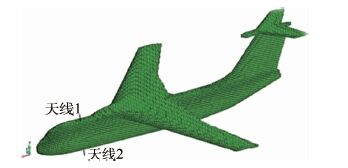
FDTD在计算电大尺寸平台,比如装载有天线的运八飞机平台时,其天线系统极其复杂,具有成千上万天线单元并包含细小结构。采用一体化模型对载机平台及其天线系统进行数值模拟具有相当大的难度。如图 6所示天线系统有许多细小结构和包含有介质,计算时根据稳定性条件需要采用细网格剖分,而飞机平台可以看成是金属,网格剖分时可以采用粗网格,两个计算域可以实现协同计算。先计算天线系统的辐射问题,得到FDTD外推面上的电磁流,然后通过近场外推得到粗网格计算域连接边界上的入射场,将该辐射场作为预警机平台的照射源,计算预警机平台在天线激励下的辐射;对天线的直接辐射场和机体受天线照射下的辐射场进行矢量叠加运算。
|
| 图 6 FDTD计算网格 Fig. 6 FDTD computing grid |
如图 7所示,上面源所在区域表示天线所在的 FDTD计算域,该计算域由于微带天线的细小结构和介质的存在而需要很细的网格划分,下面的区域表示平台存在的计算域,该计算域由于目标几何尺寸大而同样需要消耗大量的计算机内存,本算例使用集群环境下的多核CPU进行计算。

|
| 图 7 计算区域的划分 Fig. 7 Dividing the computational domain |
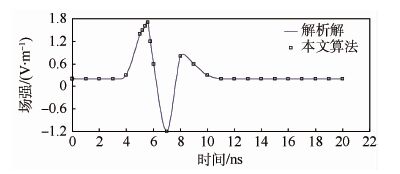
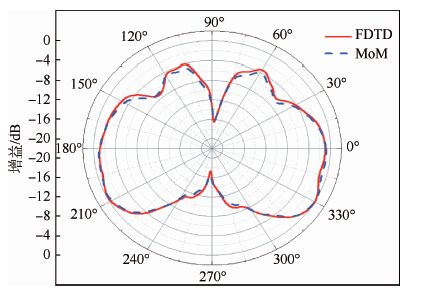
在上面计算域放置一个偶极子,通过近场外推在下面计算域观察点得到的结果。作为比较,图 8给出了本文算法的计算结果和解析解对比图;同时还将FDTD计算所得的机载天线辐射方向图和矩量法(MoM)计算结果对比(见图 9)。数据显示计算结果吻合,同时也证明FDTD算法的准确性。
|
| 图 8 经过近场外推后子域观察点场值和解析结果的比较 Fig. 8 Comparison between subdomain observation pointfield values and analysis results after near extrapolation |
|
| 图 9 FDTD计算所得的机载天线辐射方向图和矩量法的比较 Fig. 9 Comparison between FDTD calculated airborneantenna radiation pattern and moment method |
表 2给出了Mur吸收边界条件下、多个CUDA 线程、多个元胞下的加速比。
| Yee 元胞数 | CUDA 模块 |
CPU 时间/ms |
GPU 时间/ms |
加速比 |
| 32×32×32 | 8×8 | 1.57 | 0.24 | 6.54 |
| 64×64×64 | 16×16 | 14.16 | 0.78 | 18.10 |
| 128×128×128 | 32×32 | 118.28 | 2.37 | 49.90 |
| 256×256×256 | 64×64 | 975.31 | 17.89 | 54.50 |
| 512×512×512 | 128×128 | 7 843.85 | 150.87 | 51.90 |
| 1 024×1 024×1 024 | 256×256 | 62 748.45 | 1 394.18 | 45.00 |
从表 2可以看出:并行计算的加速比与计算域网格数量保持一定的线性增长关系,加速比最大值出现在网格数107量级,然后减小。考虑到时间步的叠加和CPU内核的调整都需要消耗时间,实际上,网格数目少的时候,加速比也较小。但是,其总时间基本上保持一定,加速比随着计算网格增加到一定程度后难以掩盖访问的延迟,从而出现总体加速比下降的情况。
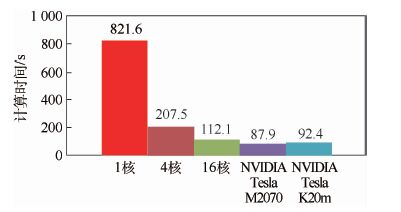
选取Yee元胞数的规模为256×256×256,开展1核、4核、16核、NVIDIA Tesla M2070、NVIDIA Tesla K20 m计算时间对比测试。CPU多核采用MPI数据调度和通信,GPU使用OpenCL调度,一个CPU核控制一块GPU,也就是以一个MPI进程控制一块GPU。如图 10可见,在该元胞数下GPU相对于CPU的加速比达到8.89。虽然在CPU多核情况下,计算时间随着核数的增加迅速减少,计算效率快速提高,但是也达不到GPU的加速性能。
|
| 图 10 1核、4核、16核、NVIDIA Tesla M2070、NVIDIA Tesla K20 m计算性能对比 Fig. 10 Comparison of computing performance among 1 core,4 cores,16 cores,NVIDIA Tesla M2070 and NVIDIA Tesla K20m |
图 11显示的是在该Yee元胞数规模下的各个GPU优化的核心函数和CPU程序中对应函数的执行时间对比。数据表明:主要函数的运行时间 遵从表 1的时间百分比分布规律;更新E和H场域计算密度较高,加速比也较大,达到6倍多。

|
| 图 11 1核、4核、16核、NVIDIA Tesla M2070、NVIDIA Tesla K20m计算时间对比 Fig. 11 Comparison of computing time among 1 core,4 cores,16 cores,NVIDIA Tesla M2070 and NVIDIA Tesla K20m |
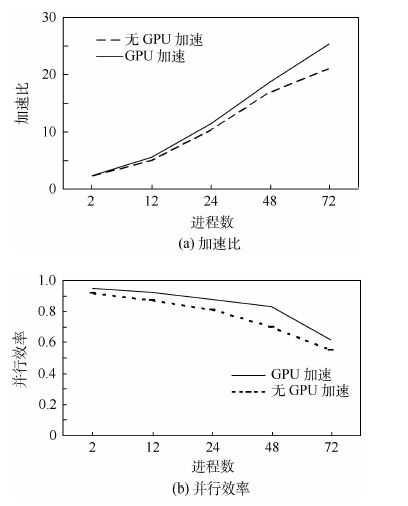
选取Yee元胞数的规模为512×512×512,分别使用2、12、24、48、72块NVIDIA Tesla K20m进行加速测试。测试结果如图 12所示(“无GPU加速”表示未使用优化虚拟拓扑策略获得的并行效率;“GPU加速”表示使用了优化虚拟拓扑策略获得的并行效率)。结果表明:GPU的并行效率随着核数的增加出现下降的趋势;优化虚拟拓扑策略对并行效率的提升有一定的作用,优化效果随着GPU块数的增加而凸显出来,在48块GPU时达到最好,然后开始下降。原因之一可能是:计算区域的体积决定了计算时间的长短,计算区域的表面积决定了通信时间的长短,在GPU块数增加时,通信时间的减少程度较小,而计算时间的减少程度较大,两者的比值变化大。原因之二可能是:在GPU块运行过程中存在host与device之间额外的数据传输,增加了计算时间。所以,在GPU块数增加的情况下,纯程序计算时间与消耗的总时间的比例将逐渐降低,导致加速比减小、并行效率下降。
|
| 图 12 有无GPU加速比与并行效率对比 Fig. 12 Comparison of acceleration ratio and parallelefficiency with and without GPU |
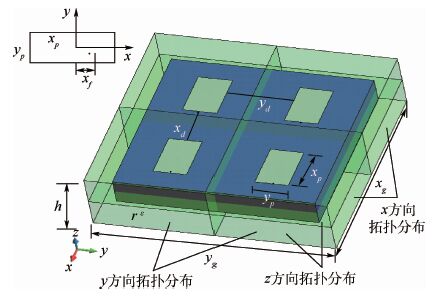
以一个2×2微带阵列为测试模型进行拓扑优化研究,并在集群平台上进行了测试。微带模型及MPI进程虚拟拓扑示意图见图 13,测试参数:中心频率为4.97 GHz,xp=14 mm,yp=9.6 mm,xd=15 mm,εr=4.34,h=0.8 mm,xg=60 mm,yg=60 mm,xf=3.6 mm,网格大小为dx=dy=dz=0.4 mm。
|
| 图 13 微带模型及MPI进程虚拟拓扑示意图 Fig. 13 Schematic diagram of micro-strip model andMPI progress virtual topology |
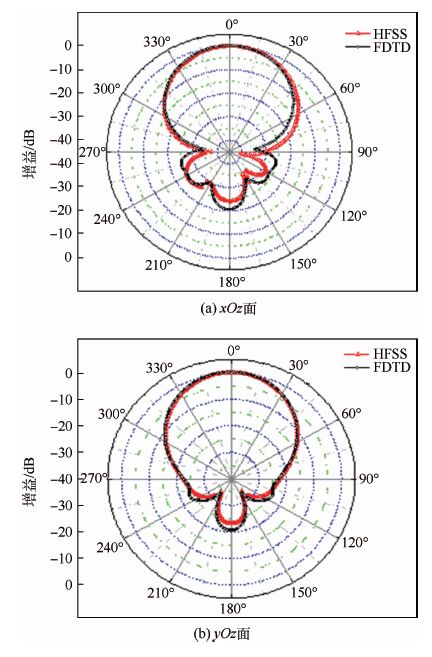
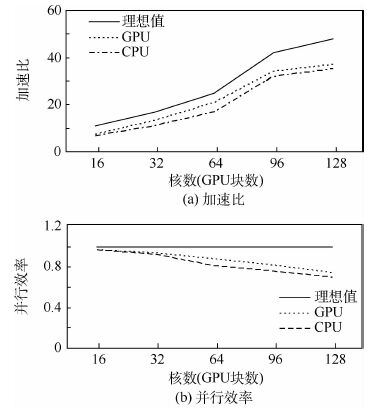
本测试的总网格区域为1 200×1 200×300,时间步为2 000步,测试最大核数为128(CPU),96(GPU)。该阵列的方向图如图 14所示,其结果与商业软件HFSS仿真结果进行了对比,吻合良好。加速比和并行效率曲线如图 15所示。
从图 15中可以看出,以16核为基准,加速比达到7倍以上,FDTD并行程序在32核下的并行效率可达80%以上。以48核为基准,加速比达到10倍以上,FDTD并行程序的并行效率也可达70%以上,结果同CPU、GPU测试基本吻合。
|
| 图 14 2×2微带阵列方向图 Fig. 14 2×2 micro-strip array pattern |
|
| 图 15 加速比和并行效率随核数的变化 Fig. 15 Acceleration ratio and parallel efficiency varywith number of cores |
本文基于分布式平台开展一种新的FDTD并行算法研究,利用上海交通大学高性能计算中心GPU集群、上海超级计算机中心的“魔方”商用超级计算机以及国家超级计算济南中心的“神威蓝光”国产超级计算机平台开展测试。实验平台包括NVIDIA Tesla M2070(GPU)、NVIDIA Tesla K20m(GPU),机群使用MellanoxInfiniband FDR交换机、Intel Xeon E5-2670等计算设备。算法在通信过程中采用异步数据传输方案,使用CUDA中的流(Stream)控制机制和异步内存复制函数进行管理,提高了GPU中资源的使用率,同时考虑了计算资源的充分利用,采用多个Stream进行任务并行操作,避免网格数量过少,同时保证与其余Stream负载的平衡以及GPU的运算能力。本文还对GPU并行效率进行了研究,根据大量的测试数据,得到效率提升的经验公式(目前国内相关的文献很少有提到如何提升并行效率,也没有固定的计算公式可以遵循),总结提出了3种优化虚拟拓扑策略。
通过纯CPU、GPU以及CPU和GPU的混合使用测试,证明本文算法在线程的调度水平、核心函数处理速度等方面有所提升,减少了通信执行时间比例,最终体现在加速比、并行效率方面有一定的提高,同时也表明:
1) FDTD在计算电大尺寸特别是有复杂天线系统的平台时,由于天线单元具有成千上万个细小结构,采用一体化模型对载机平台及其天线系统进行数值模拟具有相当大的难度。建议在保证稳定性条件下,可以开展区别对待的网格剖分形式,同时针对不同区域采用协同求解的方法(可以是单算法的协同,也可以是多算法的协同求解)。
2) 在GPU核运行过程中存在host与device之间额外的数据传输,增加了计算时间。但这种影响对整个计算过程到底会产生多大的影响,产生这些影响的原因有哪些,以及GPU和CPU混合执行时与MPI之间的数据通信是否会产生堵塞等问题值得后期进一步研究。
| [1] | YEE K S. Numerical solution of initial boundary value problems involving Maxwell's equations in isotropic media[J]. IEEE Transactions on Antennas and Propagation, 1966, 4 (14) : 302 –307. |
| [2] | SU M F,EI-KADY I,BADER D A,et al.A novel FDTD application featuring OpenMP-MPI hybrid parallelization[C]//Proceedings of the International Conference on Parallel Processing,2004 ICPP 2004.Piscataway,NJ:IEEE Press,2004:373-379. |
| [3] | YU W H, Y J, SU T, et al. A robust parallel conformal finite-difference time-domain processing package us in the MPI library[J]. IEEE Antennas and Propagation, 2005, 47 (3) : 39 –59. DOI:10.1109/MAP.2005.1532540 |
| [4] | KRAKIWSKY S E,TURNER L E,OKONIEWSKI M M.Acceleration of finite-difference time-domain (FDTD) using graphics processor units (GPU) [C]//Proceedings of the IEEE MITTS International Microwave Symposium Digest.Piscataway,NJ:IEEE Press,2004,2:1033-1036. |
| [5] | ADAMS S,PAYNE J,BOPPANA R.Finite difference time domain (FDTD) simulations using graphics processors[C]//Proceedings of the DoD High Performance Computing Modernization Program Users Group Conference.Piscataway,NJ:IEEE Press,2007:334-338. |
| [6] | DU L G,LI K,KONG F M.Parallel 3D finite difference time domain simulations on graphics processors with CUDA[C]//Proceedings of the International Conference on Computational Intelligence and Software Engineering (CISE '09).Piscataway,NJ:IEEE Press,2009:145-147. |
| [7] | LIU Y, LIANG Z, YANG Z Q. A novel FDTD approach featuring two-level parallelization on PC cluster[J]. Progress in Electromagnetics Research-Pier, 2008, 80 : 393 –408. DOI:10.2528/PIER07120703 |
| [8] | KOMATITSCH D, GODDEKE D, ERLEBACHER G, et al. Modeling the propagation of elastic waves using spectral elements on a cluster of 192 GPUs[J]. Computer Science-Research and Development, 2010, 25 (1-2) : 75 –82. DOI:10.1007/s00450-010-0109-1 |
| [9] | JACOBSEN D A,THIBAULT J C,SENOCAK I.An MPI-CUDA implementation for massively parallel incompressible flow computations on multi-GPU clusters [C]//Proceedings of 48th AIAA Aerospace Sciences Meeting.Piscataway,NJ:IEEE Press,2010:1-16. |
| [10] | NAGAOKA T,WATANABE S.Accelerating three-dimensional FDTD calculations on GPU clusters for electromagnetic field simulation[C]//Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society(EMBC12).Piscataway,NJ:IEEE Press,2012:5691-5694. |
| [11] | YANG C T, HUANG C L, LIN C F. Hybrid CUDA,OpenMP,and MPI parallel programming on multi-core GPU clusters[J]. Computer Physics Communications, 2011, 182 (1) : 266 –269. DOI:10.1016/j.cpc.2010.06.035 |
| [12] | KIM K H, PARK Q H. Overlapping computation and communication of three-dimensional FDTD on a GPU cluster[J]. Computer Physics Communications, 2012, 183 (11) : 2364 –2369. DOI:10.1016/j.cpc.2012.06.003 |
| [13] | XU L, XU Y, JIANG R L, et al. Implementation and optimization of three-dimensional UPML-FDTD algorithm on GPU cluster[J]. Computer Engineering & Science, 2013, 35 (11) : 160 –167. |
| [14] | TAFLOVE A, BRODWIN M E. Numerical solution of steady-state electromagnetic scattering problems using the time-dependent Maxwell's equation[J]. IEEE Transactions on Microware Theory Techniques, 1995, 23 (8) : 623 –630. |
| [15] | GE D B, YAN Y B. Finite-difference time-domain method for electromagnetic wavess[M]. 3rd ed Xi'an: Xidian University Press, 2011 : 37 -38. |
| [16] | ENGQUIST B, MAJDA A. Absorbing boundary conditions for the numerical simulation of waves[J]. Mathematics of Computation, 1977, 31 (139) : 629 –651. DOI:10.1090/S0025-5718-1977-0436612-4 |



