2. 海军航空工程学院 训练部, 烟台 264001
2. Department of Command, Naval Aeronautical and Astronautical University, Yantai 264001, China
传统的基于退化数据的可靠性建模方法都是采用固定参数退化模型,近些年,随机参数退化模型已成为研究热点。Wang[1]研究了具有随机参数的Wiener过程,并使用最大期望(Expectation Maximization,EM)算法估计随机参数的超参数值。Si等[2]研究了利用随机参数Wiener过程预测装备剩余有效寿命的方法,并提出联合使用递归滤波算法和EM算法进行参数值估计。刘君强等[3]利用多阶段随机参数Wiener过程实现了航空发动机个体剩余寿命的实时预测。Lawless 和 Crowder[4]提出了基于随机参数Gamma过程的性能退化建模方法,用于分析某产品裂纹增长数据。Wang等[5]在假定Gamma过程的随机参数服从共轭先验分布的基础上,研究了融合历史退化数据与现场退化数据的建模方法。Tsai等[6]提出了基于随机参数Gamma过程的退化试验最优设计方法。逆高斯(Inverse Gaussian)过程同Gamma过程一样适用于对严格单调退化过程进行建模,Wang和Xu[7]、Peng等[8]、Ye 和 Chen[9]以及Peng[10]分别研究了随机参数Inverse Gaussian过程在性能退化建模中的应用。以上研究结果表明随机参数退化模型比固定参数退化模型具有更优的拟合效果和预测能力。
加速退化试验(Accelerated Degradation Test,ADT)已经广泛用于快速评估退化失效型产品的可靠性[11-14],然而目前的随机参数退化模型大都以同一应力下的退化数据为对象,缺少在ADT中应用的研究。Peng[10]对随机参数Inverse Gaussian过程在加速退化建模中的应用进行了有益的探索,然而研究工作是根据主观判断建立随机参数及其超参数与加速应力之间的关系,容易因为建模不合理导致外推到正常应力下的可靠性指标不准确。为了提高ADT中可靠性评估结果的准确性,本文以Inverse Gaussian过程为例研究了基于随机参数退化模型的加速退化建模方法,其主要特点是利用加速系数将加速退化数据都折算到工作应力下进行统一处理。首先,利用加速系数不变原则推导出退化模型的各参数在不同应力下应满足的关系式,由此建立参数的加速模型;接着,计算出各加速应力相对于工作应力的加速系数,进而将加速应力下的退化数据等效折算到工作应力下;然后,给出了参数估计方法,为了便于统计分析采用了随机参数的共轭先验分布,并且利用EM算法估计随机参数的超参数值;最后,通过仿真试验和实例应用对所提的方法进行了验证。
1 Inverse Gaussian过程 1.1 固定参数Inverse Gaussian过程Inverse Gaussian过程{Y(t),t≥0},t为时间,具有下列3条性质:①Y(t)在t=0在处连续,Y(0)=0且以概率1成立;②Y(t)具有独立增量,即对任意0≤t1<t2≤t3<t4,Y(t2)-Y(t1)与Y(t4)-Y(t3)相互独立;③独立增量ΔY(t)=Y(t+Δt)-Y(t)服从ΔY(t)~IG(μΔΛ(t),λΔΛ2(t)),IG(·,·)表示Inverse Gaussian分布,Λ(t)为时间函数且Λ(0)=0,ΔΛ(t)=Λ(t+Δt)-Λ(t),Δt为时间增量;μ为均值参数;λ为尺度参数。
可推导出Inverse Gaussian过程Y(t)~IG(μΛ(t),λΛ(t)2),Y(t)的概率密度函数(PDF)可表示为
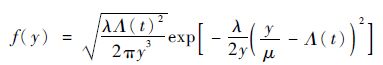
|
(1) |
设D为产品的失效阈值,则Y(t)首次到达D的时间为产品的寿命ξ=inf{t|Y(t)≥D}。ξ的累积分布函数(CDF)可由式(2)推出。
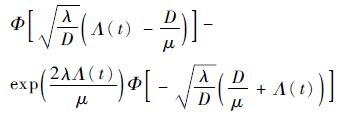
|
(2) |
式中:Φ(·)为标准正态分布CDF。
1.2 随机参数Inverse Gaussian过程为了描述产品个体之间的退化过程差异,提高退化模型的预测能力,采用了文献[10]提出的随机参数Inverse Gaussian过程:将μ、λ作为随机参数。为了便于统计分析,采用了μ、λ的共轭先验分布:假定λ服从Gamma分布λ~Ga(a,b),其PDF表示为
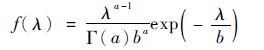
|
(3) |
假定δ=1/μ服从条件正态分布δ|λ~N(c,d/λ),其PDF为
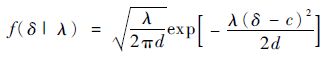
|
(4) |
对于随机参数Inverse Gaussian过程,产品的可靠度函数可表示为

|
(5) |
由式(5)可知,确定可靠度函数R(t)需要估计出 θ =(a,b,c,d,Λ)。为了从加速退化数据中估计出 θ ,本文提出了基于加速退化数据等效折算的解决方案,利用加速系数将各加速应力下的退化数据都折算到工作应力下。
2.1 推导加速系数表达式性能退化模型的某型参数值会随着应力水平的改变而变化,加速模型用于描述这些参数值随应力水平的变化规律[13]。ADT建模的重要环节之一是要正确判断出性能退化模型的哪些参数会随着加速应力发生变化,否则无法准确外推出产品在正常应力下的可靠性指标。本节利用加速系数不变原则[13, 15]推导Inverse Gaussian过程的哪些参数随着加速应力发生变化,进而确定加速系数表达式。
假设Fk(tk)和Fh(th)分别表示产品在任 2个应力水平Sk和Sh下的累积失效概率,tk和th分别为Sk和Sh下的时间,如有Fk(tk)=Fh(th),则可将应力Sk相当于应力Sh的加速系数Ak,h定义为

|
(6) |
加速系数不变原则是指在一个有效的加速试验中,产品在2个加速应力间的加速系数值不随着试验时间的长短而变化。如果加速系数随试验时间发生了变化,说明产品在此2个加速应力下的失效机理并不一致[15-16],其加速退化数据不能用于外推产品在正常应力下的可靠性指标。据此,Ak,h应为一个与试验时间长短无关的常数,式(7)对任意tk恒成立:
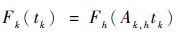
|
(7) |
将式(2)代入式(7),得
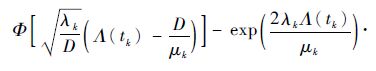
|

|
(8) |
为了式(8)对任意tk恒成立,需要满足:
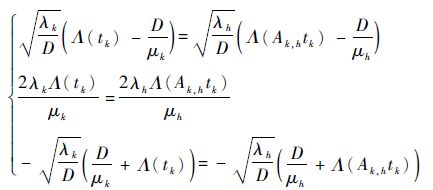
|
(9) |
式中:λk和λh分别为Sk和Sh下的尺度参数;μk和μh分别为Sk和Sh下的均值参数。
设时间函数Λ(t)=tr,r为形状参数,此函数有很好的拟合特性,可以对凸型、凹型、线型退化过程进行建模。为了保证式(9)对任意tk恒成立,需要满足

|
(10) |
式中:rk和rh分别为Sk和Sh下的形状参数。
可知r不随着应力水平发生变化,但是μ和λ会随着应力水平的改变而变化。假定加速应力为温度T,并选择Arrhenius方程作为加速模型。为了使μ和λ在任2个加速应力下都满足式(10)中的比例关系(μk/μh= 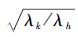
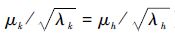
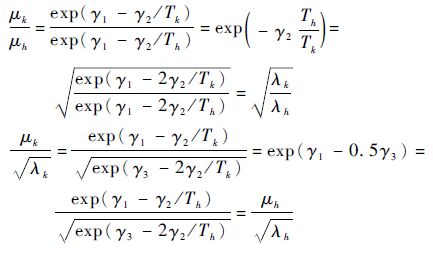
|
根据式(10)可得加速系数表达式为
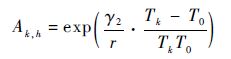
|
(11) |
设T0为产品的工作温度,ti,j,k为Tk下第i个产品的第j次测量时间,y(ti,j,k)为对应的退化测量值,Λi,j,k=Λ(ti,j,k)-Λ(ti,j-1,k)为时间函数Λ(ti,j,k)的增量,yi,j,k=y(ti,j,k)-y(ti,j-1,k)为退化增量,k=1,2,…,Q,Q为加速应力总数;i=1,2,…,Nk,Nk为Tk下的产品数量;j=1,2,…,Mi,k,Mi,k为Tk下第i个产品的测量次数。根据Inverse Guassian 分布的统计特性yi,j,k~ IG(exp(γ1-γ2/Ti)Λi,j,k,exp(γ3-2γ2/Ti)Λi,j,k2),建立似然函数:
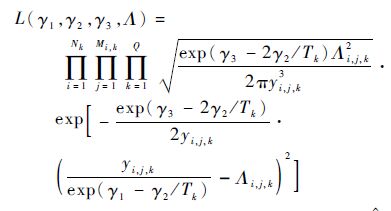
|
(12) |
可解得极大似然估计值
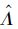
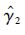
根据式(6)对加速退化数据进行折算,在保持退化测量值y(ti,j,k)不变的同时对测量时间ti,j,k进行折算:
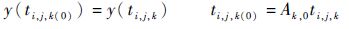
|
(13) |
式中:y(ti,j,k(0))和ti,j,k(0)为从Tk折算到T0的退化数据。为了表达方便,y(ti,j)和ti,j分别为折算后的退化测量值和测量时间,此时i=1,2,…,n,n为ADT中的样品总数;j=1,2,…,mi,mi第i个产品的测量次数。
3 参数估计方法设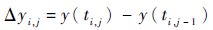

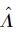
根据Inverse Gaussian过程的统计特性Δyi,j~IG(μiΔΛi,j,λiΔΛi,j2),建立似然函数为
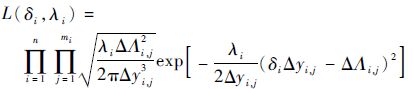
|
(14) |
结合式(3)及式(4),建立完全对数似然函数为
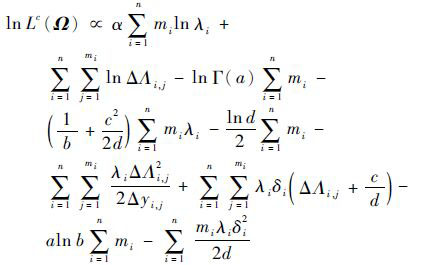
|
(15) |
设f(δi,λi)为随机参数δi、λi的联合先验概率密度函数,则有f(δi,λi)=f(λi)f(δi|λi),则联合后验概率密度函数f(δi,λi|Δ y i),可通过Bayesian公式f(δi,λi|Δ y i)∝L(δi,λi)f(δi,λi)推导出,可得随机参数δi、λi的后验分布为

|
(16) |
其中:
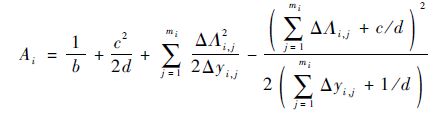
|
式(15)中的λi、ln λi、λiδi和λiδi2为含有随机参数的隐含数据项,因此无法直接极大化式(15)估计得 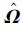
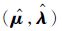
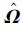

|
(17) |
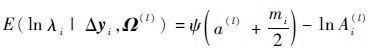
|
(18) |
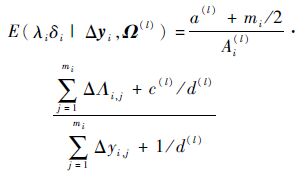
|
(19) |
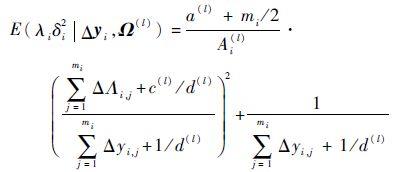
|
(20) |
式中:ψ(·)为digamma函数。
将式(15)中的各隐含数据项利用对应的期望值代替后,M步的任务是极大化式(15),解得c(l+1)、d(l+1)、b(l+1)及a(l+1)的表达式分别为

|
(21) |
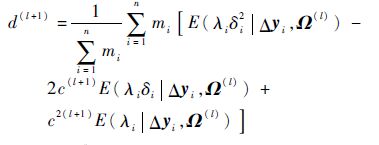
|
(22) |
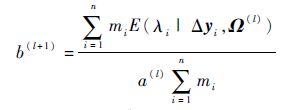
|
(23) |
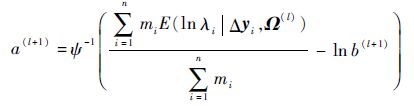
|
(24) |
式中:ψ-1(·)为逆digamma函数。
EM算法的执行过程描述如下。
初始化:设 l=0,Ω (0)=(1,1,1,1);
第l+1次迭代:
E步:计算E(λi|Δ y i,Ω (l)),E(ln λi|Δ y i,Ω (l)),E(λiδi|Δ y i,Ω (l))及E(λiδi2|Δ y i,Ω (l));
M步 : 解得c(l+1)、d(l+1)、b(l+1)及a(l+1),将 Ω (l)更新为 Ω (l+1);
结束条件:max( Ω (l+1)- Ω (l))<10-7或 l达到最大迭代数。
4 仿真验证 4.1 验证加速系数不变原则的推导结论第2节通过加速系数不变原则推导出了Inverse Gaussian过程各参数的变化规律,本节通过仿真试验对推导结论公式进行验证,仿真模型为
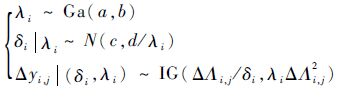
|
(25) |
仿真模型的参数值设置为:(a,b)=(2,1);(c,d)=(0.5,0.1);i=1,2,…,20;j=1,2,…,10;∀i,ti,j=10,20,…,100;Λ(ti,j)=ti,jr,r=0.5,1.0,2.0。验证步骤如下:
1) 利用仿真模型生成产品在应力Sk下的退化增量数据Δyi,j,k、ΔΛi,j,k。
2) 利用Δyi,j,k、ΔΛi,j,k解得Sk下的参数估计值

3) 分别设加速系数Ak,h为0.4,4,根据式(13)计算出折算到Sh下的退化增量数据Δyi,j,h、ΔΛi,j,h。
4) 利用Δyi,j,h、ΔΛi,j,h解得Sh下的参数估计值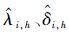

5) 计算出
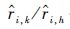
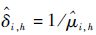
结果表明
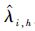
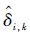
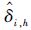
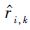


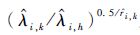
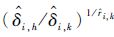
| r | Ak,h=0.4 | Ak,h=4 | ||||
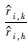 的均值 的均值 |
 的均值 的均值 |
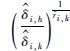 的均值 的均值 |
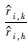 的均值 的均值 |
 的均值 的均值 |
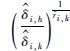 的均值 的均值 |
|
| 0.5 | 1.000 0 | 0.400 1 | 0.400 1 | 1.000 0 | 4.000 2 | 4.000 1 |
| 1.0 | 1.000 1 | 0.400 0 | 0.400 0 | 1.000 0 | 4.000 0 | 4.000 0 |
| 2.0 | 1.000 0 | 0.400 2 | 0.400 0 | 1.000 0 | 3.999 9 | 4.000 0 |
4.2 验证本文所提的建模方法
通过仿真模型生成产品在工作应力下和3个加速应力下的性能退化数据,分别利用固定参数和随机参数Inverse Gaussian过程对加速退化数据建模,外推出产品在工作应力下的可靠度。将利用工作应力下性能退化数据获取的产品可靠度作为标准值,评价本文所提建模方法是否比传统的固定参数建模方法更优。仿真模型为

|
(26) |
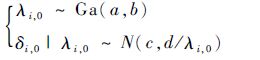
|
(27) |
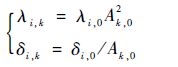
|
(28) |

|
(29) |
验证步骤如下:
1) 设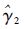
2) 设(a,b,c,d)=(2.0,1.0,0.5,0.1),由式(27)生成T0下的随机参数(λi,0,δi,0),i=1,2,…,20。
3) 由式(28)生成Tk下的随机参数(λi,k,δi,k),k=1,2,3。
4) 设∀i,ti,j=1,2,…,10 a,利用(λi,0,δi,0)由式(29) 生成T0下的退化增量数据(Δyi,j,0,Δti,j)。
5) 利用(λi,k,δi,k)由式(29) 生成Tk下的退化增量数据(Δyi,j,k,Δti,j),k=1,2,3。
6) 设失效阈值D=2,利用随机参数Inverse Gaussian模型对(Δyi,j,0,Δti,j)建模,获得可靠度函数R(0)(t)作为标准值。
7) 利用随机参数Inverse Gaussian模型对(Δyi,j,k,Δti,j)建模,获得可靠度函数R(1)(t)。
8) 利用固定参数Inverse Gaussian模型对(Δyi,j,k,Δti,j)建模,获得可靠度函数R(2)(t)。
9) 判断R(1)(t)和R(2)(t)哪个与R(0)(t)更接近。
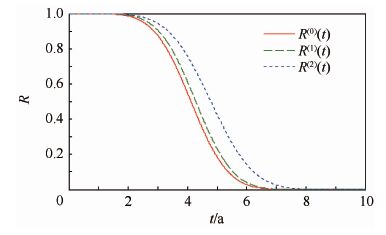
R(0)(t)、R(1)(t)和R(2)(t)的变化曲线如图 1所示,可见R(1)(t)与R(0)(t)更接近,说明本文所提的建模方法相比传统的固定参数建模方法提高了可靠性评估的准确性。
|
| 图 1 可靠度曲线 Fig. 1 Reliability curves |
Meeker 和 Escobar[20]提供了某型碳膜电阻在恒定应力ADT中的退化数据。3组加速温度应力分别为83、133和173℃,产品的工作温度为50℃,试验过程中所有样品同时测量,测量时刻为452、 1 030、4 341和8 084 h,退化参量为电阻值的百分比增量。 更为详细的试验数据见文献[20]中的Table C.3,因为第27个样品的退化数据不是单调递增,本文剔除了第27个样品的退化数据。
首先对每个产品的退化过程是否服从Inverse Gaussian过程进行验证。由式(14)解出每个产品对应的参数估计值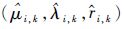
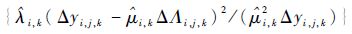

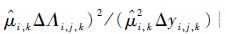
接着利用式(12)解得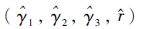
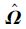

|
| 图 2 超参数估计值的迭代收敛过程 Fig. 2 Iterative convergence process ofhyper-parameter estimates |
最后将
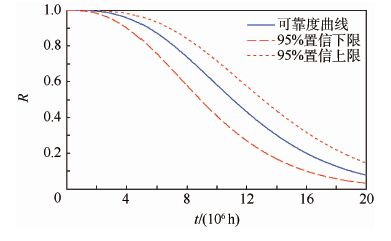
|
| 图 3 产品在50℃下的可靠度曲线 Fig. 3 Reliability curves of product under 50℃ |
为了将随机参数退化模型应用于ADT以提高可靠性评估结果的准确性,本文以Inverse Gaussian过程为例提出了基于随机参数退化模型的加速退化建模方法。
1) 随机参数Inverse Gaussian过程具备很好的统计特性,适合对严格单调退化过程建模,是除了Wiener过程和Gamma过程之外另一种应用性较好的随机过程模型。
2) 根据加速系数不变原则可推导出退化模型各参数在各加速应力下应满足的关系式,为获得各种退化模型的加速系数表达式提供了一种可行方法。
3) 利用加速系数可实现加速退化数据的等效折算,这种处理思路还可为解决加速退化建模的其他难题提供有益参考。
4) 与传统的基于固定参数的建模方法相比,本文提出的基于随机参数退化模型的建模方法具有更好的拟合效果,能够提高可靠性评估的准确性。
| [1] | WANG X. Wiener processes with random effects for degradation data[J]. Journal of Multivariate Analysis, 2010, 101 (2) : 340 –351. DOI:10.1016/j.jmva.2008.12.007 |
| [2] | SI X S, WANG W B, HU C H, et al. A Wiener-process-based degradation model with a recursive filter algorithm for remaining useful life estimation[J]. Mechanical Systems and Signal Processing, 2013, 35 (1-2) : 219 –237. DOI:10.1016/j.ymssp.2012.08.016 |
| [3] | 刘君强, 谢吉伟, 左洪福, 等. 基于随机Wiener过程的航空发动机剩余寿命预测[J]. 航空学报, 2015, 36 (2) : 564 –574. LIU J Q, XIE Z W, ZUO H F, et al. Residual lifetime prediction for aeroengines based on Wiener process with random effects[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36 (2) : 564 –574. (in Chinese) |
| [4] | LAWLESS J, CROWDER M. Covariates and random effects in a Gamma process model with application to degradation and failure[J]. Lifetime Data Analysis, 2004, 10 (3) : 213 –227. DOI:10.1023/B:LIDA.0000036389.14073.dd |
| [5] | WANG H W, XU T X, MI Q L. Lifetime prediction based on Gamma processes from accelerated degradation data[J]. Chinese Journal of Aeronautics, 2015, 28 (1) : 172 –179. DOI:10.1016/j.cja.2014.12.015 |
| [6] | TSAI C C, TSENG S T, BALAKRISHNAN N. Optimal design for degradation tests based on Gamma processes with random effects[J]. IEEE Transactions on Reliability, 2012, 61 (2) : 604 –613. DOI:10.1109/TR.2012.2194351 |
| [7] | WANG X, XU D. An inverse Gaussian process model for degradation data[J]. Technometrics, 2010, 52 (2) : 188 –197. DOI:10.1198/TECH.2009.08197 |
| [8] | PENG W W, LI Y F, YANG Y J, et al. Inverse Gaussian process models for degradation analysis:A Bayesian perspective[J]. Reliability Engineering and System Safety, 2014, 130 : 175 –189. |
| [9] | YE Z S, CHEN N. The inverse Gaussian process as degradation model[J]. Technometrics, 2014, 56 (3) : 302 –311. DOI:10.1080/00401706.2013.830074 |
| [10] | PENG C Y. Inverse Gaussian processes with random effects and explanatory variables for degradation data[J]. Technometrics, 2015, 57 (1) : 100 –111. DOI:10.1080/00401706.2013.879077 |
| [11] | PARK C, PADGETT W J. Accelerated degradation models for failure based on geometric Brownian motion and Gamma processes[J]. Lifetime Data Analysis, 2005, 11 (4) : 511 –527. DOI:10.1007/s10985-005-5237-8 |
| [12] | YE Z S, CHEN L P, TANG L C, et al. Accelerated degradation test planning using the Inverse Gaussian process[J]. IEEE Transactions on Reliability, 2014, 63 (3) : 750 –763. DOI:10.1109/TR.2014.2315773 |
| [13] | 王浩伟, 徐廷学, 赵建忠. 融合加速退化和现场实测退化数据的剩余寿命预测方法[J]. 航空学报, 2014, 35 (12) : 3350 –3357. WANG H W, XU T X, ZHAO J Z. Residual life prediction method fusing accelerated degradation and field degradation data[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35 (12) : 3350 –3357. (in Chinese) |
| [14] | LING M H, TSUI K L, BALAKRISHNAN N. Accelerated degradation analysis for the quality of a system based on the Gamma process[J]. IEEE Transactions on Reliability, 2015, 64 (1) : 463 –472. DOI:10.1109/TR.2014.2337071 |
| [15] | 周源泉, 翁朝曦, 叶喜涛. 论加速系数与失效机理不变的条件(Ⅰ)-寿命型随机变量的情况[J]. 系统工程与电子技术, 1996, 18 (1) : 55 –67. ZHOU Y Q, WENG Z X, YE X T. Study on accelerated factor and condition for constant failure mechanism (Ⅰ)-The case for lifetime is a random variable[J]. System Engineering and Electronics, 1996, 18 (1) : 55 –67. (in Chinese) |
| [16] | 王浩伟, 徐廷学, 王伟亚. 基于退化模型的失效机理一致性检验方法[J]. 航空学报, 2015, 36 (3) : 889 –897. WANG H W, XU T X, WANG W Y. Test method of failure mechanism consistency based on degradation model[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36 (3) : 889 –897. (in Chinese) |
| [17] | BALAKRISHNAN N, LING M H. EM algorithm for one-shot device testing under the exponential distribution[J]. Computational Statistics & Data Analysis, 2012, 56 (3) : 502 –509. |
| [18] | 韩立岩, 蔡明生, 尹力博. 正态逼近与基于覆盖宽度的EM估计[J]. 北京航空航天大学学报, 2013, 39 (5) : 654 –659. HAN L Y, CAI M S, YIN L B. Approximation by normal distribution with covering width based on EM estimation[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39 (5) : 654 –659. (in Chinese) |
| [19] | 徐廷学, 王浩伟, 张鑫. EM算法在Wiener过程随机参数的超参数值估计中的应用[J]. 系统工程与电子技术, 2015, 37 (3) : 707 –712. XU T X, WANG H W, ZHANG X. Application of EM algorithm to estimate hyper parameters of the random parameters of Wiener processes[J]. Journal of Systems Engineering and Electronics, 2015, 37 (3) : 707 –712. (in Chinese) |
| [20] | MEEKER W Q, ESCOBAR A. Statistical methods for reliability data[M]. New York: John Wiley & Sons, 1998 : 630 -640. |
| [21] | EFRON B. Better bootstrap confidence intervals[J]. Journal of American Statistical Association, 1987, 82 (397) : 171 –185. DOI:10.1080/01621459.1987.10478410 |
| [22] | MARKS C E, GLEN A G, ROBINSON M W, et al. Applying bootstrap methods to system reliability[J]. The American Statistician, 2014, 68 (3) : 174 –180. DOI:10.1080/00031305.2014.928232 |



