2. 贵州大学 理学院 系统科学及信息技术研究所, 贵阳 550025
2. Institute of System Science and Information Technology, College of Science, Guizhou University, Guiyang 550025, China
机会约束规划 (Chance-Constrained Programming,CCP)[1]是一类含机会约束或概率不等式的随机规划。依据目标函数表现形式的不同,CCP包含两类模型,即目标函数是期望值函数的E-模型和目标函数满足概率不等式的P-模型 (即概率优化模型)。大量实际优化问题均可经由P-模型加以描述和解决,如电力市场报价、资源优化、水库优化调度和炼油厂冶炼原油规划等[2-3]。由于此类问题的目标值需在给定置信水平下经由机会约束确定,加之目标值的估计质量与随机变量的样本大小紧密相连,因此,探讨效率和效果均较为突出且噪声抑制能力强的智能优化算法是求解此类问题的关键。 特别地,在随机变量分布特性已知的情况下,P-模型可以被转化为具有解析形式的规划模型,进而利用已有约束优化算法求解[2]。
当随机变量的分布信息未知时,智能优化算法已成为求解P-模型的主要方法。已有算法成果均在要求随机变量的样本大小保持不变下,借助Monte Carlo、Sugeno模拟或神经网络估计个体的适应度,然后设计改进型遗传算法(GA)[3-8]、粒子群优化(PSO)算法[9-13]和免疫优化算法[14]。例如,文献[4-6] 研究了含模糊和随机参数的混合P-模型,其利用模糊模拟、随机模拟估计个体的适应度,利用遗传算法、同步扰动随机逼近算法(SPSA)和神经网络等设计混合遗传算法。其次,粒子群优化算法具有参数少、优化效率高、结构简单和易于应用等优点,与神经网络结合求解P-模型已成为一种主要方法,但由于此类算法易陷入局部搜索,加之神经网络的网络权值极大依赖于样本量和样本的分布,导致该算法最终获得的效果不理想。例如,文献[13]通过设置惯性权重为零来增强局部搜索能力,一旦出现当前、历史最优位置相同状况时,借助随机粒子弥补群体多样性,获得改进型粒子群优化算法。免疫优化算法求解P-模型已得到初步研究,文献[14]利用神经网络估计个体的目标值;利用双克隆和双变异策略改进克隆选择算法,获得改进型免疫优化算法,并应用于水库优化调度问题。
综上可知,近年来求解P-模型的研究集中在探讨静态采样下的智能优化算法,但算法的计算资源占用多,计算开销较大,因此,如何高效估计问题的目标值,以及如何有效处理机会约束条件,探讨应用能力强的智能优化算法已成为解决P-模型的关键[6]。为此,本文从生物免疫学中危险理论蕴涵的生物机理出发,设计求解单目标P-模型的微种群免疫优化算法(Micro-Immune Optimization Algorithm,μIOA)。数值比较性实验显示,μIOA在寻优效率、搜索效果和噪声抑制能力等方面均具有明显优势。
1 问题描述考虑如下单目标概率优化问题(P):
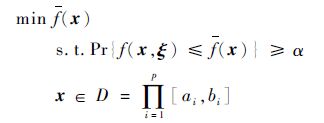
|
式中:D为决策区域; x 为p维决策向量;ai为解向量的分量区间左端点;bi为解向量的分量区间右端点; ξ ∈ R q为分布特性未知的有界随机向量;Pr{·}为概率算子;α为置信水平,0<α≤1;f( x ,ξ )为关于 x 的非线性有界随机函数。 x *∈D称为问题(P)的最优解,若满足以上机会约束的任意 x ∈D,均有f ( x *)≤f ( x )。当在点 x 处 ξ 的样本大小M(简称为 x 的样本大小)给定后,可经由Monte Carlo随机模拟确定f ( x )的估计值[3],即若 ξ 的M个样本为 ξ i,1≤i≤M,不妨设f( x ,ξ i)≤f( x ,ξ i+1),则f ( x )的近似值为f( x ,ξ k),k=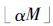
危险理论[15]作为一种较为流行的免疫学理论,是描述免疫系统感知外来物质后,依据免疫细胞受损程度作出相应反应的过程。该理论认为,引起免疫应答的因素不是所有非自我物质,而是损害机体的危险信号(danger),也即只有当受损细胞产生有害信号且触及到抗原呈递细胞(Antigen Presenting Cells,APCs)后,免疫系统才产生应答,而对机体无害的非自我物质不作任何应答。具体而言,当机体中出现被扭曲或凋亡的细胞时,APC是否能被激活依赖于第0信号和邻近细胞的健康情况;一旦它被激活,则向辅助性T细胞传递第1、2信号,其中,第1信号向辅助性T细胞暗示免疫系统已发现危害物质,并发送此物质的危害程度信息,第2信号促使辅助性T细胞产生淋巴因子,致使免疫系统开始应答。从细胞感染角度,免疫细胞分为未感染细胞、易感染细胞和已感染细胞。应答开始时,免疫系统会形成免疫细胞危险区域,通过B细胞的应答,清除危险区域内的已感染细胞。
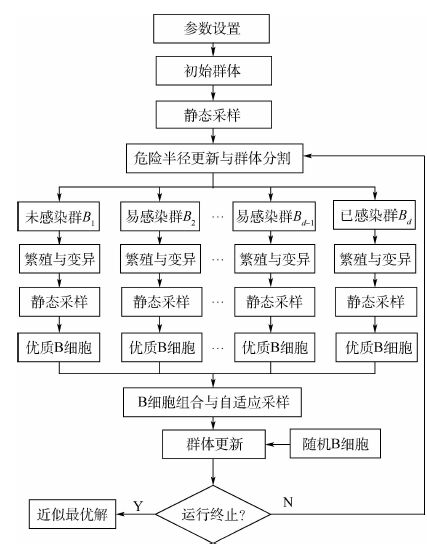
基于以上免疫理论和问题(P),μIOA的运行机制如图 1所示。可知,静态采样的作用是依据相同的样本大小,计算各B细胞的亲和力;进化群体中每个B细胞作为未感染、已感染或易感染细胞,有自身的危险区域;危险半径更新与群体分割是依据算法的迭代数和问题(P)的决策区域对B细胞的危险半径作动态调整,并依据进化群体中B细胞的分布和危险半径将群体划分为未感染、已感染或易感染子群。各子群依据不同的繁殖和变异方式实施进化,然后选出每个进化后的子群中最好的B细胞(各B细胞的危险半径为初始半径)与现存的危险区域中代表性B细胞组合。群体更新是依据组合后 的群体中B细胞的危险半径划分为未感染、已感染或易感染子群,然后抽出各子群中最好的B细胞与随机生成的新B细胞组合,构成新的进化群。
|
| 图 1 μIOA的流程图 Fig. 1 Flowchart of μIOA |
危险理论描述了B细胞如何清除危险信号的过程,为设计μIOA求解P-模型提供了新思路。将危险信号视为问题本身,B细胞视为优化问题(P)的候选解,其包含3种类型:未感染、已感染和易感染B细胞。细胞 x 的亲和力由Sigmoid函数确定:
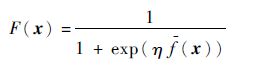
|
(1) |
式中:η∈(0,1)。
基于图 1和问题(P),μIOA可描述如下:
步骤1 输入参数:群体规模N,最大迭代次数Gmax,初始危险半径R,初始最小和最大样本大小m和M,样本参数v。
步骤2 置n←1,随机产生群体规模为N的初始B细胞群A={ x 1,x 2,…,x N} ,依据m和M,计算A中所有B细胞的亲和力,在此
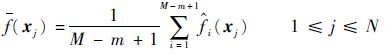
|
(2) |
式中:
步骤3 危险半径更新和群体分割: 依据亲和力,降幂排序群体A中B细胞,借助危险区域,产生未感染群B1,易感染群B2,B3,…,Bd-1和已感染群Bd,d由B细胞的危险半径和亲和力确定,d≤5。
步骤4 A中第i个B细胞繁殖N+2-i个克隆,总繁殖数为N(N+3)/2。
步骤5 Bi中B细胞克隆的变异概率为
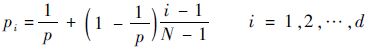
|
(3) |
B1中B细胞克隆实施高斯变异,B2中B细胞克隆实施柯西变异,B3中B细胞克隆实施多项式变异,B4~Bd-1中B细胞克隆实施非均匀变异,Bd中B细胞克隆实施柯西变异,获得变异后的群体B1*,B2*,…,Bd*。
步骤6 经由式(2),计算B1*,B2*,…,Bd*中克隆的亲和力;将各群体中亲和力最高的克隆与步骤3中各群体的最好B细胞组合构成C。
步骤7 执行自适应采样方案,C中B细胞依据获得的样本大小和m,经由式(2),获得各自的亲和力。
步骤8 借助初始危险半径R,按照步骤3的方式产生未感染群、易感染群和已感染群;抽取各子群中亲和力最高的B细胞构成群体F。
步骤9 若|F|< N,则F中的B细胞与随机生成的B细胞构成规模为N的新群体A,其中新的B细胞依据式(2),计算各自的亲和力;若|F|≥N,则F中亲和力较高的N个B细胞更新群体A。其中,|F|为群体F的成员个数。
步骤10 置n←n+1;若n>Gmax,则结束,输出结果;否则,转步骤3。
以上算法中,R在w/(4N)~w/N之间取值,w为决策向量中所有分量的变化幅度的最大值。步骤3的目的是依据B细胞的亲和力,将群体A划分为B1,B2,…,Bd,B1中B细胞的亲和力高于B2中B细胞的亲和力,B2中B细胞的亲和力高于B3中B细胞的亲和力,依此类推。值得指出的是,以上子群划分的方法不同于小生境方法。步骤5要求不同类型的子群依据自身的变异概率,采用不同变异方式对B细胞实施变异,使B细胞多方位勘测局部区域,同时多渠道搜寻高质量和多样的B细胞。步骤8对组合群体进行分割后,在各子群中选出最好B细胞构成新群体,目的在于确保新进化群有足够的多样性。另外,尽管要求步骤4的进化群体的克隆数为N(N+3)/2,但因该算法是小种群优化方法,N被要求取较小的值(5~8之间)[16-18],所以整个算法的搜索效率能得到保证。其次,该算法在步骤7中自适应地确定B细胞的样本大小,进而计算B细胞的亲和力,此有助于提高算法搜索效率和增强辨析进化群体中优质抗体的能力。步骤3和步骤7的具体设计如下:
1) 危险半径更新: x i的危险半径为
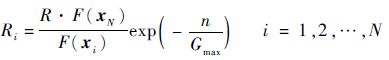
|
(4) |
危险区域为决策区域D中如下超正方体:
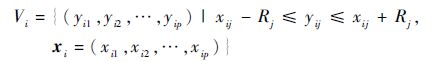
|
2) 群体分割:基于危险半径更新,A中落入超正方体V1中的B细胞构成未感染群B1,然后将B1中的B细胞从A中删除,余下的B细胞中,由亲和力最高的B细胞和其危险区域按同样方式产生子群B2,依此重复,直到产生最后一个子群,不妨设共有d个子群。第2~d-1个子群称为易感染群,第d个子群称为已感染子群Bd。
3) 自适应采样:对于规模为J的B细胞群C,由于随机因素的影响,很容易误认为较差B细胞是优质的,而最好的B细胞是劣质的,因此为了削减计算开销和提高寻优效率,优质B细胞被分配大的样本大小,而劣质B细胞被分配小的样本大小。为此,记C={ x 1,x 2,…,x J}。群体C的样本大小设置为
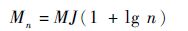
|
(5) |
B细胞 x i依据式(6)获得样本大小:

|
(6) |
另外,随着n的增大,Mn也逐渐增大。为了防止因采样规模过大,导致算法的运行效率受到影响,采用动态的样本规模阈值mn控制B细胞的采样大小,即

|
(7) |
由此,B细胞 x i的样本大小为
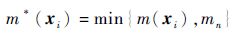
|
(8) |
根据第3节算法描述,μIOA的计算复杂度由步骤3~步骤8确定。在一次迭代周期内,步骤3需将进化群体A划分为子群B1,B2,…,Bd,依次判断B细胞是否在危险区域,因此其计算复杂度为O(N2);步骤4、步骤5执行繁殖和变异,共运行N(N+3)p/2次;步骤6由初始样本大小m和克隆数确定其计算复杂度,即O(mN2);步骤7在最坏情形下,计算复杂度为mn(mn+m)|C|;在步骤8中,群体C中B细胞需依据亲和力进行降幂排序和群体分割,均需运行|C|(|C|-1)/2 次,所以步骤8的计算复杂度为O(|C|2)。概括起来,结合|C|≤2N以及m较小,μIOA在最坏情形下的计算复杂度为
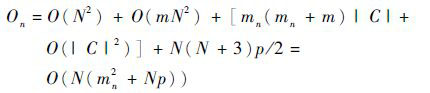
|
(9) |
由于问题(P)包含随机向量,当样本大小较大时,常规智能优化算法求解此问题均需较大计算量,特别当采用静态采样方法计算目标函数值时,若试图获得较好效果,必借助较大的样本大小来补偿算法的噪声抑制能力。然而,由式(9)获知,μIOA是一种自适应采样优化算法,其计算复杂度由N、p和mn确定;算法在进化初期,搜索速度快且执行大范围搜索;在进化后期,搜索偏慢,执行局部搜索。
5 数值实验本实验在Window XP/CPU/3.30 GHz,RAM/2.98 GB,VC+ +环境下进行。为比较分析μIOA的性能,选取具有代表性的三种智能优化算法参与比较,即Xiao-SPSO[13]、Ai-SPSO[12]和GA[3]。测试事例包括3个理论测试问题和1个工程优化问题。为避免随机因素对算法搜索质量的影响,每种算法对每个测试问题均独立运行100次。之后,各自获得的100个结果被用于执行统计分析。各算法的终止准则是评价次数为104。另外,参与比较的算法在相应文献中均要求个体具有较大样本大小,这使得算法的搜索效率受到极大影响;经由算法调试,以及兼顾效率和效果等因素,设置个体样本大小为300,其他参数的设置由相应文献获知。其次,μIOA主要包括3个可调参数:R、M和v。M和v为控制个体采样大小的参数,若M和v偏小,搜索效果不理想;反之,则算法搜索效率降低;它们可在5~10之间取值。进一步,R是一个子群划分参数,当R较小时,算法群体多样 性受影响;反之,则算法进化单一。R在w/(4N)~ w/N之间取值。算法调试后,μIOA的参数设置为N=5,R=1,m=2,M=10,v=5,η依问题而定。为使各算法获得的目标值与理论值贴近,所获解均需重新估计其目标值,样本大小为105。
问题1
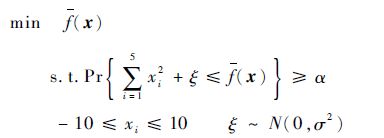
|
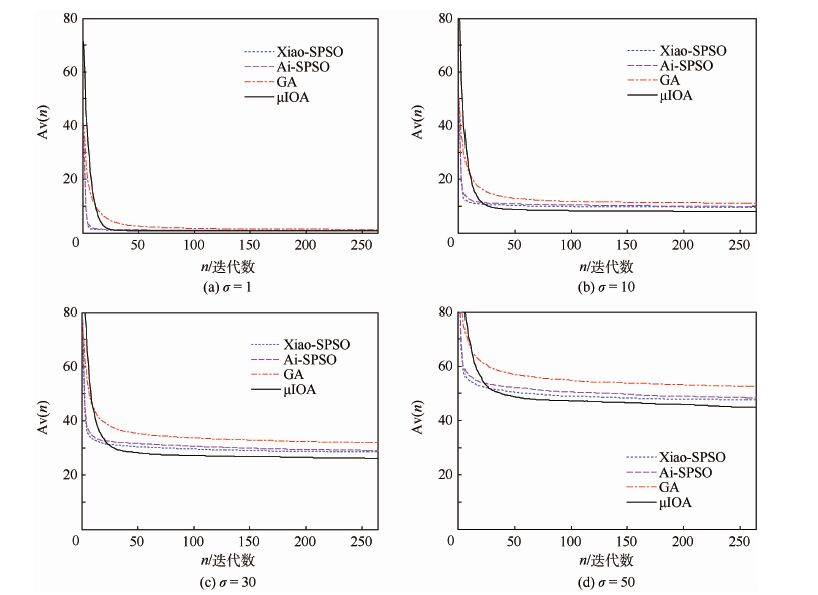
该问题是经由文献[18]的Sphere函数转化获得。尽管此问题是一个5维的简单随机优化问题,但噪声强度σ取较大值时,随机因素对优化质量的影响较大,求解变得困难,取α=0.9。若σ取1、10、30或50,则该问题的理论最优值依次为1.281 6、12.816 0、38.450 0和64.083 3。各算法求解100次后,获得的最好目标值的统计结果和平均运行时间如表 1所示,平均搜索曲线如图 2所示。表 1中:min、max、mean和St.Dev为算法100次运行获得100解的最小、最大、平均目标值和目标值的均方差;CI和AR分别为置信区间和平均执行时间。图 2中:Av(n)为算法100次运行后获得第n代群体的最小目标值的均值。
| σ | 算法 | min | max | mean | St.Dev | CI | AR/(′′) |
| 1 | Xiao-SPSO | 1.280 1 | 1.423 1 | 1.322 8 | 0.028 6 | [1.318 1,1.327 6] | 1.53 |
| Ai-SPSO | 1.282 2 | 1.432 8 | 1.324 6 | 0.030 5 | [1.319 5,1.329 6] | 1.50 | |
| GA | 1.324 8 | 1.883 1 | 1.537 8 | 0.135 4 | [1.515 4,1.560 3] | 1.49 | |
| μIOA | 1.277 9 | 1.377 3 | 1.311 9 | 0.019 7 | [1.308 7,1.315 2] | 0.63 | |
| 10 | Xiao-SPSO | 12.833 4 | 13.618 8 | 13.140 5 | 0.176 1 | [13.111 3,13.169 8] | 1.50 |
| Ai-SPSO | 12.754 5 | 14.009 9 | 13.160 4 | 0.252 5 | [13.118 5,13.202 3] | 1.50 | |
| GA | 12.883 5 | 15.606 0 | 13.888 8 | 0.589 3 | [13.790 9,13.986 6] | 1.49 | |
| μIOA | 12.781 7 | 13.549 6 | 13.111 2 | 0.179 8 | [13.081 4,13.141 1] | 0.64 | |
| 30 | Xiao-SPSO | 38.273 9 | 41.828 7 | 39.319 6 | 0.685 5 | [39.205 7,39.433 4] | 1.50 |
| Ai-SPSO | 38.285 0 | 42.274 9 | 39.403 7 | 0.661 5 | [39.293 8,39.513 5] | 1.50 | |
| GA | 38.743 7 | 45.725 2 | 40.830 7 | 1.367 3 | [40.603 7,41.057 7] | 1.50 | |
| μIOA | 38.478 5 | 41.435 1 | 39.405 7 | 0.553 6 | [39.313 7,39.497 6] | 0.83 | |
| 50 | Xiao-SPSO | 63.915 0 | 70.895 6 | 65.731 9 | 1.164 6 | [65.538 5,65.925 3] | 1.50 |
| Ai-SPSO | 63.732 3 | 68.823 8 | 65.573 3 | 1.075 8 | [65.394 7,65.751 9] | 1.50 | |
| GA | 64.476 6 | 74.933 1 | 68.000 4 | 2.271 7 | [67.623 2,68.377 6] | 1.50 | |
| μIOA | 63.883 7 | 70.992 7 | 66.456 7 | 1.517 0 | [66.204 8,66.708 6] | 1.15 |
|
| 图 2 问题1的平均搜索曲线比较 Fig. 2 Comparison of average search curves for Problem 1 |
由表 1可知,当噪声强度σ=1或10时,μIOA比Xiao-SPSO 和Ai-SPSO能获得更好的解质量,Xiao-SPSO 和Ai-SPSO的解质量相近,GA的解质量较差,此可由图 2得到验证。另一方面,μIOA、Xiao-SPSO 和Ai-SPSO的搜索效果较稳定,各自在不同噪声强度下获得的平均值与理论值的偏差较小,且获得的置信区间较窄,但GA较差。当σ=30时,μIOA、Xiao-SPSO 和Ai-SPSO的解质量相近,GA的解质量较差,μIOA的搜索效果最稳定,且获得的置信区间较窄。当σ=50时,Xiao-SPSO 和Ai-SPSO获得的效果比μIOA获得的效果稍好。从执行效率看,μIOA的执行效率明显高于其他算法的执行效率; 参与比较的算法的平均执行效率相差不明显。整体上,μIOA求解问题1有一定的优势。另外,表 1也表明,随着噪声强度的增大,以上各项指标的值相应增大,问题求解的难度相应加大。
问题2

|
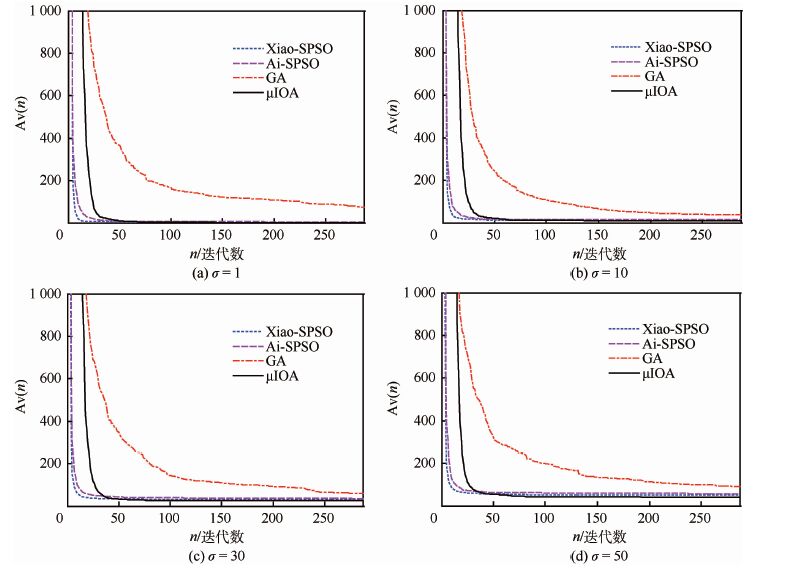
该问题是经由文献[18]的Rosenbrock函数转化获得,其变量之间存在较强的耦合性,搜索其最优解较难。取置信水平α=0.9。由于此问题的机会约束条件中确定性函数的最小值为0,所以当σ为1、10、30或50时,该问题的理论最优值依次与问题1获得的理论值是相同的。以上算法获得的统计结果如表 2所示,平均搜索曲线如图 3所示。
| σ | 算法 | min | max | mean | St.Dev | CI | AR/(′′) |
| 1 | Xiao-SPSO | 1.285 1 | 9.834 6 | 3.610 5 | 1.295 8 | [3.395 3,3.825 6] | 1.72 |
| Ai-SPSO | 1.817 6 | 12.659 6 | 4.329 7 | 1.502 6 | [4.080 2,4.579 2] | 1.68 | |
| GA | 3.100 3 | 889.281 0 | 63.838 3 | 152.833 0 | [38.461 9,89.214 7] | 1.69 | |
| μIOA | 1.287 3 | 5.873 1 | 2.417 6 | 1.102 2 | [2.234 6,2.600 6] | 0.75 | |
| 10 | Xiao-SPSO | 12.863 9 | 19.934 3 | 15.711 2 | 1.337 6 | [15.489 1,15.933 3] | 1.70 |
| Ai-SPSO | 13.536 9 | 23.544 1 | 16.370 1 | 1.698 8 | [16.088 0,16.652 1] | 1.69 | |
| GA | 15.483 2 | 318.454 0 | 36.822 2 | 52.716 7 | [28.069 1,45.575 3] | 1.68 | |
| μIOA | 12.757 2 | 17.835 4 | 14.299 5 | 1.298 5 | [14.083 9,14.515 1] | 0.73 | |
| 30 | Xiao-SPSO | 38.906 6 | 45.734 8 | 42.096 9 | 1.491 9 | [41.849 2,42.344 7] | 1.70 |
| Ai-SPSO | 38.364 2 | 46.901 1 | 42.886 8 | 1.669 9 | [42.609 6,43.164 1] | 1.68 | |
| GA | 40.001 0 | 341.166 0 | 65.544 4 | 47.410 7 | [57.672 3,73.416 5] | 1.69 | |
| μIOA | 39.064 8 | 44.282 8 | 41.080 8 | 1.362 3 | [40.854 6,41.307 0] | 0.73 | |
| 50 | Xiao-SPSO | 64.491 9 | 73.881 8 | 68.375 1 | 1.692 6 | [68.094 0,68.656 1] | 1.69 |
| Ai-SPSO | 65.139 6 | 75.697 2 | 69.772 2 | 2.183 3 | [69.409 7,70.134 8] | 1.68 | |
| GA | 68.293 3 | 349.510 0 | 98.991 4 | 58.956 7 | [89.202 3,108.781 0] | 1.68 | |
| μIOA | 64.492 9 | 74.245 5 | 67.943 3 | 1.958 1 | [67.618 2,68.268 4] | 0.73 |
|
| 图 3 问题2的平均搜索曲线比较 Fig. 3 Comparison of average search curves for Problem 2 |
表 2中的平均值说明,μIOA所获解质量明显优于参与比较的算法的解质量,Xiao-SPSO和 Ai-SPSO次之,而GA获得的效果最差。另一方面,经由以上均方差,μIOA、Xiao-SPSO 和Ai-SPSO的搜索效果较为稳定(见图 3),而GA较差。其次,经由以上平均运行时间,参与比较的算法的执行效率没有明显差异,μIOA的执行效率是这些算法的2倍多。因此,μIOA求解问题2具有明显优势。
问题3
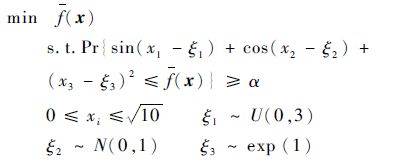
|
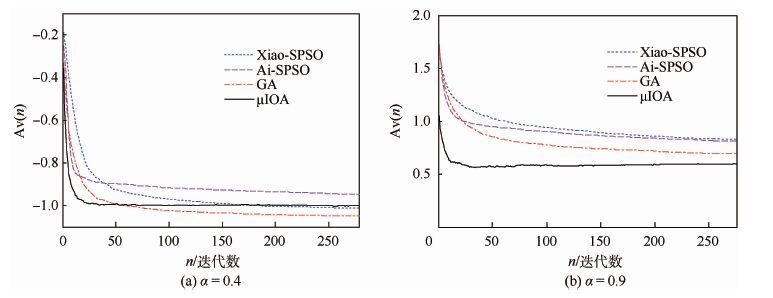
该问题是经由文献[12]中E-模型转化获得的多模态概率优化问题。由于随机变量的分布类型多样化,机会约束中决策变量受到随机变量扰动的干扰,所以算法求解较为困难。取置信水平α为0.4、0.9,该问题的理论最优解尚不清楚。以上算法获得的统计结果如表 3所示,平均搜索曲线如图 4所示。
| α | 算法 | min | max | mean | St.Dev | CI | AR/(′′) |
| 0.4 | Xiao-SPSO | -0.817 2 | -0.028 9 | -0.755 0 | 0.122 8 | [-0.775 3,-0.734 6] | 4.71 |
| Ai-SPSO | -0.811 7 | -0.055 8 | -0.708 7 | 0.183 5 | [-0.739 1,-0.678 2] | 4.63 | |
| GA | -0.827 5 | -0.747 8 | -0.800 9 | 0.015 3 | [-0.803 4,-0.798 3] | 4.64 | |
| μIOA | -0.823 6 | -0.700 9 | -0.790 6 | 0.020 8 | [-0.794 1,-0.787 1] | 1.11 | |
| 0.9 | Xiao-SPSO | 1.212 4 | 2.181 2 | 1.518 6 | 0.237 2 | [1.479 2,1.558 0] | 2.73 |
| Ai-SPSO | 1.224 1 | 2.204 7 | 1.502 9 | 0.216 0 | [1.467 0,1.538 7] | 2.71 | |
| GA | 1.186 7 | 2.059 6 | 1.350 3 | 0.192 0 | [1.318 5,1.382 2] | 2.71 | |
| μIOA | 1.187 7 | 1.513 0 | 1.280 0 | 0.069 8 | [1.268 4,1.291 6] | 1.23 |
|
| 图 4 问题3的平均搜索曲线比较 Fig. 4 Comparison of average search curves for Problem 3 |
经由表 3的平均值获知,在低置信水平下(α=0.4),以上问题的解的可信度低,求解较易;GA和μIOA获得的解质量较贴近且较好;经由均方差值获知,此两算法的搜索效果较稳定;然而,Xiao-SPSO和Ai-SPSO的解质量相对较差,搜索效果欠稳定。在高置信水平下(α=0.9),以上问题的解的可信度高,但求解偏难。
在此情形下,μIOA在所获解质量和搜索效果的稳定性方面均优于其他算法,GA次之;Xiao-SPSO和 Ai-SPSO的解质量相近,且劣于μIOA和GA。 特别值得强调的是,与GA相比,Xiao-SPSO和 Ai-SPSO求解问题1和问题2能获得较好解质量,但求解问题3获得的解质量差于GA获得的解质量,表明Xiao-SPSO和 Ai-SPSO求解多模态概率优化问题时存在群体多样性不足的缺陷。另一方面,在执行效率方面,参与比较的算法具有相近的执行效率,μIOA的执行效率至少是这些算法的2倍。
问题4 公交车调度
将每天公交车运营时间分成K个时段,xi为公交车发车间隔,1≤i≤K,N(xi)为第i个时段内发车间隔为xi情况下的乘客总数,r为单一公交票价,μs为单位乘客剩余的货币价值,ef和ew分别为票价和发车间隔的乘客需求弹性因子,μ0为单位车辆在单位时间内的运营成本,ti为运行时间段,tir为第i个时段开出的第r班车全程的开行时间,τ为平均一位乘客用于上下车的平均值,μw为乘客等待时间的时间价值。基于此,文献[19]获得多时段公交发车间隔优化问题的E-模型,现将其转化为P-模型:
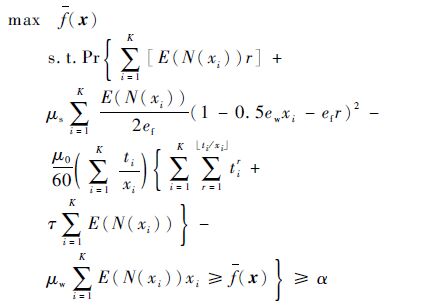
|
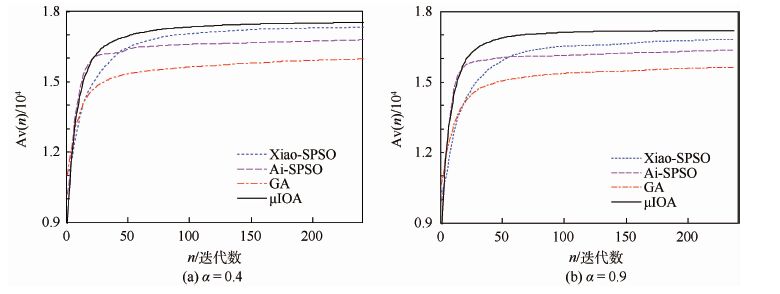
模型中的参数设置由文献[19]获知,特别地,K=6。此问题是一种非连续、非线性的机会约束规划问题。取置信水平α为0.4、0.9,以上算法获得的统计结果如表 4所示,算法的平均搜索曲线如图 5所示。
经由表 4可知,在不同置信水平下,μIOA所获解的平均值均大于其他算法获得的平均值,且均方差均小于其他算法获得的均方差,因此μIOA获得的解质量最好且搜索效果最稳定; 其次,Xiao-SPSO的解质量和搜索效果次之,Ai-SPSO的解质量和搜索效果比GA好。另外,在以上置信水平设置下,参与比较的算法的执行效率差异不明显;μIOA的执行效率至少是这些算法的1.5倍。
| α | 算法 | min | max | mean | St.Dev | CI | AR/(′′) |
| 0.4 | Xiao-SPSO | 16 506.8 | 17 498.7 | 17 292.9 | 257.449 0 | [17 250.1,17 335.6] | 488.53 |
| Ai-SPSO | 14 149.9 | 17 430.8 | 16 770.5 | 547.360 0 | [16 679.6,16 861.3] | 507.26 | |
| GA | 12 357.1 | 17 414.4 | 15 954.0 | 832.824 0 | [15 815.7,16 092.2] | 444.24 | |
| μIOA | 17 231.9 | 17 505.4 | 17 436.5 | 52.579 8 | [17 427.8,17 445.2] | 269.99 | |
| 0.9 | Xiao-SPSO | 16 010.2 | 17 029.9 | 16 752.5 | 289.599 0 | [16 704.4,16 800.6] | 493.90 |
| Ai-SPSO | 12 148.8 | 16 969.9 | 16 324.8 | 703.621 0 | [16 208.0,16 441.7] | 534.86 | |
| GA | 13 081.7 | 16 857.9 | 15 573.8 | 781.660 0 | [15 444.0,15 703.6] | 516.73 | |
| μIOA | 16 849.0 | 17 212.5 | 17 003.0 | 39.528 4 | [16 996.4,17 009.5] | 271.18 |
|
| 图 5 问题4的平均搜索曲线比较 Fig. 5 Comparison of average search curves for Problem 4 |
鉴于概率优化是一类具有广泛应用背景和求解较难的不确定性规划问题,基于免疫学中较为关注的危险理论和问题具有的固有特性,建立适用于此类问题的微种群免疫优化算法(μIOA)。μIOA经理论分析和实验验证表明:
1) 计算复杂度依赖于迭代数、变量维数和群体规模。
2) 具有群体规模小、可调参数少、自适应能力强和执行效率高等优点。
3) 搜索效果具有明显优势,噪声抑制能力强,对复杂的P-模型具有一定的应用潜力。
尽管μIOA已具有明显优势,但在处理复杂优化问题(如问题4)时,搜索效果欠稳定,辨析优质个体的能力有待增强。
| [1] | LIU B D. Uncertainty theory:A branch of mathematics for modeling human uncertainty[M]. Berlin: Springer-Varlag, 2010 : 81 -113. |
| [2] | 麻倩倩.一类随机机会约束规划的算法及应用研究[D].保定:华北电力大学,2006:1-28. MA Q Q.Research on the algorithm and application for a class of stochastic chance-constrained programming[D].Baoding:North China Electric Power University,2006:1-28(in Chinese). |
| [3] | LIU B D. Theory and practice of uncertain programming[M]. 2nd ed Berlin: Springer-Varlag, 2009 : 25 -55. |
| [4] | 丁晓东, 吴让泉, 邵世煌. 含有模糊和随机参数的混合机会约束规划模型[J]. 控制与决策, 2002, 17 (5) : 587 –590. DING X D, WU R Q, SHAO S H. Hybrid programming model with fuzzy and stochastic parameters[J]. Control and Decision, 2002, 17 (5) : 587 –590. (in Chinese) |
| [5] | NING Y,TANG W,WANG H.Hybrid genetic-SPSA algorithm based on random fuzzy simulation for chance-constrained programming[M]//WANG L,JIN Y.Fuzzy systems and know-ledge discovery.Berlin:Springer-Varlag,2005:332-335. |
| [6] | 刘宝碇, 赵瑞清. 随机规划与模糊规划[M]. 北京: 清华大学出版社, 1998 : 74 -94. LIU B D, ZHAO R Q. Stochastic programming and fuzzy programming[M]. Beijing: Tsinghua University Press, 1998 : 74 -94. (in Chinese) |
| [7] | LIU X, LIN L, ZANG D. Stochastic programming models and hybrid intelligent algorithm for unbalanced bidding problem[J]. Computer and Information Science, 2009, 2 (1) : 188 –194. |
| [8] | ZHANG H, HA M, XING H. Chance-constrained programming on Sugeno measure space[J]. Expert Systems with Applications, 2011, 38 (9) : 11527 –11533. DOI:10.1016/j.eswa.2011.03.029 |
| [9] | 肖宁, 曾建潮. 基于随机模拟与 PSO 算法相结合的随机机会约束规划算法[J]. 计算机应用与软件, 2009, 26 (4) : 40 –41. XIAO N, ZENG J C. Algorithm of stochastic chance-constrained programming based on combination of random simulation and PSO algorithm[J]. Computer Application and Software, 2009, 26 (4) : 40 –41. (in Chinese) |
| [10] | 肖宁. 求解随机机会约束规划的混合智能算法[J]. 计算机工程与应用, 2010, 46 (22) : 43 –46. XIAO N. Solving stochastic chance-constrained programming problems with hybrid intelligent algorithm[J]. Computer Engineering and Applications, 2010, 46 (22) : 43 –46. (in Chinese) |
| [11] | 卢福强, 黄敏, 王兴伟. 虚拟企业风险管理的机会约束规划模型及算法[J]. 信息与控制, 2009, 38 (4) : 399 –405. LU F Q, HUANG M, WANG X W. Chance-constraint programming model and algorithm for risk management of virtual enterprise[J]. Information and Control, 2009, 38 (4) : 399 –405. (in Chinese) |
| [12] | 艾宁宁.基于混合智能算法求解随机期望值模型和机会约束规划[D].西安:长安大学,2012:1-41. AI N N.A study hybrid algorithm solving stochastic expected value models and chance-constrained programming[D].Xi'an:Chang'an University,2012:1-41(in Chinese). http://cdmd.cnki.com.cn/article/cdmd-10710-1013017779.htm |
| [13] | XIAO N. An algorithm for solving stochastic chance-constrained programming problem[J]. Advanced Materials Research, 2014, 912-914 : 1138 –1141. DOI:10.4028/www.scientific.net/AMR.912-914 |
| [14] | 段富, 杨茸. 求解随机机会约束规划的混合智能算法及应用[J]. 计算机应用, 2012, 32 (8) : 2230 –2234. DUAN F, YANG R. Hybrid intelligent algorithm for solving stochastic chance-constrained programming and its application[J]. Journal of Computer Applications, 2012, 32 (8) : 2230 –2234. (in Chinese) |
| [15] | MATZINGER P. Tolerance,danger,and the extended family[J]. Annual Review of Immunology, 1994, 12 : 991 –1045. DOI:10.1146/annurev.iy.12.040194.005015 |
| [16] | WU D, GAN D Q, JIANG J N. An improved micro-particle swarm optimization algorithm and its application in transient stability constrained optimal power flow[J]. International Transactions on Electrical Energy Systems, 2014, 24 : 395 –411. DOI:10.1002/etep.v24.3 |
| [17] | VIVEROS-JIMÉNEZ F, MEZURA-MONTES E, GELBUKH A. Empirical analysis of a micro-evolutionary algorithm for numerical optimization[J]. International Journal of Physical Sciences, 2012, 7 (8) : 1235 –1258. |
| [18] | ABIYEV R H, TUNAY M. Optimization of high-dimensional functions through hypercube evaluation[J]. Computational Intelligence and Neuroscience, 2015, 2015 : 1 –11. |
| [19] | 许旺土, 何世伟, 宋瑞, 等. 多时段公交发车间隔优化的随机期望值模型[J]. 北京理工大学学报, 2009, 29 (8) : 676 –679. XU W T, HE S W, SONG R, et al. Stochastic expected value model for multiple bus headways optimization[J]. Transaction of Beijing Institute of Technology, 2009, 29 (8) : 676 –679. (in Chinese) |



