2. 北京航空航天大学 可靠性与环境工程技术国防科技重点实验室, 北京 100083
2. Science and Technology on Reliability and Engineering Laboratory, Beijing University of Aeronautics and Astronautics, Beijing 100083, China
由于航天在轨产品服役期内无法维护,在研制时需要对其整个服役期内的可靠度进行分析评价,而其中机械产品由于样本量少或样本缺失使得一些参数除随机性外,往往还存在大量的模糊性问题,此时不能采用常规的概率理论的处理方式[1-2]。国内外学者关于机械产品模糊时变可靠性的研究起步较晚。Ayyub和Lai[3]在机械零部件的模糊可靠性的求解问题上进行了初步的研究,提出了模糊可靠度定义;国内学者黄洪钟[4-5]和王磊[6]等对广义应力和强度在模糊随机变量的问题进行了一系列研究,但这些研究都是处于静态的可靠性分析范畴之内。考虑机械产品的广义强度的退化性,Sickert等[7]提出了基于模糊随机过程的结构时变可靠性分析方法;方永峰[8]、Gao[9]和Wang[10]等提出了多次载荷作用下的基于广义应力强度干涉模型的模糊应力以及随机强度过程的模糊可靠度求解方法,但上述研究并未考虑失效准则的模糊性,即认为产品只有“成功”和“失效”两个状态,但实际工况中,由于对故障机理、失效模式等的认知不确定性,使得常规“两态”假设无法满足实际要求,因此在上述分析的基础上,对于失效判据的模糊推广很有必要和实际价值。
针对机械产品的时变可靠性分析问题,Andrieu-Renaud等[11]提出了一种结构可靠度计算方法—PHI2,通过计算极限状态面在单位时间从安全域到失效域的平均穿阈次数进而得到可靠度或失效概率。Cognard等[12]在此方法的基础上改进了上穿率的计算,提出了新PHI2方法。这种方法采用随机过程描述广义强度或应力,考虑了随机过程中的时间相关性,目前应用较广泛。
本文在以上关于机械产品模糊时变可靠性研究的基础上,针对机械产品存在退化强度、广义模糊应力和模糊判据的情况进行可靠性建模分析,应用相关概率理论、模糊理论对问题进行处理和转化,应用广义应力强度干涉模型建立产品的模糊时变可靠性模型,并采用FPHI2(Fuzzy PHI2)方法进行时变可靠度求解。最后,用此方法对数值算例和空间双轴驱动机构中谐波减速器的磨损失效问题进行模糊时变可靠性建模分析,验证此方法的工程实用性。
1 模糊时变可靠性模型 1.1 模糊随机应力强度干涉模型定义[8] 某一时间段[0,t]内,对于∀τ∈[0,t],


|
(1) |
在τ时刻,假设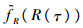
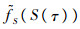

|
(2) |
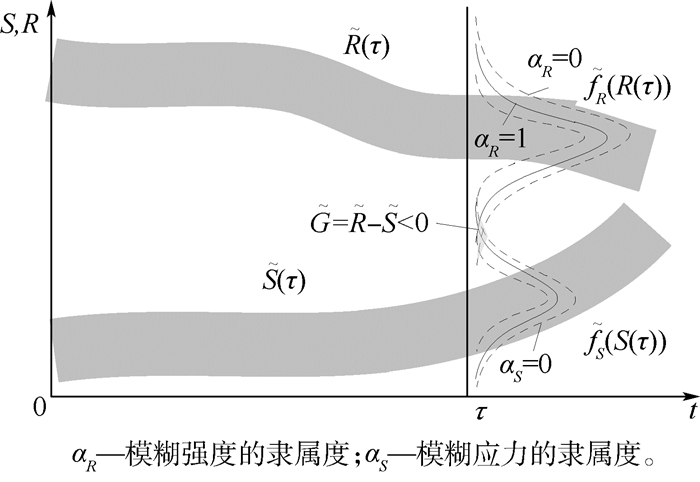
在时间[0,t]内模糊应力-强度干涉模型如图 1所示。
|
| 图 1 在时间τ内的模糊随机应力-强度干涉模型 Fig. 1 Fuzzy random stress-resistance interference model in time τ |
设τ时刻的模糊极限状态面为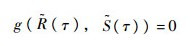

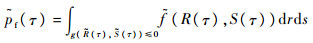
|
(3) |
把失效准则看作模糊事件,机械产品功能函数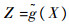
1) Z<0不表示产品完全失效,只是其适用性有所降低,Z值越小,降低的程度越多。
2) Z>0不表示产品一定处于安全区域。
3) Z=0不是产品可靠和失效状态的界限。
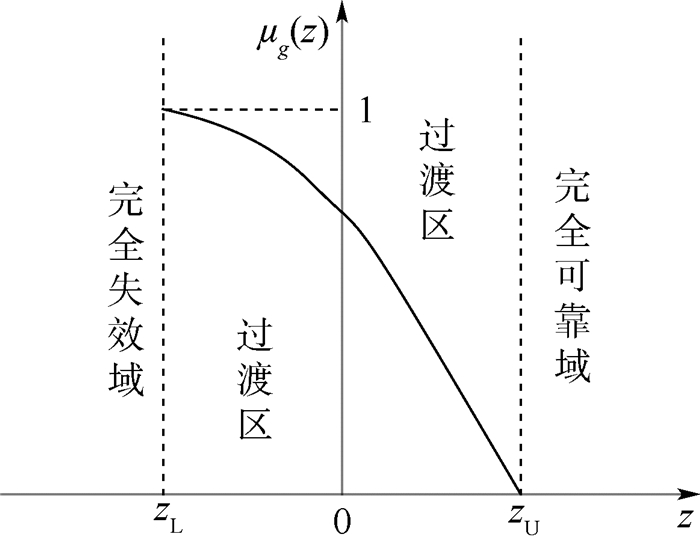
通过将原有的确定失效判据进行拓展,结合工程经验和专家意见得到一个表示产品从完全失效到完全完好的区间[zL,zU],描述事件状态程度隶属函数μg(z)可以用来表示这一过渡情况,其数值越大则产品失效的倾向越大,数值越小,失效的倾向越小,如图 2所示。
|
| 图 2 模糊失效判据 Fig. 2 Fuzzy failure criterion |
设产品的失效模糊随机事件可表示为
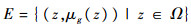
|
(4) |
式中:z∈Ω为产品模糊随机空间Ω中的随机变量;μg(z)为描述事件状态程度的隶属函数,设z的概率密度函数为fZ(z),则产品失效事件E的概率为

|
(5) |
式中:μg(z)应为递减函数,使得产品的失效程度随z值的减小而增大[14],其范围为0≤μg(z)≤1。
假设随机变量X的联合概率密度函数可表示为fX(x),产品的失效事件E的概率可表示为
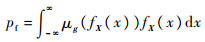
|
(6) |
根据前面的描述,结合随机变量的概率分布函数的定义,可以把1-μg(z)看作一个新的随机变量(记为Z′)的概率分布函数,则[14]
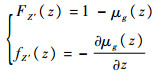
|
(7) |
式中:FZ′(z)和fZ′(z)分别为Z′的分布函数和概率密度函数。
于是产品的模糊随机失效域可以描述为{X|g(X)≤Z′},等效的功能函数为Ze=g(X)-Z′,且仅含随机变量,此时可以采用常规的概率可靠度求解方法进行计算。
若μg(z)为递增函数则可以把μg(z)看作一个新的随机变量(记为Z")的概率分布函数,同理[14]:

|
(8) |
这种情况下产品的失效域描述为{X|g(X)≥Z"},对应的等效功能函数为Ze=Z"-g(X),也可以使用常规的概率可靠度求解方法计算产品的失效概率和可靠度。
1.3 广义模糊应力的处理产品的功能函数中存在模糊随机变量,记为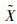
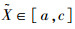

|
(9) |
根据模糊理论,给定α水平下的截集为

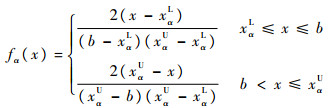
|
(10) |
因此可以把模糊随机变量处理成为概率密度函数中含有参数α的随机变量,其中0≤α≤1。
1.4 模糊时变可靠性模型的建立综合上述情况,用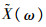
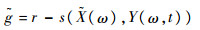
|
(11) |
设产品的失效模糊随机事件可表示为
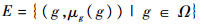
|
(12) |
式中:Ω为模糊随机空间;μg(g)为模糊失效状态的隶属函数,且0≤μg(g)≤1。
设μg(g)为增函数,根据1.2节的方法,引入随机变量Z"来表示失效判据的模糊性,它的概率分布函数和概率密度函数形如式(8),得到此时的模糊失效域和等效的功能函数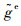
采用1.3节的方法处理模糊随机变量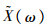
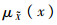
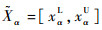
至此,含有模糊随机变量和模糊判据情况下的等效功能函数转化为给定α水平下的仅含随机变量的功能函数geα:
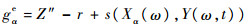
|
(13) |
进而给定α水平下的产品的失效概率为

|
(14) |
后续通过对α的积分可以求得产品的失效概率。
2 模糊时变可靠度求解 2.1 时变可靠度求解方法在时间区间[0,t]内,对∀τ∈[0,t],设产品的极限状态函数为g(τ,X(τ,ω)),产品失效集可通过以下事件来表示:
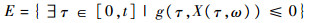
|
(15) |
产品在时间区间[0,t]内的累积失效概率为

|
(16) |
在τ时刻的瞬时失效概率定义为
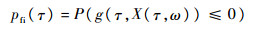
|
(17) |
定义上穿率为[11]
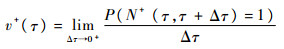
|
(18) |
式中:N+(τ,τ+Δτ)为时间段[τ,τ+Δτ]内的穿阈次数。根据文献[16]中的方法,上穿率的计算方法为
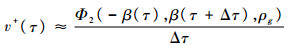
|
(19) |
式中:Φ2为二维正态分布的概率分布函数;β(τ)和β(τ+Δτ)分别为通过静态可靠度算法如一阶可靠性方法(First Order Reliability Method,FORM)、二阶可靠性方法(Second Order Reliability Method,SORM)计算得到的τ和τ+Δτ时刻的可靠性指标;ρg为相关系数。
于是累积失效概率为
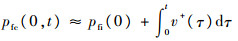
|
(20) |
在时间区间[0,t]内,α水平下产品失效集可通过下列事件来表示:
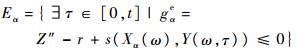
|
(21) |
α水平下产品在时间区间[0,t]内的累积失效概率表示为
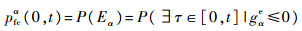
|
(22) |
在τ时刻的瞬时失效概率定义为
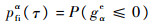
|
(23) |
当α水平下的等效极限状态函数中包含随机过程时,由于随机过程的时间相关性,不同时间点的可靠度具有相关性,因此基于上穿方法处理。设Nα+(0,t)表示α水平下的等效极限状态曲面在[0,t]内从安全域向失效域的上穿次数,则[0,t]内的累积失效概率为

|
(24) |
若产品在0时刻失效,则该动态问题等效于0时刻的静态问题,可用静态可靠性方法计算。若产品在0时刻没有失效,则这个问题等效于条件概率

|
(25) |
在时刻τ∈[0,t],α水平下的上穿率为
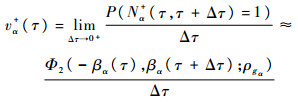
|
(26) |
式中:βα(τ)和βα(τ+Δτ)分别为α水平下利用静态可靠度算法FORM,计算的τ和τ+Δτ时刻的可靠度指标,通过等概率转换得到二维标准正态空间中的示意图,见图 3;ρgα表示α水平下的相关系数,计算方法如下:

|
(27) |
式中:nα(τ)和nα(τ+Δτ)分别为α水平下τ和τ+Δτ时刻下二维标准正态空间中极限状态面的单位外法向量,具体见图 3所示。
所以[0,t]内α水平下的累积失效概率为

|
(28) |
考虑模糊随机变量的隶属度水平,则在[0,t]内产品的累积失效概率为

|
| 图 3 根据FORM计算两时刻的可靠度指标 Fig. 3 Computation of reliability index of two instances according to FORM |
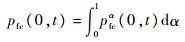
|
(29) |

|
(30) |
设某产品的功能函数为

考虑失效判据的模糊性,设极限状态的隶属函数为

|
(31) |
则引入随机变量Z′使得
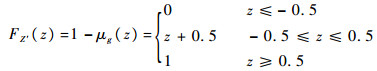
|
(32) |
等效功能函数为
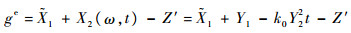
|
(33) |
设模糊随机变量

|
(34) |
用截集法处理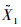
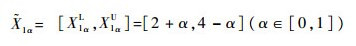
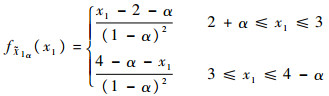
|
(35) |
所以α水平下的等效功能函数为

|
(36) |
式(36)中各个随机变量的分布表见表 1。
| 变量 | 分布类型 | 均值 | 标准差 |
| Y1 | 正态分布 | 0 | 0.01 |
| Y2 | 正态分布 | 480 | 48 |
| Z′ | 均匀分布 | 0 | 1/12 |
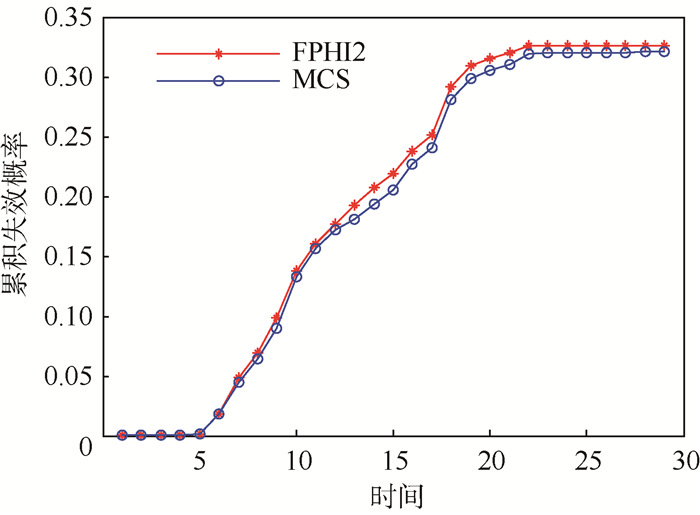
利用本文提出的可靠度计算方法可以求得此数值案例的累积失效概率,见图 4。
|
| 图 4 累积失效概率 Fig. 4 Cumulative failure probability |
从图 4中可以看出采用本文提出的模糊时变可靠性建模及可靠度求解方法得到的累积失效概率随时间呈上升趋势,在t≤5时可靠度很高,之后的5<t≤20时,累积失效概率随时间增长较快,达到0.32,最后的时间内趋于平缓,这是符合实际的。另外FPHI2和蒙特卡罗仿真(Monte Carlo Simulation,MCS)两条曲线贴合程度较高,其相对误差最大不超过10%,可见本文中的方法是相对准确的。
3.2 工程案例谐波减速器是卫星天线的动力传输部分,主要由带有内齿圈的刚性齿轮,带有外齿圈的柔性齿轮和波发生器组成,具体结构如图 5所示。

|
| 图 5 谐波减速器 Fig. 5 Harmonic reducer |
谐波减速器的故障模式主要由磨损机理引起的,磨损是接触表面在相对运动过程中造成的固体表面损伤,它包括表面活性层的材料改变,表面局部材料的断裂,磨粒形成并脱离接触区等十分复杂的过程[17]。为计算简化,以Archard磨损公式建立退化模型,对磨损过程进行建模以做近似的估算和预计[18]。
接触表面相对滑动时,磨损体积W可用式(37)进行计算:

|
(37) |
式中:k为磨损系数;P为接触面间的法向载荷;S为相对滑动位移;H为材料硬度。
在使用中,实际磨损量是随时间变化的,另外零件加工制造过程中的热处理、表面处理等工艺措施会导致材料硬度属于模糊随机变量,所以
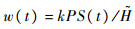
|
(38) |
根据实际测量数据和相关的专家经验,认为硬度

|
(39) |
则α水平下的概率密度函数为

|
(40) |
通过计算可得α水平下材料硬度的均值和方差分别为

|
(41) |
根据Hertz接触理论和轮齿啮合的相关几何条件计算接触面间的法向载荷[18]:

|
(42) |
式中:σ为接触应力,通过多次有限元仿真结果,认为它服从均值为106.111 5 MPa、变异系数为0.14的极值I型分布;L为接触线长度;m为模数;z1和z2分别为刚性齿轮和柔性齿轮的齿数;ν1和ν2分别为刚性齿轮和柔性齿轮的泊松比;E1和E2分别为刚性齿轮和柔性齿轮的弹性模量;θ为压力角。
已知k=10-9,m=0.2,z1=202,z2=200,sinθ=0.342,假设谐波减速器的输入转速为200(°)/s,这里S(t)=1.752×107St。[W]为许用磨损量,将其看成均值为5 mm3、变异系数为0.1的正态分布随机变量[19]。式(38)代入相关数据整理得
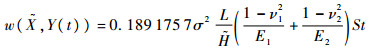
|
(43) |
所以谐波减速器的功能函数为

|
(44) |
考虑模糊判据,认为磨损状态为模糊随机变量,其隶属函数为[15]

|
(45) |
式中:δ为由模糊失效判据造成的磨损状态变化值。本例中取δ=0.05 mm3,对应引入的随机变量为Z",它的概率分布函数为
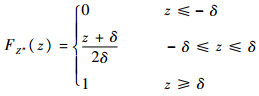
|
(46) |
所以α水平下的等效的功能函数为

|
(47) |
考虑各个随机变量的分散特性,结合相应的工程经验,取定各个随机变量的参数分布,如表 2所示。
| 变量 | 分布类型 | 均值 | 标准差 |
| [W] | 正态分布 | 5 | 0.5 |
| σ | 极值I型分布 | 106.111 5 | 15 |
| L | 正态分布 | 12.5 | 0.125 |
| S | 正态分布 | 0.467 7 | 0.004 677 |
| Z" | 均匀分布 | 0 | 0.028 868 |
| ν1 | 正态分布 | 0.295 | 0.014 75 |
| E1 | 正态分布 | 209 | 10.45 |
| ν2 | 正态分布 | 0.3 | 0.015 |
| E2 | 正态分布 | 206 | 10.3 |
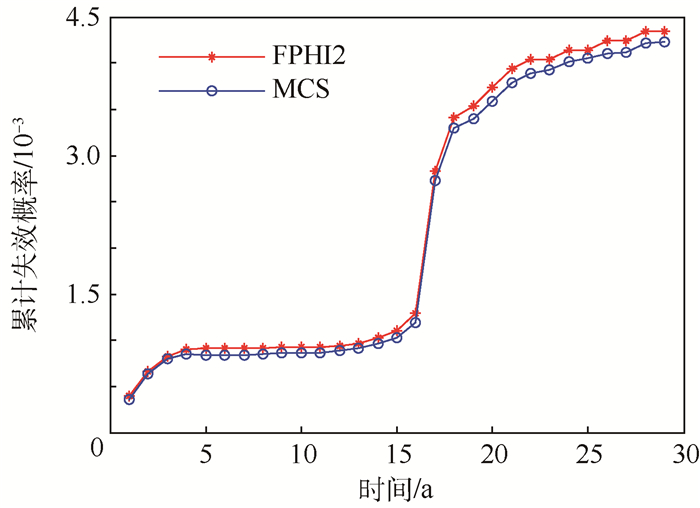
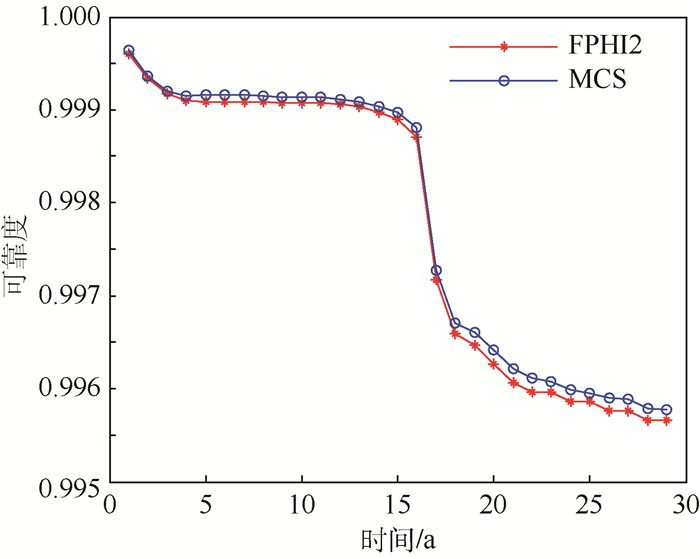
在谐波减速器的输入转速为200(°)/s,使用期限为25 a时,利用2.2节的可靠性方法计算,可以得到谐波减速器的累积失效概率和可靠度分别如图 6和图 7所示。
|
| 图 6 谐波减速器的累积失效概率 Fig. 6 Cumulative failure probability of harmonic reducer |
|
| 图 7 谐波减速器的可靠度 Fig. 7 Reliability of harmonic reducer |
通过图 6、图 7中的曲线可以看出:当工作时间小于15 a,曲线较为平滑,累积失效概率低于1.1×10-3;当工作时间为15 a以上,曲线变化剧烈,柔性齿轮磨损严重;当工作时间高于20 a,累积失效概率也进一步加大,可靠度低于0.996 5。
1) 根据相关项目要求,谐波减速器服役期为12 a,要求在12 a末产品的可靠度仍需达到0.999,计算结果表明考虑失效判据以及相关变量的模糊性时,产品时变失效概率较低,14 a末可靠度大于0.999,超过了设计要求,即产品在服役期内是可靠的。这样的分析结果也是符合实际的,因此对相关单位具有一定的指导意义。
2) 失效概率曲线图表明模糊时变可靠度计算方法与MCS方法在失效概率的计算上差别较小,计算结果准确度可以认为满足工程分析要求,对工程实际应用有一定的参考价值。
4 结 论本文针对航天在轨机械产品服役期内的时变可靠性建模分析问题,综合考虑了模糊性和随机性,建立了机械产品模糊时变可靠性模型,提出了模糊时变可靠度求解方法——FPHI2,经具体案例验证表明:
1) 本文提出的模糊时变可靠度求解方法求解方便,计算误差较小,对工程应用具有一定的指导意义,例如数值案例中两种方法的计算误差最大不超过10%,工程案例中可靠度和累计失效概率曲线贴合度较高。
2) 该方法建立的航空在轨机械产品的模糊时变可靠性模型形式简单,便于后续的模糊时变可靠度求解。
3) 本文提出的机械产品模糊时变可靠性分析方法也适用于航空、通用机械等领域的类似可靠性分析问题。
为使本文提出的方法在可靠性建模分析中应用更广,建模处理的准确度需进一步研究和验证。
| [1] | LI L Y, LU Z Z. Interval optimization based line sampling method for fuzzy and random reliability analysis[J]. Applied Mathematical Modeling, 2014, 38 (13) : 3124 –3135. DOI:10.1016/j.apm.2013.11.027 |
| [2] | 何世禹. 航天器在轨寿命预测与可靠性评价[J]. 航天器环境工程, 2008, 25 (3) : 209 –211. HE S Y. On-orbit lifetime prediction and reliability evaluation of spacecraft[J]. Spacecraft Environment Engineering, 2008, 25 (3) : 209 –211. (in Chinese) |
| [3] | AYYUB B M, LAI K L. Structural reliability assessment with ambiguity and vagueness in failure[J]. Naval Engineering Journal, 1992, 104 (3) : 21 –35. DOI:10.1111/nej.1992.104.issue-3 |
| [4] | 黄洪钟. 基于模糊失效准则的机械结构广义静强度的模糊可靠性计算理论[J]. 机械强度, 2000, 22 (3) : 36 –41. HUANG H Z. Fuzzy reliability analysis of generalized static strength of mechanical structure based on fuzzy failure criterion[J]. Journal of Mechanical Strength, 2000, 22 (3) : 36 –41. (in Chinese) |
| [5] | 黄洪钟, 田志刚. 基于广义模糊随机强度的模糊可靠性计算理论[J]. 机械工程学报, 2002, 38 (8) : 50 –53. HUANG H Z, TIAN Z G. Fuzzy reliability analysis based on generalized fuzzy random strength[J]. Chinese Journal Of Mechanical Engineering, 2002, 38 (8) : 50 –53. DOI:10.3901/JME.2002.08.050 (in Chinese) |
| [6] | 王磊, 刘文珽. 基于随机模糊参数的结构模糊可靠性分析模型[J]. 北京航空航天大学学报, 2005, 31 (4) : 412 –415. WANG L, LIU W T. Model for structural fuzzy reliability analysis based on fuzzy random parameter[J]. Journal of Beijing University of Aeronautics and Astronautics, 2005, 31 (4) : 412 –415. (in Chinese) |
| [7] | SICKERT J U,GRAF W,REUTER U,et al.Application of fuzzy randomness to time-dependent reliability[C]//Proceedings on Safety and Reliability of Engineering Systems and Structures.Rotterdam:Mill Press,2005:1709-1716. |
| [8] | 方永峰, 陈建军, 曹鸿钧. 多次模糊载荷下结构动态模糊可靠性分析[J]. 机械工程学报, 2014, 50 (3) : 192 –196. FANG Y F, CHEN J J, CAO H J. Structural dynamic reliability under Fuzzy loads with some times and fuzzy strength[J]. Journal of Mechanical Engineering, 2014, 50 (3) : 192 –196. (in Chinese) |
| [9] | GAO P, YAN S Z, XIE L Y. Dynamic fuzzy reliability models of degraded hold-down structures for folded solar array[J]. Applied Mathematical Modeling, 2014, 38 (2) : 4354 –4370. |
| [10] | WANG Z L, HUANG H Z, LI Y F, et al. An approach to system reliability analysis with fuzzy random variables[J]. Mechanism and Machine Theory, 2012, 52 : 35 –46. DOI:10.1016/j.mechmachtheory.2012.01.007 |
| [11] | ANDRIEU-RENAUD C, SUDRET B, LEMAIRE M, et al. The PHI2 method:A way to compute time-variant reliability[J]. Reliability Engineering and System Safety, 2004, 84 (1) : 75 –86. DOI:10.1016/j.ress.2003.10.005 |
| [12] | MEJRI M, CAZUGUEL M, COGNARD J Y, et al. A time-variant reliability approach for ageing marine structures with non-linear behavior[J]. Computers & Structures, 2011, 89 (19-20) : 1743 –1753. |
| [13] | 李广博.Fourier正交基神经网络加权响应面法的结构可靠性分析[D].长春:吉林大学,2014:57-60. LI G B.Structural reliability analysis based on Fourier orthogonal neutral network weighted response surface method[D].Changchun:Jinlin Universty,2014:57-60(in Chinese). |
| [14] | 张明. 结构可靠度分析——方法与程序[M]. 北京: 科学出版社, 2009 : 204 -206. ZHANG M. Structural reliability analysis:Method and procedures[M]. Beijing: Science Press, 2009 : 204 -206. (in Chinese) |
| [15] | 张萌, 陆山. 模糊可靠性模型的收敛性及改进的截集分布[J]. 北京航空航天大学学报, 2014, 40 (8) : 1109 –1115. ZHANG M, LU S. Convergence of fuzzy reliability models and an improved cut-set distribution[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40 (8) : 1109 –1115. (in Chinese) |
| [16] | ELLISHKOFF I. Essay on uncertainties in elastic and viscoelastic structures:Form A.M.Freudenthal's criticisms to modern convex modeling[J]. Computers & Structures, 1995, 56 (6) : 871 –895. |
| [17] | 刘晓叙, 陈敏. 机械零件磨损寿命计算方法的比较与探讨[J]. 机械工程师, 2010 (4) : 38 –39. LIU X X, CHEN M. The comparison and approach of the wear life calculation methods for mechanical part[J]. Journal of Mechanical Engineer, 2010 (4) : 38 –39. (in Chinese) |
| [18] | GAO Z B,ZHANG J G,KAN L J.Fuzzy time-dependent reliability modeling and analysis method for mechanisms based on strength degradation[C]//60th Annual Reliability and Maintainability Symposium,RAMS 2014.Piscataway,NJ:IEEE Press,2014:140-153. |
| [19] | 赵鸣, 刘朝英. 轴颈磨损寿命的模糊可靠性计算[J]. 吉林建筑工程学院学报, 2008, 25 (1) : 78 –80. ZHAO M, LIU C Y. Calculating for the vague reliability of journal wear life[J]. Journal of Jilin Architectural and Civil Engineering Institute, 2008, 25 (1) : 78 –80. (in Chinese) |



