2. 上海交通大学 数学系, 上海 200240;
3. 上海第二工业大学 理学院, 上海 201209
2. Department of Mathematics, Shanghai Jiao Tong University, Shanghai 200240, China ;
3. Department of Mathematics, Shanghai Second Polytechnic University, Shanghai 201209, China
辛结构是Hamilton动力系统的重要性质,数值方法应当尽可能地保持Hamilton系统固有特性。文献[1-3]系统地提出Hamilton的辛几何算法,以及构造诸多类型的辛几何算法:生成函数法、辛RK等。现有的辛几何算法可以保证系统的辛结构,因此具有较好的数值稳定性以及较好的长时间跟踪能力。尽管现有辛算法不存在数值的耗散,但是,这类方法仍然具有较大的相位误差。文献[4-6]对辛差分方法存在的数值误差存在的相位误差给出分析和矫正方案。文献[7]系统地分析了几种常见的保结构方法(平均向量场法、对角Padé逼近、生成函数法)的相位误差及修正给出详尽的分析,然而,基于相位误差分析的辛算法较少讨论Hamilton系统的另外一个很重要特性:保能量。
近年来,辛方法的相位漂移现象越来越引起国内外学者关注,辛Runge-Kutta-Nystrom(RKN)格式方法[8-9]和辛分块Runge-Kutta(SPRK)方法[10-12],这类算法通过研究构造算法的泰勒展开阶数研究算法的相位误差。从而推导出很多相位误差较小的计算格式,这类方法需要求解代数方程组,得到优化的参数,从而满足相位误差最小的条件,文章显示,这类参数相对比较复杂。向前Euler方法的相位误差为正,而向后Euler方法相位误差为负分数步对称辛算法(FSJS)方法[13]利用这一特性,提出分数步计算方案,即在每个计算单元内,分别使用数次向前Euler和向后Euler方法,极大地减小相位误差,但是每一步计算过程中都要计算分数步数步,从而增加了计算量。
文献[14-17]利用时间有限元方法解Hamilton系统,该方法显示对线性Hamilton系统连续有限元方法可以保证Hamilton系统的辛结构以及Hamilton函数的守恒。文献[18]提出平均间断有限元方法可以保证Hamilton系统的动量守恒,且平均间断有限元方法不保辛。对于Hamilton系统,优异的算法需要保持系统辛结构、系统所固有的守恒规律以及具有较小的相位误差。
间断有限元方法[19]求解时间常微分方程问题,由于其有较好的A稳定性以及较高的计算精度,近年来,得到了广泛的应用,间断有限元方法求解在单元节点是间断的。这给后续计算带来很多处理方法。
利用间断有限元方法在节点间断,相位误差为零的计算格式——极小化相位误差加权间断有限元辛方法(WDG-PF)。该方法在极小化相位误差的前提下,可以保证Hamilton系统的辛结构。相位误差和能量误差几乎达到计算机精度。对于高低混频系统,传统计算方法很难做到在较大步长,同时实现对高低频信号的精确仿真,本文的方法可以对这样的混频系统精确地计算,数值实验显示,在满足保辛和保能量的前提下,本文的方法高频和低频信号计算误差都达到计算机精度。
1 Hamilton系统及相位误差考虑如下Hamilton正则方程:

|
(1) |
式中:ω为系统的频率。给定初始条件x(0)=x0,y(0)=y0。
方程式(1)对应的Hamilton函数:
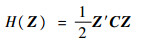
|
式中: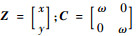
式(1)可以化为

|
(2) |
式中: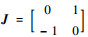
方程式(1)对应的解析解为
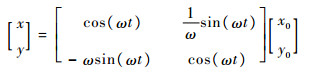
|
用辛差分方法(如辛Runge-Kutta,Euler中点)求解方程式(2)的一般递推公式为
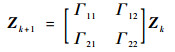
|
(3) |
为了分析式(3)的幅值和相位精度,需要求解Jacobi矩阵

|
其中: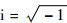
则Jacobi矩阵
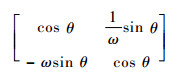
|
从而可得式(3)的相位误差为
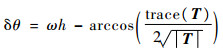
|
(4) |
式中:θ为单步相位角;Δθ为单步相位误差。
2 加权间断有限元方法对式(2)采用加权间断有限元方法,将时间域[0, +∞)剖分:0=t0 < t1 < … < tN-1 < tN < …,记剖分单元[tj, tj+1]=Ij,j∈[0,N]。
定义1 m(m≥0)次间断有限元空间Sh={Z|Ij是m次多项式, Z在tj和tj+1处可以不连续}

|
初值Z0-=Z0。
间断有限元方法求解方程式(2)
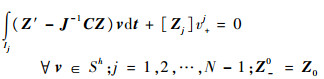
|
(5) |
取形函数
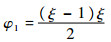
|
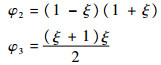
|
则
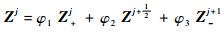
|
(6) |
同时:
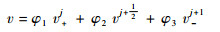
|
(7) |
将式(6)和式(7)代入式(5)可得

|
(8) |

|
(9) |
式中:
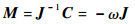
|
计算过程如图 1所示。

|
| 图 1 计算过程 Fig. 1 Computational procedure |
由式(8)和式(9)可知,每次计算在节点tj+1处存在两个计算值,即改点的左右极限值Zj+1-和Zj+1+。
间断有限元在节点的灵活性,给后续设计计算格式带来灵活性。
现引入参变量α,使得
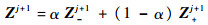
|
(10) |
文献[20]也用过类似的数值技巧,不同的是本文所引入的参变量α,“一次计算,终身使用”。即对于给定的Hamilton以及给定的单元长度,只需计算第一个单元极小化相位误差所需的参变量α,后续单元计算,完全使用相同参变量数值。
3 极小化相位误差一次加权间断有限元方法求解方程式(2),得式(11),如下:
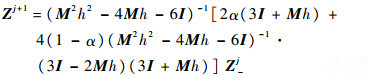
|
(11) |
记
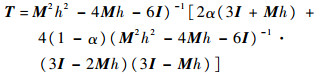
|
其中Jacobi矩阵T的性质影响计算的幅值和相位误差。文献[4-7, 13-14]给出传递矩阵对相位误差的影响。对于线性Hamilton系统,单步的相位误差可以通过式(4)求解。
定理1 若

|
(12) |
则式(11)的相位误差为零。
式中:

|
证明 将式(12)代入式(11),演算,易证。
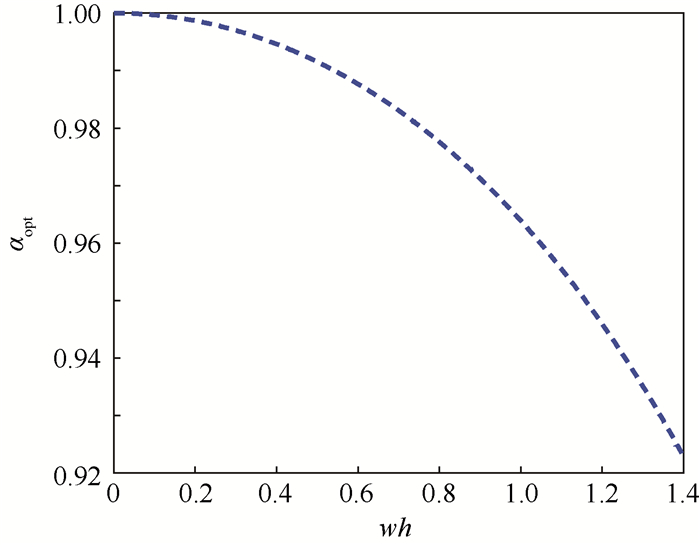
同理, 可得二次加权间断有限元方法相位误差为零时的最优加权系数αopt(见图 2)。
|
| 图 2 ωh和最优权重αopt的关系 Fig. 2 Relationship between ωh and αopt |
从图 2可以看出,不同的h、ω,对应唯一最优的权重αopt。
这样的权重α,仅需在第一个单元中计算一次,后续单元利用第一个单元计算所得权重α,进行迭代。这样就得到极小化相位误差的传递矩阵
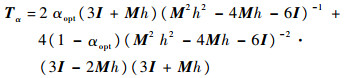
|
对于Hamilton系统,长时间的仿真要求传递矩阵是辛矩阵,从而可以很好地控制幅值误差。可以验证极小化相位误差的传递矩阵Tα不是辛矩阵。仍需要对极小化相位误差的传递矩阵进行处理,使得算法可以很好地控制幅值。
引理[2] 矩阵A是辛矩阵的充要条件为A′JA=J
定理2 若2×2矩阵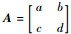
证明 若|A|=1即ad-bc=1则

|
即A是辛矩阵。
对极小化相位误差的传递矩阵Tα进行如下处理:

|
(13) |
因为Tα是2×2的矩阵,所以
定理3 对极小化相位误差的矩阵Tα进行如式(8)的处理得到的矩阵Tα_sym是辛矩阵。
证明

|
定理4 极小化相位误差的传递矩阵Tα和处理后的传递矩阵Tα_sym具有相同的相位误差。
证明 若极小化相位误差的Jacobi矩阵Tα的特征值可以写成
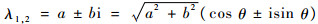
|
其中:b≠0;单步相位角θ定义为
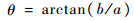
|
则由式(8)可得Tα_sym的特征值为
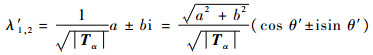
|
单步相位角为
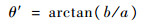
|
即θ=θ′,所以Tα和Tα_sym具有相同的相位误差。即对极小化相位误差的矩阵Tα进行式(13)的变换,得到新的Jacobi矩阵Tα_sym同样具有极小的相位误差。
由定理2~4可得:传递矩阵Tα_sym可以使得计算的相位误差极小,同时满足保辛性要求。
4 数值算例 4.1 椭圆型Hamilton系统考察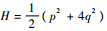
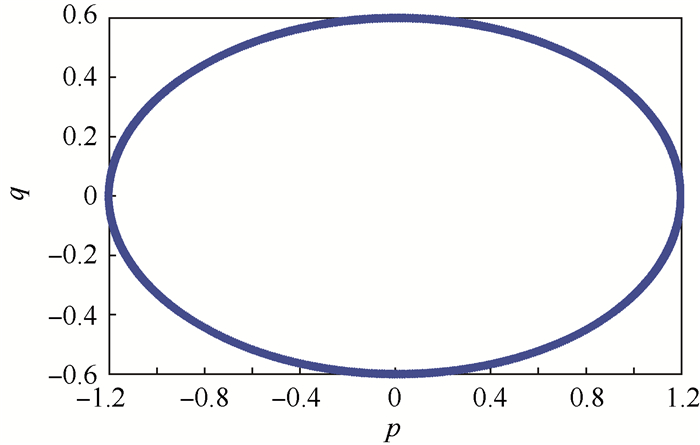
为了更好地表现WDG-PF方法的保结构特性,相图是计算了[0, 10 000]s内辛结构的守恒规律,相图如图 3所示。从图 3可以直观看出长时间计算,WDG-PF方法可以很好地保持Hamilton系统的辛结构,不会出现数值耗散,具体数值结果如表 1所示。
|
| 图 3 相图 Fig. 3 Phase portrait |
对于周期系统,相位误差也会出现周期现象,所以在比较算法精确性方面,因此较在[0, 100]s时间域内,比较不同算法数值解在时域上的误差绝对值的最大值,如表 1所示。
从表 1可以看出,WDG-PF方法和保能量算法(二次连续有限元(TFE2)和平均向量场(AVF))一样可以保证Hamilton函数的守恒性。其中AVF方法多项式可以写出积分表达式。但是,可以看出本文方法WDG-PF可以精确地保证数值解在时域上的精度,计算误差几乎达到计算机精度。其中能量指的是Hamilton函数H=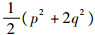
表 2为几种方法求解Hamilton系统时域上的误差。从表 2可以看出本文方法WDG-PF方法可以很好地保证Hamilton系统的能量守恒性,同时,相对于针对减少相位误差所设计的计算格式分数步对称辛算法(FSJS)、辛Runge-Kutta-Nystrom格式(RKN)和P辛Runge-Kutta-Nystrom格式(RKN)方法,WDG-PF方法的相位误差更小,这是现有专门方法所无法比拟的。
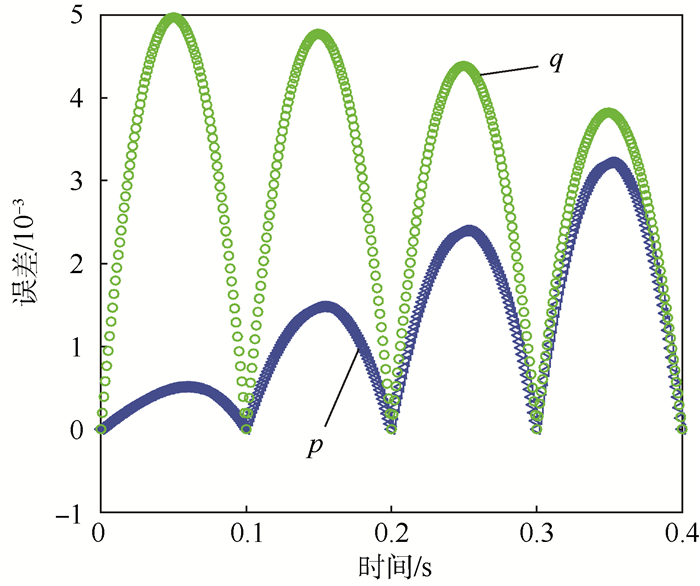
图 4为一次极小化相位误差加权间断有限元方法计算单元内部误差分布。
|
| 图 4 一次加权间断元方法在前4个单元内部误差图(h=0.1) Fig. 4 Error distribution of one-order WDG-PF in first four elements(h=0.1) |
从图 4可以看出一次极小化相位误差加权间断有限元方法在单元节点误差极小(几乎为零), 在单元内部误差较大。
4.2 高低混频Hamilton系统Hamilton函数:

|
正则方程组为
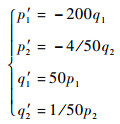
|
初值:
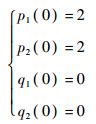
|
解析解为
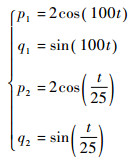
|
分别用WDG-PF(h=0.02),TFE1[15] (h=0.000 1)、FSJS[13] (h=0.01)SPRK[10] (h=0.001)方法,计算区域为[0,600] s。
图 5(a)和图 5(b)为高频信号p1(t)、q1(t)计算情况;图 5(c)和图 5(d)为低频信号p2(t)、q2(t)计算情况。从图中可以看出对于传统方法TFE、FSJS和SP辛RKN采用较小的步长,可以实现低频信号的精度很高,但很难在较大步长下实现对高低频信号的同时精确仿真。而WDG-PF方法因为极小化相位误差,使得算法可以在大步长下对高低混频系统的精确仿真。

|
| 图 5 几种不同方法求解p1、q1、p2和q2误差 Fig. 5 Errors of p1, q1, p2 and q2 solved by different methods |
表 3中是Hamilton函数H=(p1, q1, p2, q2)=
有限元或间断元在单元内部存在超收敛现象。
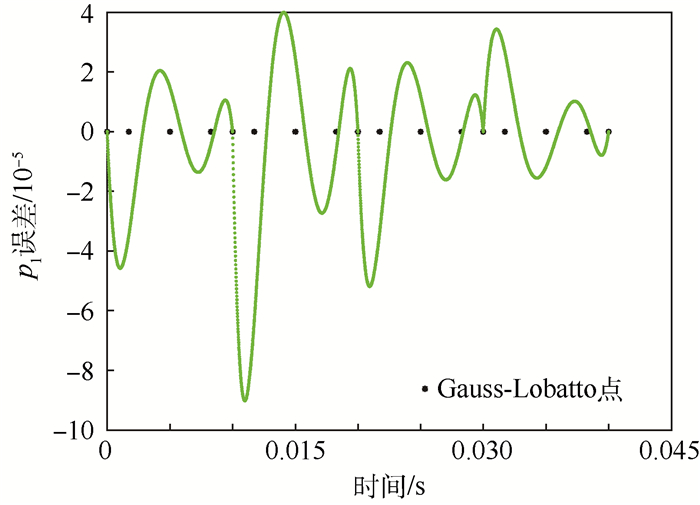
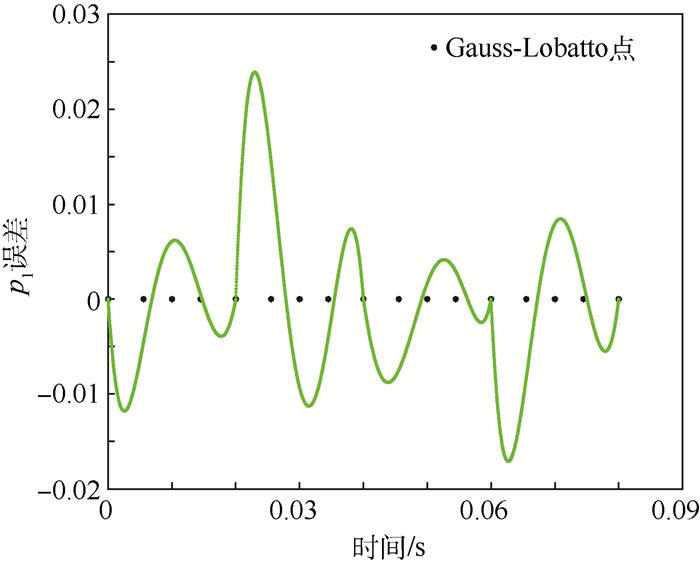
图 6和图 7为高频信号p1分别用4次加权间断有限元方法和3次加权间断有限元方法在前4个单元的误差分布情况。从图 6和图 7可看出,极小化相位误差的加权间断在Gauss-Lobatto点附近有超收敛现象。
|
| 图 6 4次WDG-PF在前4个单元内部误差情况 Fig. 6 Error distribution for four-order WDG-PF in first four elements |
|
| 图 7 3次WDG-PF在前4个单元内部误差情况 Fig. 7 Error distribution for third-order WDG-PF in first four elements |
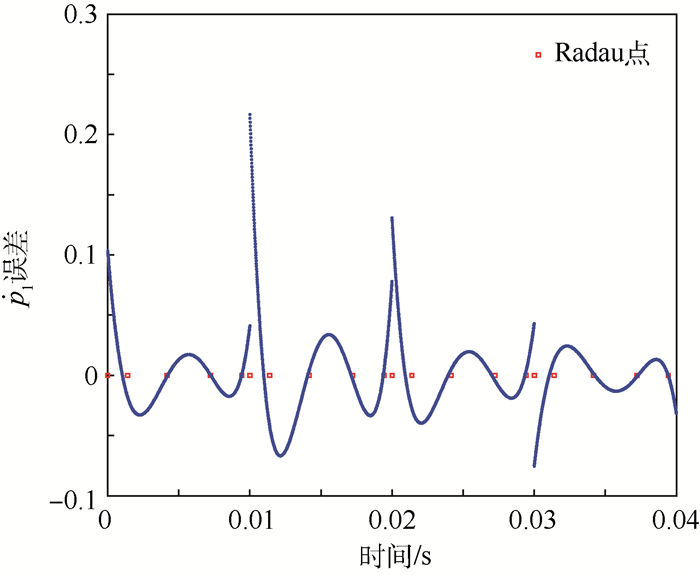
图 8和图 9为高频信号极小化相位误差加权间断有限元方法一阶导数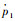
|
| 图 8 4次WDG-PF在前4个单元内部导数误差情况 Fig. 8 Derivative error distribution for four-order WDG-PF in first four elements |

|
| 图 9 3次WDG-PF在前4个单元内部导数误差情况 Fig. 9 Derivative error distribution for third-order WDG-PF in first four elements |
从高低混频Hamilton系统算例可以看出本文的方法WDG-PF,可以保证系统的Hamilton函数守恒以及保证系统的辛结构。不需要非常小的计算步长就可以极好地仿真高频和低频信号,即高低频信号的相位误差均极小,同时单元内部存在超收敛现象,这个优良的特性是其他方法所没有的。
5 结论极小化相位误差加权间断有限元辛方法具有如下优越性:
1) 对于给定的Hamilton系统和单元长度,使得相位误差极小且保辛,权重α“一次计算,终身使用”。
2) 可以解决间断有限元方法不能保证Hamilton系统辛结构的缺点,具有极小的相位误差和极高精度的保能量特性,几乎达到计算机精度。
3) 这种加权间断有限单元有超收敛点。
4) 特别针对高低混频Hamilton系统或者刚性问题,WDG-PF方法可以在大步长下同时实现对高频和低频信号的准确仿真。
| [1] | FENG K. Difference schemes for Hamiltonian formalism andsymplectic geometry[J]. Journal of Computational Mathematics, 1986, 4 (3) : 279 –289. |
| [2] | FENG K., QIN M. Symplectic geometric algorithms for Hamiltonian systems[M]. Heidelberg: Springer, 2010 : 279 -289. |
| [3] | CALVO M P. Numerical Hamiltonian problems[M]. London: CRC Press, 1994 : 315 -356. |
| [4] | BRUSA L, NIGRO L. A one-step method for direct integration of structural dynamic equations[J]. International Journal for Numerical Methods in Engineering, 1980, 15 (5) : 685 –699. DOI:10.1002/(ISSN)1097-0207 |
| [5] | 邢誉峰, 杨蓉. 单步辛算法的相位误差分析及修正[J]. 力学学报, 2007, 39 (5) : 668 –671. XING Y F, YANG R. Phase errors and their correction in symplectic implicit single-step algorithm[J]. Chinese Journal of Theoretical and Applied Mechanics, 2007, 39 (5) : 668 –671. (in Chinese) |
| [6] | 邢誉峰, 冯伟. 李级数算法和显式辛算法的相位分析[J]. 计算力学学报, 2009, 26 (2) : 167 –171. XING Y F, FENG W. Phase analysis of Lie series algorithm and explicit symplectic algorithm[J]. Chinese Journal of Computational Mechanics, 2009, 26 (2) : 167 –171. (in Chinese) |
| [7] | 陈璐, 王雨顺. 保结构算法的相位误差分析及其修正[J]. 计算数学, 2014, 36 (3) : 271 –290. CHEN L, WANG Y S. Phase error analysis and correction of structure preserving algorithms[J]. Mathematica Numerica Sinica, 2014, 36 (3) : 271 –290. (in Chinese) |
| [8] | VYVER H V D. A symplectic Runge-Kutta-Nystrom method with minimal phase-lag[J]. Physics Letters A, 2007, 367 (1) : 16 –24. |
| [9] | MONOVASILIS T, KALOGIRATOU Z, SIMOS T E. Exponentially fitted symplectic runge-Kutta-Nyströmethods[J]. Applied Mathematics & Information Sciences, 2013, 7 (1) : 81 –85. |
| [10] | MONOVASILIS T, KALOGIRATOU Z, SIMOS T E. Symplectic Partitioned Runge-Kutta methods with minimal phase-lag[J]. Computer Physics Communications, 2010, 181 (7) : 1251 –1254. DOI:10.1016/j.cpc.2010.03.013 |
| [11] | SIMOS T E. A two-step method with vanished phase-lag and its first two derivatives for the numerical solution of the Schr dinger equation[J]. Journal of Mathematical Chemistry, 2011, 49 (10) : 2486 –2518. DOI:10.1007/s10910-011-9897-1 |
| [12] | MONOVASILIS T, KALOGIRATOU Z, SIMOS T E. Two new phase-fitted symplectic partitioned Runge-Kutta methods[J]. International Journal of Modern Physics C, 2011, 22 (12) : 1343 –1355. DOI:10.1142/S0129183111016932 |
| [13] | 刘晓梅, 周钢, 王永泓, 等. 辛算法的纠飘研究[J]. 北京航空航天大学学报, 2013, 39 (1) : 22 –26. LIU X M, ZHOU G, WANG Y H, et al. Rectifying drifts of symplectic algorithm[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39 (1) : 22 –26. (in Chinese) |
| [14] | TANG W, SUN Y. Time finite element methods:A unified framework for numerical discretizations of ODEs[J]. Applied Mathematics & Computation, 2012, 219 (4) : 2158 –2179. |
| [15] | 汤琼, 陈传淼. Hamilton系统的连续有限元法[J]. 应用数学和力学, 2007, 28 (8) : 958 –966. TANG Q, CHEN C M. Continuous finite element methods of Hamiltonian systems[J]. Applied Mathematics and Mechanics, 2007, 28 (8) : 958 –966. (in Chinese) |
| [16] | 陈传淼, 汤琼. Hamilton系统的有限元研究[J]. 数学物理学报, 2011, 31A (1) : 18 –33. CHEN C M, TANG Q. Study of finite element for Hamiltonian systems[J]. Acta Mathematica Scientia, 2011, 31A (1) : 18 –33. (in Chinese) |
| [17] | HU S F, CHEN C M. Runge-Kutta method finite element method and regular algorithms for Hamiltonian system[J]. Applied Mathematics & Mechanics:English Edition, 2013, 34 (6) : 747 –760. |
| [18] | LI C H, CHEN C M. Ultraconvergence for averaging discontinuous finite elements and its applications in Hamiltonian system[J]. Applied Mathematics & Mechanics:English Edition, 2011, 32 (7) : 943 –956. |
| [19] | DELFOUR M, HAGER W, TROCHU F. Discontinuous Galerkin methods for ordinary differential equations[J]. Mathematics of Computation, 1981, 36 (154) : 455 –473. DOI:10.1090/S0025-5718-1981-0606506-0 |
| [20] | WANG D, XIAO A, LI X. Parametric symplectic partitioned Runge-Kutta methods with energy-preserving properties for Hamiltonian systems[J]. Computer Physics Communications, 2013, 184 (2) : 303 –310. DOI:10.1016/j.cpc.2012.09.012 |
| [21] | QUISPEL G R W, MCLAREN D I. A new class of energy-preserving numerical integration methods[J]. Journal of Physics A Mathematical & Theoretical, 2008, 41 (4) : 75 –97. |



