2. 北京航空航天大学 交通科学与工程学院, 北京 100083
2. School of Transportation Science and Engineering, Beijing University of Aeronautics and Astronautics, Beijing 100083, China
微重力水气分离技术是环境控制与生命保障系统为载人航天提供水和空气保障的关键技术之一。膜式静态水气分离器效率高,功耗小,没有降低可靠性的运动部件。美国、俄罗斯和欧洲太空局均已研制出相应的产品,并成功应用于国际空间站环控生保系统[1]。在各国研制新一代环控生保系统的背景下,技术或单机小型化、轻量化的需求日益强烈。由于膜式水气分离依靠膜的选择渗透性实现分离,与膜-液接触面积、膜两侧局部压差相关,开展流道弯曲度对微重力膜式水气分离性能影响的基础研究,对中国载人航天环控生保系统水气分离技术设计与预研具有重要的工程意义。
膜式水气分离器仿真涉及入口流型问题和分离膜边界问题。由于缺乏实验数据和理论认识,难以给出仿真所需的真实的微重力条件下气液两相流动入口边界。如何从平均的两相流动参数计算得到具有几何尺度的气液界面,是一个特殊的气液界面多尺度问题。传统的气液两相流仿真模型,例如流体体积法(Volume of Fluid,VOF)、欧拉双流体模型(Two-Fluid Model,TFM),源于网格尺度制约、模型边界缺少,难以解决入口边界的可计算性问题[2]。针对气液两相流界面多尺度问题,研究者发展出TFM嵌入式[3-7]和耦合式模型[8-9]。从模型实现和应用的角度出发,TFM嵌入式比耦合式模型更为简便,通用性更好,然而前者在锐化和捕捉大尺度界面时也具有一定的不确定性。同时,μm量级的膜厚使处理分离膜边界问题时难以建立真实的几何模型,需借助数学模型描述膜特性,以此作为水气两相在流道中的物理边界条件。Vieira等[10]在油水分离仿真研究中采用动量源项法实现陶瓷膜中两相渗透过程,但未体现膜的选择性。孙春平等[11]在膜式静态水气分离仿真研究中采用质量源项法描述膜的单相渗透过程,但未考虑膜渗透过程反过来对膜附近局部压力、速度的影响,且未考虑两相流动情况。
本文提出基于界面概率近似方法的欧拉双流体模型(Eulerian Two-Fluid Model with an Interface Probability Approximation Method, TFM-IPAM)解决气液界面多尺度问题,为膜式水气分离仿真提供合理的入口流型,同时为避免几何多尺度问题,提出动量源项法模拟膜选择与渗透特性,开展微重力膜式水气分离仿真研究,重点研究在典型结构和工作参数下流道弯曲度θ对膜分离性能的影响。
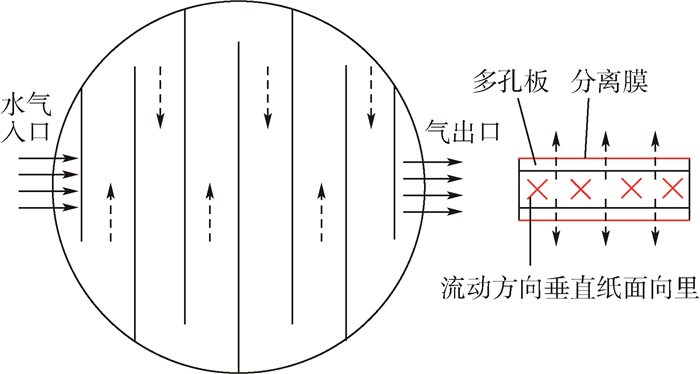
1 模型与算法 1.1 几何模型图 1为膜式静态水气分离器结构,包括水气混合入口管道、气路出口管道、分离膜、多孔板、分离流道等静态部件[12]。其中分离膜是指透水不透气的选择性渗透膜,是水气分离的核心部件。多孔板为膜的支撑部件,增加机械强度。
|
| 图 1 膜式静态水气分离器结构 Fig. 1 Membrane static gas-liquid separator structure |
工作原理:水气混合物在外部输运压力作用下进入分离流道,液相碰到分离膜后被吸附并在膜两侧压差的作用下,穿过膜的孔隙进入积液腔,气体从气出口排出,从而实现水气分离的宏观过程。膜的分离机理采用优先吸附-毛细管流动模型[13]解释。由于膜材料亲水特性以及孔隙的设计,膜会优先吸附水,并在膜孔和膜面上形成纯水吸附层,阻隔气相穿透。水在膜两侧压差推动力作用下通过膜孔,实现水气分离的微观过程。
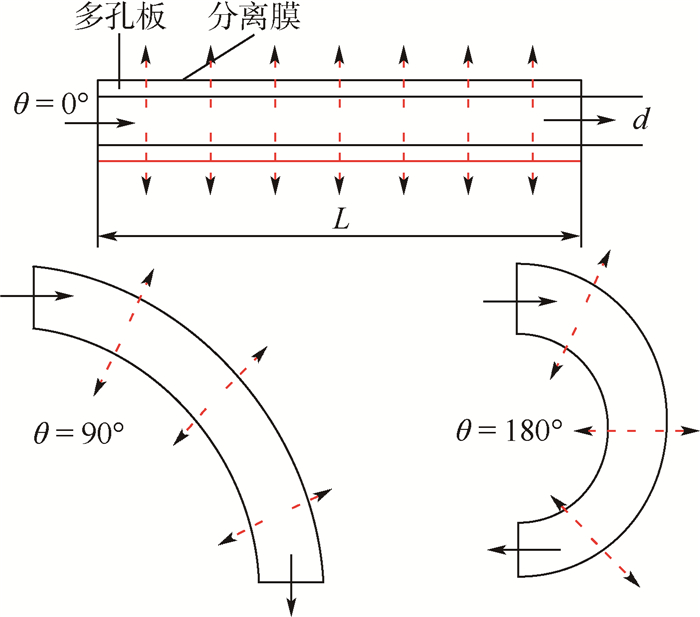
流道弯曲度研究采用矩形截面流道(长为L,宽为d,高为h,假定h远大于d),渗透方向沿宽度方向,并设计3种流道弯曲度θ=180L/(rπ)(见图 2),r为曲率半径。为不失一般性,模型有效性验证采用直圆管流道(长为L,直径为d)。为减弱进出口影响,进口和出口均按直通道延长L。具体计算参数为:L=200 mm;d=10 mm;θ=0°,90°,180°;分离膜背压取-50 kPa;气出口背压为0 kPa;表面张力σ=0.07 N/m,壁面接触角β=60°;网格尺度Δx=0.5 mm。
|
| 图 2 3种流道弯曲度 Fig. 2 Three kinds of channel curvatures |
TFM-IPAM通过界面概率近似方法将计算域划分为界面层和离散流区域,在界面层将连续气相与液相之间的大尺度(大于网格尺度)界面处理为基于网格尺度的显式几何边界,在界面位置计入气液界面摩擦力;在离散流区域,采用基于平均场的隐式物理尺度处理连续气/液相和离散液/气相之间的小尺度(小于网格尺度)界面,补充传统相间作用力。其中界面动量传输项(气液界面摩擦力与传统相间作用力)和湍流封闭关系是模型基本方程求解的必要条件。暂未考虑隐式物理尺度的分布性,仅采用离散相Sauter平均直径作为隐式物理尺度,该值通常由实验测量、理论计算或合理假设确定,本文取1/2Δx。
1.2.1 基本方程对于绝热的不可压两相流系统,TFM中气液两相的连续方程和动量方程的通用表达式为[14]
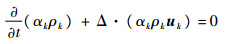
|
(1) |
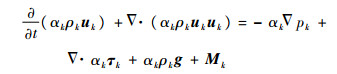
|
(2) |
式中:α为相体积分数, 下标k代表气相(g)或液相(l);ρ为密度;u为速度;p为压力;t为时间;τ为应力;g为重力加速度;M为界面动量传输量。式(2)等号右边第1项为压力梯度项;第2项为应力项,包括粘性应力和雷诺湍流应力,本文对后者采用k-ω离散湍流模型封闭,同时采用Troshko-Hassan模型[15]考虑湍流交互;第3项为重力项,微重力时忽略该项;第4项为界面动量传输项,将在1.2.3节界面传输详细阐述。在多孔区域中基本方程须乘以多孔介质孔隙率ε。
1.2.2 界面概率近似方法为追求方法较好的适应性,同时保持基本方程的物理意义及不引入过多的不确定性,将VOF方法的高精度压缩差分格式——任意网格界面压缩捕捉格式(Compressive Interface Capturing Scheme for Arbitrary Meshes,CICSAM)[16]应用于TFM-IPAM中大尺度界面数值扩散的处理,并在离散流区域使用CICSAM与二阶迎风的调和格式,调和系数选取0.5。然而CICSAM能有效控制但不能完全消除数值扩散,界面横跨数个网格,其几何边界仍具有不确定性。因此,提出界面统计方法捕捉大尺度界面,以单层网格描述其几何边界,标定出界面层和离散流区域,为局部化界面动量传输提供准确的位置信息。
首先,算法基于一个等价关系,即物理意义上相分数为单元中一相的体积含量,等价于概率意义上一相出现在该单元中的概率。当某网格单元一相的α大于临界相分数αc(例如,本文αc取0.99)时,根据概率近似可将一相出现在该单元的概率视为1,判定该相完全占据当前网格单元。其次,基于一个类比关系,即相分数α等值线/面至α=1等值线/面之间的差值|1-α|可视为相分数意义上的距离函数。因此,可借助Level-set方法中的海维赛德函数[17]实现相分数概率近似及相界面锐化调节的数学描述。
当|1-α| < |1-αc|(即α>αc)时,则在概率意义上一相出现在该单元的概率为1,即经概率近似调节之后的相分数αs=1;当|1-α|>|αc|(即α < 1-αc)时,则αs=0;当|1-αc|≤|1-α|≤|αc|(即1-αc≤α≤αc)时,实施归一化处理,调和αs至范围(0, 1)。从而实现相分数的第1次近似及相界面的第1次锐化调节。而后,以小步-多次的方式进行N次调节(一般N取10即可),将相分数为(0, 1)的区域压缩消除(因界面数值扩散并非完全对称,可能会存在极个别网格相分数处于0~1之间),使全场相分数梯度处于2个极端,0或1/Δx。相分数梯度为非零值的网格标记为大尺度界面的几何边界(界面层);整体计算域被界面层分割为气泡流和液滴流区域。其中经横坐标平移变换后的海维赛德函数表达式为
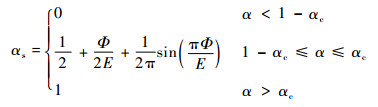
|
(3) |
式中:Φ=α-0.5;Ε=αc-0.5。
算法基于概率近似方法将由不可避免的数值扩散造成的数值上不确定的界面转化为概率上确定的界面,基于Level-set方法简化了界面锐化和捕捉的近似过程。
1.2.3 界面传输TFM-IPAM对不同尺度的界面分别采用不同的处理方式,因此界面动量传输的表达式也不同。在界面层,施加气液界面摩擦力:

|
(4) |
式中:界面面积密度Afs =|Δαl|,αl为液相体积分数;混合密度ρm=αlρl+ αgρg,αg为液相体积分数,ρl和ρg分别为液相和气相密度;气液速度差|U|=|ul-ug|。参考AIAD模型[5],界面摩擦系数为
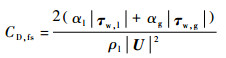
|
(5) |
式中:气液之间切应力为
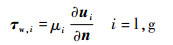
|
(6) |
式中:μi为动力粘度;n为法向向量。
在离散流区域,计入传统相间作用力。传统相间作用力包括阻力和非阻力,阻力Fd, k通常为界面动量传输项Mk的主要贡献力,可暂不考虑非阻力贡献。在气泡流区域,阻力表达式为

|
(7) |
式中:界面面积密度Ab=6αg/db,db为气泡直径;阻力系数CD, b采用Grace等[18]的模型。
在液滴流区域,阻力表达式为
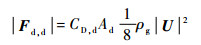
|
(8) |
式中:界面面积密度Ad=6αl/dd,dd为液滴直径;阻力系数CD, d采用Ishii-Zuber模型[19]。
考虑表面张力FS, k,采用Brackbill等[20]的连续表面力模型计算并计入到界面动量传输Mk中。
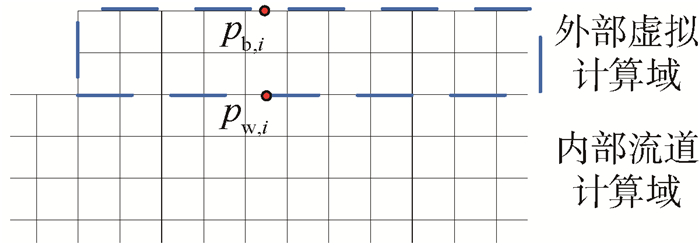
1.3 膜边界模型 1.3.1 动量源项法模型假设:①将膜视为具有一定厚度(远小于流道当量直径)的多孔壁面,定义为外部虚拟计算域(见图 3),本文取壁厚Lt=1 mm;②不考虑膜内真实流动;③忽略多孔板流阻;④膜形成纯液相吸附层,即虚拟计算域充满液相。
|
| pb, i—虚拟计算域外壁局部压力;pw, i—膜壁面局部压力。 图 3 虚拟和流道计算域 Fig. 3 Virtual and channel computing domain |
通过对虚拟计算域液相动量方程添加源项实现分离膜的渗透性。对于均匀的多孔介质,动量源项为

|
(9) |
式中:μk为流体动力粘度;1/K为多孔介质粘性阻力系数;C2为惯性阻力系数。1/K和C2由Ergun[21]半经验关系式确定:
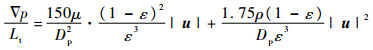
|
(10) |
式中:Dp为多孔粒子平均直径;比较式(9)与式(10),得到
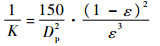
|
(11) |
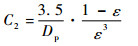
|
(12) |
根据分离膜渗透实验值:压差Δp为50 kPa时,液相质量通量为0.033 kg/(m2·s-1),建立线性的体积通量特性,体积通量为
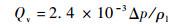
|
(13) |
将式(13)代入式(10),同时假定膜内部流动为层流,则式(10)等式右边第2项可忽略,由此匹配出孔隙参数Dp=0.15 mm,ε=0.016,代入式(11)得到1/K=1.49×1015 m-2。
分离膜的选择性(透水不透气)采用同样办法,对虚拟计算域气相动量方程添加极大值源项,取参数1/K=1020 m-2。
1.3.2 膜渗透流量及通量计算当流动动态平衡时采用膜分离流量的时空平均值(即膜通量时均值)作为膜分离性能评估参数:
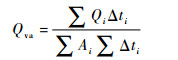
|
(14) |
式中:Qi为瞬时局部化膜流量;Ai为单位长度膜面积,其中圆形截面管道Ai=πdΔL,矩形截面管道Ai=2hΔL,膜的单位长度ΔL=Δx;Δti为时间步长。其第1种计算方法基于膜边界的液相渗透速度:
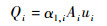
|
(15) |
式中:αl, i为膜内侧相邻单元网格局部化的液相体积分数;ui为局部化膜渗透速度,方向垂直膜面向外。
第2种方法为工程计算方法,基于膜两侧的压差:
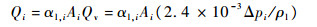
|
(16) |
式中:膜两侧局部压差Δpi=pw, i-pb, i。第1种方法结果视为仿真值,第2种方法结果视为工程值,二者相互校核可用于验证膜渗透模型的有效性。
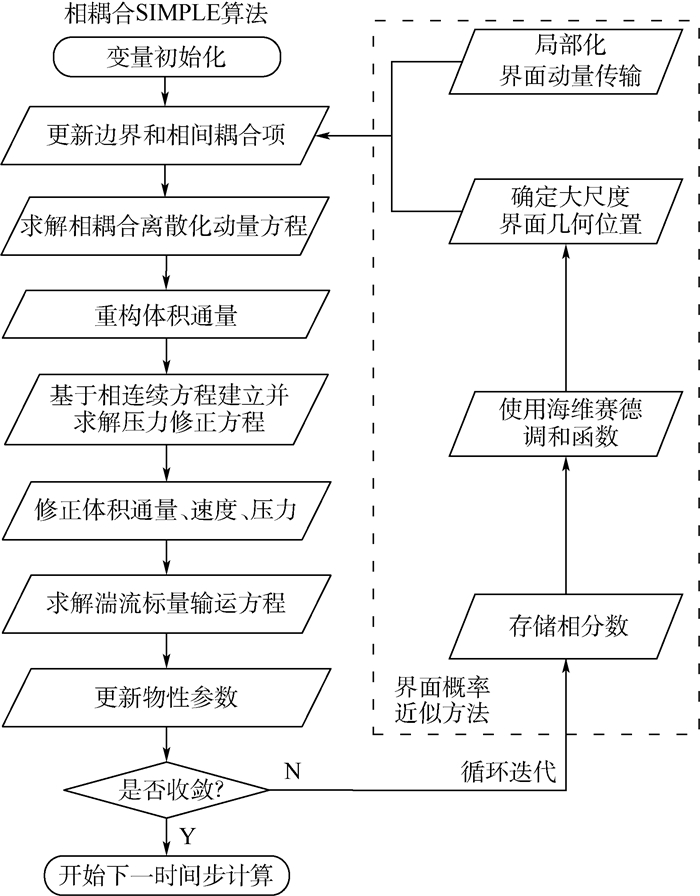
1.4 数值算法TFM-IPAM基本方程采用相耦合SIMPLE算法[22]求解。在方程空间离散方面,动量和湍流方程采用一阶迎风差分格式;基本方程中对流和扩散项中的梯度项计算采用Green-Gauss梯度方法;相连续方程采用1.2.2节所述差分格式策略。时间离散采用二阶精度隐式格式。采用商业软件FLUENT版本14.5 (ANSYS, Inc., Canonsburg, PA, USA)实现上述离散和求解算法。局部化的离散格式、几何边界以及界面动量传输则通过自定义函数UDF嵌入FLUENT求解器中。图 4为TFM-IPAM的整体求解流程,虚线框部分为本文核心算法。时间步长中的每一次迭代计算后,实施界面概率近似方法,更新界面的几何边界和动量传输。
|
| 图 4 TFM-IPAM整体求解流程 Fig. 4 Entire solution procedure for TFM-IPAM |
以不渗透的直圆管为研究对象,设计了4种微重力流型验证工况(见表 1),其中气液表观速度usg和usl按入口流量(前3个工况为1 L/min、第4个工况为22.15 L/min)、截面面积、入口含气率αg=0.1,0.5,0.9,0.96换算得到。
| 工况 | usl/(m·s-1) | usg/(m·s-1) | usl/usg | Wel | Weg | Wel/Weg | 微重力流型结果 | |
| 仿真 | 文献 | |||||||
| 1 | 0.19 | 0.02 | 9.00 | 0.46 | 0.05 | 9.00 | 泡状 | 泡状[24, 25, 26, 27, 28, 29] |
| 2 | 0.11 | 0.11 | 1.00 | 0.25 | 0.25 | 1.00 | 弹状 | 弹状[24, 25, 26, 27, 28, 29] |
| 3 | 0.02 | 0.19 | 0.11 | 0.05 | 0.46 | 0.11 | 弹状 | 弹状[24, 25, 26, 27, 28, 29] |
| 4 | 0.20 | 4.50 | 0.04 | 0.48 | 10.76 | 0.04 | 环状 | 环状[23] |
| 注:Weg,Wel—气相和液相韦伯数。 | ||||||||
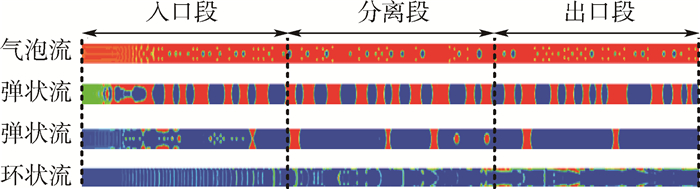
首先采用TFM-IPAM计算得到较为真实的入口流型分布。图 5为4种工况微重力流型仿真结果。图中红色代表液相,蓝色代表气相,其他颜色代表混合相。随着usg增大,工况1~工况4仿真预测流型分别为泡状流、弹状流、弹状流、环状流。同时结果表明,各工况均按气液两相均匀混合的形式给定入口流入形态,在TFM-IPAM几何边界和界面动量传输的约束下,气液两相自动形成与入口流动参数匹配的流动形态。形态转化呈现一定程度的气液界面多尺度现象,TFM-IPAM成功捕捉到流动中典型的大尺度界面特征,对小尺度界面具有过滤作用,实现了界面多尺度问题中大小尺度界面的层次化处理,有效避免了传统计算方法适应性和可计算性差等问题。
|
| 图 5 微重力流型仿真结果 Fig. 5 Simulation results of microgravity flow patterns |
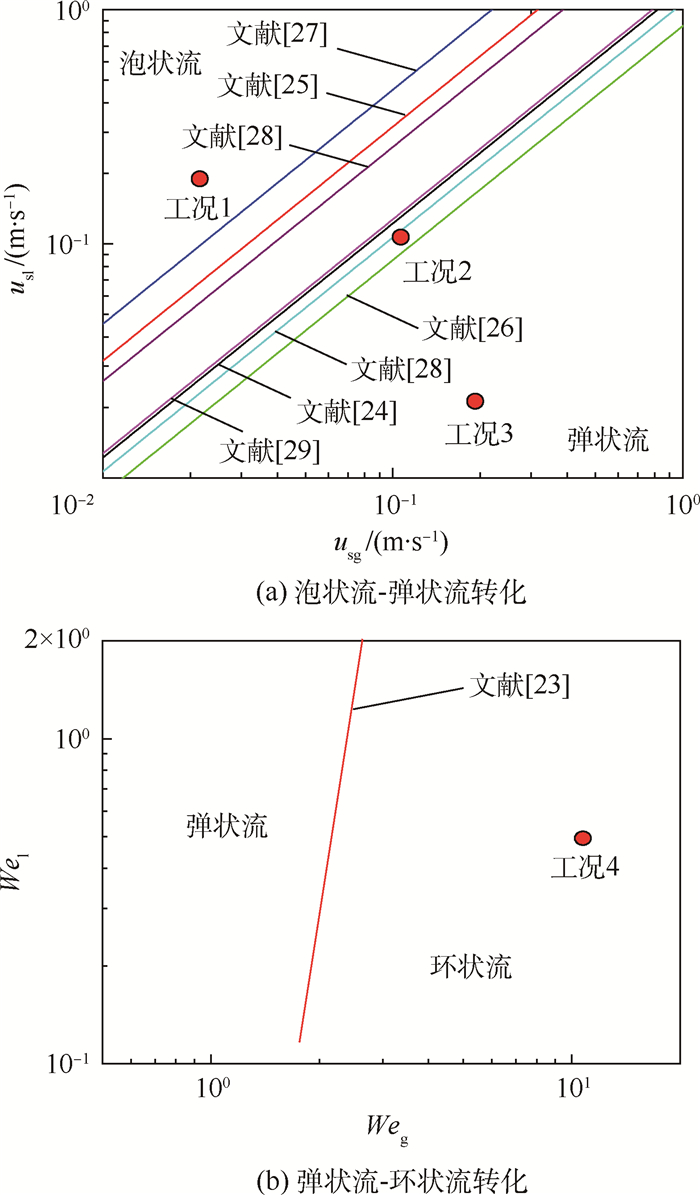
其次与文献[23-29]微重力实验得到的流型图进行对比验证。
1) 微重力条件下泡状流-弹状流之间的转变采用Zuber-Findlay空隙率模型[30]预测,转化条件为
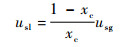
|
(17) |
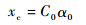
|
(18) |
式中:xc为临界参数;气相分布参数C0和临界空隙率α0由实验测定或用实验经验关系式算出。
2) 微重力条件下弹状流-环状流之间的转变,采用Zhao-Hu半理论Weber数模型[23],转化条件为

|
(19) |
式中:Wel=usl/u0=(Weslρg/ρl)1/2,u0=(ρga/σ)1/2为特征速度,a为圆管直径或矩形截面边长,Wesl=ρlusl2a/σ为液相表观韦伯数;Weg=usg/u0=(Wesg)1/2,Wesg=ρgusg2a/σ为气相表观韦伯数。
图 6对比了仿真预测结果与由微重力实验确定的流型图[23-29]预测结果。由于不同研究者的实验工质、管径、管型均不相同,难以得到统一的参数值,具有一定的不确定性,故工况2的点位于近似平行的分割带中,但总体上4个工况的仿真结果与2个流型图预测结果具有很好的一致性,验证了TFM-IPAM在解决入口流型仿真问题(即入口边界气液界面多尺度仿真问题)的有效性。
2.2 膜渗透模型有效性以渗透的直圆管为研究对象,以准稳态时刻(取10 s)液相渗透总流量∑Qi为验证指标,通过对比仿真值与工程值验证膜渗透模型的有效性。验证工况及结果见表 2。
| 工况 | usl/(m·s-1) | usg/(m·s-1) | ∑Qi | ||
| 仿真值/(mL·s-1) | 工程值/(mL·s-1) | 误差/% | |||
| 1 | 0.21 | 0 | 0.210 0 | 0.210 0 | 0 |
| 2 | 0.19 | 0.02 | 0.210 2 | 0.209 8 | 0.2 |
| 3 | 0.11 | 0.11 | 0.163 0 | 0.160 0 | 1.9 |
| 4 | 0.02 | 0.19 | 0.043 2 | 0.039 4 | 9.6 |
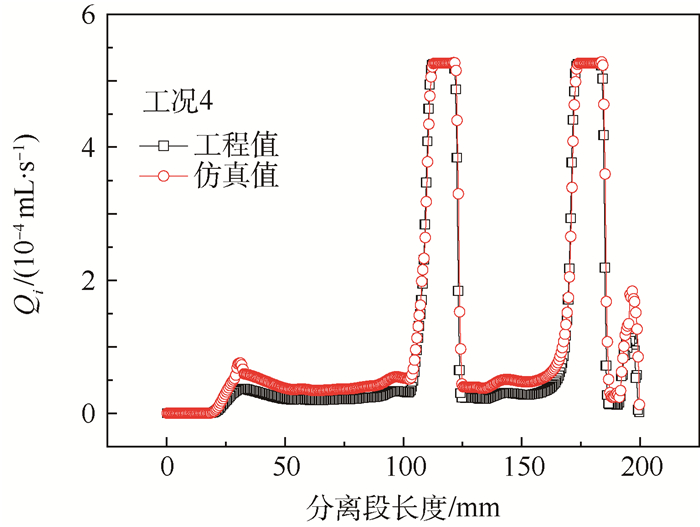
结果表明∑Qi的仿真值与工程值最大误差小于10%,平均误差小于3%。图 7以工况4为例,给出了膜渗透局部流量的沿程变化曲线,仿真计算曲线与工程计算曲线具有高度一致的变化趋势, 从而在定量和定性2个方面验证了膜渗透模型的有效性。
|
| 图 7 仿真与工程值对比 Fig. 7 Comparison between simulation and engineering values |
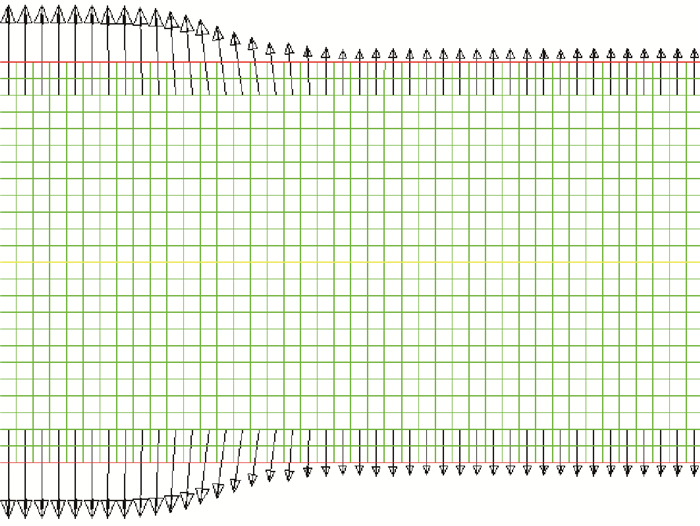
同时液相渗透速度矢量局部放大图(见图 8)表明在外部虚拟计算域和内部流道计算域之间的面上,液相渗透速度矢量的大小具有分布性,相比于质量源项法,动量源项法更为真实地模拟了分离膜的渗透过程。此外,膜面上并无气相渗透速度产生,说明模型能有效阻挡气体穿透,实现了分离膜对水的选择性。
|
| 图 8 液相渗透速度矢量 Fig. 8 Permeability velocity vector of liquid phase |
以渗透的矩形截面流道为研究对象,以准稳态时段(10~15 s)的时均膜通量Qva为膜式水气分离性能指标,考查典型工作参数下不同流道弯曲度对性能的影响。仿真工况及结果见表 3。其中:u0=0.21C m/s,C为速度倍率因子;usl=(1-αg)u0 m/s;usg=αgu0 m/s。
| θ/(°) | C | Qva /(mL·m-2·s-1) | |||
| αg=0 | αg=0.1 | αg=0.5 | αg=0.9 | ||
| 0 | 1.0 | 33.464 | 33.355 | 26.201 | 7.037 |
| 0.5 | 33.460 | 33.326 | 25.109 | 4.994 | |
| 90 | 1.0 | 33.479 | 33.270 | 23.765 | 6.896 |
| 0.5 | 33.479 | 33.124 | 23.422 | 4.852 | |
| 180 | 1.0 | 33.479 | 32.970 | 22.211 | 6.938 |
| 0.5 | 33.465 | 32.718 | 20.381 | 4.800 | |
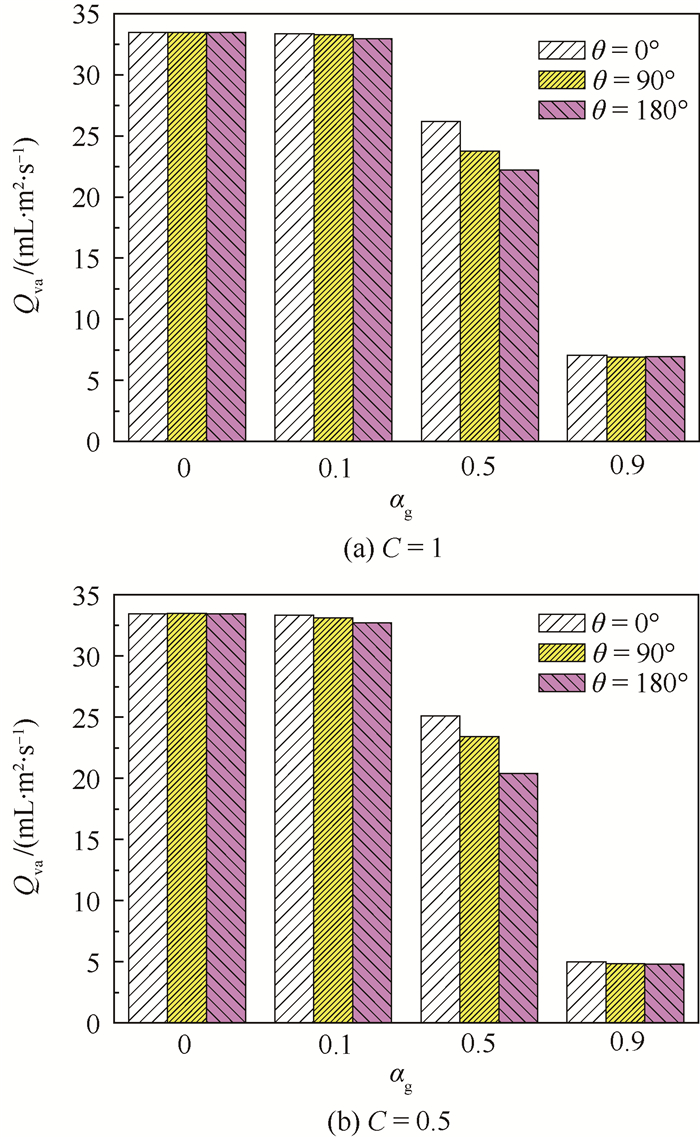
图 9对比了典型工作参数下不同流道弯曲度的时均膜通量。结果表明:①同一θ的工况下,Qva整体上随αg增大而减小。因Qva与膜面局部含液率相关,而局部含液率受αg和局部流动形态综合影响,故Qva与αg呈非线性变化;②同一αg的工况下,Qva随θ的变化规律具有差异。
|
| 图 9 不同θ工况下Qva对比 Fig. 9 Qva comparison between different θ |
在αg=0时,膜面含液率全局一致,Qva仅受局部压差影响,θ变化造成局部压力增大,使Qva略有增大,相对改变率ηθ的平均值小于0.06%。其中相对改变率ηθ定义为
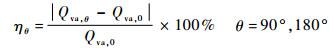
|
(20) |
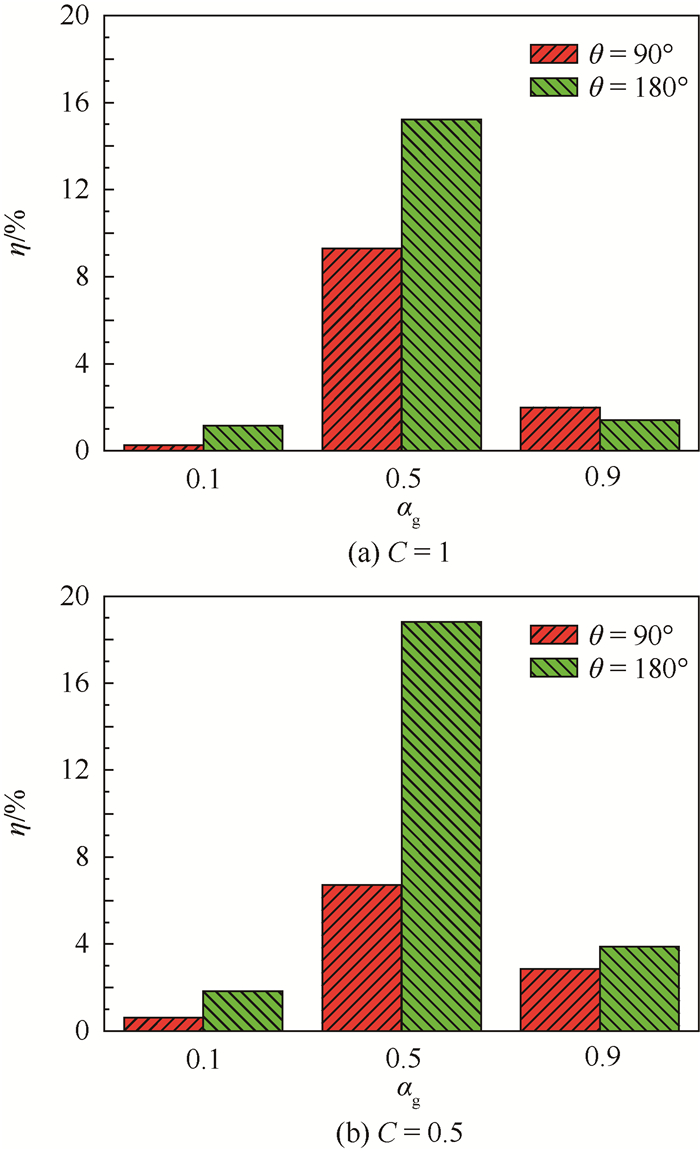
对于两相情况,总体表现为Qva随θ增大而减小,不同αg导致不同变化量。图 10表明:①在C=1、αg=0.1时,η90和η180分别为0.3%、1.2%,均值为0.75%;αg=0.5时,η90和η180分别为9.3%、15.2%,均值为12.3%;αg=0.9时,η90和η180分别为2.0%、1.4%,均值为1.7%;②在C=0.5、αg=0.1时,η90和η180分别为0.6%、1.8%,均值为1.2%;αg=0.5时,η90和η180分别为6.7%、18.8%,均值为12.8%;αg=0.9时,η90和η180分别为2.8%、3.9%,均值为3.4%。
|
| 图 10 不同θ工况下ηθ对比 Fig. 10 ηθ comparis on between different θ |
由此得出:多水和多气的工况,流道弯曲度变化对时均膜通量影响相对较小,相对变化率随速度倍率因子减小而增大;当αg=0.5时,时均膜通量受流道弯曲度影响显著,相对变化率随速度倍率因子变化无明显规律。
从宏观流动形态分析,以C=1、不同αg、不同θ工况下动态平衡时的瞬时流动形态(见图 11)为例。由于膜分离段长度较短,膜两侧压差变化可忽略,则Qva直接取决于膜面含液率。如图 11所示,θ直接影响膜面含液率,间接影响Qva。

|
| 图 11 不同θ工况下流动形态(C=1) Fig. 11 Flow morphologies under different θ(C=1) |
αg=0.1为典型多水工况,形态为泡状流,气泡尺度始终小于流道特征尺度d。θ=0°时,气泡在轴中央附近沿轴向运动,膜面含液率近似为1;θ=90°时,受离心力作用,液相流动偏离轴线,沿流道曲率半径向外流动,气泡沿曲率半径向里运动。此时离心力和液相阻力的综合作用不足以使气泡全部到达流道内侧壁面;θ=180°时,曲率半径减半,离心力加倍,气泡与内侧壁面接触面积相对增加,膜面含液率减小,Qva随之减小。
αg=0.5工况,形态为弹状流,气泡急剧形成并增大至流道特征尺度d。θ=0°时,在液膜粘性力作用下,气泡变为典型的前窄后宽的泰勒泡;θ=90°时,液柱外缘长度略大于内缘长度,但离心力仍不足以克服液柱内缘液膜粘性力,使液柱断裂形成气泡贯通或气液分层;θ=180°时,液柱出现局部贯通现象。然而由于水气比相当,当前流动形态不足以明显判定膜面含液率变化,需另作分析。
αg=0.9为典型多气工况,形态为弹状流,气泡尺度远大于流道特征尺度d。随θ增大,整体流动出现液滴脱落并跟随气流运动现象,导致膜面含液率减小,从而Qva减小。但由于流道整体含液量较少,故Qva受θ的影响相对较小。
从作用力贡献分析,采用当量弗劳德数无量纲方法,将由流道弯曲造成的离心场视为特殊形式的重力场,则当量弗劳德数为
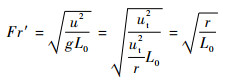
|
(21) |
式中:ut为切向速度;r为曲率半径;L0为特征长度。对于两相情况,流道弯曲造成的离心场由两相表观速度之和共同贡献,又气相和液相各自存在表观速度,则气液相的当量弗劳德数分别为
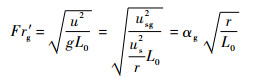
|
(22) |
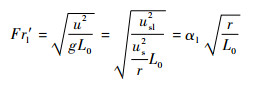
|
(23) |
式中:us为表观速度;r和l0定义为

|
(24) |

|
(25) |
式(24)和式(25)代入式(22)和式(23)可得
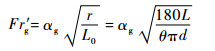
|
(26) |

|
(27) |
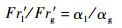
|
(28) |
式(27)表明:Fr′l随θ增大而减小。然而对于液相,除了自身惯性力和离心力,还受气相惯性力影响。采用Fr′l/ Fr′g反映液相惯性力与气相惯性力的主导关系,则θ对液相的影响,取决于Fr′l和Fr′l/ Fr′g二者的大小关系。
θ=90°:当αl=0.1时,Fr′l=0.36说明离心力对于液相惯性力占主导作用,但此时Fr′l/Fr′g=0.11,说明气相惯性力对液相的作用远大于离心力对液相的作用;当αl=0.9时,Fr′l=3.21表明液相惯性力占主导作用,同时Fr′l/ Fr′g=9说明相比于气相惯性力,液相惯性力仍然起主导作用;当αl=0.5时,Fr′l=1.78,Fr′l/Fr′g=1,说明液相惯性力与气相惯性力相当,离心力作用将凸显。上述分析从作用力贡献角度定性说明,在多水和多气工况,θ对Qva影响相对较小,同时解释了当αl=0.5时,Qva受θ影响显著的原因。θ=180°的影响分析与θ=90°类似。
4 结 论提出TFM-IPAM和动量源项法应用于微重力膜式水气分离性能仿真研究,得到以下结论:
1) TFM-IPAM具有捕捉和过滤不同尺度界面的功能,能增强计算方法的适应性和问题的可计算性;动量源项法能实现膜的选择性和渗透性,更为真实地模拟膜边界渗透过程。模型与方法能有效解决这一类仿真技术问题,具有重要的工程应用价值。
2) 时均膜通量随入口含气率增大而减小,存在显著的非线性关系;随流道弯曲度增大而降低,降低程度与αg相关。在典型的多气和多水工况下,流道弯曲度影响的相对变化率小于5%;当αg=0.5时,流道弯曲度对时均膜通量影响凸显,相对变化率均值大于12%。
3) 直流道(θ=0°)适于选作膜式静态水气分离器主要流道形式。流道弯曲度对膜特性影响规律以及当量弗劳德数无量纲分析方法为今后产品设计和技术改进提供了有益的参考。
| [1] | 张文伟, 杨春信. 再生式环控生保系统水气分离技术研究进展[J]. 航天医学与医学工程, 2011, 24 (6) : 444 –450. ZHANG W W, YANG C X. Progress of research on gas/liquid separation technology of regenerative environment control and life support system[J]. Space Medicine and Medical Engineering, 2011, 24 (6) : 444 –450. (in Chinese) |
| [2] | 张文伟, 柯鹏, 杨春信, 等. 气液两相流界面多尺度问题可计算性研究进展[J]. 化工学报, 2014, 65 (12) : 4645 –4654. ZHANG W W, KE P, YANG C X, et al. Progress of computability of multi-scale interface problems in gas-liquid two-phase flow[J]. CIESC Journal, 2014, 65 (12) : 4645 –4654. (in Chinese) |
| [3] | ŠTRUBELJL, TISELJI, MAVKOB. Simulations of free surface flows with implementation of surface tension and interface sharpening in the two-fluid model[J]. International Journal of Heat and Fluid Flow, 2009, 30 (4) : 741 –750. |
| [4] | HÖHNE T, VALLÉE C. Experiments and numerical simulations of horizontal two-phase flow regimes using an interfacial area density model[J]. Journal of Computational Multiphase Flows, 2010, 2 : 131 –143. DOI:10.1260/1757-482X.2.3.131 |
| [5] | YOON H Y, CHO H K, LEE J R, et al. Multi-scale thermal-hydraulic analysis of PWRS using the CUPID code[J]. Nuclear Engineering and Technology, 2012, 44 (8) : 831 –846. DOI:10.5516/NET.02.2012.716 |
| [6] | HÄNSCH S, LUCAS D, KREPPER E, et al. A multi-field two-fluid concept for transitions between different scales of interfacial structures[J]. International Journal of Multiphase Flow, 2012, 47 : 171 –182. DOI:10.1016/j.ijmultiphaseflow.2012.07.007 |
| [7] | COSTE P. A Large interface model for two-phase CFD[J]. Nuclear Engineering and Design, 2013, 255 : 38 –50. DOI:10.1016/j.nucengdes.2012.10.008 |
| [8] | ČERNEG, PETELINS, TISELJI. Coupling of the interface tracking and the two-fluid models for the simulation of incompressible two-phase flow[J]. International Journal of Multiphase Flow, 2001, 171 (2) : 776 –804. |
| [9] | WARDLE K, WELLER H. Hybrid multiphase CFD solver for coupled disperse segregated flows in liquid-liquid extraction[J]. International Journal of Chemical Engineering, 2013, 2013 : 1 –13. |
| [10] | VIEIRA T M, SOUZA J S, BARBOSA E S, et al. Numerical study of oil/water separation by ceramic membranes in the presence of turbulent flow[J]. Advances in Chemical Engineering and Science, 2012, 2 (2) : 257 –265. DOI:10.4236/aces.2012.22030 |
| [11] | 孙春平, 柯鹏, 杨春信. CFD技术在膜式静态水分离器中的应用方法研究[J]. 航天医学与医学工程, 2013, 26 (3) : 202 –205. SUN C P, KE P, YANG C X. Study on application of CFD technology in membrane static water separator[J]. Space Medicine and Medical Engineering, 2013, 26 (3) : 202 –205. (in Chinese) |
| [12] | 赵建福, 彭超, 李晶, 等. 静态水气分离特性的失重飞机实验研究[J]. 工程热物理学报, 2011, 32 (5) : 799 –802. ZHAO J F, PENG C, LI J, et al. Experimental study on performance of a static water-air two-phase separator aboard reduced gravity airplane[J]. Journal of Engineering Thermophysics, 2011, 32 (5) : 799 –802. (in Chinese) |
| [13] | 贾志谦. 膜科学与技术基础[M]. 北京: 化学工业出版社, 2012 : 61 -63. JIA Z Q. Membrane science and technology foundation[M]. Beijing: Chemical Industry Press, 2012 : 61 -63. (in Chinese) |
| [14] | ISHII M, HIBIKI T. Thermo-fluid dynamics of two-phase flow[M]. New York: Springer, 2006 : 156 -162. |
| [15] | TROSHKO A A, HASSAN Y A. A two-equation turbulence model of turbulent bubbly flows[J]. International Journal of Multiphase Flow, 2000, 27 (11) : 1965 –2000. |
| [16] | UBBINK O.Numerical prediction of two fluid systems with sharp interfaces[D].London:Imperial College of Science, Technology and Medicine, 1997. |
| [17] | OLSSON E, KREISS G. A conservative level set method for two phase flow[J]. Journal of Computational Physics, 2005, 210 (1) : 225 –246. DOI:10.1016/j.jcp.2005.04.007 |
| [18] | CLIFT R, GRACE J R, WEBER M E. Bubbles, drops, and particles[M]. London: Academic Press, 1978 : 111 -116. |
| [19] | ISHⅡ M, ZUBER N. Drag coefficient and relative velocity in bubbly, droplet or particulate flows[J]. AIChE Journal, 1979, 25 (5) : 843 –855. DOI:10.1002/(ISSN)1547-5905 |
| [20] | BRACKBILL J U, KOTHE D B, ZEMACH C. A continuum method for modeling surface tension[J]. Journal of Computational Physics, 1992, 100 (2) : 335 –354. DOI:10.1016/0021-9991(92)90240-Y |
| [21] | ERGUN S. Fluid flow through packed columns[J]. Chemical Engineering Progress, 1952, 48 (2) : 89 –84. |
| [22] | VASQUEZ S A, IVANOV V A.A phase coupled method for solving multiphase problems on unstructured meshes[C]//Proceedings of ASME 2000 Fluids Engineering Division Summer Meeting.Boston:ASME, 2000:743-748. |
| [23] | ZHAO J F, HU W R. Slug to annular flow transition of microgravity two-phase flow[J]. International Journal of Multiphase Flow, 2000, 20 (8) : 1295 –1304. |
| [24] | DUKLER A E, FABRE J, MCQUILLEN J B, et al. Gas-liquid flow at microgravity conditions flow patterns and their thansitions[J]. International Journal of Multiphase Flow, 1988, 14 (5) : 389 –400. |
| [25] | COLIN C, FABRE J, DUKLER A E. Gas-liquid flow at microgravity conditions-I dispersed bubble and slug flow[J]. International Journal of Multiphase Flow, 1993, 17 (4) : 533 –544. |
| [26] | COLIN C, FABRE J. Gas-liquid pipe flow under microgravity conditions:Influence of tube diameter on flow patterns and pressure drop[J]. Advances in Space Research, 1995, 16 (7) : 137 –142. DOI:10.1016/0273-1177(95)00148-8 |
| [27] | ZHAO L, REZKALLAH K S. Pressure drop in gas-liquid flow at microgravity conditions[J]. International Journal of Multiphase Flow, 1995, 21 (5) : 837 –849. DOI:10.1016/0301-9322(94)00089-3 |
| [28] | BOUSMAN W S, MCQUILLEN J B, WRITE L C. Gas-liquid flow patterns in microgravity:Effects of tube diameter, liquid viscosity and surface tension[J]. International Journal of Multiphase Flow, 1996, 22 (6) : 1035 –1053. DOI:10.1016/0301-9322(96)00023-7 |
| [29] | 赵建福, 林海, 解京昌, 等. 失重飞机搭载气/液两相流实验研究[J]. 空间科学学报, 2000, 20 (4) : 340 –347. ZHAO J F, LIN H, XIE J C, et al. Experimental investigation of gas-liquid two-phase flow utilizing reduced gravity airplane[J]. Chinese Journal of Space Science, 2000, 20 (4) : 340 –347. (in Chinese) |
| [30] | ZUBER N, FINDLAY J A. Average volumetric concentration in two-phase flow systems[J]. Journal of Heat Transfer, 1965, 87 (4) : 453 –468. DOI:10.1115/1.3689137 |