在航空航天的结构中存在着大量的开口薄壁结构,由于开口薄壁结构的抗扭性能较差,而横向加强构件的存在可以大大改善开口薄壁结构受扭后的变形应力状态。因此,为了提高其抗扭性能,通常在结构中使用有横向加强构件的开口薄壁梁。由于横向加强构件的存在,使得结构的建模通常采用壳单元或实体单元。实体单元虽然可以很好地模拟真实结构,但通常所需单元的数量较大,计算代价高昂。而使用壳单元虽能有效地减小单元数量,但是薄壁构件通常存在大量的圆角,壳单元对圆角进行建模通常很困难且步骤繁琐[1]。因此,为了更有效地对有横向加强构件的薄壁杆件建模,本文提出运用开口薄壁梁单元对其进行等效建模,单元的截面参数可以通过参数辨识的方法得到。这种方法可以大幅度地减小单元数量与计算规模并且有很高的精度。
Arpaci等[2-3]研究了考虑扭转效应的开口薄壁梁的耦合振动特性。Prokić [4]研究了任意截面形状的开口薄壁梁的动力学特性。Ambrosini等[5-6]运用Vlasov理论计算了任意截面开口薄壁梁的振动频率。Prokić [7]考虑了复杂薄壁梁振动的耦合效应。本文在此基础上建立了有横向加强构件的开口薄壁梁的弯扭耦合振动方程。通过实验测得的固有频率,分别采用有限元法、传递矩阵法和解析法对模型进行参数优化辨识,从而建立了等效梁单元模型,通过与实测频率进行对比,验证了方法的正确性与精确性。
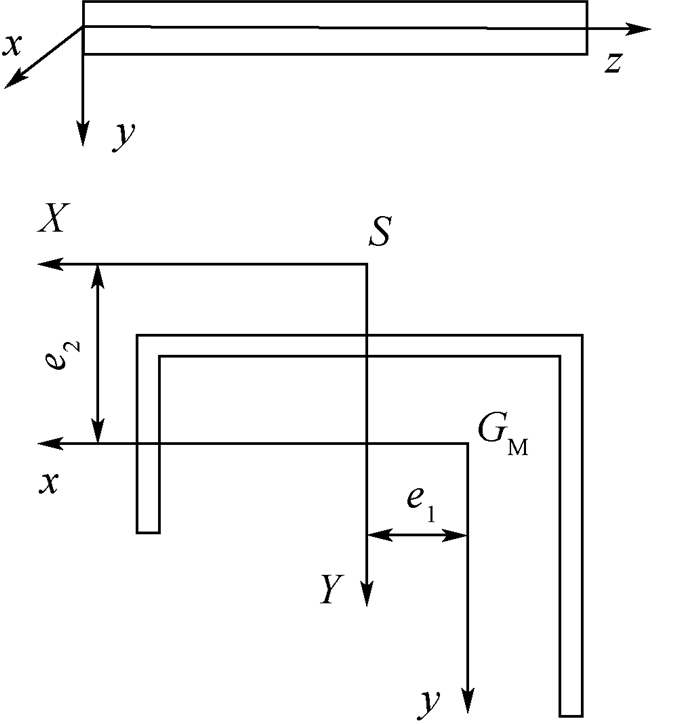
1 开口薄壁杆件弯扭耦合振动方程图 1为开口薄壁梁横截面。考虑图 1所示的弯扭耦合非对称薄壁梁单元截面, X和Y轴通过截面剪切中心(剪心)S且平行于过形心的坐标轴x和y,S点与GM点为横截面的剪心与质心,剪心与质心之间的2个坐标轴之间的距离分别为e1和e2。一般细长的开口薄壁杆件弯扭耦合振动方程[8]为
|
| 图 1 开口薄壁梁横截面 Fig. 1 Cross-section of open thin-walled beam |
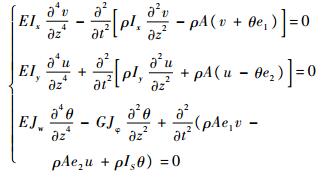
|
(1) |
式中:v为横截面剪心沿y方向的位移;u为剪心沿x轴方向的位移;θ为横截面扭转角;ρ为材料密度;Ix和Iy为截面关于x轴与y轴的惯性矩;Jw和Jφ为截面翘曲常数和扭转常数;E为材料的弹性模量;IS为截面关于剪心的极惯性矩;t为时间;A为隔板区域面积;G为剪切模量。
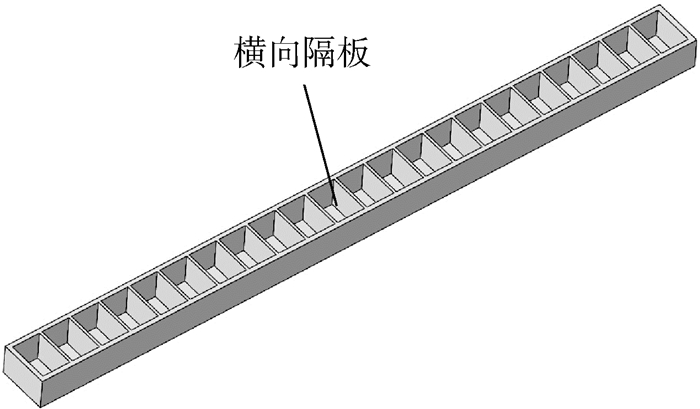
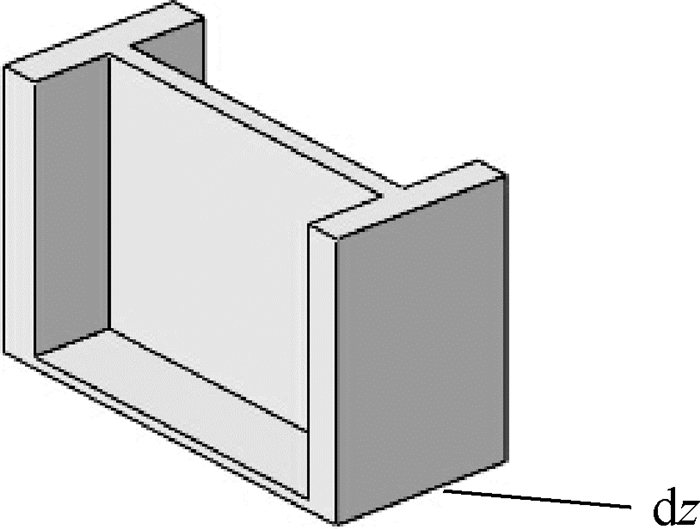
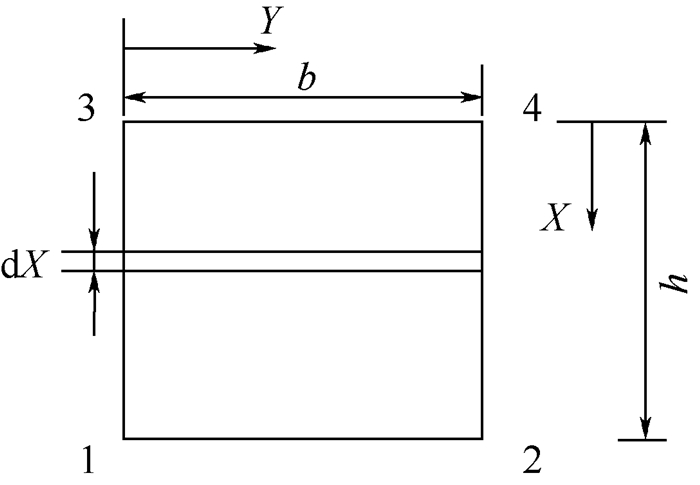
2 横向加强构件作用下的开口薄壁杆件横向隔板构件作用下的开口杆件如图 2所示,由于隔板对于杆件的翘曲有一定的抑制作用,因此杆件的弯扭耦合运动方程与开口杆件将是有差别的[9],容易证明,对于纯弯曲变形状态,这种杆件可以等效为普通的开口薄壁梁。而对于纯扭转变形,本节将会证明有隔板加强杆件的运动方程与普通开口薄壁杆件运动方程在形式上也是一致的。当有横向隔板构件作用下的薄壁杆件发生整体扭转变形时,由于隔板与杆件连接处横向弯矩与剪力的作用,隔板除了产生扭曲以外还会发生弯曲。从杆件中取出含有隔板的一个微段dz,如图 3所示。隔板的厚度为d,长宽分别为b和h,隔板平面示意图如图 4所示。
|
| 图 2 横向隔板构件作用下的开口杆件 Fig. 2 Open bar under action of transverse partition member |
|
| 图 3 含有横向隔板的一个微段 Fig. 3 micro-segment containing transverse partition member |
|
| 图 4 横向隔板示意图 Fig. 4 Schematic diagram of transverse partition member |
若不考虑连接处的弯矩作用,隔板相当于铰接在槽型杆件上,由虚位移原理可以得到微段的平衡微分方程[9]:
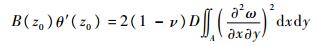
|
(2) |
式中:D为隔板抗弯刚度;ν为材料泊松比;B(z0)为隔板对槽型截面作用的双力矩,z0为轴向坐标;ω为隔板的面外位移,与杆件轴向平行。根据薄板理论,由于不考虑连接处横向弯矩作用,隔板只承受扭矩,板的面外位移为
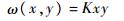
|
(3) |
式中:K为任意常数,可以通过边界条件确定。当杆件只承受扭矩作用时,槽型杆件周边纵向位移为
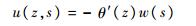
|
(4) |
式中:w(s)为以隔板中心为极点的扇形坐标, s为周向曲线坐标。联立式(2)~式(4)可以得到
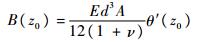
|
(5) |
由式(5)推导可知横向隔板对该槽型截面处的作用相当于一双力矩。
若考虑隔板与槽型截面连接处的弯矩时,将隔板可以看作一系列宽为dx、长为b的梁所组成,如图 4所示,由于1和2边不受外力,因此可以忽略梁与梁之间的内力,考虑到槽型截面外形轮廓线上各点的翘曲不同,隔板将会发生面外弯曲。将宽为dx且两端固支的梁由中间位置截开。在切口处作用一对方向沿杆轴线的单位剪力。
可以由图乘法计算得到切口两端相对位移为
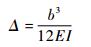
|
(6) |
式中:I为梁的截面惯性矩:
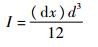
|
(7) |
开口截面薄壁杆件受扭矩作用时,梁切口两端的位移δ可以由单位力法求解得到

|
(8) |
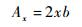
|
(9) |
式中:Ax为隔板面积。由于切口两端相对位移为0,将式(6)~式(9)代入力法方程,可以得到
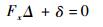
|
(10) |
式中:Fx为切口两端作用力:
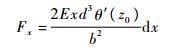
|
(11) |
因此力Fx在槽型截面上引起的双力矩为
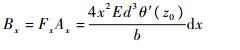
|
(12) |
式中:Bx为长为b的梁在槽型截面z0处的双力矩。现在对Bx从0到h进行积分,可以得到隔板整体对槽型截面的双力矩B(z0)为
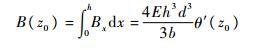
|
(13) |
考虑到隔板同时发生弯曲与扭转变形,因此总的双力矩为二者的叠加,即

|
(14) |
由于杆件为周期薄壁结构,且隔板沿杆纵向布置较密,可以采用连续化处理方法,将多层隔板等效成为连续的弹性介质,弹性介质对槽型截面的双力矩集度可由式(15)等效计算:

|
(15) |
式中:B(z)为双力矩;Lc为隔板之间的间距。槽型截面剪力流为
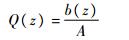
|
(16) |
根据有加强构件的开口薄壁梁的连续化解法,可以得到一般意义下的有加强构件薄壁杆件受静态扭转载荷作用的平衡微分方程[9]为
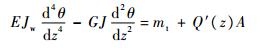
|
(17) |
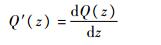
|
(18) |
式中:mt为沿杆长分布的外扭矩;J为扭转惯性矩。
将式(14)~式(16)代入式(17)和式(18)中,可以得到微段受扭矩作用的平衡微分方程:
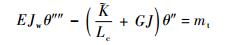
|
(19) |

|
(20) |
式中: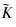
一般非对称开口薄壁杆件受静态扭转载荷作用的平衡微分方程为
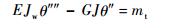
|
(21) |
对比式(19)与式(21)可知,有隔板作用下的开口薄壁杆件受扭静态平衡方程与一般开口薄壁杆件方程形式相同,只是在扭转刚度GJ上增加了一个修正项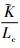
正确的辨识等效截面参数首先需要建立正确的数学模型。本节通过有限元法建立考虑剪切变形的开口薄壁梁单元的数学模型。王晓峰[10]、Mohri[11]和Kim[12]等分别建立了考虑剪切变形的空间薄壁梁单元。这种单元基于Timoshenko梁理论和Vlasov薄壁杆件约束扭转理论,通过设置单元内部结点,对弯曲转角和翘曲角采用独立插值的方法,薄壁杆件横截面正应力对应的余能为
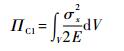
|
(22) |
式中:V为体积;σx为正应力。
剪应力对应的余能为
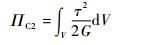
|
(23) |
式中:τ为剪应力。
圣维南剪力所对应的余能为
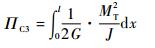
|
(24) |
式中:MT为转矩; l为梁的长度。
因此单元的总余能为三者的叠加, 即
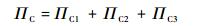
|
(25) |
根据Hellinger-Reissner广义变分原理,推得可同时考虑剪切变形及弯扭耦合等因素的空间薄壁梁单元刚度矩阵。单元每个节点有7个自由度:{u, v, w, θx, θy, θz, θ},u、v和w为沿3个坐标轴方向的横向位移,θx、θy和θz为绕3个坐标轴的转角。通过引入单元内部节点,由插值函数建立单元位移场,通过虚功原理建立单元平衡微分方程,同时将单元内部自由度凝聚后可以得到单元刚度矩阵K,同理用类似的方法可以得到单元的质量矩阵,以上所描述的有限元模型在一般的有限元通用程序中均有相应的单元,例如ABAQUS中开口薄壁梁单元。
3.2 传递矩阵模型Ambrosini[13]建立了考虑剪切效应与转动惯量的开口薄壁梁单元的传递矩阵模型,即

|
(26) |
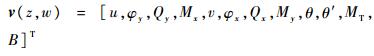
|
式中: v (z, ωf)为状态矢量,ωf为圆频率; φx和φy为绕x轴和y轴的截面转角; Qx和Qy为截面剪力; Mx和My为弯曲力矩; θ′为θ沿薄壁梁轴向坐标的一阶微分; B为双力矩; 矩阵A的具体形式可以参见文献[12]。式(26)适用于非对称开口薄壁杆件,并且由于考虑了剪切效应,因此也适用于深梁。因此状态矢量可以表示为
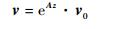
|
(27) |
式中:v0为初始状态矢量。将eAz展开成级数的形式, 即
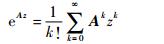
|
(28) |
式中:A为12阶×12阶函数传递矩阵。对于固支边界条件、简支边界条件和自由边界条件依次有
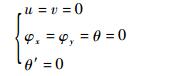
|
(29) |
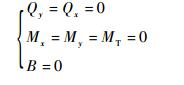
|
(30) |
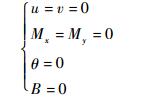
|
(31) |
根据开口薄壁梁两端的边界条件可以求出固有频率。
3.3 解析模型开口薄壁杆件振动微分方程式(1)并未考虑梁的剪切效应,因此仅对于细长梁有较高的精度。令
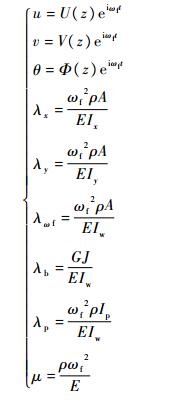
|
(32) |
式中:Iw为翘曲系数;Ip为极惯性矩;U(z)为横向位移幅值;V(z)为纵向位移幅值;Φ(z)为转角位移幅值,假设:
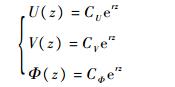
|
(33) |
式中:CU为横向位移常数;CV为纵向位移常数;CΦ为转角位移常数;r为常数。
将式(32)和式(33)代入振动微分方程式(1)并化简可以得到其矩阵形式为
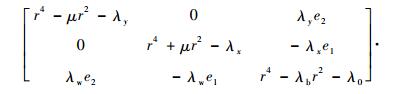
|
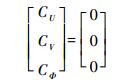
|
(34) |
若方程式(34)存在非零解, 则其系数行列式应为0,于是有
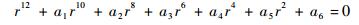
|
(35) |
式中:
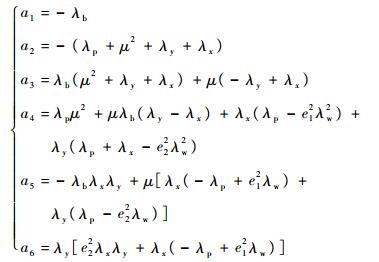
|
可以通过数值计算求解方程式(35)的根,因此可以得到U(z)、V(z)和Φ(z)的一般表达式为
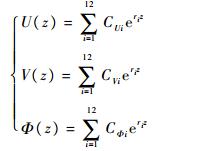
|
(36) |
式中:ri为常数,未知量CUi、CVi和CΦi可以由边界条件得到。边界条件与式(29)~式(31)相同。
3.4 截面参数优化识别流程 3.4.1 目标函数建立进行参数优化识别首先要建立正确的目标函数,目标函数的好坏将会直接影响到辨识参数的精度,本文通过采用3种不同的目标函数对参数进行辨识,并同时比较3种辨识结果的精度。目标函数为
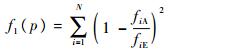
|
(37) |
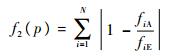
|
(38) |

|
(39) |
式中:p为需要辨识的参数;fiA为计算固有频率;fiE为实验频率或目标频率。后2种目标函数是非光滑的函数,可以通过变换将其转化为光滑优化问题。
对于目标函数式(38),可以将其转化为
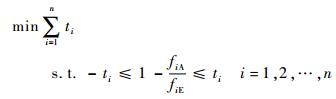
|
(40) |
对于目标函数式(39),可以将其转化为
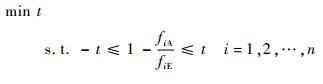
|
(41) |
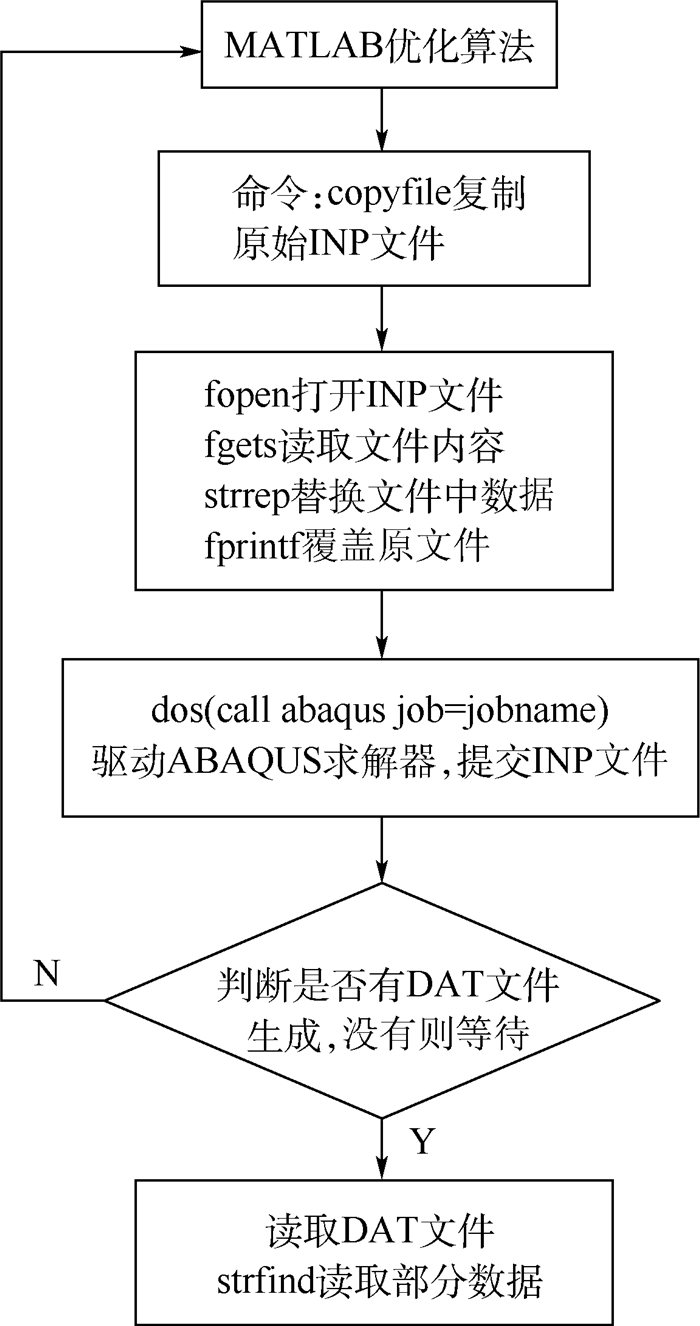
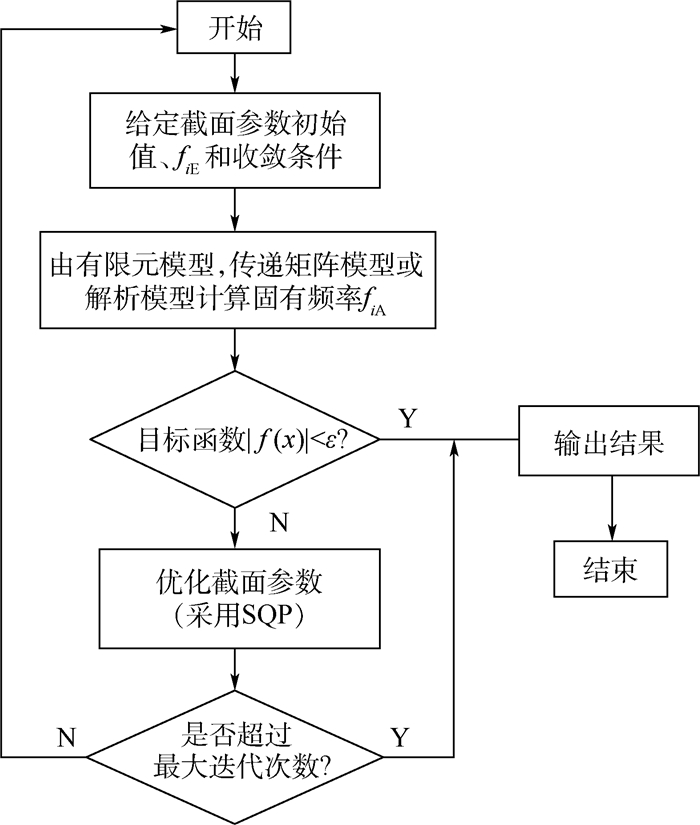
通过以上变量替换将截面参数辨识问题转化为带约束的非线性优化问题。序列二次规划(SQP)[14-16]算法是求解中小规模约束最优化问题的一类有效算法。SQP的基本思想是用一系列二次规划问题来逼近带约束的非线性优化问题的解。本文采用全局SQP方法对截面参数进行优化,截面参数优化识别流程如图 5和图 6所示。
|
| 图 5 MATLAB与ABAQUS交互优化流程 Fig. 5 MATLAB and ABAQUS interactive optimization process |
|
| 图 6 截面参数识别流程 Fig. 6 Cross-section parameter identification procedure |
MATLAB是一种影响大、流行广的科学计算语言,其中拥有大量优秀的数值算法,而ABAQUS是一款非常强大的有限元分析软件,可以模拟非常复杂的模型。在运用有限元模型进行参数辨识的过程中,本文将结合二者的优点,同时使用MATLAB和ABAQUS进行交互式的优化参数辨识。INP文件是ABAQUS的输入文件,它包含了对整个模型的完整描述,而INP文件本质上是一种文本文件,因此MATLAB可以对其进行读写从而控制ABAQUS的分析过程。ABAQUS通常可以将其计算结果输出至DAT文件,MATLAB可以直接读取DAT文件中的数据,由此可知只需要通过文件之间的交换即可实现MATLAB与ABAQUS联合优化。
在优化过程中,每一步迭代,MATLAB中可以通过修改INP文件中的部分数据然后运用dos命令驱动ABAQUS程序进行计算,同时MATLAB可以判断是否有DAT结果文件生成从而读取其中的结果数据,由结果数据通过优化算法进行一步迭代得到一组新的数据作为ABAQUS输入数据,从而完成一次循环。MATLAB与ABAQUS交互优化流程如图 5所示。
3.4.3 截面参数初始值估算截面参数初始值对参数优化将会产生较大的影响。合理的设置初始值才能得到正确的结果。初始值的估计可以通过对结构施加静态载荷,运用有限元程序计算得到的静态位移估算截面的等效参数。截面等效惯性矩Ix和Iy的估计可以通过对一端固支的实体在另一端分别施加弯矩Mx和My,通过实体单元计算截面端部的位移wx和wy,由材料力学可知
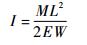
|
(42) |
式中:M为端部所受的力矩;W为端部位移;L(0≤L≤1)为隔板沿轴向厚度之和与结构的总长度之比。
截面的扭转常数Jφ与翘曲常数Jw对结构的固有频率的影响很大,因此合理的设置初值可以提高截面参数的辨识精度。
工况1 考虑将结构的一端固支,在另一端施加扭矩mt。采用里兹法求解截面扭转角,开口截面薄壁杆件的约束扭转势能可以表示为

|
(43) |
由于薄壁杆件的一端完全固支,因此在固定端处的扭转角θ和翘曲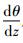
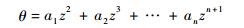
|
(44) |
易知式(44)满足位移边界条件。将式(44)代入式(43),得
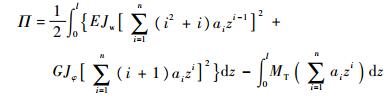
|
(45) |
由势能驻值原理可以得到
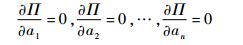
|
(46) |
由此可以解出n个参数。当令n→∞,可以解得精确解为
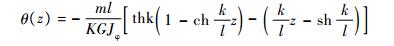
|
(47) |
式中: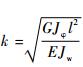
工况2 考虑将结构的两端均固支,在杆件的1/2截面处施加扭矩MT,由于在固定端处要满足位移边界条件,可以假设扭转角θ为
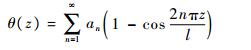
|
(48) |
易知式(48)满足两端固支的边界条件,因此开口薄壁杆件的应变能为
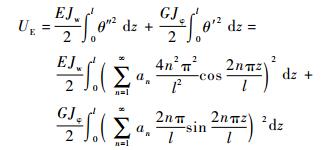
|
(49) |
利用积分公式,当n≠m时有
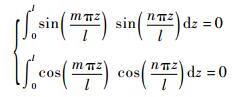
|
(50) |
当n=m时有

|
(51) |
因此式(49)可以化简为

|
(52) |
载荷势能为
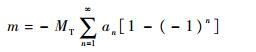
|
(53) |
因此薄壁杆件的总势能为
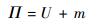
|
(54) |
根据势能驻值条件可以得到
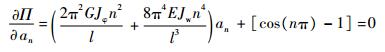
|
(55) |
可以得到
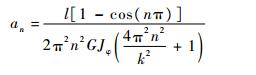
|
(56) |
由此可以得到扭转角θ(z)的解析式,令z=l 2可以得到扭矩作用点处的扭转角。实际使用中,通常取解析式的前3项来近似扭转角θ(z)。本节推导了2种不同工况下扭转角θ(z)的解析式。对于扭转常数Jφ与翘曲常数Jw初值的估算,可以在有限元程序中运用实体单元计算2种工况下结构的静态位移,然后联立式(47)和式(48)可以得到关于Jφ与Jw的非线性方程组。非线性方程组可以采用牛顿法进行求解进而得到Jφ与Jw的初始估计值。
4 仿真算例运用有横向隔板构件加强的薄壁结构进行仿真验证,槽型横截面宽0.1 m,高0.1 m,壁厚0.008 m,隔板厚度为0.005 m,隔板的间距为0.071 m,薄壁构件的总长为1.5 m,材料弹性模量为71 GPa,材料的密度为2.78×103 kg/m3。在ABAQUS中运用实体单元计算结构两端自由时的前10阶固有频率,建立目标函数,设置辨识参数的初始值然后进行参数优化,x轴与y轴为过截面形心的主惯性轴,且y轴为截面对称轴,如图 1所示。易知剪心在此对称轴上,由此可知e1=0,因此需要辨识的参数有7个,辨识结果如表 1所示。表 2为简化模型计算所得的各阶频率与真实模型频率的误差绝对值。
| 截面参数 | 梁单元模型 | 传递矩阵模型 | 解析模型 | ||
| 二范数 | 无穷范数 | 一范数 | |||
| Ix/(10-6m4) | 2.26 | 2.34 | 2.24 | 2.16 | 2.30 |
| Iy/(10-6m4) | 3.88 | 2.50 | 3.76 | 3.76 | 3.71 |
| Jφ/(10-7m4) | 1.47 | 1.44 | 1.42 | 1.39 | 1.44 |
| Jw/(10-9m6) | 2.08 | 2.19 | 2.06 | 2.17 | 2.13 |
| e1/m | 0 | 0 | 0 | 0 | 0 |
| e2/mm | 66.4 | 68.4 | 65.8 | 68.2 | 67.2 |
| Kx | 0.837 | 0.905 | 0.824 | 0.788 | |
| Ky | 0.411 | 0.443 | 0.424 | 0.352 | |
| % | |||||
| 模态 阶次 |
梁单元模型 | 传递矩阵模型 | 解析模型 | ||
| 二范数 | 无穷范数 | 一范数 | |||
| 1 | 0.37 | 2.12 | 0.29 | 0.01 | 0.27 |
| 2 | 1.08 | 0.98 | 1.06 | 0.08 | 0.80 |
| 3 | 0.09 | 1.91 | 0.15 | 1.40 | 0.88 |
| 4 | 0.57 | 2.11 | 1.05 | 1.71 | 1.36 |
| 5 | 1.68 | 2.02 | 2.18 | 1.22 | 1.77 |
| 6 | 0.07 | 1.99 | 0.06 | 0.18 | 0.57 |
| 7 | 0.45 | 0.45 | 1.01 | 0.20 | 0.53 |
| 8 | 0.67 | 0.92 | 0.72 | 0.22 | 0.63 |
| 9 | 0.02 | 2.13 | 0.09 | 2.35 | 1.15 |
| 10 | 2.07 | 2.18 | 2.06 | 2.19 | 2.12 |
| 11 | 2.05 | 2.08 | 1.11 | 2.18 | 1.85 |
表 1中, Kx和Ky为x方向和y方向的横向剪切刚度系数。由表 1可以看出,目标函数为二范数与无穷范数辨识所得的结果相接近,并且由表 2反映上述2种模型计算的结果相对于其他模型更加接近真实值。当目标函数为二范数时,等效模型与真实模型的模态应变能及其误差如表 3所示,由于模态应变能不仅包含各阶模态的刚度信息,同时还包含振型的相关信息,因此表 3的结果可以说明等效梁单元计算精度可以逼近真实解且误差在工程要求的范围之内。
| 模态 阶次 |
模态应变能/(N·m) | 模态应变能误差/% | |
| 真实模型 | 等效模型 | ||
| 1 | 530 070 | 538 680 | 1.62 |
| 2 | 595 130 | 604 227 | 1.51 |
| 3 | 923 810 | 922 350 | -0.16 |
| 4 | 2 421 200 | 2 362 411 | -2.41 |
| 5 | 5 509 182 | 5 574 967 | 1.18 |
| 6 | 6.456×106 | 6.460×106 | 0.06 |
| 7 | 7.208×106 | 7 040 179 | -2.33 |
| 8 | 1.419×107 | 1.396×107 | -1.62 |
| 9 | 2.215×107 | 2.226×107 | 0.49 |
| 10 | 2.733×107 | 2.790×107 | 2.01 |
| 11 | 3.067×107 | 3.129×107 | 1.96 |
有横向隔板的开口结构的扭转刚度与翘曲刚度介于普通的开口结构与闭口结构之间,随着横向隔板数量的增加,其结构的力学性能在理论上应接近于闭口结构,反之,应接近于无横向加强的薄壁开口结构,为了验证此结论,定义式(42)中的L,对于开口截面与闭口截面均可以得到其等效扭转常数的精确解。对于开口截面,截面的扭转常数精确解为[17]

|
(57) |
对于闭口截面,截面扭转常数的精确解为
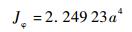
|
(58) |
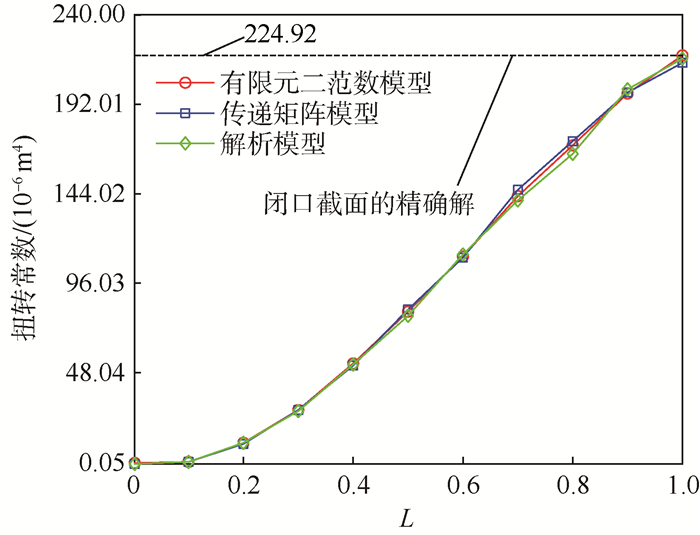
式中:a为槽型截面尺寸;δt为槽型截面的壁厚。图 7反映了随着隔板数量与厚度的增加,等效截面扭转常数可以趋近于闭口截面的精确解2.249 2×10-4m4,而随着隔板数量与厚度的减少, 等效截面扭转常数可以趋近于槽形开口截面扭转常数精确解5.091 3×10-8m4。由此可以说明等效梁模型的正确性与合理性。
|
| 图 7 等效截面扭转常数与L的关系曲线 Fig. 7 Relationship curves between equivalent cross-section torsion constant and L |
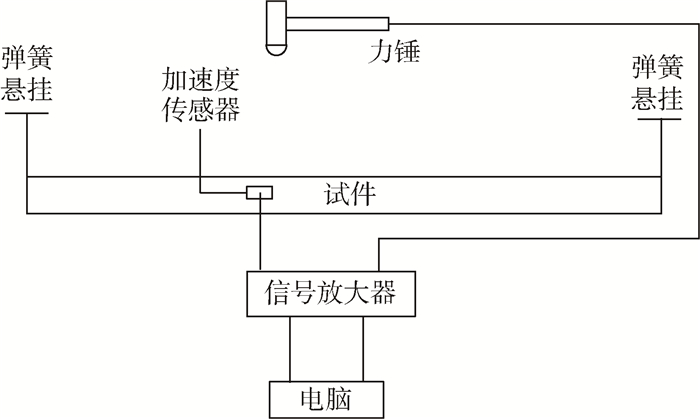
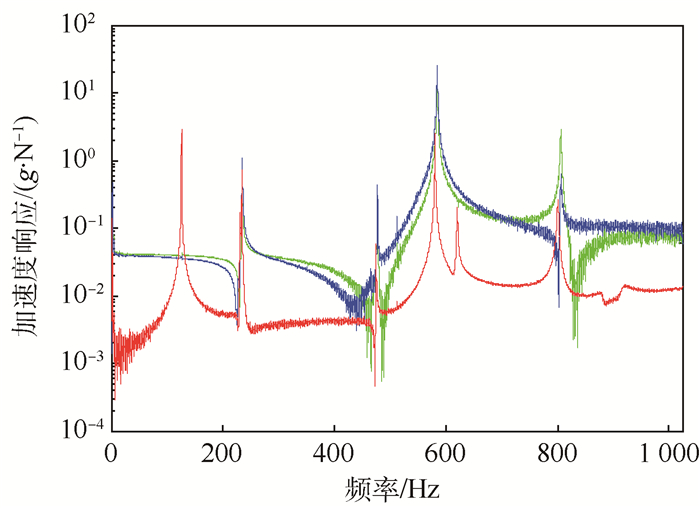
某测试结构长1.1 m,槽型截面宽0.1 m,高0.06 m,壁厚5 mm,隔板厚度3 mm,隔板间距0.1 m,材料弹性模量为71GPa,材料的密度为2 780 kg/m3。测试结构如图 2所示。通过锤击法模态测试测量结构的固有频率。将结构用软弹簧悬挂,设置LMS振动噪声测试系统的采样时间为8 s,分析带宽1 024 Hz,触发电压为65.399 mV,测量的平均次数为5次。由于所需测量频带较宽,因此使用硬锤头,测试方法采用单输入多输出识别法。沿薄壁结构轴向布置多个加速度传感器,加速度传感器的响应信号由LMS系统采集。结构测试的示意图如图 8所示,薄壁结构部分测量点的加速度频响函数Bode图如图 9所示。
|
| 图 8 实验模态测试示意图 Fig. 8 Schematic diagram of experimental modal testing |
|
| 图 9 不同测点的加速度频响函数Bode图 Fig. 9 Bode diagram of acceleration frequency response function at different points |
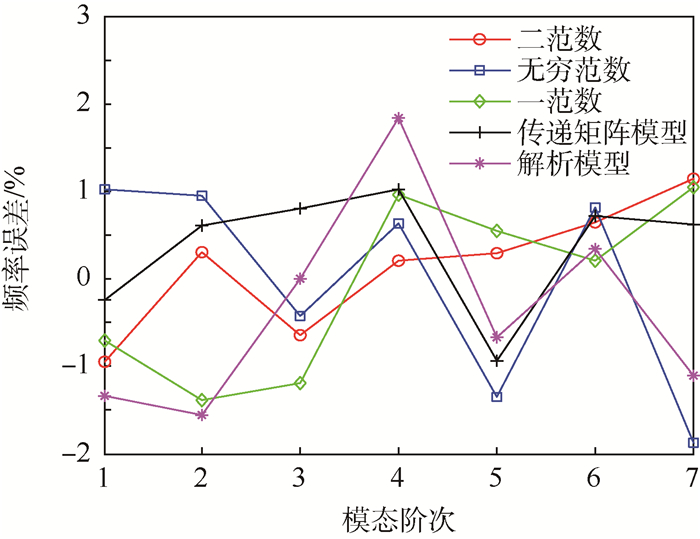
根据频响函数可以得到结构的各阶频率,等效截面参数的辨识结果如表 4所示,表 5为等效梁单元计算频率与实验频率对比。图 10为各阶模态频率误差。由图 10计算结果可以看出,由梁单元计算所得的频率与实验频率误差基本在2%以内,计算与实验误差主要来源于3个方面:①结构的几何模型误差,由于薄壁结构中往往存在着大量的圆角,而圆角对结构的扭转频率影响较大,因此圆角的加工误差通常会造成结构频率的改变从而导致理论模型与真实结构的差异;②理论模型或者有限元模型本身的计算精度所引入的误差,由于有限元模型通常只能在低频段有较高的计算精度,而等效梁模型本身就是对真实结构的近似,这是计算与实验之间误差的主要来源;③优化程序与目标函数所带来的误差,由表 4的结果可以看出不同的目标函数对计算结果的影响较大,同时优化算法本身的性能也会对结果产生一定的影响。
| 截面参数 | 梁单元模型 | 传递矩阵模型 | 解析模型 | ||
| 二范数 | 无穷范数 | 一范数 | |||
| Ix/(10-7m4) | 3.07 | 3.07 | 3.07 | 3.07 | 3.07 |
| Iy/(10-6m4) | 1.20 | 1.23 | 1.19 | 1.17 | 1.22 |
| Jφ/(10-8m4) | 1.09 | 1.05 | 1.07 | 1.06 | 1.07 |
| Jw/(10-10m6) | 2.11 | 2.06 | 2.16 | 2.15 | 2.10 |
| e1/m | 0 | 0 | 0 | 0 | 0 |
| e2/m | 0.064 5 | 0.063 1 | 0.065 6 | 0.066 3 | 0.064 2 |
| 模态 阶次 |
实验 频率 |
计算频率 | ||||
| 二范数 | 无穷范数 | 一范数 | 传递矩阵模型 | 解析模型 | ||
| 1 | 126.8 | 125.6 | 128.1 | 125.9 | 126.5 | 125.1 |
| 2 | 231.1 | 231.8 | 233.3 | 227.9 | 232.5 | 227.5 |
| 3 | 234.9 | 233.4 | 233.9 | 232.1 | 236.8 | 234.9 |
| 4 | 477.4 | 478.4 | 480.4 | 482.0 | 482.3 | 486.2 |
| 5 | 585.2 | 586.9 | 577.3 | 588.4 | 579.7 | 581.3 |
| 6 | 621.6 | 625.6 | 626.7 | 622.9 | 626.1 | 623.7 |
| 7 | 806.4 | 815.6 | 791.3 | 814.8 | 811.4 | 797.5 |
|
| 图 10 模态频率误差 Fig. 10 Modal frequency error |
1)本文提出用开口薄壁梁来等效近似计算有均匀分布横向加强构件的薄壁杆件,这种等效方法不仅适用于有隔板的构件,对于缀板或缀条加强的薄壁杆件也有同样的适用性,具有一定的通用性。
2)本文建立了3种开口薄壁梁模型,通过对比不同模型辨识结果说明目标函数为二范数与一范数的有限元模型的精度普遍高于其他模型。
3)本文提出了通过实体有限元在静态载荷作用下产生的静态位移来估算等效截面的扭转常数与翘曲常数,并且这种估计方法有较强的通用性。
4)本文所使用的ABAQUS与MATLAB交互式的参数优化辨识方法,可以有效地将MATLAB中各种优化算法与有限元程序相结合,实现了对ABAQUS的二次开发。
5)用梁来等效替代横向构件作用的薄壁结构可以大幅度缩减单元的数量,同时在一定的频率范围内有较高的精度。
6)本文所提出的等效模型物理意义明确,不仅适用于结构模型修正,同时也适用于结构动态载荷识别与损伤识别,模型应用范围广。
| [1] | BROWN A M, SEUGLING R M. Using plate finite elements for modeling fillets in global response analysis[J]. Finite Elements in Analysis and Design, 2004, 40 (13-14) : 1963 –1975. DOI:10.1016/j.finel.2004.01.008 |
| [2] | ARPACI A, BOZDAG E. On free vibration analysis of thin-walled beams with nonsymmetrical open cross-sections[J]. Computers and Structures, 2002, 80 (7-8) : 691 –695. DOI:10.1016/S0045-7949(02)00025-1 |
| [3] | ARPACI A, BOZDAG S E, SUNBULOGLU E. Triply coupled vibrations of thin-walled open cross-section beams including rotary inertia effects[J]. Journal of Sound and Vibration, 2003, 260 (5) : 889 –900. DOI:10.1016/S0022-460X(02)00935-5 |
| [4] | PROKIĆ A. On triply coupled vibrations of thin-walled beams with arbitrary cross-section[J]. Journal of Sound and Vibration, 2005, 279 (3-5) : 723 –737. DOI:10.1016/j.jsv.2003.11.053 |
| [5] | AMBROSINI R D. A modified Vlasov theory for dynamic analysis of thin-walled and variable open section beams[J]. Engineering Structures, 2000, 22 (8) : 890 –900. DOI:10.1016/S0141-0296(99)00043-7 |
| [6] | AMBROSINI R D, RIERA J D, DANESI R F. Dynamic analysis of thin-walled and variable open section beams with shear flexibility[J]. International Journal for Numerical Methods in Engineering, 1995, 38 (17) : 2867 –2885. DOI:10.1002/(ISSN)1097-0207 |
| [7] | PROKIĆ A. On fivefold coupled vibrations of Timoshenko thin-walled beams[J]. Engineering Structures, 2006 (28) : 54 –62. |
| [8] | YAMAN Y. Vibrations of open-section channels:A coupled flexural and torsional wave analysis[J]. Journal of Sound and Vibration, 1997, 204 (1) : 131 –158. DOI:10.1006/jsvi.1997.0933 |
| [9] | 包世华, 周坚. 薄壁杆件结构力学[M]. 北京: 中国建筑工业出版社, 2006 : 190 -193. BAO S H, ZHOU J. Structural mechanics of thin-walled rod member[M]. Beijing: China Building Industry Press, 2006 : 190 -193. (in Chinese) |
| [10] | 王晓峰, 张其林, 杨庆山. 新型空间薄壁梁单元[J]. 应用数学和力学, 2010, 31 (9) : 1089 –1100. WANG X F, ZHANG Q L, YANG Q S. New finite element of spatial thin-walled beams[J]. Applied Mathematics and Mechanics, 2010, 31 (9) : 1089 –1100. (in Chinese) |
| [11] | MOHRI F, EDDINARI A, DAMIL N, et al. A beam finite element for non-linear analyses of thin walled elements[J]. Thin-Walled Structures, 2008, 46 (7-9) : 981 –990. DOI:10.1016/j.tws.2008.01.028 |
| [12] | KIM N, KIM M Y. Exact dynamic/static stiffness matrices of non-symmetric thin-walled beams considering coupled shear deformation effects[J]. Thin-Walled Structures, 2005, 43 (5) : 701 –734. DOI:10.1016/j.tws.2005.01.004 |
| [13] | AMBROSINI D. On free vibration of nonsymmetrical thin-walled beams[J]. Thin-Walled Structures, 2009, 47 (6-7) : 629 –636. DOI:10.1016/j.tws.2008.11.003 |
| [14] | HAN S P. Super linearly convergent variable metric algorithms for general nonlinear programming problems[J]. Mathematical Programming, 1976, 11 (1) : 263 –282. DOI:10.1007/BF01580395 |
| [15] | HAN S P. A globally convergent method for nonlinear programming[J]. Journal of Optimization Theory and Applications, 1977, 22 (3) : 297 –309. DOI:10.1007/BF00932858 |
| [16] | POWELL M J D.A fast algorithms for nonlinearly constrainted optimization calculations [M]//WATSON G.Numerical analysis.Heidelberg:Springer, 1978:144-157. |
| [17] | 钱伟长, 林鸿荪, 胡海昌. 弹性柱体扭转理论[M]. 北京: 科学出版社, 1956 : 178 -179. QAN W C, LIN H S, HU H C. Torsion bar elastic theory[M]. Beijing: Science Press, 1956 : 178 -179. (in Chinese) |



