伪卫星是一种成本低廉、易于部署的导航增强平台。在一些导航卫星可视性降低、卫星导航信号被干扰的情况下,通过部署伪卫星,可在卫星导航服务性能下降的情况下为特定区域的用户提供导航增强服务。根据部署空间区域的不同,伪卫星可分为空基和地基(海基)两类。与地基伪卫星相比,空基伪卫星无论是在覆盖范围还是部署灵活性方面都具有前者不可比拟的优势。在各类空基平台中,临近空间飞艇飞行动态性较小、工作高度较高,且具有一定的悬停能力,不仅有利于平台本身的定位,而且具有更大的导航增强服务范围。因此,基于临近空间飞艇的空基伪卫星技术已经成为当前区域导航增强领域的研究热点。
目前,澳大利亚、美国、印度和日本等国已经对基于临近空间飞艇的伪卫星导航增强系统进行了建模仿真和半实物外场试验。文献[1]将伪卫星作为差分基准站,对伪卫星位置误差、信号的多径效应和对流层延迟进行了建模仿真;文献[2]模拟了城市峡谷环境,对部署伪卫星来改善导航源的几何精度因子(Geometric Dilution Of Precision,GDOP)和提高用户可见星数量进行了仿真分析;文献[3]分析了空基和地基伪卫星的协同定位问题,通过采用载波相位二次差分的办法来提高定位精度,对伪卫星GDOP恶劣导致的用户定位精度下降进行补偿;文献[4]模拟了由4颗基于平流层飞艇的空基伪卫星、6个地面监测站和1个控制中心组成的导航增强系统,对GPS不可用情况下的用户伪距测量误差进行了仿真分析;文献[5-6]重点研究了利用地面监测站对基于平流层飞艇的空基伪卫星进行“倒GPS”定位的方法, 并进行了半实物外场试验,通过差分来提高对伪卫星的定位精度。
国内对基于临近空间飞艇的相关研究重点集中于伪卫星平台的组网方案和编队控制上。文献[7]提出了一种利用平流层飞艇提高北斗区域导航系统GDOP性能的方法;文献[8-10]重点分析了空基伪卫星高度角和方位角等因素对GDOP的影响,并以此为基础提出了空基伪卫星的布局方案;文献[11]则采用遗传算法来计算使GDOP最优的伪卫星几何布局;文献[12]考虑了基于无人机的空基伪卫星编队的协同控制问题,采用“长机-僚机”方式的控制策略,设计了一种基于神经网络的编队控制器。
从国内外的研究现状可知,空基伪卫星组网的主要任务之一是设计伪卫星平台的最优几何构型来降低用户定位误差,具体表现为以GDOP作为优化目标,通过采用经验法或最优化算法来计算伪卫星的最优部署位置。这些研究通常仅给出伪卫星最终的静态组网结果,而未考虑伪卫星以什么样的方式到达部署位置。事实上,伪卫星在部署时总是存在从初始位置向目标位置的运动过程,此时伪卫星编队的几何构型将会随着伪卫星本身运动状态的变化而变化,导致用户所在区域的GDOP也在不断改变。
临近空间飞艇运动速度较慢,组网部署通常需要一定时间。一般用户普遍对导航服务有着连续性和完好性的要求,在伪卫星部署过程中也可能会有定位和定时方面的需求。因此,针对国内外相关研究的不足之处,有必要研究飞艇编队在组网部署过程中的航路规划问题,通过设计合适的航路,使飞艇编队在运动过程中尽量保持良好的几何构型,降低用户在伪卫星组网过程中的定位误差。针对此问题,本文首先梳理了空基伪卫星平台组网性能指标;然后指出了伪卫星航路规划问题中不同于一般无人飞行器航路规划的特殊性,设计了一种基于稀疏A*算法的伪卫星航路规划算法;最后对提出的空基伪卫星航路规划算法进行了仿真验证。
1 空基伪卫星组网性能指标从用户定位和定时的角度出发,伪卫星组网性能的优劣可用GDOP来衡量。GDOP定义为用户伪距测量误差到定位定时误差的放大倍数,其反映了导航源几何位置对用户定位误差的影响。GDOP的计算方法如下:
设用户接收机的三维位置和钟差分别为(xu, yu, zu)和tu,在校正对流层传播延迟等误差项后,用户接收机到伪卫星的伪距测量值为
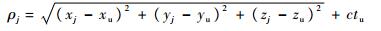
|
(1) |
式中:(xj, yj, zj)为第j颗伪卫星的三维位置坐标;c为光速。
设用户近似位置和近似钟差分别为(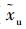
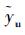
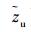
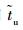
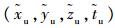
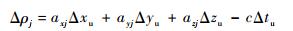
|
(2) |
式中:(Δxu, Δyu, Δzu)为用户近似位置与真实位置之差;(axj, ayj, azj)为用户位置到第j颗伪卫星的方向余弦。
假设伪卫星数量为n,则式(2)可扩展为矩阵形式:

|
(3) |
式中:

|
(4) |
由式(3),采用最小二乘法,得到用户位置和时间偏差为
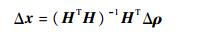
|
(5) |
式(5)中,若Δx存在扰动,则可得Δx的条件数为
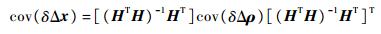
|
(6) |
式中:δΔx为用户接收机的定位和定时误差;δΔρ为用户接收机伪距测距标准差。
若各伪卫星的测距误差统计独立,均值为0,方差为δ2,则由式(6)有
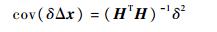
|
(7) |
由式(7)可见,(HTH)-1体现了用户接收机的定位定时误差与伪距测量误差的关系,称为精度衰减矩阵。GDOP定义为(HTH)-1迹运算的平方根:
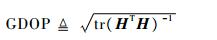
|
(8) |
通常而言,将伪卫星所覆盖的服务区域内进行均匀采样,将采样点的GDOP求和后进行平均,就可得到伪卫星网络对服务区域的定位增强性能优劣程度:
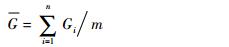
|
(9) |
式中:G为增强区域的GDOP均值;Gi为采样点i处的GDOP值;m为覆盖区域的有效采样点数。所谓有效指的是覆盖区域某个采样点到各伪卫星的方向余弦满足HTH可逆的条件,此时该采样点对应的GDOP可被求解。
2 空基伪卫星航路规划算法设计空基伪卫星航路规划指的是在规划区域内,在给定约束条件下寻找一条从起始点到目标点的最优或可行的飞行轨迹。根据空基伪卫星的业务性质,动态组网过程中的航路代价可分为伪卫星距离代价和覆盖区域GDOP代价2个方面。出于导航定位的需要,伪卫星数量通常在4个以上。这样,空基伪卫星的航路规划是一个编队协同航路规划问题。
由GDOP的定义可知,GDOP代价始终随着各伪卫星的运动而变化。这种航路代价与运动状态的耦合关系,使空基伪卫星的航路规划问题存在不同于一般飞行器航路规划的特殊性:在对一般飞行器进行协同规划时,规划区域中的威胁源/障碍往往不随飞行器的运动而发生变化,这就可以先对每个飞行器单独进行航路规划,然后再考虑时间上的协同;然而,对空基伪卫星而言,GDOP代价是由多颗伪卫星的运动状态所共同决定的,因此在协同航路规划中,无法为每个伪卫星单独规划相应的航路,而必须将多颗伪卫星作为一个整体来进行规划。
2.1 航路规划代价函数设计A*算法是一种标准启发式搜索算法,在路径规划和图搜索领域中应用非常广泛。在利用A*算法进行航路搜索时,通常将规划环境表示为网格的形式,通过预先设定的代价函数寻找最小代价航路。算法对当前位置的每一个可能到达网格单元计算代价函数,然后选择代价函数最低的网格单元加入搜索空间。加入搜索空间的这一新网格单元又被用来进行下一次的搜索,产生更多的可能路径[13]。
A*算法的代价函数定义为
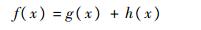
|
(10) |
式中:g(x)为实际代价函数;h(x)为启发代价函数。
本文定义g(t)为从起始时刻运动到当前时刻t的实际代价。设空基伪卫星数量为n,则本文将g(t)设计为
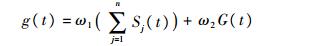
|
(11) |
式中:Sj(x)为第j颗伪卫星从起始时刻到当前时刻t的运动距离;G(t)为在当前时刻t条件下,增强服务区域各采样点对应的GDOP值的总和;ω1和ω2分别为伪卫星距离代价和GDOP代价的权重,调节ω1、ω2的大小可决定伪卫星是选择优先保障航路上GDOP最优而增加距离代价,还是减少距离代价而牺牲GDOP性能。
定义h(t)为从当前时刻t运动到最终目标位置的估计代价,h(t)可设计为
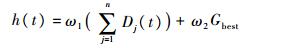
|
(12) |
式中:Dj(t)为第j颗伪卫星从当前时刻t所在位置与目标部署位置的欧氏距离;Gbest为伪卫星全部位于目标部署位置时对应的增强区域各采样点的GDOP总和,也是GDOP代价的最优值;权重ω1、ω2取值与式(11)相同。
文献[13]的相关研究已经证明,只要启发式函数满足一致性(h(t)组成结构与g(t)相同)和可接纳性(h(t)小于或等于从当前时刻t所处位置到目标位置的真实代价),并且搜索空间中存在可行解,那么A*算法就一定能找到其中的最优解。由式(11)可知,h(t)满足一致性和可接纳性。因此,采用式(11)和式(12)的A*算法可以找到全局最优解。
2.2 代价函数权重自适应调整空基伪卫星在从初始位置向目标位置的组网部署过程中,距离代价和GDOP代价始终随伪卫星编队运动状态的改变而不断变化。若伪卫星编队初始位置对应的GDOP代价远高于最终目标位置对应的最优GDOP,则伪卫星在运动的初期就有必要为提高用户定位精度而增加GDOP代价的权重,对应的航路规划就需要尽量使伪卫星编队保持良好的几何构型;而随着伪卫星逐渐接近目标位置,GDOP代价也逐渐收敛于最优值,当GDOP代价与最优值的偏差小到一定程度时,则可以考虑增大距离代价的权重,使伪卫星能够沿着较短的路径尽快到达目标位置,以减少燃料和时间的消耗。
由此可见,为使伪卫星在动态组网时能够根据当前的运动状态调节代价函数f(t),需要在航路规划时对距离代价和GDOP代价的权重进行自适应调整。针对式(11)中GDOP代价的权重ω2,本文将ω2设计为关于当前时刻t的函数:
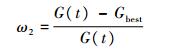
|
(13) |
相应地,距离代价权重ω1表示为
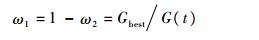
|
(14) |
由式(13)和式(14)可见,在当前时刻t,若伪卫星编队的GDOP代价G(t)接近最优值Gbest,那么在下一时刻的航路规划中就相应地减小GDOP代价权重ω2,而增加距离代价的权重ω1,使航路尽量接近飞艇当前位置与目标位置的最短距离,这样在飞艇匀速运动的情况下,将会缩短飞艇到达目标所需时间;反之,若伪卫星编队几何结构在当前时刻t比较恶劣,则GDOP代价权重ω2也相应较高,下一时刻航路规划将朝着降低GDOP代价的方向进行。
2.3 航路规划约束条件采用A*算法进行航路搜索,在扩展节点时需要搜索当前节点邻域中的所有网格单元。这样,算法收敛到最优解的时间会随着规划区域的增大而呈指数增长,并且生成的航路不一定满足伪卫星运动的物理约束条件。因此,结合第2.1节中航路规划代价函数设计,本文考虑基于稀疏A*算法来进行空基伪卫星的三维航路搜索。稀疏A*算法与普通A*算法的不同之处在于:在扩展节点时,稀疏A*算法通过把约束条件结合到搜索算法中去,减少节点需要搜索的邻域网格单元,有效缩短搜索时间。
在Szczerba等[14]提出的稀疏A*算法中,主要考虑的约束条件为飞行器运动时的几何约束,包括最小航迹段步长Lmin、最大水平拐弯角Φmax等。由于稀疏A*算法是在离散的网格单元中搜索,规划出的路径由一系列的折线段所组成,并不满足飞行器的运动特性。因此,为规划出可飞行的航路,还需考虑飞行器动力学方面的约束。
飞行器的动力学特性主要包括在机体表面产生力和力矩的空气动力,这些力和力矩产生了侧向、纵向和滚转加速度[15]。为生成可飞行航路,在规划航路时需要考虑飞艇转弯速率的约束,在三维空间中可转化为航路中的曲率和挠率约束。曲率和挠率分别与加速度满足如下关系:
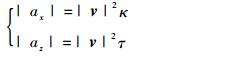
|
(15) |
式中:v为飞行器的速度;ax为侧向加速度;az为俯仰加速度;κ为曲率;τ为挠率。
由式(15)可知,曲率(挠率)与加速度成正比,因此规划路径上任意一点的曲率(挠率)应小于飞行器可达到的最大曲率(挠率)。
Dubins曲线由一系列圆弧及其切线组成,已被证明是在满足一定曲率条件下,连接给定方向向量的两点间的最短轨迹曲线[15]。这样,在给定飞艇最大曲率(挠率)的情况下,可以采用Dubins曲线对由传统稀疏A*算法规划出的路径进行平滑处理,得到可飞行路径。
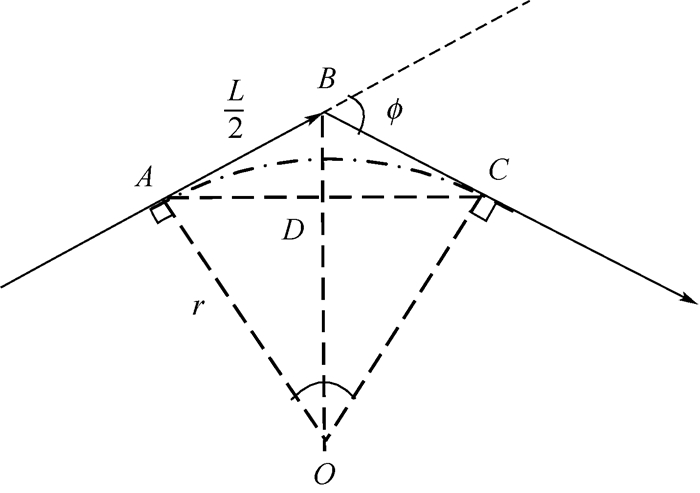
下面以二维平面情况为例说明Dubins曲线的曲率与稀疏A*算法中最大水平拐弯角的约束关系。如图 1所示,A、B和C为稀疏A*算法规划出的航路上的3个位置点,航路在B点转弯;r为曲率半径;Φ为航路水平拐弯角;L为航路步长。由曲率与曲率半径的关系κ=1/r可知,κ越大,则r越小;当κ达到最大值κmax,r对应为最小值rmin。此外,由图 1不难得到以下关系:
|
| 图 1 Dubins曲线平滑处理原理 Fig. 1 Principle of smoothing with Dubins curve |
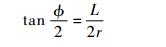
|
(16) |
式(16)表明,当L一定时,r越小,则Φ越大;当L=Lmax,r=rmin时,Φ达到最大值Φmax,Φmax即为稀疏A*算法中的最大水平拐弯角。此外,为能够对航路中可能出现连续的折线段进行平滑,取线段AB和BC的长度均为L/2。
因此,在二维情况下,若在航路规划时能给出约束条件最大航路步长Lmax和飞艇最大曲率κmax,就可以计算出航路最大水平拐弯角Φmax,从而通过稀疏A*算法进行航路规划,规划完成后再采用Dubins曲线对航路进行平滑处理。推广到三维空间,约束条件除Lmax和κmax外,若再给定飞艇最大挠率τmax,可计算出最大水平拐弯角Φmax和最大俯仰角θmax,再结合高程约束,就可以对三维空间中的航路进行规划和平滑。
航路规划约束也包括航迹段长度的约束。由式(16)可知,在曲率一定的条件下,如果航迹段步长L值较大,则水平拐弯角Φ也将增大,这样稀疏A*算法在每次扩展节点时就要搜索更多的邻域网格,增加了时间和空间代价;结合图 1还可见,B点是从A点扩展而来的航路代价最小点,而飞艇实际却是沿AC运动,若L过大,则B与AC的距离也更长,航路代价也相差更大。当航路代价相差到一定程度时,B点实际上就不能作为A点在约束条件下扩展出来的航路代价最小点,成为无效点。若L取得过小,在规划空间较大时,不仅航路规划时间将会指数增长,而且飞艇将会增加更多的转弯机动。然而,以飞艇为平台的空基伪卫星作为导航源,只有在本身位置能够精确测量的前提下才能为用户提供导航增强服务,如果飞艇机动较多,将不利于飞艇本身位置的确定,从而影响用户定位。因此,在确定航迹段步长L时,应结合曲率等约束条件,在可接受的上限以内合理选择其大小。
对飞艇编队进行航路规划时,除了单个飞艇的动力学约束外,还需考虑各飞艇之间相对状态的约束,主要包括碰撞条件约束和能量消耗均衡性约束。对于碰撞条件约束,可通过设置飞艇间距阈值进行判断,在航路规划过程中,若飞艇间距小于阈值,就认为存在碰撞危险;对于能量消耗均衡性约束,可在航路规划之前预先进行任务分配,避免个别飞艇距离目标位置过长或过短。具体方法是:以各伪卫星到目标部署位置的欧式距离均方差最小为准则,遍历初始位置与目标位置的所有排列组合情况,选出最优组合。
2.4 基于稀疏A*算法的航路规划算法稀疏A*算法是在隐式图中进行搜索,图中的节点在图搜索过程中可分为3类:已被扩展的节点;当前已经产生但尚未扩展的节点;尚未产生的节点。其中,第1类节点称为封闭节点,在搜索过程中存放在CLOSED表中;第2类节点是当前已经产生、正在等待扩展的节点,称为开放节点,在搜索过程中存放在OPEN表中[16]。
基于权重自适应调整的改进稀疏A*算法的空基伪卫星航路规划算法流程如下:
步骤1 对各个飞艇进行任务分配,确定各飞艇所对应的目标部署位置。同时,根据输入曲率和挠率的最大值约束,计算曲率半径和挠率半径。设置航迹段步长L,由式(15)计算最大水平拐弯角Φmax和最大俯仰角θmax。
步骤2 将各伪卫星初始位置点插入OPEN表中,将CLOSED表置空。
步骤3 如果OPEN表为空,算法以搜索失败结束。调整算法参数(相邻网格单元),然后重新运行规划算法。
步骤4 按式(10)计算节点代价f(t),从OPEN表中移出代价最小的元素作为各伪卫星的开放节点,将它放入CLOSED表中,同时更新GDOP代价和距离代价的权重值。
步骤5 如果伪卫星当前节点与目标点之间的距离小于航迹段步长,则将目标点的父节点指针指向当前节点,航路搜索过程结束。从目标点开始向上回溯至起始位置,得到从起始点到目标的最小代价路径。
步骤6 扩展各伪卫星的开放节点。扩展过程如下:
1)对每颗伪卫星构造当前节点待扩展区。待扩展区的水平剖面是夹角大小为Φmax的2倍的扇面,扇面的半径在数值上等于航迹段步长L。并以进入当前节点速度在水平面上投影的方向为对称轴。垂直剖面的夹角大小为θmax的2倍,关于水平方向对称。
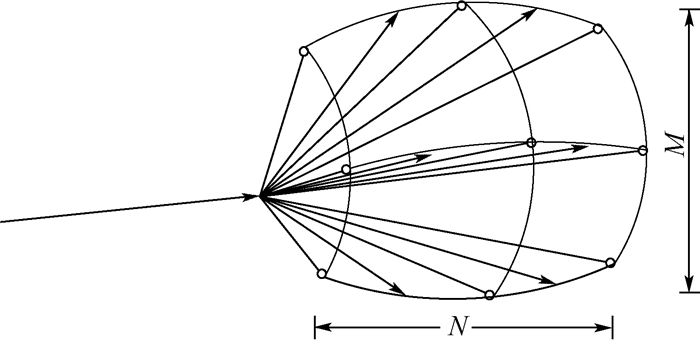
2)分割各颗伪卫星当前位置点的待扩展区。如图 2所示,首先在垂直剖面内均匀取M个方向,得到M个2倍于Φmax大小的扇面;然后把每一个扇面均匀分为N个扇区,这样可得到M×N个小扇区,共形成M×(N+1)个扩展节点。判断每个扩展节点位置坐标是否满足飞行高度约束,若不满足,则将该节点位置高度限制为高程约束的边界值。
|
| 图 2 开放节点扩展示意图 Fig. 2 Schematic diagram of expanding open nodes |
3)将n个伪卫星对应的待扩展区组合成一个搜索空间,各个伪卫星分别遍历各自对应的待扩展区,经排列组合后共形成[M×(N+1)]n种组网方式。
4)设置伪卫星之间碰撞危险的距离阈值dmin,遍历检测搜索空间,检测各个伪卫星的间距。若在某种组网方式中,存在2个及以上的伪卫星的间距距离小于距离阈值,则将该组网方式从搜索空间中剔除。若剔除以后搜索空间为空集,则OPEN表置空,返回步骤3。
5)将第3)步计算得到的每种组网情况对应的各伪卫星位置坐标集合,插入到OPEN表中。
6)返回步骤3。
步骤7 对规划出的路径采用Dubins曲线进行平滑。结合图 1,平滑方法如下:
1)沿航路前行方向,每隔L/2的距离选取一个航路上的位置点(大地坐标系),组成位置点序列,设第一个位置点为当前位置点。
2)从当前位置点开始,依次往后连续取3个点,分别设为A(xA, yA, zA)、B(xB, yB, zB)和C(xC, yC, zC)。计算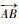
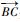
3)计算水平拐弯角Φ,若Φ为钝角,则Φ的值用π-Φ替代。根据式(16)计算曲率半径r;同时,根据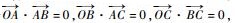
4)设D为AC与OB的交点,根据图 1中几何关系,计算得到如下向量长度:
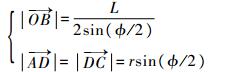
|
(17) |
构造本地坐标系:以O为本地坐标系原点,以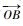
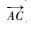
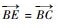
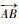
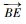
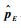
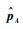
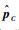
令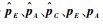
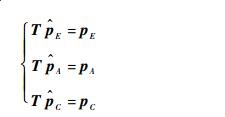
|
(18) |
通过求解式(18)的方程组,可求解出转换矩阵T中各个元素。由于E、A和C在本地坐标系中的坐标并不在同一个坐标轴平面上,因此,式(18)中的9个方程互不相关,T中的9个未知数均可被求解。
5)设置旋转角度步长Δω,在本地坐标系中将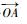
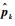
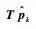
6)连接A、C及采样点,得到Dubins曲线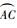
7)若C
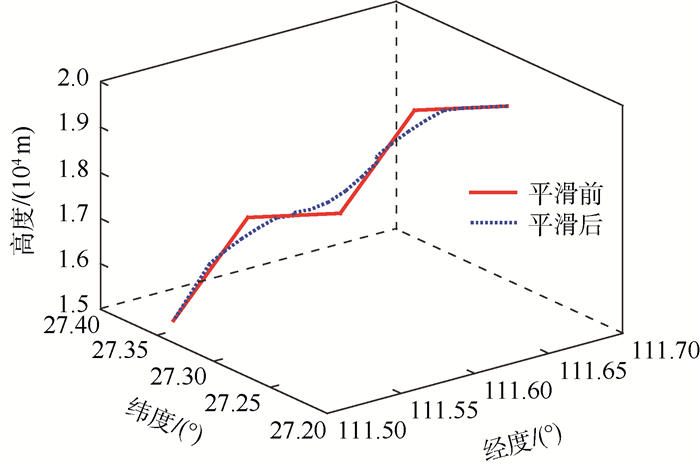
图 3显示了基于Dubins曲线平滑前后的航路对比。可见,平滑后的航路更加符合飞艇的实际运动轨迹。
|
| 图 3 Dubins曲线平滑前后的航路对比 Fig. 3 Comparison of route with and without smoothing by Dubins curve |
本文仿真实验采用临近空间飞艇作为空基伪卫星平台。由于飞艇的数量、初始位置和初始速度方向等因素由飞艇放飞地点、飞艇前期任务规划等诸多因素决定,存在很大的随机性。因此,本文仿真实验对于飞艇数量、初始位置和初始速度方向参数不作特别要求。
仿真实验的相关参数见表 1。飞艇的初始速度方向假设为从正南至正北方向,速度大小恒定。仿真平台采用MATLAB R2015a。
| 参数 | 数值 |
| 飞艇数量 | 5 |
| 飞艇编队初始位置 | 1号艇:(122.0,24.5,10 000) |
| (经度/(°),纬度/(°),高度/m) | 2号艇:(122.5,25.0,10 000) |
| 3号艇:(123.0,25.5,10 000) | |
| 4号艇:(123.5,25.0,10 000) | |
| 5号艇:(124.0,24.5,10 000) | |
| 飞艇高程范围/m | [2 000,30 000] |
| 航迹段长度(步长)/m | 5 000 |
| 最小曲率半径/m | 4 330 |
| 最小挠率半径/m | 4 330 |
| 最小间距阈值/m | 5 000 |
| 服务区域经度范围/(°) | [112.0,114.0] |
| 服务区域纬度范围/(°) | [25.5,27.5] |
| 垂直方向搜索扇面数 | 3 |
| 水平方向搜索扇区数 | 4 |
3.1 离线航路规划仿真
离线航路规划指在飞艇编队组网部署之前规划出各飞艇的预定航路。本文分别在4种不同权重条件下对飞艇航路规划进行仿真,这4组不同权重条件分别如下:
1)距离代价权重与GDOP代价权重按式(13)和式(14)进行自适应调节。
2)距离代价权重优先,GDOP代价权重为0。
3) GDOP代价权重优先,距离代价权重为0。
4)距离代价与GDOP代价权重为固定值1/2。
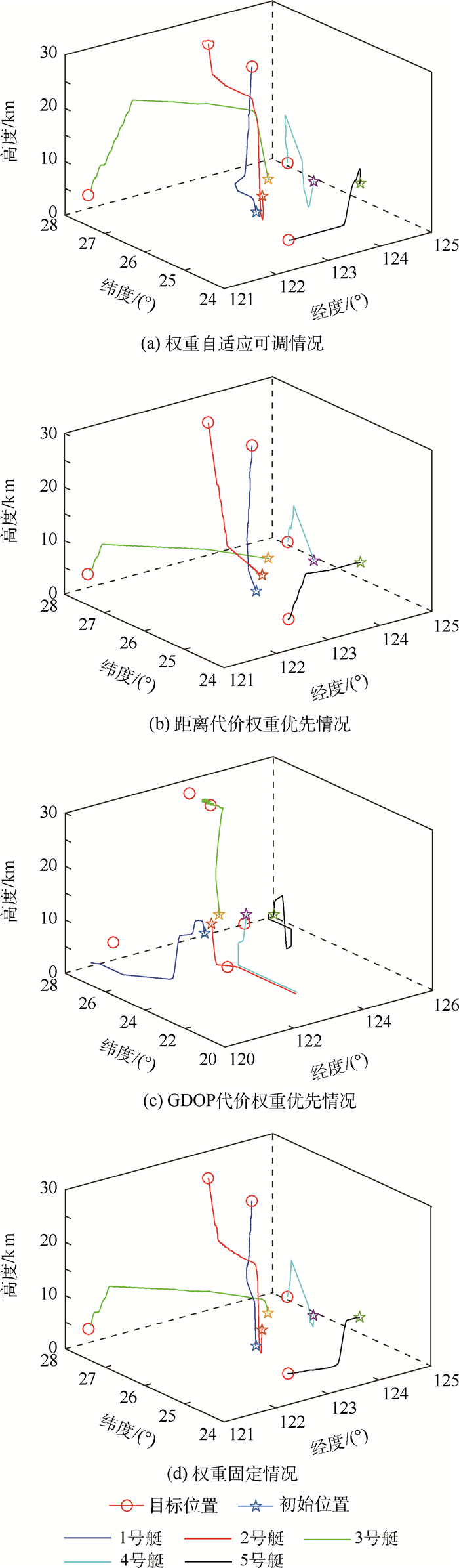
在以上4组不同权重条件下,飞艇航路规划仿真结果如图 4所示。由于飞艇具有一定的悬停能力,因此对于先到达目标部署位置的飞艇,本文假定其到达目标部署位置后即悬停不动,相应的路径不再继续规划。飞艇编队的目标部署位置在航路规划前采用粒子群搜索算法[17, 18]求出。
|
| 图 4 不同权重条件下的三维航路规划结果 Fig. 4 3D route planning of airships in different conditions of weight |
由图 4可见,对于权重自适应可调、距离代价权重优先以及权重固定3种情况,航路规划算法均可以收敛,飞艇最终运动到目标部署位置;只有在GDOP代价权重优先的情况下,航路规划算法不能使飞艇收敛到目标部署位置。
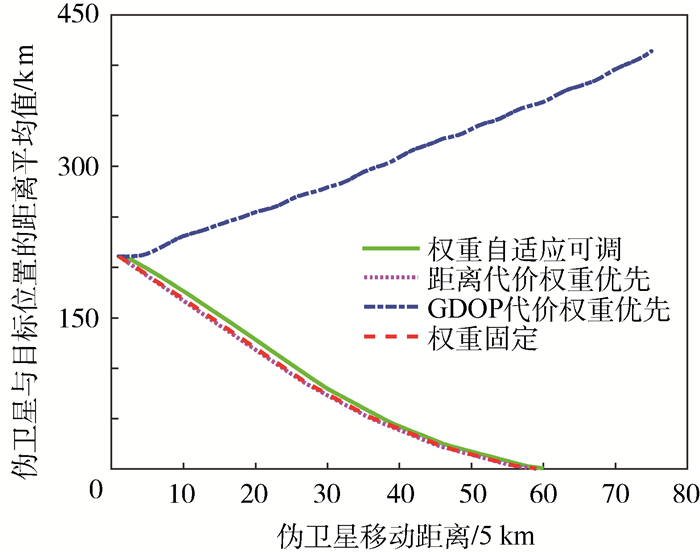
基于上述4种权重条件下的航路规划结果,可分析各飞艇在沿相应航路运动时,飞艇与目标部署位置的距离以及导航增强服务区域的GDOP变化情况。各飞艇与目标部署位置的平均距离变化如图 5所示。
|
| 图 5 不同权重条件下航路规划中各飞艇与目标部署位置平均距离变化曲线 Fig. 5 Curves of average distance from airships' position to deployed target position in different conditions of weight during route planning |
由图 5可见,对于GDOP代价权重优先的情况,由于算法中没有目标部署位置的信息,导致航路规划过程中飞艇与目标部署位置的偏离越来越大,而对于其他3种情况,算法在每一次搜索中都包含了目标部署位置信息,因而飞艇总是会最终收敛于目标部署位置。此外,在权重自适应可调情况下进行航路规划时,飞艇距离代价与距离权重优先条件下的距离代价比较接近。这表明采用基于权重自适应可调情况下的航路规划算法,不会明显地增加飞艇组网部署的时间开销。
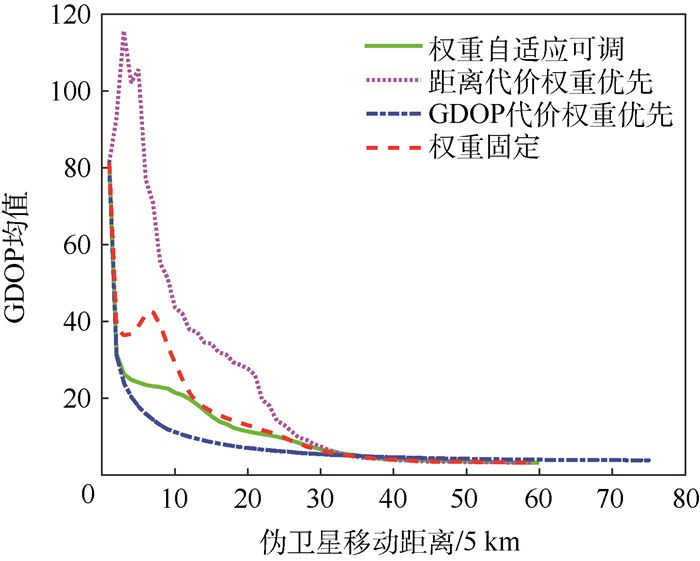
在上述4种权重条件下,航路规划中GDOP代价权重变化情况如图 6所示。可见,对于距离代价权重优先的情况,由于算法在搜索过程中没有考虑GDOP因素,因此航路规划过程中导航增强服务区域的GDOP均值没有像其他3种权重条件下那样快速下降。而对于权重自适应可调和固定权重2种情况,前者对应的航路规划中的GDOP均值下降更快,更加接近于GDOP代价权重优先条件下的GDOP均值。
结合图 5和图 6可知,与其他相比,采用权重自适应可调的航路规划算法,能够在不明显增加距离代价的情况下使飞艇编队保持良好的几何构型,有效降低GDOP代价,体现了在距离代价和GDOP代价之间的调节能力。
|
| 图 6 不同代价权重条件下航路规划中的GDOP代价变化曲线 Fig. 6 Curves of GDOP cost in different conditions of weight during route planning |
离线航路规划为每个飞艇确定了预定的飞行路径。然而,飞艇在实际飞行时,难免会受到风场等外界因素的影响而偏离预定航路。在这种情况下,需要对飞艇编队的航路进行在线重规划。本文考虑在单个飞艇偏离预定航路情况下,飞艇编队在线航路重规划的2种方法:基于单艇调整的在线航路重规划和基于编队调整的在线航路重规划。
基于单艇调整的在线航路重规划仅对偏离预定航路的飞艇进行航路重规划,其他飞艇则继续按原定航路运动。这样,航路重规划在搜索时,搜索空间仅为单个飞艇的待扩展区,与飞艇编队整体的航路规划相比,搜索空间大大减小,具有较好的实时性。
由于单个飞艇偏离原定航路破坏了飞艇编队的整体几何构型,因此基于编队调整的在线航路重规划将从修正编队几何构型的角度考虑,采用的方法与离线航路规划方法相同。由于基于编队调整的航路重规划重新优化了编队的几何结构,因而与基于单艇调整的航路重规划而言,具有更低的GDOP代价。
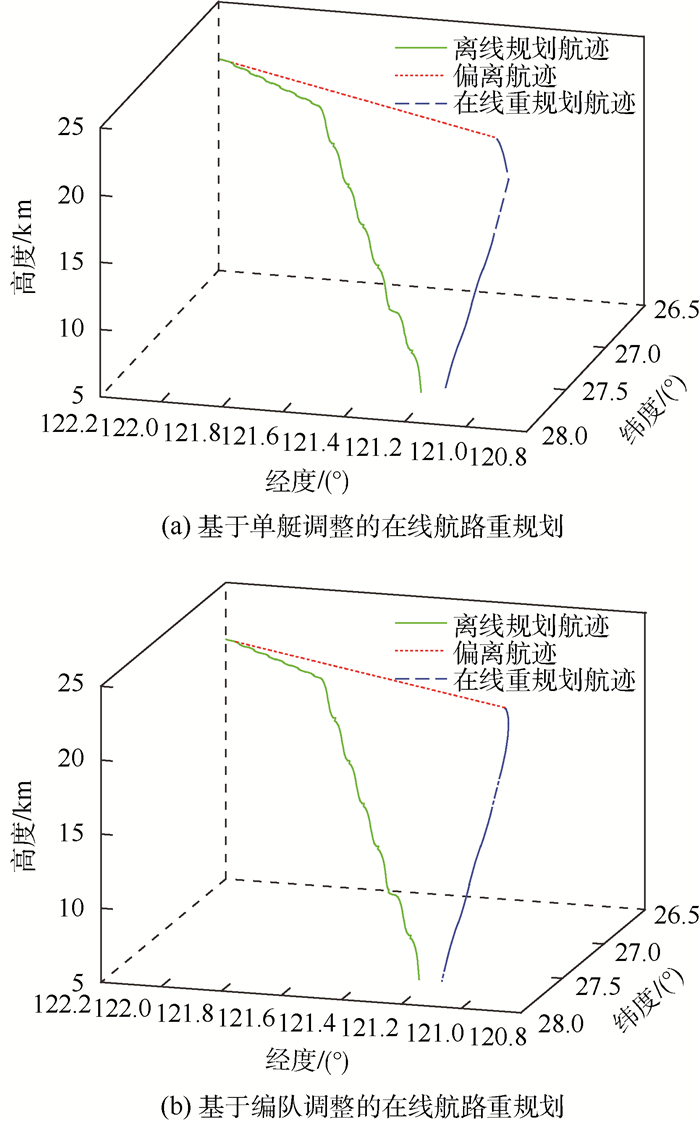
在本节仿真中,假设图 4(a)仿真中的3号艇(绿色)在沿预定航路运动到经度为122.125 2°、纬度为26.765 7°、高度为22 500 m的位置后开始发生偏离,继续运动至经度为120.999 4°、纬度为27.415 1°、高度为22 500 m的位置后,飞艇检测到自身已偏离预定航路,并开始在线航路重规划。3号艇的在线航路重规划结果如图 7所示。图 7(a)为基于3号艇自身调整的在线航路重规划结果,图 7(b)所示为基于编队调整的在线航路重规划结果。可见,2种方法规划出的航路都可收敛于原定航路。
|
| 图 7 3号艇在线航路重规划的仿真 Fig. 7 Simulation of online route re-planning of No.3 airship |
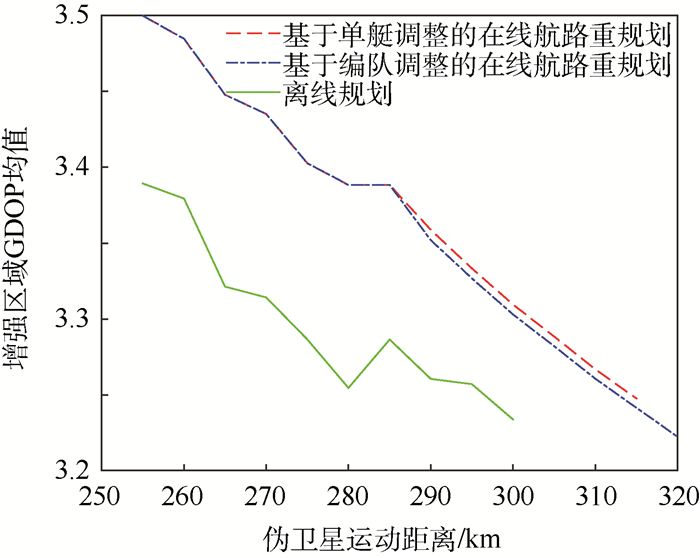
图 8显示了3号艇在线航路规划前后,增强服务区域GDOP均值的变化情况。可见,虽然基于编队调整的在线航路重规划与基于单艇调整的在线航路重规划相比,GDOP代价有所降低,但降幅仅约为0.006,相应的航路代价却增加了一个步长(5 km)。这表明在线航路重规划若对整个编队的几何构型进行调整,不仅算法搜索时间增多,而且飞艇沿规划航路运动的时间也更长。考虑到在线航路重规划对实时性的要求,实际中可能更适合采用基于单艇调整的在线航路重规划方法。
|
| 图 8 在线航路重规划的GDOP代价对比 Fig. 8 Comparison of GDOP cost of online route re-planning |
本文在相关研究的基础上,提出了空基伪卫星从初始位置到目标位置如何进行组网部署的问题。在稀疏A*算法的基础上,结合相关约束,提出了距离代价和GDOP代价权重自适应可调节的空基伪卫星航路规划算法。通过仿真实验,得出如下结论:
1)采用权重自适应可调的航路规划算法,规划的航路一方面能够有效降低导航增强服务区域的GDOP值,提高用户定位精度;另一方面又能够使飞艇较快到达目标部署位置,不会明显增加飞艇运动的时间和燃料消耗,表明航路规划算法具有良好的经济性。
2)当编队中的个别飞艇在运动过程中偏离预定航路时,可采用基于单艇调整和基于编队调整2种在线航路重规划方法,前者的算法搜索速度更快,规划路径更短,而GDOP代价与后者相比相差并不大,因此更适合在线实时的航路重规划。
本文的仿真实验中,均假定飞艇在运动过程中保持匀速。实际上,飞艇在运动过程中受风场、空气密度等环境因素的影响,很难始终保持匀速运动。飞艇运动过程中的速度变化将会实时改变编队的几何构型,从而对GDOP代价产生扰动。后续工作将进一步重点研究变速情况下的在线航路规划。
| [1] | DAI L W, WANG J L, TSUJII T, et al.Pseudolite applications in positioning and navigation:Modeling and geometric analysis[C]//International Symposium on Kinematic System in Geodesy, Geomatics & Navigation.Berlin:Springer, 2001:482-489. |
| [2] | OKTAY H, STEPANIAK M.Airborne pseudolite in a global positioning system degraded environment[C]//2011 5th International Conference on Recent Advances in Space Technologies (RAST).Piscataway, NJ:IEEE Press, 2011:280-285. |
| [3] | TIWARY K, BEHERA S, SHARADA G, et al. Modelling and simulation of pseudolite-based navigation:A GPS-independent radio navigation system[J]. Defence Science Journal, 2010, 60 (5) : 541 –550. DOI:10.14429/dsj |
| [4] | CHANDU B, PANT R, MOUDGALYA K.Modeling and simulation of a precision navigation system using pseudolites mounted on airships:AIAA-2007-7746[R].Reston:AIAA, 2007. http://arc.aiaa.org/doi/pdf/10.2514/6.2007-7746 |
| [5] | WANG J. Pseudolite applications in positioning and navigation:Progress and problems[J]. Journal of Global Positioning Systems, 2002, 1 (1) : 48 –56. DOI:10.5081/jgps |
| [6] | TSUJII T.Experiments of inverted pseudolite positioning for airship-based GPS augmentation system[C]//Proceedings of the 15th International Technical Meeting of the Satellite Division of the U.S.Institute of Navigation.Manassas:Institute of Navigation, 2002:1689-1695. |
| [7] | MA W H, YUAN J P, LUO J J.Airborne pseudolite aiding BeiDou system to improve positioning precision in low latitude areas[C]//International Conference on Space Information Technology.Bellingham:SPIE Press, 2006, 5985:955-959. |
| [8] | 杨一, 高社生, 阎海峰. 临近空间伪卫星几何布局方案设计[J]. 系统工程与电子技术, 2014, 36 (3) : 532 –538. YANG Y, GAO S S, YAN H F. Design on geometric configuration schemes of pseudolite in near space[J]. Systems Engineering & Electronics, 2014, 36 (3) : 532 –538. (in Chinese) |
| [9] | 呼玮, 杨建军, 何苹. 基于临近空间飞艇定位的伪卫星布局研究[J]. 无线电工程, 2009, 39 (10) : 24 –27. HU W, YANG J J, HE P. Study on psedulite configuration scheme based on near space airships[J]. Radio Engineering, 2009, 39 (10) : 24 –27. (in Chinese) |
| [10] | 孟键, 孙付平, 丛佃伟. 伪卫星增强区域卫星导航系统组网仿真[J]. 测绘科学技术学报, 2008, 25 (3) : 213 –215. MENG J, SUN F P, CONG D W. Plans of agumenting regional satellite navigation using PLs[J]. Journal of Geomatics Science and Technology, 2008, 25 (3) : 213 –215. (in Chinese) |
| [11] | 杨龙, 周建华, 陈金平. 基于遗传算法的空基伪卫星导航信号增强平台组网优化方法研究[J]. 全球定位系统, 2008, 33 (3) : 9 –13. YANG L, ZHOU J H, CHEN J P. The study of optimization of formation flying navigation agumentation platforms based on genetic algorithm[J]. GNSS World of China, 2008, 33 (3) : 9 –13. (in Chinese) |
| [12] | 党进伟, 高社生, 张极. 伪卫星协同编队控制与仿真[J]. 测控技术, 2013, 32 (11) : 76 –79. DANG J W, GAO S S, ZHANG J. Control and simulation of collaborative formation for pseudolites[J]. Measurement & Control Technology, 2013, 32 (11) : 76 –79. (in Chinese) |
| [13] | HART P E, NILSSON N J, RAPHAEL B. A formal basis for the heuristic determination of minimum cost routes[J]. IEEE Transactions on Systems Science and Cybernetics, 1968, 4 (2) : 100 –107. DOI:10.1109/TSSC.1968.300136 |
| [14] | SZCZERBA R J, GALKOWSKI P, GLICKSTEIN I S, et al. Robust algorithm for real-time route planning[J]. IEEE Transactions on Aerospace and Electronic Systems, 2000, 36 (3) : 869 –878. DOI:10.1109/7.869506 |
| [15] | TSOURDOS A, WHITE B, SHANMUGAVEL M.无人机协同路径规划[M].祝小平, 周洲, 王怿, 译.北京:国防工业出版社, 2013:27-56. TSOURDOS A, WHITE B, SHANMUGAVEL M.Cooperative path planning of unmanned aerial vehicles[M].ZHU X P, ZHOU Z, WANG Y, translated.Beijing:National Defense Industry Press, 2013:27-56(in Chinese). |
| [16] | 丁明跃, 郑昌文, 周成平, 等. 无人飞行器航迹规划[M]. 北京: 电子工业出版社, 2009 : 46 -57. DING M Y, ZHENG C W, ZHOU C P, et al. Route planning for unmanned aerial vehicles[M]. Beijing: Publishing House of Electronics Industry, 2009 : 46 -57. (in Chinese) |
| [17] | 朱志良, 叶宁, 刘军, 等. 基于临近空间飞行器的区域自组网优化部署算法[J]. 电子与信息学报, 2011, 33 (4) : 915 –921. ZHU Z L, YE N, LIU J, et al. Deployment optimization algorithm for regional MANET containing near space vehicles as a part[J]. Journal of Electronics & Information Technology, 2011, 33 (4) : 915 –921. (in Chinese) |
| [18] | LI D P, DENG P K, LIU B, et al.Research on the dynamic configuration of air-based pseudolite network[C]//China Satellite Navigation Conference (CSNC) 2015 Proceedings:VolumeⅡ.Berlin:Springer, 2015, 341:357-367. https://www.researchgate.net/publication/281561057_Research_on_the_Dynamic_Configuration_of_Air-Based_Pseudolite_Network |



