2. 中国飞行试验研究院 测试所, 西安 710089
2. Measurement Technology Institute, Chinese Flight Test Establishment, Xi'an 710089, China
卫星总体参数设计涉及结构、轨道控制、姿态控制和电源分系统等,是典型的多学科优化问题,各学科的数学模型各不相同,难以统一并转化为一个模型,必须各分系统独立操作,各分系统间存在由于变量共享产生的相互制约,所以,卫星总体设计是典型的多学科优化问题[1]。
工程实际中卫星总体设计可以分成总体设计层和分系统设计层。总体设计层根据卫星任务目标,确定卫星设计的关键参数及取值,提出对各分系统的要求。分系统设计层在总体设计层指定的要求下,对各个分系统进行设计。这是自上而下的设计算法。
协同优化算法模拟这一过程,系统级模型模拟总体设计层,根据卫星设计总目标进行优化设计;N个分系统级模型模拟分系统设计层,以共享变量在分系统级和系统级模型中取值一致作为优化目标[2-3]。该算法使用N+1个优化模型同时进行优化设计,采用计算机进行迭代计算可以获得比实际设计师的协商更高的效率,同时由于该算法最大限度地保持了学科的自治性和模块化,广泛应用于卫星总体设计[2-3]、汽车减速器设计、亚声速喷气式客机总体设计、卫星结构设计[4]和液体火箭发动机设计[5]等。
然而,共享变量在系统级和分系统级的一致性要求导致优化过程收敛困难计算量大。李邦国等[6]通过定义约束的最优灵敏度,把系统级约束转换为动态约束,提高了计算效率。杨希祥等[7]通过采用支持向量回归机算法构造系统级约束条件的近似模型,提高计算效率。龙腾和刘莉[8]采用了2-范数形式的一致性约束方程。龙腾等[9]利用学科间动态不一致信息更新系统级优化中的罚因子,提高了学科级优化的效率。魏锋涛等[10]利用凝聚约束处理算法,将系统级优化的多个等式约束凝聚成一个单约束。杨丽丽等[4]采用超球子空间思想通过缩小变量在不同分系统取值的距离的算法实现一致性约束。Darabi等[5]通过在系统级和分系统级优化时同时考虑一致性约束,降低一致性约束的收敛难度。朱崎峰和宋保维[11]将系统优化的全部设计变量分为全局设计变量和局部设计变量两部分,基于学科状态方程,在系统级和学科级同时构建共享变量的一致性约束条件,保证更严格的共享变量一致性。Qiao等[12]通过将参数固定到典型值进而缩小参数可行域,以降低一致性约束时的计算量。Ji等[13]通过引入动态松弛因子,提高了一致性约束的收敛速度。这些改进措施只是从一定程度简化了一致性约束,但是,一致性约束仍然存在。另外,各分系统的优化目标是共享变量的一致性,并没对自身进行优化,所以,设计结果虽然可以保证系统级模型是最优的,但是无法保证分系统级也是最优的。
为了解决上述问题,本文将劝说式多Agent协商算法[14-15]引入到采用协同优化算法的卫星总体优化设计中,将系统级模型和分系统级模型都升级为智能体模型,提出了基于多Agent协商的协同优化算法。该算法中系统级Agent模型除进行系统级优化外,主动提议共享变量并通过与各分系统协商确定共享变量满足各分系统一致性的取值,系统级优化模型中不再需要一致性约束;分系统级Agent模型在与系统级模型协商确定共享变量取值之前,先进行自身优化,保证各分系统是最优的。
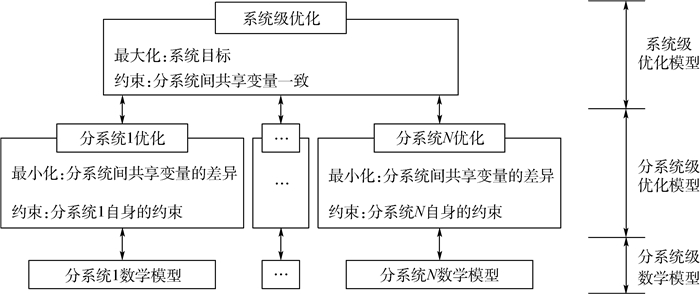
1 引入劝说式多Agent协商的协同优化算法 1.1 协同优化算法协同优化算法是一种针对复杂系统设计问题的分布式的、多级的优化算法[2]。它将复杂优化设计问题分解为不同学科的优化设计问题,并通过系统级约束条件来协调各学科之间的共享变量。其基本框架如图 1所示,包含系统级优化模型、分系统优化模型和分系统级数学模型。
|
| 图 1 协同优化的基本框架 Fig. 1 Basic frame of collaborative optimization |
系统级优化的目的是使系统级优化模型达到最优,同时采用等式约束条件来保证各分系统之间共享变量的一致性。分系统级优化模型的设计变量包括共享变量和只属于本分系统的局部变量,约束条件为对该分系统自身的要求,优化目标是使该分系统包含的共享变量与系统级取值一致。通过系统级优化和分系统级优化之间的多次迭代,最终找到一个使系统级优化模型达到最优并且共享变量在分系统级与系统级取值一致的优化结果。不同分系统有各自的优化模型,可以保证在不同的卫星设计阶段,通过改变分系统级数学模型的详细程度,得到不同设计阶段的优化结果[2-3]。
由图 1可见,共享变量的协调一致在系统级优化时作为约束,在分系统级优化时作为优化目标。系统级模型中共享变量可以任意取值,但是共享变量在分系统级中通常不相互独立,因此共享变量在分系统级很难取得与系统级一致的结果,导致计算量大[2]。另外,所谓的分系统级优化模型其实是各分系统对共享变量的协调,各分系统内部并没有对本分系统自身进行优化,这样不能保证系统级最优时分系统级也是最优,也就难以保证整个系统是最优的。
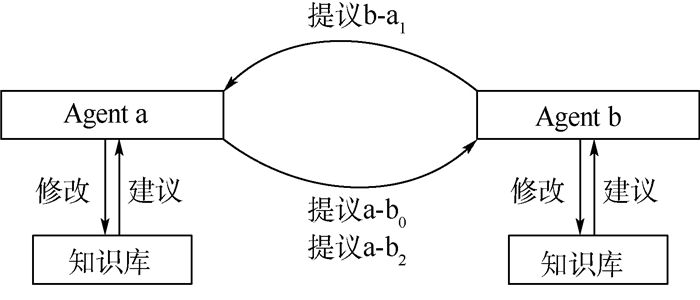
1.2 劝说式多Agent协商算法多Agent协商算法是处理多议题协调关系最有效的算法之一[16-17]。如果将共享变量在系统级和分系统级协调一致看作是议题的协商,则多Agent协商可以用于变量的协调一致。多Agent协商算法有基于辩论的协商算法[18-19]、基于学习的协商算法[20]和基于劝说的协商算法[14-15]等。其中劝说式多Agent协商借助信念修正这一推理工具,可以加快协商进程[15]。2个Agent参与的劝说式协商算法的一次协商过程如图 2所示。
|
| 图 2 劝说式多Agent协商算法的协商过程 Fig. 2 Negotiation process of persuasive multi-Agent negotiation algorithm |
以Agent a发起协商为例,Agent a提出提议a-b0之后,发给Agent b。Agent b根据自己的知识库分析提议a-b0,如果同意则结束协商,协商结果为a-b0;如果不能接受,则Agent b参考提议a-b0调整自己的知识库并提出反提议b-a1,发送给Agent a。Agent a根据自己的知识库分析提议b-a1,如果同意则结束协商,协商结果为b-a1;如果不能接受,则Agent a参考提议b-a1调整自己的知识库并提出反提议a-b2,依次循环。
由图 2可见,劝说式多Agent协商就是参与协商的多个Agent不断交换提议与反提议,直到一方可以满足对方的要求,结束协商。双方的要求一直在变化,提议也逐渐变化,最终协商结果是双方能接受的与初始提议最接近的结果,可以与初始提议不同。协商过程是双方共同参与的,双方同时根据对方的提议修改自己的知识库,可以保证最终取得一致结论。
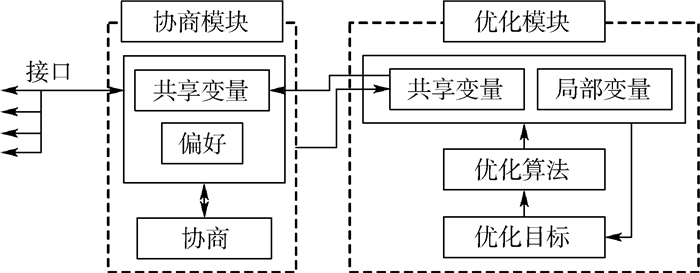
1.3 基于劝说式多Agent协商的协同优化算法基本框架如果在协同优化算法中增加协商模块来保证共享变量在系统级和分系统级中的一致性,系统级优化模型不再存在一致性约束,分系统级优化模型的优化目标可以不再是分系统级包含的共享变量与系统级取值一致,而变为自身最优(比如目标为质量最小、功率最小等)。
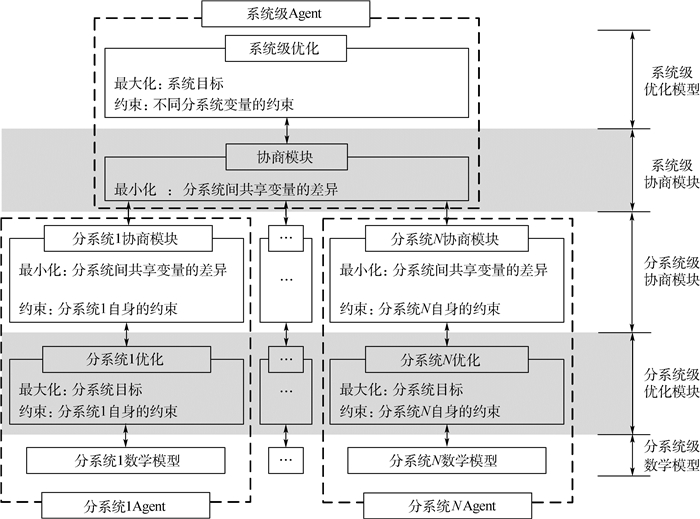
在系统级模型中增加协商模块,在分系统级模型中增加自身优化模块,图 1中的系统级模型和分系统级模型不再是单一的优化模型,而是具有了一定的自治性、适应性和能动性的智能体(Agent),最终形成了基于劝说式多Agent协商的协同优化算法,算法的原理如图 3所示(灰色底色为增加的模块)。
|
| 图 3 基于劝说式多Agent协商的协同优化算法基本框架 Fig. 3 Basic frame of collaborative optimization algorithm based on persuasive multi-Agent negotiation |
图 3中,系统级和分系统级模型中的协商模块将系统级优化时的每一个解通过协商生成一个满足共享变量一致性要求的可行解,然后用可行解代替原来的解。协商模块使得系统级优化时每个解都满足共享变量一致性要求。
图 3中,分系统级优化模块以本系统协商模块提议的共享变量中本分系统的自变量取值为条件对本分系统进行优化,协商模块提议的共享变量中本分系统的因变量均根据优化结果计算。优化模块保证分系统级提议满足各分系统最优。
2 对地观测卫星的协同优化模型对地观测卫星的总体优化设计涉及多个学科,本节应用协同优化算法对对地观测卫星进行结构、轨道控制、姿态控制以及电源分系统的一体化设计。
2.1 系统级Agent模型系统级Agent模型主要完成共享变量协商和系统级优化2个功能,工作流程如图 4所示。
|
| 图 4 系统级Agent模型的工作流程图 Fig. 4 Workflow of system-level Agent-based model |
系统级优化模块使用遗传算法进行优化,具体工作流程如下:
1) 系统级优化模块中的遗传算法生成一代个体,每个个体包含系统的共享变量和只在系统级存在的局部变量。
2) 针对系统级优化模块的一个个体,系统级协商模块为每一个共享变量分配一个偏好。针对每一个分系统,协商模块提取相关共享变量和对应的偏好形成提议。本文中分系统共有4个,针对系统级优化模块的一个个体,系统级协商模块分别形成4个提议并传给相应的分系统Agent。每个提议如式(1)所示。
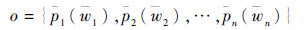
|
(1) |
式中:pi为共享变量;wi为共享变量的偏好,共有n个共享变量。
3) 每个分系统Agent模型形成一个与接收到提议的共享变量最接近的提议,返回给系统级协商模块(详见第2.2节)。系统级协商模块比较发出和收到的2种提议中的共享变量,如果2种共享变量近似相等则转入步骤4),否则系统级协商模块将同一共享变量从不同分系统返回的值进行平均,并把同一共享变量的偏好从不同分系统返回的值进行平均,形成新的提议传给分系统级Agent,重新执行步骤3)。
4) 用步骤3)中共享变量的取值替换步骤1)个体中的共享变量。优化模块采用新个体进行系统级优化。
系统级优化模块的优化目标是卫星总质量最小,变量是各个分系统的质量,系统级优化采用遗传算法进行。系统级优化设计问题的数学模型为
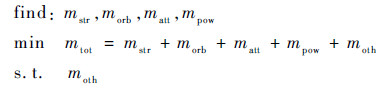
|
(2) |
式中:mtot为卫星总质量;mstr为结构分系统质量;morb为轨道控制分系统质量;matt为姿态控制分系统质量;mpow为电源分系统质量;moth为除结构、轨道控制、姿态控制和电源分系统外其他分系统的总质量。
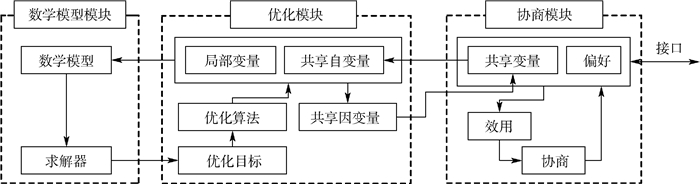
2.2 分系统级Agent模型分系统级Agent模型的工作流程如图 5所示,主要包括协商模块、优化模块和数学模型模块。
|
| 图 5 分系统级Agent模型的工作流程 Fig. 5 Workflow of subsystem Agent-based model |
分系统级协商模块的作用是在分系统级中通过优化迭代找到与系统级协商模块的提议最接近的提议。分系统级优化模块用来保证分系统级协商模块的提议同时满足本分系统自身要求和使本分系统最优2个条件。分系统级优化模块和协商模块都使用遗传算法进行优化。具体工作流程如下:
1) 分系统级协商模块接收系统级提议,形如式(1)。在分系统级中共享变量可以分为2种,分别是本分系统的自变量和本分系统的因变量。假设共享变量中分别有r个自变量和s个因变量(r+s=n),则共享变量可以写为

|
(3) |
2) 在分系统级协商模块中,遗传算法的一个个体由所有共享变量组成。遗传算法随机生成个体时每个个体只包含自变量部分:
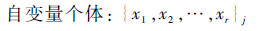
|
(4) |
式中:j为个体编号。遗传操作时,也仅对个体中的自变量进行操作。
3) 每个个体的因变量部分由分系统级优化模块计算。针对每个自变量个体,分系统级优化模块以自变量取值{x1,x2,…,xr}j作为已知条件,利用数学模型,根据每个分系统自身优化目标,对本分系统局部自变量{x1,x2,…,xt}(假设局部自变量共有t个)进行优化。优化完成后,本分系统的所有自变量为{x1,x2,…,xr,x1op,x2op,…,xtop}(上标op代表本分系统达到最优时局部自变量的值),利用上述自变量可以计算共享变量中本分系统的因变量y1,y2,…,ys。形成第j个完整个体:
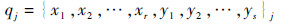
|
(5) |
4) 分系统级协商模块以完整个体与式(1)最接近为目标,利用遗传算法不断优化完整个体。将与式(1)最接近的完整个体中的共享变量取值,作为本分系统的提议。
遗传算法优化过程中在第k代时,第j个个体的适应度函数如下:
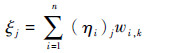
|
(6) |
式中:(ηi)j为共享变量的归一化系数;wi,k为共享变量在第k代时的偏好。
对于共享变量中的自变量,归一化系数(ηi)j的计算算法如下:
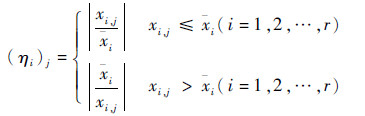
|
(7) |
对于共享变量中的因变量,归一化系数(ηi)j的计算算法如下:
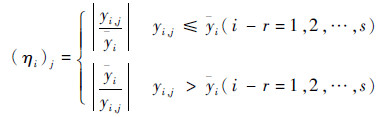
|
(8) |
适应度函数最大为优化目标。利用上述算法可以得到与系统级提议o的共享变量最接近的共享变量个体qop。
5) 在分系统级协商模块中,为了尽快获得qop,参考Agent协商理论中对知识库进行修改的策略,提出了分系统级协商模块对每一个共享变量的偏好进行修改的策略如下:
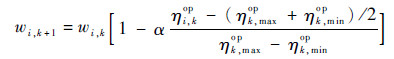
|
(9) |
式中:ηi,kop为第k代最优个体的第i个变量的归一化系数;ηk,maxop为第k代最优个体的所有n个变量的归一化系数中的最大值;ηk,minop为第k代最优个体的所有n个变量的归一化系数中的最小值;α为偏好的进化系数,假设为0.1。式(9)会降低与系统级提议接近的共享变量的偏好,提高与系统级提议差别大的共享变量的偏好。
6) 分系统级协商模块将qop和获得qop时新的偏好形成形似式(1)的提议o′,并发送给系统级协商模块。
结构、轨道控制、姿态控制和电源分系统的数学模型采用经验公式,参见文献[21],不再赘述。
2.2.1 结构分系统的协商模型和优化模型结构分系统的协商模型,以共享变量为参数,在满足本分系统对共享变量范围的要求下,目标是使得本分系统共享变量的取值与系统级提议中的共享变量最接近,协商模型为
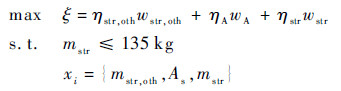
|
(10) |
式中:mstr,oth为卫星除了结构分系统外其他分系统的总质量;As为卫星横截面积;w为对应的偏好,在协商过程中会根据式(9)变化;ηstr,oth为其他分系统总质量的归一化系数;ηA为卫星横截面积的归一化系数;ηstr为结构分系统质量的归一化系数。其中mstr,oth和As为结构分系统的自变量,mstr为结构分系统的因变量。
结构分系统的优化模型以协商模型每个个体共享变量中本分系统的自变量为已知条件,通过优化本分系统局部自变量,使卫星结构在满足刚度(频率)、强度和稳定性要求下,达到结构分系统质量最小。优化模型为
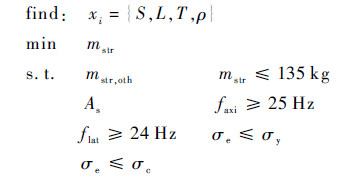
|
(11) |
式中:S为卫星构形;L为卫星高度;T为卫星结构壁厚;ρ为材料类型;faxi为卫星轴向基频;flat为卫星侧向基频;σe为卫星等效轴向应力;σy为材料屈服应力;σc为结构失稳临界应力。
2.2.2 轨道控制分系统的协商模型和优化模型轨道控制分系统的协商模型为
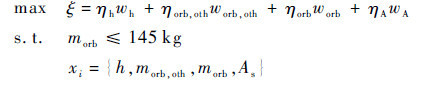
|
(12) |
式中:ηh为卫星轨道高度的归一化系数;
轨道控制分系统的优化模型是根据轨道高度h、其他分系统总质量morb,oth和卫星横截面积As,通过选择推进剂类型,使轨道控制分系统的质量最小。优化模型为

|
(13) |
式中:pt为推进剂类型。
2.2.3 姿态控制分系统协商模型和优化模型姿态控制分系统协商模型为
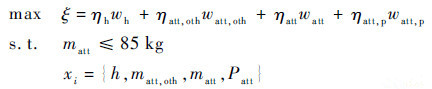
|
(14) |
式中: ηatt,oth、ηatt和ηatt,p分别为卫星除了姿态控制分系统外其他分系统的总质量、姿态控制分系统的质量和功率的归一化系数;matt,oth为除姿态控制分系统外其他分系统的总质量;Patt为姿态控制分系统的功率。其中h和matt,oth为自变量,matt和Patt为因变量。
姿态控制分系统的优化模型是以卫星h、matt,oth和控制精度cp为已知条件,对卫星稳定方式st和控制方式ct进行优化,使姿态控制分系统的质量最小。
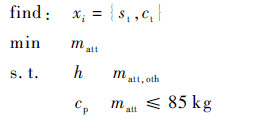
|
(15) |
电源分系统协商模型为
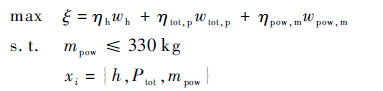
|
(16) |
式中: ηtot,p和ηpow,m分别为卫星总功率需求和电源分系统质量的归一化系数;Ptot为卫星总功率需求;其中h和Ptot为自变量,mpow为因变量。
电源分系统是以h和Ptot为已知条件,对太阳电池类型St、太阳帆板安装方式it、蓄电池类型bt和卫星设计寿命tl进行优化,使电源分系统的质量最小。优化模型为
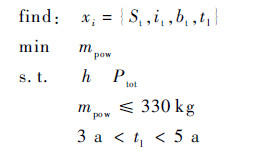
|
(17) |
采用JADE平台建立卫星协同优化的系统级和分系统级Agent模型,对对地观测卫星进行优化设计。优化时所有遗传算法中每一代的个体数均为50。本文首先研究协商模块对共享变量的一致性的作用和分系统级优化模块对各分系统质量的优化作用,然后给出基于劝说式多Agent协商的协同优化结果以证明本文算法的可行性。
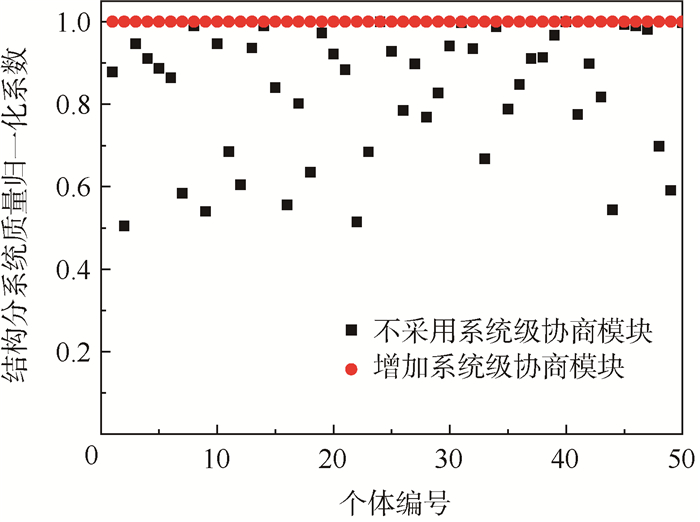
3.1 协商模块和分系统优化模块的作用协商模块可以保证系统级优化时每个解都满足共享变量一致性要求。图 6给出增加协商模块和不采用协商模块时,结构分系统质量的归一化系数的比较情况。
|
| 图 6 协商模块对结构分系统质量归一化系数的影响 Fig. 6 Effect of negotiation module on normalization coefficient of structure subsystem mass |
由图 6可见,经过系统级协商模块和结构分系统协商模块的协商之后,结构分系统质量的归一化系数均为1,表明:结构分系统质量这一共享变量在结构分系统与系统级优化模型中一致。不采用协商模块时,在结构分系统优化模型得到的结构分系统质量只有很少一部分与系统级优化模块中接近,这是因为,针对系统级优化时随机生成的一代个体,结构分系统质量这一共享变量在结构分系统中很难与系统级取得相同的值。因此,协商模块可以保证分系统级模型与系统级模型中共享变量的一致性。
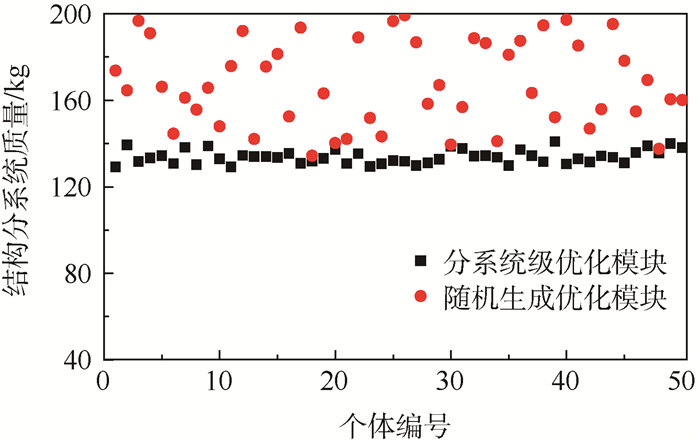
以结构分系统为例分析分系统级优化模块的作用。不采用分系统级优化模块时,结构分系统的3个共享变量在满足结构分系统自身约束条件下直接随机生成,假设为m′str,oth、A′s和m′str。采用分系统级优化模块时,首先只随机生成m′str,oth和A′s,然后在满足结构分系统自身约束条件下对结构分系统的参数如卫星构形、卫星高度、卫星结构壁厚和材料类型等进行优化,得到满足给定m′str,oth和A′s及结构分系统自身约束条件下结构分系统质量的最小值(mstr)min。很明显,优化后的(mstr)min不会大于随机生成的m′str。图 7给出结构分系统质量采用随机生成和通过分系统级优化模块生成时两者的比较情况。
|
| 图 7 分系统级优化模块对结构分系统质量的优化作用 Fig. 7 Effect of subsystem optimization module on mass of structure subsystem |
由图 7可见,经过结构分系统优化模块优化后的结构分系统质量均小于在满足条件下随机生成的结构分系统质量。表明对各分系统进行优化设计,可以保证各分系统最优。
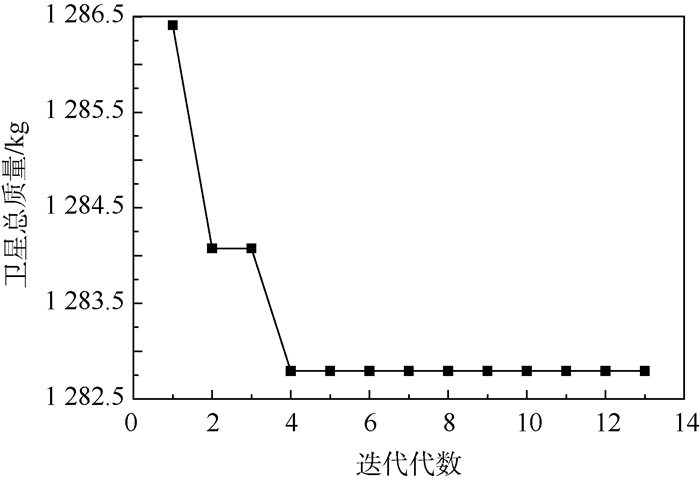
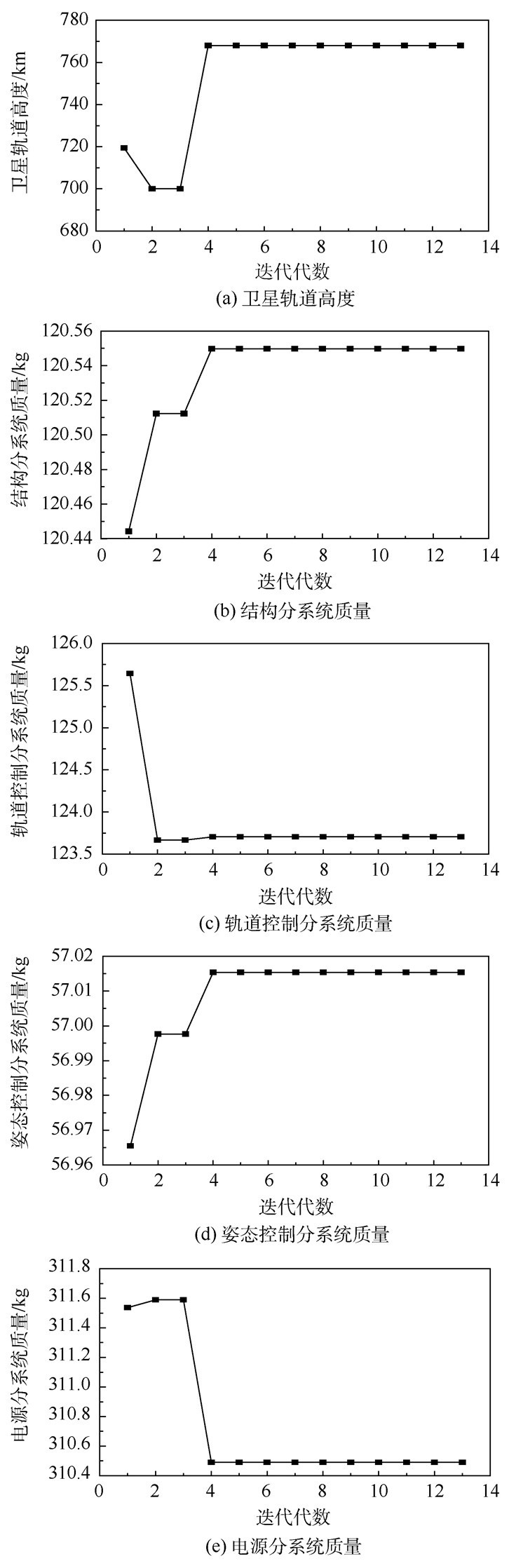
3.2 基于劝说式多Agent协商的协同优化结果图 8和图 9给出基于劝说式多Agent协商的协同优化结果。其中,图 8为卫星总质量的优化历程,图 9为卫星共享变量中卫星轨道高度、结构分系统质量、轨道控制分系统质量、姿态控制分系统质量及电源分系统质量的优化历程。
|
| 图 8 卫星总质量优化历程 Fig. 8 History process of optimization for total satellite mass |
|
| 图 9 卫星共享变量优化历程 Fig. 9 History process of optimization for satellite shared variables |
由图 8可见,卫星总质量先随着优化代数逐渐下降,然后趋于不变,表明卫星的整体优化达到收敛;另外,卫星的总质量在优化的第4代即达到稳定状态,表明算法的收敛速度快,因此本文算法具有较好的收敛性。由图 8和图 9可见,在第2~3代之间,所有变量出现了平台状的变化趋势,到第4代时所有变量又发生了变化。这一过程表明,本文算法以卫星轨道高度、结构分系统质量和姿态控制分系统质量的增加为代价,降低了卫星的总质量。这体现了本算法克服局部最优解的能力。
表 1给出采用文献[3]算法和本文算法分别进行协同优化设计时的优化结果。由表 1可得,本文算法的优化结果与文献[3]的结果基本吻合,这证明了本文算法的有效性。
4 结论
1) 本文针对协同优化算法中共享变量在系统级优化模型和分系统级优化模型间的一致性问题及分系统自身优化问题,提出了基于劝说式多Agent协商的协同优化算法。
2) 以某对地观测卫星为例,建立了基于多Agent协商的协同优化模型,优化结果表明,基于多Agent协商的协同优化算法可以保证共享变量的一致性;在协同优化算法中增加分系统自身优化模块,可以保证系统级优化在分系统最优解中进行,并且最终该算法得到了合理的优化结果。
3) 各个分系统Agent模型具有很强的相互独立性可以很容易地修改,也可以很容易地增加分系统数量,本文为进一步研究更为复杂的、集合更多卫星分系统的多学科设计优化问题提供了重要的参考方法。
考虑到优化模型中各分系统的数学模型为粗糙的经验公式并且遗传算法的计算量较大,特别是当数学模型复杂化并且精度提高之后,采用遗传算法优化时计算量难以接受,可以进一步研究的工作包括:①考虑更多的卫星分系统;②采用精度更高的分系统级数学模型,比如结构分系统的应力状态采用有限元模型进行分析等;③采用计算量更小的优化求解方法。
| [1] | 谭春林, 庞宝君, 张凌燕, 等. 对地观测卫星总体参数多学科优化[J]. 北京航空航天大学学报,2008, 34 (5) : 529 –532. TAN C L, PANG B J, ZHANG L Y, et al. Multi-disciplinary optimization in earth observation satellite main parameters[J]. Journal of Beijing University of Aeronautics and Astronautics,2008, 34 (5) : 529 –532. (in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [2] | 裴晓强, 黄海. 协同优化在卫星多学科设计优化中的初步应用[J]. 宇航学报,2006, 27 (5) : 1054 –1058. PEI X Q, HUANG H. Multidisciplinary design optimization of satellite using collaborative optimization[J]. Journal of Astronautics,2006, 27 (5) : 1054 –1058. (in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [3] | 吴文瑞, 黄海, 吴蓓蓓. 遥感卫星总体参数设计的建模与协同优化[J]. 北京航空航天大学学报,2012, 38 (10) : 1363 –1368. WU W R, HUANG H, WU B B. Modeling and collaborative optimization of remote sensing satellite system parameters design[J]. Journal of Beijing University of Aeronautics and Astronautics,2012, 38 (10) : 1363 –1368. (in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [4] | 杨丽丽, 陈昌亚, 王德禹. 基于多目标协同优化算法的卫星结构优化设计[J]. 上海交通大学学报,2014, 48 (10) : 1446 –1450. YANG L L, CHEN C Y, WANG D Y. Structural optimization of satellite based on multi-objective collaborative optimization algorithm[J]. Journal of Shanghai Jiao Tong University,2014, 48 (10) : 1446 –1450. (in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [5] | DARABI H, ROSHANIAN J, ZARE H. Design of liquid-propellant engine using collaborative optimization and evolutionary algorithms[J]. Proceedings of the Institution of Mechanical Engineers,Part G:Journal of Aerospace Engineering,2015, 229 (2) : 232 –242. |
| Click to display the text | |
| [6] | 李邦国, 陈潇凯, 林逸. 协同优化方法的改进及应用[J]. 吉林大学学报(工学版),2010, 40 (6) : 1497 –1501. LI B G, CHEN X K, LIN Y. Reformed collaborative optimization method and its application[J]. Journal of Jilin University (Engineering and Technology Edition),2010, 40 (6) : 1497 –1501. (in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [7] | 杨希祥, 杨慧欣, 江振宇, 等. 基于支持向量回归机和粒子群算法的改进协同优化方法[J]. 湖南大学学报(自然科学版),2011, 38 (3) : 34 –39. YAND X X, YANG H X, JIANG Z Y, et al. Improved collaborative optimization based on support vector regression and particle swarm optimization[J]. Journal of Hunan University(Natural Sciences),2011, 38 (3) : 34 –39. (in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [8] | 龙腾, 刘莉. 改进的Pareto多目标协同优化策略[J]. 系统工程与电子技术,2012, 34 (9) : 1834 –1840. LONG T, LIU L. Enhanced Pareto multi-objective collaborative optimization strategy[J]. Systems Engineering and Electronics,2012, 34 (9) : 1834 –1840. (in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [9] | 龙腾, 刘莉, 彭磊. 基于可行方向序列无约束极小化技术外点法的改进协同优化策略[J]. 机械工程学报,2013, 49 (3) : 153 –162. LONG T, LIU L, PENG L. Enhanced collaborative optimization strategy based on feasible direction SUMT exterior method[J]. Journal of Mechanical Engineering,2013, 49 (3) : 153 –162. (in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [10] | 魏锋涛, 宋俐, 李言, 等. 改进的多学科协同优化方法[J]. 计算机集成制造系统,2013, 19 (9) : 2116 –2122. WEI F T, SONG L, LI Y, et al. Improved multidisciplinary collaborative optimization method[J]. Computer Integrated Manufacturing Systems,2013, 19 (9) : 2116 –2122. (in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [11] | 朱崎峰, 宋保维. 一种改进的快速收敛多学科设计协同优化方法[J]. 华中科技大学学报(自然科学版),2014, 42 (2) : 116 –120. ZHU Q F, SONG B W. An improved fast converging collaborative optimization method of multidisciplinary design optimization[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition),2014, 42 (2) : 116 –120. (in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [12] | QIAO F,ZHU J,NI J C.Collaborative optimization model of cost and energy consumption for sintering burden[C]//World Congress on Intelligent Control and Automation (WCICA).Piscataway,NJ:IEEE Press,2014:2316-2321. |
| Click to display the text | |
| [13] | JI A M, YIN X, YUAN M H. Hybrid collaborative optimization based on selection strategy of initial point and adaptive relaxation[J]. Journal of Mechanical Science and Technology,2015, 29 (9) : 3841 –3854. |
| Click to display the text | |
| [14] | KHAN R F, SUTCLIFFE A. Attractive agents are more persuasive[J]. International Journal of Human-Computer Interaction,2014, 30 (2) : 142 –150. |
| Click to display the text | |
| [15] | 杨佩, 高阳, 陈兆乾. 一种劝说式多Agent多议题协商方法[J]. 计算机研究与发展,2006, 43 (7) : 1149 –1154. YANG P, GAO Y, CHEN Z Q. Persuasive multi-Agent multi-issue negotiation[J]. Journal of Computer Research and Development,2006, 43 (7) : 1149 –1154. (in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [16] | ROSENSCHEIN J S, ZLOTKIN G. Rules of encounter:Designing conventions for automated negotiation among computers[M]. Cambridge,MA : MIT Press , 1994 : 29 -46. |
| Click to display the text | |
| [17] | JENNINGS N R, FARATIN D, JOHNSONM J, et al. Agent-based business process management[J]. Journal of Cooperative Information Systems,1996, 5 (2-3) : 105 –130. |
| Click to display the text | |
| [18] | PILOTTI P, CASALI A, CHESNEVAR C. A belief revision approach for argumentation-based negotiation agents[J]. International Journal of Applied Mathematics and Computer Science,2015, 25 (3) : 455 –470. |
| Click to display the text | |
| [19] | MAREY O, BENTAHAR J, KHOSROWSHAHI-ASLE E, et al. Decision making under subjective uncertainty in argumentation-based agent negotiation[J]. Journal of Ambient Intelligence and Humanized Computing,2015, 6 (3) : 307 –323. |
| Click to display the text | |
| [20] | ZHANG J H, REN F H, ZHANG M J. Bayesian-based preference prediction in bilateral multi-issue negotiation between intelligent agents[J]. Knowledge-Based Systems,2015, 84 : 108 –120. |
| Click to display the text | |
| [21] | LARSON W J, WERTZ J R. Space mission analysis and design[M]. 2nd ed Torrance : Microcosm Inc , 1992 : 353 -497. |
| Click to display the text | |



