灵敏度分析主要研究模型的输出不确定性是如何分配到输入不确定性的[1]。研究输入对输出不确定性的影响程度,有助于设计者选择更全面、合理和有效减小模型输出不确定性的方案。通常,灵敏度分为局部灵敏度、全局灵敏度和区域灵敏度。局部灵敏度不能反映输入变量整个分布范围对输出响应不确定性的影响,而全局灵敏度反映的是输入变量在其整个分布范围的不确定性对输出响应不确定的影响程度,更具有实际应用的潜能。目前,全局灵敏度的分析模型主要分为3类:非参模型(相关系数模型)[2]、基于方差的模型[3, 4]和矩独立模型[5, 6]。在这些分析模型中,基于方差的模型应用最为广泛,由Sobol和Kucherenko[3]提出,满足“全局性、可量化性和模型独立性”。全局灵敏度分析这种平均的思想可以简单直观地从总体上把握输入变量对输出性能的影响,但由于全局灵敏度是在全域内取平均,因而有可能掩盖输入变量取值区域对输出影响的重要信息,因此,进行区域灵敏度分析至关重要,其主要度量的是输入变量不同取值区间对输出不确定性的贡献程度。Bolado-Lavin等[7]提出样本均值贡献(Contribution to Sample Mean,CSM)曲线,其衡量的是输入变量分布区间减缩时,输出均值的变化。受CSM的启发,Tarantola等[8]提出了样本方差贡献(Contribution to Sample Variance,CSV)曲线及相应的方差比函数。Wei等[9]又对CSM、CSV及相应的均值比函数和方差比函数做了改进,改进后的指标更真实地反映了输入变量的区间减缩后对输出均值和方差的贡献。在基于方差的区域灵敏度分析的基础上,Wei等[10]提出了基于方差的W指标,其反映的是输入变量取不同取值区间对输出方差的平均影响,但是不能反映输入变量取不同取值区间时对输出方差影响的变异性。
因此,本文对基于方差的W指标进行改进,改进后的指标既包含输入变量取不同取值区间对输出方差的平均影响,又包含不同取值区间对输出方差影响的变异性,使得改进后的W指标能够提供更为全面合理的输入变量的灵敏度信息。除此之外,本文还将空间分割(Space-Partition,SP)、无迹变换(Unscented Transformation,UT)[11]和函数插值技术相结合构造了一类计算方法,只需一组UT样本点就可以近似计算基于方差的全局灵敏度指标、基于方差的区域灵敏度指标、基于方差的W指标和改进的基于方差的W指标,以便为设计人员提供更多重要性分析的有用信息。数值算例和工程算例的计算结果验证了本文方法的准确性和高效性。
1 各类基于方差的灵敏度指标 1.1 基于方差的全局灵敏度指标设Y=g(X),X=(X1,X2,…,Xn)为n维随机变量,Xi对Y方差贡献的1阶指标定义如下[4]:
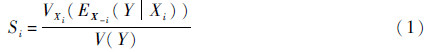
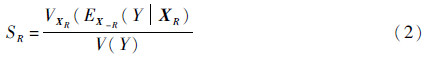
1阶方差贡献总指标以及r阶方差贡献总指标定义如下:
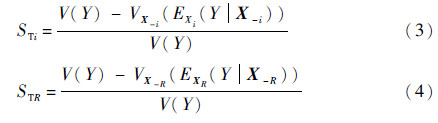
本文采用Wei等[9]改进的区域灵敏度指标进行计算分析。当Xi的分布范围从原始的[-∞,+∞]减缩到[u,v]时,模型输出均值为
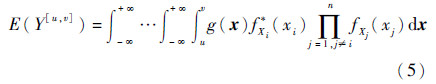
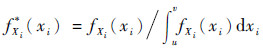 为Xi在减缩区间内的概率密度函数;u=FXi-1(q1);v=FXi-1(q2)(FXi-1(·)为第i个输入变量的累积分布函数的逆函数,q2>q1∈[0,1])。
为Xi在减缩区间内的概率密度函数;u=FXi-1(q1);v=FXi-1(q2)(FXi-1(·)为第i个输入变量的累积分布函数的逆函数,q2>q1∈[0,1])。
输入变量Xi的均值比函数定义如下:
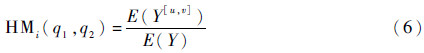
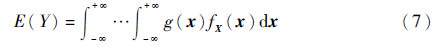
类似地,当Xi的分布范围从原始的[-∞,+∞]减缩到[u,v]时,模型输出方差为
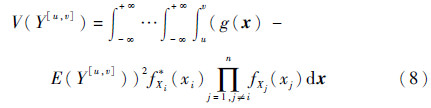
相应地,输入变量Xi的方差比函数定义如下:
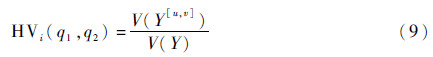
通过三维的HMi(q1,q2)和HVi(q1,q2)图像可以清楚地读出Xi变量减缩到任意区间[FXi-1(q1),FXi-1(q2)]时所对应的均值与原始均值的比值以及方差与原始方差的比值,从而直接为设计人员提供更多有用的减小输出不确定性的信息。
1.3 基于方差的W指标文献[10]对于输入变量Xi定义了其基于方差的W指标如下:
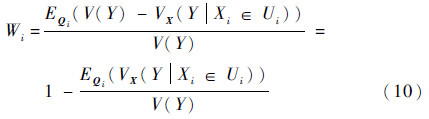
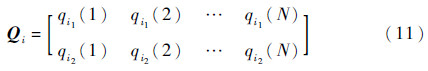
VX(Y|Xi∈Ui)为Xi属于Ui区间而X-i变量在其整个分布范围内变化时所对应的输出方差。Qi包括了Ui的所有可能,因此,基于方差的W指标反映的是输入变量固定在其分布范围的任意子区间内对输出方差的平均影响。对于W总指标,文献[10]也给出了相应的定义:
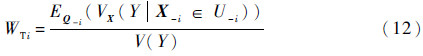
文献[10]同时证明了基于方差的W指标与方差比函数HVi(q1,q2)的关系:
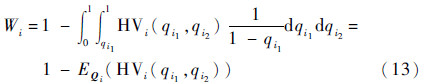
从基于方差的W指标的定义可以看出,其仅是Xi取所有可能的分布子区间时对输出方差的平均影响,可能掩盖了Xi在某个子区间对输出方差V(Y)的较大影响项,因此,更合理的基于方差的W指标的定义不仅需包含平均影响项(即原始的基于方差的W指标所提供的信息),还需包含影响Xi取不同分布子区间对输出方差影响的变异性,基于此,本文在第2节将对原始的基于方差的W指标进行修正。
2 改进的基于方差的W指标第1.3节分析了原始的基于方差的W指标存在的不足,本节将对其进行一定的修正。为避免Xi取不同分布子区间时对输出方差影响的正负抵消,对原始的基于方差的W指标的改进如下:
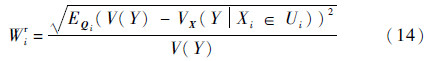
通过平方项的添加,使原本影响的正负抵消现象得以消除,取而代之的是正负抵消项的累加,这更能真实反映Xi在不同分布子区间内对输出方差的平均影响。对式(14)作进一步推导可得
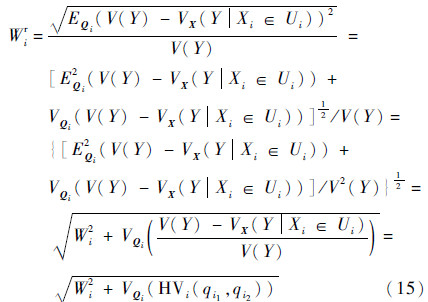
从式(15)可以看出,改进的基于方差的W指标既包含了原始的基于方差的W指标,又包含了Xi在不同分布子区间内对输出方差影响的变异性,因而改进的基于方差的W指标较原始的基于方差的W指标更全面。
3 各类基于方差灵敏度指标的近似计算方法通过第1节对各类基于方差的灵敏度指标的回顾以及第2节对原始的基于方差的W指标的改进,可以看出,不同的灵敏度指标侧重反映不同的信息,为了给设计人员提供全方位、多角度的输入变量重要性信息,需要从区域和全局双重的角度进行研究,这样可以在把握输入变量对输出性能影响的总体信息的基础上,全面把握输入变量随机取值的任意区域对输出性能影响的详细信息,既不因总体上的综合而遮盖区域的重要影响信息,又不因区域的繁多信息而影响对输入不确定性影响的总体上的把握。本节将空间分割、UT和函数插值技术相结合构造一种近似计算方法,其只需一组UT样本点就可以同时近似计算各类基于方差的灵敏度指标。
3.1 输出响应均值和方差的计算
由文献[11]可知,UT方法首先根据输入变量概率分布的一些特征(如均值和协方差)确定产生一组Sigma点以及相应的权重。然后将Sigma点代入非线性函数中,得到变换的Sigma点,这些变换后的Sigma点可以用来估计非线性函数的均值和协方差。低阶UT在仅匹配先验状态均值和协方差的情况下,对非线性函数Y=g(X)的均值和方差的估计: 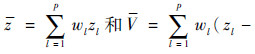
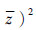 可以达到3阶精度[12],wl为相应的权值,p为Sigma点个数,zl为Sigma点代入到非线性函数中得到的变换的样本点,
可以达到3阶精度[12],wl为相应的权值,p为Sigma点个数,zl为Sigma点代入到非线性函数中得到的变换的样本点,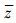 为非线性函数g(X)的均值估计值,
为非线性函数g(X)的均值估计值,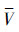 为非线性函数g(X)的方差估计值。对于高度非线性的输出响应函数均值和方差的计算,UT方法将失效。本文将空间分割和UT方法结合,计算非线性程度较高的输出响应函数的均值和方差。其基本思想为:将求解E(Y)和V(Y)的积分全域进行分割,则在子空间内局部函数的非线性程度将大大低于全域函数的非线性程度,使得在局部区域采用UT方法可得到高精度的解。输入变量组成的积分全域分割也为本文利用一组UT样本点计算各类方差指标创造了良好的前期准备条件。
为非线性函数g(X)的方差估计值。对于高度非线性的输出响应函数均值和方差的计算,UT方法将失效。本文将空间分割和UT方法结合,计算非线性程度较高的输出响应函数的均值和方差。其基本思想为:将求解E(Y)和V(Y)的积分全域进行分割,则在子空间内局部函数的非线性程度将大大低于全域函数的非线性程度,使得在局部区域采用UT方法可得到高精度的解。输入变量组成的积分全域分割也为本文利用一组UT样本点计算各类方差指标创造了良好的前期准备条件。
空间分割结合UT方法(SP-UT)计算E(Y)和V(Y)的步骤如下:将每一维输入空间Xi(i=1,2,…,n)等概率地划分为Ni个互不重叠且充满整个取值区域的子区间Aji=[aji-1,aji](ji=1,2,…,Ni),在此划分下输出响应Y的均值E(Y)和方差V(Y)如下:
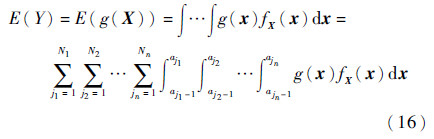
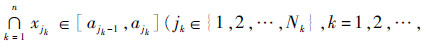 n)中,X的联合密度函数变为
n)中,X的联合密度函数变为
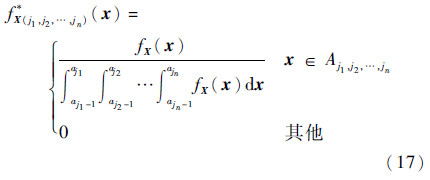
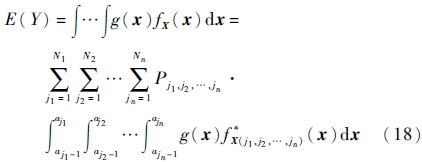
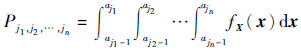 为x∈Aj1,j2,…,jn的概率。在减缩的子空间Aj1,j2,…,jn内应用UT方法可得
为x∈Aj1,j2,…,jn的概率。在减缩的子空间Aj1,j2,…,jn内应用UT方法可得
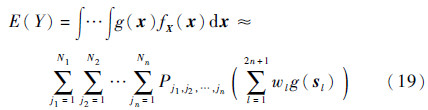
类似地,输出响应的方差为
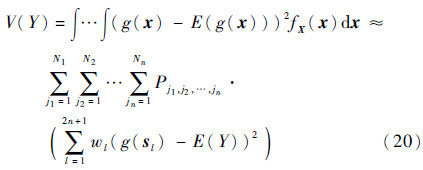
文献[13]给出了基于方差的全局灵敏度指标的近似计算公式,对于1阶方差指标有如下近似:
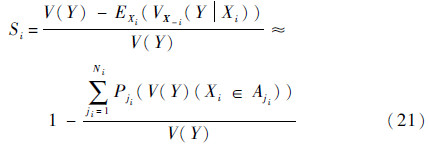
式(21)的前提假设是:当输入变量Xi所对应的取值区间划分较小时,近似计算值收敛于真值。本节主要给出重复利用UT样本计算1阶方差全局灵敏度指标的近似表达:
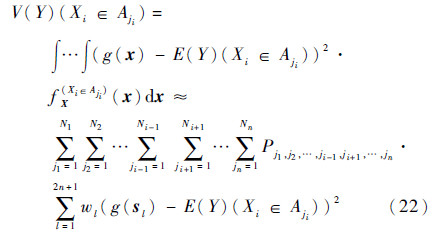
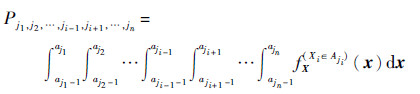
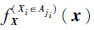 为Xi属于Aji子区间而其他变量处于原始积分域的联合概率密度函数,即
为Xi属于Aji子区间而其他变量处于原始积分域的联合概率密度函数,即
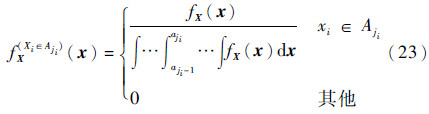
wl和sl则是由如下密度函数产生的X的第l个权值及相应的n维Sigma点。
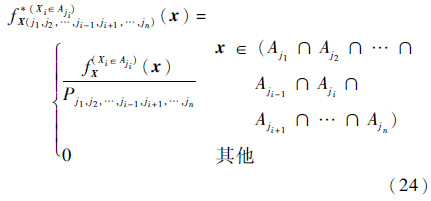
E(Y)(Xi∈Aji)采用SP-UT估算的表达式为
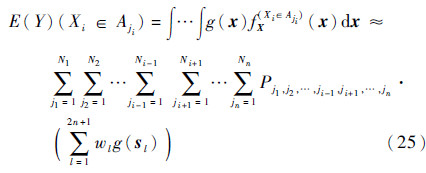
重复利用计算无条件均值和方差所产生的子空间内的UT样本点近似计算方差全局灵敏度指标的公式如下:
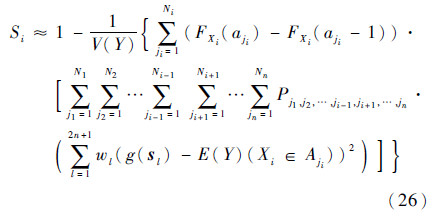
重复利用计算无条件均值和方差所产生的空间划分及相应的样本点得到均值比函数和方差比函数的三维图像的具体流程如下。
1) 在计算无条件均值和方差中,每一维输入变量区间被划分为Ni个子区间,则Xi变量分布区间相应分位数向量B为: 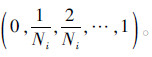
2) 满足q1,q2∈B且q2>q1的区间有Ni(Ni+1)/2个,计算每一个可能区间的HMi和HVi,如下:
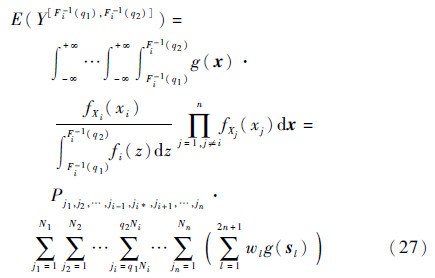
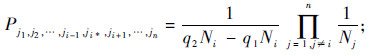 ;wl和sl为由如下密度函数产生的X的第l个权值和相应的n维Sigma点。
;wl和sl为由如下密度函数产生的X的第l个权值和相应的n维Sigma点。
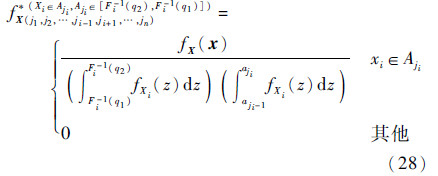
类似地,计算  如下:
如下:
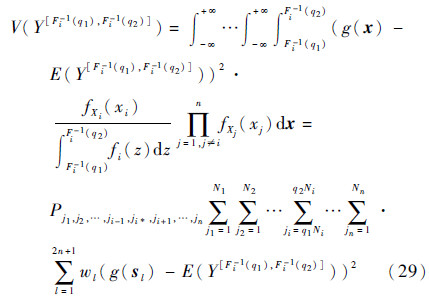
3) 根据步骤2)计算的结果画出HMi和HVi与分位数q1、q2的关系图。
式(13)和式(15)分别建立了方差比函数和基于方差的W指标及改进的基于方差的W指标的关系,则在计算得到的HV图中,可以通过函数插值技术得到任意区间对应的输出响应函数的方差值,进而近似得到对应的基于方差的W指标和改进的基于方差的W指标。
3.4 SP-UT方法的计算量
采用标准UT,每个子空间内产生p=2n+1个Sigma点,由于w0=0,因此每个子空间内实际模型调用次数为p=2n,总计算量为: 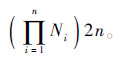 。可以看出,本文方法主要针对输入变量维数较低的问题。
。可以看出,本文方法主要针对输入变量维数较低的问题。
算例1 Sobol’s G函数[14]。由于其强的非单调性和强的非线性,在灵敏度分析中被广泛作为验证算例。数学表达式如下:
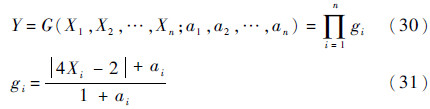
 |
| 图 1 Sobol’s G函数均值比函数三维图 Fig. 1 3D plots of mean ratio functions of Sobol’s G function |
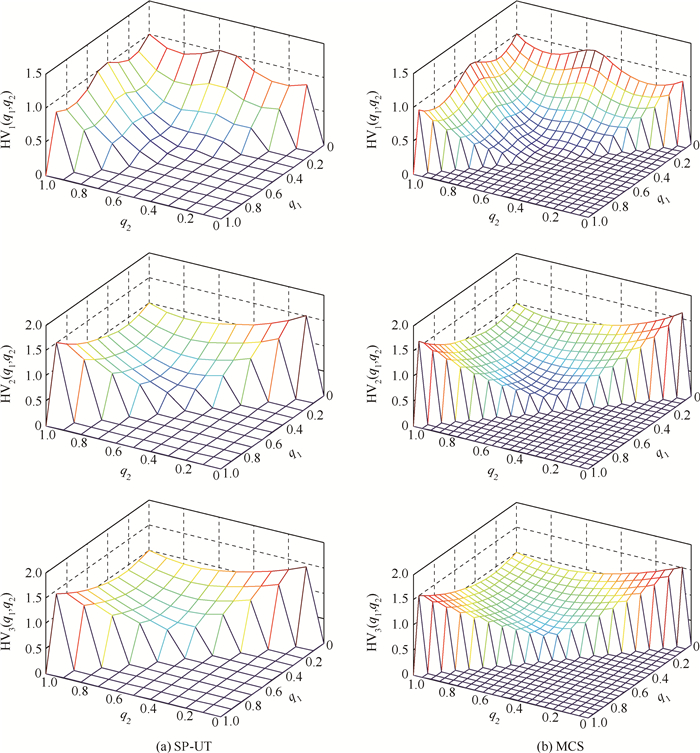 |
| 图 2 Sobol’s G函数方差比函数三维图 Fig. 2 3D plots of variance ratio functions of Sobol’s G function |
| 方法 | W1 | W2 | W3 | WT1 | WT2 | WT3 |
| SP-UT | 0.5240 | 0.2020 | 0.1056 | 0.6923 | 0.3933 | 0.3252 |
| (0.0062) | (0.0066) | (0.0052) | (0.0084) | (0.0084) | (0.0059) | |
| MCS | 0.5291 | 0.1615 | 0.0830 | 0.7716 | 0.3966 | 0.3137 |
| 注:小括号中的数表示抽取30组2000个插值区间计算出的基于方差的W指标的标准差,MCS的计算量为6×106。 | ||||||
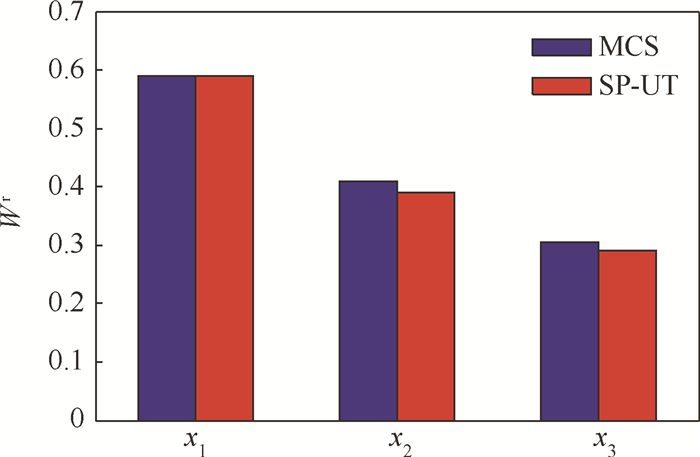 |
| 图 3 Sobol’s G函数的改进的基于方差的W指标的计算结果 Fig. 3 Calculation results of variance-based modified W indices of Sobol’s G function |
算例2 一根钢筋混凝土梁[15],其极限状态函数为
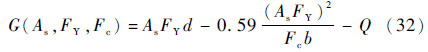
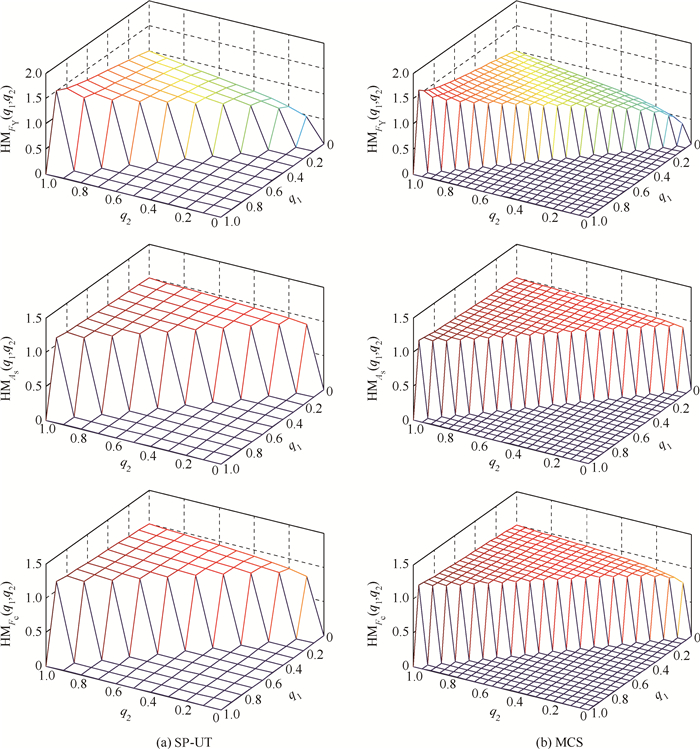 |
| 图 4 钢筋混凝土梁结构的均值比函数三维图 Fig. 4 3D plots of mean ratio functions of reinforced concrete beam |
| 输入变量 | 均值 | 变异系数 | 分布类型 |
| FY/(kN·cm-2) | 44 | 0.105 | 正态 |
| As/cm2 | 4.08 | 0.02 | 正态 |
| Fc/(kN·cm-2) | 3.12 | 0.14 | 正态 |
| 方法 | SFY | SAs | SFc | SFYAs | SFYFc | SAsFc |
| SP-UT | 0.8424 | 0.0304 | 0.0805 | 0.8767 | 0.9231 | 0.1169 |
| MCS | 0.8686 | 0.0312 | 0.0871 | 0.8988 | 0.9575 | 0.1221 |
| 注:MCS的计算量为1.001×106。 | ||||||
| 方法 | WFY | WAs | WFc | WTFY | WTAs | WTFc |
| SP-UT | 0.7509 | 0.0187 | 0.0372 | 0.9417 | 0.1698 | 0.2245 |
| (0.0027) | (0.00023) | (0.016) | (0.002) | (0.0036) | (0.0036) | |
| MCS | 0.7784 | 0.0155 | 0.0361 | 0.9457 | 0.1268 | 0.1966 |
| 注:小括号中的数表示抽取30组2000个插值区间计算出的基于方差的W指标的标准差,MCS的计算量为6×106。 | ||||||
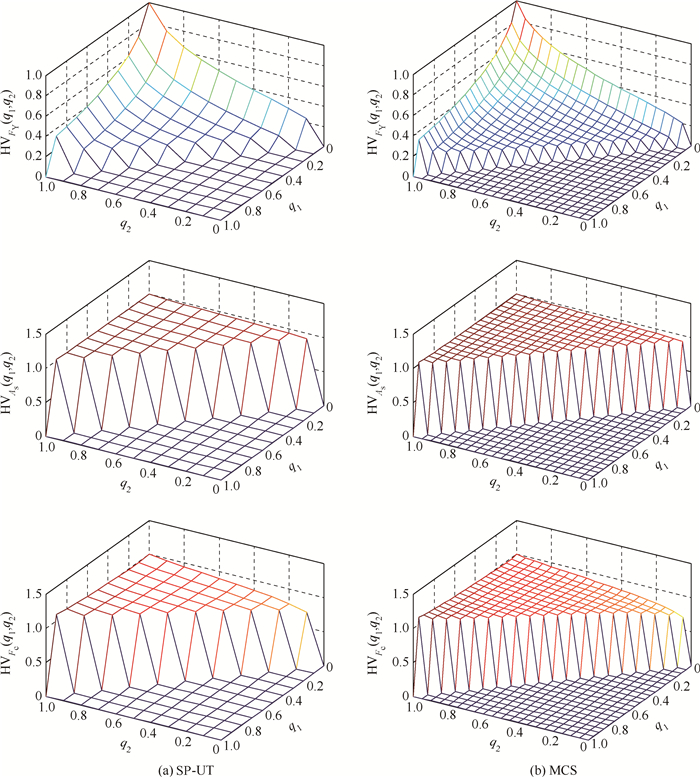 |
| 图 5 钢筋混凝土梁结构的方差比函数三维图 Fig. 5 3D plots of variance ratio functions of reinforced concrete beam |
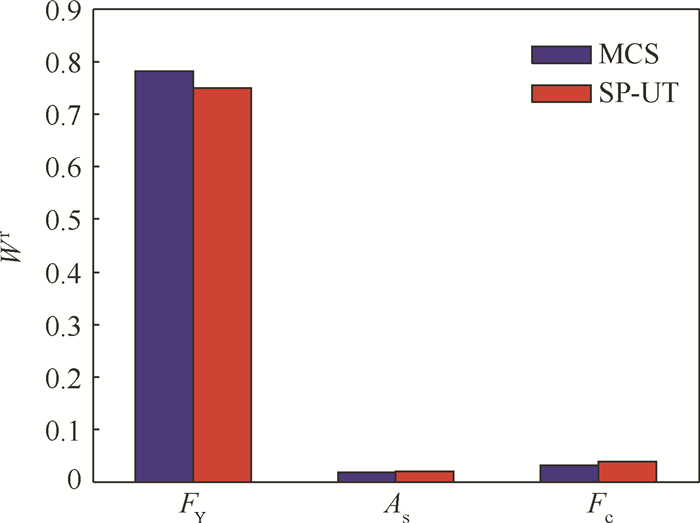 |
| 图 6 钢筋混凝土梁结构的改进的基于方差的W指标的计算结果 Fig. 6 Calculation results of variance-based modified W indices of reinforced concrete beam |
通过与大量样本下MCS计算结果的对比可以看出,本文方法通过一组样本点近似各类方差重要性指标的准确性和高效性。通过各指标的计算结果可以得出,钢的屈服强度不论从全局还是局部的角度来看,都是对输出不确定性影响最大的变量,因此,可以通过调整其取值范围来降低输出的不确定性。
5 结 论1) 本文对原始的基于方差的W指标进行了改进,使其在包含原始指标所提供的信息外,还包含了Xi在不同分布子区间内对输出方差影响的变异性,更全面合理地反映了Xi取不同实现区间时对输出方差的平均影响。
2) 鉴于各类基于方差的灵敏度指标从不同的角度衡量了输入变量的重要性,提出了高效的同时计算这些指标的基于空间分割、UT和函数插值技术的方法,该方法利用一组UT样本点就能计算出所有指标,从而高效地从多角度为设计人员提供更有价值的输入变量的重要性信息。
3) 本文方法可以适用于复杂的非线性响应函数,通过算例进行了验证。
4) 由于本文方法的计算量会随输入变量维数的增加而呈指数增长,因此,其仅适用于输入变量维数较低的问题。
| [1] | SALTELLI A. Sensitivity analysis for importance assessment[J].Risk Analysis,2002,22(3):579-590. |
| Click to display the text | |
| [2] | SALTELLI A, MARIVOET J.Non-parametric statistics in sensitivity analysis for model output:A comparison of selected techniques[J].Reliability Engineering and System Safety,1990,28(2): 229-253. |
| Click to display the text | |
| [3] | SOBOL I M, KUCHERENKO S.Derivative based global sensitivity measures and their link with global sensitivity indices[J].Mathematics and Computers in Simulation,2009,79(10): 3009-3017. |
| Click to display the text | |
| [4] | SALTELLI A, ANNONI P,AZZINI I,et al.Variance based sensitivity analysis of model output.Design and estimator for the total sensitivity index[J].Computation Physics Communications,2010,181(2):259-270. |
| Click to display the text | |
| [5] | BORGONOVO E. A new uncertainty importance measure[J].Reliability Engineering and System Safety,2007,92(6):771-784. |
| Click to display the text | |
| [6] | BORGONOVO E, CASTAINGS W,TARANTOLA S.Moment independent importance measures:New results and analytical test cases[J].Risk Analysis,2011,31(3):404-428. |
| Click to display the text | |
| [7] | BOLADO-LAVIN R, CASTAINGS W,TARANTOLA S.Contribution to the sample mean plot for graphical and numerical sensitivity analysis[J].Reliability Engineering and System Safety,2009,94(6):1041-1049. |
| Click to display the text | |
| [8] | TARANTOLA S, KOPUSTINSKAS V,BOLADO-LAVIN R,et al.Sensitivity analysis using contribution to sample variance plot:Application to a water hammer model[J].Reliability Engineering and System Safety,2012,99(2):62-73. |
| Click to display the text | |
| [9] | WEI P F, LU Z Z,RUAN W B,et al.Regional sensitivity analysis using revised mean and variance ratio functions[J].Reliability Engineering and System Safety,2014,121(1):121-135. |
| Click to display the text | |
| [10] | WEI P F, LU Z Z,SONG J W.A new variance-based global sensitivity analysis technique[J].Computer Physics Communications,2013,184(11):2540-2551. |
| Click to display the text | |
| [11] | SANSEVERINO C M R, RAMIREZ-MARQUEZ J E.Uncertainty propagation and sensitivity analysis in system reliability assessment via unscented transformation[J].Reliability Engineering and System Safety,2014,132:176-185. |
| Click to display the text | |
| [12] | MCNAMEE J, STENGER F.Construction of fully symmetric numerical integration formulas[J].Numerische Mathematik,1967,10(4):327-344. |
| Click to display the text | |
| [13] | ZHAI Q Q, YANG J,ZHAO Y.Space-partition method for the variance-based sensitivity analysis:Optimal partition scheme and comparative study[J].Reliability Engineering and System Safety,2014,131(6):66-82. |
| Click to display the text | |
| [14] | ARCHER G, SALTELLI A,SOBOL I M.Sensitivity measures ANOVA-like techniques and the use of bootstrap[J].Journal of Statistical Computation and Simulation,1997,58(2):99-120. |
| Click to display the text | |
| [15] | NOWAK A S, COLLINS K R.Reliability of structures[M].New York:McGraw-Hill,2000:359. |



