2. 中国航天科技集团公司, 北京 100048
2. China Aerospace Science and Technology Corporation, Beijing 100048, China
升力式再入飞行器通常具有飞行状态跨度大、飞行环境恶劣及动力学特性复杂等特点[1],为适应不同飞行环境,通常配备了反作用力控制系统(RCS)和多种气动舵面,如体襟翼、副翼、升降舵、V形垂尾等。以HTV-2为代表的升力式再入飞行器,出于任务要求只配置了左右体襟翼和RCS,主要依靠体襟翼完成姿态控制(考虑到经济性和有效性,RCS一般作为辅助实现控制)。左右体襟翼只能通过同向偏转、差动偏转实现等效于升降舵和副翼的控制,直接作用到俯仰通道和滚转通道,无法实现对偏航通道的直接控制。一般来说再入姿态控制选取攻角和倾侧角作为跟踪指令[2],以倾侧角为输出、副翼为输入时横侧向通道将存在内动态,通常引入零动态来考察内动态的稳定性[3]。对飞行器而言,其动力学特性决定了在飞行包线内系统极易出现零动态不稳定的情况,此时系统表现为非最小相位特性。而对于非最小相位系统,若不处理不稳定零动态,用传统的控制方法实现跟踪控制将需要无限大的控制能力[4],这给控制器的设计提出了很大的挑战。
为解决非最小相位系统的控制问题,均需要考虑如何处理不稳定零动态。文献[5]综述了目前非线性非最小相位系统的研究成果,并对其镇定、轨迹跟踪及路径跟踪等控制方法进行了分析比较。国内外对非最小相位系统轨迹跟踪的研究主要可分为近似线性化、输出重定义、动态滑模控制、MIMO系统分解方法和最小范数控制策略等。Benvenuti等[6]通过去除线性化后原系统右半平面的一个零点,来局部重新定义一个输出,使得新的系统是最小相位。这种方法处理弱非最小相位系统结果尚可,却无法解决强非最小相位系统问题。Martin等[7]为解决强非最小相位系统问题,提出了输出重定义方法。通过选择合适的输出,可以使响应的系统不含零动态或内动态,进而实现全状态反馈线性化,但由于无法总结出系统的方法选择合适的输出,故实施起来需要不断尝试。文献[8, 9]基于动态滑模方法研究了非最小相位系统的输出跟踪,这种方法结合了传统滑模控制和动态补偿的优点,性能比静态反馈更强,但对被控对象的形式需要做出较强的假设,而且控制律非连续,可能引起输出抖振。文献[10]利用坐标变换把非最小相位系统的输出跟踪问题转变成跟踪误差的镇定问题,再运用系统分解方法把原系统分为最小相位子系统和非最小相位子系统分别设计镇定控制器,可以极大降低设计控制律的难度。文献[11]应用最小范数控制策略设计了由线性静态反馈项、切换项和非线性辅助输入项组成的跟踪控制器,确保输出跟踪误差与内动态具有鲁棒镇定特性。此外,神经网络控制[12]、模糊滑模控制[13]以及迭代学习控制方法[14]均被用来实现非最小相位系统的跟踪控制。
考虑到系统分解的思路与升力式再入飞行器三通道耦合控制问题的相似性,引入系统分解可降低待求解问题的维数。而动态逆和状态反馈技术成熟,可以很方便地实现线性化系统的控制。同时运用最小范数控制策略可以辅助解决整个闭环系统的镇定问题,本文综合上述各项技术,针对升力式再入飞行器模型,提出了一种仅利用体襟翼完成三通道控制的姿态控制方法。首先选定合适的局部微分同胚将原系统转换为正则形式,并对得到的内动态进行稳定性分析,提出系统非最小相位特性的判据。运用此判据可判定在副翼反效的飞行状态下该系统为非最小相位系统。针对这一问题,依据与内动态是否线性相关把系统的外部动态分为两部分,其中线性相关的外部动态和内动态组合在一起形成新的非最小相位子系统,剩余与内动态线性无关的部分为最小相位子系统。运用动态逆控制技术对这2个子系统分别设计镇定控制器,并基于Lyapunov方程和最小范数控制策略在非最小相位子系统中引入一个非线性辅助控制输入来镇定整个姿控回路。仿真结果表明,该控制器在仅用体襟翼实现三通道姿态控制的情况下对跟踪控制指令具有良好的跟踪效果并能够镇定内动态。
1 问题描述 1.1 姿态输入-输出模型正则形式升力式再入飞行器姿态运动方程组[2]为
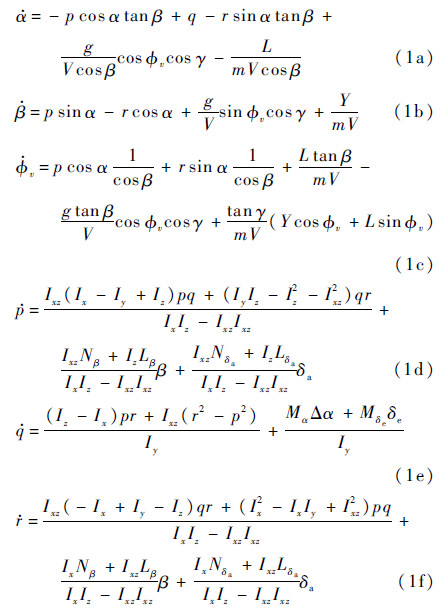
用Δα=α-αT、Δδe=δe-δeT表示实测攻角与配平攻角、实测升降舵偏角与配平升降舵的偏差。由于在姿态控制研究的过程中,从轨迹上所选的工作点均为配平状态下的工作点,这样就有
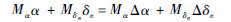
为方便控制器的推导,这里定义
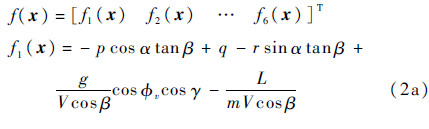
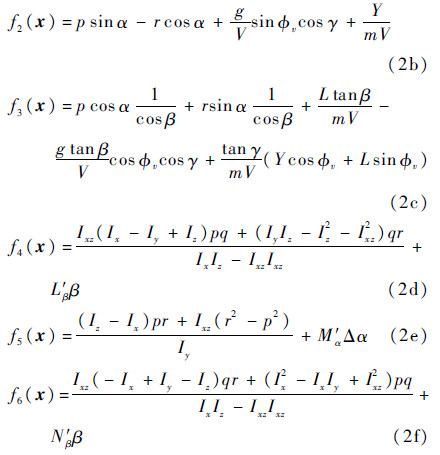
输入矩阵可写成
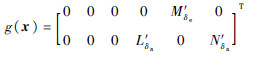
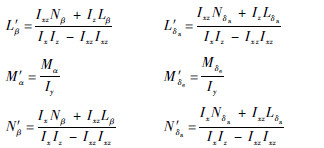
通常制导系统将攻角和倾侧角作为指令信号传给控制系统,选定系统输出为
将式(3)和式(4)组成一个姿态输入-输出模型:
从式(1)、式(4)中不难看出向量的相对阶为[2 2],系统的相对阶为r=4,小于状态量个数,说明系统存在内动态。此时存在一个局部微分同胚:Φ(x):x→(ξ,η),将式(5)转化为正则形式[16],转化后的正则形式可表示为
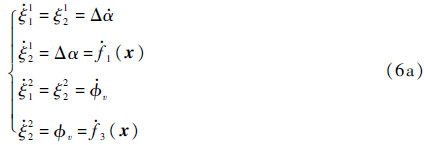
为验证该正则模型为非最小相位系统,引入零动态来考察该系统的内动态稳定性
假定α=α0,γ≈0,q≈0,将式(8)代入式(6a)和式(6b)中,可得
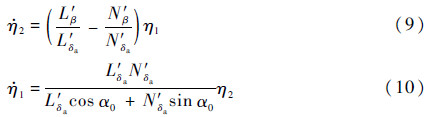
对式(9)求一阶导并将式(10)代入,有
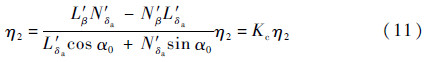
当系数Kc≤0时,式(11)对应二阶系统有2个零根或一对纯虚根,处于临界稳定的状态;当Kc>0时,式(11)对应二阶系统有一个正根一个负根,说明此时内动态η2不稳定,系统为非最小相位系统。可以得出如下判据。
判据 当飞行器的工作状态满足
注意到
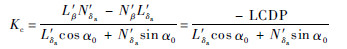
通常来说式(12)中分母为正,Kc的正负主要取决于横向操纵偏航发散参数(LCDP)[17]的极性。对于Kc>0,有LCDP <0,飞行器副翼反效,主要表现为当试图获得向左(或右)的滚转机动时飞行器开始缓慢向正确的方向滚转,然后转而向反方向快速滚转。这与经典单输入单输出非最小相位系统中的“负调”现象类似。这种情况如不能及时发现,无论是驾驶员还是自动驾驶仪均无法做出正确的机动。对应第3节中仿真结果,内动态无控的控制器即是只针对输出状态进行反馈线性化完成状态反馈后设计的控制器,可以看出开始该控制器能够对指令有正确的响应,随着副翼进一步响应,由于此时工作在内动态不稳定的状态(对应LCDP为负),倾侧角向反方向发散,侧滑开始振荡,最终引起攻角的振荡,飞行器失控。此判据可预判飞行器的非最小相位特性,与LCDP有判断副翼反效有着相似的作用。与LCDP不同的是,判据从系统的内动态稳定性角度出发判定了是否为非最小相位系统,是非线性控制理论体系下的结论,而LCDP是基于飞行器横侧向线性化模型从飞行力学角度出发推得,二者有异曲同工之妙。
2 姿态输出跟踪控制器1.2节中已根据式(12)的判据判定了系统式(6)为非最小相位系统,本节针对该系统设计姿态输出跟踪控制器。首先运用系统分解方法将原系统分解为最小相位子系统和非最小相位子系统,然后基于动态逆技术分别对2个子系统设计状态反馈控制器,最后依据最小范数控制策略在非最小相位子系统的控制器中增加非线性辅助控制项用来镇定整个姿控回路。
2.1 系统分解对最小相位系统来说运用传统的状态反馈控制器即可很好地实现跟踪控制,而对高阶非最小相位系统来说,由于内动态的不可观测,用状态反馈控制需要完成很复杂的调参工作[3]。系统分解的好处就在于能够将原系统拆分为最小相位和非最小相位子系统,针对子系统分别设计控制器使内动态局部稳定。这可以降低非最小相位系统的阶数,把原问题变成一个更容易求解的非最小相位问题。
通常系统分解采取如下分解步骤[5]:基于正则形式,①把外部动态分为和内动态线性相关、线性无关的两部分,把内动态和与之线性相关的外部动态组合成一个新的子系统,为非最小相位子系统,另一部分为最小相位子系统;②分别设计镇定控制器,确保子系统的稳定性。
对式(7)进行处理,将其线性部分从非线性形式中分离出，即
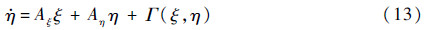
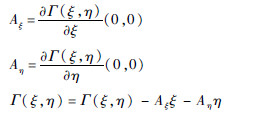
这样可以将式(13)具体写为
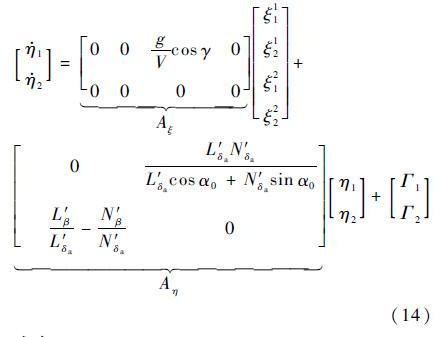
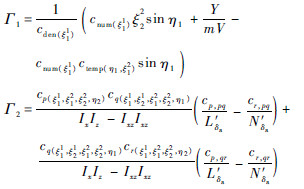
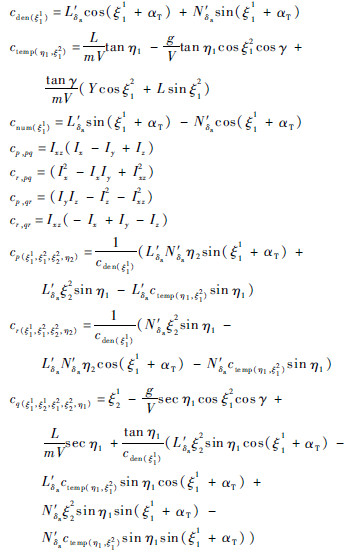
从式(14)中Aξ可看到,内动态与ξ11、ξ21线性无关,与ξ12、ξ22线性相关。据此将正则形式(6)拆分为最小相位子系统式(15a)和非最小相位子系统式(15b):
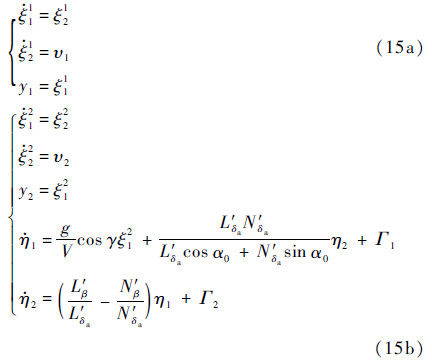
针对2个子系统式(15a)、式(15b)的伪控制量分别设计状态反馈控制器实现对指令的跟踪控制,然后利用动态逆控制技术即可建立起伪控制量和控制量之间的关系。下面分别求取2个子系统伪控制量的状态反馈控制律。
2.2.1 纵向通道控制器(最小相位子系统)将最小相位子系统式(15a)写成矩阵形式：
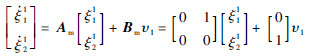
选取增益矩阵Km=[k1 k2],设计纵向通道控制器为
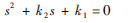
对于非最小相位子系统式(15b),选取变量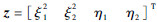 
,将其写成矩阵形式[18]:
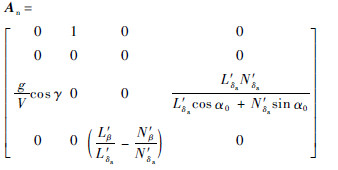
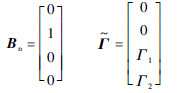
为消去式(17)中的非线性项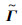 
从而实现对z的线性反馈、镇定内动态,令υ2=υn-Knz,选取合适的增益矩阵Kn使得 
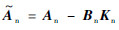为Hurwitz矩阵。此时式(17)变为
对任意给定的对称正定矩阵Q,存在P使得Lyapunov方程成立
对式(18)选取Lyapunov函数
对式(20)求一阶导并将式(19)代入,有
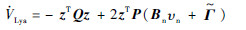
选取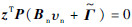 
,则有
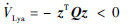
子系统式(15b)镇定。
考虑到 
中υn解不唯一,基于最小范数控制策略,有
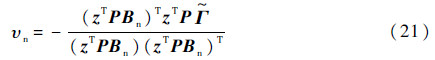
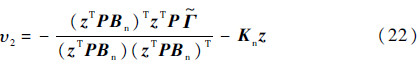
对原系统式(1a)、式(1c)两边求导得
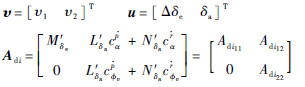
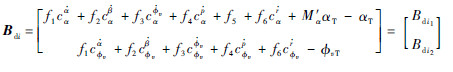
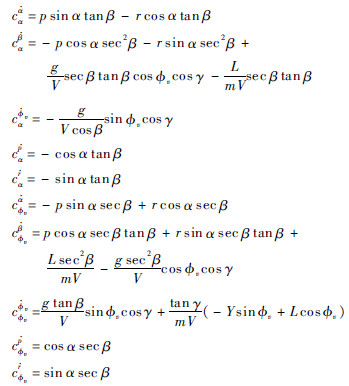
将式(16)、式(22)代入式(23)中,可得原系统的姿态输出跟踪控制器:
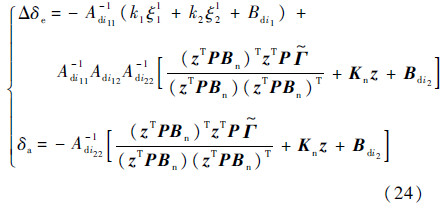
从控制器的设计过程可知,该控制方法并未对原系统进行三通道解耦,只是根据正则形式中状态量之间的线性相关度对原系统进行了分解,对分解后的最小相位子系统和非最小相位子系统分别进行反馈控制。同时充分考虑内动态的非线性,基于Lyapunov方程和最小范数控制策略,增加了非线性辅助控制输入项式(21)来镇定姿态控制回路,这与高超声速飞行器再入过程中强耦合、非线性的特点是吻合的。最终得到的姿态输出跟踪控制器通过调节Km、Kn,将各偏差量反馈到升降舵和副翼,实现对飞行器的姿态控制。
3 仿真结果
选择飞行器状态:速度为1341.7m/s,高度为34.07km时进行仿真验证该控制器,选定初始攻角α=8°,初始侧滑角β=0°,初始倾侧角Φv=0°,对阶跃指令进行跟踪,令攻角指令αc=18°,倾侧角指令Φvc=10°,保持零侧滑角βc=0°。经过检验,飞行器此时LCDP为-0.0145,符合判据式(12)中Kc>0的情况,说明此时系统为非最小相位系统。为进一步验证飞行器内动态的不稳定并与本文所设计的控制器做对比,选取式(15)中的4个状态量(不包括内动态),用w=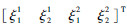 
表示。将式(15)中与w相关的公式用矩阵形式表示为
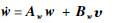
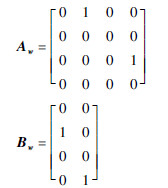
设计内动态无控的控制器为υ=-Kww,其中参数选取
此时极点为
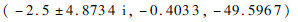
子系统式(15a)、式(15b)的极点为
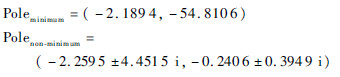
将内动态无控的控制器与本文所设计的姿态输出跟踪控制器做对比,如图 1~图 4所示。
 |
| 图 1 攻角、侧滑角和倾侧角响应曲线 Fig. 1 Response curves of angle of attack (AOA), sideslip angle and bank angle |
 |
| 图 2 升降舵、副翼偏转角 Fig. 2 Deflection angles of elevator and aileron |
 |
| 图 3 姿态角速率响应曲线 Fig. 3 Response curves of attitude angle rates |
 |
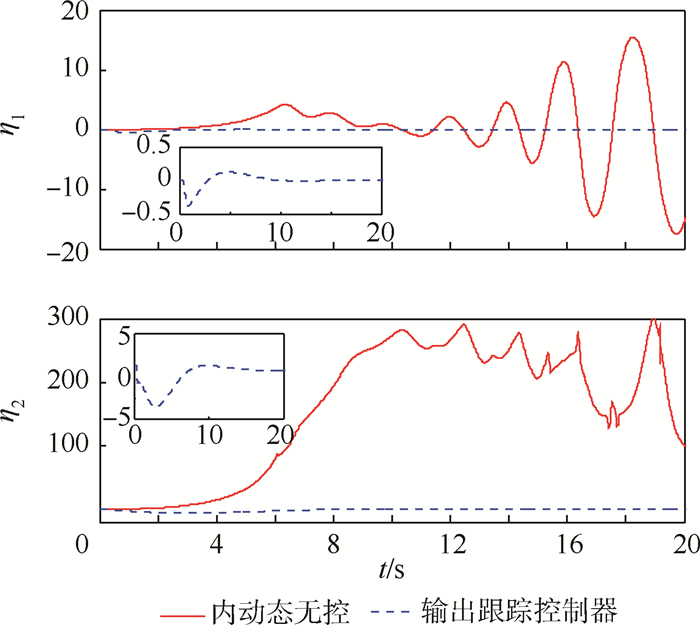| 图 4 内动态响应曲线 Fig. 4 Response curves of internal dynamics |
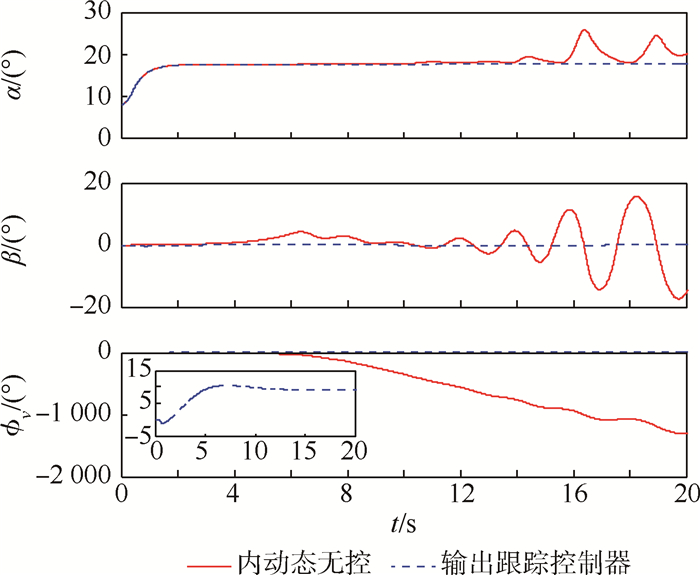
图 1为攻角、侧滑角和倾侧角的跟踪曲线。可以看出在当前控制器参数下,本文提出的控制器可以实现攻角、倾侧角指令的跟踪,同时镇定侧滑角,且从图 1中可看出倾侧角开始有“负调”现象;而对内动态不加控制的极点配置方法,开始攻角指令响应良好,在5s时由于侧滑角(内动态η1)不稳定,首先引起了倾侧角的负向持续增大,然后随着侧滑角进一步振荡发散,在15s前后由于运动耦合诱发了攻角的振荡,最终攻角发散。
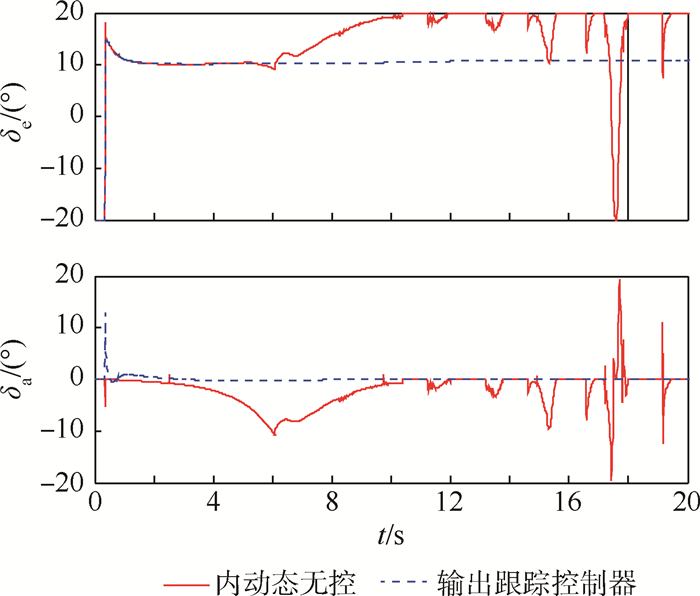
图 2为升降舵、副翼随时间变化的曲线。在经过3s之后用姿态输出跟踪控制器升降舵已稳定,副翼为0°;而对内动态无控的控制来说,在5s之后升降舵突然发生变化,直到15s之后和副翼交替突变,飞行器失控。
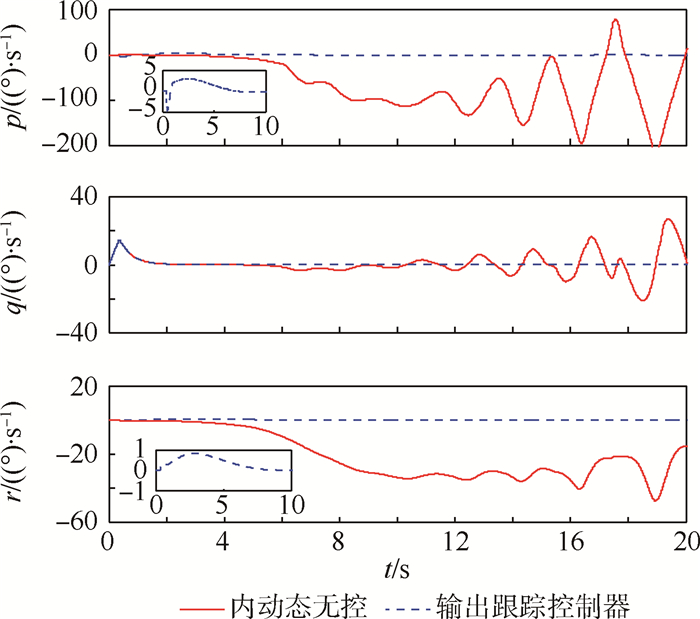
图 3表示飞行器三通道角速率p、q、r随时间的变化。对于姿态输出跟踪控制器来说,滚转角速率p和偏航角速率r均在10s内稳定,俯仰角速率q更是在3s内稳定;而对内动态无控的控制来说,5s之内q基本稳定,而p和r均出现了较大的数值,对应内动态η2开始发散。5s之后p、q、r均开始振荡,由于惯性耦合,起初振荡只表现在偏航通道的侧滑角上,侧滑角的进一步振荡诱发了运动耦合,攻角随即振荡发散。
图 4为飞行器2个内动态η1、η2随时间的变化。其中可明显看出,在内动态无控的情况下η1和η2均已发散,而本文设计的控制器很好地获得了稳定的内动态。其中η2开始表现为负值,这与图 3中p和r在仿真初期的正负是相关的。
为验证该控制器的鲁棒性,另选一组飞行状态:速度为4170m/s,高度为50km。选定初始攻角α=8°,初始侧滑角β=0°,初始倾侧角Φv=0°,同样对阶跃指令进行跟踪,令攻角指令αc=18°,倾侧角指令Φvc=50°,保持零侧滑角βc=0°,飞行器此时LCDP为-0.1255。表 1中给出了再入飞行器蒙特卡罗仿真所用的不确定性参数模型。无气动扰动时与蒙特卡罗100组的仿真结果对比如图 5~图 8所示,其中红色曲线表示无扰动时的仿真结果,蓝色曲线表示100组气动、大气密度扰动情况下的蒙特卡罗仿真结果。
| 不确定性种类 | 分布类型 | 误差大小(3σ)/% |
| 气动力系数 | 正态分布 | 30 |
| 气动力矩系数 | 正态分布 | 50 |
| 大气密度 | 正态分布 | 30 |
 |
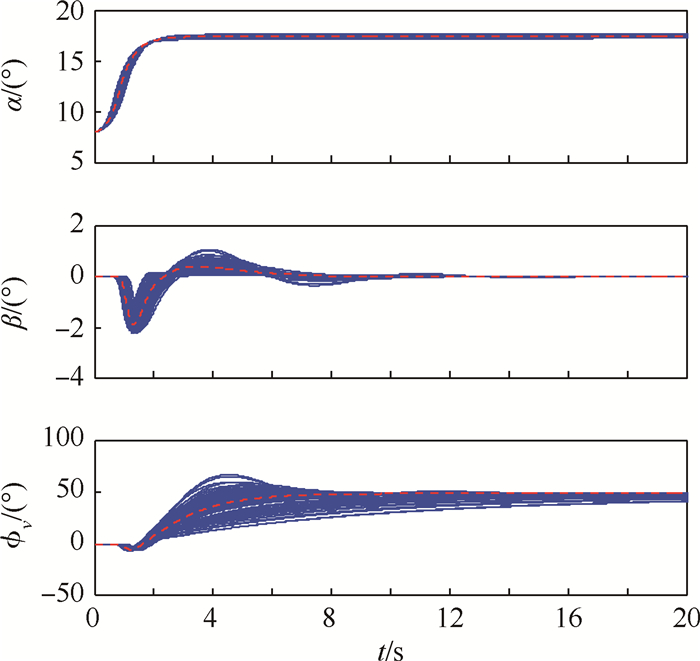| 图 5 气动扰动情况下攻角、侧滑角和倾侧角响应曲线 Fig. 5 Response curves of AOA, sideslip angle and bank angle with aerodynamic disturbances |
 |
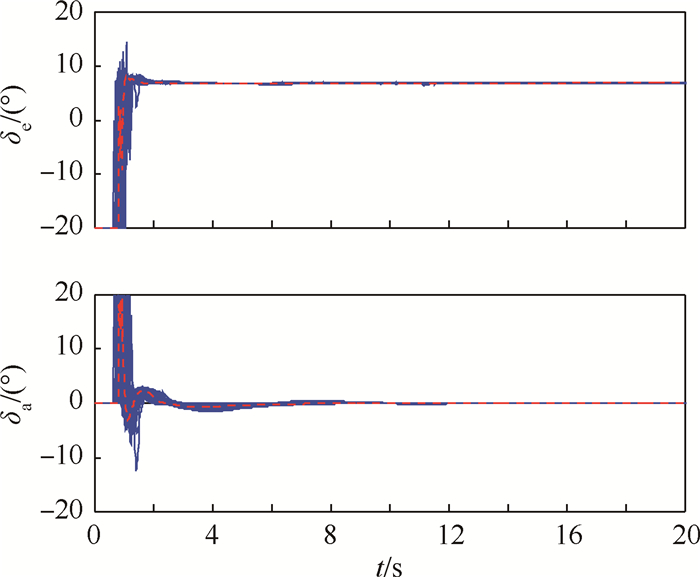| 图 6 气动扰动情况下升降舵、副翼偏转角 Fig. 6 Deflection angles of elevator and aileron with aerodynamic disturbances |
 |
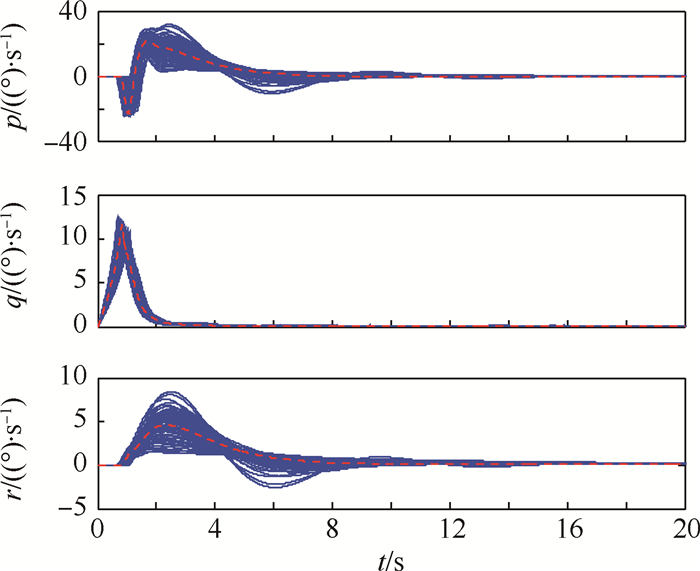| 图 7 气动扰动情况下姿态角速率响应曲线 Fig. 7 Response curves of attitude angle rates with aerodynamic disturbances |
 |
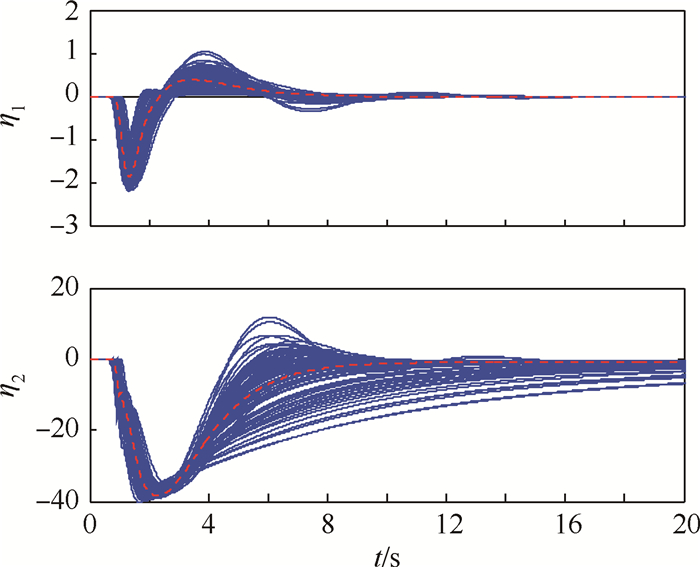| 图 8 气动扰动情况下内动态响应曲线 Fig. 8 Response curves of internal dynamics with aerodynamic disturbances |
选取攻角指令稳态跟踪误差αerror和倾侧角指令稳态跟踪误差Φv-error作为蒙特卡罗仿真评估标准,依据工程经验选取αerror≤0.5°和Φv-error≤2°作为干扰情况下可以接受的指令跟踪结果。通过分析仿真结果可以发现,100组中共有87组在上述选定范围内,可以说明该控制方法在所选扰动情况下具有较强的鲁棒性。
从蒙特卡罗仿真结果可以看出,飞行器在该控制器作用下,在马赫数为12左右时可以实现指令跟踪,对大的倾侧角指令(50°)同样能够很好地跟踪且不失快速性,同时在气动参数和大气密度受扰的情况下该控制方法具有较强的鲁棒性。此外通过仿真发现,υn的量级较小,相较式(22)中的Knz来说是小量,说明该控制器的鲁棒性主要由Knz实现。
4 结 论本文针对升力式再入飞行器提出了一个判定非线性系统为非最小相位系统的判据,并针对非最小相位系统的姿态控制问题,给出了一种仅用体襟翼控制三通道的姿态输出跟踪控制方法。
1) 本文提出的系统非最小相位特性判据判定了副翼反效与非最小相位特性之间的关联性:若飞行器副翼反效,则当前系统为非最小相位系统。
2) 通过与内动态无控的控制器对比,该控制方法能够镇定非线性系统的内动态,并对控制指令起到了预期的跟踪效果。
3) 该方法降低了非最小相位特性模型的复杂度,同时引入了非线性辅助控制输入项进一步镇定了整个姿态控制回路,蒙特卡罗仿真验证了该控制方法具有一定的鲁棒性。
| [1] | 包为民. 航天飞行器控制技术研究现状与发展趋势[J].自动化学报,2013,39(6):697-702. BAO W M.Present situation and development tendency of aerospace control techniques[J].Acta Automatica Sinica,2013,39(6):697-702(in Chinese). |
| Cited By in Cnki (22) | Click to display the text | |
| [2] | 李惠峰. 高超声速飞行器制导与控制技术[M].北京:中国宇航出版社,2012:518-536. LI H F.Hypersonic aircraft guidance and control technology[M].Beijing:China Astronautic Publishing House,2012:518-536(in Chinese). |
| [3] | ISIDORI A. Nonlinear control systems[M].Beijing:Publish House of Electronics Industry,2006:127-135. |
| [4] | SLOTINE J E. Applied nonlinear control[M].Beijing:China Machine Press,2006:144-152. |
| [5] | 苏善伟,朱波, 向锦武,等.非线性非最小相位系统的控制研究综述[J].自动化学报,2015,41(1):9-21. SU S W,ZHU B,XIANG J W,et al.A survey on the control of nonlinear non-minimum phase systems[J].Acta Automatica Sinica,2015,41(1):9-21(in Chinese). |
| Cited By in Cnki | Click to display the text | |
| [6] | BENVENUTI L, DI BENEDETTO M D,GRIZZLE J W.Approximate output tracking for nonlinear non-minimum phase systems with an application to flight control[J].International Journal of Robust and Nonlinear Control,1994,4(3):397-414. |
| Click to display the text | |
| [7] | MARTIN P, DEVASIA S,PADEN B.A different look at output tracking:Control of a VTOL aircraft[J].Automatica,1996,32(1):101-107. |
| Click to display the text | |
| [8] | SIRA-RAMIREZ H. A dynamical variable structure control strategy in asymptotic output tracking problems[J].IEEE Transactions on Automatic Control,1993,38(4):615-620. |
| Click to display the text | |
| [9] | SHTESSEL Y B. Nonlinear output tracking in conventional and dynamic sliding manifolds[J].IEEE Transactions on Automatic Control,1997,42(9):1282-1286. |
| Click to display the text | |
| [10] | AL-HIDDABI S A, MCCLAMROCH N H.Tracking and maneuver regulation control for nonlinear nonminimum phase systems:Application to flight control[J].IEEE Transactions on Control Systems Technology,2002,10(6):780-792. |
| Click to display the text | |
| [11] | ZHU B, WANG X H,CAI K Y.Approximate trajectory tracking of input-disturbed PVTOL aircraft with delayed attitude measurements[J].International Journal of Robust and Nonlinear Control,2010,20(14):1610-1621. |
| Click to display the text | |
| [12] | TALEBI H A, PATEL R V,KHORASANI K.A neural network controller for a class of nonlinear non-minimum phase systems with application to a flexible-link manipulator[J].Journal of Dynamic Systems,Measurement,and Control,2005,127(2):289-294. |
| Click to display the text | |
| [13] | BABAEI A R, MORTAZAVI M,MORADI M H.Fuzzy sliding mode autopilot design for nonminimum phase and nonlinear UAV[J].Journal of Intelligent & Fuzzy Systems,2013,24(3):499-509. |
| Click to display the text | |
| [14] | 刘山,吴铁军. 基于稳定逆的非最小相位系统的迭代学习控制[J].控制理论与应用,2003,20(6):831-837. LIU S,WU T J.Stable-inversion based iterative learning control for non-minimum phase plants[J].Control Theory and Applications,2003,20(6):831-837(in Chinese). |
| Cited By in Cnki (13) | Click to display the text | |
| [15] | 史丽楠,张冉, 李昭莹,等.基于输出重定义的再入飞行器动态逆姿态控制[J].北京航空航天大学学报,2014,40(9):1291-1298. SHI L N,ZHANG R,LI Z Y,et al.Inverse dynamic attitude control for re-entry vehicle based on output redefinition[J].Journal of Beijing University of Aeronautics and Astronautics,2014,40(9):1291-1298(in Chinese). |
| Cited By in Cnki (2) | Click to display the text | |
| [16] | WALLNER E M, WELL K H.Attitude control of a reentry vehicle with internal dynamics[J].Journal of Guidance,Control,and Dynamics,2003,26(6):846-854. |
| Click to display the text | |
| [17] | LUTZE F H, DURHAM W C,MASON W H.Unified development of lateral-directional departure criteria[J].Journal of Guidance,Control,and Dynamics,1996,19(2):489-493. |
| Click to display the text | |
| [18] | SU S W, LIN Y.Robust output tracking control for a velocity-sensorless vertical take-off and landing aircraft with input disturbances and unmatched uncertainties[J].International Journal of Robust and Nonlinear Control,2013,23(11):1198-1213. |
| Click to display the text | |
| [19] | HUANG C S, YUAN K.Output tracking of a nonlinear non-minimum phase PVTOL aircraft based on nonlinear state feedback control[J].International Journal of Control,2002,75(6):466-473. |
| Click to display the text |