2. 哈尔滨工业大学机器人技术与系统国家重点实验室, 哈尔滨 150080
2. State Key Laboratory of Robotics and System, Harbin Institute of Technology, Harbin 150080, China
移动机器人可代替人类在复杂危险的环境下从事各种工作,如深空探测、野外救援和反恐防暴等,其运动机构主要有轮式、腿式、履带式以及复合式。单一运动机构的移动机器人仅能适用于某些特定条件的外部地形环境;而复合式运动机构的移动机器人结合了多种运动机构的优点,具有更强的复杂地形适应性,能更好地适应外部环境[1]。例如轮行模式能够快速通过平整的地面,而步行模式则能灵活地通过崎岖不平的路面,轮腿式机器人集合了轮式的快速性和腿式的灵活性,因此受到广泛的研究。
六腿机器人容易实现静态稳定行走,且是一个冗余系统,当其1条腿或2条腿损坏时,仍可用剩余的腿来实现行走。六腿机器人的1条腿或2条腿可以作为通用的机械臂来使用,以完成复杂的操作任务。多于六腿结构的机器人更容易获得静态稳定性,但其结构和控制变得更为复杂,而且多于6条腿不会提高行走速度[2],因此六腿结构是一个较好的选择。典型的六腿机器人按照本体形状可以分为2种:矩形本体和六边形本体[3]。矩形本体六腿机器人的6条腿轴对称安装在机器人本体的两侧,每侧3条腿[4, 5];六边形本体六腿机器人的6条腿圆周对称布置在本体四周,本体为六边形或圆形[6, 7]。由于圆周对称分布的六腿机器人比矩形本体六腿机器人拥有更多的对称轴(或对称面),这种对称优势使圆周对称分布的六腿机器人可以拥有更多的前进方向,可实现零半径转弯,比矩形本体六腿机器人有更好的转向灵活性。因此,圆周对称分布结构优于矩形本体结构。
轮腿式机器人的轮腿机构组合方式是设计中需要考虑的主要问题。现有的轮腿组合方式主要有3种:①轮、腿独立式;②轮、腿结合式;③轮即是腿/腿即是轮式。轮、腿独立式机器人的轮子和腿相对独立,分别独立安装在机器人的本体上,当腿折叠收起时,轮子与地面接触,机器人可轮式运动;当腿伸展站立时,轮子与地面脱离,机器人可腿式步行。日本东北大学的Chariot[8]机器人是轮、腿独立式机器人的典型代表,这类机器人结构和控制相对简单,但其运动灵活性和地形适应性较差。轮、腿结合式机器人的轮安装在机器人的腿上。现有这类机器人将轮子直接安装在腿的末端,轮子锁定可直接当作机器人的足,如芬兰赫尔辛基大学的Workpartner[9]机器人、美国JPL实验室的ATHLETE[10]机器人、中国哈尔滨工业大学的HITAN[11]机器人和北京航空航天大学的轮腿式变结构机器人[12]等。这类机器人可通过改变自身构型以调整运动模式,具有很好的灵活性,但在步行行走时,轮子的某一局部长时间与地面接触摩擦,造成轮子不规则的磨损,会使轮子变得不是一个完整的圆形,对轮行方式造成不利影响。这种安装方式可以设计相应的步行足,使足、轮分开,但需要增加额外的驱动,主动改变腿的构态:轮行时,轮子与地面接触;步行时,足与地面接触。额外驱动使机器人结构和控制变得复杂。轮即是腿/腿即是轮式机器人拥有特殊结构的“轮/腿”,当其伸展开来时,是普通腿分支,当其折叠时变成环形结构,成为轮子,特殊的“轮/腿”结构使加工制造变得相对困难,且地形适应性有限。这类机器人代表有美国盐湖城Jacobsen等[13]发明的一种可重构的特殊结构轮腿装置、日本东北大学Rohmer等[14]开发的LEON机器人等。
针对现有轮腿式机器人轮腿机构组合方式中存在的问题,本文设计了一种新型轮、腿结合式的圆周对称式六轮腿式机器人NOROS,在不引入新关节(或驱动)的情况下,通过改变机器人的构态,就能实现腿式运动模式与轮行运动模式的切换。本文详细介绍了机器人结构、运动模式、运动模式切换规划,并进行了试验研究。
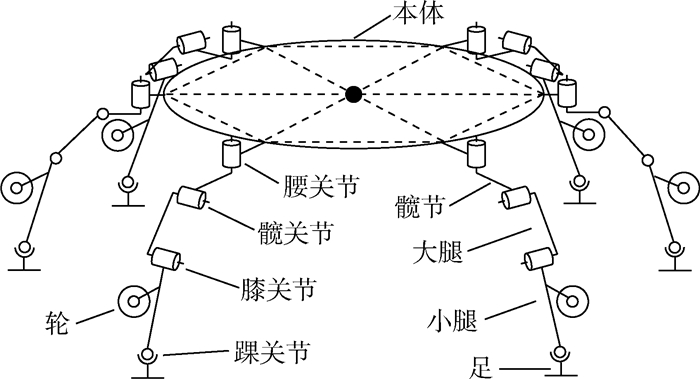
1 NOROS机器人结构设计 1.1 方案设计NOROS机器人选用六分支结构,采用圆周对称的布置方式,每条腿有3个主动关节(自由度):腰关节、髋关节和膝关节。由于自然界中拥有六腿结构的动物主要是昆虫,因此机器人的腿关节布置仿照昆虫结构进行设计:腰关节和髋关节轴线相互垂直,膝关节轴线和髋关节轴线互相平行。机器人足与小腿的连接为一个球铰结构,足在与支撑面的接触过程中被动地适应支撑面。轮子安装在机器人的小腿上,当机器人站立步行时,轮子不会与地面接触,当机器人小腿折叠时,轮子与地面接触,便可以实现轮行。图 1所示为NOROS机器人的机构设计简图。
|
| 图 1机器人机构设计简图 Fig. 1 Robot mechanism design sketch |
NOROS机器人整机共有18个主动关节,每个主动关节处采用舵机作为驱动,轮子采用直流电机驱动。图 2所示为NOROS机器人的三维虚拟样机结构和实体样机。机器人本体是一个半球结构,底盘为上下两层结构,与腰关节旋转轴安装在一起,半球形的外壳罩在本体底盘上。锂电池安装在机器人的双层结构的本体内,机器人的控制系统等电子硬件安装在半球壳内部的底盘上部,采用这种设计,机器人关键电子部件都安装在半球壳内部,受到很好的保护。6条结构相同的轮腿均布安装在机器人两层结构的底盘上,因此整体结构存在6个对称面。

|
| 图 2 机器人实体样机 Fig. 2 Robot physical prototype |
多腿机器人的运动是通过各条腿的协调运动来实现的。机器人步态是指机器人的每条腿按一定顺序和轨迹运动的过程,分为规则步态(周期步态)和非规则步态(自由步态)2种。规则步态指机器人的腿按固定的顺序和轨迹进行运动的过程,这种步态决定了机器人只可以在较平整的路面上步行。非规则步态指机器人腿的运动顺序和足端运动轨迹是非固定的,机器人能够根据步行环境的变化改变腿的摆动次序及足的运动轨迹,所以理想的非规则步态也可以称为自适应步态或智能步态。在复杂地形条件下,机器人必须采用非规则步态行进,较具有代表性的有:①基于局部规则。如德国Cruse等[15, 16]通过对竹节虫的研究,提出了作用在腿间的6条基本规则;文献[17]同样基于竹节虫生物试验得到的一组规则,提出了一种适用于六腿机器人稳定步行的分布式控制策略。基于局部规则的方法只根据腿间的简单规则以及机器人与环境的简单交互即能实现对机器人步态的规划,简单可行且具有一定的柔性和鲁棒性。②基于中枢模式发生器(Central Patten Generation,CPG)理论。利用 CPG 方法能够在不利用传感器的情况下生成节律式步态,模拟生物低级神经中枢使机器人自发地生成有一定规律的步态来控制机器人行走。CPG 方法在控制机器人快速行走的情况下比较有优势,但当涉及到步行落足点等细节时,其就不如局部规则。
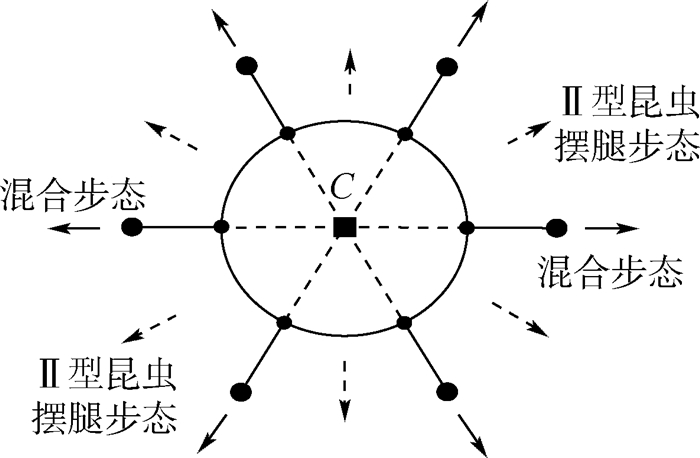
2.1 典型三角步态这里讨论机器人的规则步态,由于NOROS机器人采用圆周对称的结构,因此其6条腿的布置可以有多种方式。王志英等在文献[6]中提出了3种典型的“3+3”周期步态:昆虫摆腿步态、哺乳动物踢腿步态和混合步态。事实上,还有1种不同于这3种步态的昆虫摆腿步态。将王志英提出的昆虫摆腿步态命名为Ⅰ型昆虫摆腿步态,另1种昆虫摆腿步态命名为Ⅱ型昆虫摆腿步态。上述4种典型“3+3”三角步态根据初始站立姿态(或支撑三角形)可分为2类:①Ⅰ型昆虫摆腿步态和哺乳动物踢腿步态。在初始站立姿态下,6条腿分为2组分别平行地布置在机器人本体的两侧,如图 3所示。从图 3中可以看出,Ⅰ型昆虫摆腿步态的前进方向与哺乳动物踢腿步态的前进方向垂直,且每种步态可以沿同一直线的2个方向行进。②Ⅱ型昆虫摆腿步态和混合步态。在初始站立姿态下,6条腿均匀布置在机器人本体的四周,如图 4所示。从图 4中可以看出,混合步态的行进方向可沿任意1条腿的指向方向,而Ⅱ型昆虫摆腿步态的行进方向可以沿任意相邻2条腿角平分线的方向,因此Ⅱ型昆虫摆腿步态的行进方向与混合步态行进方向呈30°角,且每种步态可以沿6个方向前进。

|
| 图 3腿平行布置姿态 Fig. 3 Leg parallel arrangement |
|
| 图 4 腿分散布置姿态 Fig. 4 Leg disperse arrangement |
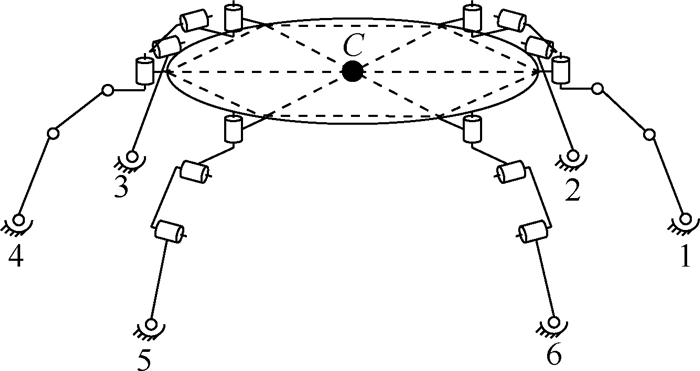
机器人在地面步行行走过程中,假设足与地面接触无相对滑动,机器人六腿支撑等效机构简图如图 5所示。
|
| 图 5 机器人六腿支撑等效机构 Fig. 5 Robot six legs support equivalent mechanism |
机器人在直线行走过程中,保持自身本体姿态不变,则机器人的腰关节轴线始终与地面垂直。
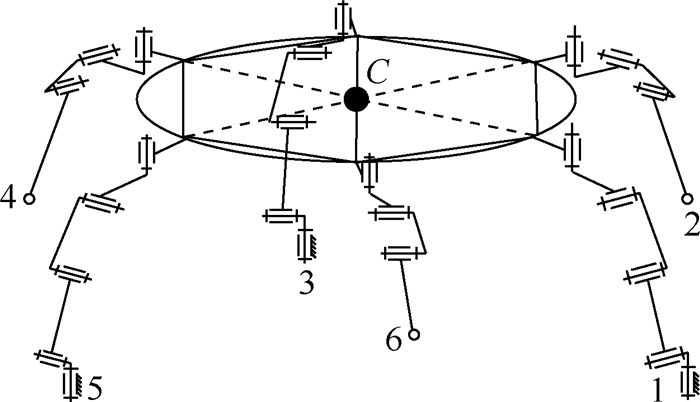
在Ⅰ型和Ⅱ型昆虫摆腿步态直线行走过程中,踝关节的运动相当于2个相互垂直的铰链运动,2种昆虫步态行走过程中的机构简图类似,仅腿的布置位置有所差异。因此在昆虫步态行走过程中,1、3和5腿支撑,2、4和6腿抬起时的等效机构简图如图 6所示。
|
| 图 6 昆虫摆腿步态等效机构 Fig. 6 Insect swing leg gait equivalent mechanism |
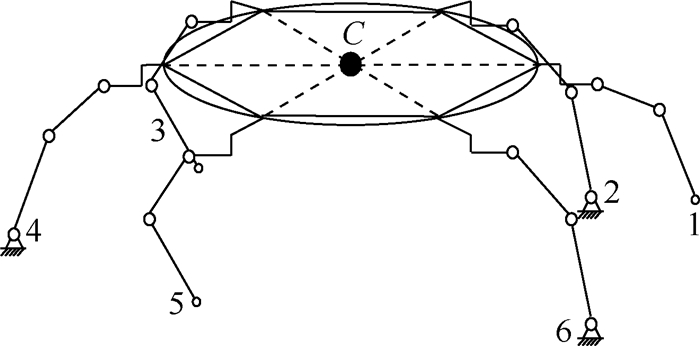
在哺乳动物踢腿步态直线行走过程中,腿无左右摆动,所以腰关节相当于锁紧,支撑腿踝关节的运动相当于一个旋转铰链运动。1、3和5腿抬起,2、4和6腿支撑时的等效机构简图如图 7所示。
|
| 图 7 哺乳动物踢腿步态等效机构 Fig. 7 Mammal kick leg gait equivalent mechanism |
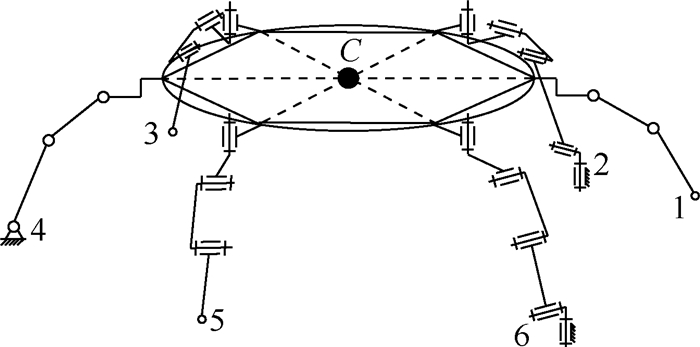
在混合步态直线行走过程中,等效机构如图 8所示。从图 8中可以看出,混合步态等效机构的1条支撑腿支链和哺乳动物踢腿步态的支撑腿机构相同,其余2条支撑腿支链和昆虫摆腿步态的支撑腿机构相同,混合步态综合了昆虫摆腿步态和哺乳动物踢腿步态的特点。
|
| 图 8 混合步态等效机构 Fig. 8Mix gait equivalent mechanism |
从稳定性角度来说[6],上面所指的混合步态最好;虽然从纵向稳定性角度来说踢腿步态最好,但由于运动学限制而无法实现。昆虫的摆腿步态消耗的能量最小[6],且可以在不改变身高的情况下跨越高于自身高度的障碍物,其直线行走控制简单,适当调整初始位姿条件,可行步态和稳定性都可得到较大提高。哺乳动物的踢腿步态由于所需道路宽度较其他2种小,因此可穿过较窄的道路。但混合步态的转弯性能和稳定性最好,其他性能则处于中间。因此,混合步态综合性能最好。在实际应用中,可根据具体情况选择最优步态。
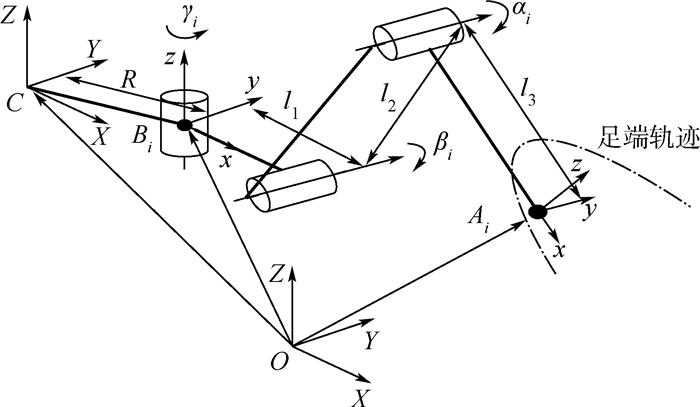
六腿机器人的行走主要根据机器人的运动学进行规划控制,首先分析抬起腿的正向运动学。图 9所示为抬起腿的机构简图。为求解机器人抬起腿的正向运动学,首先建立4个坐标系:全局坐标系{O}、本体坐标系{C}、腰关节坐标系{Bi}以及足端坐标系{Ai}。全局坐标系{O}是建立在机器人所处的环境中;本体坐标系{C}是建立在机器人的本体底盘上,其原点与机器人本体结构的几何中心重合;腰关节坐标系{Bi}的z轴与腰关节旋转轴线重合,并固结在本体的底盘上;足端坐标系{Ai}的原点与足重合,x轴沿着小腿的方向,取机器人腿完全展开时的位形为初始位形。坐标系参数如图 9所示。
|
| 图 9 抬起腿机构简图 Fig. 9 Lifting leg mechanism sketch |
由于本体坐标系和腰关节坐标系都固结在机器人本体上,因此从坐标系{C}到坐标系{Bi}的变换矩阵也固定不变,可描述为

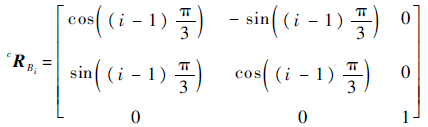
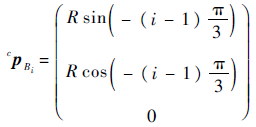
初始位形下,从坐标系{Bi}到坐标系{Ai}的变换矩阵为
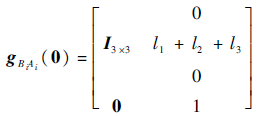
运动旋量 ξ ij 描述的是第i条腿的第j个关节的旋转运动,每个旋转关节的运动旋量可以表述为

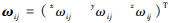 为旋转轴线的方向;
为旋转轴线的方向; 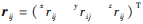 为旋转轴线上任意一点的向量。
为旋转轴线上任意一点的向量。
因此,抬起腿的正向运动学可以用指数积公式表示为
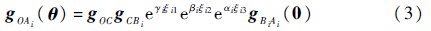
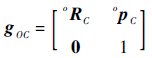
机器人的尺寸及关节旋转角度限制见表 1。
| R/mm | l1/mm | l2/mm | l3/mm | α/(°) | β/(°) | γ/(°) |
| 150 | 50 | 120 | 130 | (-40,160) | (-80,100) | (-65,65) |
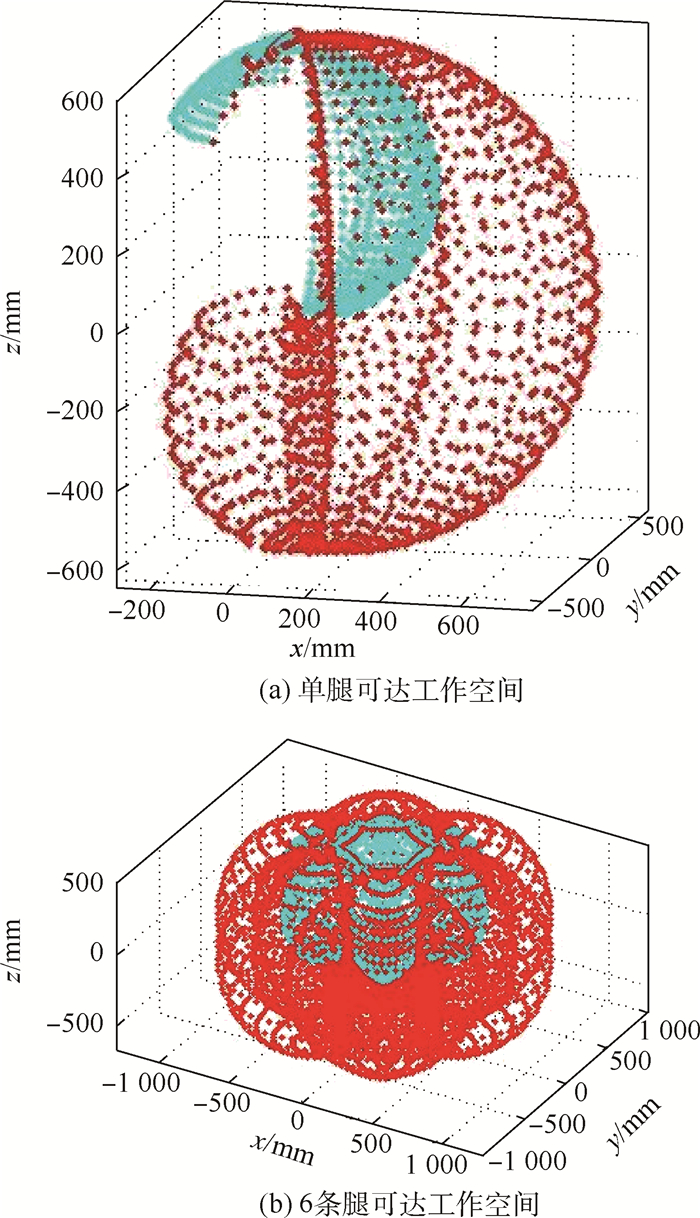
根据前述抬起腿的正运动学和机器人的主要参数,经仿真得到机器人单腿可达工作空间和6条腿的可达工作空间,如图 10所示。
|
| 图 10 腿的工作空间 Fig. 10 Working space of legs |
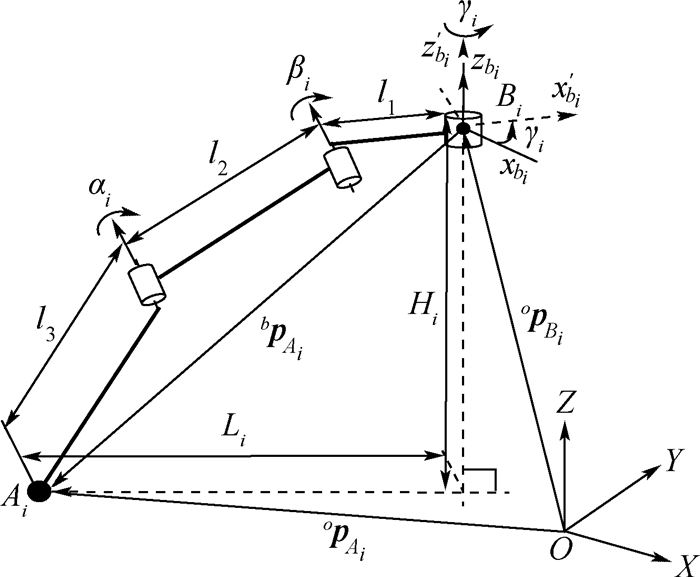
多腿机器人的运动是通过控制所有腿的驱动关节来实现的,因此需要通过机器人的逆运动学求解所有腿的驱动关节角度。由于NOROS机器人腿结构简单,具有3个旋转关节,可以通过几何方法来求解其逆运动学,将空间问题转化为平面问题,降低求解难度。图 11所示为第i条腿的空间机构简图。图中已知 opBi、oBiR 和opAi,而驱动关节变量αi、βi和γi未知。
|
| 图 11 第i条腿空间机构简图 Fig. 11 No.i leg’s space mechanism sketch |
根据矢量在坐标系间的变换关系,可得

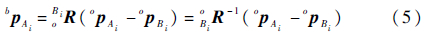
在小腿、大腿与腰关节轴线所在的平面,以及垂直于腰关节轴线的本体平面内,存在如式(6)所示几何关系:
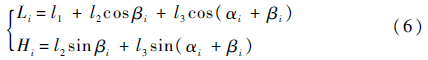
根据图 11所示的几何关系,还可以得到
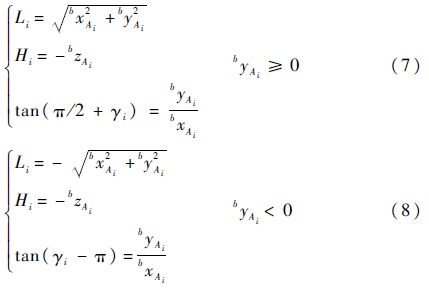
圆周对称的六腿机器人有以上4种典型“3+3”三角周期步态。静止状态下,机器人可以调整腿的布置方式,改变自身站立姿态,可以选取不同的步态行走。在行走过程中,机器人可以改变行走步态,以适应不同的地形环境。这里讨论行走过程中4种典型周期步态之间的切换问题。
4种步态按照初始站立姿态(或行走过程中的支撑三角形)分为2类:①同类支撑三角形下的步态行走过程中可直接切换,机器人仅改变了行进方向而未改变行走过程中的支撑三角形(如Ⅰ型昆虫摆腿步态和哺乳动物踢腿步态之间的转换及Ⅱ型昆虫摆腿步态和混合步态之间的转换)。②不同类支撑三角形下的步态行走过程中步态切换要改变其支撑三角形,也就是行走过程中改变机器人腿的布置方式。
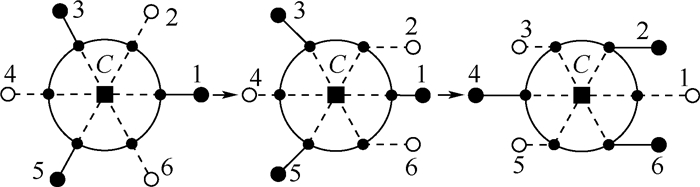
1) 在行走过程中,混合步态变换成哺乳动物踢腿步态过程只需要2步,1个步态周期便能完成切换,如图 12所示。 图中:虚线表示摆动腿,实线表示支撑腿。第1步,支撑腿(1、3和5)支撑本体并后蹬,摆动腿(2、4和6)改变摆动姿态,调整腰关节角度到哺乳动物踢腿步态的位置后,支撑腿和摆动腿互换;第2步,支撑腿(2、4和6)支撑本体并后蹬,摆动腿(1、3和5)调整腰关节角度到哺乳动物踢腿步态的位置,完成从混合步态到哺乳动物踢腿步态的切换。从哺乳动物踢腿步态到混合步态的切换过程则是这一过程的逆过程。
|
| 图 12 混合步态切换成哺乳动物踢腿步态 Fig. 12 Mix gait switch to mammal kick leg gait |
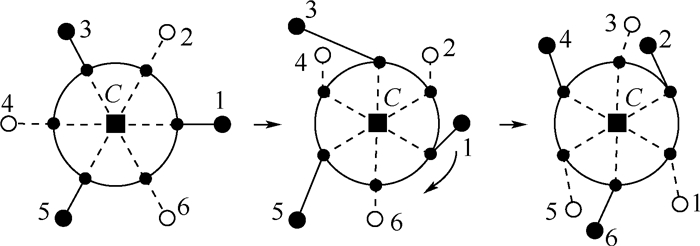
2) 混合步态变换成Ⅰ型昆虫摆腿步态的过程如图 13所示。第1步,支撑腿(1、3和5)支撑本体后蹬并旋转,机器人本体在支撑腿的作用下旋转60°,摆动腿(2、4和6)摆动调整腰关节角度到Ⅰ型昆虫摆腿步态的位置后,支撑腿和摆动腿互换;第2步,支撑腿(2、4和6)支撑本体并后蹬,摆动腿(1、3和5)调整腰关节角度到Ⅰ型昆虫摆腿步态的位置,完成从混合步态到Ⅰ型昆虫摆腿步态的切换。从Ⅰ型昆虫摆腿步态到混合步态的切换过程则是这一过程的逆过程。
|
| 图 13 混合步态切换成Ⅰ型昆虫摆腿步态 Fig. 13 Mix gait switch to insect swing leg gait Ⅰ |
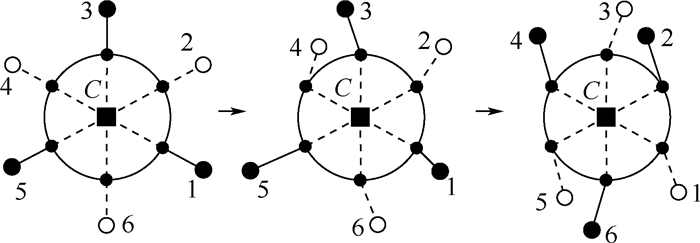
3) 行走过程中,Ⅱ型昆虫摆腿步态变换成Ⅰ型昆虫摆腿步态过程也需要2步,在1个步态周期内便能完成变换,如图 14所示。第1步,支撑腿(1、3和5)支撑本体并后蹬,摆动腿(2、4和6)摆动调整腰关节角度到Ⅰ型昆虫摆腿步态的位置后,支撑腿和摆动腿互换;第2步,支撑腿(2、4和6)支撑本体并后蹬,摆动腿(1、3和5)调整腰关节角度到Ⅰ型昆虫摆腿步态的位置,完成从Ⅱ型昆虫摆腿步态到Ⅰ型昆虫摆腿步态的切换。从Ⅰ型昆虫摆腿步态到Ⅱ型昆虫摆腿步态的切换过程则是这一过程的逆过程。
|
| 图 14 Ⅱ型昆虫摆腿步态切换成Ⅰ型昆虫摆腿步态 Fig. 14 Insect swing leg gait Ⅱ switch to insect swing leg gait Ⅰ |
4) Ⅱ型昆虫摆腿步态变换成哺乳动物踢腿步态过程如图 15所示。第1步,支撑腿(1、3和5)支撑本体后蹬并旋转,机器人本体在支撑腿的作用下旋转60°,摆动腿(2、4和6)摆动调整腰关节角度到哺乳动物踢腿步态的位置后,支撑腿和摆动腿互换;第2步,支撑腿(2、4和6)支撑本体并后蹬,摆动腿(1、3和5)调整腰关节角度到哺乳动物踢腿步态的位置,完成从Ⅱ型昆虫摆腿步态到哺乳动物踢腿步态的切换。从哺乳动物踢腿步态到Ⅱ型昆虫摆腿步态的切换过程则是这一过程的逆过程。

|
| 图 15 Ⅱ型昆虫摆腿步态切换成哺乳动物踢腿步态 Fig. 15 Insect swing leg gait Ⅱ switch to mammal kick leg gait |
NOROS机器人可以在腿步行运动模式和轮行运动模式下运动,不同运动模式间的相互转变就需要相应的轮腿运动模式切换规划。不同的轮腿式机器人也需要相应的轮腿运动模式切换规划来适应自己的轮腿结构。由于NOROS机器人特殊的轮腿结构,其切换规划相对较复杂,需要一系列动作序列完成轮腿运动模式的相互切换;但是其结构相对简单,包含轮子在内每条腿仅有4个转动关节。
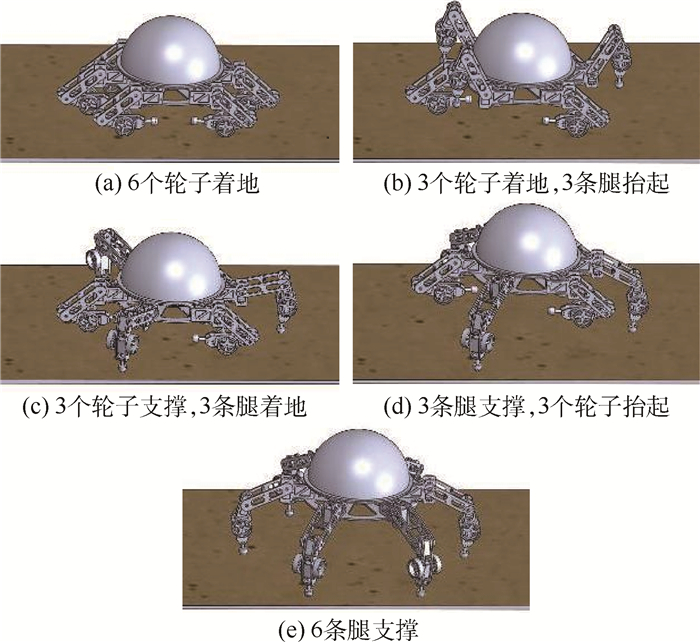
轮腿运动模式切换规划包括步行变轮行切换和轮行变步行切换2种规划,这2种运动切换规划是2个相反的过程,也就是说,其中1个切换规划的逆过程是另1个切换规划。图 16展示了小NOROS机器人从轮行模式到步行模式切换的过程。图 16(a)为机器人6个轮子着地的支撑状态;图 16(b)为机器人3个轮子支撑本体,其余3条轮腿抬起切换;图 16(c)为3条切换腿足刚好与地面接触,3个支撑轮未抬离地面;图 16(d)为3条支撑腿支撑本体升高,支撑轮离开地面进行切换;图 16(e)为机器人完成模式切换,6条腿支撑地面。
|
| 图 16 轮行到步行运动模式切换规划 Fig. 16 Wheel moving to leg moving switch planning |
图 16所示的轮行到步行运动模式切换规划的逆过程((e)—(d)—(c)—(b)—(a))便是步行运动模式到轮行运动模式切换规划。由于机器人在3个轮子支撑时,其本体也能够实现静态稳定,因此机器人也可以在3个轮子支撑时进行轮行运动,如图 16 (b)所示。3轮着地轮行模式到步行模式的切换过程为 (b)—(c)—(d)—(e);从步行模式到3轮着地轮行模式的切换过程为(e)—(d)—(c)—(b)。
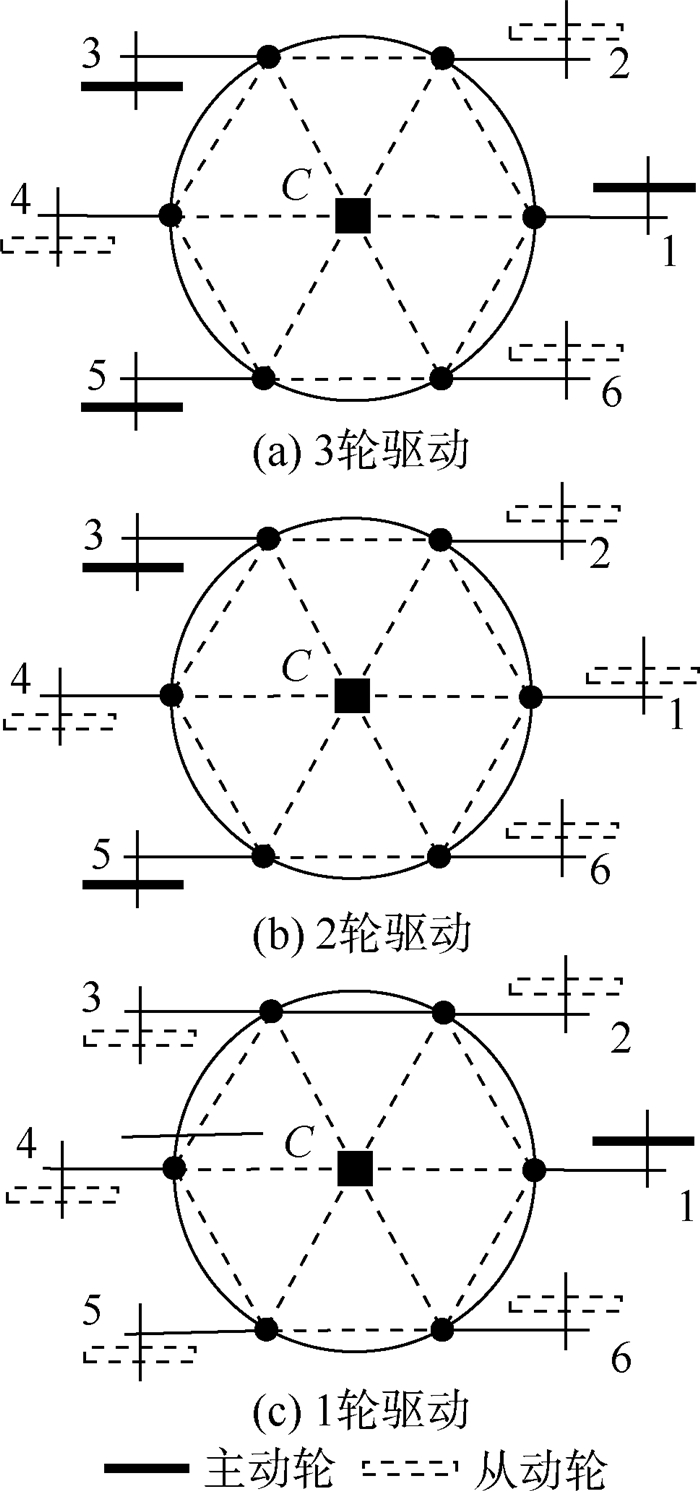
4 轮行运动模式机器人在6轮着地的行驶过程中,可由1轮驱动、2轮驱动、3轮驱动或者更多轮驱动。图 17(a)所示为6轮着地轮行时3轮驱动方式;腿1的主动轮变成从动轮后就是2轮驱动方式,如图 17(b)所示;而腿3、腿5的主动轮变成从动轮后机器人就是1轮驱动方式,如图 17(c)所示。同样的,3轮着地轮行时也存在1轮驱动、2轮驱动、3轮驱动3种方式。由于机器人本体的圆周对称结构,在腿1、腿3和腿5上安装3个主动轮,而在腿2、腿4和腿6上安装3个从动轮(即3个主动轮和3个从动轮交叉安装),当机器人切换到轮行运动模式时,无论6条腿如何布置成2组,总会在一侧有2个驱动轮、1个从动轮,而在另外一侧有1个驱动轮、2个从动轮,如图 18所示。因此,圆周对称结构的六轮腿式机器人间隔安装3个主动轮和3个从动轮就完全满足轮行要求。
|
| 图 17 不同数目驱动轮驱动方式 Fig. 17 Drive mode of different numbers of driving wheels |

|
| 图 18 轮行模式下腿的不同分组 Fig. 18 Different groupings of legs under wheel moving mode |
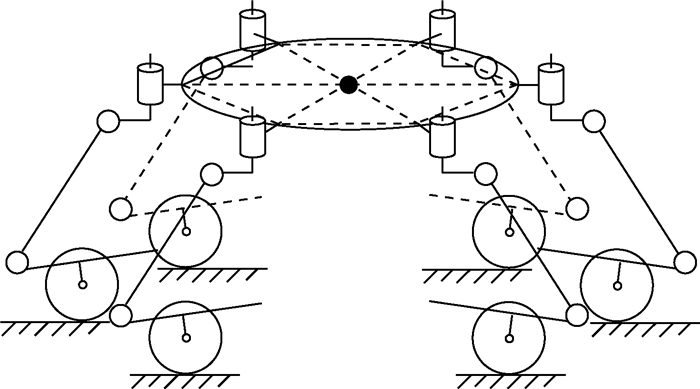
由于NOROS机器人的轮子安装在其小腿膝关节处,在轮行运动模式下,机器人可以调整膝关节和髋关节的角度,以调整本体高度,腰关节可控制轮子的方向。机器人在轮行直线快速前进时,调整膝关节和髋关节的角度,从而降低本体高度,以提高机器人轮行行进的稳定性。NOROS机器人轮行运动模式下的机构简图如图 19所示。从图 19可以看出,NOROS机器人在轮行运动模式下是一种摇臂轮式结构。
|
| 图 19 NOROS机器人轮行运动模式下机构简图 Fig. 19 Mechanism sketch of NOROS robot under wheel moving mode |
机器人在6轮着地轮行转向过程中,如果本体高度较低,轮子轴线到腰关节轴线的距离就会过远,调整腿关节角度,抬高本体高度,会缩短轮子轴线到腰关节轴线的距离。NOROS机器人的轮行转弯情况分为2种:静止原地转弯和直线行进过程中转弯。
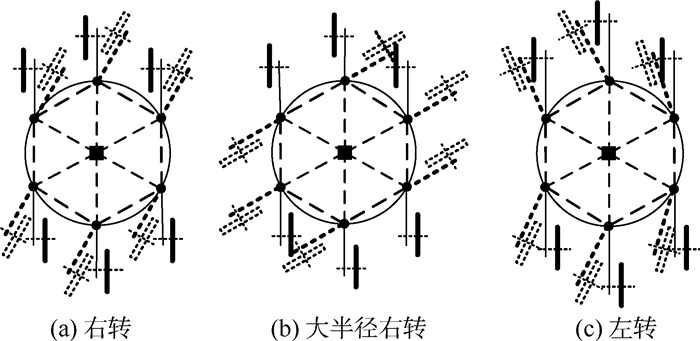
NOROS机器人的轮腿结构,使其在静止原地转弯时,可以通过抬起腿,使轮子离开地面,腰关节摆动,重新安排腿的布置情况,使轮子的行进方向改变来实现转向,这种方式可以使NOROS机器人在轮行运动模式静止的情况下实现零半径转弯。图 20所示为机器人静止原地转弯的3种情形。图 21所示为机器人6轮着地直线轮行时转弯的一种情况。每个轮子受地面摩擦力的作用如图 21中所示,可以得到每个轮子所受地面摩擦力矩为
|
| 图 20 机器人通过改变腿的布置实现转向的几种情形 Fig. 20 Different cases of robot turning via changing arrangement of legs |

|
| 图 21 轮子受摩擦力简图 Fig. 21 Frictional force sketch of wheels |
从图 21中可以看出,行进方向前侧3个轮子所受地面摩擦力在其转向方向上都会存在阻力矩,而行进方向后侧的3个轮子所受地面摩擦力在其转向方向上都会存在一个与阻力矩方向相反的力矩。存在该力矩的轮子转向可依靠地面的摩擦 力被动转向,而存在阻力矩的轮子转向必须通 过腿的腰关节主动转动来实现,如果轮子轴线到腰关节轴线的距离过远,根据式(9)可知,在腰关节控制轮子的方向时,势必受到地面很大的摩擦力矩的作用,可能导致转向失败或者破坏机器人结构,所以不适合在轮行运动模式下转弯。
因此,机器人在6轮着地直线轮行过程中转向时,要调整腿关节角度使轮子轴线与腰关节轴线相交或尽可能接近,使地面对转向中轮子产生的摩擦力尽可能小,从而减小地面摩擦力矩。当6轮同时着地进行转向时,可分为以下2种情况讨论:
1) 图 22所示为机器人一种可行轮行运动模式下转弯的机构简图。此种情况下,使轮子的轴线与腰关节的轴线相交,减小地面摩擦力矩。假设机器人轮子满足纯滚动条件,机器人的运动在某一瞬时是围绕瞬时转动中心(ICR)的回转运动。建立2个坐标系{O}、{C},其中{O}为全局坐标系,原点为O点,{C}为机器人本体参考坐标系,其原点位于机器人本体的中心C点,Φc为坐 标系{C}的y轴与坐标系{O}的X轴的夹角,机器人本体在全局坐标系中的位姿坐标为(xc,yc,c)T,其中xc与yc表示机器人在全局坐标系中的位置。图 22中,ri为第i条腿腰关节轴线到ICR的距离;vc为机器人本体关于ICR的线速度;ω为机器人本体关于ICR的角速度。

|
| 图 22 机器人6轮转向机构简图Ⅰ Fig. 22 Mechanism sketch Ⅰ of robot turning by six wheels |
机器人在此情况下的运动学方程为

根据图 22中的几何关系,可以得到如式(11)所示方程:
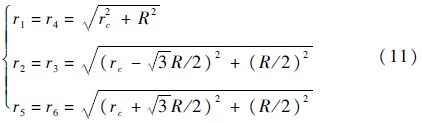
由此可以得到机器人各个轮子的转向角为

机器人各个轮子轴线在前进方向的速度为

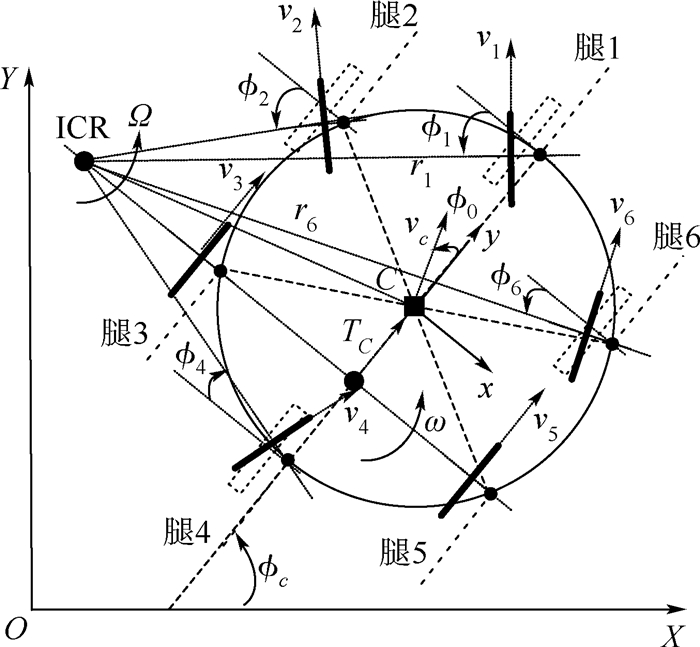
2) 图 23所示为机器人另一种6轮着地轮行运动模式下转弯的机构简图。参照前例建立参考坐标系,可以得到机器人在此情况下的运动学方程为
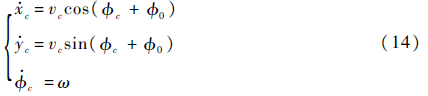

|
| 图 23 机器人6轮转向机构简图Ⅱ Fig. 23 Mechanism sketch Ⅱ of robot turning by six wheels |
由此得到点TC处的转动半径为
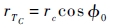
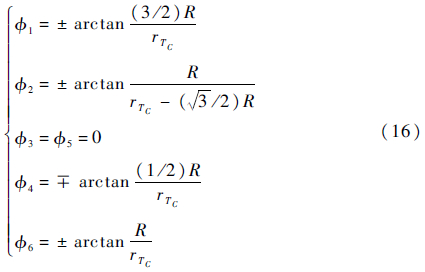
除上述2种转弯形式外,机器人还可以在3轮着地行驶过程中转弯。3轮着地行驶过程中,轮轴线和腰关节轴线相交时,与上述2种转弯情况一致;图 24所示为3轮着地行驶过程中轮轴线和腰关节轴线无相交的情况。

|
| 图 24 机器人3轮转向机构简图 Fig. 24 Mechanism sketch of robot turning by three wheels |
参照前例建立参考坐标系,图 24中Li为第i条腿轮子轴线到腰关节轴线的距离,由于机器人本体始终和地面平行,轮子轴线到其所在腿的腰关节轴线的距离就存在以下关系:L2=L4=L6=L。
机器人在此情况下的运动学方程为
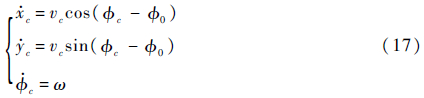
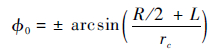
轮子和地面的纯滚动会引入非完整约束,使机器人的运动方向受到限制,未转向两轮连线中点TC运动方向始终垂直于两轮连线,因此点TC处速度始终与机器人本体坐标系y轴重合。由此得到3个轮子的转弯半径为

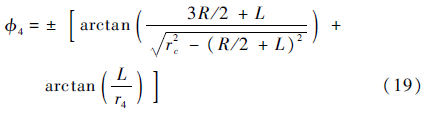
机器人各个轮子轴线在前进方向的速度为

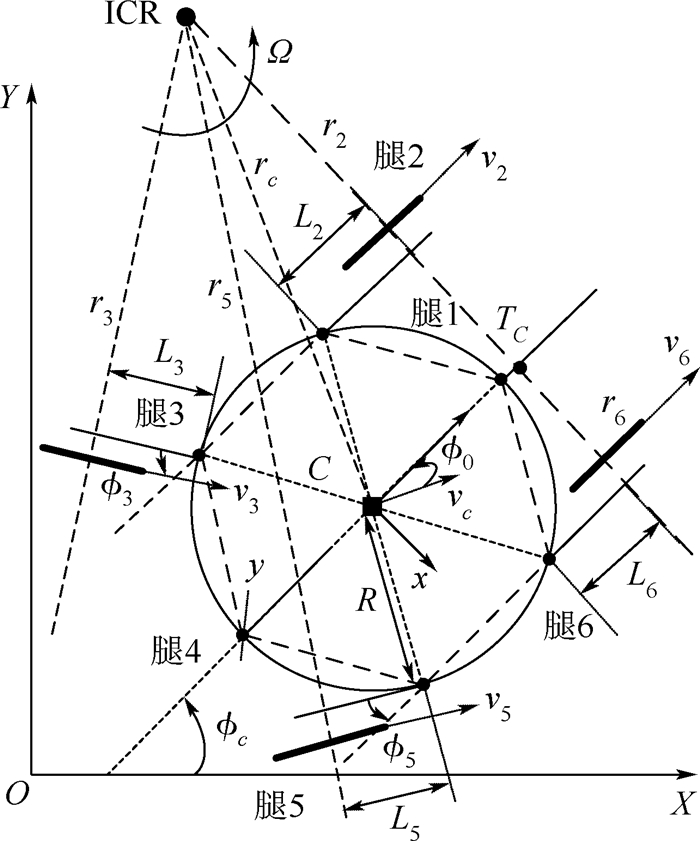
机器人还可以在4轮着地行驶过程中转弯。这里讨论4轮着地行驶过程中轮轴线和腰关节轴线无相交的情况,如图 25所示。
|
| 图 25 机器人4轮转向机构简图 Fig. 25 Mechanism sketch of robot turning by four wheels |
图 25中,Li为第i条腿轮子轴线到腰关节轴线的距离,由于机器人本体始终和地面平行,轮子轴线到其所在腿的腰关节轴线的距离就存在以下关系:L2=L3=L5=L6=L。
机器人在此情况下的运动学方程为
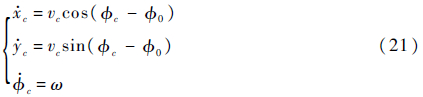
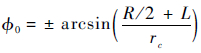
由几何关系可得此4个轮子的转弯半径分别为
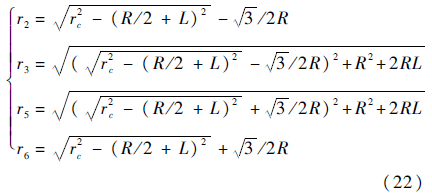
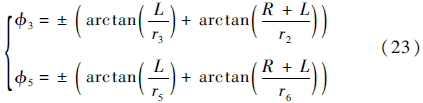
机器人各个轮子轴线在前进方向的速度为

利用机器人样机进行了机器人样机的步态行走试验,机器人能够完全按照设计的周期规则步态进行步行行走。图 26所示为机器人以哺乳动物踢腿步态行走爬坡试验过程。

|
| 图 26 机器人步行爬坡试验 Fig. 26 Test of robot climbing slope by legs |
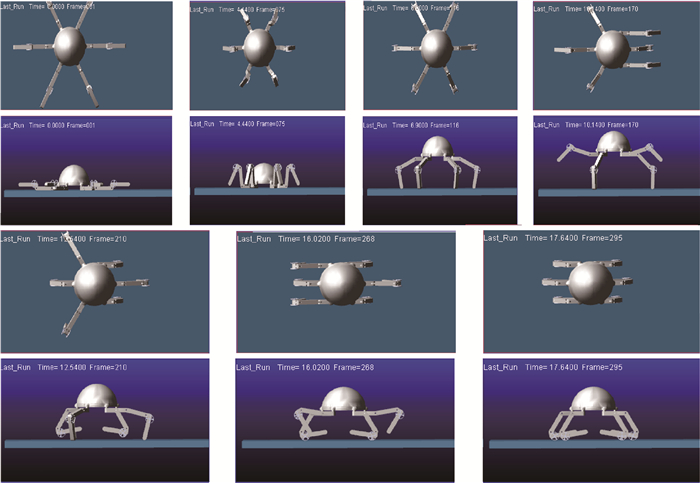
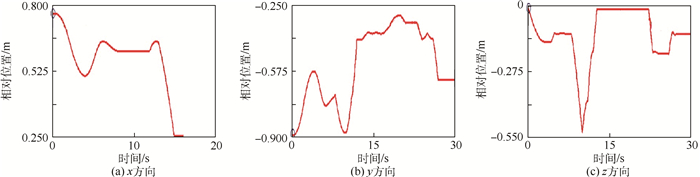
按照第3节的轮腿运动模式切换规划,先使用ADAMS进行了运动仿真,图 27所示为机器人从倒伏到站立再到轮行的过程,图 28为足端在x、y和z 3个方向相对于地面的位置变化曲线。由仿真结果可知,机器人可以顺利实现站立和轮腿切换任务,不会发生干涉、倾倒等问题。利用机器人样机进行了运动模式切换试验,机器人按照切换规划顺利实现不同运动模式的切换。图 29展示了机器人从腿步行运动模式到轮行运动模式的切换过程,其逆过程则是轮行运动模式到腿步行运动模式的切换过程。
|
| 图 27 仿真过程 Fig. 27 Simulation process |
|
| 图 28 足端位置曲线 Fig. 28Position curves of foot |

|
| 图 29 机器人运动模式切换试验 Fig. 29 Robot motion mode switching test |
利用机器人样机进行了轮行6轮转弯和爬坡试验,如图 30和图 31所示。

|
| 图 30 机器人轮行转弯试验 Fig. 30Test of robot turning by wheels |

|
| 图 31 机器人轮行爬坡试验 Fig. 31Test of robot climbing slope by wheels |
试验表明,NOROS机器人可以在4种典型“3+3”三角周期步态下行走,并能按运动规划实现轮腿运动模式切换,进行轮行运动,顺利实现轮行爬坡。
6 结 论1) 设计了一种新型圆周对称结构的六轮腿式机器人,该机器人在不增加驱动的情况下,通过改变自身构态,实现足或轮与地面接触,完成轮行和步行运动模式的切换,避免了轮子当作足使用时在步行行走过程中对轮子局部磨损造成的不利影响。
2) 给出了4种典型“3+3”三角周期步态,分析了不同步态间的切换问题,根据机器人特殊的轮腿结构,研究了其相应的轮腿运动切换规划,并进行了试验验证,试验表明机器人在此运动规划下可顺利完成轮行和步行运动模式的切换。
3) 分析了轮行运动模式,并进行了试验验证。根据机器人轮行运动过程中腿的布置情况,得出间隔布置3个驱动轮和3个从动轮是最佳布置方式。分析转弯过程中轮子的受力情况,给出了轮行转弯的可行方法,并建立了4种机器人轮行运动过程中的转弯运动学模型。
| [1] | 田娜,丁希仑,戴建生.一种新型的变结构轮腿式探测车机构设计与分析[J].机械设计与研究,2004,20(z1):268-270. TIAN N,DING X L,DAI J S.Design and analysis of a novel metamorphic wheel-legged rover mechanism[J].Journal of Machine Design and Research,2004,20(z1):268-270(in Chinese). |
| Cited By in Cnki (2) | Click to display the text | |
| [2] | PREUMONT A,ALEXANDRE P,GHUYS D.Gait analysis and implementation of a six leg walking machine[C]//5th International Conference on Advanced Robotics,Robots in Unstructured Environments,IEEE.Piscataway,NJ:IEEE Press,1991:941-945. |
| Click to display the text | |
| [3] | CHU S K K,PANG G K H.Comparison between different model of hexapod robot in fault-tolerant gait[J].IEEE Transactions on Systems,Man,and Cybernetics,2002,32(6):752-756. |
| Click to display the text | |
| [4] | 苏军,陈学东,田文罡.六足步行机器人全方位的步态研究[J].机械与电子,2004(3):48-52. SU J,CHEN X D,TIAN W G.A study of the omnidirectional gait for hexapod walking robot[J].Machinery & Electronics,2004(3):48-52(in Chinese). |
| Cited By in Cnki (40) | Click to display the text | |
| [5] | 韩宝玲,王秋丽,罗庆生.六足仿生步行机器人足端工作空间和灵活度研究[J].机械设计与研究,2006,22(4):10-12. HAN B L,WANG Q L,LUO Q S.Mechanical optimization and analyses of hexapod walking bio-robot[J].Machine Design and Research,2006,22(4):10-12(in Chinese). |
| Cited By in Cnki (28) | Click to display the text | |
| [6] | 丁希仑,王志英,ROVETTA A.六边形对称分布六腿机器人的典型步态及运动性能分析[J].机器人,2010,32(6):759-765. DING X L,WANG Z Y,ROVETTA A.Typical gaits and motion analysis of a hexagonal symmetrical hexapod robot[J].Robot,2010,32(6):759-765(in Chinese). |
| Cited By in Cnki (9) | Click to display the text | |
| [7] | 徐坤,丁希仑,李可佳.圆周对称分布六腿机器人三种典型行走步态步长及稳定性分析[J].机器人,2012,34(2):231-241. XU K,DING X L,LI K J.Stride size and stability analysis of a radially symmetrical hexapod robot in three typical gaits[J].Robot,2012,34(2):231-241(in Chinese). |
| Cited By in Cnki (3) | Click to display the text | |
| [8] | SHNRO N,EIJI N,TAKAYUKI T.Motion control technique for practical use of a leg-wheel robot on unknown outdoor rough terrains[C]//Proceedings of 2004 IEEE/RSJ International Conference on Intelligent Robots and Systems,IEEE.Piscataway,NJ:IEEE Press,2004:1353-1358. |
| Click to display the text | |
| [9] | YLONEN S J,HALME A J.Workpartner-Centaur like service robot[C]//Proceedings of the 2002 IEEE/RSJ International Conference on Intelligent Robots and Systems,IEEE.Piscataway,NJ:IEEE Press,2002:727-732. |
| Click to display the text | |
| [10] | WILCOX B H.ATHLETE:An option for mobile lunar landers[C]//2008 IEEE Aerospace Conference,IEEE.Piscataway,NJ:IEEE Press,2008:1-8. |
| Click to display the text | |
| [11] | WANG P F,HUANG B,SUN L N.Walking research on multi motion mode quadruped bionic robot based on moving ZMP[C]//IEEE International Conference on Mechatronics and Automation,IEEE.Piscataway,NJ:IEEE Press,2005:1935-1940. |
| Click to display the text | |
| [12] | 丁希仑,徐坤.一种新型变结构轮腿式机器人的设计与分析[J].中南大学学报,2009,40(S1):91-101. DING X L,XU K.Design and analysis of a novel metamorphic wheel-legged rover mechanism[J].Journal of Central South University,2009,40(S1):91-101(in Chinese). |
| Cited By in Cnki (10) | Click to display the text | |
| [13] | JACOBSEN S,SMITH F M,OLIVIER M,et al.Reconfigurable articulated leg and wheel:US7017687B1[P].2006-03-28. |
| Click to display the text | |
| [14] | ROHMER E,REINA G,YOSHIDA K.Dynamic simulation-based action planner for a reconfigurable hybrid legwheel planetary exploration rover[J].Advanced Robotics,2010,24(8-9):1219-1238. |
| Click to display the text | |
| [15] | CRUSE H.What mechanisms coordinate leg movement in walking arthropods?[J].Trends in Neurosciences,1990,13(1):15-21. |
| Click to display the text | |
| [16] | CRUSE H,WEHNER R.No need for a cognitive map:Decentralized memory for insect navigation[J].PLoS Computational Biology,2011,7(3):1-10. |
| Click to display the text | |
| [17] | BENDER J A,SIMPSON E M,TIETZ B R,et al.Kinematic and behavioral evidence for a distinction between trotting and ambling gaits in the cockroach Blaberus discoidalis[J].The Journal of Experimental Biology,2011,214(12):2057-2064. |
| Click to display the text |



