2. 北京航空航天大学无人驾驶飞行器研究所, 北京 100083
2. Research Institute of Unmanned Aerial Vehicle, Beijing University of Aeronautics and Astronautics, Beijing 100083, China
概率分布的参数估计是根据从总体中抽取的样本估计总体分布中包含的未知参数的方法,在可靠性数据分析中,通过获取产品故障数据、选择寿命分布类型、进行参数估计后,最终关注的是产品可靠度随时间的变化情况[1]。常用的点估计方法有:矩估计、最小二乘法估计、极大似然估计和图估计等。矩估计法由英国统计学家Pearson于1894年提出,可以在不知道母体的分布的情况下进行参数估计。最小二乘法于18世纪初提出,主要用于线性统计模型中的参数估计问题。极大似然估计法由英国统计学家费希尔于1912年提出,是可靠性数据分析中应用最为广泛的方法之一,该方法的理论依据是极大似然原理,极大似然原理可理解为“使当前样本中各个体故障时的故障密度估计值之积最大”,但这与评估的最终目标“使当前样本中各个体故障时的可靠度估计值最合理”并不等价,因此从理论上讲在可靠度的研究中使用极大似然估计是存在一定问题的[2, 3, 4, 5]。贝叶斯估计法是利用参数的后验分布对参数进行估计的方法。其中,期望型贝叶斯估计是使用最多的一种贝叶斯估计方法。
除了传统的点估计方法以外,很多学者在原有估计的基础上,提出了一些其他的估计方法,如在寿命分布估计中常使用的最佳线性无偏估计(BLUE)[6],弥补BLUE只能适用于小样本缺点的简单线性无偏估计(GLUE)[7]等。还有一些研究者研究了如何以可靠度估计值构造似然函数进行参数估计,例如极大间距估计方法(maximum spacing estimation)[8, 9, 10, 11],它将相邻试件故障时的可靠度估计值之差,作为评价估计合理程度的标准,认为一个合理的估计结果应当使各相邻的试件故障时的可靠度估计值之差更接近。但显然极大间距估计方法也并未涉及可靠度估计值本身的合理性。结合β分布的性质和可靠度定义之间的关系[12, 13, 14, 15, 16, 17],本文以可靠度估计值的合理程度构造β似然函数,得出的分布参数估计方法适用于可靠度、生存率等关注事件发生比例的研究领域。
1 β似然函数的构造考虑有某种产品共h个,考虑其中某个具体产品的寿命长短,因为产品之间谁先失效谁后失效是等可能的,所以该个产品在所有h个产品中第几个失效(从1~h)也是等可能的。当产品个数h趋近于无穷大时,该个产品失效时还未故障产品所占比例也就是等可能的(从0~1),然而此时还未故障产品所占比例即为产品的可靠度。由此可知对某种产品,若仅知道其中一个具体产品的寿命值,则可认为该时刻产品的可靠度服从0~1上的均匀分布U[0,1],由此可得出结论 1。
结论 1 对一件产品进行寿命试验,在该件产品失效时间t时刻,该种产品的可靠度服从U[0,1]。
将可靠度服从U[0,1]看作向线段[0,1]上等可能地投一个点,则当对多个产品进行寿命试验时,由于各个产品的寿命互相独立,可看作向线段[0,1]上等可能地投多个点。根据有关β分布的2个定理[18]:
定理 1 向线段[0,1]上独立地投h个随机点,假设每个点都服从U[0,1],则左起第i(i=1,2,…,h)个落点的概率分布为β(i,h-i+1)。
定理 2 若X~β(a,b),则1-X~β(b,a)。 由此可知:
结论 2 对h个寿命独立同分布的产品进行寿命试验,则第i个产品故障时产品的可靠度服从分布β(h-i+1,i)。
事实上,可靠度非参数估计中的β分布法就是应用结论2来对产品的经验分布函数进行计算。 假设对某产品n个试件进行寿命试验,记试验开始时为零时刻,试验中共m(m≤n)个试件发生故障,l(l≤n)个试件中途由于其他原因撤离(如未发生故障而中途退出试验、由非试验规定条件的意外因素致使试件故障),剩余n-m-l个试件直至试验终止未发生故障。其中试件发生故障的时间依次为t1,t2,…,ti,…,tm,故障时间和撤离时间共同排序为t1,t2,…,tj,…,tm+l。
由结论 2可知寿命试验中不同时刻产品可靠度服从的分布。在有试件中途撤离时,由于无法得知这些试件将在何时故障而无法直接使用该结论,此时需假设中途撤离试件将等可能地在其撤离后的试件故障之间发生故障,则可对真实故障试件在所有试件中的故障序号的期望(即平均秩次Ai)进行计算,进而使用平均秩次Ai作为β分布法中的序号,即:对n个寿命独立同分布的产品进行寿命试验,则第i个产品故障时(此时的故障时间和撤离时间的共同排序号为j)产品的可靠度服从分布β(n-Ai+1,Ai)。直接通过求期望计算平均秩次Ai比较复杂,可选择通过递推公式计算:
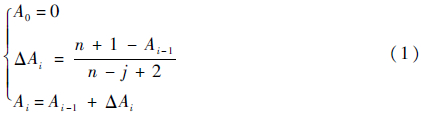
显然在无中途撤离的情况下Ai=i=j,此时与原β分布法的结论一致。
为了以可靠度估计值构造似然函数,需假设所选寿命分布的可靠度函数为R(t,θ),其中θ为待估参数,因此第i个故障发生时的可靠度估计值为R(ti,θ)。考虑到第i个故障发生时的产品的可靠度服从分布β(n-Ai+1,Ai),根据β分布的定义可知此时的可靠度估计值R(ti,θ)在可靠度分布β(n-Ai+1,Ai)中的概率密度为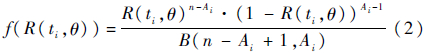
其中B(n-Ai+1,Ai)为β函数:
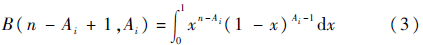
认为对应概率密度较大的可靠度估计值更合理,用该概率密度f(R(ti,θ))的大小评价该试件故障时可靠度估计值的合理程度,以各个试件故障时的f(R(ti,θ))的乘积评价估计结果对整组数据估计的合理程度,由此得到β似然函数为
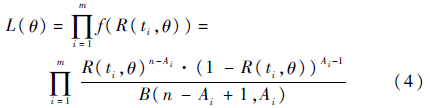
显然,在确定的寿命数据和可靠度函数R(t,θ)下,β似然函数是关于待估参数θ的函数,其反映的是不同参数θ取值下可靠度估计值的合理程度。注意到似然函数中的B(n-Ai+1,Ai)与待估参数无关而不会影响到函数的单调性,因此β似然函数也可写为
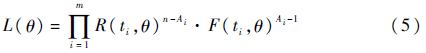
类似极大似然估计,β似然估计选择使β似然函数取值最大的参数值作为估计结果,表明此时各试件故障时的可靠度估计值总体最合理。
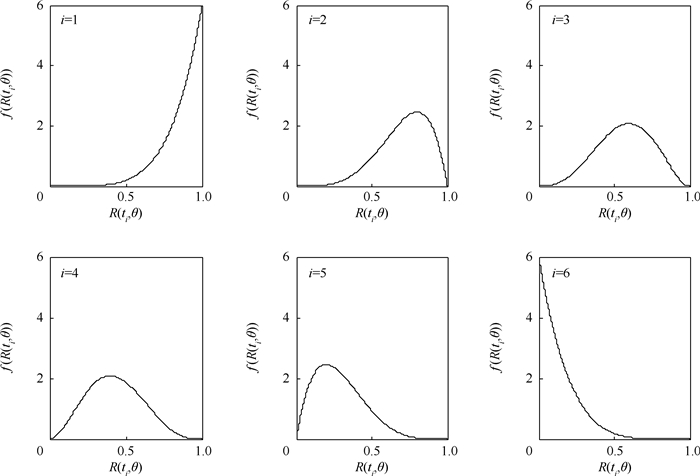
在β似然函数中,由于n为正整数、1≤Ai≤n,因此无论可靠度估计值R(ti,θ)为[0,1]之间的何值,其概率密度值f(R(ti,θ))都在一个有限的范围内,不会出现似然函数中有无穷大项的情况。对n>1的这些分布的概率密度曲线在Ai=1时单调递增、1 < Ai < n时为单峰曲线、Ai=n时单调递减(如图 1为n=6,Ai=i(i=1,2,…,6)时的概率密度曲线),即各试件故障时的最佳可靠度估计值只有一个,由β分布的性质可知该值为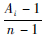 。因此对在分布的取值区间内且样本量n>1的寿命数据,无论所选寿命分布为何种数学形式,不同参数取值下其β似然函数都是存在最大值的,即β似然估计都存在。但需要指出的是,由于β似然函数可能存在多个极大值,当多个极大值相等且为最值时β似然估计的结果不唯一;另外β似然估计在样本量n=1时失效,因为唯一的试件失效时产品的可靠度服从分布β(1,1)即均匀分布,此时无论可靠度的估计值为何值,对应的概率密度都一样,也就无从进行比较。
。因此对在分布的取值区间内且样本量n>1的寿命数据,无论所选寿命分布为何种数学形式,不同参数取值下其β似然函数都是存在最大值的,即β似然估计都存在。但需要指出的是,由于β似然函数可能存在多个极大值,当多个极大值相等且为最值时β似然估计的结果不唯一;另外β似然估计在样本量n=1时失效,因为唯一的试件失效时产品的可靠度服从分布β(1,1)即均匀分布,此时无论可靠度的估计值为何值,对应的概率密度都一样,也就无从进行比较。
|
| 图 1 β分布的概率密度曲线 Fig. 1 Probability density curves of β distribution |
从计算的难易角度讲,β似然估计是优于矩估计的,特别是随着分布参数的增加,矩估计需要求解多元非线性方程组,而目前对于很多类型的方程组都是无法通过数值计算进行求解的,所以矩估计在参数较多时使用起来并不方便。β似然估计在多参数时只需求解多元函数的极值即可,具体计算时可以借用成熟的商业数学软件,如MATLAB实现求解。
3 仿真分析为了验证β似然估计方法在实际数据处理中的表现,本文采用了指数分布和威布尔分布仿真再估计的方法,将β似然估计与极大似然估计进行了比较,其具体步骤如下:
1) 随机确定分布参数(指数分布的故障率λ、威布尔分布的形状参数β和尺度参数α)。
2) 使用仿真的方法分别获取该参数下服从指数分布和威布尔分布的失效数据。
3) 分别选择指数分布和威布尔分布作为寿命分布模型,使用极大似然估计和β似然估计对这失效数据进行参数估计,得到指数分布的故障率λ1和λ2及威布尔分布的参数α1β1和α2β2。
4) 比较2个估计得到的故障率λ1和λ2与原始故障率λ的接近程度、比较参数α1β1和α2β2与原始参数αβ之差的绝对值之和的大小关系。
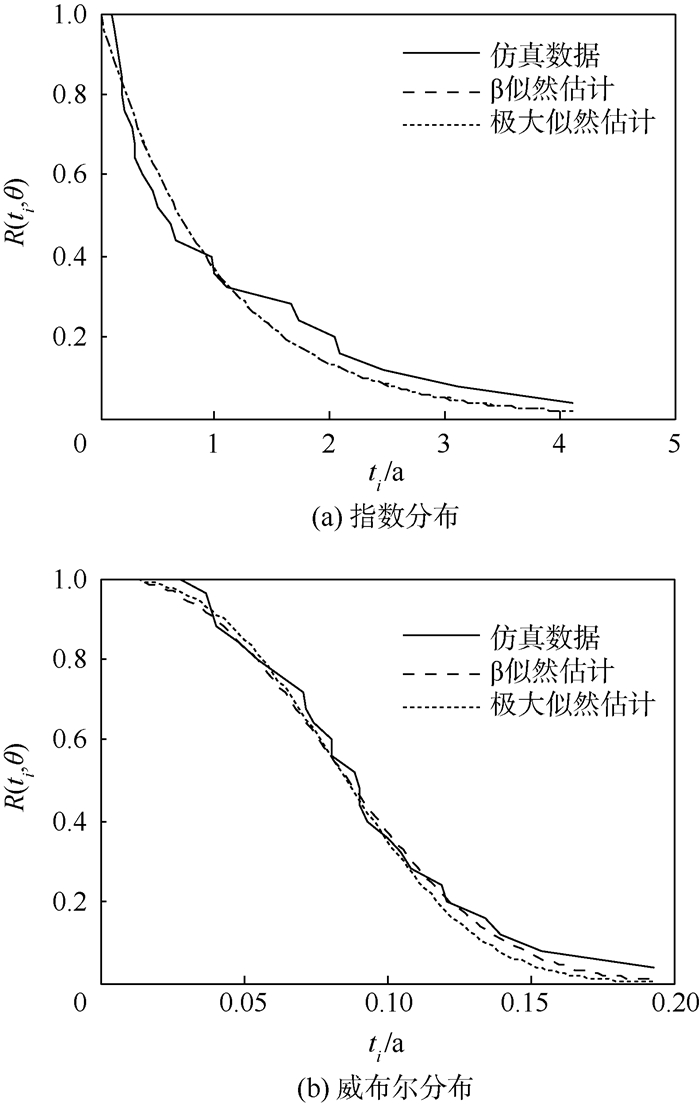
5) 重复以上步骤,直到记录下足够多次的比较结果。 使用计算机进行1 000次上述仿真比较后,统计的结果为使用极大似然估计得到的λ1较使用β似然估计λ2更接近原始λ的次数为568次,反之432次;使用极大似然估计得到的|α1-α|+|β1-β|较使用β似然估计得到的|α2-α|+|β2-β|更大的次数为383次,且2种方法对各组数据的估计结果相差往往都很小。图 2为指数分布和威布尔分布下的其中各一次仿真再估计得到的可靠度曲线。
|
| 图 2 仿真结果对比 Fig. 2 Comparison of simulation results |
由此可认为2种方法对指数分布和威布尔分布的参数估计结果相差极小,可以认为2种方法对指数分布和威布尔分布都是适用的。
4 应用举例对某产品10件进行1 000 h定时截尾的寿命试验,试验中记录了试件的故障情况和撤离情况如表 1所示,其中3号试件为未故障撤离,现使用本文所述方法对该产品可靠度为0.7下的可靠寿命进行估计。
| 试件序号 | 工作时间/h | 试验终止原因 |
| 1 | 216 | 故障 |
| 2 | 50 | 故障 |
| 3 | 514 | 撤离 |
| 4 | 565 | 故障 |
| 5 | 298 | 故障 |
| 6 | 460 | 故障 |
| 7 | 1 000 | 截尾 |
| 8 | 183 | 故障 |
| 9 | 131 | 故障 |
| 10 | 940 | 故障 |
对试验数据进行整理知,试件数量为10,发生故障的试件数量为8,进行排序并计算故障件的平均秩次如表 2所示。
| 共同排序号 j | 故障排序号 i | 工作时间 t i/h | 平均秩次 A i |
| 1 | 1 | 50 | 1 |
| 2 | 2 | 131 | 2 |
| 3 | 3 | 183 | 3 |
| 4 | 4 | 216 | 4 |
| 5 | 5 | 298 | 5 |
| 6 | 6 | 460 | 6 |
| 7 | / | 514 | / |
| 8 | 7 | 565 | 7.25 |
| 9 | 8 | 940 | 8.5 |
选择指数分布作为产品的寿命分布,其可靠度函数为

对应β似然函数为

式中:Ai和ti取值见表 2。使用MATLAB提供的数值方法[19]易求得当λ取0.001 7时L(λ)取到极大值5 811,即参数λ的β似然估计值为0.001 7。由此可知产品可靠度0.7下的可靠寿命为
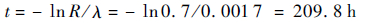
使用平均秩计算产品的经验分布函数为
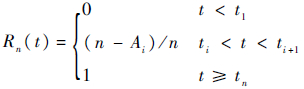
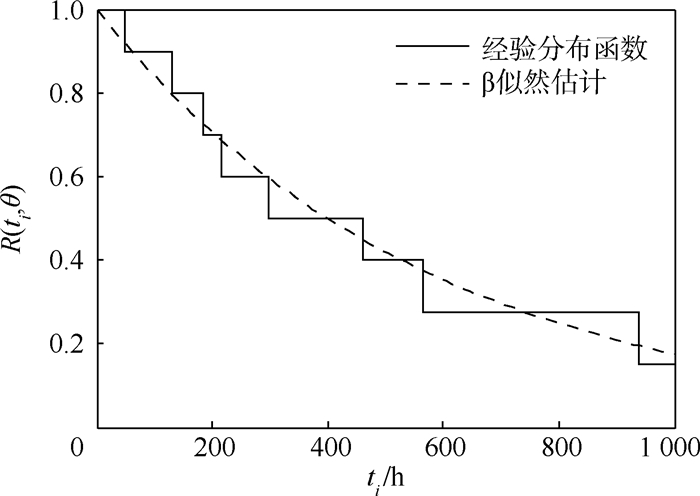
该经验分布函数与β似然估计结果R(t)=exp(-0.001 7t)的比较如图 3所示,可见β似然估计结果与经验分布直观上也是一致的。
|
| 图 3 估计结果对比 Fig. 3 Comparison of estimation results |
本文针对寿命分布的参数估计提出了一种基于β似然函数的β似然估计方法,该方法以可靠度估计值的合理性为核心,根据可靠度非参数估计中的β分布法得到试件故障时可靠度所服从的分布,进而使用该分布的概率密度来度量试件故障时可靠度估计值的合理程度,以该合理程度之积构造β似然函数,将使β似然函数取值最大的参数取值作为估计结果。本文方法具有以下特点:
1) 具有较强的理论支撑:β似然函数推导过程使用的“β分布法”和平均秩次的计算都非常成熟,前者可被严格证明、后者在无法得知准确故障秩次时使用秩次的期望值也是合理的。
2) 适用于各种寿命分布类型:无论分布的数学形式如何,β似然函数的取值都在一个有限的范围内,不会出现类似极大似然函数取值可能无穷大的情况,因此β似然估计都是存在的(仅要求样本量n > 1);另外随着分布参数的增加,β似然函数作为多元函数,其求极值在数值计算中容易实现,其难度低于矩估计中需要进行的多元非线性方程组求解。
3) 估计结果合理可信:β似然函数的推导就是以评价可靠度估计值的合理性为出发点,故本方法适用于可靠度、生存率等关注事件发生比例的研究领域。 基于以上特点,本方法在浴盆曲线模型等较为复杂的分布参数估计中有较为突出的优点,克服了极大似然估计结果不存在的问题。
| [1] | 赵军圣,庄光明,王增桂.极大似然估计方法介绍[J].长春理工大学学报,2010,5(6):53-54. ZHAO J S,ZHUANG G M,WANG Z G.An introduction about maximum likelihood estimation[J].Journal of Changchun University of Science and Technology,2010,5(6):53-54(in Chinese). |
| Click to display the text (12) | |
| [2] | BO R.The maximum spacing method:An estimation method related to the maximum likelihood method[J].Scandinavian Journal of Statistics,1984,11(2):93-112. |
| Click to display the text | |
| [3] | EKSTRÖM M.On the consistency of the maximum spacing method[J].Journal of Statistical Planning and Inference,1998,70(2):209-224. |
| Click to display the text | |
| [4] | GHOSH K,JAMMALAMADAKA S R.A general estimation method using spacings[J].Journal of Statistical Planning and Inference,2001,93(1):71-82. |
| Click to display the text | |
| [5] | EKSTROM M.Consistency of generalized maximum spacing estimates[J].Scandinavian Journal of Statistics,2001,28(2):343-354. |
| Cited By in Cnki | Click to display the text | |
| [6] | 孙振东,王喜山.一种计算电子元器件工作寿命的方法——最好线性无偏估计(BLUE)法[J].烟台大学学报(自然科学与工程版),1994(4):10-17. SUN Z D,WANG X S.A method to calculate lifetime of electronic devices-the best linear undistorted estimation[J].Journal of Yantai University(Natural Science and Engineering),1994(4):10-17(in Chinese). |
| Cited By in Cnki | Click to display the text | |
| [7] | 徐安.BLUE和GLUE及主要点估计方法的评价[J].济南交通高等专科学校学报,1994(1):37-44. XU A.Assessment of BLUE and GLUE and the main point estimation method[J].Journal of Jinan Communications College,1994(1):37-44(in Chinese). |
| Cited By in Cnki (1) | Click to display the text (1) | |
| [8] | SHAO Y.Consistency of the maximum product of spacing method and estimation of a unimodal distribution[J].Statistica Sinica,2001,11(4):1125-1140. |
| Click to display the text | |
| [9] | EKSTRÖM M.Alternatives to maximum likelihood estimation based on spacings and the Kullback-Leibler divergence[J].Journal of Statistical Planning and Inference,2008,138(6):1778-1791. |
| Click to display the text | |
| [10] | RANNEBY B,JAMMALAMADAKA S R,TETERUKOVSKIY A.The maximum spacing estimation for multivariate observations[J].Journal of Statistical Planning and Inference,2005,129(1):427-446. |
| Click to display the text (13) | |
| [11] | EL HAJE HUSSEIN F,GOLUBEV Y.On entropy estimation by m-spacing method[J].Journal of Mathematical Sciences,2009,163(3):290-309. |
| Click to display the text | |
| [12] | GOMES A E,DA SILVA C Q,CORDEIRO G M.The beta Burr III model for lifetime data[J] Brazilian Journal of Probability and Statistics,2013,27(4):502-543. |
| Click to display the text (2) | |
| [13] | BADSHA MD.B,MOLLAH MD.N H,JAHAN N,et al.Robust complementary hierarchical clustering for gene expression data analysisby β-divergence[J].Journal of Bioscience and Bioengineering,2013,116(3):397-407. |
| Click to display the text (3) | |
| [14] | CORDEIRO G M,NADARAJAH S,ORTEGA E M M.General results for the beta Weibull distribution[J].Journal of Statistical Computation and Simulation,2013,83(6):1082-1114. |
| Click to display the text | |
| [15] | CORDEIRO G M,LEMONTE A J.The β-Birnbaum-Saunders distribution:An improved distribution for fatigue life modeling[J].Computational Statistics and Data Analysis,2011,55(3):1445-1461. |
| Click to display the text | |
| [16] | PARANAÍBA P F,ORTEGA E M M,CORDEIRO G M,et al.The beta Burr XII distribution with application to lifetime data[J].Computational Statistics and Data Analysis,2011,55(2):1118-1136. |
| Click to display the text | |
| [17] | SILVA G O,ORTEGA E M M,CORDEIRO G M.The beta modified Weibull distribution[J].Lifetime Data Analysis,2010,16(3):409-430. |
| Click to display the text | |
| [18] | 赵宇,杨军,马小兵.可靠性数据分析教程[M].北京:北京航空航天大学出版社,2009:150-151. ZHAO Y,YANG J,MA X B.Data analysis of reliability[M].Beijing:Beihang Uuiversity Press,2009:150-151(in Chinese). |
| [19] | 周品,赵新芬.MATLAB数理统计分析[M].北京:国防工业出版社,2009:200-204. ZHOU P,ZHAO X F.MATLAB statistics analysis[M].Beijing:National Defense Industry Press,2009:200-204(in Chinese). |



